Abstract
Rule-based and information-integration category learning were compared under minimal and full feedback conditions. Rule-based category structures are those for which the optimal rule is verbalizable. Information-integration category structures are those for which the optimal rule is not verbalizable. With minimal feedback subjects are told whether their response was correct or incorrect, but are not informed of the correct category assignment. With full feedback subjects are informed of the correctness of their response and are also informed of the correct category assignment. An examination of the distinct neural circuits that subserve rule-based and information-integration category learning leads to the counterintuitive prediction that full feedback should facilitate rule-based learning but should also hinder information-integration learning. This prediction was supported in the experiment reported below. The implications of these results for theories of learning are discussed.
Keywords: Perceptual categorization, Cognitive neuroscience of categorization, Reinforcement learning, Dopamine, Striatum, Bayesian hypothesis testing, Feedback
1. Introduction
Categorization is a fundamental cognitive operation that is relevant to all aspects of daily life, allowing us to meaningfully parse the world and help guide behavior. Categorization is also a critical component for a broad range of tasks including identifying threats, choosing solution paths in math problems, and hitting a softball. Given categorization’s ubiquity, it is not surprising that the study of category learning has been a focus of research in cognitive science.
Perhaps it is also not surprising that simple explanations for such a central cognitive function have fallen short in some regards. Simple model-based accounts of how people learn categories from examples, such as prototype- (e.g., Posner & Keele, 1968), exemplar- (Estes, 1994; Nosofsky, 1986; Smith & Medin, 1981), and rule-based (e.g., Bruner, Goodnow, & Austin, 1956; Feldman, 2003) models, have given way to proposals that posit multiple category learning systems (e.g., Ashby, Alfonso-Reese, Turken, & Waldron, 1998; Erickson & Kruschke, 1998; Love, Medin, & Gureckis, 2004; Nosofsky, Palmeri, & McKinley, 1994). The rise in the popularity of multiple system theories coincides with a surge of interest and advances in understanding the neural basis of category learning (Aron et al., 2004; Ashby et al., 1998; Ashby & Maddox, 2005; Love & Gureckis, 2007; Reber, Gitelman, Parrish, & Mesulam, 2003; Seger & Cincotta, 2005, 2006).
Two neural circuits that subserve distinct category learning systems have been of particular interest (e.g., Ashby, Ennis, & Spiering, 2007). One system is a rule system that learns and reasons in an explicit fashion. The rule system’s hypothesis-testing processes are consciously accessible. Introspection allows for accurate verbal report of discovered rules. In contrast, the procedural learning system is not consciously penetrable and instead operates by associating regions of perceptual space with actions that lead to reward. The rule and procedural systems rely on distinct neural substrates. The rule system is implemented by a circuit involving dorsolateral prefrontal cortex, anterior cingulate and the head of the caudate nucleus (Ashby & Maddox, 2005; Filoteo et al., 2005; Love & Gureckis, 2007; Seger & Cincotta, 2005, 2006), whereas the procedural system is implemented by a circuit involving inferotemporal cortex and the posterior caudate nucleus (Ashby et al., 1998; Nomura et al., 2007; Seger & Cincotta, 2005; Wilson, 1995).
The rule and procedural system are complementary in that the two systems excel with different types of category structures and under different task conditions. The rule system engages working memory (WM) and executive attention processes and is not vulnerable to feedback manipulations that delay feedback following a response to a stimulus presentation or deliver feedback prior to stimulus presentation, whereas the procedural system only performs well when feedback closely follows a response to a stimulus presentation (Ashby, Maddox, & Bohil, 2002; Maddox, Ashby, & Bohil, 2003; Maddox & Ing, 2005). These differences in feedback processing are readily explained by the nature of the circuits supporting the rule and procedural systems. The rule system invokes WM processes that allow for more flexibility in terms of how feedback is processed. In contrast, the procedural system does not interact with WM processes and instead relies on dopamine-mediated reward learning in the caudate nucleus (Beninger, 1983; Miller, Sanghera, & German, 1981; Montague, Dayan, & Sejnowski, 1996; Wickens, 1993).
One advantage of the procedural system is that it is unaffected by concurrent or sequential working memory demands, whereas the rule system is bound by working memory resources (DeCaro, Thomas, & Beilock, 2008; Maddox, Ashby, Ing, & Pickering, 2004; Waldron & Ashby, 2001; Zeithamova & Maddox, 2006, 2007). These limited resources place an upper-limit on the kind of rules that can be learned. In particular, people seem to be limited to mastering category structures for which optimal responding involves verbalizable rules along psychologically privileged stimulus dimensions. Category structures that are learnable by the rule system, like that shown in Fig. 1A, are referred to as rule-based structures. The optimal rule (denoted by the solid horizontal and vertical lines) is to “respond A to short, shallow angle lines, B to short, steep angle lines, C to long, shallow angle lines, and D to long, steep angle lines”. The structure in Fig. 1B is unlearnable by the rule system because the optimal rule (denoted by the solid diagonal lines) is not verbalizable (i.e., length and orientation involve incommensurable units). Such structures are referred to as information-integration category structures.
Fig. 1.
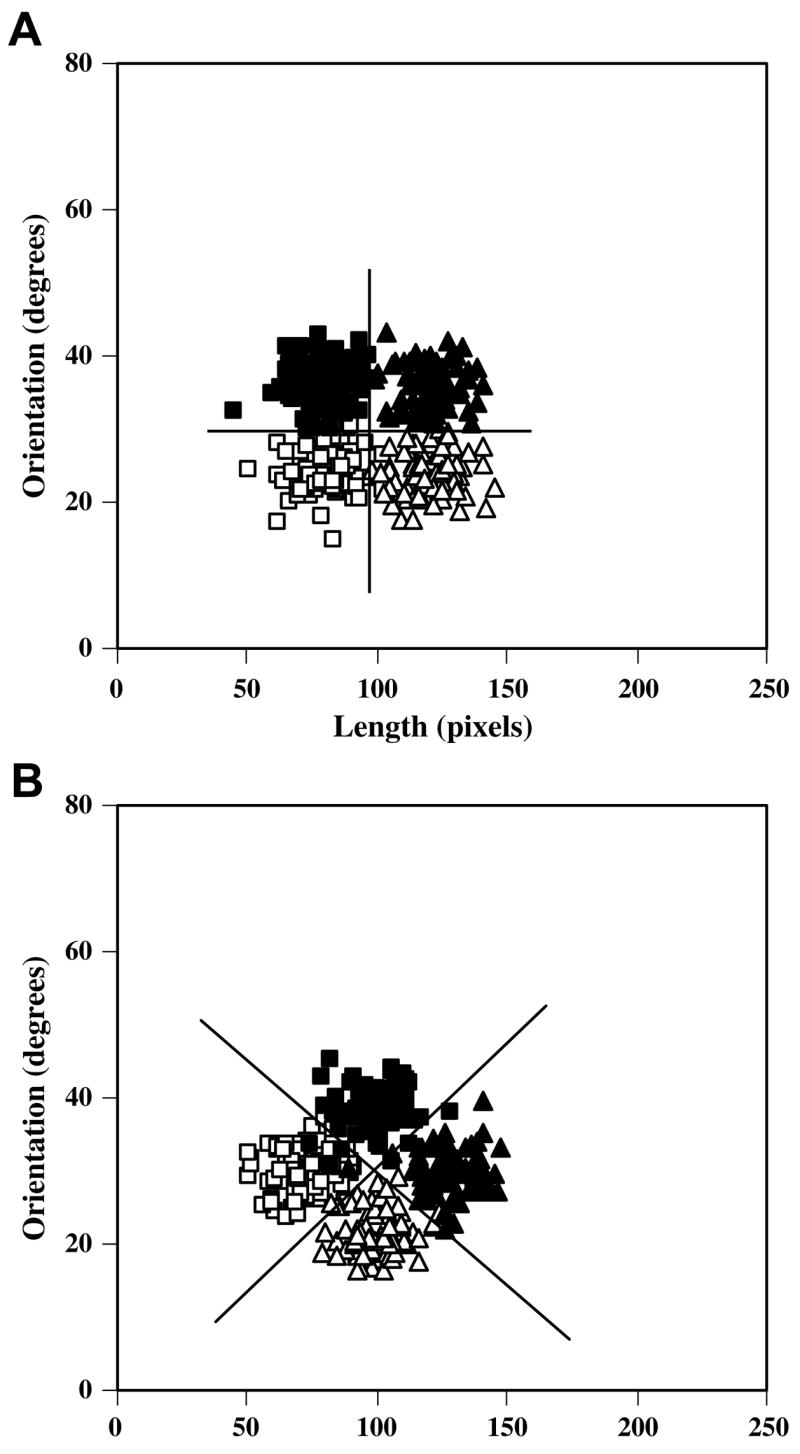
Category structures used in the rule-based (A) and information-integration conditions (B). Solid lines denote the optimal decision bounds, and the open squares, filled squares, open triangles, and filled triangles denote stimuli from categories A–D, respectively. Each category was defined as a bivariate normal distribution along the two stimulus dimensions with mean vectors μA, μB, μC, and μD (in length-orientation stimulus space) and common variance–covariance matrix Σ: μA = [72 100]′, μB = [100 128]′, μC = [100 72]′, μD = [128 100]′ and Σ = ΣA = ΣB = ΣC = ΣD = [100 0; 0 100]. Optimal accuracy was 95%. Twenty-five random samples were drawn from each of these category distributions for a total of 100 unique stimuli. Each sample was linearly transformed so that the sample mean vector and sample variance–covariance matrix exactly equaled the population mean vector and variance–covariance matrix. Each random sample (x, y) was converted to a stimulus by deriving the length in pixels l = x, and the orientation (in degrees counterclockwise from horizontal) as o = yπ/600. These scaling factors were chosen to roughly equate the salience of each dimension. The resulting 100 stimuli were randomized separately for each participant in each block.
Rather than rely on working memory processes to construct verbalizable rules, the procedural system uses dopamine-mediated reward learning to associate regions of the stimulus space with a response (Ashby et al., 1998). Although both systems are thought to be operative on each trial, an initial bias toward the hypothesis-testing system is assumed. Only when the procedural system begins to generate consistently more accurate responses (or the hypothesis-testing system consistently fewer) is control passed to this system. If the hypothesis-testing system generates accurate responses, control may not be passed to the procedural system. One possibility is that the rule system acts as a gating mechanism for the procedural system – when the rule system is meeting with success, it governs responding; otherwise, control is passed to the procedural system. Given that the rule system is subject to introspection and cognitive control, it is plausible that the rule system guides the interactions between the learning systems.1
This theory makes surprising predictions with respect to the impact of the nature of feedback. For example, individuals with low working memory span capacity should actually perform better in information-integration tasks because the rule system is at a disadvantage and therefore will more readily pass control to the procedural system, a prediction that was recently supported (DeCaro et al., 2008). When the theory is cast in terms of popular rule and procedural learning computational formalisms, other surprising behavioral predictions can be derived and tested. The focus of the remainder of this contribution is on deriving and testing these predictions.
1.1. Computational instantiation and behavioral predictions
Here, we provide a qualitative description of a two system model that illustrates our theory. One natural way to characterize the rule system is as a Bayesian hypothesis-testing system that disambiguates between competing hypotheses during training. For the four choice category problems like those shown in Fig. 1, the hypothesis space would conform to all possible verbalizable rules that divide the two dimensional stimulus space into four regions by the intersection of the two perpendicular decision bounds that each run parallel to a stimulus dimension. The Bayesian system learns the probability of each of the potential hypotheses, and generates a predicted categorization response by weighting each of these probabilities by the prior probability associated with each hypothesis. These priors could be uniformor biased toward decision bounds that divide the space into four regions of approximately equal size. The optimal decision bounds shown in Fig. 1A correspond to one such hypothesis. Fig. 2 provides another example hypothesis. Setting aside category overlap, this Bayesian system asymptotes to 100% performance for rule-based category structures (Fig. 1A) compared to 50% for (rotated) information-integration category structures (Fig. 1B).
Fig. 2.
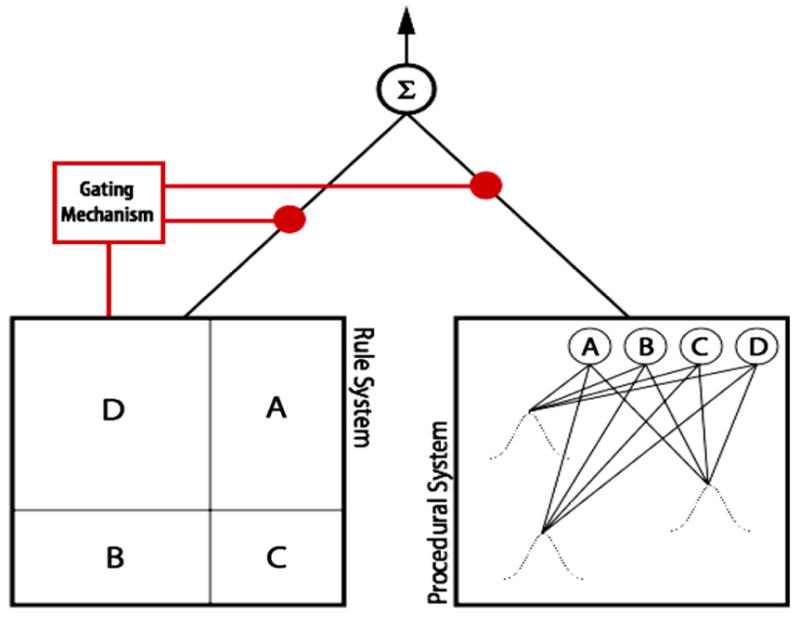
One possible instantiation of the rule and procedural systems. The rule system is modeled as a Bayesian model that optimally updates the probability of each hypothesis according to the current stimulus and the feedback. Full feedback is more effective in discriminating among competing hypotheses than is minimal feedback. Each hypothesis corresponds to two intersecting and perpendicular decision bounds with each rectangular region assigned to one of the four possible categories. One such hypothesis is shown in the left side of the figure. The procedural system uses reinforcement learning and a covering map of Gaussian receptive fields to estimate the value of each action (i.e., the anticipated accuracy of responding A, B, C, or D) for each stimulus location. Because this system estimates rewards, rather than updating hypothesis probabilities, it is only concerned with the correctness of its responses, which is equivalently signaled by minimal and full feedback. The performance of the rule system governs whether the rule system or the procedural system determines the overall response. When the rule system is performing at a high level, the gating mechanism is more likely to allow the rule system to continue determining the overall response rather than passing control to the procedural system.
Key to the present investigation, the Bayesian system optimally utilizes all aspects of feedback when calculating the likelihood of the competing hypotheses. When feedback is full (i.e., when the participant is told both whether they were correct or incorrect as well as whether the stimulus belongs to category A, B, C, or D), the Bayesian system will converge to asymptote more quickly than when minimal feedback is used (i.e., the participant is simply told that they are correct or incorrect). When the Bayesian rule system’s response is correct, the model can strengthen consistent hypotheses under both minimal and full feedback. However, when the Bayesian system is wrong, under full feedback the system can both strengthen consistent hypotheses and weaken inconsistent hypotheses, whereas under minimal feedback only inconsistent hypotheses are weakened. Thus, the Bayesian system learns faster under full feedback.
One natural way to characterize the procedural learning system is as a biologically-inspired reinforcement learning system that estimates the value (equivalent to accuracy in the current experiment) of taking each of the four possible actions (i.e., category choices) for every stimulus location. Fig. 2 illustrates one such system. This estimation process is implemented by randomly placing some number of radial basis functions, akin to the receptive fields found in the tail of the caudate nucleus (Wilson, 1995), at locations corresponding to points in the two dimensional stimulus space shown in Fig. 1. The connection weights from these receptive fields to output nodes that estimate the value of each classification response are updated using reinforcement learning procedures (Schultz, Dayan, & Montague, 1997; Sutton & Barto, 1998). The procedural system learns at the same rate regardless of category or feedback type because the learning system is only concerned with stimulus location and feedback valence (i.e., reward present or absent). Performance of the procedural system asymptotes at 100% minus errors arising from exploration processes (Sutton & Barto, 1998).
The properties of these two systems and their functional association predict a surprising relationship between type of category structure (rule-based or information-integration) and feedback (minimal or full). In particular, overall performance should be better with full feedback for rule-based structures and (counterintuitively) be better with minimal feedback for information-integration structures. With rule-based categories, the Bayesian system can solve the task. Since full feedback leads to more rapid rule learning, there should be a performance advantage for the full feedback condition relative to the minimal feedback condition. This should be especially apparent early in learning. With information-integration categories, the Bayesian system cannot solve the task, but instead must pass control to the procedural system. Because full feedback leads to more rapid rule learning, it should lead to a greater, more sustained reliance on the Bayesian system, thus leading to a performance disadvantage for full feedback relative to minimal feedback for information-integration learning. This disadvantage for full feedback should be especially apparent later in learning as the procedural system’s accuracy improves, but control is not entirely passed along to this system. The following experiment tests these counter intuitive predictions.
2. Current experiment
2.1. Methods
2.1.1. Participants
One-hundred-sixteen participants completed the study and received course credit for their participation. All participants had normal or corrected to normal vision, and no participant completed more than one condition. A learning criterion [defined as achieving at least 40% correct (25% is chance) during the final (6th) 100-trial block] was applied to ensure that only participants who showed at least minimal learning were included in the analyses. Of the 116 participants, 107 met the learning criterion [Information-Integration-Full-Feedback: N = 32 (3 excluded); Information-Integration-Minimal-Feedback: N = 30 (2 excluded); Rule-Based-Full-Feedback: N = 27 (2 excluded); Rule-Based-Minimal-Feedback: N = 27 (2 excluded)].
2.1.2. Stimuli and stimulus generation
The stimuli and stimulus generation algorithm are detailed in Fig. 1.
2.1.3. Procedure
Participants were randomly assigned to one of the four experimental conditions: Information-Integration-Full-Feedback, Information-Integration-Minimal-Feedback, Rule-Based-Full-Feedback, and Rule-Based-Minimal-Feedback. Each condition consisted of 6, 100-trial blocks with a participant controlled rest period between each block. Participants were told that they were to categorize lines on the basis of their length and orientation, that there were four equally-likely categories, and that high levels of accuracy could be achieved. On each trial, a stimulus appeared and remained on the screen until the participant generated a response by pressing one of four buttons that were labeled “A”, “B”, “C”, or “D”. Following the response, corrective feedback was provided for 1 s. A 1-s ITI followed the feedback and the next trial was initiated.
Participants received either Full Feedback or Minimal Feedback on each trial. An example of the feedback provided in the Full and Minimal Feedback conditions on correct and error trials is presented below:
Full Feedback, Correct: “Correct, that was an X”, where X is the correct category response
Full Feedback, Error: “No, that was an X”, where X is the correct category response
Minimal Feedback, Correct: “Correct”
Minimal Feedback, Error: “No”
Thus, the only difference across the Full and Minimal Feedback conditions was in the explicit specification of the correct category label. On every trial, in both conditions, participants were told whether their response was correct or incorrect.
2.2. Results
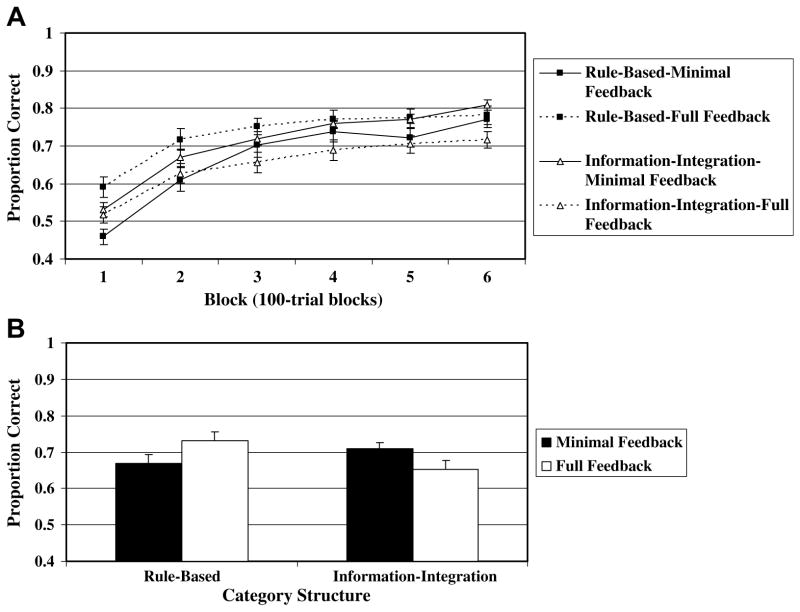
The learning curves for all four conditions across the 6 100-trial blocks are presented in Fig. 3A. A 2 category structure (information-integration vs. rule-based) × 2 feedback condition (full vs. minimal) × 6 block ANOVA was conducted on the data. The main effect of block [F(5, 515) = 153.03, p < .001, MSE = .006], and the feedback × block interaction was significant [F(5, 515) = 6.30, p < .001, MSE = .006]. Importantly, the category structure × feedback condition interaction was significant [F(1, 103) = 9.90, p < .01, MSE = .060], and is displayed in Fig. 3B. All other effects were non-significant. As predicted, for the rule-based condition, full feedback (.73) led to better performance than minimal feedback (.67) [t(48) = 2.09, p < .05], whereas for the information-integration condition, full feedback (.65) led to worse performance then minimal feedback (.71) [t(55) = 2.37, p < .05].
Fig. 3.
(A) Proportion correct (averaged across participants) for each 100-trial block from the experiment. (B) Proportion correct averaged across participants and blocks. Standard error bars included.
Although we expected, and observed, an advantage for full feedback in the rule-based condition, and minimal feedback in the information-integration condition, we speculated that the effect would weaken with experience in the rule-based condition, but would strengthen in the information-integration condition. As a test of this prediction we compared performance in the full and minimal feedback conditions on a block-by-block basis separately for the rule-based and information-integration conditions. For the rule-based condition, full feedback led to significantly better performance (p < .05) in blocks 1 and 2 (i.e., during the first 200 trials), but by the third block the effect was not significant. For the information-integration condition, there was no significant performance difference in blocks 1–3, but the effect was significant in blocks 4 (p < .05), 5 (p < .05), and 6 (p < .01).2
4. Discussion
Virtually every theory of learning holds that more informative feedback should result in better performance. The results for the information-integration condition run counter to this widely held belief – subjects performed better when feedback was minimal. This result is surprising given that minimal feedback is strictly less informative than full feedback. Full feedback indicates both correctness (as minimal feedback does) and the target category.
This surprising outcome is anticipated by a two system model in which overt behavioral decisions are determined by either a rule or procedural learning system (see Fig. 2). These two systems are motivated by known neurobiology, results from behavioral experiments, and computational considerations. The rule system is modeled as a Bayesian hypothesis-testing system that optimally utilizes feedback. This system more readily discriminates among competing hypotheses when full feedback is employed. In contrast, the procedural learning system uses reinforcement learning and is only concerned with the valence of feedback, which is equally supplied by minimal and full feedback. A gating system determines whether the rule or procedural system executes the overt response, with the rule system maintaining control unless it is performing at a low level.
The observed interaction in the experiment arises because the procedural system is best suited to information-integration categories whereas the rule system is best suited to rule-based categories (e.g., Ashby et al., 1998; Ashby & Maddox, 2005). However, for both category structures learned under full feedback, the rule-based system will tend to respond above chance early in learning. Even for information-integration categories, the rule system can approach 50% accuracy, which is far above the 25% chance level. These early successes delay the transfer of control to the procedural system, which hurts performance in the Information-Integration-Minimal-Feedback condition after the initial training blocks.
One key question for our theory is why would evolution give rise to a procedural system that does not make optimal use of full feedback? It would seem that such a basic learning system, especially one that is phylogenetically older, should optimally leverage feedback from the environment. We believe the answer lies in the other functions that the procedural system serves and the concordant computational demands placed on the system. The procedural system is primarily concerned with proceduralizing complex behaviors or skills. These skills often involve sequencing actions in a proper order. For example, hitting a softball does not involve one decision per trial as in our experiment, but involves a multitude of cascading actions with each action impacting the future state of the system. Perhaps even more challenging from a learning perspective, the reward signal for such dynamic tasks often appears only at the end of a sequence of actions (e.g., when the softball is hit or missed). The only known learning systems that can effectively learn in these situations without explicit planning, which would require WM resources, are reinforcement learning systems that process rewards as in our proposed procedural system (e.g., Nagy et al., 2007). Thus, the computational requirements, along with what we know of the neurobiology of dopamine-mediated learning, point to a system that would not distinguish between minimal and full feedback, but nevertheless could be interfered with if the Bayesian system were to be operative (such as when full feedback is given).
One important point to make is that we do not deny that there are other systems that contribute to category learning. For example, it is clear that aspects of category learning are mediated by a hippocampal learning system (Foerde, Knowlton, & Poldrack, 2006; Love & Gureckis, 2007), and we have shown that this system may be involved in certain aspects of rule learning (Nomura et al., 2007). However, the present experiment was designed to differentially tap the rule and procedural systems. A complete theory will have to take into account the hippocampal and other learning systems. The present contribution is speculative, but demonstrates that valuable predictions can be made by working with models inspired by know neurobiology. Regardless of the ultimate correctness of our proposal, we believe the current results speak to the utility of this basic approach.
Footnotes
This research was supported in part by National Institute of Health Grant R01 MH59196, and AFOSR Grant FA9550-06-1-0204 to W.T.M., AFOSR Grant FA9550-07-1-0178 and NSF CAREER Grant #0349101 to B.C.L., and a National Institute of Health Grant R01 NS41372 to J.V.F.
A second possibility is that there is a third “control” mechanism that manages the gating of the systems. For the present purposes, both mechanisms make the same predictions regarding the effects of feedback on learning.
A series of decision bound models were also applied to the data from each participant in each block of trials. Each model instantiated either a rule-based or a procedural strategy. Standard parameter estimation and model fitting procedures based on maximum likelihood were utilized to identify the best model for each data set. As expected, in the information-integration conditions, the proportion of participants whose data was best fit by a rule-based strategy was higher in the full feedback condition (39% of data sets across blocks) then in the minimal feedback condition (26% of data sets across blocks), with this difference increasing across blocks. In the rule-based conditions, on the other hand, the proportion of participants using rule-based strategies was high (82% and 84% of data sets across blocks for the full and minimal feedback conditions, respectively), but participants in the full feedback condition converged more quickly on the optimal rule and optimal decision criteria.
This article appeared in a journal published by Elsevier. The attached copy is furnished to the author for internal non-commercial research and education use, including for instruction at the authors institution and sharing with colleagues. Other uses, including reproduction and distribution, or selling or licensing copies, or posting to personal, institutional or third party websites are prohibited. In most cases authors are permitted to post their version of the article (e.g. in Word or Tex form) to their personal website or institutional repository. Authors requiring further information regarding Elsevier’s archiving and manuscript policies are encouraged to visit:
References
- Aron AR, Shohamy D, Clark J, Myers C, Gluck MA, Poldrack RA. Human midbrain sensitivity to cognitive feedback and uncertainty during classification learning. Journal of Neurophysiology. 2004;92(2):1144–1152. doi: 10.1152/jn.01209.2003. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Alfonso-Reese LA, Turken AU, Waldron EM. A neuropsychological theory of multiple systems in category learning. Psychological Review. 1998;105:442–481. doi: 10.1037/0033-295x.105.3.442. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Ennis JM, Spiering BJ. A neurobiological theory of automaticity in perceptual categorization. Psychological Review. 2007;114(3):632–656. doi: 10.1037/0033-295X.114.3.632. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Maddox WT. Human category learning. Annual Review of Psychology. 2005;56:149–178. doi: 10.1146/annurev.psych.56.091103.070217. [DOI] [PubMed] [Google Scholar]
- Ashby FG, Maddox WT, Bohil CJ. Observational versus feedback training in rule-based and information-integration category learning. Memory & Cognition. 2002;30(5):666–677. doi: 10.3758/bf03196423. [DOI] [PubMed] [Google Scholar]
- Beninger RJ. The role of dopamine in locomotor activity and learning. Brain Research. 1983;287(2):173–196. doi: 10.1016/0165-0173(83)90038-3. [DOI] [PubMed] [Google Scholar]
- Bruner JS, Goodnow J, Austin G. A study of thinking. New York: Wiley; 1956. [Google Scholar]
- DeCaro MS, Thomas RD, Beilock SL. Individual differences in category learning: Sometimes less working memory capacity is better than more. Cognition. 2008;107:284–294. doi: 10.1016/j.cognition.2007.07.001. [DOI] [PubMed] [Google Scholar]
- Erickson MA, Kruschke JK. Rules and exemplars in category learning. Journal of Experimental Psychology: Learning, Memory, and Cognition. 1998;127:107–140. doi: 10.1037//0096-3445.127.2.107. [DOI] [PubMed] [Google Scholar]
- Estes WK. Classification and cognition. New York: Oxford University Press; 1994. [Google Scholar]
- Feldman J. The simplicity principle in human concept learning. Current Directions in Psychological Science. 2003;12(6):227–232. [Google Scholar]
- Filoteo JV, Maddox WT, Simmons AN, Ing AD, Cagigas XE, Matthews S, et al. Cortical and subcortical brain regions involved in rule-based category learning. Neuroreport. 2005;16(2):111–115. doi: 10.1097/00001756-200502080-00007. [DOI] [PubMed] [Google Scholar]
- Foerde K, Knowlton BJ, Poldrack RA. Modulation of competing memory systems by distraction. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(31):11778–11783. doi: 10.1073/pnas.0602659103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Love BC, Gureckis TM. Models in search of a brain. Cognitive, Affective & Behavioral Neuroscience. 2007;7(2):90–108. doi: 10.3758/cabn.7.2.90. [DOI] [PubMed] [Google Scholar]
- Love BC, Medin DL, Gureckis TM. SUSTAIN: A network model of category learning. Psychological Review. 2004;111(2):309–332. doi: 10.1037/0033-295X.111.2.309. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Ashby FG, Bohil CJ. Delayed feedback effects on rule-based and information-integration category learning. Journal of Experimental Psychology: Learning, Memory, and Cognition. 2003;29(4):650–662. doi: 10.1037/0278-7393.29.4.650. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Ashby FG, Ing AD, Pickering AD. Disrupting feedback processing interferes with rule-based but not information-integration category learning. Memory & Cognition. 2004;32(4):582–591. doi: 10.3758/bf03195849. [DOI] [PubMed] [Google Scholar]
- Maddox WT, Ing AD. Delayed feedback disrupts the procedural-learning system but not the hypothesis-testing system in perceptual category learning. Journal of Experimental Psychology: Learning, Memory, & Cognition. 2005;31(1):100–107. doi: 10.1037/0278-7393.31.1.100. [DOI] [PubMed] [Google Scholar]
- Miller JD, Sanghera MK, German DC. Mesencephalic dopaminergic unit activity in the behaviorally conditioned rat. Life Science. 1981;29(12):1255–1263. doi: 10.1016/0024-3205(81)90231-9. [DOI] [PubMed] [Google Scholar]
- Montague PR, Dayan P, Sejnowski TJ. A framework for mesencephalic dopamine systems based on predictive Hebbian learning. The Journal of Neuroscience. 1996;16(5):1936–1947. doi: 10.1523/JNEUROSCI.16-05-01936.1996. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nagy O, Kelemen O, Benedek G, Myers CE, Shohamy D, Gluck MA, et al. Dopaminergic contribution to cognitive sequence learning. Journal of Neural Transmission. 2007;114(5):607–612. doi: 10.1007/s00702-007-0654-3. [DOI] [PubMed] [Google Scholar]
- Nomura EM, Maddox WT, Filoteo JV, Ing AD, Gitelman DR, Parrish TB, et al. Neural correlates of rule-based and information-integration visual category learning. Cerebral Cortex. 2007;17(1):37–43. doi: 10.1093/cercor/bhj122. [DOI] [PubMed] [Google Scholar]
- Nosofsky RM. Attention, similarity, and the identification–categorization relationship. Journal of Experimental Psychology: General. 1986;115:39–57. doi: 10.1037//0096-3445.115.1.39. [DOI] [PubMed] [Google Scholar]
- Nosofsky RM, Palmeri TJ, McKinley SC. A rule-plus-exception model of classification learning. Psychological Review. 1994;101:53–79. doi: 10.1037/0033-295x.101.1.53. [DOI] [PubMed] [Google Scholar]
- Posner MI, Keele SW. On the genesis of abstract ideas. Journal of Experimental Psychology. 1968;77:304–363. doi: 10.1037/h0025953. [DOI] [PubMed] [Google Scholar]
- Reber PJ, Gitelman DR, Parrish TB, Mesulam MM. Dissociating explicit and implicit category knowledge with fMRI. Journal of Cognitive Neuroscience. 2003;15(4):574–583. doi: 10.1162/089892903321662958. [DOI] [PubMed] [Google Scholar]
- Schultz W, Dayan P, Montague PR. A neural substrate of prediction and reward. Science. 1997;275(5306):1593–1599. doi: 10.1126/science.275.5306.1593. [DOI] [PubMed] [Google Scholar]
- Seger CA, Cincotta CM. The roles of the caudate nucleus in human classification learning. Journal of Neuroscience. 2005;25(11):2941–2951. doi: 10.1523/JNEUROSCI.3401-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Seger CA, Cincotta CM. Dynamics of frontal, striatal, and hippocampal systems during rule learning. Cerebral Cortex. 2006;16(11):1546–1555. doi: 10.1093/cercor/bhj092. [DOI] [PubMed] [Google Scholar]
- Smith EE, Medin DL. Categories and concepts. Cambridge, MA: Harvard University Press; 1981. [Google Scholar]
- Sutton RS, Barto AG. Reinforcement learning: An introduction. Cambridge, MA: MIT Press; 1998. [Google Scholar]
- Waldron EM, Ashby FG. The effects of concurrent task interference on category learning: Evidence for multiple category learning systems. Psychonomic Bulletin & Review. 2001;8(1):168–176. doi: 10.3758/bf03196154. [DOI] [PubMed] [Google Scholar]
- Wickens J. A theory of the striatum. New York: Pergamon Press; 1993. [Google Scholar]
- Wilson CJ. The contribution of cortical neurons to the firing pattern of striatal spiny neurons. Cambridge: MIT Press; 1995. [Google Scholar]
- Zeithamova D, Maddox WT. Dual task interference in perceptual category learning. Memory & Cognition. 2006;34:387–398. doi: 10.3758/bf03193416. [DOI] [PubMed] [Google Scholar]
- Zeithamova D, Maddox WT. The role of visuo-spatial and verbal working memory in perceptual category learning. Memory & Cognition. 2007;35(6):1380–1398. doi: 10.3758/bf03193609. [DOI] [PubMed] [Google Scholar]