The structure and precision of retinal spike trains

Abstract

Assessing the reliability of neuronal spike trains is fundamental to an understanding of the neural code. We measured the reproducibility of retinal responses to repeated visual stimuli. In both tiger salamander and rabbit, the retinal ganglion cells responded to random flicker with discrete, brief periods of firing. For any given cell, these firing events covered only a small fraction of the total stimulus time, often less than 5%. Firing events were very reproducible from trial to trial: the timing jitter of individual spikes was as low as 1 msec, and the standard deviation in spike count was often less than 0.5 spikes. Comparing the precision of spike timing to that of the spike count showed that the timing of a firing event conveyed several times more visual information than its spike count. This sparseness and precision were general characteristics of ganglion cell responses, maintained over the broad ensemble of stimulus waveforms produced by random flicker, and over a range of contrasts. Thus, the responses of retinal ganglion cells are not properly described by a firing probability that varies continuously with the stimulus. Instead, these neurons elicit discrete firing events that may be the fundamental coding symbols in retinal spike trains.

All of our visual experience derives from sequences of action potentials traveling down the optic nerve. Many theories have been proposed to explain how these spike trains from retinal ganglion cells encode the visual world (1–4). Fundamental to such an understanding is the reproducibility of these neural symbols to repeated presentations of the same stimulus. If retinal spike trains are highly deterministic, then individual visual messages can be attached to each spike; whereas, if they are highly stochastic, then the brain must average over many spikes to obtain an equally informative visual message.

As far back as 1928, Adrian (5) proposed that information about the sensory environment is conveyed in the time-varying firing rate of spiking sensory neurons—a view that has been influential to neuroscience ever since (6–8). As a result, many researchers have concentrated on estimates of the firing rate derived from averages over long time windows or multiple stimulus presentations (9, 10). Measurements of response reliability have often focused on the trial-to-trial variance in this spike count: in the visual cortex, this variance is found to be greater than the mean (11, 12), whereas similar experiments in the thalamus and retina have found variance-to-mean ratios both above and below one (13–15). The picture emerging from this work is that spike trains in the visual system are intrinsically stochastic; that, at best, one can determine the instantaneous probability that the neuron will fire, and that this firing rate depends in some smooth fashion on the sensory stimulus. However, poor reproducibility can also arise from confounding factors (16), such as anesthesia (13), uncontrolled eye movements (17, 18), or ongoing brain activity (19). Furthermore, the response precision may depend on the stimulus. For example, a sudden step change in illumination can reproducibly elicit precisely timed action potentials from retinal ganglion cells (20–22). The importance of precise spike timing has long been appreciated in the auditory system, where it is known to convey information essential for sound localization (23). If high-precision spike trains were common also among visual neurons, their information capacity could be significantly higher than previously estimated (24–26).

To assess the reproducibility of retinal responses, the retina was repeatedly presented with the same visual input and spike trains were recorded simultaneously from many ganglion cells. The isolated retina preparation eliminated any effects of anesthesia or eye movements. The stimulus consisted of spatially uniform illumination that flickered randomly with a Gaussian intensity distribution. This stimulus ensemble presents the retina with a wide variety of temporal waveforms, which are essential for investigating the generality of retinal precision. Some experiments also provided spatial modulation, by flickering different parts of the field independently. By comparing responses to many repeats of the same stimulus, we found that individual neurons responded with brief, highly precise periods of firing, separated by intervals of complete silence. The measured spike trains were found to be qualitatively and quantitatively inconsistent with the conventional model, in which a ganglion cell’s firing rate depends smoothly on the preceding visual stimulus. These observations have important consequences for our understanding of both the neural code of the retina and visual responses in subsequent regions of the brain.

METHODS AND ANALYSIS

Recording and Stimulation.

Experiments were performed on both the larval tiger salamander and the Dutch-belted rabbit to sample different retinal architectures. The isolated retina was superfused with oxygenated Ringer’s solution (salamander) or Ames medium maintained at 37°C (rabbit). Action potentials from retinal ganglion cells were recorded extracellularly with a multi-electrode array, and their spike times measured relative to the beginning of each stimulus repeat (27, 28). Spatially uniform white light was projected from a computer monitor onto the photoreceptor layer. The intensity was flickered by choosing a new value at random from a Gaussian distribution (mean I, standard deviation δI) every 30 msec. The mean light level (I = 4 × 10⁻³ W/m²) corresponded to photopic vision. Contrast C is defined here as the temporal root-mean-squared average of the light intensity divided by the mean, C = δI/I. A spatially modulated “checkerboard” stimulus consisted of an array of square regions, 134 μm on a side, whose intensity values were chosen independently every 30 msec as described above (27, 28). Recordings extended over 100 repeats of a 20-sec segment of random flicker or 30 repeats of an 800-sec segment. This report is based on 137 cells from 10 retinae in salamander and 45 cells from 2 retinae in rabbit.

Firing Event Identification.

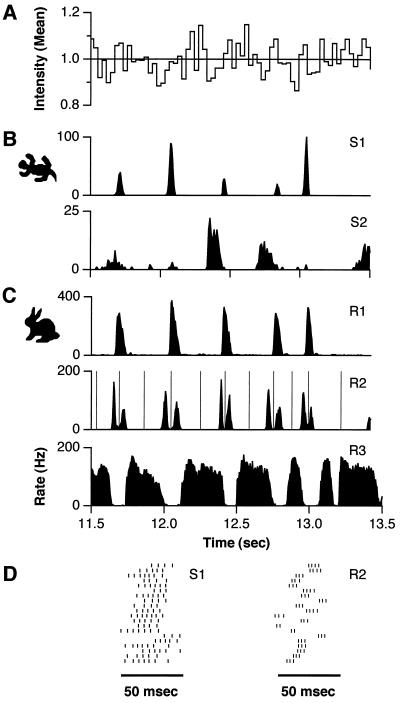
Discrete episodes of ganglion cell firing were evident in response to random flicker stimulation (Fig. 1). In many cases (e.g., S1 in Fig. 1), firing events were clearly recognized from the post-stimulus time histogram (PSTH) as a contiguous period of firing bounded by periods of complete silence. For other cells (e.g., R2 in Fig. 1), the PSTH showed sharp peaks but did not necessarily drop to zero in between. To provide a consistent demarcation of firing events, we drew the boundaries of a firing event at minima ν in the PSTH that were significantly lower than neighboring maxima p₁ and p₂, such that 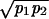/ν ≥ φ with 95% confidence. The threshold φ was chosen as 1.5, and the results of event identification depended only weakly on φ. With these boundaries defined, every spike in each trial was assigned to exactly one firing event.

Figure 1.

Retinal ganglion cell responses to spatially uniform random flicker at 9% contrast. (A) Stimulus intensity in units of the mean for 2 sec of the 20-sec segment. Post-stimulus time histograms for representative salamander (B) and rabbit (C) ganglion cells were accumulated over 100 repeated stimulus presentations with 5-msec time bins. Comparing the stimulus to the response, one finds that salamander cell S1 is driven by decreases in illumination (OFF-type) and cell S2 is ON-type. Rabbit cell R1 is very similar to salamander S1. Cell R2 responds to the same stimulus features with pairs of bursts. Vertical lines in this PSTH are boundaries between identified firing events. Cell R3 fires at a sustained rate and is interrupted transiently with great timing precision, making its response the “complement” of cells R1 and R2. Several other response types could be distinguished in the rabbit. (D) Twenty consecutive spike trains from cells S1 and R2 showing the firing event near t = 12 sec in B and C.

Before identifying minima, we smoothed each PSTH with a Gaussian filter of width σ equal to the time scale of modulations in the firing rate. For each cell, this time scale was determined from the shuffled auto-correlation function a(t), a histogram of time differences between all pairs of spikes on two different trials. σ was taken as the width of a Gaussian curve fit to a(t) divided by 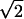, since the interspike time interval is affected by the temporal jitter of both spikes. Once event boundaries were set, the event precision (δT and δN², see Results) was measured directly from spike times and no longer depended sensitively on the choice of smoothing. For example, when σ was varied over a 3-fold range for cell S1 in Fig. 1, the timing jitter τ changed by only 0.6% and the Fano factor F by 1.2% (see Results for definitions of τ and F). Other methods for identifying statistically significant firing events in neural spike trains have been proposed (29, 30). In addition, an excess of short interspike intervals may enable event identification from a single trial (31).

Sparseness of Spike Trains.

We measured the sparseness of a ganglion cell’s response by the fraction α of time bins in the PSTH during which the cell fired above a certain threshold rate, which was chosen as 5% of the cell’s maximal firing rate. For this purpose, the PSTH was calculated with time bins equal to the median temporal precision τ of a given cell’s firing events (see Results). The value of α was not very sensitive to the choice of time bin: when the bin size was varied over a 3-fold range around τ for cell S1 in Fig. 1, α changed by only 14%. The 5% threshold was low enough to capture almost all the cell’s firing: for the same cell, 95% of the spikes were in time bins exceeding the threshold.

Information Calculations.

We calculated the Shannon information (32) conveyed for two different properties of firing events: the time of its first spike and its total number of spikes. Here we present a simple heuristic formula that relies on the fact that the entropy S in a Gaussian signal with variance Δ² is given by S = const + log₂Δ. If the distribution of interevent time intervals is Gaussian across events and trials with standard deviation ΔU (see Fig. 5A) and the distribution across trials for event i is Gaussian with standard deviation δU_i (see Fig. 5A Inset), then the average information per event conveyed by spike timing is I_T ≈ log₂ΔU − 〈log₂δU〉. Here 〈 . . . 〉 is an average over events. If all firing events have similar temporal precision δU = 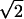δT (see Fig. 2A), then this formula simplifies to I_T ≈ log₂(ΔU/δU) = log₂(ΔU/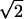δT). Notice that the ratio ΔU/δU is the number of distinguishable interevent intervals. Similarly, the information in spike counts is I_N ≈ log₂ΔN − 〈log₂δN〉, where ΔN is the standard deviation of the distribution of spike counts accumulated over all trials. Finally, if the distribution of spike counts is given by Poisson statistics, then δN_i = 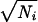for every event. The resulting information in spike counts assuming Poisson statistics is I_P ≈ log₂ΔN − 〈log₂N^1/2〉. Though the measured distributions of these quantities were clearly not Gaussian in detail, we have performed a more accurate information calculation that treats non-Poisson spiking statistics (33), yielding results very similar to the simple approximation presented here.

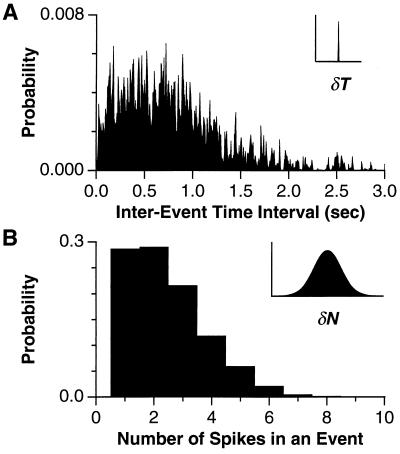
Figure 5.

Histogram of the distribution of (A) time intervals between the first spike of two consecutive firing events and (B) number of spikes in an event, accumulated over 30 trials of an 800-sec segment of random flicker for a salamander ganglion cell at 35% contrast. (Insets) For comparison on the same abscissa, a Gaussian distribution is shown with a standard deviation given by the median temporal jitter and number jitter, respectively.

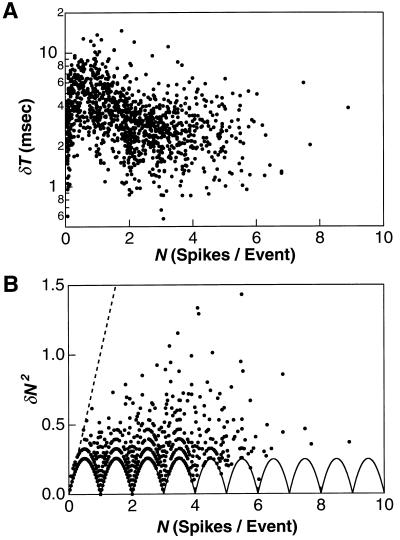
Figure 2.

Statistics of firing events for a salamander ganglion cell stimulated at 35% contrast. (A) The temporal jitter δT of the first spike versus the average spike count N in the event. (B) The variance in spike count δN² versus the average spike count N. Each dot represents the precision of 1 of 1152 firing events accumulated during 30 repeated trials of an 800-sec segment of random flicker. The variance for a Poisson process is shown (broken line) along with the lower bound on the variance (solid line) arising from the fact that each trial generates an integer number of spikes.

RESULTS

The qualitative features of ganglion cell responses to random flicker stimulation at 9% contrast (see Methods and Analysis) are seen in Fig. 1. First, spike trains had extensive periods in which no spikes were seen in 100 repeated trials. Many spike trains were sparse, in that the silent periods covered a large fraction of the total stimulus time. Second, during periods of firing, the PSTH rose from zero to the maximum firing rate (≈100 Hz) on a time scale comparable to the time interval between spikes (≈10 msec). Together these observations suggest that the response is better viewed as a set of discrete firing “events” than as a continuously varying firing rate. In general, the firing events were bursts containing more than one spike (Fig. 1D). Identifiable firing events were seen across cell types and across species. In fact, some rabbit and salamander cells responded at nearly identical sets of times (cells S1 and R1 in Fig. 1). However, the rabbit retina displayed a greater variety of distinctive firing patterns (Fig. 1C).

Measurements of both timing and number precision can be obtained if the spike train is parsed into such firing events (see Methods and Analysis). For each firing event i, we accumulated the distribution of spike times across trials and calculated several statistics: the average time T_i of the first spike in the event and its standard deviation δT_i across trials, which quantified the temporal jitter of the first spike; similarly, the average number N_i of spikes in the event and its variance δN_i² across trials, which quantified the precision of spike number. In trials that contained zero spikes for event i, no contribution was made to T_i or δT_i, while a value of zero was included in the calculation of N_i and δN_i². Finally, the sparseness of a cell’s response was measured by the fraction of time α, during which the cell fired at more than 5% of its maximal rate. We will now use these measures to explore the generality of retinal precision and sparseness for different stimulus conditions and different ganglion cell types.

Fig. 2A plots the temporal jitter δT of the first spike in an event against the number of spikes N for roughly 1,000 firing events from a salamander ganglion cell at high contrast (35%). The jitter δT was very small (1–10 msec) and decreased slightly with N. Thus, repeated trials of the same stimulus can elicit action potentials with a timing uncertainty of less than 1 msec. This precision is remarkable, because salamander photoreceptors have a visual integration time of ≈100 msec (34, 35). More noteworthy perhaps than the events with the best timing precision are the events with the worst, whose jitter rarely exceeded 10 msec. Because the random flicker stimulus ensemble includes intensity fluctuations with a wide range of sizes, durations, and stimulus histories, one might have expected a wide range of timing jitters. Together, the narrow distribution of event timing jitters and their small values suggest that the timing of firing events is an important aspect of visual signaling for these ganglion cells.

Fig. 2B shows that the variance δN² in the spike count was remarkably low at 35% contrast (36): it often approached the lower bound imposed by the fact that individual trials necessarily produce integer spike counts (33). The sets of arches traced out correspond to the smallest, second smallest, and third smallest variance δN² at any given value of N. This high precision, with the majority of events having δN < 0.5 spikes, indicates that firing events differing by only a single spike can be distinguished reliably. If a spike train were completely characterized by its time-varying firing rate, then the number of spikes counted over any given time interval would be distributed with Poisson statistics. In particular, the variance in that spike count would be equal to the mean (37). The fact that, instead, δN² ≪ N for all events constitutes clear evidence that the ganglion cell spike trains cannot be completely characterized by their firing rate.

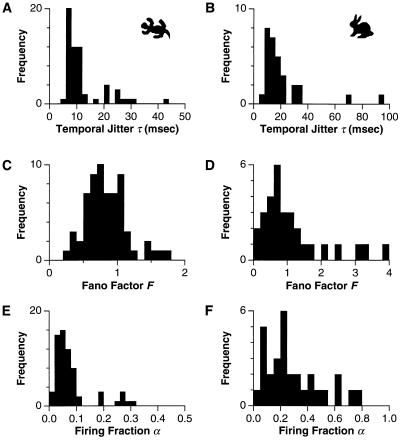
As seen in Fig. 1, the precision and sparseness of the response varied across the population of ganglion cells. Fig. 3 summarizes these results. For each cell, the temporal jitter of all firing events was distilled into a single number τ by taking the median over all events. At moderate contrast (9%) salamander cells fell into a high-precision group with τ = 6–12 msec and another with τ > 15 msec (Fig. 3A). All cells in the former group (e.g., cell S1 in Fig. 1) were “fast OFF” cells, as identified by the time course of the reverse correlation function (38). The rabbit retina exhibited a group of ganglion cells with τ = 5–20 msec, as well as several cells with larger values (Fig. 3B). The spike number precision of each cell was assessed by computing the average variance over events and dividing by the average spike count: F = 〈δN²〉/〈N〉. This quantity, also known as the Fano factor, has a value of one for a Poisson process (37). Most salamander and rabbit ganglion cells had values broadly centered on F ≈ 0.7; both retinas also exhibited cells with F > 1 (Fig. 3 C and D). In addition, most salamander cells had very sparse responses (Fig. 3E), with firing fractions in the range α = 0.03–0.1. The rabbit retina showed a wider distribution of firing fractions (Fig. 3F), with peaks around α ≈ 0.1 (e.g., cell R1 in Fig. 1) and α ≈ 0.2 (e.g., cell R2 in Fig. 1), as well as values up to α = 0.76 (cell R3 in Fig. 1). This diversity is not surprising given the greater variety of ganglion cell types in this species (39–41). Although rabbit ganglion cell spike trains were not always sparse, they still had clear periods of silence that allowed the identification of firing events (e.g., cell R3 in Fig. 1).

Figure 3.

Histograms of spike train statistics for 65 salamander cells from 4 retinae (Left) and 30 rabbit cells from 2 retinae (Right), measured at 9% contrast. (A and B) The median temporal jitter τ of the first spike of an event. (C and D) The variance-to-mean ratio (Fano factor) F of the spike count in an event. (E and F) The fraction of time spent firing α.

Preliminary measurements indicate that the response to a spatially modulated checkerboard stimulus (see Methods and Analysis) has the same character. Firing events were identified for all seven fast OFF ganglion cells in one salamander retina. At 24% contrast, their temporal jitter was τ = 8.7 ± 0.6 msec (mean ± SEM), the Fano factor was F = 0.34 ± 0.02, and the firing fraction was α = 0.020 ± 0.003. The receptive field center (measured by reverse correlation, ref. 38) typically spanned six checkers. Since each checker flickered independently, the effective contrast integrated over the receptive field was only ≈10%. For the same cells stimulated with spatially uniform flicker at 9% contrast, the temporal jitter was τ = 11 ± 0.5 msec, the Fano factor was F = 0.80 ± 0.04, and the firing fraction was α = 0.031 ± 0.005. Thus, the temporal precision and firing fraction under a spatially modulated stimulus are close to that under a uniform stimulus with the same effective contrast, while the number precision is better.

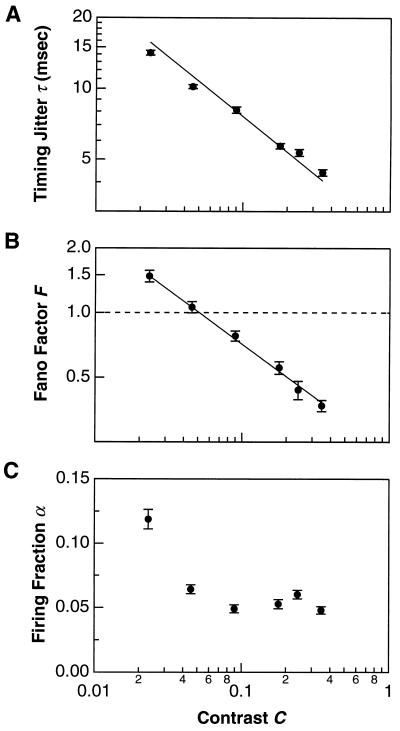
Does a highly precise retinal response only occur for “strong” visual stimuli? To answer this question, we varied the intensity contrast over a 15-fold range: from 2.3% (barely visible to the experimenters) to 35% (roughly the contrast of natural scenes, refs. 42–44). The analysis was restricted to the fast OFF cell type in the salamander. Fig. 4A shows that the average temporal jitter τ rose from 4.4 msec at the highest contrast (35%) to 14 msec at the lowest (2.3%). As seen in Fig. 4B, the Fano factor was considerably below one at high contrast, but increased above one at low contrast. The contrast dependence of both τ and F was well described by a power law ∝C^γ with γ = −0.5. Interestingly, Fig. 4C shows that the firing fraction α was roughly constant until the lowest values of contrast. From Fig. 4A, one might have expected the firing fraction to increase as contrast is lowered, but a decrease in the frequency of firing events at lower contrast compensated for the increase in timing jitter.

Figure 4.

Dependence of retinal precision on stimulus contrast. (A) The temporal jitter τ. (B) The Fano factor F. (C) The firing fraction α. All data (•) are plotted as mean ± SEM of a population of salamander ganglion cells (fast OFF-type), pooled over 50/6, 15/1, 31/3, 40/4, 31/3, and 32/3 cells/retinae at each contrast value ranging from highest to lowest. Solid lines are one-parameter curve fits proportional to Contrast^−0.5.

While the precision of both spike timing and spike number degrades similarly as contrast is lowered, the retina’s temporal precision is far better when judged on an absolute scale. Fig. 5A shows that interevent time intervals for a salamander ganglion cell range up to ≈2 sec, while the temporal jitter for this cell is only 3.1 msec. Thus, the time intervals between successive events on a single trial can be significant to better than 1 part in 500. In contrast, Fig. 5B reveals that the range of event spike counts is only a few times larger than the trial-to-trial variability in spike count for any given event. Thus, the dominant form of variability in retinal spike trains is the addition or omission of spikes, rather than the jitter of spike times (45).

This difference between spike timing and spike number precision can be quantified using an information theoretic measure. Because the temporal jitter is so small compared with the range of interevent time intervals that a ganglion cell can generate, many different time intervals can be distinguished reliably. The information measures, on a logarithmic scale, the number of distinguishable intervals elicited by the visual stimulus (see Methods and Analysis). For the ganglion cell in Fig. 5, the information per event from spike timing was I_T = 7.3 bits. Similarly, the number of distinguishable spike counts yields the information conveyed by the spike number: I_N = 1.7 bits. Thus, the time of occurrence of a firing event carries far more visual information than the number of spikes in that event. This observation held over the entire range of contrasts tested, consistent with the fact that timing precision and number precision show the same functional dependence on contrast (Fig. 4). Still, at high contrast, the spike number was more precise than predicted for a Poisson process with the same PSTH. In the case of a Poisson process, δN_i = 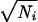for each event, resulting in an information I_P = 0.7 bits for the same ganglion cell. Thus, a typical firing event at 35% contrast carries more than twice the information in spike number than one might have assumed before measuring the precision.

DISCUSSION

In summary, we have found that many retinal ganglion cells, in response to dynamic stimuli, produce spike trains with rapid modulations of the firing rate upon a background of essentially zero firing. Because these cells make rapid transitions between silence and maximal activity, rather than sampling a continuum of intermediate values, describing this process by a time-varying firing rate is awkward. Instead, the response is better viewed as a discrete function comprised of silent periods interrupted by firing events with several spikes. These qualitative features have been seen in other visual areas. When driven by repeated presentations of natural movies, X cells in the lateral geniculate nucleus of the cat responded with sparse and rapidly modulated episodes of firing, although the authors did not draw attention to these features (46). Similarly, many neurons in cortical area MT of awake monkeys responded to random dot motion with identifiable firing events (30). Even so, difficulties in controlling eye movements (17, 18) or ongoing brain activity (19) may have reduced the observed response precision in such experiments.

Why was no maintained firing rate observed? An extensive literature has studied the statistics of maintained firing of retinal ganglion cells both in darkness and under constant illumination (47–49). This firing rate was found to depend only weakly on the light level, leading to the speculation that maintained firing is a generic noise source against which visual responses must always be discriminated. However, phenomena such as contrast gain control (50, 51) and contrast adaptation (28) suggest that retinal function depends not just on the mean light level but also on the recent history of contrast. The present observations imply that the maintained firing observed under constant illumination is not an additive component of the stimulus-driven response. We suggest, instead, that under conditions of low contrast, such as constant illumination, the sensitivity of the retina increases to the point where ganglion cell firing can be elicited by cellular fluctuations within the network. In fact, the increase of the firing fraction at the lowest contrast (see Fig. 4C) may reflect a measurable increase in the maintained discharge. When the stimulus contrast is increased, this spontaneous firing disappears, because the network adjusts to a lower sensitivity (28).

Another major result of this work is the high precision of the retinal response to dynamic visual stimuli. Relatively few experiments have measured retinal precision, but inspection of published PSTHs reveals poor stimulus-locking under a variety of stimulus conditions (9, 52), in particular for slowly varying stimuli and low contrast. However, following a sudden step in illumination, the first few spikes often have high timing precision (20, 21) and number precision (15, but see ref. 13). Interestingly, recent experiments in other systems have found that neurons respond with greater timing precision to rapidly varying inputs than to sustained inputs (29, 30, 33). The present work shows that many ganglion cells, when driven by a broad mixture of fast and slow stimulus waveforms, respond to a small subset of stimulus features with high precision and simply do not respond to the others. Thus, high response precision is a generic feature of these ganglion cells, holding over the range of stimulus patterns in the random flicker ensemble and over a wide range of contrasts. The smallest values of timing jitter were very similar in salamander and rabbit. Since mammalian cones have faster kinetics than those of amphibians, it appears that—at least under photopic conditions—the phototransduction process does not limit the precision of ganglion cell firing.

What does response precision tell us about the neural code of the retina? Superimposed upon a background of zero firing, precise firing events are highly informative. In fact, each firing event produced by the ganglion cell in Fig. 5 can convey up to I_T + I_N ≈ 9 bits of visual information (assuming that event timing and spike count are uncorrelated). This amounts to 3.6 bits per spike and strengthens the impression that information rates of order several bits per spike are universal across many sensory systems (37, 53). Furthermore, the observed sub-Poisson variability in the spike count means that a description of ganglion cell firing by a continuously varying firing rate is not only poorly matched to the phenomenology, but fundamentally incomplete. Firing events containing single spikes or bursts of spikes are elicited precisely enough to convey distinct packets of visual information, and hence may constitute the fundamental symbols in the neural code of the retina.

The identification of firing events makes it possible to distinguish information about what kind of visual stimulus pattern occurred from when it occurred. The “when” information is conveyed by the time of a firing event and is measured by I_T. The “what” information is conveyed by all other features of an event and is measured in part by I_N (31). We have found that for retinal ganglion cells stimulated by random flicker, information about “when” dominates that about what. For instance, the ganglion cell in Fig. 5 can discriminate at least 2^I_N = 3 different stimulus features, but can localize them to one of 2^I_T = 160 different time bins. The dominance of I_T over I_N held over the entire range of stimulus contrasts studied, as well as for a spatially modulated stimulus. To further assess the role of timing precision in visual processing, it will be instructive to determine how it fares under stimuli drawn from the natural world.

This distinction between what and when information is subject to several caveats. First, it assumes that firing events are generated independently of each other, whereas there is evidence against this simple notion. Because the random flicker ensemble should produce excitatory stimuli with roughly constant probability per unit time, independently generated firing events would exhibit an exponential interval distribution. But the measured distribution (Fig. 5A) is approximately flat out to intervals of 1 sec. If successive events are not produced independently, then their relative timing might help discriminate among different stimulus features. Second, groups of nearby ganglion cells show a strong tendency toward synchronized firing (38, 54). As a result, the concept of a firing event may need to be generalized to involve a local group of cells. The spike count N could be replaced by a list of counts from m such ganglion cells (N₁, . . . N_m), which would identify what stimulus feature caused the event, while the event time again would mark when that feature occurred. Clearly, further statistical analysis of these firing events will help in understanding the nature of this neural code.

Does the brain use all of the information in retinal spike trains? The analysis of retinal recordings alone cannot answer this question. Instead, it establishes bounds within which the brain’s visual computations must occur. For progress on this challenging question, future studies must address the relationship between spiking patterns in retina and those in subsequent visual circuits.

ABBREVIATION

PSTH

post-stimulus time histogram