Abstract
Follicular dendritic cells (FDC) provide a reservoir for HIV type 1 (HIV-1) that may reignite infection if highly active antiretroviral therapy (HAART) is withdrawn before virus on FDC is cleared. To estimate the treatment time required to eliminate HIV-1 on FDC, we develop deterministic and stochastic models for the reversible binding of HIV-1 to FDC via ligand–receptor interactions and examine the consequences of reducing the virus available for binding to FDC. Analysis of these models shows that the rate at which HIV-1 dissociates from FDC during HAART is biphasic, with an initial period of rapid decay followed by a period of slower exponential decay. The speed of the slower second stage of dissociation and the treatment time required to eradicate the FDC reservoir of HIV-1 are insensitive to the number of virions bound and their degree of attachment to FDC before treatment. In contrast, the expected time required for dissociation of an individual virion from FDC varies sensitively with the number of ligands attached to the virion that are available to interact with receptors on FDC. Although most virions may dissociate from FDC on the time scale of days to weeks, virions coupled to a higher-than-average number of ligands may persist on FDC for years. This result suggests that HAART may not be able to clear all HIV-1 trapped on FDC and that, even if clearance is possible, years of treatment will be required.
The pool of HIV type 1 (HIV-1) on follicular dendritic cells (FDC) is an important reservoir that has the potential to perpetuate infection (1–3). Although antiretroviral therapies that block viral replication have no direct effect on viral clearance, these therapies are associated with loss of HIV-1 from FDC (4–7). Cavert et al. (4) observed that the amount of HIV-1 on FDC, estimated as ≈1011 virions, decreased by up to 5-fold during the first 2 d of potent antiretroviral therapy and by up to more than four orders of magnitude after 6 mo. This clearance of FDC-associated HIV-1 during antiretroviral therapy suggested that HIV-1 might be eradicated from the FDC reservoir, and an estimate of 30 mo to eradication was proposed (4).
To evaluate further the prospect of eradicating or substantially reducing FDC-associated HIV-1 through highly active antiretroviral therapy (HAART), we develop and analyze two related mathematical models for the reversible binding of HIV-1 to FDC via ligand–receptor interactions. One model is a deterministic mass-action model that allows us to follow the time course of dissociation for a population of virions initially on FDC when therapy reduces the pool of virus available for binding to FDC. This model is useful for examining early events during treatment. The other model is a stochastic model that allows us to determine the distribution of dissociation times for individual virions. This model is useful for examining late events during treatment and assessing the treatment time required to eliminate HIV-1 on FDC. These models also allow us to determine how physical quantities, such as the surface density of receptors or the valence of a virion, influence the dissociation process.
The mathematical models developed here are based on our current understanding of the physical chemistry of antigen trapping by FDC (8). HIV-1 is held on the surface of FDC through interactions with complement receptors (9) and possibly Fc receptors that bind antibodies attached to HIV-1. FDC express complement receptors CR1, CR2, and CR3 (10). These receptors bind proteolytic fragments of complement component C3 (11): CR1 binds C3b; CR2 binds iC3b, C3dg, and C3d; and CR3 binds iC3b. Ligands of CR2 have been detected on plasma virus (12, 13). One mechanism that contributes to C3 deposition on HIV-1 is direct binding of C1q to sites on the HIV-1 transmembrane glycoprotein gp41 (14), which leads to activation of complement via the classical pathway (15). In our models, we focus on interactions of CR2 on FDC with terminal C3 fragments (C3dg and C3d) on HIV-1. By focusing on this subset of interactions involved in binding of HIV-1 to FDC, we obtain a minimal estimate of the treatment time required to eliminate FDC-associated HIV-1.
Models
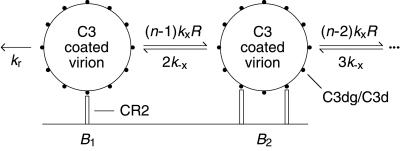
Models are based on the reaction scheme illustrated in Fig. 1. We treat CR2 as a monovalent cell-surface receptor, which is consistent with the observed stoichiometry of CR2 binding to C3dg (16), and we treat a complement coated virion as a multivalent ligand that expresses a set of equivalent binding sites for CR2. The assumption of equivalent sites is a useful simplification (17). We characterize the number of CR2-binding sites on a virion by the effective valence n, which is defined as the maximum number of sites on the virion at which CR2 can bind simultaneously (17). Although we develop our models in terms of interactions between CR2 and terminal fragments of C3, the models are also valid for the interaction of Fc receptors with antigen–antibody complexes.
Figure 1.
Reaction scheme. Complement opsonized virus is held on FDC through interactions between CR2 and terminal C3 fragments on HIV-1.
Mass-Action Model.
A mass-action model based on Fig. 1, which is closely related to earlier models for multivalent ligand–receptor binding and viral attachment to cell surfaces (17, 18), is defined by
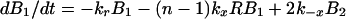 |
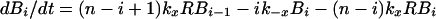 |
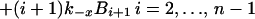 |
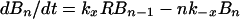 |
1 |
and
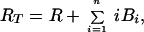 |
2 |
where Bi is the surface density of virions bound at i sites, R is the surface density of unbound CR2, RT is the total surface density of CR2 (i.e., the average number of CR2 per unit area on FDC), kx is the single site rate constant for addition of a receptor to a HIV-CR2 complex, k−x is the single site rate constant for removal of a receptor from a HIV–CR2 complex, and kr is the effective rate constant for detachment of a virion from FDC, which in general depends on the diffusion properties of HIV-1 and the surface density of CR2 (19, 20). The association and dissociation terms in Eq. 1 include factors that account for the number of free and bound sites on a virion. Drug treatment begins at time t = 0. We assume that therapy, in combination with viral clearance, eliminates the pool of virus available for binding to FDC. This assumption is reflected in Eq. 1 by the absence of terms for attachment of HIV-1 to FDC. Because some attachment of HIV-1 to FDC can be expected during HAART, Eq. 1 underestimates the number of virions on FDC at any given time. We also assume that RT in Eq. 2 is constant, because antigens, including HIV-1, are retained on the surface of FDC without significant internalization (8, 9, 21).
To calculate the time course of dissociation induced by therapy, we solve the initial value problem defined by Eqs. 1 and 2 after parameter values and an initial condition are specified. We consider the limiting initial condition of receptor saturation, in which each CR2 is bound to a single virion (R = 0, B1 = RT, and Bi = 0 for i = 2, … , n at t = 0), and a more realistic initial condition, in which virions are attached to multiple receptors in a pretreatment steady state. The pretreatment state is determined by solving the steady-state form of Eqs. 1 and 2 when an associative rate αVR is included in the expression for dB1/dt, where α is an apparent rate constant for association, and V is the steady-state concentration of free virus. (The steady-state form of Eq. 1 is obtained by setting dBi/dt = 0 for all i.) The value of αV is chosen so that the number of bound virions per receptor, Σi=1n Bi/RT, is equal to a specified value.
Birth–Death Model.
A stochastic model, based on the scheme in Fig. 1, allows us to estimate the expected time that an individual virion remains bound to FDC during treatment. A virion with i of n sites bound to CR2 can participate in either of two transitions: a bond can break, resulting in i − 1 bound sites, or a bond can form, resulting in i + 1 bound sites. The rate of transition to the state with i − 1 bound sites is kr for i = 1 and ik−x for i > 1, and the rate of transition to the state with i + 1 bound sites is (n − i)kxR.
If only a small fraction of CR2 are bound to HIV-1, such that R ≈ RT (a condition that will eventually be reached as virus dissociates), then R can be replaced with RT in the transition rate equations, and these equations then lead to the following system of linear algebraic equations (22):
 |
3 |
where ti is the expected time required for a virion bound at i sites to dissociate from FDC during treatment, t0 = 0, λi = (n − i)kxRT, μ1 = kr, and μi = ik−x for i > 1. The first term in Eq. 3, 1/(λi + μi), is the expected time required for a virion initially bound at i sites to make a transition. The next term is the probability that the transition is formation of a bond, λi/(λi + μi), multiplied by the expected time required for dissociation after this transition, ti+1. The last term is the probability that the transition is the opening of a bond, μi/(λi + μi), multiplied by the expected time required for dissociation after this transition, ti−1. From the analytical solution of Eq. 3 (22), we find:
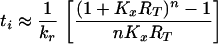 |
4 |
where Kx = kx/k−x. This equation is exact for the special case i = 1. For other values of i, Eq. 4 underestimates the expected dissociation time (see Appendix).
The expected lifetime of a virion on FDC does not tell the whole story; some virions will dissociate sooner and others later. The probability that a virion remains bound to FDC after a specified treatment time is obtained by solving the forward Kolmogorov equations (22) for the reaction scheme illustrated in Fig. 1:
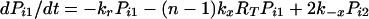 |
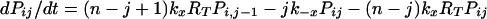 |
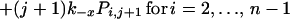 |
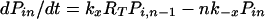 |
5 |
with the initial condition Pii = 1 and Pij = 0 for j ≠ i at t = 0. Here, Pij is the probability that a virion bound initially at i sites is bound to FDC at j sites after treatment time t. The probability that a virion starting with i attachments is still bound after time t is given by Σj=1n Pij. This sum can also be interpreted as the fraction of virions initially bound at i sites that remain bound to FDC after time t.
Parameter Estimates.
Valence.
Thieblemont et al. (23) quantified the deposition of C3b/iC3b on recombinant HIV-1 glycoprotein gp160 in the presence of normal human serum. A binding stoichiometry of 1:1 was estimated. Because there are 72 spikes on an ideal immature virus (24), which corresponds to 216 gp160 molecules (25), a virion has the potential to bind several hundred C3 fragments. We focus on values of n between 10 and 100.
Receptor surface density.
The surface density of CR2 on FDC is unknown; however, it is higher than that on B cells (10). The number of CR2 per B cell is between 10,000 and 30,000 (26, 27). On the basis of 30,000 CR2 per B cell and a B cell diameter of 10 μm, the surface density of CR2 on B cells is approximately 9.6 × 109 receptors per square centimeter. Thus, RT > 1.6 × 10−14 mol/cm2.
Equilibrium crosslinking constant.
An estimate of the crosslinking constant Kx can be obtained from the relation Kx = K/d (28), where K is the equilibrium constant for binding of CR2 to C3dg/C3d in solution, and d is a length that characterizes the volume in which CR2-binding sites are restricted when a complement-opsonized virion is anchored to the cell surface. The affinity of CR2 for C3dg determined by sucrose gradient ultracentrifugation is 3.64 × 104 M−1 (16). The affinity of CR2 for C3d is reportedly the same as that for C3dg (29). Thus, K = 3.64 × 104 M−1. This is perhaps an underestimate, because the affinity of CR2 for iC3b determined by BIAcore measurement is 8 − 34 × 106 M−1 (30), and CR2 has been found to bind C3dg/C3d and iC3b with similar affinities (31, 32). We take d = 120 nm, the diameter of a mature virion (33), because no CR2-binding site can be further than this distance from the anchor point. By using this value of d, we underestimate the value of Kx, because some CR2-binding sites will be at distances less than 120 nm. Thus, Kx > 3 × 1012 cm2/mol and KxRT > 0.05.
Dissociation rate constants.
Binding of iC3b to CR2 has been monitored with the BIAcore instrument (30). Although a value for the dissociation constant is not reported in this study, it is apparent that iC3b dissociates from CR2 with a half-life of less than 10 s. We estimate t1/2 = 5 s, which corresponds to a dissociation rate constant of (ln 2)/t1/2 ≈ 0.1 s−1. We assume that kinetic interactions of CR2 with iC3b and C3dg/C3d are similar and base our calculations on kr = k−x = 0.1 s−1.
Results
By focusing on interactions between terminal C3 fragments and CR2 (Fig. 1), we have developed both a deterministic (Eqs. 1 and 2) and stochastic model (Eqs. 3–5) for binding of HIV-1 to FDC. We now use these models to examine the effect of HAART on dissociation of HIV-1 from FDC. In our models, therapy, in combination with viral clearance, causes dissociation of HIV-1 from FDC by eliminating the pool of virus available for binding to FDC.
Time Course of Dissociation.
Cavert et al. (4) have shown that more than 99.9% of HIV-1 on FDC is cleared after 180 d of potent antiretroviral therapy. In some cases, the reduction in viral load on FDC was greater than 10,000-fold. Fig. 2 shows a time course of dissociation derived from our mass-action model that is consistent with these observations. Similar time courses are obtained with various combinations of parameter values (Table 1). Although Fig. 2 is based on particular parameter values, it illustrates typical features of time courses derived from Eqs. 1 and 2.
Figure 2.
Dissociation of HIV-1 from FDC during HAART. The number of bound virions per CR2 on FDC, Σi=1n Bi/RT, is plotted as a function of time t. Treatment begins at t = 0. For t > 0, we assume there is no attachment of HIV-1 to FDC. The time course of dissociation during (a) the first 2 d of treatment or (b) the first 200 d of treatment is determined from Eqs. 1 and 2 with n = 20, KxRT = 1.1427 and kr = k−x = 0.1 s−1. After the value of n is specified, the value of KxRT is chosen so that the level of virus on FDC after 180 d of treatment is 10,000-fold less than that after 2 d of treatment. The dotted line in a is based on the initial condition B1 = RT (each receptor is initially bound to a single virion). The solid line is based on a more realistic initial condition, which is determined from the steady-state form of Eqs. 1 and 2 with the associative rate αVR (αV = 3.5576 × 10−6 s−1) added to the expression for dB1/dt in Eq. 1. With this initial condition, Σi=1n Bi/RT = 0.05, and virions are distributed in various bound states at t = 0.
Table 1.
Persistence of HIV-1 on FDC
| Nominal (mean) valence n | Best-fit crosslinking constant KxRT | Expected dissociation time t1, days | Extinction time, days | Smallest valence for which
|
|
|---|---|---|---|---|---|
| t1 > 1 yr | t1 > 10 yr | ||||
| 10 | 3.840 | 21 | 555 | 12 | 14 |
| 20 | 1.1427 | 21 | 561 | 24 | 28 |
| 30 | 0.6533 | 21 | 562 | 37 | 41 |
| 40 | 0.45527 | 21 | 564 | 49 | 55 |
| 50 | 0.34885 | 21 | 564 | 61 | 69 |
| 60 | 0.2826 | 21 | 564 | 73 | 83 |
| 70 | 0.23742 | 21 | 564 | 85 | 96 |
| 80 | 0.20468 | 21 | 565 | 97 | 110 |
| 90 | 0.17986 | 21 | 565 | 109 | 124 |
| 100 | 0.1604 | 21 | 566 | 121 | 137 |
The values of n and KxRT given in each row result, according to Eqs. 1 and 2, in a 10,000-fold drop in viral load on FDC between days 2 and 180 of treatment, consistent with the drop observed by Cavert et al. (4). A fitting procedure (bisection) was used to determine KxRT after a nominal value was specified for n. The expected dissociation time t1 in column 3 is calculated from Eq. 4. The extinction time in column 4 is the time required to reduce the mean number of bound virions from 1011 virions, which is the estimated total number of virions on FDC (3), to a single virion. The extinction time is calculated from Eq. 5 with the initial condition P11 = 1 (each virion is initially bound at a single site). The valences given in columns 5 and 6 are the smallest valences for which t1 is greater than or equal to 1 yr and 10 yr, respectively, according to Eq. 4 (on the basis of the value of KxRT in column 2). All calculations assume kr = k−x = 0.1 s−1.
The Rate of Dissociation Is Biphasic.
Fig. 2 shows that there is an early stage of fast decay, which lasts on the order of a week, followed by a late stage of slower exponential decay, which lasts many months. This late stage of decay is characterized by a half-life of approximately 15 d, which is consistent with the half-life calculated from the data of Cavert et al. (4) collected at days 22 and 180 (the half-life for eight patients ranged from 26 d to less than 15 d).
The Late Stage of Dissociation Is Insensitive to the Pretreatment Steady State.
To evaluate the importance of the pretreatment steady state, we considered a range of initial conditions when calculating time courses of dissociation. Time courses are shown in Fig. 2a for two initial conditions. One time course corresponds to the pretreatment state in which the number of bound virions is initially equal to the number of CR2 receptors. The other corresponds to a more realistic but still speculative pretreatment state in which the number of bound virions is initially 20-fold less than the number of CR2 receptors, and virions are initially present in a distribution of bound states. With this latter initial condition, the level of virus on FDC falls approximately 3-fold during the first 2 d of therapy, consistent with the observations of Cavert et al. (4). The influence of the initial condition rapidly diminishes with time; the two time courses in Fig. 2a converge within a day, which is typical. A time course similar to that shown in Fig. 2b is obtained over a wide range of initial conditions. We conclude that the pretreatment steady state has little influence on the treatment time required to eliminate FDC-associated HIV-1.
Expected Dissociation Time and Extinction Time.
The vast majority of virus is predicted to dissociate quickly (Fig. 2). Consequently, except during the early stage of dissociation, the number of bound virions should be much less than the number of CR2 receptors. Thus, the stochastic model (Eqs. 3–5), which is valid when most receptors are free (R ≈ RT), should be applicable for most of the dissociation process. By using this model, we find that, regardless of the particular values of the valence, n, and dimensionless crosslinking constant, KxRT, chosen to reproduce the observations of Cavert et al. (4), the mean time a virion remains bound to FDC is approximately 3 wk, and the expected level of virus falls 1011-fold after approximately 18 mo of treatment (Table 1, columns 3 and 4).
The Persistence of a Virion on FDC Is Sensitive to Its Valence.
Because the valence of a virion is related to the number of C3 fragments deposited on the virion through a random process, we expect a distribution of valences for virions on FDC. The influence of a virion's valence on its expected dissociation time is illustrated in Fig. 3. In Fig. 3a, the expected dissociation time for a virion is plotted as a function of valence for two fixed values of KxRT. As can be seen, the expected retention time increases exponentially with increasing valence for each case. Thus, a virion with higher-than-average valence will take much longer to dissociate than a virion with average valence. Note that the time scale in this figure ranges from 1 d to more than 25 yr, but the valences considered range from 16 to 28 (circles) and 47 to 86 (squares). Fig. 3b illustrates that dissociation time is a sensitive function of KxRT when valence is held fixed, and that it is also a sensitive function of valence over a wide range of values for KxRT.
Figure 3.
Influence of (a) valence n and (b) dimensionless crosslinking constant KxRT on the expected dissociation time of an individual virion, t1. In a, t1 is plotted as a function of n for KxRT = 1.1427 (circles) and KxRT = 0.2826 (squares) (cf. Table 1). In b, t1 is plotted as a function of KxRT for n = 10, … , 100. Dissociation times are determined from Eq. 4 with kr = 0.1 s−1.
To quantify the variability in valence required to substantially increase the treatment time required to eradicate FDC-associated HIV-1, we interpret each valence given in column 1 of Table 1 as the mean valence for a population of virions. For each case, we then use Eq. 4 to determine the valence required to increase the mean lifetime of a virion from 21 d to 1 yr and from 21 d to 10 yr. For example, if we use the same dimensionless crosslinking constant KxRT = 1.1427 that was determined on the basis of n = 20, we find that for a virion with valence n = 24, the expected dissociation time increases to 370 d and for a virion with valence n = 28, the expected dissociation time increases to 18 yr. Results are summarized in columns 5 and 6 of Table 1. We conclude that the valence of a virion need not be much larger than the mean valence that characterizes the initial population on FDC to increase the expected dissociation time for a virion by an order of magnitude or more.
The Probability That a Virion Remains Bound to FDC Declines Exponentially with Time.
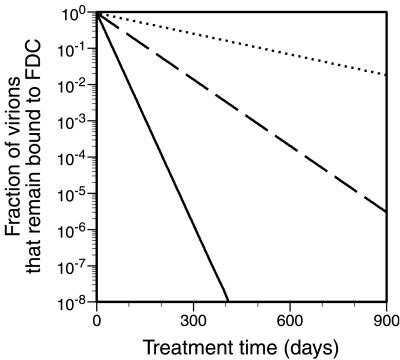
The dissociation time can vary for identical virions; some will dissociate faster and some slower than the expected dissociation time. As illustrated in Fig. 4, and as is typical for cases that we have considered, the probability that a virion remains attached to FDC declines exponentially with treatment time. Furthermore, the rate of exponential decay is inversely proportional to the expected lifetime of a virion, t1. As a result, the treatment time required to reduce an initial pool of N virions to a single virion is approximated by the simple formula t1 ln N. This formula indicates that the treatment time required to reduce a pool of 108 virions to a single virion is ≈18 t1, whereas the treatment time required to reduce a pool of 1011 virions to a single virion is ≈25 t1. We conclude that the treatment time required to eradicate the FDC pool of HIV-1 is relatively insensitive to the number of virions in this pool.
Figure 4.
Fraction of virions initially on FDC that remain on FDC after treatment time t. The quantity Σjn=1 P1j, determined from Eq. 5, is plotted as a function of t for three cases: n = 60 (solid line), n = 65 (broken line), and n = 70 (dotted line). In all cases, kr = k−x = 0.1 s−1 and KxRT = 0.2826 (cf. Table 1).
The formula t1 ln N can be used to estimate the time required to extinguish a pool of virions with higher-than-average valence. For example, if we consider virions with valence n = 73 and KxRT = 0.2826 (cf. Table 1), then t1 = 1.2 years (Eq. 4) and the extinction time for a pool of 106 virions is 1.2 ln (106) ≈ 16 yr. The pool size of 106 virions considered here is rather small compared with the estimated total viral burden of 1011 virions (3) but presumably still large enough to perpetuate infection, given the highly infectious nature of HIV-1 on FDC (2).
Discussion
Complement receptors, interacting with C3 fragments, play an important role in trapping HIV-1 on FDC (9). It is likely that most C3 fragments on FDC-associated virus are processed to generate CR2 ligands, because Factor I, which cleaves C3b to generate iC3b and C3dg (34), is present in lymphoid follicles in close association with FDC (35), and also because CR1, which is a cofactor for Factor I (34), is abundant on FDC (10). Thus, the receptor most likely to be involved in long-term retention of HIV-1 on FDC is CR2, the receptor on FDC that binds the terminal products of C3 cleavage (C3dg and C3d) (11). Focusing on the interaction of CR2 on FDC with terminal C3 fragments on HIV-1 (Fig. 1), we developed a mass-action model (Eqs. 1 and 2) and a stochastic birth–death model (Eqs. 3–5) for the binding of HIV-1 to FDC. We then used these models to determine how retention of HIV-1 on FDC is influenced by antiretroviral therapy that reduces the pool of virus available for binding to FDC. The binding parameters in our models can be estimated from available data, but each of these parameters is uncertain to some extent. Although these parameters are clearly important and deserve further study, our key results are largely independent of particular parameter values.
The mass-action model, with reasonable parameter values (Table 1; Fig. 2), is capable of reproducing the observations of Cavert et al. (4) of fast and then slow decay of FDC-associated HIV-1 with loss of more than 99.9% of virions after 6 mo of therapy. Analysis of this model shows that dissociation of HIV-1 from FDC during therapy is expected to be biphasic (Fig. 2). This can be attributed to multivalent binding. Initially, each virion is held on FDC via some average number of bonds. As bonds break, some virions dissociate, which increases the number of receptors available to interact with virions that remain on FDC. Thus, as the extent of dissociation increases, the average number of bonds that hold a virion on the cell surface also increases, and as a result the rate of dissociation slows. The rate of dissociation reaches a steady level when the surface density of unbound receptors approximates the total surface density of receptors (R ≈ RT). We also found that the slow phase of decay is insensitive to the initial pretreatment steady state (Fig. 2a). As a result, it is not essential to fully characterize the pretreatment steady state. These results together indicate that estimates of the treatment time required to clear HIV-1 on FDC can be obtained by focusing on the period after most of the virus has dissociated, the period during which our stochastic model is applicable.
Analysis of the stochastic model indicates that the expected dissociation time for an individual virion is extremely sensitive to the virion's valence (Fig. 3), which is related to the number of C3 fragments available for interacting with CR2 on FDC. This raises the possibility that virions with higher-than-average valence may be retained on FDC for considerably longer times than would be expected from the measured decay at early time points. Most virions that dissociate early will have average or below average valence. The results summarized in Table 1 indicate that the variability in valence required to increase the mean dissociation time of a virion from 21 d, the value consistent with a 10,000-fold drop in virus after 6 mo of therapy (4), to 1 yr or 10 yr is small. Thus, key information that determines whether HAART has the potential to eradicate the FDC pool of virus is the distribution of valences for virions on FDC. Unless the distribution is extremely narrow, HAART is unlikely to completely clear FDC-associated virus, even though it may reduce the viral load substantially. Analysis of the stochastic model also indicates, as illustrated in Fig. 4, that the treatment time required to reduce a pool of N FDC-bound virions with the same valence to a single virion is given approximately by the product of ln N and t1, the expected dissociation time of an individual virion. This indicates that the treatment time for eradication of HIV-1 from FDC is relatively insensitive to the number of virions on FDC.
The treatment times estimated here are likely to be underestimates. Factors that can be expected to contribute to longer treatment times, which we have not considered in our models, include receptors other than CR2 that interact with HIV-1, such as Fc receptors, and attachment of both previously dissociated and newly generated HIV-1 to FDC during HAART, particularly as recent results suggest that HAART may not fully block viral replication (36, 37). Other complications not considered, which may speed loss of HIV-1 from FDC, include turnover of FDC, shedding of iccosomes (38), structural degradation of virions, binding of virions to CD4+ cells, uptake of virions by antigen presenting cells, and secretion of soluble CR2 by lymphocytes (30) and FDC (39). Soluble CR2 might compete with surface CR2 for sites on HIV-1 (40). However, surface receptors are likely to have a considerable advantage in this competition (41), because HIV-1 is tethered to the cell surface in the vicinity of these receptors. Thus, surface CR2 receptors see a high local concentration of HIV-1, which is not the case for soluble CR2 receptors.
We have focused on one aspect of HIV-1 trapping by FDC: the interaction of CR2 with terminal C3 fragments. The models developed here are the first for HIV-1 binding to FDC. Predictive mathematical models such as these are perhaps the only feasible approach available for investigating events after the viral load on FDC falls to undetectable levels, levels that may still be sufficiently high to perpetuate infection (42). The single most important result obtained from analysis of these models is that low-affinity interactions between HIV-1 and FDC are sufficient to retain a fraction of HIV-1 on FDC for very long times, even if the vast majority of virus dissociates quickly during HAART. In light of this result, it would seem prudent to pursue intervention strategies not only for ridding the body of latently infected cells (43) but also for speeding the release of HIV-1 from FDC. One strategy that might be considered is a C3 competitor that binds to CR2 on FDC (44).
Acknowledgments
We thank G. F. Burton, B. Goldstein, J. E. Mittler, J. K. Percus, and O. E. Percus for helpful discussions. This work was performed in part under the auspices of the U.S. Department of Energy and was supported by National Institutes of Health grants RR06555 and AI28433 (A.S.P.) and National Science Foundation grant MCB9723897 (C.W.).
Abbreviations
- HIV-1
HIV type 1
- FDC
follicular dendritic cells
- HAART
highly active antiretroviral therapy
Appendix
The solution of Eq. 3 is:
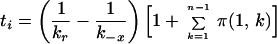 |
6 |
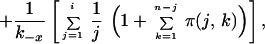 |
where
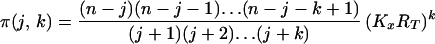 |
For a virion that is initially bound at only a single site, Eq. 6 becomes
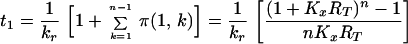 |
7 |
Because t1 < ti for i > 1, Eq. 7 provides a lower bound on the expected dissociation time for a virion initially attached to CR2 at any number of sites. As can be easily confirmed, ti ≈ t1.
References
- 1.Pantaleo G, Graziosi C, Demarest J F, Butini L, Montroni M, Fox C H, Orenstein J M, Kotler D P, Fauci A S. Nature (London) 1993;362:355–358. doi: 10.1038/362355a0. [DOI] [PubMed] [Google Scholar]
- 2.Heath S L, Tew J G, Tew J G, Szakal A K, Burton G F. Nature (London) 1995;377:740–744. doi: 10.1038/377740a0. [DOI] [PubMed] [Google Scholar]
- 3.Haase A T, Henry K, Zupancic M, Sedgewick G, Faust R A, Melroe H, Cavert W, Gebhard K, Staskus K, Zhang Z-Q, et al. Science. 1996;274:985–989. doi: 10.1126/science.274.5289.985. [DOI] [PubMed] [Google Scholar]
- 4.Cavert W, Notermans D W, Staskus K, Wietgrefe S W, Zupancic M, Gebhard K, Henry K, Zhang Z-Q, Mills R, McDade H, et al. Science. 1997;276:960–964. doi: 10.1126/science.276.5314.960. [DOI] [PubMed] [Google Scholar]
- 5.Wong J K, Gunthard H F, Havlir D V, Zhang Z-Q, Haase A T, Ignacio C C, Kwok S, Emini E, Richman D D. Proc Natl Acad Sci USA. 1997;94:12574–12579. doi: 10.1073/pnas.94.23.12574. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Stellbrink H-J, van Lunzen J, Hufert F T, Fröschle G, Wolf-Vorbeck G, Zöllner B, Albrecht H, Greten H, Racz P, Tenner-Racz K. AIDS. 1997;11:1103–1110. doi: 10.1097/00002030-199709000-00004. [DOI] [PubMed] [Google Scholar]
- 7.Tenner-Racz K, Stellbrink H-J, van Lunzen J, Schneider C, Jacobs J-P, Raschdorff B, Großschupff G, Steinman R M, Racz P. J Exp Med. 1998;187:949–959. doi: 10.1084/jem.187.6.949. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Mandel T E, Phipps R P, Abbot A, Tew J G. Immunol Rev. 1980;53:29–59. doi: 10.1111/j.1600-065x.1980.tb01039.x. [DOI] [PubMed] [Google Scholar]
- 9.Joling P, Bakker L J, Van Strijp J A G, Meerloo T, de Graaf L, Dekker M E M, Goudsmit J, Verhoef J, Schuurman H-J. J Immunol. 1993;150:1065–1073. [PubMed] [Google Scholar]
- 10.Reynes M, Aubert J P, Cohen J H M, Audouin J, Tricottet V, Diebold J, Kazatchkine M D. J Immunol. 1985;135:2687–2694. [PubMed] [Google Scholar]
- 11.Ross G D, Medof M E. Adv Immunol. 1985;37:217–267. doi: 10.1016/s0065-2776(08)60341-7. [DOI] [PubMed] [Google Scholar]
- 12.Sullivan B L, Knopoff E J, Saifuddin M, Takefman D M, Saarloos M-N, Sha B E, Spear G T. J Immunol. 1996;157:1791–1798. [PubMed] [Google Scholar]
- 13.Sullivan B L, Takefman D M, Spear G T. Virology. 1998;248:173–181. doi: 10.1006/viro.1998.9289. [DOI] [PubMed] [Google Scholar]
- 14.Ebenbichler C F, Thielens N M, Vornhagen R, Marschang P, Arlaud G J, Dierich M P. J Exp Med. 1991;174:1417–1424. doi: 10.1084/jem.174.6.1417. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Tacnet-Delorme P, Boyer V, Thielens N M, Hernandez J-F, Bally I, Sim R B, Desgranges C, Arlaud G J. J Immunol. 1999;162:4088–4093. [PubMed] [Google Scholar]
- 16.Moore M D, DiScipio R G, Cooper N R, Nemerow G R. J Biol Chem. 1989;264:20576–20582. [PubMed] [Google Scholar]
- 17.Perelson A S. Math Biosci. 1981;53:1–39. [Google Scholar]
- 18.Wickham T J, Granados R R, Wood H A, Hammer D A, Shuler M L. Biophys J. 1990;58:1501–1516. doi: 10.1016/S0006-3495(90)82495-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Shoup D, Szabo A. Biophys J. 1982;40:33–39. doi: 10.1016/S0006-3495(82)84455-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.DeLisi C, Wiegel F W. Proc Natl Acad Sci USA. 1981;78:5569–5572. doi: 10.1073/pnas.78.9.5569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Schmitz J, van Lunzen J, Tenner-Racz K, Großschupff G, Racz P, Schmitz H, Dietrich M, Hufert F T. J Immunol. 1994;153:1352–1359. [PubMed] [Google Scholar]
- 22.Taylor H M, Karlin S. An Introduction to Stochastic Modeling. 3rd Ed. San Diego: Academic; 1998. pp. 333–417. [Google Scholar]
- 23.Thieblemont N, Haeffner-Cavaillon N, Weiss L, Maillet F, Kazatchkine M D. AIDS Res Hum Retroviruses. 1993;9:229–233. doi: 10.1089/aid.1993.9.229. [DOI] [PubMed] [Google Scholar]
- 24.Gelderblom H R, Hausmann E H S, Özel M, Pauli G, Koch M A. Virology. 1987;156:171–176. doi: 10.1016/0042-6822(87)90449-1. [DOI] [PubMed] [Google Scholar]
- 25.Wyatt R, Sodroski J. Science. 1998;280:1884–1888. doi: 10.1126/science.280.5371.1884. [DOI] [PubMed] [Google Scholar]
- 26.Rasmussen J M, Marquart H V, Rask R, Jepsen H H, Svehag S-E. Complement. 1988;5:98–107. doi: 10.1159/000463040. [DOI] [PubMed] [Google Scholar]
- 27.Tooze J A, Bevan D H. Clin Exp Immunol. 1991;83:423–429. doi: 10.1111/j.1365-2249.1991.tb05655.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Goldstein B, Wofsy C. Lect Math Life Sci. 1994;24:109–135. [Google Scholar]
- 29.Nagar B, Jones R G, Diefenbach R J, Isenman D E, Rini J M. Science. 1998;280:1277–1281. doi: 10.1126/science.280.5367.1277. [DOI] [PubMed] [Google Scholar]
- 30.Frémeaux-Bacchi V, Bernard I, Maillet F, Mani J-C, Fontaine M, Bonnefoy J-Y, Kazatchkine M D, Fischer E. Eur J Immunol. 1996;26:1497–1503. doi: 10.1002/eji.1830260714. [DOI] [PubMed] [Google Scholar]
- 31.Kalli K R, Ahearn J M, Fearon D T. J Immunol. 1991;147:590–594. [PubMed] [Google Scholar]
- 32.Diefenbach R J, Isenman D E. J Immunol. 1995;154:2303–2320. [PubMed] [Google Scholar]
- 33.Gentile M, Adrian T, Scheidler A, Ewald M, Dianzani F, Pauli G, Gelderblom H R. J Virol Methods. 1994;48:43–52. doi: 10.1016/0166-0934(94)90087-6. [DOI] [PubMed] [Google Scholar]
- 34.Liszewski M K, Farries T C, Lublin D M, Rooney I A, Atkinson J P. Adv Immunol. 1996;61:201–283. doi: 10.1016/s0065-2776(08)60868-8. [DOI] [PubMed] [Google Scholar]
- 35.Yamakawa M, Imai Y. Immunology. 1992;76:378–384. [PMC free article] [PubMed] [Google Scholar]
- 36.Zhang L, Ramratnam B, Tenner-Racz K, He Y, Vesanen M, Lewin S, Talal A, Racz P, Perelson A S, Korber B T, et al. N Engl J Med. 1999;340:1605–1613. doi: 10.1056/NEJM199905273402101. [DOI] [PubMed] [Google Scholar]
- 37.Furtado M R, Callaway D S, Phair J P, Kunstman K J, Stanton J L, Macken C A, Perelson A S, Wolinksy S M. N Engl J Med. 1999;340:1614–1622. doi: 10.1056/NEJM199905273402102. [DOI] [PubMed] [Google Scholar]
- 38.Szakal A K, Kosco M H, Tew J G. J Immunol. 1988;140:341–353. [PubMed] [Google Scholar]
- 39.Ling N R, Hardie D L, Johnson G D, MacLennan I C M. Clin Exp Immunol. 1998;113:360–366. doi: 10.1046/j.1365-2249.1998.00668.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Wickham T J, Shuler M L, Hammer D A. Biotechnol Prog. 1995;11:164–170. doi: 10.1021/bp00032a008. [DOI] [PubMed] [Google Scholar]
- 41.Goldstein B, Posner R G, Torney D C, Erickson J, Holowka D, Baird B. Biophys J. 1989;56:955–966. doi: 10.1016/S0006-3495(89)82741-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 42.Burton G F, Masuda A, Heath S L, Smith B A, Tew J G, Szakal A K. Immunol Rev. 1997;156:185–197. doi: 10.1111/j.1600-065x.1997.tb00968.x. [DOI] [PubMed] [Google Scholar]
- 43.Chun T-W, Fauci A S. Proc Natl Acad Sci USA. 1999;96:10958–10961. doi: 10.1073/pnas.96.20.10958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Goldstein B, Wofsy C. Immunol Today. 1996;17:77–80. doi: 10.1016/0167-5699(96)80583-4. [DOI] [PubMed] [Google Scholar]