Patterned library analysis: A method for the quantitative assessment of hypotheses concerning the determinants of protein structure

Abstract

Site-directed mutagenesis and combinatorial libraries are powerful tools for providing information about the relationship between protein sequence and structure. Here we report two extensions that expand the utility of combinatorial mutagenesis for the quantitative assessment of hypotheses about the determinants of protein structure. First, we show that resin-splitting technology, which allows the construction of arbitrarily complex libraries of degenerate oligonucleotides, can be used to construct more complex protein libraries for hypothesis testing than can be constructed from oligonucleotides limited to degenerate codons. Second, using eglin c as a model protein, we show that regression analysis of activity scores from library data can be used to assess the relative contributions to the specific activity of the amino acids that were varied in the library. The regression parameters derived from the analysis of a 455-member sample from a library wherein four solvent-exposed sites in an α-helix can contain any of nine different amino acids are highly correlated (P < 0.0001, R² = 0.97) to the relative helix propensities for those amino acids, as estimated by a variety of biophysical and computational techniques.

Site-directed mutagenesis (1) and combinatorial libraries (2–19) have been used to generate considerable information about the structure-determining elements in proteins. The fraction of variants in combinatorial libraries containing randomized residues (2–8) or residues constrained to be hydrophobic (9–15) that pass some test have been used as semiquantitative assessments of the role of the targeted residues or motifs. A more hypothesis-oriented approach used degenerate codons to construct binary or hydrophobic–hydrophilic patterns in library variants whose effects on protein structure could then be tested (16–19). However, only a limited number of types of hypotheses can be tested if one uses degenerate codons (codons with mixed nucleotides at one or more sites) to introduce variability into a library. We report here two tools to extend the range of hypotheses that can be quantitatively assessed with combinatorial libraries.

The first extension involves the use of resin-splitting technology (20) to facilitate the construction of arbitrarily complex libraries that are free of the constraints imposed by the genetic code. Libraries can be constructed so that all of their members conform to some hypothesis, and members can then be scored by some structurally related test. As in previous applications, the successful fraction of variants serves as a relative “score” of the hypothesis, but the arbitrarily complex nature of the hypotheses made possible by split-resin technology extends the range of what can be tested.

The second extension involves the use of regression analysis to expand the analytical power of combinatorial library experiments. In an ideal case, one would be able to assess a hypothesis concerning the determinants of protein structure by making a small number of carefully chosen mutations and determining the changes in protein stability. In reality, the change in stability that occurs on mutation at even the simplest sites depends on multiple factors. Regression analysis provides a well-developed formalism for the assessment of the contributions of multiple effects even in the context of the presence of unknown effects. Appropriate selection of the nature of variants in a combinatorial library and the use of regression analysis make possible the quantitative assessment of specific hypotheses and, by averaging over the effects of many factors, to extract accurate information regarding partial effects contributing to protein structure formation. Regression analysis can also be used to assess several competing hypotheses by using a single library, in contrast to the approach using the fraction of the library variants that remains active as the metric. Split-resin technology provides the means to attain adequate signal-to-noise ratio in the libraries such that regression analysis can be effective. Regression analysis provides access to new information by providing a formalism for the quantitative evaluation of the consequences of the effects defined in a hypothesis and a statistical assessment of the degree to which variant behavior can be attributed to them (21–23).

Materials and Methods

Reagents.

Coomassie Plus reagent was obtained from Pierce, Suc-Ala-Ala-Pro-Phe-pNA from Bachem, dibromomethane from Aldrich, restriction enzymes and ligase from New England Biolabs, Ni-NTA spin columns from Qiagen, and proteinase K from Qiagen.

Oligonucleotide Synthesis.

To synthesize the desired degenerate oligonucleotides, synthesis on a Beckman Oligo 1000 apparatus (Beckman Coulter) was interrupted at the positions of interest, the columns opened, and the resin removed into an isodense solution (dibromomethane plus 29.4% vol/vol acetonitrile) to facilitate apportioning. The resin was then allocated into empty Beckman synthesis columns and the appropriate codons added to the growing oligonucleotide chain. The columns were then reopened and the resin from the several columns mixed and returned to another column for continued synthesis. A metal clamp to hold the tops onto the used columns was fabricated to allow their reuse.

Library Construction.

A synthetic gene for eglin c was inserted into the pET28a (Novagen) expression vector, which adds a his-tag to the N terminus of eglin to aid purification (24). One PCR primer degenerate at the sites of interest and a second primer, both containing an EarI site on their 3′ ends, were used to amplify the entire wild-type eglin c template vector (pET28a). The amplified DNA was gel purified, cleaved with EarI, ligated with T4 ligase, and transformed into Escherichia coli NovaBlue (Novagen). Each library contained any of seven amino acids at four positions (22, 23, 26, and 27; all residue positions are with respect to the first codon in wild-type eglin c being position 1). The residues at the four variable positions in the libraries are in wild-type R, E, T, and L, respectively. Six of the seven amino acids were the same in all three libraries (K, Q, E, D, N, and H). Our sample from the library with P as the seventh amino acid contained 114 members, 32% of which have one or more prolines; our sample from the A library had 187 members, of which 33% contain at least one alanine; and our sample from the G library had 154 members, of which 63% have one or more glycines.

DNA Sequencing.

Two hundred eleven of the variants were sequenced in the University of North Carolina DNA sequencing facility from double-stranded DNA prepared by PCR from colonies of variants. For these variants, sequence was determined for the first 61 of the 76 codons of the his-tagged version of eglin c. The remaining 244 variants were sequenced from single-stranded DNA by using the dideoxy-termination method (Amersham T7 sequenase 2.0 sequencing kit). For these variants, sequence was read for codons 10 through 33.

Protein Preparation.

To obtain variant proteins for specific activity measurements, 1.5-ml cultures were grown in 2 × YT medium (per liter: 16 g trytone, 10 q yeast extract, 5 q NaCl and adjusted to pH 7.0 with NaOH), induced with 1-mM isopropyl-d-thiogalactoside for eglin expression at 0.6 OD₆₅₀, and incubated at 37°C for 2 hr. The cultures were then spun at 3,000 × g in a Beckman GM-3.8 horizontal rotor and the pellets harvested and frozen at −70°C. Cell pellets were later thawed at room temperature and resuspended in 1 ml of 50 mM Tris, pH 8.5. An equal volume of lysis buffer (50 mM Tris, pH 8.5/2% Tween 20/2 mg/ml lysozyme) was added and the mixture allowed to incubate for 20 min at room temperature. Viscosity was reduced by adding 1 M MgCl₂ to a final concentration of 10 mM and DNase to a final concentration of 13 units/ml. Debris was removed by centrifugation at 3,000 × g in a refrigerated centrifuge. NaCl (4 M) was added to the supernatant to a final concentration of 300 mM. This solution was added to Qiagen Ni-NTA spin columns prepared per manufacturer's directions, washed two times with 600 μl of 50 mM Tris, pH 6.4/300 mM NaCl, and eluted twice with 180 μl of 25 mM citrate, pH 4.5/300 mM NaCl, all by centrifugation at 700 × g, per the manufacturer's directions. The bulk of the purified protein elutes in the first fraction.

Relative Specific Activity Measurements.

These assays were carried out by using a Biomek 2000 robotic liquid handling apparatus (Beckman Coulter). Protein concentrations were determined by mixing 75 μl of sample with 75 μl of Coomassie Plus reagent in a 96-well plate. After 60 min of color development, the optical densities of the wells at 562 or 595 nm were determined by using a Molecular Devices 96-well plate reader. Values from triplicate aliquots were converted to μg/ml of eglin c from a standard curve of purified his-tagged wild-type eglin c assayed on the same plate.

Eglin c activity measurements were made by mixing 25 μl of various dilutions of the sample with 40 μl of proteinase K at 0.8 μg/ml in 50 mM Tris, pH 8.5. After a 10-min incubation at room temperature, 40 μl of substrate (Suc-Ala-Ala-Pro-Phe-pNA) at 0.6 mg/ml in 175 mM Tris, pH 8.5, was added. After 30 min of color development, the OD₄₀₅ of the sample was determined in a Molecular Devices 96-well plate reader. Activity (in wild-type equivalent micrograms) was determined by the dilution factor, giving rise to 50% of maximal color development referenced to a sample of purified his-tagged wild-type eglin at 50 μg/ml assayed on the same plate.

The relative specific activity was calculated by dividing the activity of the variant in wild-type eglin equivalent μg/ml by the protein concentration of the variant in wild-type eglin equivalent μg/ml. The detection limit of sensitivity of this measurement is 0.02 relative specific activity.

Regression Analyses.

Regression analyses were carried out with the jmp software package, ver. 3 (SAS Institute, Cary, NC).

Results and Discussion

To explore the utility of using split-resin technology to construct libraries of arbitrarily complex patterns, we asked whether “patterned” libraries, in which each library member conforms to some complex pattern or hypothesis, could be used to reproduce a known feature of helix stability, namely the intrinsic tendency of amino acids to adopt helical dihedral angles (α-helix propensities). We chose eglin c as our model protein because it is a small 70-residue protein with both an α-helix and a β-sheet and no cysteines. Its structure is known both from NMR (25) and x-ray crystallography (26), its denaturation thermodynamics is well defined (27, 28), and its structural homologue, CI-2, has proven to be a useful model protein for folding (29–31) and mutagenesis studies (32, 33). We also wanted a protein with a straightforward activity assay so that we could use high-throughput methods to monitor the consequences of mutation. Eglin c is a proteinase inhibitor that acts by binding very tightly to its target in the Michaelis complex (34). The proteinase-binding site is contained within a 10-aa loop that is on the opposite side of eglin from the α-helix that contains the mutated residues in our libraries (Fig. 1). Hence, it is plausible that substitutions in the helix might affect binding only via changes in stability.

Figure 1.

Ribbon diagram of eglin c. The proteinase-binding site in eglin c is contained within the 10-aa loop (Upper Left) of the diagram. The solvent-exposed residues in the α-helix that are varied in the libraries (R22, E23, T26, and L27) are shown in stick-ball format.

Percent-Passed Analysis.

To determine the feasibility of testing more complex patterns, made possible by split-resin technology, we constructed three libraries designed to test three hypotheses concerning α-helix propensity. Extensive studies on amino acid propensities in helices (35–41) indicate that variants with hydrophilic amino acids plus alanine substitutions at solvent-exposed sites (but not in the N-cap or C-cap) would do well, that variants with hydrophilic amino acids plus proline substitutions at those sites would do poorly, and that variants with hydrophilic amino acids plus glycine would be intermediate. Libraries that can test the effects of incorporating alanine, proline, or glycine into a common set of hydrophilic amino acids cannot be constructed by using degenerate codons. Using split-resin technology, we constructed libraries in which each variant in a given library has substitutions at four solvent-exposed positions in the eglin α-helix (Fig. 1). At each of the four positions, a variant could have any of seven different amino acids. Six of the amino acids (E, K, Q, D, N, and H) are hydrophilic and common to all three libraries. The seventh amino acid is P for one library, G for another, and A for the third.

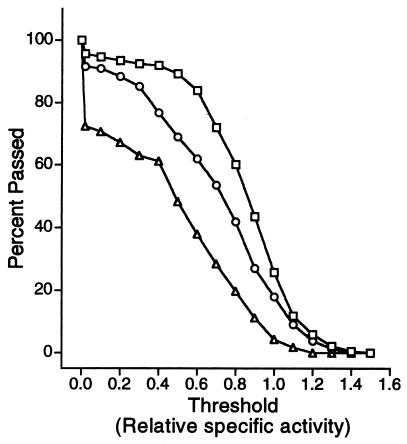
Transformants were selected from each library at random, DNA sequence from the eglin c coding region of each variant was collected to verify consistency with the library design, variant protein was purified by use of the N-terminal his-tag, and the relative specific activity of each variant was measured. We used the percent of each library that was active as the metric for the quality of the library and hence for the hypothesis that it encoded. Because the amount of activity that qualifies a variant as inactive is arbitrary, we measured the percent active by using successively higher values of activity as the threshold to determine whether a variant was active or inactive. This statistical device, called a survival curve, is used in many applications. Comparing the survival curves for the three libraries, we find that they order as expected (Fig. 2); for any activity threshold, the proline library has the smallest fraction above threshold, the glycine library a higher fraction, and the alanine library the highest. However, the glycine library has a larger fraction of variants containing the differential substituent. If a glycine library is constructed by removing, at random, enough glycine containers to match the other two libraries (33% glycine containers), then the glycine survival curve does not become distinguishable from the alanine library until a specific activity threshold of 0.75 is reached. Thus, for the four eglin helix positions, the use of alanine led to the highest “survival rate,” supporting the hypothesis that alanine stabilizes α-helices, whereas proline disrupts them.

Figure 2.

Percentage of variants in the libraries that have relative specific activities above a given threshold. The wild-type sequence is defined to have a relative specific activity of 1.00. The library with the six common hydrophilic residues and alanine, 187 members, is indicated with a (□); the hydrophilic residues plus glycine library, 154 members, (○); and hydrophilic residues plus proline, 114 members, (▵).

Regression Analysis: Intrinsic Helix Propensities.

Regression analysis tools can be used to extend the capacity to extract information from these libraries. The combined libraries comprise 455 variants whose specific activities span a 40-fold range. The size of this random sample, combined with the variance of their activities, affords an opportunity to go beyond the conclusions drawn from a percent-passed analysis and to assess the relative contributions to activity of all of the amino acids that were varied in the libraries. We turned to regression methods because many factors are thought to contribute to α-helix stability. Amino acids have different intrinsic tendencies to form helical dihedral angles (39–41); their sidechains interact differently with the helix macrodipole (42) as well as with each other (43–45); and certain combinations facilitate helix capping (46–51). Regression analysis gives an appropriate evaluation of parameters in a partially correct linear model, as long as the predictor variables are uncorrelated (23). Here we ask how well a model does that assumes: (i) that additivity is appropriate; (ii) that the four mutated positions are equivalent; and (iii) that the predictor variables (number of the amino acids in the four substitution sites) are not correlated with other effects. The regression model tested (Eq. 1) is that some

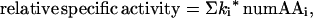1

portion of the response, here eglin relative specific activity, is a linear sum of effects from amino acids in the varied positions, where the parameter k_i represents the contribution of the ith amino acid type at any of the four positions to the activity of a variant and the predictor variable, numAA_i, represents the number of the ith amino acid type in the four substitution sites. That is, numAA_i ranges from 0 to 4, but the sum (Σ numAA_i) for a given variant must always equal four, making this a special kind of regression model, that is, a “mixture” model in which there is no intercept term (52). Least-squares minimization of the difference between predicted and measured relative specific activities generates estimates for the parameters k_i.

All of the parameters (Table 1) determined from the relative specific activity data for the combined libraries containing 455 variants have P values at least an order of magnitude smaller than that generally taken as a standard for significance (P < 0.05). The model as a whole is highly significant (P < 0.0001). As expected for a partial model for helix stability, the model does not account for all of the variance seen in the activities of the library members, accounting for only 31% of that variance. This observation illustrates one of the attractive features of regression analysis, that is, its capacity to give appropriate values for effects in the model even when other important effects are neglected. For example, in our collection of variants, we might expect to find mutations other than those introduced by design, but these adventitious mutations do not interfere with our capacity to evaluate the impact of the modeled effects. We estimate that the standard deviation for the specific activity measurements is 6.3%, the standard error of the mean is 2.6%, and the irreducible variance in our data, that is, the average difference in activity between variants with the same amino acid composition but different sequence, is 7.9%. This latter value is surprisingly small, given the fact that there are other known factors that impact on stability.

Table 1.

Regression analysis parameters for effects of amino acid composition in four helix sites on activity

Amino acid	ki	StdErr	P>|t|
K	0.248	0.020	<0.0001
E	0.233	0.016	<0.0001
A	0.217	0.034	<0.0001
Q	0.217	0.016	<0.0001
N	0.165	0.019	<0.0001
D	0.150	0.019	<0.0001
H	0.139	0.016	<0.0001
G	0.052	0.018	0.0051
P	−0.295	0.043	<0.0001

The parameter (k_i) represent the fraction of the relative specific activity contributed by that amino acid and hence are unitless. StdErr, estimate of the standard deviation of the distribution of the parameter estimate. P>|t|, is probability of getting an even greater t statistic given the hypothesis that the parameter is zero, that is, that there is no correlation between the particular amino acid composition and the relative specific activity. 

Two lines of evidence support the notion that these regression parameters represent helix propensities. First, they accurately reproduce similar estimates for helix propensities obtained by a variety of computational and biophysical methods. Second, they are quite robust, in that they do not vary significantly with the choice of data set or regression model.

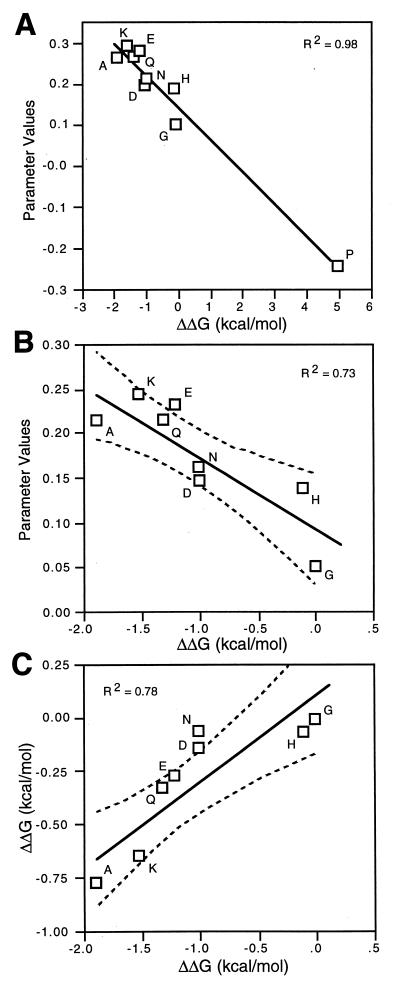
Our regression parameters correlate well (Fig. 3A) with the helix propensity values determined from physical measurements in host-guest experiments (P < 0.0001, R² = 0.98, ref. 38, and P < 0.0001 R² = 0.97, ref. 35). These physical measurements are based on the fraction of model peptides folded and the application of helix-coil transition theory. Our regression parameters also correlate well with propensity values derived from changes in the free energy of denaturation after mutating solvent exposed positions at internal sites in α-helices in globular proteins (P < 0.0001, R² = 0.97 barnase, ref. 43, and P < 0.0001, R² = 0.98 T4 lysozyme, ref. 38) and with propensities derived from statistical analyses (P < 0.0001, R² = 0.99, ref. 39).

Figure 3.

Correlation between intrinsic helix propensity values for amino acids determined by biophysical methods and by regression analysis of a patterned library. A compares the regression analysis parameters of all nine amino acids that were variant in our library with α-helical propensity values derived from biophysical measurements (guest-host experiments in alanine peptides) on peptides in aqueous solution (40). B compares regression parameter values of the variant amino acids minus proline with α-helical propensity values derived from biophysical measurements (40). C compares α-helical propensity values derived from biophysical measurements from the laboratories of Baldwin (40) and DeGrado (35). The solid lines have been fit by least squares, and the dotted curves represent the 95% confidence limits of the fit.

Although these correlations are as good as that obtained from comparing biophysical helix propensity data from different laboratories [e.g., comparing data from the DeGrado (35) and Baldwin (40) laboratories gives P < 0.0001, R² = 0.93], the correlations are dominated by a single point, the value for proline. However, the correlations between the propensity values for the eight nonproline residues, although lower (Fig. 3B), are also as good as the correlation between biophysical data from two different laboratories for those same eight amino acids (Fig. 3C). The probability of finding this level of correlation (for the eight amino acids) by chance in a population where there is no correlation between the parameters and activity is less than 1 in 10,000.

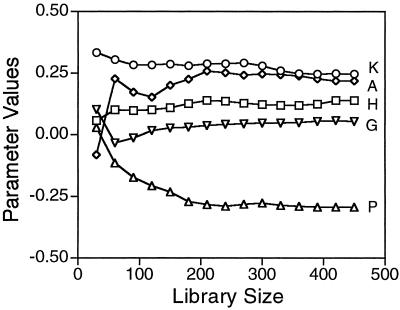
How robust are these regression parameters? We initially analyzed a subset of 192 variants using lysate activity instead of specific activity. Although the coefficient of variation of those activity measurements is large (30%), similar regression parameters were obtained (data not shown) as when we used specific activities. Analyzing subsets of the specific activity data shows that there is considerable fluctuation in the regression parameters until the size of the library analyzed reaches 200 to 300 variants (Fig. 4). The t test probability value for the regression parameters for E, K, D, and N goes below 5% after analyzing only 30 variants, the parameters for Q and H after 60, for P after 90, for A after 150, and for G not until 270 variants are analyzed. If the data are analyzed with a partial model containing only the six hydrophilic residues in common in the three libraries, then the six regression parameters correlate with an R² of 0.96 with those from the model with all nine variant residues. If the subset of 375 variants that have a relative specific activity of greater than 0.3 are analyzed separately, the regression parameters obtained correlate with an R² of 0.99 with those obtained from the complete data set, and the reduced data set accounts for about the same proportion of the variance.

Figure 4.

Regression parameters vs. library size. Regression parameters for the effects of nine variant amino acids were calculated for subsets of the libraries to determine how they varied as a function of library size. Five of the parameters covering the range of behaviors are shown. The subsets contained equal numbers of variants from the three libraries until a subset size of 360, at which point the 120 variants from the proline library were exhausted. The variants in the subsets were chosen in the order they were picked from the transformation plates.

Conclusions

Both the percent-passed and regression analysis approaches for utilizing patterned libraries to assess hypotheses concerning the determinants of protein structure reproduce the known effects of amino acid propensity on α-helix stability. However, regression analysis is less stringent in its requirements for use than the percent-passed approach. In the percent-passed approach, all of the members of the library must conform to the hypothesis to be tested and, as a consequence, only a single hypothesis can be tested per library. This requirement also places a serious burden on library construction to prevent the inclusion of variants that do not conform to the design criteria and to make sure that the various libraries to be compared have similar compositions. None of these constraints applies to regression analysis.

This use of regression analysis to assess the effects of helix propensity might suggest that randomized libraries would be more useful than patterned ones because, in our case, we might have been able to collect information about all 20 of the amino acids. However, one cannot explore all of the relevant sequence space in mutagenesis experiments. To achieve a useful signal-to-noise ratio, a library must contain a significant number of variants that satisfy the hypothesis if it is to be adequately tested by either percent-passed or regression analysis (Fig. 4). This is particularly true if the analysis is of effects that involve more than one residue, such as side-chain interaction effects. In such cases, the sample size necessary to contain enough of the hypothesis-testing variants to attain statistically significant results increases as the degree of patterning decreases.

Our quantitative analysis of patterned libraries extends the traditional anecdotal uses of mutagenesis to test hypotheses. Traditionally, one uses the functionality of variants to confirm the capacity of a hypothesis to predict variant behavior, whereas unexpected variant behavior suggests the need for modified hypotheses. The percent-passed approach reformulates the former analysis in more quantitative terms. The regression model approach provides access to new information by providing a formalism for quantitative expression of effects in a hypothesis and a statistical assessment of the degree to which variant behavior can be attributed to them. In our case, these proof-of-principle experiments produce an independent and reliable index of helix propensities, by virtue of the ability of randomized sampling to average over the effects of potentially confounding effects, correctly revealing partial contributors to helix stability. It is impressive that the simplified model tested, a model without position effects or side-chain interaction effects, can accurately reproduce stability-based helix propensity values.

In addition to quantifying the predictive power of the hypothesis, regression analysis also identifies variants whose behavior deviates from the hypothesis expressed in the model, that is, those with large differences between observed and calculated behavior. These outliers are a rich source of new indications on which the iteration of hypothesis generation, testing, and revision depends.

Studies of the effects of amino acids in a model protein are always subject to the idiosyncratic features of that protein. Nevertheless, there are contexts where it is useful to determine the idiosyncratic properties for their own sake. For example, threading algorithms are often designed to utilize idiosyncratic features of the target protein to assess the likelihood that a different sequence is compatible with the target fold. That is, a context is defined for a given residue, and probability tables are derived for the amino acids within that idiosyncratic context (53). The results presented here suggest that the analysis of patterned libraries will provide an additional tool for the determination of those probability tables.

Intrinsic α-helix propensity values have been previously derived from several different types of studies. The free energies from various biophysical analyses of peptides (35, 36, 40) and model proteins (38, 43, 48) and the pseudo-energy terms derived from statistical analyses of the protein database (39) agree remarkably well (41, 45). Parameters derived from our analyses of patterned libraries correlate with these previously derived values to the same degree that the previously derived values correlate with each other. This agreement encourages us to believe that our approach can provide quantitative assessments of many hypotheses about the relations between amino acid sequence, stability, and structure.