Abstract
We consider general fluctuating copolymerization processes, with or without underlying templates. The dissipation associated with these nonequilibrium processes turns out to be closely related to the information generated. This shows in particular how information acquisition results from the interplay between stored patterns and dynamical evolution in nonequilibrium environments. In addition, we apply these results to the process of DNA replication.
Keywords: DNA replication, entropy production, nonequilibrium fluctuations, self-organization
The origin of biological information is one of the major challenges for our understanding of living organisms. Since the discovery of DNA, the biochemical support for the storage of genetic information has been known. DNA is a copolymer that keeps the memory of information on the living organism in its structure. This molecular structure is stable at ambient temperatures because of the binding energy between the nucleotides, allowing the heredity of genetic information across generations. As observed in vitro in evolution experiments on RNA and viruses (1, 2), the processing of biological information can be discussed in terms of the dynamics of populations associated with the different possible genetic sequences, the populations evolving by replications and mutations into quasispecies (3, 4). Such population dynamics are nonequilibrium processes where dissipation is compensated by energy supply, and the entropy produced by dissipation is evacuated to the environment of these open systems. However, this view relies on macroscopic concepts such as population size, which are largely separated from the nanoscale of the genetic sequences. Moreover, observations reveal that biological systems have structures and functions at every scale down to the molecular level, and the understanding of their origin is a challenge.
Actually, the information in DNA copolymers is processed and replicated by mechanisms taking place at the molecular level in the presence of thermal fluctuations. These fluctuations are due to the random motion of the atoms and molecules composing DNA, the transcription or replication machinery, and their environment. In this regard, biological information processing is ruled by the statistical laws of motion and thermodynamics. At thermodynamic equilibrium, the principle of detailed balance implies that no information can be spontaneously processed or generated because each random motion is statistically balanced by the corresponding reverse motion. Therefore, equilibrium is the stage of erratic motion where information generation is highly improbable.
Recently, it has been shown that nonequilibrium fluctuating systems present a time asymmetry in which the typical random paths followed by the system during its time evolution turn out to be more probable than their time reversal (5–8). The remarkable result is that this temporal ordering of nonequilibrium fluctuations is the consequence of the second law of thermodynamics. This phenomenon explains that dynamical order can be naturally generated in molecular motion under nonequilibrium conditions.
The goal of this article is thus to show that the implication of this nonequilibrium temporal ordering in copolymerization processes is the generation of information. Indeed, copolymerization can store in space the dynamical order that is generated in time by nonequilibrium processes, establishing a coupling from time back to the spatial support of information. The possibility of such transfers of information has already been envisaged at the macroscopic level (9) and is here shown to arise at the molecular level. With this aim, we study copolymerization processes with or without the presence of an underlying template. Such processes have the ability to store information in the copolymer pattern, which in turn, influences the dynamics of the system. Information generation can thus be understood as a natural consequence of driving out of equilibrium systems with the ability to store and retrieve molecular information.
We first explain the tradeoff between dissipation and information in copolymerization processes in the framework of nonequilibrium statistical thermodynamics. We then proceed with the illustration of these results in the case of DNA replication.
Dissipation–Information Tradeoff
Copolymerization processes can be described at the macroscopic level in terms of population sizes, i.e., the chemical concentrations of the monomers, dimers, trimers, etc. In this macroscopic description, the rate of dissipation, in particular, due to metabolism can be estimated by the thermodynamic entropy production given in terms of the chemical concentrations (10). Because we are interested in the molecular structure generated during copolymerization, we adopt a mesoscopic description at the scale of a single copolymer chain.
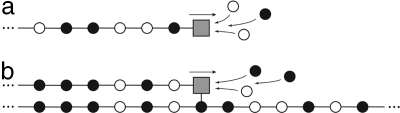
We first consider a copolymerization process without template and with M different monomers (see Fig. 1a). We denote by ω a copolymer chain of finite length surrounded by a solution containing monomers m at given concentrations. The solution surrounding each single copolymer chain is assumed to be sufficiently large to play the role of a reservoir that is continually replenished with new monomers so as to keep their concentrations fixed. In this situation, an arbitrary chain ω can grow by adding a monomer m: ω+ m → ωm. This copolymerization step is driven by the free-enthalpy change of the reaction. If the latter is high enough, the monomers attach to but never detach from the chain, and the process is totally irreversible. For instance, if the binding rates k+m only depend on the monomer m added to the chain, the growth proceeds by the random addition of monomers at the velocity v = Σm k+m. The insertion probabilities are here given by ηm = k+m/Σn k+n, showing that the chain may be disordered because of the multiplicity of the monomer species composing the copolymer. However, such totally irreversible processes could only happen in the extreme case where the copolymerization is driven arbitrarily far from equilibrium. In general, the free-enthalpy differences between the reactants ω + m and the products ωm are finite and reversed reactions are possible. Accordingly, the chain ω may grow not only by the addition of monomers but also shorten by removing the last monomer m of the actual chain: ω + m 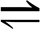 ωm. The closer to equilibrium the process is, the more probable the reversed reactive events are. Consequently, the configurational disorder of the chain can be larger if it is grown under low driving forces in the vicinity of the thermodynamic equilibrium.
ωm. The closer to equilibrium the process is, the more probable the reversed reactive events are. Consequently, the configurational disorder of the chain can be larger if it is grown under low driving forces in the vicinity of the thermodynamic equilibrium.
Fig. 1.
Schematic representations of a copolymerization process without a template (a) and a copolymerization process with a template (b). The circles depict the monomers and the square depicts the catalyst of polymerization.
The general framework to study such processes is provided by the stochastic theory of nonequilibrium processes (11, 12). At the mesoscopic level, many phenomena such as nonequilibrium reactions are successfully described in terms of continuous-time random processes. In this framework, the probability Pt(ω) to find the copolymer chain ω at time t is ruled by the evolution equation:
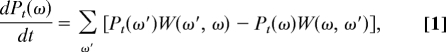 |
where the coefficients W(ω, ω′) denote the rates of the transitions ω → ω′ (11, 12). For many processes at fixed pressure and temperature T, the ratio of forward-to-backward transition rates can be expressed in terms of the free enthalpy G(ω) of a single copolymer chain ω surrounded by the solution, according to
where kB is Boltzmann's constant (13). We notice that the transition rates W(ω, ω′) as well as the free enthalpies G(ω) will in general depend on the concentrations of monomers m in the solution surrounding the chain ω (11–13).
A key concept for our purposes is the thermodynamic entropy of the system:
where S(ω) is the entropy of the copolymer chain ω in solution (14). The entropy (Eq. 3) varies in time with the probability distribution ruled by the evolution equation (Eq. 1). It is known that these variations dS/dt are due to both the exchange of entropy with the environment deS/dt and the internal production of entropy
which is always nonnegative, in agreement with the second law of thermodynamics (11, 12, 15). The exchange of entropy is given by
in terms of the time variation of the mean enthalpy of the system: 〈H〉t = Σω Pt(ω)H(ω) (14, 15). The enthalpy H(ω) of the copolymer ω is related to the corresponding free enthalpy and entropy by G(ω) = H(ω) − TS(ω). We notice that the exchange of entropy during the time interval Δt is equal to the heat of copolymerization Δ〈H〉 over the temperature T according to ΔeS = Δ〈H〉/T.
It is assumed that, for fixed concentrations of monomers, the growth process can go on without limit and possibly reach a regime where the synthesized copolymer has stationary statistical properties (16, 17). In such a stationary regime, the mean length of the chains grows at some fixed average velocity
The mean length is evaluated as 〈l〉t = Σl pt(l) × l in terms of the probability distribution pt(l) of the chain lengths l at time t. The statistical composition of the copolymer in the stationary regime is described by the probability distribution μl(ω) to have a chain ω, provided that its length is l. This distribution is normalized as Σωμl(ω) = 1, where the sum is restricted to all of the chains ω of length l. Accordingly, the probability to have a certain chain ω at time t becomes
in the stationary regime (16, 17).
The entropy (Eq. 3) can thus be rewritten as
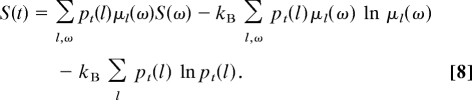 |
The first term is the contribution from the thermodynamic entropy S(ω) of the copolymer ω in its environment. In the stationary regime, we may introduce the mean entropy per monomer as
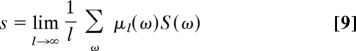 |
so that the first term becomes 〈l〉t × s, in the long-time limit.
The second term in Eq. 8 can be expressed in terms of the disorder in the composition of the copolymer. This disorder can be characterized by the Shannon entropy per monomer defined as
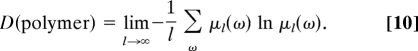 |
The disorder takes a value in the range 0 ≤ D ≤ ln M limited by the number of different monomers composing the copolymer. In the stationary regime, the second term is thus controlled by the disorder in the chain because
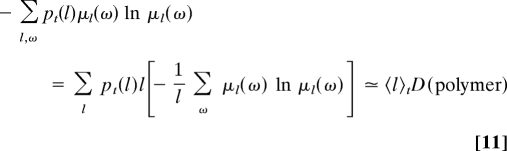 |
at long times.
The third term in Eq. 8 is the Shannon entropy of the distribution of lengths. This distribution broadens in time, and its entropy typically increases logarithmically in time. Accordingly, this term does not contribute to the variation rate of the entropy because limt→∞(−1/t)Σlpt(l) ln pt(l) = 0.
Hence, we find that the time variation of the entropy is given in the stationary regime by
with the growth velocity (Eq. 6) and physical units where kB = 1 used for the simplicity of notations. On the other hand, the entropy exchange rate (Eq. 5) is equal to
where the mean enthalpy per monomer h has a definition similar to Eq. 9. Finally, the entropy production (Eq. 4) reads
with the growth velocity (Eq. 6) and the thermodynamic force or affinity per monomer
where g = h − Ts is the free enthalpy per monomer, and ε = −g/T is the mean driving force. We note that these results do not depend on the specific choice of transition rates so that they are general in this respect. In the case where the growth velocity is positive, the affinity (Eq. 15) can be interpreted as the entropy production per added monomer. The affinity has two contributions: the first from the driving force ε given in terms of the mean free enthalpy of copolymerization and the second due to the disorder (Eq. 10) of the monomers in the chain. This shows in particular that the copolymer can grow by an entropic effect of disorder even when the driving forces are slightly negative. Indeed, the randomness incorporated in the chain has a non-negative contribution in the form of the disorder (Eq. 10) to the thermodynamic force or affinity per monomer (Eq. 15), showing how the stored pattern can influence back the dynamics of the system. Equilibrium occurs when the affinity (Eq. 15) vanishes, Aeq = 0, so that the mean driving force is equal to minus the equilibrium disorder. In this case, no systematic growth is possible, and each monomer appears with its equilibrium distribution.
In general, the transition rates W(ω, ω′) depend on the structure and composition of the whole chain ω so that nonlocal or cooperative effects can generate long-range correlations along the chain, thereby reducing the disorder (Eq. 10). However, in many cases, the transition rates only depend on the few monomers at the end of the chain, in particular, if the copolymerization process is mainly controlled by the free-enthalpy changes of bond formation in the reactions ω+ m 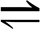 ωm. In the most local process, the transition rates only depend on the last monomer m, which is added to or removed from the chain. In this case, the transition rates are denoted as W(ω, ωm) = k+m and W(ωm, ω) = k−m, and the quantities
ωm. In the most local process, the transition rates only depend on the last monomer m, which is added to or removed from the chain. In this case, the transition rates are denoted as W(ω, ωm) = k+m and W(ωm, ω) = k−m, and the quantities
represent the driving forces favoring the chain growth. They are given by the free-enthalpy changes of the chemical reactions and are measured in units of the thermal energy: εm = [G(ω) − G(ωm)]/(kBT). In this respect, the driving forces incorporate the chemical potentials of the monomers so that they can be varied by changing control parameters such as the chemical concentrations of the different monomers in solution around the copolymer chain.
Under the assumption of Eq. 16, the mean value of the driving forces can be calculated as ε = Σm μ1(m) εm by averaging them over the normalized distribution μ1(m) of monomers. If we further assume that there is no free-enthalpy difference between the chains ωm, the driving forces are equal to each other, εm = ε for all m, whereupon equilibrium occurs when the driving force takes the value εeq = −ln M, and the disorder reaches its maximum value Deq = ln M. On the other hand, we notice that, for given positive values of the thermodynamic entropy production and the growth velocity, the disorder can be reduced at the expense of the driving force ε according to Eq. 15. Moreover, in the limit of an arbitrarily high driving force ε, no detachment of monomers occurs, and the disorder reaches the value D = −Σm ηm ln ηm, which is typically smaller than the equilibrium disorder Deq. Therefore, the nonequilibrium drive may contribute to some extent to the ordering of the copolymer.
We next consider a copolymerization process under the influence of a template, which determines the probabilities to add or remove monomers (see Fig. 1b). This is typically the case during DNA transcription or replication processes where the DNA sequence influences the probabilities to add the monomers, favoring the Watson–Crick pairing rule A-T and C-G. The template is thus composed of a chain α = α1 α2… αl…., and the transition rates now depend on this underlying substrate: W(ω, ω′∣α). In this case, the previous considerations are modified in the following way. The entropy (Eq. 3), the velocity (Eq. 6), and the mean driving force are now averaged not only over the distribution of monomers but also over the template. We suppose that the template is described by a stationary distribution νl(α) = νl(α1α2… αl), which is normalized to unity Σανl(α) = 1 for all of the chains of length l. In the stationary regime, the probability to have a chain ω at time t here takes the form
at long times, where μl (ω∣α) is the distribution of chains ω of length l grown on the template α. We expect that the template ensemble average corresponds to the average over a typical realization of the template sequence. We can here also introduce the mean entropy (Eq. 9) and enthalpy per monomer by averaging over the template. The growth speed (Eq. 6) is now obtained with a long typical sequence of the template.
On the other hand, the disorder (Eq. 10) now becomes the Shannon conditional entropy of the copolymer with respect to the template:
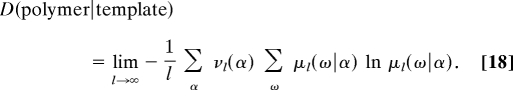 |
The conditional entropy between two random variables can also be expressed in terms of the mutual information I(X, Y) = D(X) − D(X∣Y) between the two variables (18). The mutual information is bounded according to 0 ≤ I(X, Y) ≤ min{D(X), D(Y)} and measures how much the knowledge on one of these variables reduces the uncertainty about the other. It is zero when the two variables are independent so that we recover the previous results (Eq. 10) and (Eq. 15) when the substrate does not influence the copolymerization process. Accordingly, the affinity here becomes
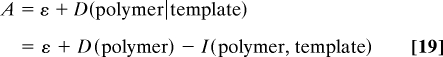 |
and is thus directly expressed in terms of the mutual information that the copolymer acquires from its template or more generally from its environment. The mean driving force is given by ε = −g/T as in Eq. 15.
To be specific, we can take transition rates of the form W(ω, ωm∣α) = k+mn and W(ωm, ω∣α) = k−mn if n = αl+1 is the template at the position l + 1, and ω is a chain of length l. The corresponding driving forces
now depend on the substrate as well. Accordingly, in the case of Eq. 20, the mean driving force is given by ε = Σm,nν1(n)μ1(m∣n)εmn, where ν1(n) is the distribution of monomers on the template.
If the copolymer grows, and v > 0, the affinity is the entropy production per added monomer so that Eq. 19 shows that substantial information can be generated if the mean driving force ε is large enough. We illustrate this fundamental result with DNA replication in the next section.
DNA Replication
In this section, we consider the process of DNA replication. In this case, the subunits of the growing polymer and the template are the four nucleotides n = A, T, C, or G. The monomers are the corresponding nucleoside triphosphates NTP, which drive the reaction by their high free enthalpy relative to the linked nucleotides. It turns out that the DNA polymerase copies the DNA with a fairly small error rate. In the actual DNA replication, an exonuclease will act as a proofreading mechanism to correct possible errors. Proofreading allows one to decrease the error rate up to the discrimination squared (19–21). This mechanism can be modeled by considering several reactions ρ during the copolymerization, namely Wρ(ω, ω′∣α). These additional pathways will change the average driving force and speed, but the disorder (Eq. 18) will remain unchanged for a given distribution of nucleotides.
To analyze purely kinetic effects, we will assume in the following that no free-enthalpy difference exists between correct and incorrect chains, implying εmn = ε. We will thus consider the different effects as a function of this parameter. The transition rates and the driving forces (Eq. 20) incorporate external conditions such as the chemical concentrations of the nucleotides, the polymerase cofactors, and the products of the polymerization. Accordingly, the driving force ε will typically be a function of such control parameters.
For concreteness, we consider the case of the DNA polymerase Pol γ, which replicates the human mitochondrial DNA. Forward kinetic constants for the incorporation of both correct and incorrect nucleotides are available (22), and we used these for our simulations. The human mitochondrial DNA is 16.5 kb long and can be obtained from GenBank (23). To have a good statistical estimation of the disorder (Eq. 18), we used longer DNA sequences generated from the same triplet distribution as the original mitochondrial DNA. Random trajectories corresponding to the master equation (Eq. 1) are obtained with Gillespie's algorithm (24).
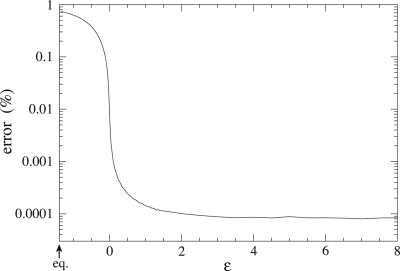
Because we assumed no free-enthalpy difference between the chains, equilibrium occurs when ε = −ln 4, where each nucleotide is inserted with equal probability regardless of the underlying template. Therefore, at equilibrium, the velocity and the mutual information vanish, and the error rate is 0.75.
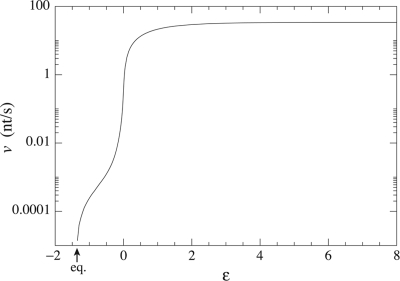
In Fig. 2, we depict the fraction of errors as a function of the driving force and, in Fig. 3, the velocity of the replication process. The key result is that the fraction of errors is a decreasing function of the driving force. The minimal error rate one can achieve is given in terms of the probability ηmn = k+mn/Σmk+mn for a base m on a template n and occurs in the infinite dissipation limit, i.e., the limit ε → ∞. Nucleotides are then inserted with rates k+mn but never detach, as shown by Eq. 20. Fig. 2 illustrates the important point that polymerases must operate far from equilibrium to achieve a high fidelity in the replication of DNA information; the same observation is expected for various biological entities that must present coherent space–time behaviors, such as molecular motors. The velocity increases with the driving force, reaching a maximal speed given by vmax−1 = Σn ν1(n)/(Σm k+mn), which is here of ≈34 bases per second. Also, both the velocity and the error rate undergo a steep transition as the driving force ε becomes positive.
Fig. 2.
Percentage of misincorporations as a function of the driving force ε. The minimal error rate is given by 1 − νA ηTA − νTηAT − νCηGC − νGηCG ≃ 8.3 10−5. The maximal error rate occurs at equilibrium where detailed balance conditions are satisfied, according to which each nucleotide insertion is balanced by its removal from the chain. Under this condition, and if εmn = ε for all m and n, every nucleotide is included with equal probability, and the error rate is 0.75. The kinetic constants of Watson–Crick pairing are taken to be k+TA = 25 s−1, k+AT = 45 s−1, k+GC = 37 s−1, and k+CG = 43 s−1 (22). The discrimination between the nucleotide m and the template n is defined as dmn = k+mn/k+rn, where r denotes the “correct” nucleotide forming the Watson–Crick pair rn with the template nucleotide n. The discriminations take the values dAA = dAG = dGA = 1/280,000, dCA = 1/210,000, dTT = 1/250,000, dCT = 1/570,000, dGT = 1/3,600, dAC = 1/71,000, dTC = 1/640,000, dCC = 1/2,300,000, dTG = 1/59,000, and dGG = 1/110,000. The reversed kinetic constants are taken as k−mn = k+mne−ε according to Eq. 20, with εmn = ε incorporating the monomer concentrations (see text section on dissipation-information trade off).
Fig. 3.
Velocity of the replication process as a function of the driving force ε. The maximal speed is given by ≈34 nt/s as explained in the text section on DNA replication.
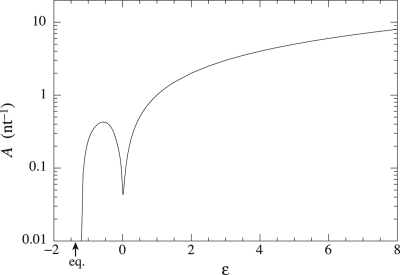
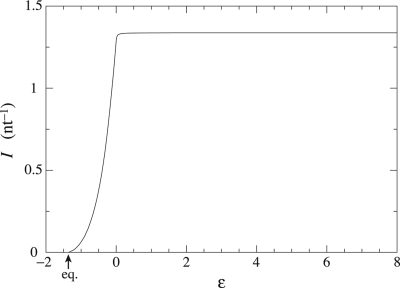
In Fig. 4, we represent the affinity (Eq. 15) per copied nucleotide, which gives the corresponding entropy production because the growth velocity is here positive. This curve is nonmonotonic and presents a minima around ε ≃ 0.015. On the left-hand side of it, the external driving force is weak or negative and dissipation occurs chiefly because of the positive driving caused by the incorporation of errors, whereas, on the right-hand side, dissipation is mainly due to the external driving force. This transition corresponds to the sharp behavior observed in the error rate and in the velocity of the process. The same behavior is also observed in the mutual information I between the original and the copied DNA strands, as depicted in Fig. 5. It increases with the driving force, nearly reaching its maximal value Imax = Σm,n ηmnν1(n) ln [ηnm/Σn ηmnν1(n)] ≃ 1.337 nats after the threshold point. Afterward, nearly all of the original information has been acquired. The result is that the increase of mutual information corresponds to a reduction of disorder and allows fidelity in the transfer of information. Contrary to the situation at equilibrium where this transfer is not possible, the nonequilibrium conditions turn out to induce the generation of mutual information.
Fig. 4.
Affinity per copied nucleotide as a function of the driving force ε. The local minimum is approximately ε ≃ 0.015 and indicates the transition between the error driven regime and the externally driven regime. Because the growth speed is positive, this affinity is the entropy production per copied nucleotide.
Fig. 5.
Mutual information between the copied DNA strand and the original strand as a function of the driving force ε. The saturation occurs after the transition between the error-driven and the externally driven regimes. The value of the mutual information at saturation is Imax ≃ 1.337 nats.
Conclusions
In this article, we have developed the nonequilibrium statistical thermodynamics of copolymerization processes, delineating the role of configurational disorder in copolymer chains. The latter plays the role of a positive driving force favoring the copolymer's growth. In particular, disorder arises from the intricate interplay between fluctuations and nonequilibrium conditions, reaching its minimal value in the infinite dissipation limit. Furthermore, we have shown how information can be generated out of equilibrium in these fluctuating processes. In this regard, we have observed a transition between two regimes. At small or negative external driving forces, the growth process is essentially driven by the incorporation of errors in the copolymer chain, whereas, beyond a threshold, it is driven by free-enthalpy sources. After this transition point, it turns out that the extra dissipation does not lead to a substantial increase in the fidelity of the replicated strands, as measured by the error rate or the mutual information between the original and the copied DNA strand. Information acquisition thus appears to have an energy cost analogous to information erasure (25–27). Similar or enhanced effects are expected in the presence of autocatalysis (10), possibly, with different dependences on control parameters.
Albeit the results apply to every copolymerization process, they are fundamental for DNA replication and transcription and the understanding of information acquisition by biological entities. Biological systems are characterized by several properties such as metabolism and self-reproduction. Each of them can be said to be encoded in the genetic code. Whereas metabolism refers to nonequilibrium thermodynamics, self-reproduction involves information processing. The present work establishes an essential connection between both properties on the basis of nonequilibrium statistical thermodynamics. In this perspective, dissipation allows the emergence of temporal ordering and the spontaneous generation of information, explaining in this way a key feature of complex systems (28). Information generation can thus be understood as resulting from the reduction of disorder in copolymers growing out of equilibrium and the ability to store and retrieve information in nonequilibrium environments. If, furthermore, this information can be copied and processed back by the nonequilibrium dynamics of the system, the self-reproduction of biological systems could be explained. From this viewpoint, we could say that biological systems are physicochemical systems with a built-in thermodynamic arrow of time.
Acknowledgments.
The authors are grateful to G. Nicolis and R. Thomas for helpful comments and discussions. D.A. thanks the FRS–Fonds National de la Recherche Scientifique, Belgium, for financial support. This work was supported by the Belgian Federal Government (Interuniversity Attraction Poles project “NOSY”) and the “Communauté Française de Belgique” (contract “Actions de Recherche Concertées” 04/09-312).
Footnotes
The authors declare no conflict of interest.
This article is a PNAS Direct Submission.
See Commentary on page 9451.
References
- 1.Mills DR, Peterson RL, Spiegelman S. An extracellullar Darwinian experiment with a self-duplicating nucleic acid molecule. Proc Natl Acad Sci USA. 1967;58:217–224. doi: 10.1073/pnas.58.1.217. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Biebricher CK, Gardiner WC. Molecular evolution of RNA in vitro. Biophys Chem. 1997;66:179–192. doi: 10.1016/s0301-4622(97)00059-8. [DOI] [PubMed] [Google Scholar]
- 3.Eigen M, Schuster P. The Hypercycle—A Principle of Natural Self-Organization. Heidelberg: Springer; 1979. [DOI] [PubMed] [Google Scholar]
- 4.Eigen M. Steps Towards Life: A Perspective on Evolution. Oxford: Oxford Univ Press; 1992. [Google Scholar]
- 5.Gaspard P. Time-reversed dynamical entropy and irreversibility in Markovian random processes. J Stat Phys. 2004;117:599–615. [Google Scholar]
- 6.Gaspard P. Temporal ordering of nonequilibrium fluctuations as a corollary of the second law of thermodynamics. C R Phys. 2007;8:598–608. [Google Scholar]
- 7.Andrieux D, et al. Entropy production and time asymmetry in nonequilibrium fluctuations. Phys Rev Lett. 2007;98:150601. doi: 10.1103/PhysRevLett.98.150601. [DOI] [PubMed] [Google Scholar]
- 8.Andrieux D, et al. Thermodynamic time asymmetry in non-equilibrium fluctuations. J Stat Mech. 2008 P01002. [Google Scholar]
- 9.Nicolis G, Subba Rao G, Subba Rao J, Nicolis C. Generation of spatially asymmetric, information-rich structures in far from equilibrium systems. In: Christiansen PL, Parmentier RD, editors. Structure, Coherence and Chaos in Dynamical Systems. Manchester, UK: Manchester Univ Press; 1989. pp. 287–299. [Google Scholar]
- 10.Goldbeter A, Nicolis G. Far from equilibrium synthesis of small polymer chains and chemical evolution. Biophysik. 1972;8:212–226. [Google Scholar]
- 11.Schnakenberg J. Network theory of microscopic and macroscopic behavior of master equation systems. Rev Mod Phys. 1976;48:571–585. [Google Scholar]
- 12.Nicolis G, Prigogine I. Self-Organization in Nonequilibrium Systems. New York: Wiley; 1977. [Google Scholar]
- 13.Hill TL. Free Energy Transduction and Biochemical Cycle Kinetics. New York: Dover; 2005. [Google Scholar]
- 14.Gaspard P. Fluctuation theorem for nonequilibrium reactions. J Chem Phys. 2004;120:8898–8905. doi: 10.1063/1.1688758. [DOI] [PubMed] [Google Scholar]
- 15.Luo J-L, Van den Broeck C, Nicolis G. Stability criteria and fluctuations around nonequilibrium states. Z Phys B. 1984;56:165–170. [Google Scholar]
- 16.Coleman BD, Fox TG. General theory of stationary random sequences with applications to the tacticity of polymers. J Polym Sci A. 1963;1:3183–3197. [Google Scholar]
- 17.Coleman BD, Fox TG. Multistate mechanism for homogeneous ionic polymerization. I. The diastereosequence distribution. J Chem Phys. 1963;38:1065–1075. [Google Scholar]
- 18.Chaitin GJ. Toward a mathematical definition of “life”. In: Levine RD, Tribus M, editors. The Maximum Entropy Formalism. Cambridge, MA: MIT Press; 1979. pp. 477–498. [Google Scholar]
- 19.Hopfield JJ. Kinetic proofreading: A new mechanism for reducing errors in biosynthetic processes requiring high specificity. Proc Natl Acad Sci USA. 1974;71:4135–4139. doi: 10.1073/pnas.71.10.4135. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ninio J. Kinetic amplification of enzyme discrimination. Biochimie. 1975;57:587–595. doi: 10.1016/s0300-9084(75)80139-8. [DOI] [PubMed] [Google Scholar]
- 21.Bennett CH. Dissipation-error tradeoff in proofreading. Biosystems. 1979;11:85–91. doi: 10.1016/0303-2647(79)90003-0. [DOI] [PubMed] [Google Scholar]
- 22.Lee H, Johnson K. Fidelity of the human mitochondrial DNA polymerase. J Biol Chem. 2006;281:36236–36240. doi: 10.1074/jbc.M607964200. [DOI] [PubMed] [Google Scholar]
- 23. Homo sapiens DNA mitochondrion, 16569 bp, locus AC 000021, ver. GI:115315570, http://www.ncbi.nlm.nih.gov.
- 24.Gillespie DT. A general method for numerically simulating the stochastic time evolution of coupled chemical reactions. J Comp Phys. 1976;22:403–434. [Google Scholar]
- 25.Landauer R. Irreversibility and heat generation in the computing process. IBM J Res Dev. 1961;5:183–191. [Google Scholar]
- 26.Bennett CH. The thermodynamics of computation—A review. Int J Theor Phys. 1982;21:905–940. [Google Scholar]
- 27.Andrieux D, Gaspard P. Dynamical randomness, information, and Landauer's principle. Europhys Lett. 2008;81:28004. [Google Scholar]
- 28.Nicolis G, Nicolis C. Foundations of Complex Systems. Singapore: World Scientific; 2007. [Google Scholar]