Pairwise-additive hydrophobic effect for alkanes in water

Abstract

Pairwise additivity of the hydrophobic effect is indicated by reliable experimental Henry's constants for a large number of linear and branched low-molecular-weight alkanes in water. Pairwise additivity suggests that the hydrophobic effect is primarily a local phenomenon and that the hydrophobic interaction may be represented by a semiempirical force field. By representing the hydrophobic potential between two methane molecules as a linear function of the overlap volume of the hydration layers, we find that the contact value of the hydrophobic potential (−0.72 kcal/mol) is smaller than that from quantum mechanics simulations (−2.8 kcal/mol) but is close to that from classical molecular dynamics (−0.5∼−0.9 kcal/mol).

Some of the unusual properties of liquid water are intimately affiliated with a dynamic network of hydrogen bonds among water molecules (1–4). A prominent example is the hydrophobic effect that arises from a subtle variation of the hydrogen-bonding network near a nonpolar solute molecule such as a hydrocarbon (5–9). Although the hydrophobic effect has received much attention because of its important role in the function of aqueous biomacromolecules such as lipids and proteins, some aspects of the hydrophobic phenomenon remain poorly understood. Toward improved understanding, we have carefully analyzed reliable experimental Henry's constants for short alkanes in water. Our results supplement and, in part, support the comprehensive discussion by Chandler (7, 10).

Henry's constant for a nonpolar solute is directly related to the free energy of solvation, that is, the reversible work to transfer a solute molecule from an ideal gas to water. At low pressure, the solubility of a nonpolar gas in water is determined by a thermodynamic relation that governs the equilibrium between an ideal gas (IG) and an ideal liquid solution (IS), that is,

where μ stands for the chemical potential. For the solute in the ideal-gas phase,

and for the solute in the liquid solution,

where ρ denotes the number density of solute molecules, subscripts “G” and “S” denote the gas and liquid solution, respectively; k_B is the Boltzmann constant; T is temperature; and μ₀ is the chemical potential of the solute at an appropriate reference state.

The free energy of solvation for a nonpolar molecule, F_s, is associated with the interaction of a single solute molecule with its surrounding water, averaged over all possible molecular configurations of the solvent:

where ΔE represents the interaction energy of the solute molecule with all water molecules in the system and 〈⋯〉₁ denotes the ensemble average over the microstates of all water molecules.

According to Eqs. 1–4, the free energy of solvation, F_s, is related to the Ostwald coefficient, that is, the number density of the solute in the aqueous solution divided by that in the gas. Because the Ostwald coefficient is, in turn, related to Henry's constant, the free energy of solvation can be calculated from

where Henry's constant H_2,1 is in units of mol·liter⁻¹·atm⁻¹, subscript 2 stands for the solute and subscript 1 stands for water, and R = 0.082 liter·atm·mol⁻¹·K⁻¹ is the gas constant. Although the free energy of solvation defined in Eq. 4 refers to a system at constant liquid volume, experimental data for Henry's constants are usually reported at a fixed pressure. This difference is insignificant at low pressure (11, 12).

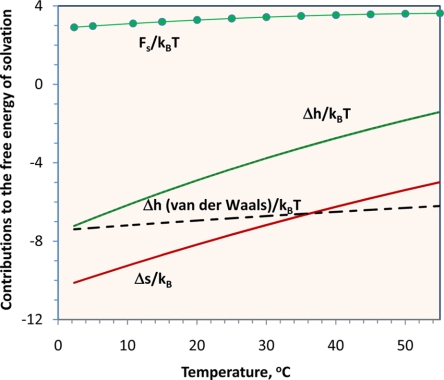
Fig. 1 shows the free energy of solvation for a methane molecule at different temperatures determined from Eq. 5. Experimental data for the gas solubility are from ref. 11. In units of thermal energy k_BT, the free energy of solvation increases from 2.9 to 3.6 as the temperature rises from 0 to 55°C; this change is much smaller than the corresponding changes in entropy or enthalpy in dimensionless units. At ambient conditions (1 atm and 25°C), the number density in the gas phase is ≈30 times higher than that in water. The tiny solubility is ascribed to the hydrophobicity of a methane molecule.

Fig. 1.

The free energy of solvation F_s for a single methane molecule in water and contributions from entropy Δs and enthalpy Δh. The dashed line gives the van der Waals attraction between a methane molecule and its surrounding water molecules estimated from the Lennard–Jones potential.

It is well documented that the hydrophobicity of a solute in water is not because of its lack of attraction with water molecules but because of the entropy penalty in reorganization of water molecules to preserve a highly organized hydrogen-bonding network. However, it is less clear to what extent a hydrophobic solute alters the probability of hydrogen bonding among the water molecules in close vicinity. The entropy and enthalpy of solvation, obtained from the derivatives of the free energy of solvation with respect to temperature, provide useful information on interactions of the solute with water:

where β = (k_BT)⁻¹. The solvation entropy arises exclusively from restrictions on the degrees of freedom of water molecules in the vicinity of the solute. Conversely, the solvation enthalpy includes a contribution from the water–solute (van der Waals) interaction energy and from the change in the hydrogen-bonding probability of the neighboring water molecules. As discussed by Pratt and Chandler (10), the water–solute interaction energy can be estimated from the water–solute Lennard–Jones (LJ) potential with conventional combining rules for the size and energy parameters. For the results shown in Fig. 1, we use the LJ parameters for methane ε_methane/k_B = 148.6 K and σ_methane = 3.9 Å, and those for water ε_water/k_B = 77 K and σ_water = 2.8 Å. The LJ parameters for methane are obtained from the literature (13) and those for water are the same as those used in standard molecular models (14). The LJ parameters for the van der Waals interaction between methane and water molecules are calculated from conventional combining rules. Except for the energy parameter for the water–methane attraction, our LJ parameters are similar to those used by Pratt and Chandler (10). In that earlier work, the water–methane energy parameter was obtained by fitting Henry's constant from an integral equation theory to the experimental result. In calculation of the total van der Waals attraction between a methane molecule with all surrounding water molecules, we assume that the number of water molecules within the first solvation of the shell of methane is fixed at 16 (15). The van der Waals energy is estimated from the attractive part of the LJ potential with the center-to-center distance between the methane molecule and its immediate neighboring water molecules fixed at ≈4.1 Å (16, 17). In our estimate of the solute–solvent van der Waals energy, we assume also that both the number of nearest neighbors and the average solute–solvent distance are invariant with temperature.

As shown in Fig. 1, near 0°C, the solvation enthalpy is nearly identical to the van der Waals attraction between a methane molecule and its immediate neighboring water molecules, implying that the extent of hydrogen bonding for water molecules within the solvation shell is similar to that in the bulk. The negative entropy is affiliated with localization of water molecules within the solvation shell, that is, partial organization of the water molecules immediately near the solute. As temperature increases, the extent of hydrogen bonding within the solvation shell is reduced in comparison with that in the bulk. The reduction in the probability of hydrogen bonding among water molecules within the solvation shell contradicts common notion that water molecules form a clathrate structure near a methane molecule. At high temperature, disruption of the hydrogen-bonding network is responsible for the absolute decrease of both solvation enthalpy and solvation entropy.

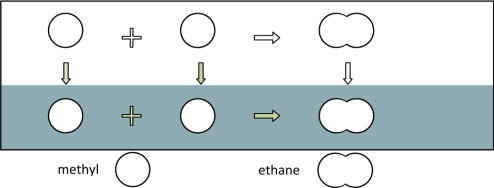
In an aqueous solution, the free energies of solvation for different alkanes (linear and branched) provide a good estimate for the multibody hydrophobic attraction among bonded methyl or methylene groups. Fig. 2 illustrates that the energetics for “formation” of an ethane molecule from two methyl groups in water include a contribution from a water-mediated hydrophobic potential in addition to that from the direct Lennard–Jones potential and to that from the “chemical” bonding energy in the absence of any water molecules. Because the contributions from the chemical bond and the direct van der Waals attraction are independent of the environment, the difference in the free energy of solvation for an ethane molecule and those for two methane molecules gives the hydrophobic potential at the bond separation

where w(r) stands for a potential of mean force, and b = 1.533 Å is the C–C bond length in ethane (11). The solvation free energies for both methane and ethane can be obtained from Henry's constants. As well documented (18), a similar procedure can be applied to linear or branched alkanes of higher molecular weight; this procedure yields a multibody hydrophobic potential

where F_s,Cn is the free energy of solvation for an alkane molecule that consists of n carbon atoms. The multibody potential defined by Eq. 9 refers to the total interaction among multiple methyl/methylene groups.

Fig. 2.

The free energy of solvation of an ethane molecule can be decomposed into those for two methyl groups and the hydrophobic potential to bring them together in an aqueous medium.

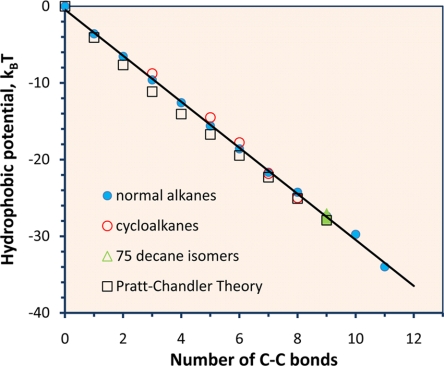
Fig. 3 presents the hydrophobic potential at 25°C for short linear alkanes, cyclo-alkanes, and 75 isomers of decane calculated from Eq. 9. All experimental data for Henry's constants are from Yaws and Yang (19). Henry's constants for long-chain alkanes (up to C20) are also available from the same reference but they are not considered here because, at room temperature, the configurational entropy becomes more significant for alkane molecules with >11 carbon numbers (20). Different from earlier simulation results (21), we find that, for short alkanes, the multibody hydrophobic potential shows a clear linear dependence on the number of C–C bonds, regardless of molecular structure. The slope (−3k_BT) corresponds to the hydrophobic attractive energy to bring two methyl/methylene groups from far apart to the bonding distance, and the intercept (−0.45k_BT) reflects the slight difference between the physical properties of methyl and methylene groups.

Fig. 3.

The multibody hydrophobic potential among methyl and methylene groups within a hydrated alkane molecule at 25°C. The linear dependence of the hydrophobic potential suggests pairwise additivity. Henry's constants, including those for 75 isomers of decane, are from Yaws and Yang (19).

Earlier, the multibody hydrophobic potential was obtained by a modified superposition approximation (10). Our results suggest that pairwise additivity holds without invoking the intramolecular degrees of freedom for alkane chains. Further, our results suggest that chain flexibility plays essentially no role in hydrophobicity, at least for short alkane chains. Indeed, Fig. 3 shows that the linear relation between the hydrophobic potential and the number of C–C bonds holds even for cycloalkanes and, to a good approximation, the hydrophobic potentials for 75 isomers of decane are all identical. Because the multibody hydrophobic potential can be perfectly reproduced by the interactions between neighboring pairs, the linear relation shown in Fig. 3 suggests that the hydrophobic interaction between carbon units is short-ranged and the overall hydrophobic potential is pairwise additive.

Pairwise additivity of the hydrophobic potential enables us to describe the free energy of solvation and solvent-mediated intermolecular interactions in water on the basis of those corresponding to individual segments (22). For example, the straight line in Fig. 3 predicts that the free energy of solvation for isobutane is −0.45k_BT − 3 × 3k_BT = 2.2 kcal/mol, in good agreement with 2.3 kcal/mol obtained from Henry's constant. The potential of mean force between two isobutane molecules can be calculated by pairwise additivity of the site–site hydrophobic potential among CH₃/CH groups. Toward that end, we need to have an expression for the hydrophobic potential of mean force as a function of the separation between two CH₃ or CH₂ or CH groups.

We expect that, to a good approximation, aqueous solvation of a hydrophobic molecule occurs primarily within a single layer of water molecules. In that case, the hydrophobic attraction must be short-ranged and must nearly disappear beyond the overlap of the solvation shells. Although distinctive oscillation was observed in molecular dynamic simulations (23), a recent quantum mechanics calculation suggests that the interaction between methane molecules in water exhibits nearly monotonic behavior (16). Because both the enthalpy and entropy of solvation scale linearly with the number of water molecules within the solvation shell, we assume that the hydrophobic potential between two methane molecules in water can be represented by a linear function of the change in the hydration volume

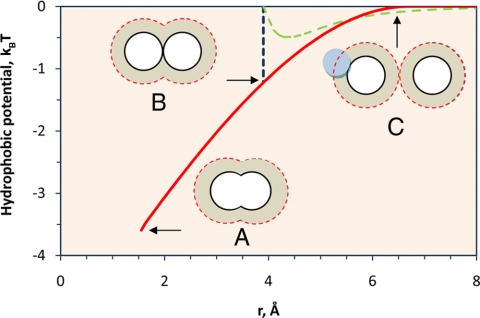
where a = 3.35 Å is the average diameter of methane and water molecules, and the proportionality constant A = 9.01 nm⁻³ is fixed by the hydrophobic potential between two CH₃ groups at the C–C bond length [T = 25°C, βw(r) = −3.59 at r = 1.533 Å]. Fig. 4 shows the hydrophobic potential between two methane molecules in water at 25°C. The contact value (−0.72 kcal/mol at r = 3.9 Å) is very much smaller than that from quantum mechanics simulations (−2.8 kcal/mol) (16) but agrees well with those from classical molecular dynamics results (−0.5∼−0.9 kcal/mol) (24, 25). For comparison with the van der Waals attractive energy, Fig. 4 also shows the Lennard–Jones potential for two isolated methane molecules. Near contact, the hydrophobic energy between methane molecules is approximately twice the maximum van der Waals energy, suggesting that in an aqueous environment the hydrophobic potential is much stronger than the direct van der Waals interaction.

Fig. 4.

The hydrophobic potential between two methane molecules in water at 25°C estimated from the change in the hydration volume. The methane molecules are separated by the C–C bond length (r = 1.533 Å) (A), are at contact (B), and have nonoverlapping solvation shells (C). For comparison, the dashed line shows the Lennard–Jones potential between two isolated methane molecules. The dotted lines show the outer boundary of the solvation shell. The perpendicular dash-dotted line shows position (B) when the methane molecules are at contact.

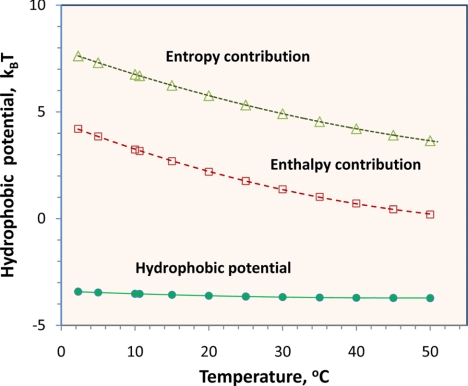
On using experimental data for Henry's constants of ethane and methane in water at different temperatures (11), we can predict the temperature dependence of the hydrophobic interaction between two methane molecules. Fig. 5 shows that, in dimensionless units, the hydrophobic potential increases only slightly with temperature whereas both enthalpic and entropic contributions decrease with temperature. Near 50°C, the hydrophobic attraction becomes purely entropic; the vanishing enthalpic contribution to the hydrophobic potential is likely because of cancellation of the solvent–solute van der Waals attraction with the variation of hydrogen-bonding potential caused by the presence of the solute. This cancellation follows because the enthalpy change must arise either from hydrogen bonding or from van der Waals attraction.

Fig. 5.

Effect of temperature on the hydrophobic potential between two methyl groups in water at a separation corresponding to the C–C bond length in an ethane molecule.

In summary, by using reliable experimental solubility data for alkanes in water over a range of temperatures, we have shown that the hydrophobic effect for low-molecular-weight alkanes in water can be accurately described by a pairwise-additive approximation. Pairwise additivity of the multibody hydrophobic potentials implies that the hydrophobic effect is most significant at small length scales (a few angstroms). Our study suggests that the hydrophobic effect is a local phenomenon most significant at a length scale comparable to the size of a water molecule. We find that near 0°C, the extent of hydrogen bonding among water molecules within the solvation shell is approximately the same as that in the bulk. As temperature increases, the extent of hydrogen bonding within the solvation shell is less than that in the bulk. Although our conclusions may not be directly applicable to protein folding or at conditions where the aggregated state of hydrophobes excludes water in the interior, we expect that the free energy of solvation and the hydrophobic interaction discussed here are relevant to the properties of hydrophobic groups at the surface of biological molecules (26).