A remark on global positioning from local distances

Abstract

Finding the global positioning of points in Euclidean space from a local or partial set of pairwise distances is a problem in geometry that emerges naturally in sensor networks and NMR spectroscopy of proteins. We observe that the eigenvectors of a certain sparse matrix exactly match the sought coordinates. This translates to a simple and efficient algorithm that is robust to noisy distance data.

Determining the configuration of N points r_i in ℝ^p (e.g., p = 2,3) given their noisy distance matrix δ_ij is a long-standing problem. For example, the points r_i may represent coordinates of cities in the United States. Distances between nearby cities, such as New York and New Haven, are known, but no information is given for the distance between New York and Chicago. In general, for every city, we are given distance measurements to its k ≪ N nearest neighbors or to neighbors that are, at most, δ away. The distance measurements δ_ij of d_ij = ‖r_i − r_j‖ may also incorporate errors. The problem is to find the unknown coordinates r_i = (x_i,y_i) of all cities from the noisy local distances.

Even in the absence of noise, the problem is solvable only if there are enough distance constraints. By solvable, we mean that there is a unique set of coordinates satisfying the given distance constraints up to rigid transformations (rotations, translations, and reflection). Alternatively, we say that the problem is solvable only if the underlying graph consisting of the N cities as vertices and the distance constraints as edges is rigid in ℝ^p (see, e.g., ref. 1). Graph rigidity had drawn a lot of attention over the years, see (1–5) for some results in this area.

When all possible N(N − 1)/2 pairwise distances are known, the corresponding complete graph is rigid, and the coordinates can be computed by using a classical method known as multidimensional scaling (MDS) (6–8). The underlying principle of MDS is to use the law of cosines to convert distances into an inner product matrix, whose eigenvectors are the sought coordinates. The eigenvectors computed by MDS are also the solution to a specific minimization problem. However, when most of the distance matrix entries are missing, this minimization becomes significantly more challenging because of the low rank-p constraint that is not convex. Various solutions to this constrained optimization problem have been proposed, including relaxation of the rank constraint by semidefinite programming (SDP) (9), regularization (10, 11), smart initialization (12), expectation maximization (13), and other relaxation schemes (14). Recently, the eigenvectors of the graph Laplacian (15) were used to approximate the large scale SDP problem by a much smaller one, noting that linear combinations of only a few Laplacian eigenvectors can well approximate the coordinates.

The problem of finding the global coordinates from noisy local distances arises naturally in localization of sensor networks (16–18) and protein structuring from NMR spectroscopy (19, 20), where noisy measurements of neighboring hydrogen atoms are inferred from the nuclear Overhauser effect (NOE). The theory and practice involves many different areas, such as machine learning (15), optimization techniques (14) and rigidity theory (1, 4, 5, 17, 21, 22). We find it practically impossible to give a fair account of all of the relevant literature and recommend the interested reader to see the references within those listed.

In this article, we describe locally rigid embedding (LRE), a simple and efficient algorithm to find the global configuration from locally noisy distances, under the simplifying assumption of local rigidity. We assume that every city, together with its neighboring cities, forms a rigid subgraph that can be embedded uniquely (up to a rigid transformation). That is, there are enough distance constraints among the neighboring cities that make the local structure rigid. The “pebble game” (23) is a fast algorithm to determine graph rigidity. Thus, given a dataset of distances, the local rigidity assumption can be tested quickly by applying the pebble game algorithm N times, once for each city. In Summary, we discuss the restrictiveness of the local rigidity assumption (see refs. 17, 21, 22 for conditions that ensure rigidity) as well as possible variants of LRE when the assumption does not hold.

The essence of LRE follows the observation that one can construct an N × N sparse weight matrix W that has the property that the coordinate vectors are an eigenspace. The matrix is constructed in linear time complexity and has only O(N) nonzero elements, which enables efficient computation of that small eigenspace. The matrix W is formed by preprocessing the local distance information to repeatedly embed each city and its neighboring points (e.g., by using MDS or SDP), which is possible by the assumption that every local neighborhood is rigid. Once the local coordinates are obtained, we calculate weights much like the locally linear embedding (LLE) recipe (24) and its multiple weights (MLLE) modification (25). Similar to recent dimensionality reduction methods (24, 26–28), the motif “think globally, fit locally” (29) is repeated here. This is just another example for the usefulness of eigenfunctions of operators on datasets and their ability to integrate local information to a consistent global solution. In contrast to propagation algorithms that start with some local embedding and incrementally embed additional points while accumulating errors, the global eigenvector computation of LRE takes into account all local information at once, which makes it robust to noise.

Locally Rigid Embedding

We start by embedding points locally. For every point r_i (i = 1, …, N) we examine its k_i neighbors r_i1, r_i2, …, r_iki for which we have distance information. We find a p-dimensional embedding of those k_i + 1 points. If the local (k_i + 1) × (k_i + 1) distance matrix is fully known, then this embedding can be obtained by using MDS. If some local distances are missing, then the embedding can be found by using SDP or other optimization methods. The assumption of local rigidity ensures that in the noise-free case, such an embedding is unique up to a rigid transformation. Note that the neighbors are not required to be physically close but can, rather, be any collection of k_i points that the distance constraints among them make them rigid. This locally rigid embedding gives local coordinates for r_i, r_i1, …, r_iki up to translation, rotation, and, perhaps, reflection. We define k_i weights W_i,ij that satisfy the following p + 1 linear constraints

The vector equation (Eq. 1) means that the point r_i is the center of mass of its k_i neighbors, and the scalar equation (Eq. 2) means that the weights sums up to 1. Together, the weights are invariant to rigid transformations (translation, rotation, and reflection) of the locally embedded points. It is possible to find such weights if k_i ≥ p + 1. In fact, for k_i > p + 1, there is an infinite number of ways in which the weights can be chosen. In practice, we choose the least-square solution, i.e., that with minΣ_j=1^k_iW_i,ij². This prevents certain weights from becoming too large and keeps the weights balanced in magnitude. We rewrite Eqs. 1 and 2 in matrix notation as

where b = (0, …, 0, 1)^T ∈ℝ^p+1, w_i = (W_i,i1, W_i,i2, …, W_i,iki)^T, and R_i is a (p + 1) × k_i matrix, whose first p rows are the relative coordinates, and the last row is the all ones vector

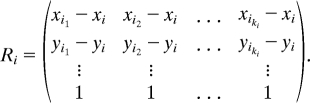It can be easily verified that the least-squares solution is

Note that some of the weights may be negative. In fact, negative weights are unavoidable for points on the boundary of the convex hull of the set.

The computed weights W_i,ij (j = 1, …, k_i) are assigned to the ith row of W, whereas all other N − k_i row entries, including the diagonal element W_i,i, are set to zero. This procedure of locally rigid embedding is repeated for every i = 1, …, N, each time filling another row of the weight matrix W. Therefore, it takes O(N) operations to complete the construction of the weight matrix W, which ends up being a sparse matrix with k̄N nonzero elements, where k̄ = 1/NΣ_i=1^N k_i is the average degree of the graph (i.e., the average number of neighbors). Both the least-squares solution and the local embedding (MDS or SDP) are polynomial in k_i, so repeating them N times is also O(N).

Next, we examine the spectrum of W. Observe that the all ones vector 1 = (1, 1, …, 1)^T satisfies

because of Eq. 2. That is, 1 is an eigenvector of W with an eigenvalue λ = 1. We will refer to 1 as the trivial eigenvector. If the locally rigid embeddings were free of any error (up to rotations and reflections), then the p coordinate vectors x = (x₁, x₂, …, x_N)^T, y = (y₁, y₂, …, y_N)^T, … are also eigenvectors of W with the same eigenvalue λ = 1

This follows immediately from Eq. 1 by reading it one coordinate at a time,

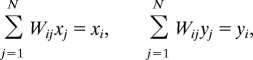Thus, the eigenvectors of W corresponding to λ = 1 give the sought coordinates, e.g., (x_i, y_i) for p = 2. It is remarkable that the eigenvectors give the global coordinates x and y despite the fact that different points have different local coordinate sets that are arbitrarily rotated, translated, and, perhaps, reflected with respect to one another.

Note that W is not symmetric, so its spectrum may be complex. Although every row of W sums up to 1, this does not prevent the possibility of eigenvalues ∣λ∣ > 1, because W is not stochastic, having negative entries. Therefore, we compute the eigenvectors with eigenvalues closest to 1 in the complex plane.

A symmetric weight matrix S with spectral properties similar to W can be constructed with the same effort (per D. A. Spielman, private communication). For each point r_i, compute an orthonormal basis w̃_{i,1, …}, w̃_i,k_i−p ∈ ℝ^k_i+1 for the nullspace of the (p + 1) × (k_i + 1) matrix R̃_i

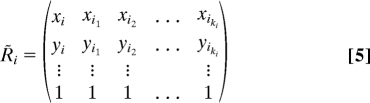In other words, we find w̃_i,j that satisfy

and

The symmetric product S_i = Σ_j=1^k_i−p w̃_i,jw̃_i,j^T of the nullspace with itself is a (k_i + 1) × (k_i + 1) positive semidefinite (PSD) matrix. We sum the N PSD matrices S_i (i = 1, …, N) to form an N × N PSD S by updating for each i only the corresponding (k_i + 1) × (k_i + 1) block of the large matrix

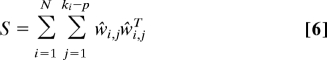where ŵ_i,j ∈ ℝ^N is obtained from w̃_i,j by padding it with zeros. Similar to the nonsymmetric case, it can be verified that the p + 1 vectors 1, x, y, … belong to the nullspace of S

In fact, because the global graph of N points is rigid, any vector in the nullspace of S is a linear combination of those p + 1 vectors (the previous construction of W may not enjoy this nice property, i.e., it is possible to create examples for which the dimension of the eigenspace of W is greater than p + 1). In rigidity theory, we would call S a stress of the framework (1).

From the computational point of view, we remark that, if needed, the eigenvector computation can be done in parallel. To multiply a given vector by the weight matrix W (or S), the storage of W (S) is distributed between the N points, such that the ith point stores only k_i values of W (S) together with k_i values of the given vector that correspond to the neighbors.

Multiplicity and Noise

The eigenvalue λ = 1 of W (or 0 for S) is degenerate with multiplicity p + 1. Hence, the corresponding p + 1 computed eigenvectors φ⁰,φ¹,…,φ^p may be any linear combination of 1, x, y, …. We may assume that φ⁰ = 1 and that 〈φ^j, 1〉 = 0 for j = 1, …, p. We now look for a p × p matrix A that represents the linear transformation from the original coordinate set r_i = (x_i,y_i, …) to the eigenmap φ_i = (φ¹_i,φ²_i, …)

The squared distance between r_i and r_j is

Every pair of points for which the distance d_ij is known gives a linear equation for the coefficients of the matrix A^T A. Solving that equation set results in A^T A, whose Cholesky decomposition yields A (up to an orthogonal transformation).

The locally rigid embedding incorporates errors when the distances are noisy. The noise breaks the degeneracy and splits the eigenvalues. If the noise level is small, then we still expect the first p nontrivial eigenvectors to match the original coordinates, because the small noise does not overcome the spectral gap

where λ_i are the eigenvalues of the noiseless W. For higher levels of noise, the noise may be large enough so that some of the first p eigenvalues cross the spectral gap, causing the coordinate vectors to spill over the remaining eigenvectors.

To overcome this problem, we allow A to be p × m instead of p × p, with m > p, but still m ≪ N. In other words, every coordinate is approximated as a linear combination of the m nontrivial eigenvectors φ¹, …, φ^m, whose eigenvalues are the closest to 1. We replace Eq. 7 by a minimization problem for the m × m PSD matrix P = A^T A

where the sum is over all pairs i ≈ j for which there exists a distance measurement Δ_ij. The least-squares solution for P is often not valid, when it ends up not being a PSD matrix or when its rank is >p. It was shown in ref. 15 that the optimization problem (Eq. 8) with the PSD constraint P ≻ 0 can be formulated as SDP by using the Schur complement lemma. The matrix A is reconstructed from the singular vectors of P corresponding to the largest p singular values.

Numerical Results

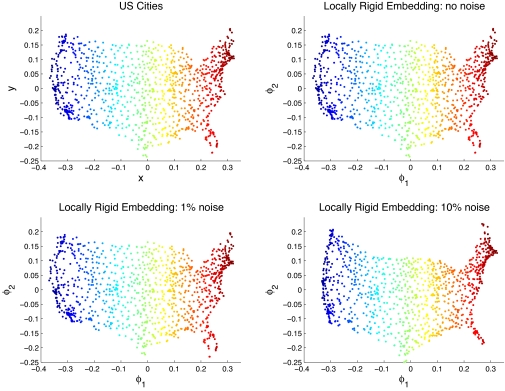
We consider a dataset of n = 1,097 cities in the United States, see Fig. 1(Upper Left). For each city, we have distance measurements to its 18 nearest cities (k_i = k = 18). For simplicity, we assume that the (₂¹⁸) distances between the neighboring cities are also collected, so that MDS is used to locally embed the neighboring cities. We tested the locally rigid embedding algorithm for three different levels of multiplicative Gaussian noise: no noise, 1% noise, and 10% noise. That is, Δ_ij = d_ij[1 + N(0,δ²)], with δ = 0,0.01,0.1. We used SeDuMi (30) for solving the SDP (Eq. 8).

Fig. 1.

Locally rigid embedding of US cities. (Upper Left) Map of 1,097 cities in the United States. (Upper Right) The locally rigid embedding obtained from clean local distances. (Lower Left) LRE with 1% noise. (Lower Right) LRE with 10% noise. Cities are colored by their x coordinate.

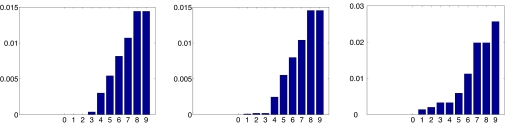
The behavior of the numerical spectrum for the different noise levels is illustrated in Fig. 2, where the magnitude of 1 − λ_i for the 10 eigenvalues that are closest to 1 is plotted. It is apparent in the noiseless case that λ = 1 is degenerated with multiplicity 3 corresponding to 1, x, y. Note that the spectral gap is quite small. The LRE finds the exact configuration without introducing any errors as can be seen in Fig. 1 (Upper Right).

Fig. 2.

Numerical spectrum of W for different levels of noise: Clean distances (Left), 1% noise (Center), and 10% noise (Right).

Adding 1% noise breaks the degeneracy and splits the eigenvalues, and because of the small spectral gap, the coordinates spill over the fourth eigenvector. Therefore, for that noise level, we solved the minimization problem (Eq. 8) with P being a 3 × 3 matrix (m = 3). The largest singular values of P were 101.7, 42.5, and 0.13, indicating a successful two-dimensional embedding.

When the noise is increased more, the spectrum changes even further. We used m = 7 for the noise level of 10%. The largest singular values of the optimal P were 76.6, 8.3, 2.0, and 0.002, which implies that the added noise effectively increased the dimension of points from two to three. The LRE distorts boundary points but does a good job in the interior.

Algorithm

In this section, we summarize the various steps of LRE that should be taken to find the global coordinates from a dataset of vertices and distances by using the symmetric matrix S.

1. Input: A weighted graph G = (V, E, Δ), δ_ij is the measured distance between vertices i and j, and ∣V∣ = N is the number of vertices. G is assumed to be locally rigid.

2. Allocate memory for a sparse N × N matrix S.

3. For i = 1 to N

   1. Set k_i to be the degree of vertex i.
   2. i₁, …, i_ki are the neighbors of i: (i, i_j) ∈ E for j = 1, …, k_i.
   3. Use SDP or MDS to find an embedding r_i, r_i1, …, r_iki of i, i₁, …, i_ki.
   4. Form the (p + 1) × (k_i + 1) matrix R̃_i following Eq. 5.
   5. Compute an orthogonal basis w̃_i,1, …, w̃_i,ki−p for the nullspace of R̃_i.
   6. Update S ← S + Σ_j=1^k_i−pŵ_i,jŵ_i,j^T. (ŵ_i,j are obtained from w̃_i,j by zero padding.).

4. Compute m + 1 eigenvectors of S with eigenvalues closest to 0: φ₀, φ₁, …, φ_m, where φ₀ is the all-ones vector.

5. Use SDP as in Eq. 8 to find coordinate vectors x₁, …, x_p as linear combinations of φ₁, …, φ_m.

Summary and Discussion

We presented an observation that leads to a simple algorithm for finding the global configuration of points from their local noisy distances under the assumption of local rigidity. The LRE algorithm that uses the matrix W is similar to the LLE algorithm (24) for dimensionality reduction. The input to LLE are high-dimensional data points for which LLE constructs the weight matrix W by repeatedly solving overdetermined linear equation systems. In the global positioning problem the input is not high-dimensional data points, but rather distance constraints that we preprocess (using MDS or SDP) to get a locally rigid low-dimensional embedding. Therefore, the weights are obtained by solving an underdetermined system (Eqs. 1–2) instead of an overdetermined system. The LRE variant that uses the symmetric matrix S is similar to the MLLE algorithm (25) in the sense that it uses more than a single weight vector, taking all basis vectors of the nullspace into account in the construction of S.

The assumption of local rigidity of the input graph is crucial for the algorithm to succeed. It is reasonable to ask whether or not this assumption holds in practice and how the algorithm can be modified to prevail even if the assumption fails to hold. These are important research questions that remain to be addressed. Even if a few vertices have corresponding subgraphs that are not rigid (nonlocalizable), so their weights are not included in the construction of the stress matrix S, the matrix S may still have a nullspace of dimension three. This can happen if the nonlocalizable vertices have enough localizable neighbors. Still, the algorithm fails when there are too many nonlocalizable vertices. For such nonlocalizable vertices, one possible approach is to consider larger subgraphs, such as the one containing all two-hop neighbors (the neighbors of the neighbors), hoping that the larger subgraph would be rigid. A different approach may be to consider smaller subgraphs, hoping that the removal of some neighbors would make the subgraph rigid. This is obviously possible if the vertex is included in a triangle (or some other small simple rigid subgraph) but at risk that the small subgraph would be too small to be rigidly connected to the remaining graph. It is not clear which approach would work better and requires numerical experiments. However, this is beyond the scope of the current article. There are many other interesting questions that follow from both the theoretical and algorithmic aspects, such as proving error bounds, finding other suitable operators for curves and surfaces, and dealing with specific constraints that arise from real-life datasets.