Repeat-protein folding: new insights into origins of cooperativity, stability, and topology

Abstract

Although our understanding of globular protein folding continues to advance, the irregular tertiary structures and high cooperativity of globular proteins complicates energetic dissection. Recently, proteins with regular, repetitive tertiary structures have been identified that sidestep limitations imposed by globular protein architecture. Here we review recent studies of repeat-protein folding. These studies uniquely advance our understanding of both the energetics and kinetics of protein folding. Equilibrium studies provide detailed maps of local stabilities, access to energy landscapes, insights into cooperativity, determination of nearest-neighbor interaction parameters using statistical thermodynamics, relationships between consensus sequences and repeat-protein stability. Kinetic studies provide insight into the influence of short-range topology on folding rates, the degree to which folding proceeds by parallel (versus localized) pathways, and the factors that select among multiple potential pathways. The recent application of force spectroscopy to repeat-protein unfolding is providing a unique route to test and extend many of these findings.

In the last twenty-five years, advances in experimental studies and in computation and theory have greatly improved our understanding of protein folding. On the experimental side, advances have come from new and improved techniques, including site-directed mutagenesis, hydrogen exchange (HX) methods, improvements to rapid mixing devices, and development of single-molecule fluorescence and force spectroscopy. Experimental advances have also come in the form of generalizations and insights from expanding databases of thermodynamic and kinetic constants for protein folding [1–5].

On the computational side, advances in our understanding of protein folding have come from huge increases in computer speed and storage capacity, in innovative methods to study energetics of folding such as ensemble-based approaches and replica exchange methods [6, 7], and distributed computing methods [8]. As with experiment, computational studies of folding, and in particular, fold prediction, have greatly benefited from expanding databases of protein structure [9, 10]. On the theoretical side, the application of ideas from condensed-matter physics and the resulting “landscape” picture of protein folding have provided a new perspective for describing folding [11–14].

Recent observations and related questions in folding of globular proteins

The advances highlighted above have provided some important insights into how proteins fold. One important insight from experimental studies is that for many proteins the rate of folding is inversely correlated to the density of sequence-distant contacts (referred to as “contact order”) in the native state [3, 15]. This correlation suggests that the overall fold or “topology” of the native-state is established in the rate-limiting step in folding [16]. At a more detailed resolution, rate-equilibrium relationships of single-residue protein variants (and so-called “Φ-values”) indicate that detailed side-chain packing interactions vary in their extent of formation in the rate-limiting, or transition-state ensemble, often remaining unformed until the native state is formed (for a review of Φ-values in globular proteins, see the article by Royer in this issue).

It is interesting to compare these two measures of the rate-limiting steps in folding with a long-standing and general observation regarding equilibrium protein folding, namely that of cooperativity. For many (but not all) globular proteins, folding appears to proceed in a thermodynamically “two-state” reaction in which all structural features of the native state are formed in a single, concerted fashion. This type of equilibrium cooperativity seems in accordance with the suggestion from the contact order correlation that the limiting step in folding is the concerted organization of the bulk of the native backbone fold. However, these two observations are less in accord with the variation of the extent of packing in the transition state ensemble suggested from Φ-value analysis. Does this packing variation indicate a specific pathway in which some tertiary interactions form late, despite their residing within a native backbone topology? Or is the backbone less native-like than the topology correlation suggests? In this regard, what are the limits of the topology-rate correlation?

The above questions raise the issue of pathways and the interactions responsible for specifying them. If there are specific pathways in which some stable structural elements form late, are these folding routes controlled kinetically, rather than reflecting the overall stability of all parts of the protein? Or does the dominant kinetic pathway genuinely reflect a low energy pathway through conformational space in a global sense? And if there is large variation in local stability, what is the glue that holds different regions of the protein together to give rise to equilibrium cooperativity?

One of the contributions of the energy landscape view of folding is a recognition that “pathways” may be much more complex than a single sequentially ordered series of well-defined intermediates. In one limiting case, that of a “folding funnel”, there is no structurally defined pathway. Rather, each structural degree of freedom (torsion angles) might “sense” the direction to the native state locally through a thermally meaningful monotonic decrease in energy, regardless of the configuration of the bulk of the chain, towards a minimum centered on the native state. This type of folding, which is referred to as “downhill” to reflect the uniform decrease in energy toward the native state, would be expected to result in very fast (potentially non-exponential) folding for even the largest conformational searches.

In a less severe barrier-limited landscape, following a partial decrease in the available conformations (perhaps by local structural propensity), folding is limited by an unbiased search (through an “entropy bottleneck”) to the native state. Although the observed topology correlation would argue against a purely native-centric downhill mechanism, the often diffuse nature of the transition states of many proteins determined by Φ-value analysis [5, 17, 18], along with a recent interpretation of the folding of a small polypeptides [19, 20],¹ are consistent with a downhill mechanism. Clearly, what is needed is a direct and detailed experimental determination of the features of the energy landscapes of protein folding.

Challenges in understanding folding using globular proteins

In motivating the study of folding using repeat proteins, it is worth identifying some of the structural features of globular proteins that limit our understanding of folding. One confounding feature of globular protein structures is that distant segments of the polypeptide chain are often in close contact (the structural basis for high contact order in globular proteins). As described below, the interconnected, “long-range” topologies of globular proteins lead to a “dissection” problem. Another confounding structural feature of globular proteins is their complex, irregular, heterogeneous architectures. Although globular proteins are constructed of a limited and fairly regular set of hydrogen bonded secondary structure elements (α-helices, β-strands, and turns), the arrangements of adjacent secondary structure elements (supersecondary structure) and the higher order tertiary structures of globular proteins are very irregular and highly variable from one protein to the next (Figure 1A). As described below, this heterogeneity leads to a “comparison” problem.

Figure 1. Comparison of globular and repeat protein structures.

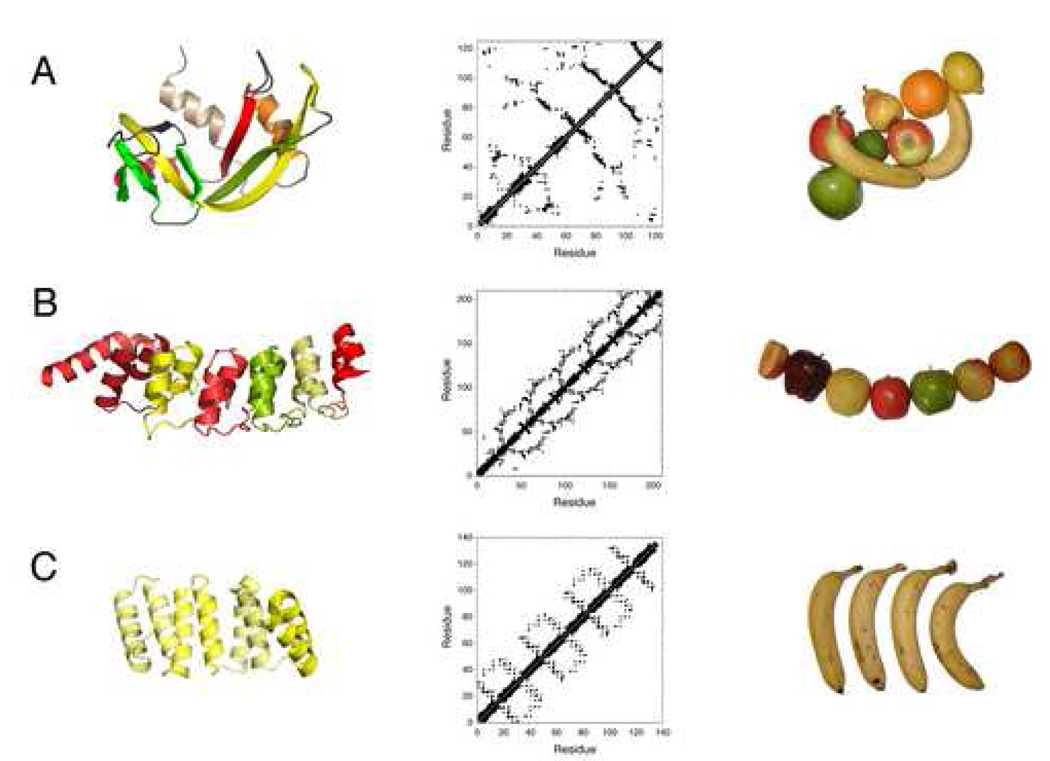
(A) A typical globular protein used in folding studies (RNase A, top; 7RSA.pdb) is compared to (B) a naturally occurring repeat protein (the Notch ankyrin domain, middle; 1OT8.pdb chain A) and to (C) a consensus repeat protein (bottom; 2FO7.pdb). Left: ribbon diagrams (prepared with MacPyMOL [107]) coloring different secondary structure elements (top) and repeats (center, bottom). Middle: contact maps, emphasizing the lack of long-range contacts in repeat proteins (center, bottom), and regular patterns of tertiary structure in different regions of repeat proteins. Right: analogy of globular and repeat proteins to assemblages of fresh fruit. Although the usual fruits of the familiar metaphorical comparison are apples and oranges, some elements of secondary structure (and whole repeat units) are elongated and can be better represented by bananas.

The dissection problem, which results from the long-range topologies of globular proteins, makes folding energy difficult to dissect because close contacts among distant chain segments are likely to promote cooperativity in folding (local loss of structure will destabilize regions that remain folded). Although concerted folding of globular proteins simplifies analysis of both equilibrium and kinetic data, it prevents dissection of energetics (and also rates of conversion) to different structural elements, which is required to construct energy landscapes for real proteins. Long-range topology is also likely to confound experimental dissection of globular proteins into fragments: in the absence of sequence distant contacts, protein fragments typically unfold and often aggregate, again preventing determination of local energetics [23].

The comparison problem, which results from the heterogeneous supersecondary and tertiary structures of globular proteins, presents a second challenge in extracting general principles in protein folding: even if local energy distribution within a globular protein can be determined, the underlying origins local energy differences is unclear. For example, in a protein with a pair of helices and a small β-sheet, it may be found that the helices are more stable than the sheet. Is this because the helices themselves are more stable than the sheet, because local packing interactions that better stabilize the helix pair, or because of burial of more hydrophobic surface area? Since the individual structural elements of globular proteins are so different and reside in different structural environments, it is difficult to answer such questions by making structural comparisons. Similar ambiguities arise in comparing of the structured and unstructured regions of kinetic intermediates, and in using Φ-values to map the structures of transition state ensembles.

Advantages of studying folding using repeat proteins

The heterogeneous structures and long-range topologies of globular proteins (Figure 1A) are contrasted by the architectural simplicity of linear repeat proteins (Figure 1B, C). Linear repeat proteins are single polypeptide chains in which a single supersecondary structure loop (containing a small number of helices and/or strands connected by turns) is repeated several times in a tandem, uninterrupted array. Adjacent repeats pack together in a more-or-less linear array, facilitating a simple linear (nearest-neighbor) representation of energetics, similar to that of DNA double helix formation. This extended architecture provides potential solutions to both problems described above—comparison and dissection—and also serves as an excellent platform for protein design [24–27].

The solution to the comparison problem provided by repeat proteins is obvious. Unlike globular proteins, where different parts of the chain differ in primary, secondary, supersecondary, and tertiary structure, for most repeat proteins there is clear repetition on all of these levels of structure. For example, the N-terminal, central, and C-terminal regions of ankyrin repeat proteins are all made of short (10–11 residue) α-helices connected by alternating short and extended turns (Figure 2A). Moreover, the supersecondary structure of each repeat (i.e. the three-dimensional arrangement of these secondary structure units) is highly similar across the entire repeat protein domain: backbone RMSD values from repeat to repeat are typically well below 1Å. In addition, the orientation of neighboring repeats relative to one another is quite conserved. This structural similarity within and between repeats leads to highly uniform tertiary structures in different regions of repeat proteins, which can be visualized clearly in the regularity of contact maps of repeat proteins (Figure 1B, C). This solution to the comparison problem can be well represented using the familiar syllogism of comparing fruits (Figure 1). Because of the structural similarity of different regions of repeat proteins, differences in the contributions of different repeats to stability and to folding kinetics can be evaluated in a much more straight-forward way.

Figure 2. Structure of various repeat proteins.

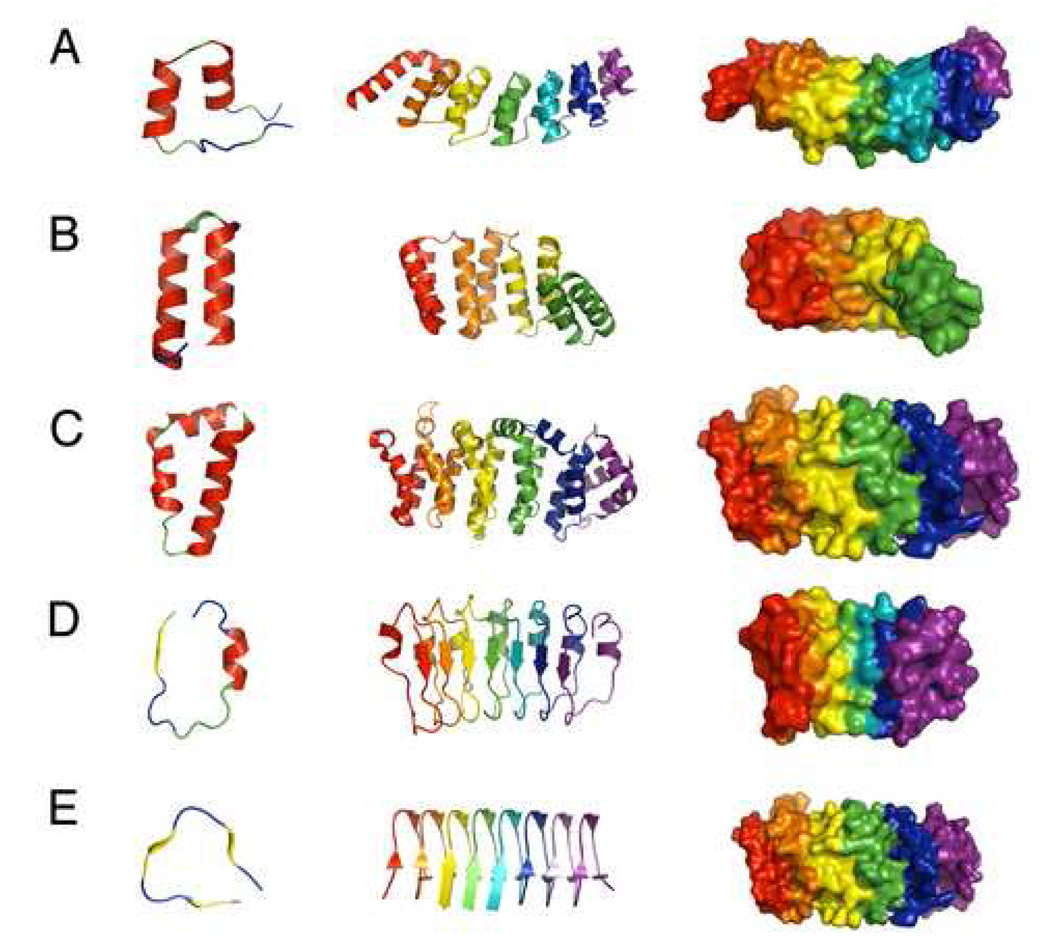
(A) the ankyrin repeats of the Notch receptor, 1O8T.pdb; (B) consensus tetratricorepeats, 2F07.pdb; (C) heat repeats; 1UPK.pdb; (D) internalin-B leucine-rich repeats, 1H62.pdb; (E) hexapeptide repeats, 1J2Z.pdb. Left: overall architecture of single repeats of some of the most common linear repeat proteins. α-helices are red, β-strands are yellow, PPII structure is green, and tight turns are blue. Center: linear arrays of these the same repeats, with adjacent repeats colored from red to purple (N to C). Right: surface representation of adjacent repeats, showing contiguous packing over the entire domain.

The solution to the dissection problem provided by repeat proteins relates to the absence of sequence-distant contacts. This can also be visualized in contact maps: whereas globular proteins have a large number of sequence-distant contacts (far off the diagonal, Figure 1A), the contacts in repeat proteins are all close-range (near the diagonal, Figure 1B, C). Because of the lack of sequence-distant contacts, distant regions of repeat proteins are not likely to directly impact each other’s structure. This suggests that the folding of different regions of repeat proteins may be studied independently of each other, either by deleting repeats from one region and studying the remaining repeats, or by characterizing partly folded states in which a subset of repeats remain structured (if such structures are significantly populated). Using these methods to dissect local stabilities in repeat proteins provides a means to experimentally map the energy landscape.

Finally, the lack of sequence distant contacts and simple topology of repeat proteins results in uniform and low contact order. Moreover, the linear structure of repeat proteins provides a means to separate relative from absolute contact order, especially when combined experimentally with length variation by deletion and insertion of repeats. Thus, repeat proteins can be used to probe the origins and limits of correlations between folding rates and topological features of the native state.

Below, we describe recent efforts to determine the equilibrium and kinetic mechanisms of repeat-protein folding, focusing on how these proteins can be used to overcome both the dissection and the comparison problems of globular proteins. We will describe recent insights into cooperativity, how repeat proteins can be used to experimentally determine energy landscapes, and the existence and specification of kinetic folding pathways. In addition, we will focus briefly on surprising findings relating consensus sequence of repeats to stability, and on the emergence of force microscopy as a promising new method to better understand the unfolding of repeat proteins.

Structural overview of linear repeat proteins

As described above, repeat proteins are constructed of tandem repeats ranging from around 20 to 40 residues in length (Table 1). These repeats are each structured similarly into a closed loop of secondary structure elements that includes either helices (typically α-helices, but sometimes and 3₁₀ or polyproline II-type helices), β-strands, or a mixture of both, connected by turns of various types (Figure 2, Table 1). In most (but not all) repeat families, partial sequence conservation is exhibited from repeat to repeat (typically around 25 percent identity).² Although this combination of modest sequence identity and small repeat size would be expected to seriously hinder sequence-based searches for single repeats, resulting in a large number of false-positives, tandem repetition in repeat arrays (typically four or more copies) greatly increases confidence in sequence searches. However, since repeat proteins are often embedded in larger, non-repeat sequences, identification of the bona fide ends of repeat proteins (and thus the overall length of the repeat domain) from sequence alone can be problematic, both because of the false-positives and false-negatives (for the latter case, terminal repeats often tend to differ in sequence from the consensus to avoid unfavorable contacts with solvent [28–30].

Table 1.

Features of repeat-protein arrays

Type	SS	<nres>	<nrep>/<nrep,gaps>	ΔASApair	ΔASApair,np	ΔASApair,p	ΔASAfold
ARM	ααα	42	5/8	1740±25	1230±22	510±13	2110±48
HEAT	ααα	41	4/13	1670±30	1190±23	480±14	2000±36
TPR1	αα	34	3/5	1125±27	810±20	320±18	1900±38
TPR2	αα	37	3/5	1880±164	1300±101)	580±69	1970±80
ANK	ααβh	33	4/5	1490±19	1010±14	470±8	1510±24
LRR1	β310,βPPII	23	7/10	1675±18	1020±11	650±9	630±11
LRR2	βα	28	7/10	1810±22	1130±18	680±12	900±17
HPR	βββ	18	4/7	1380±18	790±13	580±12	300±9

ARM, armadillo repeat; TPR1 and TPR2, tetratricopeptide repeats of different lengths; ANK, ankyrin repeat; LRR1 and LRR2, leucine-rich repeats of different lengths (and secondary structures); HPR, hexapeptide repeat. SS, secondary structure, where ααα indicates three α-helices per repeat, ααβh indicates two helices followed by a short β-hairpin, β3₁₀ and βPPII. <n_res>, average number of residues per repeat. <n_rep>, median number of repeats per tandem array, based on search results of nonredundant entries in NCBI Genbank using HMMER 2.3.2 ([100]; default settings, E-value less than 10) with hidden markov models (HMMs) from Pfam version 21.0 [101]. <n_rep,gaps>, median number or repeats per tandem array, including each gap 70% or greater the length of a repeating unit as an additional repeat. ΔASA_pair, average amount of solvent-accesible surface area (Ų) buried at the interface, obtained from the average difference in solvent accessible surface [102], between adjacent paired repeats folded in contact and individual repeats. ΔASA_pair,np and ΔASA_pair,p, interfacial nonpolar and polar surface area. ΔASA_fold, the change in surface area on folding of single unpaired repeats, using an extended polypepetide, generated by RIBOSOME (http://roselab.jhu.edu/~raj/Manuals/ribosome.html), as a simple model for the unfolded peptide structure.

In the repeat proteins described here (which include families that are abundant in sequence databases, have known high-resolution structures, and have been used as systems for studying folding), adjacent sequence repeats pack together to form an extended array (Figure 1, Figure 2). Although minor tilts and rotations about the long-axis of the array produce gradual superhelical trajectories (as elegantly detailed Kobe and Kajava [31]), the overall architecture of the repeat proteins described here can be well-approximated as linear.³

Although adjacent repeats appear to be clearly separated in ribbon representation, all-atom space-filling models demonstrate that there are substantial interactions involving high surface complementarity between repeats (Figure 2, Table 1). All linear repeat proteins bury a substantial amount of surface area at the interfaces between repeats. For helical repeat proteins (e.g. HEAT, TPR, Armadillo, Ankyrin), the amount of surface area buried per interface (~1580 Ų) is more than half that buried in individual folded repeats (1830 Ų, using an unfolded state model as a reference; Table 1). For repeats containing one or more β-strands (LLRs and HPRs), this ratio is substantially larger, owing to the smaller amount of surface area buried within individual folded repeats (~600 Ų; the amount of surface buried at interfaces in β-strand repeat proteins is similar to interfaces between α-helical repeats, at around 1650 Ų). The surface area buried between repeats is typically hydrophobic, although for the β-strand containing repeats, which form extended inter-repeat β-sheets, there are more main-chain polar groups buried and participating in inter-repeat hydrogen bonds.

Consensus Repeat arrays

The repetitive, translationally symmetric structures of repeat proteins are highly amenable to protein design. Because of the linear structures of repeat proteins, individual repeats can be combined indefinitely without size limitations, unlike globular protein for which long-range tertiary interactions inherently limit their size. Such elaboration has clearly been used by nature to expand and diversify various repeat-protein families [34, 35]. Recently, a similar approach has been particularly successful in designing new repeat proteins in the laboratory based on the consensus sequences of individual repeats, including consensus TPR [24], ankyrin [25], leucine-rich [26], and β-propeller repeats [36]. Because these repeat motifs are abundant in sequence databases, their consensus sequences are robustly determined. As described below, designed consensus repeats have been shown to adopt their target structures, and in many cases appear to possess very high thermodynamic stability. Moreover, consensus repeat proteins have been used as structural platforms to generate high-affinity protein interaction domains [37–40].

For a given repeat motif, there are a number of positions where sequence conservation is quite high; at such positions, the consensus sequence unambiguously specifies the sequence to be used in construction of a consensus repeat protein. However, there are also positions in repeat motifs where conservation is low. At such positions, several criteria have been used, such as overall composition (hydrophobic, acidic, etc.) [25], pairwise covariance [25, 26], removal of cysteine residues to improve long-term stability [24, 26], and overall protein charge [25, 26]. In addition, random substitutions along the solvent-exposed surfaces of consensus ankyrin repeats [27] and LRRs [26] have yielded libraries of designed repeat sequences that can be combined to produce novel surfaces for potential protein-protein interactions. Another important aspect of consensus repeat-protein design is the inclusion of polar, capping residues, helices and repeats at the N- and C-termini to shield hydrophobic surfaces [24, 26, 27]. Using these strategies, arrays containing up to 10 TPR, 6 ankyrin, 12 leucine-rich, and 7 β-propeller repeats have been successfully designed and constructed in vitro.

Many consensus-designed arrays of identical repeats have been found to adopt folds that closely resemble the structures of their naturally occurring counterparts. High resolution crystal structures revealed that proteins containing up to five consensus ankyrin repeats [25, 41] and up to eight consensus TPR repeats [42] adopt folds that have root-mean-square-deviations of around 0.9 and 1.6Å, respectively, from analogous structures of naturally-occurring repeat proteins. Thus, structurally speaking, this simple consensus method for repeat-protein design is highly successful. Another successful aspect of consensus design is remarkably high thermodynamic stability. Compared to their naturally-occurring sequence-variable counterparts of the same length, designed consensus repeat proteins show very high midpoints in thermal- and denaturant-induced unfolding [27, 43, 44]. Recently, it has been shown that this high stability can be thermodynamically propagated into a naturally-occurring repeat protein array by fusing consensus repeats to the naturally-occurring domain [45].

Equilibrium two-state folding, multistate folding

Because repeat proteins have modular architectures, lack long-range contacts, are often relatively large (>=200 residues), and are highly extended, they might be expected to fold and unfold in a noncooperative way, in which different repeats unfold independently of one another. Contrary to this expectation, many naturally occurring repeat proteins display highly cooperative equilibrium unfolding reactions, showing hallmarks of all-or-none transitions. This section will highlight several of these reactions, describing methods used to detect this high cooperativity. We will also highlight the unfolding transitions of several naturally-occurring repeat proteins that undergo multistate transitions, including fragments of larger repeat proteins, chimeras of natural and consensus repeat proteins, and repeat proteins with substitutions that alter local stability. For a comprehensive table of stabilities of various repeat proteins, see [44].

Cooperative equilibrium folding of repeat proteins

Among linear repeat proteins, ankyrin repeat proteins have been most extensively characterized in unfolding studies, both at equilibrium and in kinetic studies. One of the first repeat proteins for which equilibrium unfolding studies were made is p16^INK4A, a human tumor suppressor protein containing four ankyrin repeats. Tsai and coworkers found this protein to display a steep, cooperative unfolding transition when helix content was monitored by circular dichroism (CD) spectroscopy as a function of guanidine hydrochloride, although the midpoint for the unfolding transition was rather low [46]. Similar results were obtained using urea [47] and thermal denaturation [48]. Later, Itzhaki’s group examined the unfolding transition of this protein more extensively [49], and showed that similar unfolding transitions (and fitted thermodynamic parameters) are obtained when urea-induced unfolding is monitored by CD, fluorescence from two N- and C-terminal tryptophans, and gel filtration chromatography [49]. Comparison of distinct probes that monitor different structural features is a classic test for two-state unfolding. Coincidence of such probes supports an all-or-none transition between the native (N) state and denatured (D) ensemble. More recently, another four-ankyrin-repeat protein, myotrophin, has also been shown to satisfy the spectroscopic test for cooperative equilibrium two-state unfolding, and displays an appropriately high m-value in urea denaturation [50].

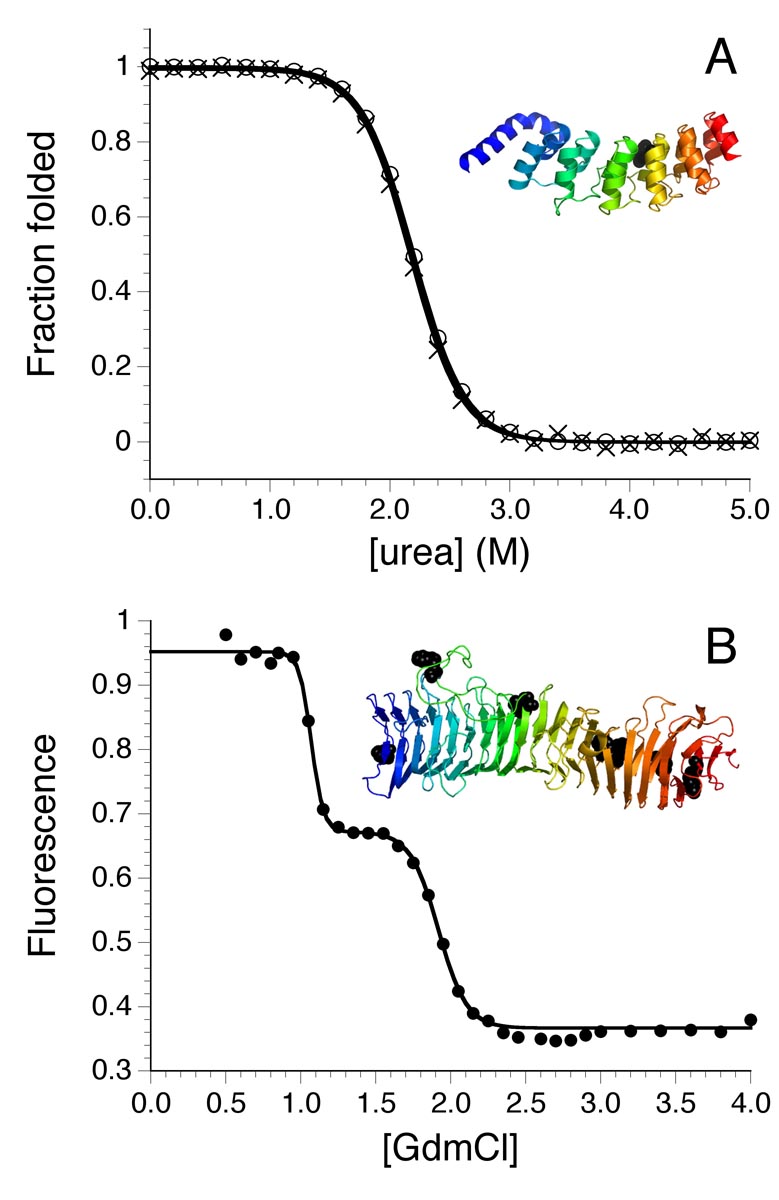
The Drosophila Notch ankyrin domain also appears to unfold via a cooperative, all-or-none mechanism. The Notch receptor contains seven ankyrin repeats, although the x-ray structure demonstrates that the most N-terminal sequence repeat is partly disordered (Figure 1) [51]. As with p16^INK4A, the Notch ankyrin domain also shows highly coincident unfolding transitions when monitored by CD in the α-helical region and by tryptophan fluorescence (Figure 3A). For Notch, there is a single tryptophan in repeat five; thus, the similarity of these two transitions indicates that to the extent that structure is disrupted at this single site, the global α-helical structure is similarly disrupted [30, 52]. Coincident spectroscopic unfolding transitions are obtained by both urea and thermal denaturation.

Figure 3. Equilibrium two-state and multistate unfolding of repeat proteins.

(A) Urea-induced unfolding of the Notch ankyrin domain, monitored by tryptophan fluorescence (circles) and CD (x’s) in the α-helical region. Data are converted to fraction folded to illustrate the coincidence of these two probes. The ribbon model shows the relative positions of the helices and the single tryptophan. Data adapted from [52]. (B) Guanidinium chloride-induced unfolding of pertactin, monitored by tryptophan fluorescence. The unfolding transition shows clear multistate reaction in which an intermediate is formed at ~1.5 M guanidinium chloride. Adapted with permission from [55].

Several other criteria have also been applied to assess the cooperativity in unfolding of the Notch ankyrin domain. One criterion is calorimetric: the enthalpy estimated from fitting a two-state model to the thermal transition (a “van’t Hoff enthalpy”) is the same, within error, as the heat of reaction determined calorimetrically, supporting a cooperative transition lacking in intermediates [30, 52]. Another criterion to assess cooperativity in unfolding of the Notch ankyrin domain comes from analysis of the sensitivity of unfolding free energy to urea (the m-value) and temperature (which reveals the change in heat capacity on unfolding, ΔC_p). Both the m-value and ΔC_p are correlated with the size of the cooperative unit; for proteins that unfold by a two-state mechanism both parameters are correlated with chain-length [2], whereas equilibrium intermediates decrease the m-value [53]. For the Notch ankyrin domain, these two parameters match what would be expected for a two-state transition [30].

Although less studied than helical repeat proteins, the equilibrium folding transitions of a few β-strand-containing repeat proteins have been also been examined. Internalin-B, a seven leucine-rich repeat protein from a pathogenic bacterium, appears to undergo a cooperative unfolding transition in which secondary structure and fluorescence are lost in a single transition [54]. In this study, reported m-values were significantly higher than expected for a two-state unfolding transition, and were interpreted as evidence of “unusually high” cooperativity, although association in the native state is an alternative explanation for such steepness. Recent results from our own laboratory demonstrate that internalin-B is monomeric in solution, although we measure m-values that are more in line with the number of residues in the equilibrium transition (NC & DB, manuscript in preparation).

Multistate equilibrium folding of repeat proteins

The examples above demonstrate that despite the modular architecture of repeat proteins (mostly α-helical ankyrin repeat proteins), a high degree of cooperativity in equilibrium folding is often observed, approaching macroscopic two-state behavior. This high level of cooperativity requires both ends of the protein to be thermodynamically coupled, despite their distance in sequence and space and their lack of direct contacts. It would be expected that surprisingly high cooperativity would be particularly difficult to maintain for repeat proteins where the ends are of very different stabilities, and for very long repeat arrays. Indeed, there are several repeat proteins that deviate from a simple two-state mechanism as a result of non-uniform stability distribution, and perhaps as a result of high repeat number.

Of the naturally occurring repeat proteins and fragments that show multistate unfolding, one of the most dramatic examples is the β-helix protein pertactin [55]. This protein, which contains roughly twenty β-helix repeats (three strands in a rough triangular arrangement), shows a clear three-state equilibrium unfolding transition, with a stable partly folded intermediate at around 1.5 M guanidine (Figure 3B). Limited proteolysis studies indicate that this intermediate is N-terminally disordered, but retains structure in the C-terminal half of the protein [55].

Another parallel β-helix protein that has been reported to show multistate unfolding is pelC, a pectate lyase from a protobacterium that causes rot in plant tissue [56]. Like pertactin, pelC contains repeats with a three-stranded triangular structure, although at seven repeats, pelC is significantly shorter than pertactin. Also, unlike pertactin, deviations from a two-state equilibrium transitions are very subtle, with minor differences between different spectroscopic probes, and a van’t Hoff enthalpy slightly lower than that reported by calorimetry [56].

Two naturally occurring helical repeat protein fragments also show evidence of multistate unfolding. p19^INK4D, another cyclin-dependent kinase inhibitor that contains five ankyrin repeats, shows a third species that forms in the transition region, as monitored by heteronuclear NMR [57]. Although unfolding transitions monitored by CD in the α-helical region match those monitored by phenylalanine fluorescence, the latter signal is likely to be distributed over four of the five repeats, and is thus likely to show a similar response to unfolding as CD, even if partly folded conformations are populated. A more dramatic multistate equilibrium unfolding transition has been observed for a large, twelve-ankyrin-repeat fragment of ankyrinR (named D34; [58]). Like pertactin, urea unfolding transitions of this large ankyrin repeat polypeptide show a clear multistate unfolding in which an intermediate is populated at moderate denaturant concentrations. Single-residue substitutions suggest that the N-terminal repeats are unstructured in this intermediate, but the C-terminal repeats remain structured [58].

Another means by which repeat proteins have been shown to populate partly folded states is in coupled folding-binding reactions, in which one or more ankyrin repeats are partly unstructured when free in solution but become structured when bound to a target protein. This type of conformational heterogeneity has been demonstrated elegantly for the six ankyrin repeats of IκBα. Hydrogen exchange studies show that ankyrin repeats 1, 5, and 6 are substantially disordered in the unbound state [59], but repeats 5 and 6 become structured on binding to NF-κB [60]. A similar disorder-order transition is seen crystallographically for the first repeat of the Notch ankyrin domain when binding the transcription factor CSL [51, 61, 62]. In both cases, this increased ordering on binding may provide allosteric regulation, promoting additional binding surfaces and repositioning key elements outside of the repeat-protein domains.

Both pertactin and the ankyrinR D34 polypeptide are longer than the repeat proteins that display two-state equilibrium unfolding, and the observations that both show clear, well-resolved equilibrium intermediates might reflect an upper size limit over which cooperativity breaks down. However, the structured regions of both intermediates are biased towards one end of the chain, suggesting that the ends differ in stability. Such a stability imbalance could promote multistate unfolding in the same way that structures made of straw, sticks, and stone display different mechanical resistance to wind shear [63].

Indeed, a number of studies have selectively destabilized (or stabilized) regions of repeat proteins, and in doing so, have converted the equilibrium mechanism from two-state to multi-state. C-terminal point substitutions of conserved residues in the Notch ankyrin domain were found to shift the equilibrium unfolding mechanism from two-state to a multistate mechanism in which the C-terminal repeats unfold at low denaturant concentrations [52]. This analysis suggested a thermodynamic coupling limit connecting the C-terminal and middle repeats, which was subsequently explored quantitatively by making multiple C-terminal substitutions [64]. In addition, when consensus repeats (described in the next section) are inserted between the central and C-terminal repeats (rather than substituting for the latter), multistate equilibrium unfolding results even without destabilizing point substitutions in the C-terminus [45]. Although analogous substitutions in the N-terminal ankyrin repeats of Notch retain equilibrium two-state character [65], these same N-terminal substitutions result in clear multistate unfolding (in which the N-terminal repeats unfold at low denaturant) in a background in which the C-terminus is stabilized by substitution with consensus repeats [45, 66].

These results suggest that one thermodynamic feature necessary for two-state folding in repeat proteins is that stability be distributed roughly uniformly, especially regarding the N- and C-termini [64]. If one terminus is substantially less stable than the other, it will not be able to retain structure under moderately destabilizing conditions, although the other (more stable) terminus will. This sensitivity to how stability is distributed along a repeat array has recently been described in analogy to a “fulcrum”, the pivot point about which a lever rotates [67]. Recent studies on the ankyrinR D34 polypeptide nicely illustrate this connection between stability distribution and cooperativity: destabilizing substitutions in the C-terminus promote suppress intermediates in the equilibrium transition, whereas analogous substitutions in the N-terminus enhance multistate unfolding [58].

Another class of repeat proteins that appear to fold via equilibrium multistate reactions is the consensus repeat proteins described above. Consensus TPR proteins containing 1- to 3-repeat capped consensus TPR proteins appear to unfold via a multistate equilibrium mechanism, based on a nonlinear length dependence of the measured m-value, and on the lower protection factors on terminal versus middle repeats[68]⁴. Multistate unfolding of consensus TPR arrays is supported by statistical thermodynamic analysis ([42], see below). A consensus ankyrin repeat protein populates equilibrium unfolding intermediates at high temperature, based on differential scanning calorimetry [69]. A consensus leucine rich repeat protein has been shown to unfold via a broad, noncooperative transition [26].

Although the structural units of globular proteins are difficult to describe architecturally, it is clear from hydrogen exchange studies that different regions of a protein have different stabilities, and undergo unfolding reactions with different probabilities [70]. In a few cases where hydrogen exchange and mutagenesis studies have begun to provide a measure of the energy distribution for globular proteins, a relationship has been found between local stability imbalance and the formation of equilibrium folding intermediates [71], and substitutions magnifying this imbalance promote multistate unfolding [53].

Mapping stability distributions and energy landscapes in repeat proteins by truncation

In principle, the degree of cooperativity in repeat protein unfolding should be able to be predicted from a quantitative description of the energy distribution among repeats. The modular architectures of repeat proteins allows the energetic contributions of different repeats to be experimentally determined through truncation, providing a quantitative test of the relationship between the uniformity of local stability and the equilibrium unfolding mechanism, and providing insights into cooperativity. Moreover, since repeats are structurally similar, differences in contributions of repeats to stability can be evaluated in terms of subtle differences within a conserved framework. Because interfaces between repeats do have some sequence variation, the easiest way to dissect the stabilities of repeats is to remove one or more repeats from the N- or C-terminus of a repeat domain. This avoids the creation of non-native interfaces.

One of the earliest experimental dissections of a repeat protein involved the 24 ankyrin-repeat domain of the protein ankyrin-R. Limited proteolysis studies showed that ankyrin-R could be separated into four folded fragments, each containing six repeats [72]. Although the crystal structure of D34, a construct containing the two C-terminal six-repeat fragments, shows a continuous stack of twelve repeats [73], the recent unfolding study of D34 [58] is consistent with a structural division proposed in the proteolysis study.

In a more quantitative dissection, p16^INK4A (four ankyrin repeats) was divided into two parts, and the C-terminal two-repeat fragment was shown to be folded and marginally stable, although the N-terminal fragment was not [74]. Further subdivision of the C-terminal fragment into single repeats led to complete unfolding. These results indicate that the energy landscape is tipped toward C-terminal structure.

The larger size of the Notch ankyrin domain, coupled with its simple equilibrium two-state folding mechanism, allowed the folding free energies of a larger deletion series to be determined [75]. By deleting single repeats from the N-terminus, the C-terminus, and both termini together, nine constructs (eight deletions and the full length protein) could be used to determine the stability distribution on a single-repeat level (constructs that contained fewer than four repeats were unfolded under the conditions used, thus their stabilities could not be quantified). Although a rough linear relationship between repeat number and folding free energy was obtained, significant variations in folding energies were seen for different constructs that contain the same number of repeats (e.g. repeats 1–5 versus 3–7) [75]. This variation reflects a local variation in the energy landscape for different partly folded states.

To take this variation, which is likely a result of differences in primary sequence among repeats, into account but retain additivity, the data were analyzed using a heterogeneous model with a free energy coefficient associated with each repeat:

$$\mathrm{\Delta }\mathit{G°}={\mathit{x}}_{\mathit{1}}\mathrm{\Delta }{\mathit{G}}_{\mathit{1}}+{\mathit{x}}_{\mathit{2}}\mathrm{\Delta }{\mathit{G}}_{\mathit{2}}+{\mathit{x}}_{\mathit{3}}\mathrm{\Delta }{\mathit{G}}_{\mathit{3}}+{\mathit{x}}_{\mathit{4}}\mathrm{\Delta }{\mathit{G}}_{\mathit{4}}+{\mathit{x}}_{\mathit{5}}\mathrm{\Delta }{\mathit{G}}_{\mathit{5}}+{\mathit{x}}_{\mathit{6}}\mathrm{\Delta }{\mathit{G}}_{\mathit{6}}+{\mathit{x}}_{\mathit{7}}\mathrm{\Delta }{\mathit{G}}_{\mathit{7}}$$ (1)

the x_i terms are simple binary variables with values of 1 or 0, depending on whether the repeat is present or absent in a particular construct [75]. The nine equations defined by the deletion series were fitted by this equation using multiple regression to estimate values for the seven free energy coefficients (ΔG_i) associated with each of the seven repeats. Assessed using cross-validation, the deletion series was well-fitted by the linear equation (1), with an unbiased correlation coefficient of 0.95 [75].

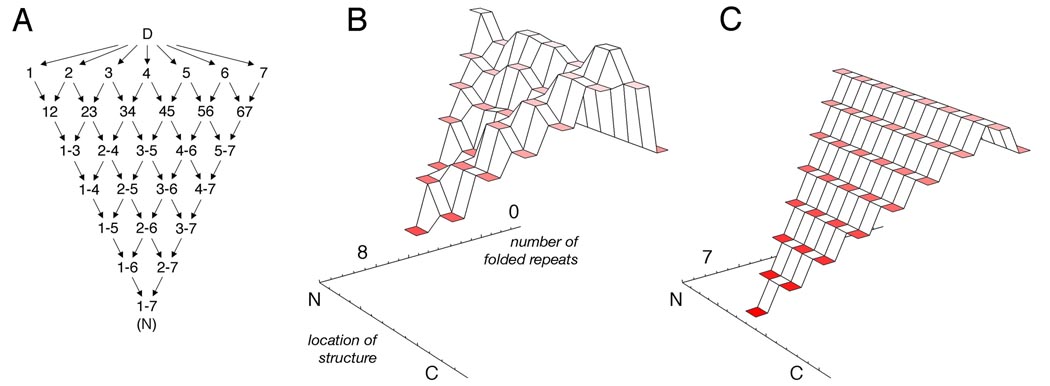
The deletion series of the Notch ankyrin domain provides a direct map of the energy landscape for constructs containing four or more folded repeats. In addition, the fitted energy coefficients for each repeat allow the energies of conformations with fewer than four repeats (which were too unstable to be analyzed in denaturation studies) to be estimated. With the assumption that interfaces between repeats are energetically equivalent (see below), these energy levels can be depicted as an energy landscape (Figure 4) [75]. Levels on this landscape correspond to constructs with a contiguous block of folded repeats, and are colored according to free energy, relative to the denatured state (green tier in the back; Figure 4B). These levels are depicted as a function of the number of folded repeats and as a function of where structure is localized (see schematic, Figure 4A). Thus, moving from the denatured ensemble to the native state corresponds to coalescing structure in neighboring repeats, and it can be done in a number of different ways, especially early in folding. Although conformations can be imagined that include non-contiguous blocks of repeats, the stability imbalance between (highly stable) interfaces and (highly unstable) single repeats strongly disfavors these conformations (see below).

Figure 4. Experimentally determined energy landscapes for helical repeat proteins.

(A) Reaction scheme for the Notch ankyrin domain showing transitions between nearest-neighbor conformations on the landscape. (B) Energy landscape of the Notch ankyrin domain. The energies of conformations with blocks of contiguous folded repeats, colored according to free energies, are shown as a function of the number of folded repeats and the location of partly folded structure (as in panel A). (C) Energy landscape for an eight helix consensus TPR construct, using the Ising analysis of Kajander ([42]; see Table 2 for energies). The landscapes in B and C are plotted on the same energy scale, and in both cases the fully folded states (right-most tier) are set to zero energy.

Several features of the energy landscape of the Notch ankyrin domain are worth further comment. First, for the most part, energy decreases in the direction of the native state as repeats are added to existing (i.e. folded) repeats (Figure 4B). In this regard, the landscape resembles a downhill “folding funnel”. An important exception is the formation of the first repeat, which is much higher in energy than the denatured state. This feature resembles an early barrier in the landscape (although there are almost certainly other, higher barriers not depicted). Second, energies vary on the landscape from one repeat to the next, creating the appearance of low-energy channels, suggestive of folding pathways. However, it should be kept in mind that since the energy landscape was determined from equilibrium studies, the kinetic routes for folding need not follow these low energy channels, depending on whether folding is under thermodynamic or kinetic control. Thus, determination of this real energy landscape from experiment prior to determining transition state structure and folding pathways experimentally provides a means to test whether pathways are chosen kinetically or thermodynamically.

A final feature of the Notch energy landscape is that although energies vary from repeat to repeat, there is an overall evenness on a length scale of two to three repeat blocks. As described above, this uniformity is likely to promote two-state equilibrium folding, whereas an imbalance in stability from one side of the landscape to the other would favor multistate unfolding. This has been tested quantitatively by deforming the Notch energy landscape so that one side is higher than the other in a way that corresponds to site-specific mutations. By raising energy levels of the C-terminal repeats, the energy landscape of the Notch ankyrin domain quantitatively predicts several aspects of the breakdown of equilibrium two-state folding for corresponding C-terminal substitutions, including sensitivity to multiple point substitutions, decreases in m-value, and deviations of spectroscopic probes from two-state behavior [64].

As an interesting comparison to the energy landscape of the Notch ankyrin domain, a similar landscape can be depicted for a variable-length consensus TPR series (described below) using the same type of coordinates. Using a nearest-neighbor approach applied by the Mochrie & Regan groups [42], conformational free energies can be plotted as a function of the extent of folding (in this case the number of helices formed) and location of structure using the energy coefficients described below. Owing to favorable nearest-neighbor interactions, the energy landscape for consensus TPR folding has the same overall shape as that for the Notch ankyrin domain, with an initial barrier followed by downhill folding to the native state, accompanied by progressive narrowing of conformational space (Figure 4C).

Unlike the energy landscape for the Notch ankyrin domain, which shows local variations suggestive of folding pathways (Figure 4B), the consensus TPR landscape is perfectly flat at each level of folding, owing to the sequence identity of repeats (Figure 4C).⁵ This evenness should strongly favor parallel folding pathways, with a weak bias for the central repeats based on the increased chances to form stabilizing interfaces compared with the end repeats. Thus, for consensus repeat proteins, experiments testing for transition state structure (such as Φ-value analysis) should show a highly delocalized transition state, reflecting multiple routes to the native state. In addition to being perfectly uniform across its width, the consensus TPR landscape differs from that of the Notch ankyrin domain in that it has a smaller initial barrier, compared to the subsequent decreases in energy resulting from adding units (in this case, folded repeats) to the growing array. This is expected to correspond to lower cooperativity for the consensus TPR arrays.

Ising models

The equilibrium thermodynamic studies of the full-length Notch ankyrin domain indicate that the entire molecule unfolds in a highly coupled single transition spanning from one end to the other [30, 52]. However, the ability of the linear model (eqn 1) to fit to the deletion series suggests that distant repeats can treated as thermodynamically independent [76]. The resolution to this paradox comes from analysis of the coefficients derived from fitting the deletion series. Each of these coefficients is defined by deletion of a repeat from the end of the ankyrin array. In such deletions, the unfolding free energy changes both from the loss of intrinsic stability of the deleted repeat (ΔG_intrinsic, the stability that the repeat would posses in isolation), and the loss of interaction of that repeat with its neighbor (ΔG_interface). Although longer-range interactions could, in principle, couple non-neighboring repeats, although due to the distance scales involved (about 10 Å per repeat), nearest-neighbor interactions are expected to dominate.

Provided that nearest-neighbor interactions are very favorable (ΔG_interface<<0), and isolated repeats are unstable (ΔG_intrinsic>0), simple nearest-neighbor interactions would be sufficient to thermodynamically couple distant repeats. As long as the interfacial free energy exceeds the intrinsic penalty, adding to the preexisting folded stack of repeats is energetically favorable. This thermodynamic profile is seen in the energy landscape of the Notch ankyrin domain (Figure 4A), and is reflected in the fitted free energy coefficients of equation 1, which give estimates of ΔG_intrinsic and ΔG_interface of +6.6 and −9.1 kcal/mol, respectively [76].

There are a number of examples in both biopolymer and material sciences where conformational transitions can be described in terms of nearest-neighbor interactions within a one-dimensional lattice. Such models are a subset of nearest-neighbor “Ising” models (after Ernst Ising [77]), and have been used to model interactions among magnetic dipoles, helix-coil transitions in peptides and nucleic acids [78–80], and protein folding [81, 82]. The advantage of Ising models, especially in a one-dimensional lattice, is that a statistical thermodynamic treatment can be used to quantitatively model the conformational equilibrium [80, 83]. Using the ΔG_intrinsic and ΔG_interface values determined from analysis of the Notch ankyrin deletion series, a partition function based on a cooperative Ising model was used to model the folding of the Notch ankyrin domain. Population analysis using this partition function supported two-state equilibrium unfolding, demonstrating that experimentally determined nearest-neighbor interaction is sufficient to couple the ends of the domain [76].

An Ising model has also been used elegantly to analyze the unfolding of variable-length consensus TPR constructs [42]. Consensus repeats are ideal for this type of analysis, because the identity of each repeat limits the number of parameters necessary to describe unfolding (ΔG_intrinsic, ΔG_interface, for example, and a perturbation parameter such as an m-value). Treating each helix (rather than each repeat, as in the analysis of the Notch ankyrin domain) as an individual Ising spin, Kajander et al were able to capture the unfolding of constructs of very different lengths, predicting a significant fraction of partly folded states, especially for the longer constructs [42]. This observation is consistent with the unfolding and hydrogen exchange studies described above [68].

Although ankyrin and TPR repeats differ in both primary sequence and structure, it is interesting to compare the intrinsic and interfacial energies determined in the Notch and consensus TPR systems. This comparison provides insight into the origins of the surprisingly high thermal stability in consensus repeat proteins, and the extent to which consensus design captures the remarkable cooperativity of repeat proteins. This comparison can be made by converting the fitted H and J terms from the analysis by Kajander et al. [42] to free energies for folding of a single unit (ΔG_intrinsic) and interfacial free energy (ΔG_interface). This is done in Table 2, where the energies of different microstates containing from zero to eight folded helices are calculated (four TPR repeats). From this, the intrinsic free energy of helix formation can be taken from the first step in folding (initiation), that is,

$$\mathrm{\Delta }{\mathit{G}}_{\text{intrinsic}}=-\mathit{2}\mathit{\text{RTH}}+\mathit{4}\mathit{\text{RTJ}}$$

Table 2.

Energy terms in an Ising for contiguous blocks of helices in a consensus TPR of eight helices (four repeats).

# folded helices	microstate	Internal: −RTHΣsi	Neighbor interaction: −RTJΣsisi+1	Ends: +RTJ(s1 + sn)	bGTotal (kcal/mol)	bStepwise ΔGi→j (kcal/mol)	bOverall ΔG0→j (kcal/mol)
0	−−−−−−−−	+8RTH	−7RTJ	−2RTJ	+RT(8H−9J)	n.a.	0
1	−−−−+−−−	+6RTH	−3RTJ	−2RTJ	+RT(6H−5J)	−2RTH+4RTJ	+2.33
2	−−−−++−−	+4RTH	−3RTJ	−2RTJ	+RT(4H−5J)	−2RTH	0.16
3	−−−+++−−	+2RTH	−3RTJ	−2RTJ	+RT(2H−5J)	−2RTH	−2.01
4	−−++++−−	0	−3RTJ	−2RTJ	−5RTJ	−2RTH	−4.18
5	−−+++++−	−2RTH	−3RTJ	−2RTJ	+RT(−2H−5J)	−2RTH	−6.35
6	−++++++−	−4RTH	−3RTJ	−2RTJ	+RT(−4H−5J)	−2RTH	−8.52
7	−+++++++	−6RTH	−5RTJ	0	+RT(−6H−5J)	−2RTH	−10.69
8	++++++++	−8RTH	−7RTJ	2RTJ	+RT(−8H−5J)	−2RTH	−12.86

H and J parameters from 1D Ising lattice treatment of Kajandar et al [42]. H represents the internal energy of a single lattice site, neglecting interaction terms with neighbors and ends, where helical (+) and unfolded (−) states have energies of +RTH and −RTH, respectively. In the Ising formalism, in which fictitious end-spins are included, H is closely related to the propagation energy (−2RTH; see entries in stepwise ΔG_i→j column). J captures interactions between adjacent sites, with a value −RTJ when adjacent sites are both helix (++) or both unfolded (−−), and +RTJ when they are in different states (+− or −+). J also captures interactions between the end sites (here positions 1 and 8) and sites off the end of the chain (fictitious positions 0 and 9) in (−) states. In the absence of denaturant, H=1.83 and J=1.9.

^bFree energies are evaluated at 298.15K.

ΔG_interface can be obtained from the free energy of adding a helix to an already formed helical stack (propagation), −2RTH. This propagation energy contains both an intrinsic free energy and an interfacial free energy; thus, the interfacial value can be obtained by difference:

$$\begin{array}{cc}-\mathit{2}\mathit{\text{RTH}}\hfill & =\mathrm{\Delta }{\mathit{G}}_{\text{intrinsic}}+\mathrm{\Delta }{\mathit{G}}_{\text{interface};}\hfill \\ \mathrm{\Delta }{\mathit{G}}_{\text{interface}}\hfill & =-\mathit{2}\mathit{\text{RTH}}-\mathrm{\Delta }{\mathit{G}}_{\text{intrinsic}}\hfill \\ \hfill & =-\mathit{2}\mathit{\text{RTH}}-(-\mathit{2}\mathit{\text{RTH}}+\mathit{4}\mathit{\text{RTJ}})\hfill \\ \hfill & =-\mathit{4}\mathit{\text{RTJ}}\hfill \end{array}$$

Numerical values for ΔG_intrinsic and ΔG_interface are obtained from substitution of the fitted parameters of J and H from Kajander et al. into the above expressions (Table 3). Comparison with the analogous free energies for the Notch ankyrin domain suggests that there is considerably less cooperativity in consensus TPR folding. The interfacial energy between ankyrin repeats is about twice the interfacial energy in the consensus TPR system.⁶ This lower cooperativity is consistent with the earlier thermodynamic studies of short consensus TPR constructs (see above; [68]). Thus, the greater stability of the consensus TPR constructs compared to the Notch ankyrin domain results from a more favorable intrinsic folding free energy (Table 3). This is especially true when comparing the intrinsic energy of folding a two-helix TPR repeat, which is 2ΔG_intrinsic+ΔG_interface=−4RTH−4RTJ=+0.16 kcal/mol, compared with ~6.6 for intrinsic folding of the Notch ankyrin domain.

Table 3.

Intrinsic and interfacial free energies from Ising analysis of repeat-protein folding

	ΔG°intrinsic (kcal/mol)	ΔG°interface (kcal/mol)
Notch ankyrin	+6.6	−9.1
Consensus TPR	+2.3 (per helix)	−4.5

ΔG° values for the Notch ankyrin domain folding are from Mello & Barrick [72]3}. ΔG° values for consensus TPR folding are from fitted J and H values Kajander et al. [42]5}, as described in the text. ΔG°_intrinsic for the consensus TPR corresponds to folding of a single helix, whereas for the Notch ankyrin domain this value corresponds to folding of an entire repeat. The intrinsic free energy for folding an entire TPR repeat corresponds to twice this value plus a single interfacial term, or +0.16 kcal/mol.

Although the above analysis is only a single comparison of a consensus and nonconsensus repeat, and although the two proteins have different architectures, the lower cooperativity and much higher intrinsic stability of the consensus repeat protein may reflect a fundamental difference between specific evolved sequences and “average” sequences. The consensus approach is likely to optimize very local energetics such as helix propensity and turn formation. In contrast, the interfacial interactions, which are longer range and involve side-chain packing and long-range hydrogen bonding interactions, involve pairwise and higher-order interactions among residues. These couplings can easily be missed in consensus sequences, which do not capture sequence covariance. This suggestion is consistent with the low cooperativity observed in the unfolding of a consensus LRR domain [26].

Kinetics of repeat-protein folding

Folding mechanisms

Although there are exceptions, equilibrium studies of repeat proteins show a surprisingly high degree of cooperativity, with many proteins conforming closely to a two-state equilibrium mechanism. In contrast, kinetic studies show a more complex picture: to date, kinetic two-state folding of repeat proteins is the exception rather than the rule. In addition to the usual complexities of proline isomerization [49, 65, 75, 84], which are often magnified in repeat proteins by the recurrence of proline residues at consensus positions, repeat proteins show additional kinetic phases in refolding and unfolding and show nonlinear “chevrons” (log relaxation constant versus denaturant concentration), often referred to as “roll-over” [85]. Although nonlinear chevrons have been suggested to result from movement of the transition state in an otherwise kinetic two-state mechanism [86], they are also consistent with (and often best explained by) a discrete on-pathway intermediate separating N and D [4, 85].

The four ankyrin-repeat protein p16^INK4A shows kinetic complexity beyond prolyl isomerization: three refolding phases are seen, and only the slowest phase can clearly be demonstrated to be influenced by prolyl isomerization [49]. The chevron plot of p16 is nonlinear, and the ratio of the folding and unfolding rate constants differs from the equilibrium constant for folding [49]. It is clear that at least one additional species is involved in the kinetics of p16^INK4A folding, although the number of intermediates and the kinetic mechanism of interconversion is unclear. Like p16^INK4A, the refolding of the five ankyrin repeat p19^INK4D shows three kinetic phases, the slowest of which is accelerated by prolyl isomerase [57]. A similar result is seen for the β-helix protein pelC, which shows four kinetic refolding phases, and appears to fold through a partly folded intermediate with substantial secondary and tertiary structure [84, 87].

The larger Notch ankyrin domain shows a single non-proline phase in folding, but two unfolding phases [75]. These two phases are associated with a roll-over in the unfolding arm of the chevron. This kinetic complexity can be fitted by a sequential three-state model with a single on-pathway intermediate separating N and D [75]. At high urea concentrations, the two unfolding steps (N→I and I→D) have similar rates, but at low urea concentrations, the first folding step (D→I) is much faster than the subsequent (I→N) step, and thus constitutes the rate-limiting process. In addition to fitting all of the kinetic data, fitted equilibrium constants and denaturant dependences from this kinetic three-state model reproduce the equilibrium values (involving just the lowest energy N and D states), supporting both the three-state kinetic and two-state equilibrium treatment [75].

Recently, the kinetics of myotrophin (four ankyrin repeats) have been reported by Itzhaki et al. [67, 88]. The chevron plot for myotrophin shows a nonlinear urea dependence. As the authors give conflicting interpretations of this curvature, suggesting both a kinetic two-state mechanism with a moving transition state [88] and a sequential on-pathway mechanism [67], the origin of this curvature is unclear.

Although it appears that consensus repeat proteins may have more complicated equilibrium folding mechanisms than do naturally occurring repeat proteins, in the limited number of published examples, folding kinetics of consensus repeats seem comparatively simple. For example, the chevron plot of E1_5, a three-repeat consensus ankyrin domain, is linear over a very broad range of urea concentrations. Moreover, the ratio of rate constants for folding and unfolding match the low-temperature two-state equilibrium constant, as does the urea dependence [69]. Likewise, two- and three-repeat consensus TPR proteins show simple linear chevrons, although measurements were restricted to a relatively narrow range of guanidine concentrations owing to the large rate constants for folding and unfolding [68]. Although more kinetic data on consensus repeat protein folding will be required before generalizations can be made, it is interesting to speculate on why these two repeat proteins fold by simple kinetic mechanisms, whereas naturally-occurring repeat proteins fold by complex kinetic mechanisms despite their simple equilibrium transitions. One simple possibility is that both consensus proteins described above are short. A second possibility is that as a result of their uniform energy landscapes, kinetic barriers involving different segments of consensus repeat proteins are all identical, and thus no particular pathways are favored. A third possibility is that, for consensus repeat proteins that have folded partway up, folding of the remaining structure would be no more difficult than the preceding steps (and if nucleation is limiting, it will be easier), thus rarifying kinetic intermediates under strongly native conditions. In contrast, for naturally occurring repeat proteins, the least stable repeats of the domain may be slow to fold and may result in a kinetic barrier that traps a partly folded state.

Overall (slow) rates of folding

Since repeat proteins all have local topology, they are all expected to fold rapidly based on contact order metrics [3]. Although rate constants vary from one repeat to the next, folding rates are generally much lower than predicted based on native state topology. For example, the Notch ankyrin domain folds approximately seven orders of magnitude slower than is predicted by relative contact order [75]. One simple source of this discrepancy is that relative contact order, which normalizes to the total chain length, is inappropriate for repeat proteins, which can be arbitrarily long (and for long repeat proteins like the Notch ankyrin domain, the transition state ensembles are likely to be substantially smaller). In support of this explanation, native-state metrics that do not normalize to chain length, such as long-range order and absolute contact order, are within three orders of magnitude.

Another possible explanation for the slow folding rates relates to the high cooperativity of naturally occurring repeat proteins, which results as much from the very low intrinsic stability of single repeats as from the stable interfaces. If the barrier for folding involves formation of two adjacent repeats without docking the repeats (interface formation would be stabilizing, and would thus be expected to be past the barrier), such a barrier would be very high in energy, and would be traversed very slowly, severely decreasing the rate of folding. Based on the analysis above of the Ising treatment, the consensus TPR repeats have much greater intrinsic stability (and lower cooperativity) than do the repeats of the Notch ankyrin domain, which may explain the much faster folding rate of the consensus constructs (for a three-repeat consensus TPR construct, the rate constant extrapolates to about 30,000 sec⁻¹ in the absence of guanidine [68]). Although the reported rate constant for folding of the three-ankyrin-repeat E1_5 consensus construct is similar to that of the naturally occurring p16^INK4A [69], E1_5 kinetics was measured at lower temperature (5 versus 25°C for p16 ^INK4A), likely slowing the rate of E1_5 folding substantially.

Transition state structures and pathways

As motivated in the beginning of this review, a key outstanding question in folding is whether folding proceeds by multiple parallel pathways (one extreme case being downhill folding) or by a restricted pathway (and if so, what determines the pathway). Given the structural redundancy of repeat proteins, folding by multiple parallel pathways involving different repeats seems quite plausible. Thus, mapping the structures of transition state ensembles and kinetic intermediates in repeat-protein folding provides a stringent test of parallel versus linear folding pathways. Moreover, the ability to experimentally determine energy landscapes for repeat proteins further motivates studies that map transition state ensembles and folding pathways, permitting the degree to which energetic biases select pathways to be determined (thermodynamic versus kinetic control).

Although bulk experimental variables (e.g. temperature, denaturant concentration, pH) can be used to learn about overall features of transition state structure, the best way to obtain high-resolution information is to make site-specific point substitutions and compare the equilibrium and kinetic effects [89, 90]. For a detailed account of results of this so-called “Φ-value” approach for globular proteins, see the review by Royer in this issue. The solution to the comparison afforded by repeat proteins simplifies Φ-value analysis, since similar substitutions (not only in amino acid type but in secondary and tertiary structure environment) can be made in different regions.

The first repeat protein for which the Φ-value method was applied to map transition state structure is p16^INK4A [91]. Because the folding reaction is complex, the authors chose to compute Φ-values for unfolding. These results indicate that the rate-limiting step in folding is the formation of repeats three and four (the two C-terminal repeats), whereas repeats one and two are unstructured [91].

More recently, the folding pathway of the Notch ankyrin domain was also analyzed by Φ-value analysis [65]. For this repeat protein, the complexity of the folding pathway is well-resolved, and the effects of analogous substitutions in each repeat on the on-pathway intermediate could be determined. Unlike p16^INK4A, the central repeats (three through five) are the first to fold, becoming partly structured in the rate-limiting step (the D to I transition) and becoming further structured in the kinetic intermediate. In contrast, repeats two, six and seven become structured only upon conversion of I to N.

Although the identities of the early-folding repeats differ in p16^INK4A and Notch, they both clearly show a preference for a discrete pathway involving two to three repeats. This pathway preference argues against a large number of parallel routes involving structure formation in different regions. The observation that more than one repeat is required in the rate-limiting step in folding is likely to result from a folding mechanism in which more than one (intrinsically unstable) repeat must be structured in the rate-limiting step in folding, but the (stabilizing) interface has yet to develop. This picture of the transition state is similar to that suggested computationally using a simplified (Go) model [92].

What determines the observed pathways for folding? For both p16^INK4A and Notch, observed folding pathways correspond to low energy routes connecting the denatured and native states. For p16^INK4A, the C-terminal folding pathway corresponds to the lowest energy substructure determined by deletion analysis [74]. For Notch, the early-folding central repeats correspond to a low energy channel through the landscape (Figure 4A [65, 76]). Thus, at least for these two proteins, folding pathway selection appears to be under thermodynamic control. Further evidence for thermodynamic control in pathway selection is provided by studies stabilizing the C-terminal repeats of Notch using consensus ankyrin repeats. This C-terminal stabilization greatly accelerates folding, suggesting that the transition state and pathway of folding has shifted, tracking the most stable region of the molecule [45]. Φ-value analysis in these consensus-stabilized constructs support this interpretation [66]. A shift in the folding pathway away from a destabilized set of ankyrin repeats has also been proposed in myotrophin [67].

Identifying the regions of greatest local stability as sites of initiation of folding is an important advance in understanding the mechanisms of protein folding. However, another important question remains: what determines the local stability of different repeats? A partial answer to this question can be found in at the primary sequence level: consensus sequences are stabilizing, thus divergence from consensus is apparently destabilizing. However, this answer is neither quantitative (it is not clear which consensus residues contribute the most to stability, and for the Notch ankyrin domain, stability differences cannot be rationalized by a simple consensus model) nor is it satisfying at a fundamental physical level.

So far, models that include greater physical detail than consensus sequence to predict ankyrin repeat protein folding have yielded mixed results. A molecular dynamics study of p16^INK4A unfolding, which included experimental Φ-value results in selecting the transition state ensemble, identified the first repeat as folded [93], in contrast to the experimental findings [91]⁷. And although a Go modeling study correctly predicted the folding pathway of p16^INK4A, the model predicted the Notch ankyrin domain to fold in an “outside-in” order (repeats two, six, and seven first; [92]) rather than the observed “inside-out” order (repeats three through five). Given the similar sequences, secondary structures, and folds of adjacent repeats, understanding the origins of free energy variation remains a key unsolved problem for predicting the folding pathways of repeat proteins (and likely globular proteins as well).

Forced unfolding by AFM

The bulk thermodynamic experiments described above are useful ways to study repeat-protein folding as they report average properties on very large populations of molecules. However, information about heterogeneity within the population is often lost due to the averaging inherent to such ensemble experiments. For this reason, it is of great interest to monitor the folding transition of single protein molecules in real-time, in hopes of gaining further insight into their folding mechanism.

One method to study unfolding of single protein molecules is force microscopy. Most forced unfolding studies have been performed using atomic force microscopy (AFM) [94, 95], although recently laser optical tweezers have also been employed to determine the forces and, importantly, the sequence of events in the folding reaction [96]. In both methods, the ends of a single polypeptide chain are attached to different surfaces, and the two surfaces are separated in a controlled way, leading to a quantifiable increasing, oppositely directed force on the termini of the polypeptide. When the force across the polypeptide chain exceeds the mechanical (kinetic) stability of the folded protein, unfolding occurs, leading to a rapid decrease in force, owing to the much greater extensibility of the unfolded chain.

Although there are many studies of the forced unfolding of globular proteins, to date there are only a few studies on repeat proteins, all using AFM. Repeat proteins are ideal candidates for single-molecule forced-unfolding studies due to their linear, modular structures and their frequent roles as structural elements in the cell. The elongated structures of these molecules suggest a linear reaction coordinate that naturally aligns with the unidirectional retraction coordinate used in force spectroscopy. In some cases, the application of force along the long axis of linear repeat proteins may be biologically relevant, as some linear repeat-containing proteins have been proposed to act as mechanical springs within the cell [97–101].

Forced unfolding studies of Ankyrin-B, a 24 repeat cytoskeletal protein have revealed two different forced unfolding events [97]. At low extensions, a linear force-displacement relationship is seen up to forces of 100pN, which the authors interpret as Hookean distortion of a fairly rigid superhelical ankyrin stack. Following an abrupt decrease in force, which the authors interpret as cooperative breakdown of tertiary structure to yield independent ankyrin repeats, additional peaks are detectable at forces less than 50pN. These smaller force peaks result in an increase in the contour length of the entire molecule of approximately 12nm each, which is the calculated contour length increment for unfolding a single ankyrin repeat, suggesting that, under force, the ankyrin repeats in this protein unfold individually in a non-cooperative manner [102]. The authors also observed refolding of individual ankyrin repeats upon relaxation of the stretching force, indicating that this process can be reversed in the AFM.

Atomic force microscopy has also been used to performed forced-unfolding studies of an ankyrin repeat-protein made of six consensus repeats, capped by two polar terminal repeats [103]. When subjected to forced unfolding, this protein also unfolds in multiple low-force transitions, each resulting in an increase of approximately 11.5nm in the total contour length, suggesting discrete unfolding transitions of full ankyrin repeat units. The forces associated with these transitions range from 30 to 70pN, similar to those observed for Ankyrin-B [102].

The stepwise unfolding of these ankyrin repeat-containing proteins under force differs from their highly cooperative behavior in bulk solution, where all repeats appear to unfold in a concerted transition. Although it might be argued that the greater level of detail revealed in the forced-unfolding studies results from observation of single molecules rather than ensemble averages, most forced unfolding studies (with the exception of transitions observed in forced-clamp format) are unique in that partial unfolding transitions relieve the destabilization on the remainder of the folded protein (owing to the substantial increase in contour length). In contrast, in bulk studies, destabilization is brought about by a uniformly-acting potential like denaturant or increased temperature, and partial unfolding of one region does not relieve the destabilization resulting on other regions. Because fragments of repeat proteins are known to be stable [74, 76], the persistence of stably folded fragments in the wake of partial forced-unfolding transitions should not be unexpected.

Since interfaces between ankyrin repeats are highly stabilizing, whereas individual repeats are unstable, the most likely scenario for forced unfolding is one in which individual repeats peel off in steps from a block of folded repeats. In this scenario, forced unfolding studies should identify the minimal number of repeats that can remain folded from the number of single-repeat transitions, as well as from the contour length increment produced in the last transition. Although this analysis was not presented for Ankyrin-B, force curves were observed to contain six (out of eight) individual consensus ankyrin unfolding transitions [103], suggesting three repeats as the minimum structure that can be folded and kinetically stable against forces of 30 pN or more. Whether the same minimal forced unfolding unit is observed in naturally occurring repeat proteins, which are of lower average stability, remains to be seen.

Conclusions and future directions

The simple architecture, dissectability and comparability of repeat proteins makes them attractive systems to learn about key issues in folding, including origins and limits of cooperativity, sequence-structure-stability relationships, energy landscapes, and kinetic pathways. Studies to date show that naturally-derived repeat proteins typically display a surprising amount of cooperativity in equilibrium unfolding transitions, provided that stability is distributed roughly evenly, on a several-repeat length scale, along the energy landscape. Studies of length dependence of stability indicate that cooperativity can be explained using nearest-neighbor statistical thermodynamics (“Ising models”) in which strongly stabilizing interfaces offset the high intrinsic instability of individual repeats. Consensus repeat proteins display surprisingly high stabilities, although they appear to be less cooperative as a result of both increased intrinsic and decreased interfacial stabilities. A quantitative understanding of the basis for consensus stability is likely to provide insight both into the underlying basis for stability and for evaluating the naturally occurring sequence variations among repeat proteins. Owing to several factors unique to single-molecule forced-unfolding studies a much higher level of detail is revealed in forced-unfolding studies, directly revealing a spectrum of partly folded states. The relationship between such states to the cooperativity in bulk needs to be better characterized.

In contrast, time-resolved studies show repeat proteins to populate transient kinetic intermediates, both in folding and unfolding. On-pathway kinetic intermediates appear to be common. For three examples to date, Φ-value analysis demonstrates that repeat proteins favor discrete pathways over parallel, distributed folding, despite their structural redundancy. Energy landscape analysis demonstrates that pathway selection is made on the basis of local free energy, and that folding pathways can be rerouted by resculpting the landscape. Although the in a few instances the kinetics of consensus repeat proteins has been examined, there is much insight to be gained in detailed kinetic studies of folding on a flat, weakly coupled landscape.