The Diffusion Decision Model: Theory and Data for Two-Choice Decision Tasks

Abstract

The diffusion decision model allows detailed explanations of behavior in two-choice discrimination tasks. In this article, the model is reviewed to show how it translates behavioral data—accuracy, mean response times, and response time distributions—into components of cognitive processing. Three experiments are used to illustrate experimental manipulations of three components: stimulus difficulty affects the quality of information on which a decision is based; instructions emphasizing either speed or accuracy affect the criterial amounts of information that a subject requires before initiating a response; and the relative proportions of the two stimuli affect biases in drift rate and starting point. The experiments also illustrate the strong constraints that ensure the model is empirically testable and potentially falsifiable. The broad range of applications of the model is also reviewed, including research in the domains of aging and neurophysiology.

1 Introduction

Diffusion models for simple, two-choice decision processes (e.g., Busemeyer & Townsend, 1993; Diederich & Busemeyer, 2003; Gold & Shadlen, 2001; Laming, 1968; Link, 1992; Link & Heath, 1975; Palmer, Huk, & Shadlen, 2005; Ratcliff, 1978, 1981, 1988, 2002; Ratcliff, Cherian, & Segraves, 2003; Ratcliff & Rouder, 1998, 2000; Ratcliff & Smith, 2004; Ratcliff, Van Zandt, & McKoon, 1999; Roe, Busemeyer, & Townsend, 2001; Stone, 1960; Voss, Rothermund, & Voss, 2004) have received increasing attention over the past 5 to 10 years for several reasons. First, in cognitive psychology research, the diffusion and other sequential sampling models (for a review, see Ratcliff & Smith, 2004) have accounted for more and more behavioral data from more and more experimental paradigms. Second, they have begun to be applied in practical domains, such as aging, where they allow new interpretations of well-known empirical phenomena. Third, the models are being applied to neurophysiological data, where they show potential for building bridges between neurophysiological and behavioral data.

This review has three major aims. The first aim is to review and explain in detail how the diffusion model (Ratcliff, 1978) accounts for the effects of various experimental manipulations on all aspects of two-choice data: accuracy, mean response times for correct responses and for error responses, and the full response time distributions for correct and error responses. In particular, it is essential to examine and evaluate the model's predictions for the shapes and behaviors of reaction time (RT) distributions and for the relative speeds of correct and error RTs. It is these aspects of data that provide strong tests of the diffusion model in particular and sequential sampling models in general. In the first half of this article, experiments 1, 2, and 3 illustrate these tests.

The second aim is to provide a diffusion model analysis of a popular experimental paradigm in the neurophysiological literature, a motion discrimination task. In this task, an array of dots is presented to the subject, and some proportion of the dots move in the same direction, either right or left, while the remainder of the dots move in random directions. The task of the subject is to determine the direction of motion of the dots moving coherently. The proportion of dots moving coherently is manipulated to provide levels of difficulty ranging from very difficult to very easy. Experiments 1, 2, and 3 investigated this task with human subjects. The data allow analyses of both correct and error RT distributions, something that has not been done before with this task with human subjects. The RT distributions are notably different in shape from those that have been obtained in the motion discrimination task with monkeys in neurophysiological research (Ditterich, 2006; Roitman & Shadlen, 2002), but they are highly consistent with results from many other paradigms with humans.

For simple two-choice decisions, empirical RT distributions for humans are generally positively skewed. Increases in the difficulty of a decision lead to increases in mean RT and decreases in accuracy. Increases in difficulty also produce regular changes in RT distributions, changes in their spread but very little change in their shape. Mosteller and Tukey (1977) pointed out that the shape of a distribution is what is left after location and scale are removed, where location is the position of the distribution (e.g., the mean) and scale is the spread (e.g., the standard deviation). One useful way of comparing RT distributions is to plot quantiles of one distribution against quantiles of another. If the distributions have the same shape, then the resulting quantile-quantile plot is linear. Later we present plots of this kind and show that the diffusion model predicts changes in mean and spread but little change in shape.

The third aim of the review is to describe how the diffusion model extracts theoretically relevant components of processing from the accuracy and RT data of two-choice tasks. Given that the model provides a qualitatively and quantitatively accurate account of data, the parameters of the model represent components of processing, and therefore the effects of experimental manipulations on the components can be observed. In other words, the model provides a decomposition of data that isolates components so that they can be individually studied. For example, the information that becomes available from stimulus encoding can be isolated, modeled, and then combined with the diffusion decision process to predict accuracy and RT distribution data. A model that explains how information is accrued from a stimulus should provide values of stimulus information that, when fed through the diffusion model, predict accuracy and RT distributions. In this way, the diffusion model can provide a meeting point between a model for stimulus encoding and representation and decision processes. Similarly, decision criterion settings can be extracted from data so that models can be developed to explain how the settings are determined by instructions, payoffs, reward contingencies, and so on. The duration of processing components outside the decision process can also be extracted and sometimes used to determine whether one experimental condition differs from another by the addition of an extra stage of processing. An extra stage is indicated when the model cannot accommodate the data under the assumption that the nondecision components have the same duration for all experimental conditions. In this case, the difference between the durations for the nondecision components would estimate the duration of the added stage.

Because the diffusion model can separate components of processing, it has come to be used in a variety of research domains, for example, to study the effects of age and aphasia on memory and decision criteria (college students to 90 year old; Ratcliff, Thapar, & McKoon, 2001, 2003, 2004; Thapar, Ratcliff, & McKoon, 2003; Ratcliff, Perea, Coleangelo, & Buchanan, 2004) and the effects of depression on information processing (White, Ratcliff, Vasey, & McKoon, 2007). Recent studies have also mapped the model's components of processing onto neural firing rate data, in part because diffusion processes appear to naturally approximate the behavior of aggregate firing rates of populations of neurons. These applications of the model are reviewed in the latter half of this review.

2 The Diffusion Model

The diffusion model is a model of the cognitive processes involved in simple two-choice decisions. It separates the quality of evidence entering the decision from decision criteria and from other, nondecision, processes such as stimulus encoding and response execution. The model should be applied only to relatively fast two-choice decisions (mean RTs less than about 1000 to 1500 ms) and only to decisions that are a single-stage decision process (as opposed to the multiple-stage processes that might be involved in, for example, reasoning tasks).

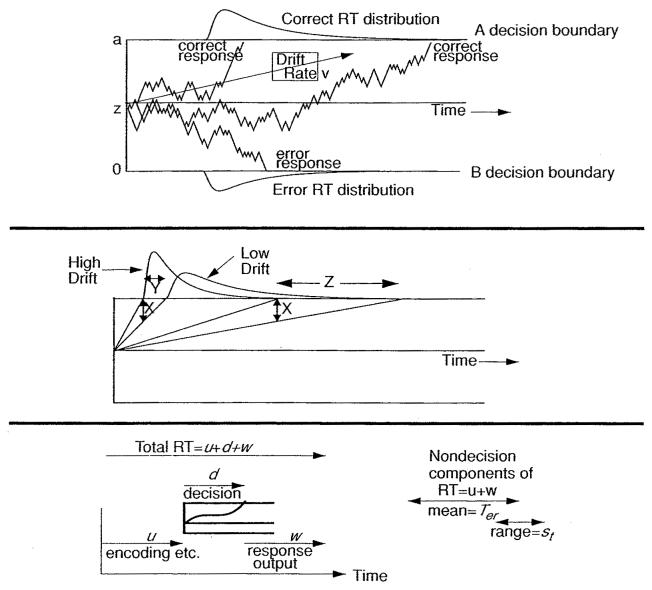
The diffusion model assumes that decisions are made by a noisy process that accumulates information over time from a starting point toward one of two response criteria or boundaries, as shown in the top panel of Figure 1. The starting point is labeled z and the boundaries are labeled a and 0. When one of the boundaries is reached, a response is initiated. The rate of accumulation of information is called the drift rate (v), and it is determined by the quality of the information extracted from the stimulus. In an experiment, the value of drift rate, v, would be different for each stimulus condition that differed in difficulty. For recognition memory, for example, drift rate would represent the quality of the match between a test word and memory. A word presented for study three times would have a higher degree of match (i.e., a higher drift rate) than a word presented once. The zero point of drift rate (the drift criterion, Ratcliff, 1985, 2002; Ratcliff et al., 1999) divides drift rates into those that have positive values, that is, mean drift rate toward the A response boundary in Figure 1, and negative values, mean drift rate toward the B boundary.

Figure 1.

The diffusion decision model. (Top panel) Three simulated paths with drift rate v, boundary separation a, and starting point z. (Middle panel) Fast and slow processes from each of two drift rates to illustrate how an equal size slowdown in drift rate (X) produces a small shift in the leading edge of the RT distribution (Y) and a larger shift in the tail (Z). (Bottom panel) Encoding time (u), decision time (d), and response output (w) time. The nondecision component is the sum of u and w with mean = T_er and with variability represented by a uniform distribution with range s_t.

There is noise (within-trial variability) in the accumulation of information so that processes with the same mean drift rate (v) do not always terminate at the same time (producing RT distributions) and do not always terminate at the same boundary (producing errors), as shown by the three processes, all with the same drift rate, in the top panel of Figure 1. Within-trial variability in drift rate (s) is a scaling parameter for the diffusion process (i.e., if it were doubled, other parameters could be multiplied or divided by two to produce exactly the same fits of the model to data). Note that for Figure 1 and all the other figures illustrating the model in this review, continuous diffusion processes were approximated by discrete random-walk processes.

Empirical RT distributions are positively skewed, and in the diffusion model, this is naturally predicted by simple geometry. In the middle panel of the figure, distributions of fast processes from a high drift rate and slower responses from a lower drift rate are shown. If the higher and lower values of drift rate are reduced by the same amount (X in the figure), then the fastest processes are slowed by an amount Y and the slowest by a much larger amount, Z.

The bottom panel of Figure 1 illustrates component processes assumed by the diffusion model: the decision process with duration d, an encoding process with duration u (this would include memory access in a memory task, lexical access in a lexical decision task, and so on), and a response output process with duration w. When the model is fit to data, u and w are combined into one parameter to encompass all the nondecision components with mean duration T_er.

The components of processing are assumed to be variable across trials. For example, all words studied three times in a recognition memory task would not have exactly the same drift rate. The across-trial variability in drift rate is assumed to be normally distributed with standard deviation η. The starting point is assumed to be uniformly distributed with range s_z, and the nondecision component is assumed to be uniformly distributed with range s_t. The first two sources of variability have consequences for the relative speeds of correct and error responses, and this will be discussed shortly. One might also expect that the decision criteria would be variable from trial to trial. However, the effects would closely approximate the effect of starting point variability, and computationally, only one integration over starting point is needed instead of two separate integrations over the two criteria.

The effect of across-trial variability in the nondecision component depends on the mean value of drift rate (Ratcliff & Tuerlinckx, 2002). With large values of drift rate, variability in the nondecision component acts to shift the leading edge of the RT distribution shorter than it would otherwise be, by as much as 10% of s_t. With smaller values of drift rate, the effect is smaller. Across-trial variability in the nondecision component allows the model to account for data that have considerable variability in the .1 quantiles of the RT distributions across experimental conditions (Ratcliff & Tuerlinckx, 2002).

The standard deviation in the duration of the nondecision component (s_t/(2 sqrt(3))) that is estimated from experimental data is typically less than one-quarter the standard deviation in the decision process, so variability in the nondecision component has little effect on the shape or standard deviation of overall RT distributions (Ratcliff & Tuerlinckx, 2002, Figure 11). For example, if s_t is 100 ms (SD = 28.9 ms) and the SD in the decision process is 100 ms, the combination (square root of the sum of squares) is 104 ms.

Figure 11.

Response proportion, mean RT for correct responses, and drift rate as a function of coherence. For the top and middle panels, the o's are data, and the x's are predictions from the diffusion model. In the bottom panel, the numerals 1, 2, and 3 refer to experiments 1, 2, and 3.

2.1 Drift Rate, Boundary Separation, and RT Distributions

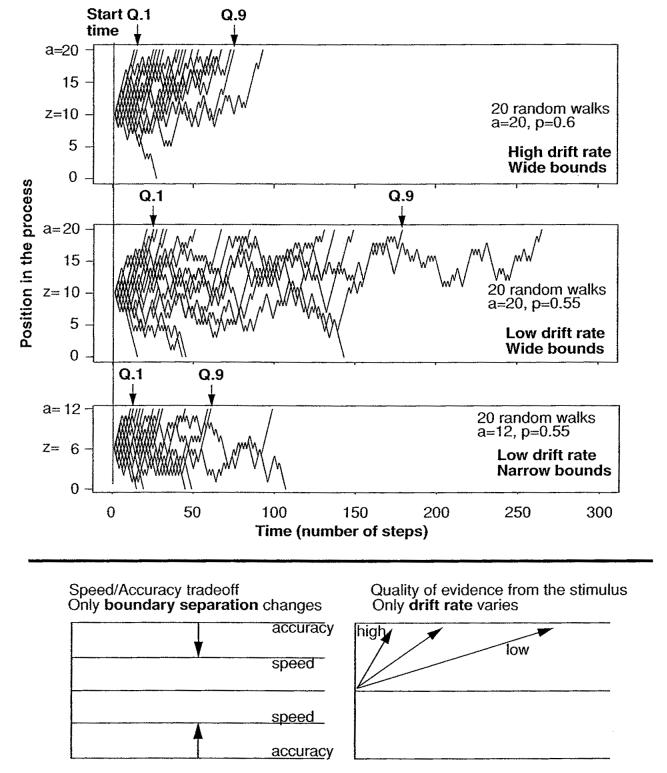
Figure 2 illustrates how RT distributions change as a function of drift rate and boundary separation, the components of processing that were manipulated in experiments 1 and 2. For each of the three simulation panels, 20 trials were simulated with the parameter values listed in the figure. p is the probability of a step toward the A response boundary in the random walk approximation of the diffusion process, the equivalent of drift rate in the continuous diffusion process. Twenty processes are sufficient to illustrate predictions of the model for RT distributions, although they are not exact (many more would be needed to obtain exact values). Each panel shows all 20 processes. The first point to note is how variable they are, which is due to within-trial variability in drift rate.

Figure 2.

Simulated diffusion processes. Each of the top three panels shows 20 processes simulated by random walks. Q.1 and Q.9 refer to the .1 and .9 quantiles of the resulting sets of RTs. For the top simulation, the upper boundary is a = 20 (the starting point is z = a/2 in each simulation), the lower boundary is 0, and the probability of taking a step toward the top boundary of .6. For the second simulation, the probability of taking a step toward the top boundary is reduced to .55, and for the third simulation, the upper boundary is reduced to a = 12. On the bottom panel, boundary separation alone changes between speed and accuracy instructions, and drift rate alone varies with stimulus difficulty.

Comparing the top and middle simulations, mean drift rate was changed from a higher to a lower value while a and z remained constant. The decrease in drift rate slows responses in the leading edge of the RT distribution (reflected in the .1 quantile of RTs) a little, and it slows responses in the tail (reflected in the .9 quantile) more. The diffusion model predicts changes in the .9 and .1 quantiles typically to be in the ratio of about 4:1. Comparing the middle and bottom simulations, boundary separation and starting point (i.e., a and z) were decreased while drift rate stayed constant. The decrease produces large changes in both the tail and the leading edge (the .9 and .1 quantiles), typically in a ratio of about 2:1. Also, decreasing the boundary separation results in a speed-accuracy trade-off: RTs decrease at the cost of more errors. As will be shown later, the model can explain the effects of manipulations of stimulus difficulty with changes only in drift rate, and it can explain the effects of speed versus accuracy instructions with changes only in boundary separation (bottom panel of Figure 2).

2.2 Response Proportions and RT Distributions

A standard manipulation in two-choice experiments in psychophysics and human performance research is to vary the relative proportions of the two responses (e.g., Swets, 1961). This can be accomplished by changing the proportions of the stimuli: stimuli for which one response is correct are presented on a larger proportion of trials than stimuli for which the other response is correct. Response proportions can also be manipulated without changing the proportions of stimuli: subjects can be asked to be more careful about one response than the other, or subjects can be rewarded to a greater degree for one response than the other.

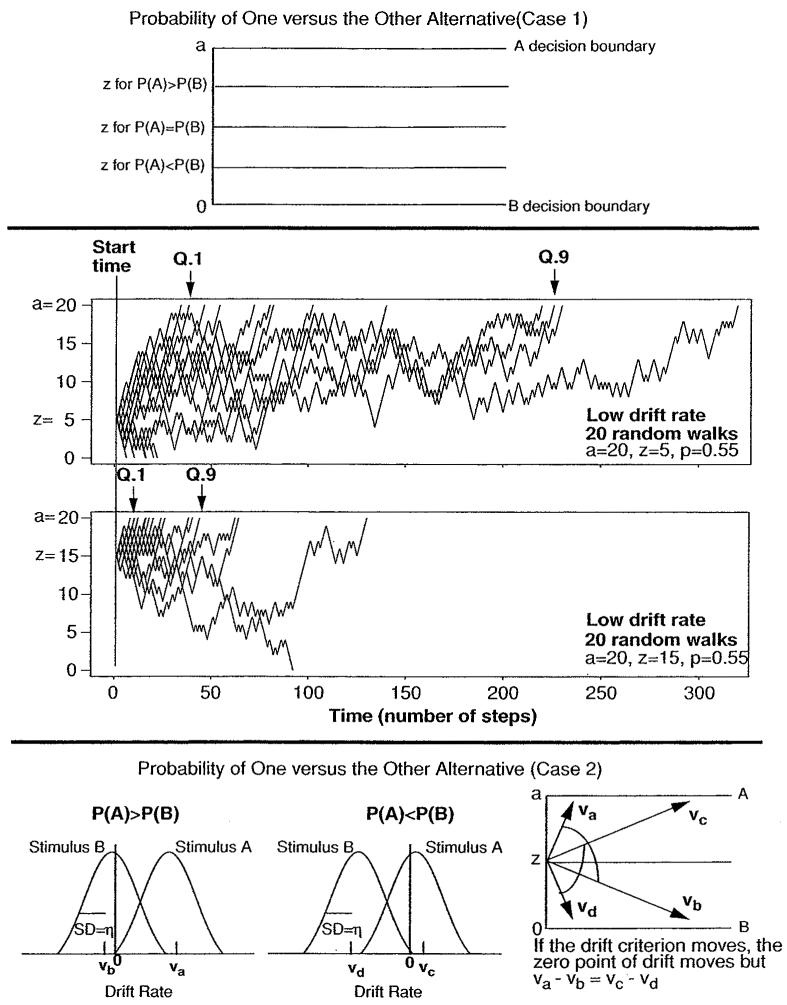
In the diffusion model, there are two ways of modeling the effects of these proportion manipulations. For one (see the top panel, Figure 3), the starting point moves closer to the more likely response. The effects are illustrated with 20-trial simulations in the second panel of Figure 3 (a was set at 20, p at .55). When the starting point is far from the boundary at which a response would be correct, the whole distribution of correct responses is shifted to longer RTs than when the starting point is equidistant between the two boundaries, with the slowest responses (e.g., .9 quantiles) slowing much more than the fastest responses (.1 quantiles). This can be seen by comparing the top simulation in Figure 3 to the middle simulation in Figure 2. When the starting point is near the boundary at which a response would be correct, the whole distribution of correct responses is shifted to shorter RTs than when the boundaries are equidistant (second simulation in Figure 3 to the middle simulation in Figure 2). In addition, there are more errors when the starting point is far from the correct boundary than when it is near.

Figure 3.

Diffusion model explanations for the effects of response probability manipulations. In the top panel, the first possible account is presented: starting point varying with probability. The effects are illustrated with two simulations in the second panel with z = 5 and z = 15. In the bottom panel, the second possibility is presented: drift criterion (the zero point) varying with probability. When the probability of response A is higher, the drift rates are v_a and v_b, with the zero point close to v_b. When the probability of response B is higher, the drift rates are v_c and v_d, and the zero point is closer to v_c. Note that this second alternative is exactly equivalent to how the criterion would change in signal detection theory from psychophysics.

The second way of modeling response proportion manipulations is to adjust the zero point of drift rate. The bottom panel of Figure 3 illustrates the distributions of drift rates for stimuli for which A is the correct response and stimuli for which B is the correct response. The distributions arise from across-trial variability in drift rate. Values of drift rate above the zero point are positive, that is, with drift toward the A boundary, and values below the zero point are negative, with drift toward the B boundary. When the probability of A being the correct response is higher (left graph), the zero point shifts toward the B distribution, and when the probability of B being the correct response is higher (right graph), the zero point shifts toward the A distribution. The differences between the means of the distributions do not change (v_a − v_b = v_c − v_d), only the zero point. The consequences for accuracy and distribution shape are the same as those for changing drift rate. In the simulations in Figure 2, a higher drift rate produces faster and more accurate responses (top simulation), while a lower drift rate produces slower and less accurate responses (second simulation). For RT distributions, this results in small changes in the position of leading edge and larger changes in the position of the tail as in Figure 2 first and second simulations.

Empirically, the two possible accounts of probability effects can be distinguished by their differing effects on RT distributions. As just explained, a shift in the starting point of the process produces large changes in both the leading edge and tail, and a shift in the zero point of drift rate produces large changes only in the tail.

Adjusting the zero point for drift rate has an exact analogy in signal detection theory. The diffusion model replaces the signal and noise distributions of signal detection theory with distributions of drift rates (Ratcliff, 1978, 1985; Ratcliff et al., 1999). In signal detection theory, the difference between the signal and noise distributions (d′) is usually invariant over probability manipulations, and in the diffusion model, the difference between the drift rate distributions is likewise invariant in at least the few cases examined so far.

2.3 Correct Versus Error RTs

Error responses are typically slower than correct responses when accuracy is stressed in instructions or in experiments where accuracy is low and errors are usually faster than correct responses when speed is stressed in instructions or when accuracy is high (Luce, 1986; Swensson, 1972).

Early random walk models could not explain these results. For example, if the two boundaries were equidistant from the starting point, the models predicted that correct RTs would be equal to error RTs, a result almost always contradicted by data (e.g., Stone, 1960). There were several partially successful attempts to produce unequal RTs (e.g., Laming, 1968; Link & Heath, 1975; Ratcliff, 1978). When Ratcliff (1978) assumed that drift rate was variable across trials, the diffusion model could predict error RTs longer than correct RTs. Laming (1968) showed that if the starting point was variable from trial to trial (hypothesized to result from sampling before the stimulus had been presented), then errors were predicted to be faster than correct responses, as they were for the choice reaction time experiments examined by Laming. Ratcliff (1981) suggested that the combination of across-trial variability in drift rate and across-trial variability in starting point might be able to account for all of the empirically observed patterns of correct and error RTs. Ratcliff et al. (1999; also Ratcliff & Rouder, 1998) later showed that this suggestion is correct. With the availability of fast computers that allowed the model to be fit to data, Ratcliff et al. demonstrated that the model could explain data from experimental conditions for which error RTs were faster than correct RTs and conditions for which they were slower, even when errors moved from being slower to being faster than correct responses in a single experiment.

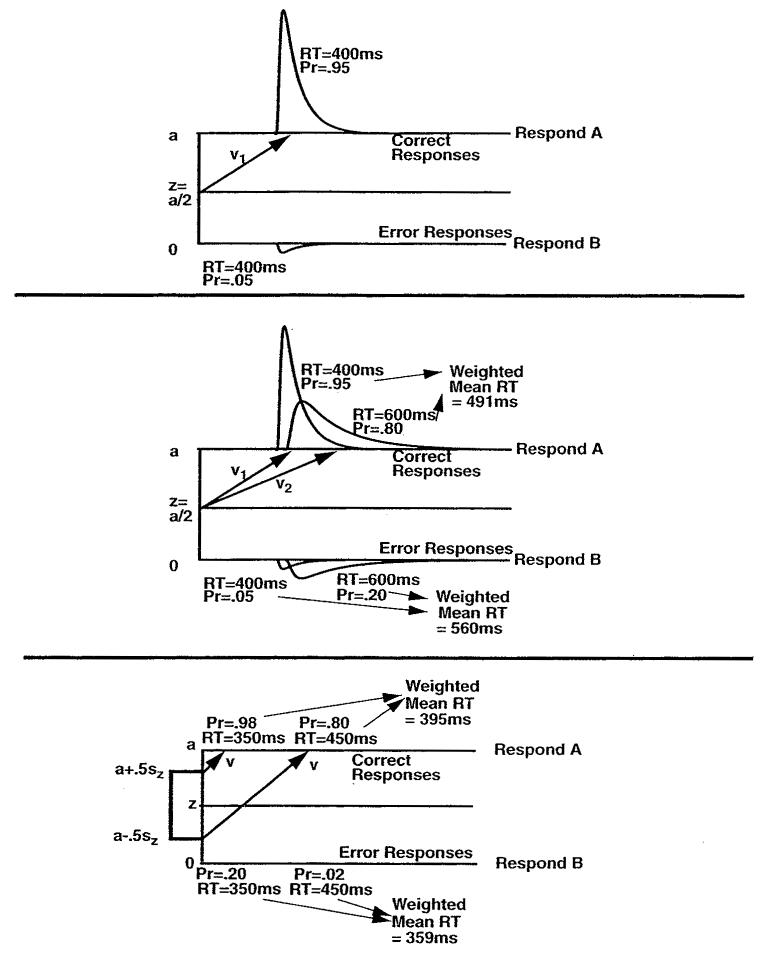
Figure 4 shows how the across-trial variabilities work to produce the relative speeds of correct and error RTs. The top panel shows a single process with mean drift rate (v) and starting point (z) midway between the two boundaries; in this case, correct and error RTs are equal. In the middle panel, the full distribution of drift rates around the mean v that results from across-trial variability is abbreviated to just two values: one (v₁) a larger value of drift rate and the other (v₂) a smaller value. Both correct and error RTs are shorter for the v₁ drift rate than the v₂ drift rate, and accuracy is better. When the two processes are combined, as they would be in the full distribution, errors are slower than correct responses because the slow error responses (RT 600 ms) from v₂ have a greater probability of occurrence (probability .20) than the fast error responses (RT 400 ms) from v₁ (probability .05).

Figure 4.

Variability in drift rate and starting point and the effects on speed and accuracy. The top panel shows RT distributions and response probabilities for correct and error responses with drift rate v. For a single drift rate, correct and error responses have equal RTs, 400 ms in the illustration. The middle panel shows two process with drift rates v₁ and v₂ and the starting point halfway between the boundaries with correct and error RTs of 400 ms for v₁ and 600 ms for v₂. Averaging these two illustrates the effects of variability in drift rate across trials and in the illustration yields error responses slower than correct responses. The bottom panel shows processes with two starting points and drift rate v. Averaging processes with starting point a + .5s_z (high accuracy and short RTs) and starting point a − .5s_z (lower accuracy and short RTs) yield error responses faster than correct responses.

In the bottom panel, the distribution in starting point due to across-trial variability is abbreviated to two values: one closer to the A boundary (at z = a + .5s_z) and one farther from the A boundary (at z = a − .5s_z). Processes starting near the incorrect boundary have a greater probability of reaching that boundary (probability .20) and are faster than those starting farther away (probability .02), so their combination leads to errors faster than correct responses.

2.4 Scaling of Accuracy and RT

A rarely discussed problem is the potentially troubling relationship between accuracy and RT. Accuracy has a scale with limits of zero and 1, while RT has a lower limit of zero and an upper limit of infinity. In addition, the standard deviations in the two measures change differently: the standard deviation in accuracy decreases as accuracy approaches 1, whereas the standard deviation in RT increases as RT slows. In the diffusion model (as well as other sequential sampling models), these relations between accuracy and RT are directly explained. The model accounts for how accuracy and RT scale relative to each other and how manipulations of experimental variables differentially affect them. This is a major advance over models that address only one dependent variable—only mean RT or only accuracy.

2.5 Summarizing RT Distribution Shape

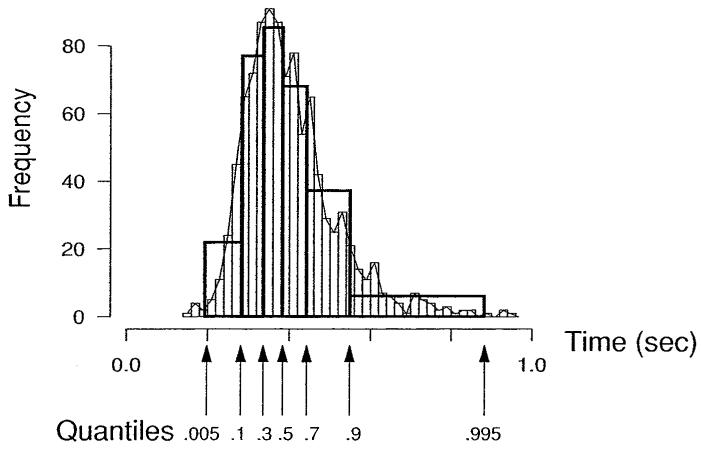
Ratcliff (1979) showed that for two-choice tasks, quantile RTs provide a good summary of the RT distribution for an experimental condition and that averaging the quantiles over subjects provides a good summary of the distribution for the average subject. To find the quantiles, RTs are ordered from shortest to longest, and the RT corresponding to the point that is 10% from the fastest response is the .1 quantile, the point that is 30% from the fastest is the .3 quantile, and so on (interpolating when necessary). In Figure 5, the RT distribution for the RTs in an experimental condition is shown as a histogram, and the .1, .3, .5, .7, and .9 quantiles are marked on the x-axis. The figure shows how the shape of the histogram can be recovered from the quantiles by constructing probability mass rectangles between a very low probability and the .1 quantile, between each pair of quantiles from .1 to .9 (probability .2 between each), and between a very high probability and the .9 quantile. In Figure 5, the lowest probability was .005 (.095 probability between .005 and .1) and the highest was .995 (.095 probability between .9 and .995). (The .005 and .995 values were used instead of 0 and 1 because a true zero probability density at the upper value is at infinity.) Over the whole distribution, the five quantile RTs provide an adequate summary for modeling purposes because they capture the typical RT distribution shape: unimodal with a relatively rapid rise to a peak followed by a longer tail.

Figure 5.

A RT distribution overlaid with .1, .3, .5, .7, and .9 quantiles, where the .1 quantile ranges from .005 to .1 and the .9 quantile from .9 to .995. The areas between each pair of middle quantiles are .2, and the areas below .1 and above .9 are .095. The quantile rectangles capture the main features of the RT distribution and therefore a reasonable summary of overall distribution shape.

2.6 Fitting the Diffusion Model to Data

Ratcliff and Tuerlinckx (2002) evaluated several methods for fitting the diffusion model to data and found that a chi-square method using quantile RTs provided the best balance between accurate recovery of parameter values (with the smallest variability in parameter estimates) and robustness to contaminant RTs (e.g., outlier RTs). The method uses quantiles of the RT distributions for correct and error responses for each condition of an experiment (the .1, .3, .5, .7, and .9 quantiles are usually used). The diffusion model predicts the cumulative probability of a response at each RT quantile. Subtracting the cumulative probabilities for each successive quantile from the next higher quantile gives the proportion of responses between adjacent quantiles. For the chi-square computation, these are the expected values, to be compared to the observed proportions of responses between the quantiles (i.e., the proportions between .1, .3, .5, .7, and .9, are each .2, and the proportions below .1 and above .9 are both .1) multiplied by the number of observations. Summing over (Observed-Expected)²/Expected for correct and error responses for each condition gives a single chi-square value that is minimized with a general SIMPLEX minimization routine. The parameter values for the model are adjusted by SIMPLEX until the minimum chi-square value is obtained (Ratcliff & Tuerlinckx, 2002).

Typically, before fitting the model to data, short and long outlier RTs are eliminated (usually no more than 2% to 3% of responses). Contaminant responses that are within the upper and lower cutoffs (e.g., from momentary lapses of attention) are modeled by including a parameter, p_o, that represents the proportion of contaminant responses in each condition of an experiment (Ratcliff & Tuerlinckx, 2002). Ratcliff and Tuerlinckx showed that excluding contaminants in this manner allows accurate recovery of the other parameters of the diffusion model (i.e., the estimates of the other components of processing); that is, explicitly modeling contaminants keeps them from affecting estimates of the other model parameters. Ratcliff and Tuerlinckx assumed that the distribution of contaminants was uniform, with maximum and minimum values corresponding to each experimental condition's maximum and minimum RTs (after cutting out short and long outliers). Ratcliff (in press) showed that the recovery of the other parameters was accurate under the assumption of a uniform distribution even if the true contaminant distribution was calculated by a constant time added to an RT from the diffusion process or by an exponential time added to an RT from the diffusion process.

3 Quantile Probability Plots and Across-Trial Variability

In order to present both the RT distributions and accuracy values for all the conditions of an experiment on the same graph, the quantiles of the RT distribution for each condition are plotted vertically on the y-axis and the proportion of correct and error responses are plotted on the x-axis. Figure 6 shows examples similar to those to be reported for experiment 1 below. For each graph, there are six conditions, varying from a high probability of one response being correct to a high probability of the other response being correct. For each condition, there are two vertical lines of quantiles: one for correct responses and one for errors. Because the probability of a correct response is usually larger than .5, quantiles for correct responses are usually on the right of .5 and quantiles for errors on the left (the two probabilities sum to 1.0). For example, if the probability of a correct response is .9, the probability of an error response is .1. The difficulty of the stimuli in each condition determines the probabilities of correct and error responses, that is, the location of the quantiles on the x-axis. The lines connecting the quantiles, from one condition to another, trace out the changes in the RT distributions across conditions.

Figure 6.

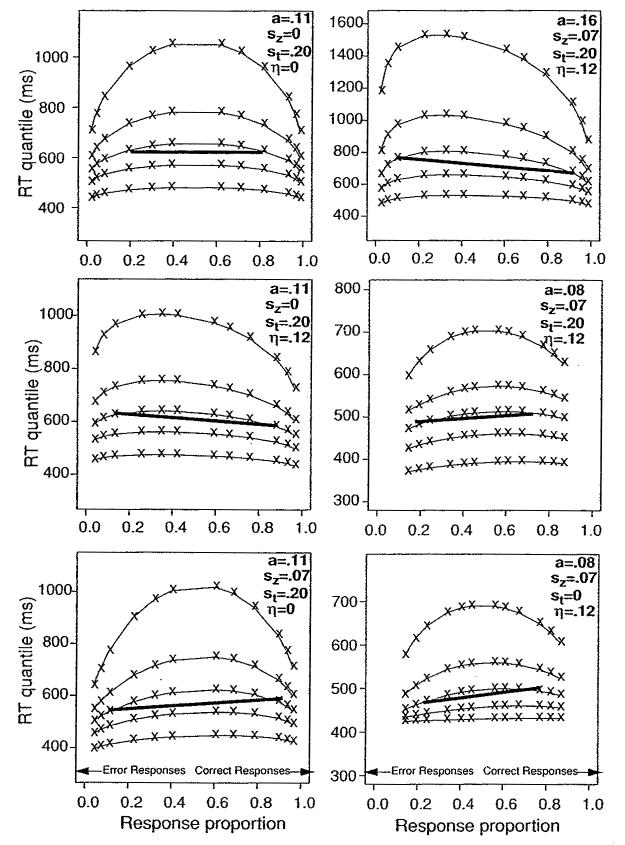
Quantile probability functions. The figures show possible outcomes for experiment 1 in which there are six levels of coherence (from 5% to 50%). Predicted quantile RTs for the .1, .3, .5 (median), .7, and .9 quantiles (stacked vertically) are plotted against response proportion for each of the six conditions. Correct responses for left- and right-moving stimuli, combined, are plotted to the right, and error responses for left- and right-moving stimuli combined are plotted to the left. The bold horizontal line in each figure connects correct and error median RTs for the third most accurate condition in order to highlight whether error responses are slower or faster than correct responses. The drift rates from which the data were simulated are those obtained in experiment 1. For all six panels, the starting point (z) was halfway between the boundaries. Across the six panels, boundary separation a takes on values of 0.16, 0.11, or 0.08; across-trial variability in starting point rate s_z takes on values of 0 or 0.07; across-trial variability in T_er, s_t, takes on values of 0 or 0.20; and across-trial variability in drift rate, η, takes on values of 0 or 0.12. T_er is the mean time taken up by the nondecision components of processing is set at 300 ms in the plots.

Quantile probability functions display all of the data that the diffusion model explains: the changes in accuracy across conditions and the changes in correct and error mean RTs and RT distributions across conditions. The structure of the model places strong constraints on how the model can fit these data. T_er determines the placement of the quantile probability functions vertically, that is, on the y-axis. The shapes of the quantile probability functions are determined by just three values: the distance between the two response boundaries a, the standard deviation in drift rate across trials, η, and the range of the starting point across trials, s_z. The drift rates for the different levels of stimulus difficulty (i.e., different conditions) sweep out the quantile probability function across response probabilities, with the parameter a being the main determinant of the spread of the RT distribution at each level of difficulty.

The left-hand plots in Figure 6 demonstrate how across-trial variability affects the relative RTs for correct and error responses. In all the plots, the starting point is midway between the two boundaries. For the top plot, across-trial variability in both drift rate and starting point is set at zero, and the quantile probability functions form symmetric inverted U's. The heavy black line connects median RTs for correct and error responses for the same condition, and this shows equal RTs for correct and error responses for the top plot. For the middle plot, across-trial variability in starting point is zero, and across-trial variability in drift rate is set at a value approximating that for experiment 1; the result is error responses slower than correct responses. In the bottom panel, across-trial variability in drift rate is zero, across-trial variability in starting point is set at a value near that of experiment 1, and error responses are faster than correct responses.

The top two right-hand panels in Figure 6 have values of variability in drift and starting point about the same as those in experiment 1, and they illustrate the effect of altering boundary separation (e.g., a speed/accuracy manipulation) on error RTs. When boundary separation, a, is a large value typical of fits to data, the range of starting point, s_z = 0.07, is small relative to the boundary separation, a = 0.16, and so error RTs are determined primarily by variability in drift across trials; the result is errors slower than correct responses. When boundary separation is decreased (middle right panel), variability in starting point is large relative to the boundary separation, a = 0.08, and starting point variability dominates variability in drift rate, resulting in shorter error than correct RTs.

The bottom right panel shows how variability in the nondecision component of processing affects distribution shape. The other five panels have variability set at a value close to that for experiment 1, and the bottom right panel has the value set at zero (i.e., s_t = 0). The lower quantiles (.1 and .3) are closer together than when s_t is larger (e.g., middle right panel). Larger values of s_t can accommodate more variability across experimental conditions in the .1 quantile RTs, as well as an increase in the separation of the .1 and .3 quantile RTs, features that are needed to fit some sets of data (see Ratcliff & Tuerlinckx, 2002, for further discussion).

The patterns of results illustrated in the six panels have all been obtained in fits to experimental data (Ratcliff, Gomez, & McKoon, 2004; Ratcliff et al., 2001; Ratcliff, Thapar, & McKoon, 2003; Ratcliff et al., 1999). We now apply the model to experiments using the motion discrimination procedure.

4 Experiments

Describing the full range of predictions from the diffusion model is most efficiently done in the context of real data. Rather than re-presenting data from already published experiments, we conducted new ones, using human subjects and the motion discrimination paradigm (Ball & Sekuler, 1982) that is currently popular in neurobiology research with monkeys (Britten, Shadlen, Newsome, & Movshon, 1992; Newsome & Pare, 1988; Roitman & Shadlen, 2002; Salzman, Murasugi, Britten, & Newsome, 1992). Experiments 1 and 2 were replications of, and experiment 3 was similar to, experiments with human subjects by Palmer et al. (2005). Palmer et al. did not examine RT distributions nor did the simplified model they presented account for error RTs (which they acknowledge). Here we use the diffusion model to account for error RTs as well as correct RTs and accuracy, and to provide comprehensive fits to RT distributions. We show that the RT distributions obtained with human subjects are quite different from those obtained with monkey subjects.

In the motion discrimination paradigm, a stimulus is composed of a set of dots in a circular window. On each trial, some proportion of the dots move in one direction (either to the left or right), and the rest move in random directions. Subjects are asked to decide whether the direction of the coherently moving dots is to the right or the left. Stimulus difficulty is varied via the proportion of dots moving in the same direction, typically from near 0% to 50%.

As stressed above, the most critical tests for evaluating sequential sampling models have to do with RT distributions. Successful models make precise predictions about the shape of RT distributions, and as a corollary, they make strong predictions about how distributions change as parameter values change. For example, as noted above, changes in drift rate lead to larger changes in the tail of the RT distribution than in the leading edge, in a ratio of about 4:1, whereas changes in boundary separation lead to changes in the leading edge that are about half the size of changes in the tail. Whether drift rate or boundary separation is varied, the shape of the RT distribution remains almost the same, as we show below.

Experiments 1 through 3 test the diffusion model and show how it captures the effects of three key manipulations: one that should affect drift rate, one that should affect boundary separation, and one that should affect either the location of the starting point or the drift rate criterion (or both). In experiment 1, stimulus difficulty was varied. According to the diffusion model, differences in difficulty should lead to differences in drift rate, which in turn predicts that most of the differences among the mean RTs should come from spreading in the tail of the RT distribution (the higher quantiles). In experiment 2, subjects were instructed to respond as accurately as possible on some blocks of trials and as quickly as possible on other blocks. In the model, this should affect boundary separation, a, predicting that the differences in mean RTs should come from both spreading in the tail of the distribution and shifting in the leading edge (the .1 quantile). In experiment 3, the proportions of stimuli for which the left and right responses were correct were varied between blocks of trials, in the ratios 75:25 and 25:75. The question was whether the resulting biases in the data would be the result of moving the starting point nearer the boundary for the most probable response or the result of a change in drift criterion or both.

In some paradigms with monkeys, RT distributions are right-skewed, and they vary across experimental conditions in the ways predicted by the diffusion model (Hanes & Schall, 1996; Ratcliff, Cherian, et al., 2003; Ratcliff, Hasegawa, Hasegawa, Smith, & Segraves, 2007). However in the motion discrimination paradigm, Ditterich (2006) found that in data collected by Roitman and Shadlen (2002), the distributions were inconsistent with the diffusion model: they were nearly symmetric in shape, widening as difficulty increased (RTs were also much longer than in data in Ratcliff, Cherian, et al., 2003, and Ratcliff, Hasegawa, et al., 2007). Ditterich proposed a model in which evidence is summed in two separate accumulators at different rates, but the rate of accumulation in both accumulators increases with time until it asymptotes at a high value after 1 s of processing. Because the drift rates increase, there is a greater and greater probability of termination as time increases, that is, an increasing hazard function, where the hazard function represents the probability that the process terminates in the next instant of time given that it has not terminated previously. This contrasts with the diffusion model's assumption that drift rate remains constant over time, which gives rise to approximately constant hazard functions (see Ratcliff et al., 1999, for further discussion). In accord with Roitman and Shadlen's data, Ditterich's model predicts RT distributions that are approximately symmetric. One of the issues addressed in experiments 1 through 3 was whether human RT distributions in the motion detection paradigm are right skewed with approximately exponential tails like other two-choice data from humans and monkeys, or approximately symmetrical as in Roitman and Shadlen's data from monkeys.

4.1 Experiment 1

The aim of experiment 1 was to replicate basic findings in the motion discrimination paradigm (Britten et al., 1992; Palmer et al., 2005; Roitman & Shadlen, 2002; Shadlen & Newsome, 2001; Salzman et al., 1992) using stimuli that span a range of levels of coherence from 5% to 50% so that accuracy varies from near ceiling (over 90% correct) to near floor (under 60% correct). The one major difference between our paradigm and the ones listed above is that in our paradigm, we did not require subjects to maintain fixation during stimulus presentation; rather, they were free to move their eyes.

4.1.1 Method: Procedure and Stimuli

The stimuli were constructed using the method presented in earlier motion discrimination experiments and the procedure followed that used in Palmer et al. (2005; see also Roitman & Shadlen, 2002). On each trial, a series of frames was displayed on a PC screen, 16.7 ms per frame. On each frame, five dots were displayed, 1 by 1 pixel in size (0.054 degree square), in a circular aperture 5.4 degrees in diameter centered on the PC screen. On the first three frames, the dots were located in random positions. On the fourth and each subsequent frame, a proportion of the dots moved coherently, that is, in the same direction for each frame, by four pixels (0.216 degrees), either left or right. For the fourth frame, the dots that moved were randomly chosen from the dots that had appeared on the first frame; for the fifth frame, they were chosen randomly from those that had appeared on the second frame; for the sixth frame, they were chosen randomly from those that had appeared on the third frame; and so on, until the subject pressed a response key. Across the frames, the movement speed of the coherently moving dots was 13 degrees per s. On each of the fourth and subsequent frames, the dots that were not chosen to move coherently appeared in random locations.

Coherence was defined as the probability across frames with which dots moved. There were 12 conditions: either the coherently moving dots moved left or right, and the probabilities of a dot moving were .05, .10, .15, .25, .35, and .50. For example, if the coherent direction was left and the probability was .05, then the probability that a dot in each frame would move left would be .05.

There were 10 blocks of 96 trials each, with a subject-paced pause between each block. Subjects were asked to respond as quickly and accurately as possible, pressing the backward slash key if the coherent motion was toward the right and the Z key if the motion was toward the left. If a response was correct, the screen was cleared, and 300 ms later, the next trial began. If a response was an error, an error message was printed for 300 ms before the 300 ms blank screen. If the RT was shorter than 250 ms or longer than 1500 ms, an additional message, “TOO FAST” or “TOO SLOW,” was presented for an additional 300 ms before the blank screen. There were few “TOO FAST” or “TOO SLOW” messages, and most of them occurred in the first trials as subjects calibrated their RTs.

4.1.2 Subjects

Fifteen college students participated in the experiment for course credit in an introductory psychology course at The Ohio State University.

4.1.3 Results

Because RTs and accuracy were about the same for responses for left-moving and right-moving stimuli, correct “left” and “right” responses were combined for analyses, and so were incorrect “left” and “right” responses. Accuracy varied across coherence levels from 0.58 to 0.94, and mean RTs varied from about 660 ms to about 550 ms. Error RTs were generally a little longer than correct RTs.

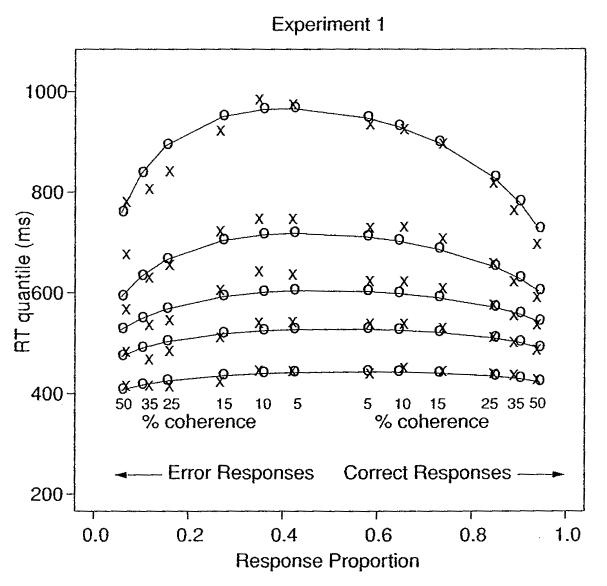
Figure 7 shows a quantile probability plot of the results. The x-axis shows the six coherence conditions, with correct responses for each condition on the right and error responses on the left. For example, for coherence of 50%, the proportion of correct responses was .94 on the far right, and the proportion of error responses was .06 on the far left. For each condition, the five vertical points (the x's) are the five quantile RTs (.1, .3, .5, .7, .9). The figure shows how the RT distributions changed across conditions. As accuracy decreased (i.e., as difficulty increased), the tails of the RT distributions spread out (the higher quantiles, by as much as 300 ms), and the leading edge changed only a little (the .1 quantile, by less than 40 ms).

Figure 7.

Quantile probability functions for experiment 1.

The data for each condition for correct responses were averaged across subjects, and so were the data for error responses. Then the chi-square method (Ratcliff & Tuerlinckx, 2002) was used to find the parameter values for the model that best fit the data (see Tables 1 and 2). The quantiles predicted from these values are plotted in Figure 7 with o's joined by lines to indicate how they varied as a function of drift rate. The predicted and observed RTs are close to each other, showing an excellent fit of the model to the data.

Table 1.

Parameters for the Diffusion Model Fits to Experiments 1 to 3.

Experiment	a1	a2	z1	z2	Ter	η	sz	st	χ2	df
1	0.111	–	0.056	–	0.418	0.122	0.067	0.199	241	55
2 (speed-accuracy)	0.109	0.152	0.055	0.076	0.414	0.073	0.065	0.243	421	78
3 (probability)	0.115	–	0.039	0.073	0.455	0.044	0.059	0.294	723	162

Notes: For experiment 2, subscript 1 for a and z refers to speed condition and subscript 2 refers to the accuracy condition. For experiment 3, subscript 1 for z refers to the condition with high probability of right responses, and subscript 2 refers to high probability of left responses, For the chi-square values to be interpretable in the standard way, they would have to be based on data from single subjects, but here they are based on averages over subjects. The chi-square values presented provide assessment of relative goodness of fit.

Table 2.

Drift Rates for the Diffusion Model Fits to Experiments 1 to 3.

Experiment	5% v1	10% v2	15% v3	25% v4	35% v5	50% v6	dc1	dc2
1	0.042	0.079	0.133	0.227	0.291	0.369	–	–
2 (speed-accuracy)	0.031	0.073	0.101	–	0.206	–	–	–
3 (probability)	0.053	0.080	0.115	–	0.229	–	−0.021	0.033

Note: The drift criterion is the amount added to the drift rates; for the condition with higher probability of right responses, dc₁ is added, and for the condition with higher probability of left responses, dc₂ is added.

Tables 1 and 2 show that the model fit the data with only drift rate varying across the six conditions of the experiment, that is, across the six levels of difficulty. All the other parameters of the model were held constant across the six conditions. Variability in drift rate and variability in starting point were moderately large, but because boundary separation was moderately large, errors were slower than correct responses.

The averaging of data over subjects might be considered a problem because the averages might not be representative of individual subjects. In 12 large studies with 30 to 40 subjects per group, Ratcliff et al. (2001), Ratcliff, Thapar, and McKoon (2003, 2004), Ratcliff, Thapar, Gomez, and McKoon (2004), and Thapar et al. (2003) showed that the parameter values obtained from fitting the model to data averaged over subjects were close to the parameter values obtained from averaging the parameters obtained from fits of the model to the data from individual subjects. In the experiments presented here, the parameter values from the two methods were within 2 standard errors with only one or two exceptions.

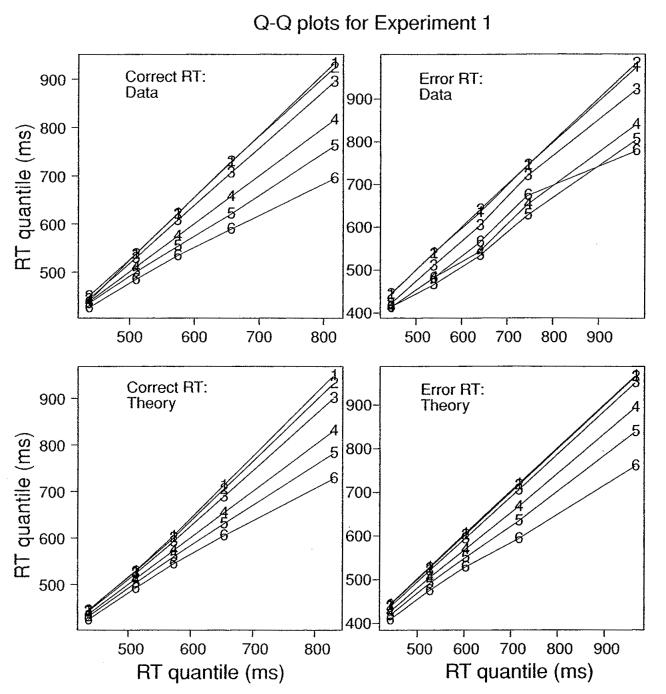
An important question is whether the RT distributions changed shape across conditions. The diffusion model predicts little change in distribution shape across conditions, that almost all the change in the distributions is in position and spread (i.e., only in location and scale; Mosteller & Tukey, 1977). Figure 8 shows quantile-quantile plots for correct and error responses for observed and predicted data from experiment 1. One condition, the 25% coherence condition, was selected, and the quantiles for responses in the other conditions were plotted against the quantiles for this condition. The 25% condition was chosen because it had moderately high accuracy, yet enough error RTs to provide reliable estimates of error RT quantiles. (The results were the same when any of the other conditions was chosen as the base for comparison). The top panels show the data. For correct responses, the quantile-quantile plots are almost linear, and for error responses, the functions are linear except for the condition with the lowest accuracy (the line marked 6 in the top right panel) where quantile RTs were highly variable because of relatively low numbers of observations. The diffusion model predicts linear functions, and the best-fitting functions from the model are shown in the bottom two panels. The findings of linear quantile-quantile plots match those from unpublished analyses from many other experiments (e.g., Ratcliff et al., 2001; Ratcliff, Thapar, & McKoon, 2003, 2004; Ratcliff, Thapar, Gomez, et al., 2004; Thapar et al., 2003). Although not presented, the model's predictions also matched the quantile-quantile plots for experiments 2 and 3 (because the model fit the quantiles separately). Also consistent with the diffusion model, plotting the quantiles from one experiment against those of other experiments shows linear functions (the Ratcliff, Thapar, and McKoon studies just cited).

Figure 8.

Quantile RTs for the six conditions in experiment 1 plotted against quantiles for the third most accurate condition (25% coherence). The top panel shows data quantiles, and the bottom panel shows quantiles predicted from the diffusion model.

The important conclusion from the quantile-quantile plots is that RT distributions show considerable invariance in shape across conditions and across experiments. This is an important regularity in experimental data in human response time studies. For a model to be successful, it has to predict this invariance in shape across the range of parameter values that give rise to RTs and accuracy values that match data.

4.2 Experiment 2

A standard experimental method of decoupling decision criteria from the stimulus information that drives the diffusion process is to vary speed and accuracy instructions. For some blocks of trials, subjects are instructed to respond as quickly as possible and for other blocks of trials as accurately as possible. In the diffusion model, speed-accuracy trade-offs are modeled by altering the boundaries of the decision process: wider boundaries require more information before a decision can be made, and this leads to more accurate and slower responses. It is important to stress that when subjects respond to speed versus accuracy instructions, all the dependent variables change (accuracy, mean RT, and RT distributions for correct and error responses). As the model has been implemented in recent studies, the effects of speed versus accuracy instructions have been explained with only boundary separation (and therefore starting point) varying. However, it is possible, as suggested by electrophysiological data from Rinkenauer, Osman, Ulrich, Muller-Gethmann, and Mattes (2004), that speed-accuracy instructions also affect nondecision components of processing; for example, speed instructions might lead to a decrease in encoding time. To allow for such effects in experiment 2, the model was implemented with different values of T_er for speed and accuracy instructions. However, the best-fitting values differed by 6 ms, so the results presented below used only a single value.

4.2.1 Method

The experiment used the same stimuli and procedure as experiment 1 with the following exceptions. First, because the speed and accuracy instruction manipulation doubled the number of conditions and halved the number of observations, the number of coherence values was reduced to four: 5%, 10%, 15%, and 35%. Second, at the beginning of each block of 96 trials, instructions were presented to indicate whether responses in the block should be made as quickly as possible or as accurately as possible. Third, there were no “TOO SLOW” messages in the blocks with accuracy instructions. Fourteen subjects from the same population as experiment 1 participated in the experiment.

4.2.2 Results

The results are displayed as quantile probability plots in Figure 9; the x's are the data, and the o's are the model predictions. The best-fitting parameter values for the model are shown in Tables 1 and 2. RTs and accuracy were about the same for left- and right-moving stimuli, for correct and error responses, so they were combined as in experiment 1. The model fit the data well, with no systematic differences between predictions and data. The predictions from the model that are displayed in Figure 9 were generated with T_er held constant across instructions.

Figure 9.

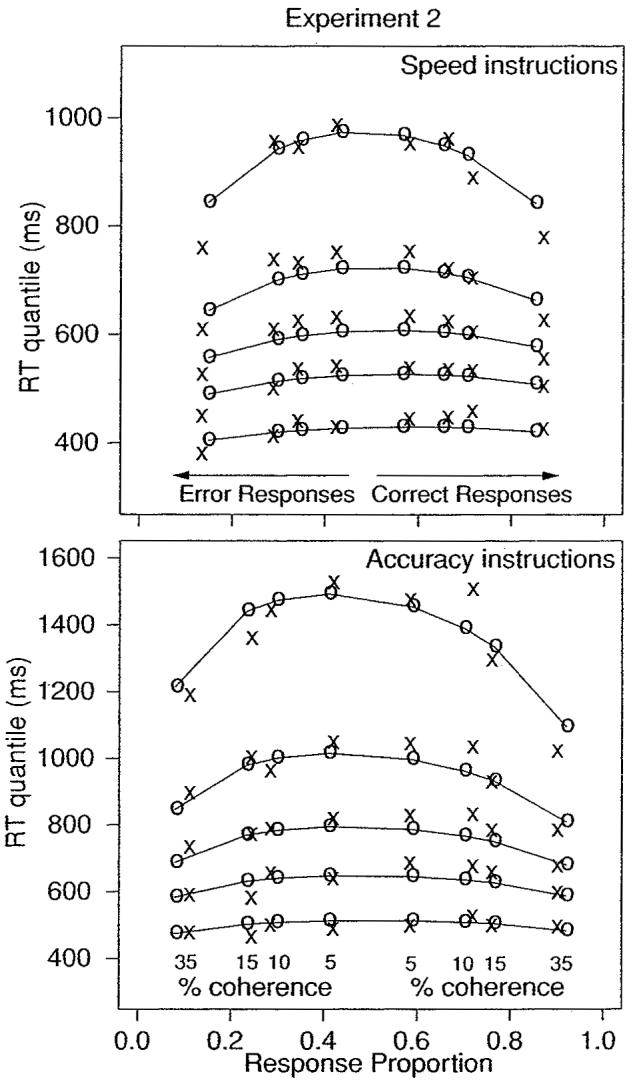
Quantile probability functions for the speed and accuracy instruction conditions for experiment 2.

As in experiment 1, the effects of stimulus difficulty were accommodated in the model by changes in drift rate. As mean RT increased across coherence levels, the .1 quantile RTs changed little (30 ms or less), but the .9 quantile RTs spread by as much as 200 ms with speed instructions and 400 ms with accuracy instructions.

RTs for error responses were about the same as for correct responses. In experiment 1, errors were slower than correct responses. However in this experiment, variability in drift rate across trials was smaller than experiment 1, producing faster errors relative to correct responses compared with experiment 1.

Speed versus accuracy instructions had small effects on accuracy, ranging from 0% to 6%. In Figure 9, higher accuracy with accuracy instructions is shown by the shift outward for correct responses toward larger proportions of correct responses (and corresponding smaller proportions of errors). In contrast, the effects of instructions on RTs were large. The effect on median RTs for correct and error responses was between 120 and 200 ms, the effect on the .1 quantiles was between 40 and 100 ms, and the effect on the .9 quantiles was between 250 and 550 ms. These effects were accommodated entirely by shifts in boundary position.

Overall, the model accounts for the data with only boundary separation varying between speed and accuracy instructions and only drift rate varying with stimulus difficulty. It simultaneously captures the small effect of difficulty on the leading edge of the RT distributions, the large effect of difficulty on the tails, the small effect of instructions on accuracy, and the large effect of instructions on RTs. The model has done equally well with these same patterns of data in many other experiments (e.g., Ratcliff, 2002, 2006; Ratcliff & Rouder, 1998; Ratcliff et al., 2001; Ratcliff, Thapar, & McKoon, 2003, 2004).

4.3 Experiment 3

Issues of current interest in the neurophysiological decision-making literature with animals concern relative response rates for the two alternatives in two-choice tasks (e.g., Bogacz, Brown, Moehlis, Holmes, & Cohen, 2006; Sugrue, Corrado, & Newsome, 2005, and references therein). Manipulations of relative weighting of the two alternatives allow investigation of response biases and how they are affected by reward rate, response proportions, relative size of rewards, feedback on response accuracy, and so on.

In experiment 3, the proportion of left-moving versus right-moving stimuli was varied in order to manipulate the relative weights assigned to the two responses. In half of the blocks of trials, 75% of the stimuli moved in one direction and 25% in the other, and in the other half of the blocks, the proportions were reversed. In the diffusion model, this manipulation could cause the starting point to move closer to the more likely decision boundary, or it could cause the drift criterion to move so that the more likely stimulus had a higher relative value of drift rate (or it could cause both). The possibilities have different behavioral signatures. If the model fits the data well, these signatures allow discrimination between the two possibilities, starting point or drift criterion, or, if the change-of-proportion manipulation affects both the starting point and the drift criterion, the model can identify how much each contributes to effects on performance.

4.3.1 Method

The stimuli and procedure were the same as for experiment 1 with the following exceptions. First, because the proportion manipulation doubled the number of conditions and halved the number of observations, the number of coherence values was reduced to the same four as in experiment 2: 5%, 10%, 15%, and 35%. Second, at the beginning of the experiment, the proportion manipulation was explained to the subjects; then, at the beginning of each block of 96 trials, subjects were informed what the relative proportion of the two stimulus types would be. Seventeen subjects from the same population as experiments 1 and 2 served in this experiment.

4.3.2 Results

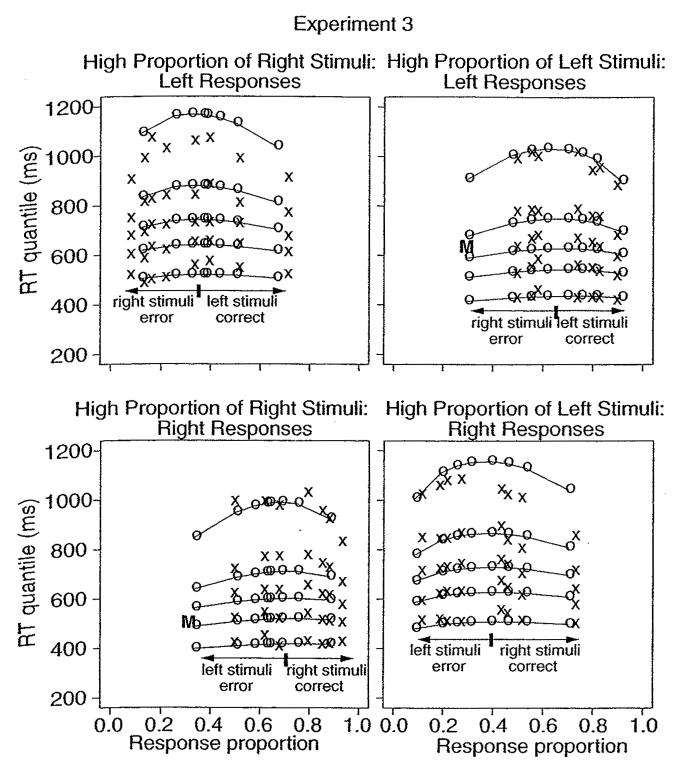
Because the proportions of the two stimuli tested for the high- versus low-probability stimuli produced an asymmetry between responses in accuracy of the two responses and also RTs for correct responses and error responses, they were not combined as they were for experiments 1 and 2. The separate quantile probability plots are shown in Figure 10, and the best-fitting parameter values are shown in Tables 1 and 2. The model fit the data well, although there were systematic misses in the .9 quantiles for error responses. These misses were systematic, but less dramatic than might appear because there were relatively few errors for these conditions.

Figure 10.

Quantile probability functions for high- and low-proportion stimuli for experiment 3.

The effects of stimulus difficulty were the same as in experiments 1 and 2. Mean RT increased across stimulus difficulty conditions with the .1 quantile RTs changing little: 15 ms or less for the high-proportion stimulus and up to 65 ms for the low-proportion stimulus. The .9 quantile RTs changed by 150 to 250 ms. In the model, the effects of difficulty were attributed solely to changes in drift rate.

The effects of the stimulus proportion manipulation were to increase accuracy and decrease RTs for the more likely stimuli. The increase in accuracy is shown by the outward shift of the RT quantiles toward a higher probability of correct responses for the bottom left and the top right panels in Figure 10 and the opposite shift from the bottom left to the bottom right panels. The decrease in RTs was due to both a shift in the leading edges (.1 quantiles) of the RT distributions, by as much as 100 ms, and a decrease in the tails (.9 quantiles), by from 100 to 150 ms.

The main question was whether the effects of stimulus proportion could be explained by a change in starting point, a change in drift criterion, or both. The shift in the leading edges of the RT distributions indicates a change in starting point (see Table 1). The starting point was about one-third of the distance between 0 and a, closer to the boundary corresponding to the high-probability stimuli. This difference in starting point accounted for most of the proportion effect. The drift criterion had only a modest effect (see Table 2). For example, in the 35% coherence condition, its value changed from high- to low-proportion stimuli by only about 10%. Fitting the model to the data with the drift criterion varying from high- to low-proportion stimuli increased the chi-square goodness of fit value by only 1%.

Error RTs are a little harder to interpret, because when there is a bias toward movement in one direction, responses to the other direction are slower. But the parameters representing variability across trials in drift rate and starting point are similar to those in experiment 2 and thus would provide about the same predictions as for experiment 2 if an unbiased condition were tested with these subjects.

4.4 Discussion of Experiments 1, 2, and 3

The three experiments demonstrate how the components of processing identified by the diffusion model work together to explain data. For all three experiments, the quantile probability plots show that the model fit the data well, including the right skew (approximately exponential) tails of the RT distributions and the changes in the distributions across experimental conditions. The only systematic misses occurred in experiment 3 for the highly variable .9 quantiles for error responses. In all three experiments, the shape of the RT distributions remained approximately constant, while experimental manipulations changed only their location and spread. The right-skewed distributions were similar to those typically found in two-choice experiments with human subjects but different from the symmetrical distributions found with monkeys in the motion discrimination paradigm (Ditterich, 2006; Roitman & Shadlen, 2002).

Stimulus difficulty was translated in the model into differences in the quality of the evidence available from the stimuli to drive the decision process (i.e., drift rate, Tables 1 and 2). The effects of speed versus accuracy instructions, experiment 2, were translated into differences in the criterial amounts of information required before a decision could be made (the distances between 0 and a, Tables 1 and 2). In experiment 3, the effects of varying the relative proportions of the stimuli were translated mainly into differences in the starting point of evidence accumulation, accompanied by a small effect on drift criterion. For all the conditions in all the experiments, the best-fitting parameters of the model successfully predicted mean RTs for correct and error responses, RT distributions, accuracy values, and the changes in these dependent variables across experimental manipulations. Also, the model can only accommodate, and the data only showed, patterns in which changes in RT distributions across manipulations occurred in the spreads or leading edges of the distribution, not their shape.

The model was successful despite the strong constraints placed on it by the data. For stimulus difficulty, only drift rate varied, not any of the other parameters, and for speed and accuracy instructions, only response criteria varied. For stimulus proportion, only starting point and (to a minor degree) drift criterion varied. In each experiment, the parameters representing the nondecision components of processing (T_er), the across-trial variability in drift rate (η), the across-trial variability in starting point (s_z), and the across-trial variability in the nondecision component (s_t) were held constant across the experimental conditions (i.e., they were not allowed to vary as a function of condition when fitting the model to the data). Boundary separation was also held constant across conditions except in experiment 2 with speed and accuracy instructions. Starting point was always halfway between the two boundaries except in experiment 3, where the relative proportions of the stimuli were varied. The best-fitting values of all of these parameters were reasonably consistent across the three experiments. The T_er values were within 40 ms of each other, and the boundary separation values were nearly the same (except with accuracy instructions in experiment 2). Estimates of the across-trial variability parameters were less consistent. Ratcliff and Tuerlinckx (2002) showed that these parameters are less accurately estimated than the other parameters. In part this is because the estimates of η and s_z depend on the relative speeds of correct and error responses, and RTs are more variable for error than correct responses because there are fewer error responses.

4.4.1 Motion Coherence and Drift Rate

A key consequence of the model's success in accounting for the data from experiments 1, 2, and 3 is that it provides an economical interpretation of the effects of the various experimental manipulations on components of processing, with the difficulty and speed and accuracy manipulations each tied to only one component and the proportion manipulation tied mainly to only one component. The components dissociated from each other so that jointly manipulating speed and accuracy instructions and difficulty, or stimulus proportion and difficulty, had separable effects on drift rate, decision criteria, and starting point.

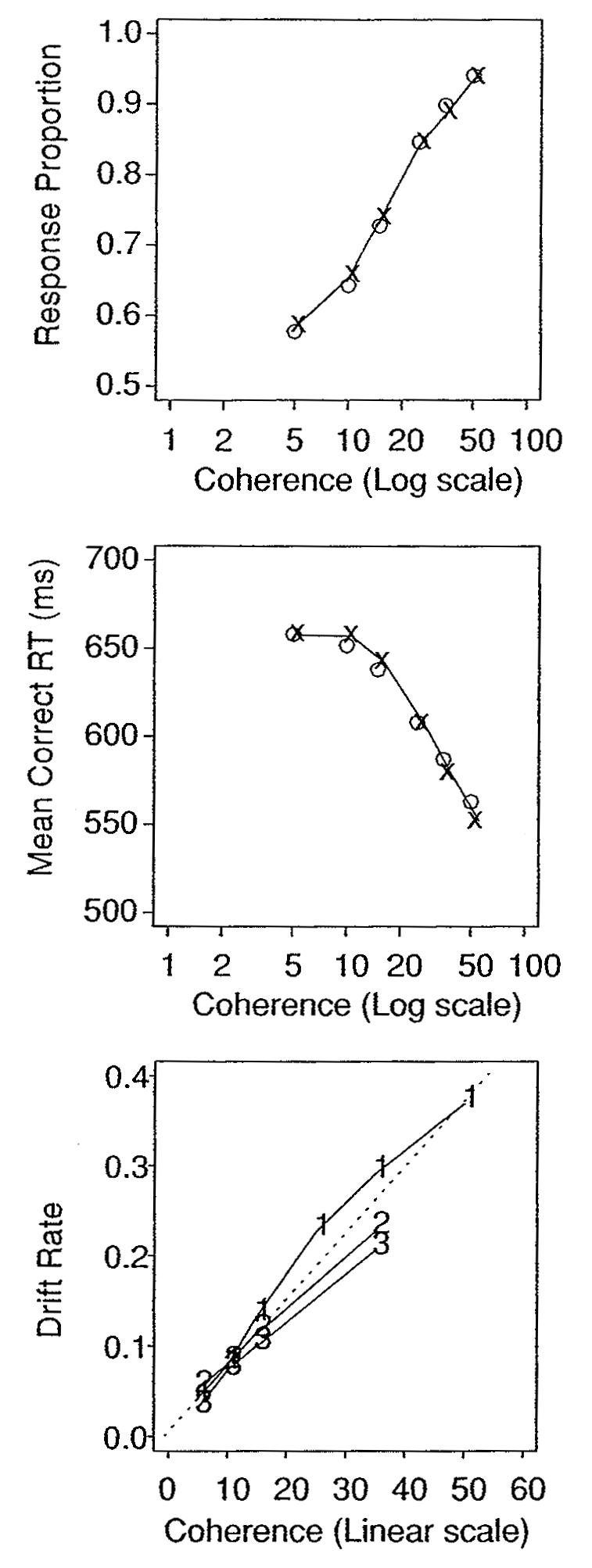
Separating drift rate from the other components of processing is essential to developing a model for how motion coherence is encoded. Drift rate represents the quality, or strength, of the information available from a stimulus. If a model for the processes that encode coherence produces appropriate drift rate values, then the values can be translated through the diffusion decision model into accurate predictions of performance (RT distributions and accuracy levels). The model for encoding coherence might relate the proportion of dots moving in the same direction to drift rate linearly, an obvious possibility, or it might relate the proportions to drift rate nonlinearly. Either way, the model can be tested by combining the predicted drift rates with the other components of the decision process and comparing the predictions to data. Figure 11 shows drift rates plotted as a function of coherence for experiments 1, 2, and 3. The functions are almost linear, but with a slight bend as coherence approaches 50%.

Palmer et al. (2005) modeled the motion discrimination task by assuming, a priori, that the relation between coherence and drift rate was linear (they checked the linearity assumption by allowing the relationship to be a power function and then finding that this function was approximately linear). Their model was a simplified diffusion model: there was no variability across trials in any of the components of processing, and the starting point was fixed at halfway between the two boundaries. Under the assumption that the relationship between drift rate and coherence was linear, they estimated model parameters from accuracy and mean RT values for correct responses alone, that is, without information about error RTs or the full RT distributions. The linear relation between drift rate and coherence was expressed as drift rate = (k) (coherence level), where k is a constant. It follows from the simplified diffusion model and the linear assumption that the coherence value for the halfway point between accuracy at floor and accuracy at ceiling, 75% correct, is 0.55/(k a′), where a′ = a/s, s is the standard deviation of within-trial noise, and a is boundary separation. Similarly, the halfway point between floor and ceiling RT is 1.92/(k a′). If these two points can be estimated from data (as in Palmer et al.), then k and a′ can be estimated. Palmer et al.'s model successfully fit accuracy values and mean RTs for correct responses. Palmer et al. did not provide predictions for RT distributions, although they could be derived from their simplified model using the full model with the variability parameters set to zero. According to their model, error and correct RTs should be equal, but the data were equivocal; on average, errors were slower than correct responses, but the difference was not consistent across subjects. Overall, it is likely that if the full diffusion model were applied to the same data as Palmer et al.'s model, the parameter estimates for the main components of processing (the nondecision component, drift rate, and boundary separation) would be similar.

For comparison to Palmer et al.'s data, Figure 11 (top two panels) shows accuracy and mean RT data from experiment 1 plotted against coherence on a log scale, the same way Palmer et al. plotted their data. The x's and lines are the predicted values from the fits of the full model to the data, and the circles are the data. The bottom panel shows drift rates plotted as a function of coherence for experiments 1, 2, and 3. The plots show that Palmer et al.'s linearity assumption is reasonable, although for experiment 1, where there was a wider range of coherence values than experiments 2 and 3, there was a slight systematic bend (that we have replicated in other experiments).

In contrast to the approach used by Palmer et al., explaining data with the full diffusion model does not require any a priori assumption about the relation between coherence values and drift rates. Palmer's method would not work if drift rate were not related to coherence by a linear function or some other simple function, or if the starting point were not equally distant from the response boundaries. In the full diffusion model, drift rates are a by-product of successfully fitting the data. The coherence–drift rate relation is constrained by all the aspects of the data and functions can be fit to the form of the relationship. In particular, the relation is constrained because it must encompass error RTs and full RT distributions, as well as accuracy and RTs for correct responses.

Below, further examples of the utility of the diffusion model in abstracting components of processing are reviewed. First, however, the model's explanations of performance in two other tasks are described and then its relationship to the general class of sequential sampling models is reviewed.

5 Modeling the Response Signal and Go–No Go Tasks

Up to this point, the only two-choice procedure that has been discussed is the standard procedure in which stimuli are presented and subjects indicate which of two response categories they belong to. The diffusion model also offers successful accounts of data from the response signal and go–no go procedures. In a response signal experiment, the time at which subjects respond is controlled. When a stimulus is presented, it is followed by a signal to respond (often a row of asterisks or a tone). Subjects are instructed to respond as quickly as possible when the signal is presented. For example, in motion discrimination, a row of asterisks might be the signal to respond, and there might be five possible response signal lags (e.g., 50, 100, 400, 700, or 1200 ms), with one of the five lags chosen randomly for each trial. Subjects are encouraged to respond quickly at the signal (e.g., within 300 ms). Because subjects respond at experimenter-determined times, the dependent variable is accuracy. Typically the shortest lag is chosen so that accuracy is at chance and the longest lag so that accuracy will be at ceiling.

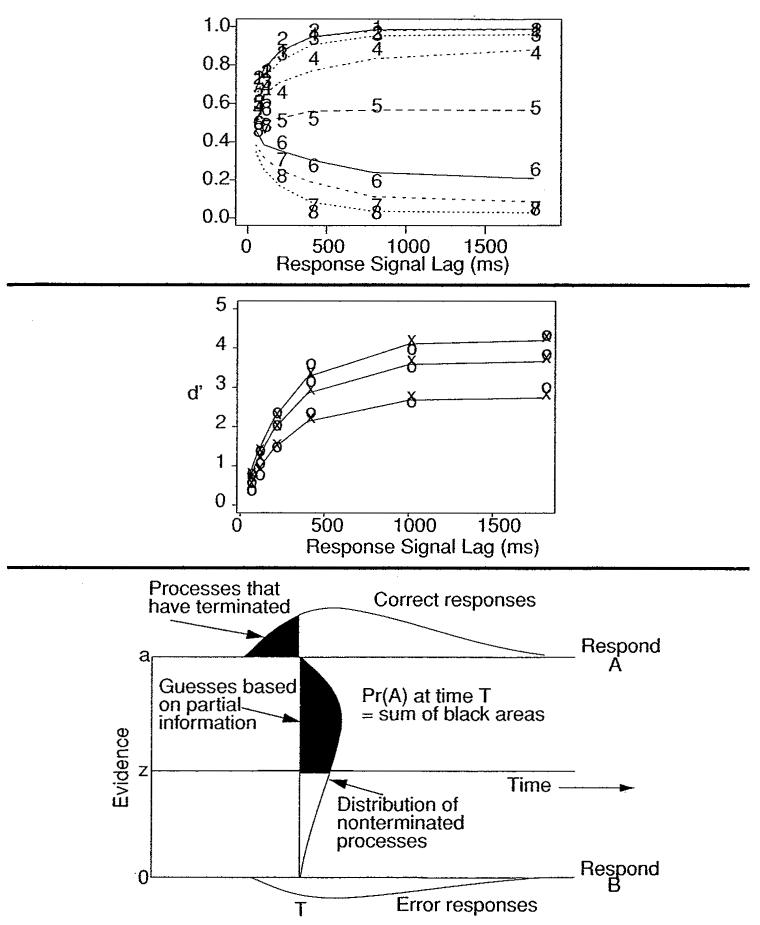
The goal is to trace out the time course of processing. The top two panels of Figure 12 show data from six conditions in a numerosity discrimination experiment. The proportion of the “large number” responses is plotted as a function of lag for each condition. Usually one of the experimental conditions is selected as a baseline condition, and d′ values are computed for each of the other conditions scaled against the baseline condition at each lag. In the middle panel of Figure 12, condition 6 was selected as the baseline, and d′ values were calculated for conditions 1, 2, and 3 in the top panel (the X's in the figure). d′ functions can usually be described as exponential growth functions (the O's in the figure). The choice of exponential functions is not based on any theoretical modeling framework; they are used because they provide a useful description of the data for testing hypotheses about processing.

Figure 12.

The response signal procedure, data, and diffusion model explanations. The top panel shows response proportion as a function of response signal lag from a numerosity discrimination experiment (Ratcliff, 2006) in which subjects judged whether the number of dots in a 10 × 10 array was greater than 50 or less or equal to 50. The eight lines represent eight groupings of numbers of dots (e.g., 13–20, 21–30, 31–40, 41–50, 51–60, 61–70, 71–80, and 81–87 dots). The middle panel shows d′ increasing as a function of lag for three well-separated positive conditions, where d′ is the difference in z-scores between each of the three conditions and a baseline condition (condition 6 from the top panel). The bottom panel shows how the diffusion model accounts for response signal data. The proportion of A responses at time T is the sum of processes that have terminated at the A boundary (the black area above the boundary) and nonterminated processes (the black area still within the diffusion process).

In early applications of sequential sampling models to response signal data, it was assumed that the diffusion process proceeds without any decision boundaries. In order to make a decision at some response signal lag, the position of the process relative to the starting point was used to make a response: if the amount of accumulated evidence was above the starting point, respond with one choice; if below, respond with the other choice (Ratcliff, 1978; Usher & McClelland, 2001).

More recently, Ratcliff (1988, 2006) explained response signal data by assuming implicit decision boundaries—the same boundaries that would be used in the standard two-choice procedure. If, when the response signal is presented, the diffusion process has already terminated at one or the other of the implicit boundaries, then that is the decision made. If the diffusion process has not terminated at a boundary, then there are two possibilities: either the decision is based on guessing or on which boundary the accumulated evidence is closest to, that is, it is based on partial information. Implicit boundaries and the probabilities of responses are illustrated in the bottom panel of Figure 12 (along with the partial information assumption). At time T, terminated processes are those above the a boundary or below the 0 boundary, while nonterminated processes are those between the boundaries. The probability of an A response is the probability of processes terminated at the A boundary (the upper black area in the figure) plus the probability the diffusion process is above the starting point (the other black area in the figure). The other assumption is that partial information is not available, and responses are based on terminated processes plus a guess for the processes not terminated.

Ratcliff (2006) collected data from the same subjects with both the standard procedure and the response signal procedure and fit the data from both simultaneously (all earlier response signal studies had not tried to fit both kinds of data simultaneously). The older version of the diffusion model, the one without boundaries, failed to account for the data, but the version with implicit boundaries was equally successful whether nonterminated processes were assumed to lead to decision based on guesses or on partial information.

Implicit boundaries are also assumed to explain data from the go–no go procedure. In this procedure, subjects are asked to make a response to a stimulus if it belongs to one of the possible response categories but to withhold responses to the other. For example, for motion discrimination, they might be asked to make a response to a right-moving stimulus and asked to not make a response to a left-moving stimulus (or vice versa). Gomez, Ratcliff, and Perea (2007) collected data from the same subjects for the standard and the go–no go procedures for lexical decision, numerosity judgments, and a recognition memory task. They tested a version of the diffusion model with an implicit boundary for no-go decisions and a version with no boundary for no-go decisions. Just as with the response signal procedure, the model fit the data well when an implicit boundary was assumed but not when no boundary was assumed.

The success of the diffusion model across the standard procedure, the response signal procedure, and the go–no go procedure derives from the model's ability to explain both RT and accuracy data; it unifies the dependent variables. A model that predicted only accuracy and not RTs could potentially explain data from the response signal paradigm but not the RTs from the standard and go–no go paradigms. A model that predicted only RTs could potentially explain data from the standard and go–no go paradigms but not the response signal paradigm. Currently, there are no models other than the diffusion model (and similar sequential sampling models) that can successfully encompass the data from these different experimental procedures.

6 Other Sequential Sampling Models

The diffusion model is a member of the general class of sequential sampling models, and so the question arises as to whether other models of the class could equally well accommodate the data of experiments 1, 2, and 3 as well as data from other two-choice studies. Broadly, there are two subclasses of sequential sampling models for simple two-choice tasks. The diffusion model and other members of its subclass assume a single quantity of evidence from a stimulus; positive evidence for one of the alternative responses is simultaneously negative evidence for the other alternative (and vice versa). Models in the other subclass, accumulator models, assume that evidence accumulates in two separate accumulators—one for each of the responses (LaBerge, 1962). Evidence toward one response does not subtract from evidence for the other. In these models, a response is initiated when the total amount of evidence in one or the other of the accumulators reaches its criterion. In early models of this type (reviewed by Vickers, Caudrey, & Willson, 1971; Luce, 1986), evidence could accumulate only positively, that is, the amounts of evidence in the accumulators could not decrease (e.g., Pike, 1966, 1973; Vickers, 1970). These models failed on a number of grounds (see Ratcliff & Smith, 2004, for details).

More recent accumulator models implement two or more diffusion processes (e.g., Bogacz et al., 2006; Ratcliff, Hasegawa, et al., 2007; Ratcliff & Smith, 2004; Usher & McClelland, 2001) and they allow the evidence in the accumulators to decrease, due to random noise and, in some cases, inhibition from one process to another. The recent accumulator models have not been tested on as many paradigms as the diffusion model or on data from large numbers of individual subjects (partly because implementing the models is computationally intensive). However, comparisons between predictions of the models (Ratcliff & Smith, 2004) and comparisons of the models using empirical data (Ratcliff, Thapar, Smith, & McKoon, 2005) indicate that they may be as successful as the single process diffusion model that has been discussed in this article.

7 Isolating Components of Processing

Experiments 1, 2, and 3 illustrate interleaved goals for the diffusion model. First, the model provides an accurate qualitative and quantitative account of the data from two-choice decision tasks. The model's predictions for RT means, distributions, and accuracy values are all close to the values obtained in the experimental data, and the changes in these dependent variables across experimental conditions are well accommodated as changes in accuracy and shifts and spreads of the RT distributions, with only minor changes in distribution shape.

Second, given the close fit of the model to data, RT and accuracy measures are decomposed by the model into components of processing. An experimental variable can affect performance in complex ways, yet the model can explain how the variable uniquely affects each of the components of processing that underlie performance. Centrally, the model allows the quality of the information available from a stimulus to be separated from the diffusion decision process that operates on that information to produce a decision. This allows processes operating prior to the decision process (e.g., perception, memory, lexical processing) to be modeled separately from the decision process, including interactions among the processes.

It is important to note that experiments 2 and 3 provide strong support for the assumption that the decision process is a diffusion process that separates evidence from the other components of processing identified by the model. Both the manipulation of speed and accuracy instructions and the manipulation of the proportions of one versus the other response have strong effects only on the decision criteria in the model, thus separating the decision process from other components.

Third, and again given the close fit of the model to data, the effects of experimental variables on performance and underlying components of processing can be investigated for individual subjects and classes of subjects. In current research, the model has been used to examine the effects of age, aphasia, and depression on cognitive processing. Also, several studies have used the diffusion model to investigate the extent to which components of processing are correlated across tasks for individual subjects. These studies are summarized below.

An important goal for the decision model is to provide a meeting point between theories. A complete explanation of performance in the motion discrimination paradigm, for example, requires a model that explains how dot motion is encoded to produce a perceptual representation that drives a decision process. In experiments 1, 2, and 3, the data were well explained with coherence nearly linearly related to drift rate, that is, the quality of information on which the decision is based. Thus, a model for dot motion encoding has a relatively straightforward task. The representation it produces must drive the diffusion decision process to produce the correct values for accuracy and RT distributions.

Another goal for the model is to bring attention to the dangers of developing models that do not fully and explicitly incorporate decision processes. Performance—RT and accuracy—is not a direct reflection of encoding processes or decision processes or any other component of processing. Instead, performance reflects the interactions and combinations of multiple components. The diffusion model offers one possible, and empirically well-supported, method of subtracting out decision process effects in order to better see underlying stimulus information effects and decision criterion effects.

As an example, consider the lexical decision task, in which letter strings are presented and subjects are asked to respond for each string “word” or “nonword.” Quite elaborate models of lexical access have been developed based on mean RTs for correct word responses in this task (e.g., Coltheart, Davelaar, Jonasson, & Besner, 1977; Forster, 1976; Morton, 1969; Paap, Newsome, McDonald & Schvaneveldt, 1982). Recently, however, Ratcliff, Gomez, et al. (2004) used the diffusion model to subtract out decision processes in order to more clearly see the relations among various types of word and nonword stimuli and how they are encoded. Ratcliff el al. found that a relatively simple hypothesis about lexical encoding accounts for all the aspects of lexical decision data (accuracy values and RT distributions for correct and error responses for words and nonwords). Specifically, the hypothesis is that encoding a letter string produces a value of how wordlike the string is. High-frequency words are more wordlike than low-frequency words, and pronounceable nonwords are more wordlike than random letter strings (e.g., nerse versus xhwut). The wordlikeness value of a letter string is translated to drift rate as input to the decision process. This interpretation of lexical decision performance is simpler than most other views. It assumes a straightforward matching process between the stimulus letter string in short-term memory and lexical information in long-term memory.

7.1 Modeling Decision Criteria and Likelihood Ratio Models

Currently, diffusion model analyses do not explain how subjects set criterion settings. There have been some proposals about how to model such settings (e.g., Bogacz et al., 2006; Triesman & Williams, 1984). But no current account can explain how human subjects set or calibrate criteria such that they are accurate on the first trial of an experiment using information presented only in verbal instructions (Ratcliff et al., 1999). Neither can current accounts (e.g., Bogacz et al., 2006), explain criterion settings when no accuracy feedback is provided. Experiments without feedback are common, especially with populations of older subjects or memory-impaired subjects. It is our belief that a significant component of criterion setting is based on a subject's history of decision making. In other words, for human subjects, reinforcement history in the experiment is not sufficient to explain a subject's criterion settings. In experiments with animal subjects, it is much more likely that the reinforcement history would be able to account for criterion setting.

The fact that human subjects can calibrate quickly based on verbal instructions has implications for likelihood-based models of decision making (e.g., Gold & Shadlen, 2001; Stone, 1960). In a likelihood-based model, the quality of a perceptual representation or information from memory produces a value on a continuum, and the likelihood of that value drives the decision process. Specifically, likelihood is the ratio of the probability density of the obtained value being a target and the probability density of the obtained value being a distractor. The problem is that human subjects with verbal instructions can calibrate in one trial, clearly not enough time to compute probability distributions for stimulus representations for positive and negative items. It requires thousands or tens of thousands of trials to estimate probability density functions by sampling observations from the distributions. For example, for a normal distribution, it takes 100 trials to get five observations (on average) beyond two standard deviations, and it would take 1000 trials to get three observations (on average) beyond three standard deviations. Even with 1000 observations, the density outside three standard deviations would be estimated poorly. Numbers of trials like these are not obtained for human subjects in most experiments.

Gold and Shadlen (2001) show that if the distributions of step size are normal, then the likelihood model is equivalent to a distance from the criterion model. We believe that the latter is plausible, but the likelihood model is not. However, for other models such as dual diffusion models with a lower bound of activation (e.g., Usher & McClelland, 2001) or models with position-varying step sizes (e.g., Ornstein-Uhlenbek models), it is not clear that there will be any equivalence between likelihood-based models and distance from the criterion models.

8 Applications of the Diffusion Model

The diffusion model has only recently come to be used as a tool for isolating component processes in cognitive tasks, but its initial success encourages future applications across widely varying tasks and subject populations. In this and the next sections, applications designed to isolate decision criteria, encoding processes, and drift rates are reviewed. The topics include aging, aphasia, short-term memory, categorization, and visual processing. Then, in the last section of the reviews, possible neural underpinnings of the diffusion decision process are described.

8.1 Individual Differences and Correlations Between Model Parameters and Data

In one of our programs of research (e.g., Ratcliff et al., 2001; Ratcliff, Thapar, & McKoon, 2003, 2004; Ratcliff, Thapar, & McKoon, 2006a, 2006b; Ratcliff, Thapar, Gomez, et al., 2004; Thapar et al., 2003), the diffusion model was fit to 18 data sets with between 30 and 40 subjects in each set, so we were able to examine correlations among mean RT, accuracy, and the model's components of processing across subjects. The consistent results across the 18 data sets were that accuracy was correlated with drift rate, and mean RT was correlated with boundary separation. In other words, the more accurate the subject, the higher was drift rate, and the slower the subject, the more widely separated were boundaries. Also in most of the studies, mean RT was correlated with the nondecision component of processing. There were no significant correlations between accuracy and mean RT, accuracy and boundary separation, mean RT and drift rate, or drift rate and boundary separation. These results suggest that across individuals, the values of the components of processing represented by drift rate (quality of evidence entering the decision process) and boundary separation (evidence needed to make a decision) are relatively independent of each other.¹

8.2 Correlations Across Tasks in Component Processes for Individual Subjects

For individual subjects, it is reasonable to assume that their performance does not change dramatically across tasks of the sort described in this review, or at least less than, it might change less than performance from one individual to another. Most things being equal, an individual who is fast at stimulus encoding and response execution on one task is likely to be fast in those components on other tasks. An individual who sets conservative criteria on one task is likely to be conservative on other tasks. The diffusion model provides a means of examining across-task performance issues like these. For example, Ratcliff et al. (2006a) used the model in this way to investigate performance on four two-choice tasks for subjects of three age groups: college age, 60 to 74 year olds, and 75 to 85 year olds (10 subjects per group). They found that for all of the subjects in all three groups, there were significant correlations across the four tasks in individuals' criteria settings (r = .32), their T_er values (r = .47), and, perhaps surprisingly, their drift rate values (r = .37). These results argue for consistent individual differences across these simple two-choice tasks.

8.2.1 Effects of Aging

For some time, it has been known that older adults (those 65 to 90 years old) are slower in two-choice tasks than young adults (college students). It was usually assumed that this slowdown in performance was the result of a general slowdown in all cognitive processes. However, recent diffusion model analyses of two-choice data from a number of tasks (six experiments with 30 or more subjects in each of three age groups per experiment) show that the slowdown is almost entirely due to older adults' conservativeness. To avoid errors, they set their decision criteria significantly further from the starting point of the decision process than young adults do. Counter to the previously held view, in most tasks, the quality of the information on which decisions are based (i.e., drift rate) is not significantly worse for the older than the young adults in the tasks we studied (Ratcliff et al., 2001, 2003, 2004, 2006a, 2006b; in press; Ratcliff, Thapar, & McKoon, 2003, 2004; Thapar, Gomez, et al., 2004; Spaniol, Madden, & Voss, 2006; Thapar et al., 2003).

8.2.2 Effects of Aphasia

In lexical decision, patients with aphasia, like older adults, perform more slowly than control subjects. Diffusion model analyses show that this comes about because they set more conservative criteria and have longer nondecision times (Ratcliff, Perea, et al., 2004). The differences in these components between aphasic subjects and normal subjects are considerably larger than the differences between college students and 60- to 75-year-old subjects. Surprisingly, and in testament to the utility of the diffusion model in isolating component processes, the mean difference in drift rates between the aphasic patients and the normal control subjects was small. The suggestion, consistent with claims by Buchanan, McEwen, Westbury, and Libben (2003), is that lexical knowledge is relatively intact in aphasic patients.

The applications summarized here outline how the diffusion model can be used to explore individual differences in a variety of domains and perhaps provide important contributions to the individual difference literature. Because the model can be applied to individual subjects, it avoids issues of averaging data across subjects, a crucial feature when individuals might show different patterns of performance.

9 Coupling Perception and Memory Models with the Diffusion Model

9.1 Short-Term Memory for Order Information and Drift Rate

A straightforward illustration of an encoding model–decision model combination was developed by Ratcliff (1981) for the representation of letter strings in short-term memory. In the task to be modeled, pairs of letter strings (five letters in length) were presented sequentially to subjects, and the subjects were asked to decide whether the strings were identical. The first string of a pair, flashed quickly, was assumed to reside in short-term memory at the time the second test string was presented. The pairs of interest were those that differed by either one or two letters. If a letter from the memory string was replaced in the test string by a new letter, then the difficulty of the decision depended on the position of the replaced letter—more difficult if it was in the middle than the ends of the string. When two letters were transposed from one to the other of the two strings, difficulty depended on the distance between the letters as well as on the letters' positions. For example, transposition of two adjacent letters was more difficult than transposition of farther-apart letters, and transpositions involving the first letter were less difficult than transpositions involving a middle letter. Ratcliff applied the diffusion model to these data and found that the model could successfully account for the data, an impressive feat given the large numbers of conditions (all the possible ways to replace or transpose letters between two strings). Most interesting was that the differences in performance across conditions were attributable solely to variations in drift rate.

Ratcliff interpreted drift rate as a measure of the degree to which the second, test letter string matched the first, short-term memory string: a higher value of drift rate indicated a higher degree of match. To produce the appropriate values of match, Ratcliff (1981) proposed an overlap model. For both the test string and the short-term memory string, it was assumed that the representation of each letter was distributed over positions in the letter string, with the distribution assumed to be gaussian with the mean centered on the letter position and the standard deviation a parameter of the model. For each letter, there was some overlap with each of the five possible positions. A middle letter, for example, would have a large overlap with the middle position (center of the gaussian) and a much lower overlap with the end positions (the tail of the gaussian). For a test pair of strings, the degree of match between them was defined as the amount of overlap between their distributed representations. This reasonably concise model for the representation of letter strings in short-term memory was able, when combined with the diffusion decision model, to correctly predict the full range of accuracy and RT data.

9.2 Early Visual Processing and Drift Rate

In the model as it has been described up to this point, it has been assumed that the value of drift rate is constant as the diffusion process proceeds from starting point to boundary. Ratcliff and Rouder (2000) explicitly investigated this assumption for letter discrimination. In their experiments, one of two letters was flashed briefly (10–40 ms) and then masked. There are two possibilities for the effect of masking. It could be that the value of drift rate is not constant; instead it increases from onset of the letter to onset of the mask and then becomes zero. This predicts dramatically slower errors than correct responses because for a process to produce an error, it has to move from the new average position, which is near the correct boundary, to the incorrect boundary. The second possibility is that drift rate is constant. It is determined by a memory representation of the stimulus that, after only a short initial rise, is constant, not erased by the mask. In this case, drift rate is constant over time, and so error RTs have the same relation to correct RTs as in all the applications of the model discussed above. In other words, error RTs are not dramatically slower than correct RTs. Ratcliff and Rouder found that data were best fit by the second, constant drift rate, assumption. This finding has been replicated in all of the experiments in which the effects of stimulus duration have been examined via the diffusion model (Ratcliff, 2002; Ratcliff & Rouder, 2000; Ratcliff, Thapar, & McKoon, 2003; Thapar et al., 2003). The conclusion is that information from a briefly displayed, masked stimulus quickly establishes a memory representation that supplies a constant value of drift rate to the decision process.

9.3 Early Visual Processing, Attention, and Drift Rate

Smith, Ratcliff, and Wolfgang (2004) proposed a significantly more comprehensive account of the connection between early visual processing and decision processes than Ratcliff and Rouder (2000). They examined the effects of contrast, attention, and masking on a simple orientation judgment. The stimuli were Gabor patches oriented in one of two directions, and subjects were to judge the orientation. Stimuli could be presented in one of four locations, and prior to stimulus onset, one position was cued as more likely than the others. Performance was better for a stimulus that appeared in the expected, that is, the attended, location than an unattended location. Also, performance was better for higher-compared to lower-contrast stimuli and better for not masked than masked stimuli.

Smith et al. (2004) combined a model of the effects of attention on early visual processing with the diffusion decision model. For the visual processing model, there were five assumptions: a stimulus produces a representation in a visual short-term memory representation; the onset of information in this representation is delayed for unattended compared to attended locations because attention has to move from the attended to the unattended location; if a stimulus is masked, the buildup of information in the representation stops when the mask is presented; after the initial buildup of information, the representation is stable (as in Ratcliff & Rouder, 2000); and the strength of the representation is a function of stimulus duration and contrast. The combination of a visual processing model based on these assumptions and the diffusion decision model provided a successful account of the data from all of the conditions formed by crossing all of these variables.

The important point from this example is that all of the interacting independent variables, common ones in the perception literature, and their effects on all of the dependent variables were explained by integrating a visual processing model consistent with current views on attention and masking with the diffusion decision model. The visual processing assumptions provided a model of drift rate and hence a meeting point between perception and decision.

9.4 Categorical Information and Drift Rate

Nosofsky and Palmeri (1997) and Ashby (2000) combined models for the representation and processing of categorical information with a sequential sampling decision process. In both of their models, a stimulus is assigned to one or the other of two categories according to how well it matches information in memory. In Nosofsky and Palmeri's model, a stimulus is matched against exemplars of the two categories. In Ashby's model, a stimulus is assumed to vary on several perceptual dimensions, and its representation on these dimensions is matched against memory. In both models, two-choice categorization decisions are made via a sequential sampling decision process. Evidence is accumulated over time toward decision boundaries—one boundary for each category.

In more detail, in Nosofsky and Palmeri's (1997) model, each time over the course of an experiment that a stimulus is presented, a representation of it is stored in memory, and these exemplars can be retrieved for use in decisions about later stimuli. The rate at which an exemplar is retrieved is a function of its strength in memory and its similarity to the stimulus. Each retrieved exemplar drives the decision process one step toward the category boundary to which the retrieved exemplar belongs. The difficulty of stimuli is varied by the frequency with which exemplars of their category are presented in an experimental session and by the similarities of the stimuli.

In Ashby's model, the representation of a stimulus is assumed to vary on several perceptual dimensions. How strongly a stimulus belongs to one or the other of the response categories depends on where it lies in the multidimensional stimulus space; the closer to the line that divides the space into two categories, the weaker the evidence for membership in the categories. Evidence is accumulated on each\of the dimensions by a diffusion process. Two decision boundaries are placed in the multidimensional space, and evidence is accumulated until one or the other is reached. Because distance from each decision boundary is one-dimensional, this reduces to the standard diffusion process.

In both Nosofsky and Palmeri's (1997) and Ashby's (2000) proposals, a model of categorization processing produces a measure of the match between a stimulus and the two response categories, and this match drives a random walk or diffusion decision process. Thus they offer two different ways of linking a stimulus representation model to a sequential sampling decision process.

10 Does the Diffusion Process Reflect Neural Activity?

As information from a stimulus is accumulated toward one or the other of the two responses in a two-choice task, the path is extremely noisy. Before culminating at a decision boundary, the total evidence accumulated can move far below the starting point and far above it. This variability over time in the diffusion process is evocative of the variability that occurs over time in neural firing rates.

One way the connection between diffusion processes and neural activity has been pursued is to simultaneously collect behavioral data and single-cell recording data. Beginning with Hanes and Schall's pioneering work (1996) and Shadlen and colleagues' (e.g., Gold & Shadlen, 2001) efforts to integrate diffusion processes and neural decision making, research in this area has rapidly advanced (Ditterich, 2006; Gold & Shadlen, 2001; Hanes & Schall, 1996; Huk & Shadlen, 2005; Mazurek, Roitman, Ditterich, & Shadlen, 2003; Roitman & Shadlen, 2002; Schall, 2003). Also, studies using event-related potential (Philiastides, Ratcliff, & Sajda, 2006) and fMRI measures (Heekeren, Marrett, Bandettini, & Ungerleider, 2004) are beginning to appear. The general questions are whether and how the components of processing recovered from behavioral data by the diffusion model or other recent sequential sampling models correspond to the physiological measures.

Research aimed at these questions is illustrated in a recent experiment by Ratcliff, Cherian, et al. (2003). Monkeys were trained to discriminate whether the distance between two dots was large or small, indicating their responses by left versus right eye movements. Which response was correct was probabilistic, defined by the history of rewards for correct responses in the experimental sessions. As the monkeys performed the task, data were collected from cells identified as buildup (or prelude) cells in the superior colliculus. The aim was to test whether the decision process and the firing rates (aggregated over individual cells and trials for each cell) were linked such that the closer the diffusion process to a decision boundary, the higher the firing rate of a cell. Ratcliff et al. applied the diffusion model to the behavioral data, fitting the data adequately and obtaining the values of the parameters that best fit the behavioral data. Then, using these parameter values, sample diffusion paths were generated, each path beginning at the starting point of the diffusion process and ending at a response boundary. These paths were averaged and the average was compared to the average, across cells and trials, of the firing rates of the buildup cells. The finding was that the average path closely matched the average neural firing rate. As the average path approached a decision boundary, the average firing rate increased.

The connection between the behavioral data and the neural data was supported by a counterintuitive feature of the data. The neural firing data were split into three groups: those for which the eye movement response was in the fastest third of responses, the intermediate third, or the slowest third. Measuring from the time of onset of a stimulus, the firing rate function for the intermediate responses was shifted in time relative to the function for the fastest responses, and the function for the slowest responses was shifted again relative to the intermediate responses. The shifts were as large as 100 ms across the experimental conditions. The shifting is counterintuitive because on average, one might expect the evidence in the diffusion process to increase gradually over time from starting point to decision boundary. However, the model predicts exactly the shifted patterns of firing rates because of the extremely large amount of noise in the diffusion processes. The noise has the consequence that processes that get near a decision criterion likely hit the criterion (noise makes them hit the criterion). So for a process to have failed to reach a criterion for a long time, it must have remained near the starting point. Therefore, the average paths for intermediate relative to fastest, and slowest relative to intermediate, processes have to remain near the starting point, accelerating to the decision criterion just before the response (see also Ratcliff, 1988). This delay followed by acceleration leads to the shifts in the firing rate functions.

In Ratcliff et al.'s experiments, recordings from cells that increased firing for one of the response categories were compared to recordings from cells that increased firing for the other of the response categories. The diffusion model accounted for the difference between the firing rates of the two types of cells, but not for the firing rates of the cells themselves.

To model the two types of cells separately, Ratcliff, Hasegawa, et al. (2006) proposed a dual diffusion model. In this model, evidence is accumulated separately for the two response alternatives as in the accumulator models described above (e.g., Usher & McClelland, 2001). For each alternative, evidence accumulation is a diffusion process. The amount of evidence at any given point in the process is subject to decay as a function of the amount of evidence in the accumulator. This model fits all the same data as the standard diffusion model described in the rest of this review. Its advantage is that it predicts the firing rates for the cells that respond in favor of one of the two types of stimuli and for the cells that respond in favor of the other type. Ratcliff, Hasegawa, et al. showed that the model provided reasonably good fits to the behavioral data, and they used the best-fitting values of the parameters to generate predicted paths for the two types of cells separately (see also Mazurek et al., 2003). The averages of the predicted paths corresponded closely to the averages of the cells' firing rates. In particular, the predicted paths showed the shift in firing rate functions from the fastest to the intermediate to the slowest thirds of the responses.

Besides these developments, there have been theoretical advances that attempt to produce models based on populations of spiking neurons, modeling the physiological behavior of neurons, synapses, and neurotransmitters (e.g., Lo & Wang, 2006; Wang, 2002; Wong & Wang, 2006). The models represent the functional architecture of the processing systems involved in making simple decisions and aim to account for physiological data from single neurons to populations while at the same time being consistent with behavioral data. One aspect of this modeling approach is to examine to what extent the behavior of populations of such units approximates diffusion processes (see Mazurek & Shadlen, 2002; Wong & Wang, 2006).

Specifically, Wong and Wang (2006) developed a spiking neuron model within a dynamical systems framework for perceptual decisions of the kind presented in experiments 1 to 3 above. They worked through a series of approximations including averaging over populations of neurons, approximating input-output relationships with linear functions and approximating slowly varying activity of some subpopulations of neurons with constant activity. The result is a simple two-unit system with self-excitation and mutual inhibition that corresponds to a dual diffusion model (e.g., Usher & McClelland, 2001). This is just one example of the advances in the theoretical literature that might provide an account of how diffusion models arise from approximations to physiologically based processes.

In the neural and functional architecture of the decision system, there are several modalities in which decisions can be expressed, such as eye movements, hand, foot, finger, head, or other limb movements, vocal responses, and so on. It is possible that each of these will implement a diffusion-like process in which evidence is accumulated in pools of neurons to criterial activity, at which time an overt response is initiated. There are many possible stimulus modalities, for example, any of a number of possible visual, auditory, tactile, smell, taste, stimulus types, as well as stimuli that require higher-level processes, for example, memory, language, and so on. Evidence from each of these possible stimulus types from the brain areas performing the computations that provide discriminative information must be able to be directed to the system that is implementing the decision. From this point of view, the decision process is a collecting point for evidence from many different processing systems, and this decision process is responsible for implementing the overt decision. Of course, this does not relegate decision processes to the very latest output stages of processing; decisions must be made internally in more complex tasks, for example planning, complex decision making, and reasoning. However, despite the possible complexity of these processing systems, simple animal models have a central place in understanding the neural systems that implement overt decisions.

11 Conclusion

It has probably not been realized in the wider scientific community that the class of diffusion models has as near to provided a solution to simple decision making as is possible in behavioral science. The models are constrained and yet have been successfully fit to many data sets, including data from a large number of individual subjects. They have proved useful in interpreting experimental results that are getting close to issues that have practical importance, for example, aging and speed of processing and aphasia. They have also provided a strong link between behavioral and neural decision making and provide a strong theoretical common language for these two domains. This review has presented the standard diffusion model in detail and has attempted to explain how it works, along with application to new experimental data using the motion coherence paradigm.