Estimating parameters of the diffusion model: Approaches to dealing with contaminant reaction times and parameter variability

Abstract

Three methods for fitting the diffusion model (Ratcliff, 1978) to experimental data are examined. Sets of simulated data were generated with known parameter values, and from fits of the model, we found that the maximum likelihood method was better than the chi-square and weighted least squares methods by criteria of bias in the parameters relative to the parameter values used to generate the data and standard deviations in the parameter estimates. The standard deviations in the parameter values can be used as measures of the variability in parameter estimates from fits to experimental data. We introduced contaminant reaction times and variability into the other components of processing besides the decision process and found that the maximum likelihood and chi-square methods failed, sometimes dramatically. But the weighted least squares method was robust to these two factors. We then present results from modifications of the maximum likelihood and chi-square methods, in which these factors are explicitly modeled, and show that the parameter values of the diffusion model are recovered well. We argue that explicit modeling is an important method for addressing contaminants and variability in nondecision processes and that it can be applied in any theoretical approach to modeling reaction time.

Sequential sampling models are currently the models most successful in accounting for data from simple two-choice tasks. Among these, diffusion models have been the ones most widely applied across a range of experimental procedures, including memory (Ratcliff, 1978, 1988), lexical decision (Ratcliff, Gomez, & McKoon, 2002), letter-matching (Ratcliff, 1981), visual search (Strayer & Kramer, 1994), decision making (Busemeyer & Townsend, 1993; Diederich, 1997; Roe, Busemeyer, & Townsend, 2001), simple reaction time (Smith, 1995), signal detection (Ratcliff & Rouder, 1998; Ratcliff, Thapar, & McKoon, 2001; Ratcliff, Van Zandt, & McKoon, 1999), and perceptual judgments (Ratcliff, 2002; Ratcliff & Rouder, 2000; Thapar, Ratcliff, & McKoon, 2002).

The experimental data to which the models are fit in two-choice tasks are accuracy rates and reaction time distributions for both correct and error responses. The ability of the models to deal with this range of data sets them apart from other models for two-choice decisions. Because multiple dependent variables need to be fit simultaneously and because the data can have contaminants, the fitting process is not straightforward. For these reasons, the model is a good testing ground for evaluating fitting methods.

In fitting any sequential sampling model to data, the aim is to find parameter values for the model that allow it to produce predicted values for reaction times and accuracy rates that are as close as possible to the empirical data. But so far in this domain, little attention has been paid to the methods for fitting. Sometimes models have been fit by eye, by simply observing that they can capture the ordinal trends in the experimental data. Sometimes a standard criterion such as chi square (e.g., Smith & Vickers, 1988), in which the difference between the observed and the predicted frequencies of reaction times in the reaction time distribution is minimized, is used. Nonstandard criteria have also been used. For example, Ratcliff and Rouder (1998) and Ratcliff et al. (1999) fitted an ex-Gaussian, summary, reaction time distribution (Ratcliff, 1979; Ratcliff & Murdock, 1976) to data and to predictions from Ratcliff’s diffusion model. Then the sum of squares for the differences between the parameters of the ex-Gaussian for predictions and for data plus the sum of squares for the differences between accuracy rates for predictions and data were minimized. Ratcliff and Rouder (2000) used a more direct sum-of-squares method in which quantile reaction times were used instead of parameters of the summary (ex-Gaussian) distribution. The statistical properties for all these fitting methods have not been examined.

In this article, we will examine three different methods for fitting the diffusion model to two-choice reaction time and accuracy data and will examine the properties of the estimators for the parameters of the model. The issues that arise have implications not only for fitting the diffusion model, but also for fitting summary models of single reaction time distributions (e.g., Heathcote, Brown, & Mewhort, 2002; Ratcliff, 1979; Van Zandt, 2000) and for fitting models in other domains. Throughout the article, we will discuss findings as they apply to the diffusion model case and also will place them in a more general context. Examples of the issues that have broad implications are the following. First, how should contaminant reaction times be handled empirically (can they be eliminated) and theoretically (can they be explicitly modeled)? Second, how robust is a method for estimating parameters either in terms of possible failures of a model’s assumptions or in terms of contaminated data? Third, there are practical considerations, including computation speed. Fourth, an optimal fitting method should provide the best possible estimates of parameters. The estimates should be unbiased— that is, they should converge on the true parameter values as the number of observations increases (i.e., they should be consistent). Fifth, the estimates should also have the smallest possible standard deviations, so that any single fit of a model to data produces estimates that are close to the true values. In Appendix A, we present a more formal discussion of the statistical factors involved in model fitting and parameter estimation.

In the model-fitting enterprise, sometimes there is no need for extremely accurate estimation of parameter values; finding a set of parameter values that produces predictions reasonably near the experimental data is enough to show that the model is capable of fitting the data. But there are many cases in which accurate estimation of parameter values is necessary. For example, any situation in which individual differences are examined requires reasonably accurate estimates of parameters. Also, if differences among the conditions in an experiment are to be examined, knowing the standard deviations in parameter estimates is important. It is toward these ends that this article will provide an evaluation of fitting methods in terms of their robustness and flexibility in fitting data, as well as in terms of their accuracy in recovering parameter values from the different fitting methods. In order to explain the fitting methods we evaluated and the results of the evaluations, we first will need to present the diffusion model, the model we used as a testing ground and the model for which we needed good fitting methods.

THE DIFFUSION MODEL

Diffusion and random walk models form one of the major classes of sequential sampling models in the reaction time domain. The diffusion process is a continuous variant of the random walk process. The models best apply in situations in which subjects make two-choice decisions that are based on a single, “one-shot” cognitive process, decisions for which reaction times do not average much over 1 sec. The basic assumption of the models is that a stimulus test item provides information that is accumulated over time toward one of two decision criteria, each criterion representing one of the two response alternatives. A response is initiated when one of the decision criteria is reached. The researchers who have developed random walk and diffusion models take the approach that all the aspects of experimental data need to be accounted for by a model. This means that a model should deal with both correct and error reaction times, with the shapes of the full distributions of reaction times, and with the probabilities of correct versus error responses. It should be stressed that dealing with all these aspects of data is much more of a challenge than dealing with accuracy alone or with reaction time alone.

Random walk models have been prominent since the 1960s (Laming, 1968; Link & Heath, 1975; Stone, 1960). Diffusion models appeared in the late 1970s (Ratcliff, 1978, 1980, 1981). The random walk and diffusion models are close cousins and are not competitors to each other, as they are with other sequential sampling models (e.g., accumulator models and counter models; see, e.g., LaBerge, 1962; Smith & Van Zandt, 2000; Smith & Vickers, 1988; Vickers, 1970, 1979; Vickers, Caudrey, & Willson, 1971). So, although we will deal with only one diffusion model in this article, most of the issues and qualitative results apply to other diffusion and random walk models, and the general approach applies to other sequential sampling models.

The earliest random walk models assumed that the accumulation of information occurred at discrete points in time, each piece of information being either fixed in size (e.g., Laming, 1968) or variable in size (Link, 1975; Link & Heath, 1975). The models were applied mainly in choice reaction time tasks and succeeded in accounting for accuracy and for mean reaction time for correct responses. They were also sometimes successful with mean error reaction times, but they rarely addressed the shapes of reaction time distributions.

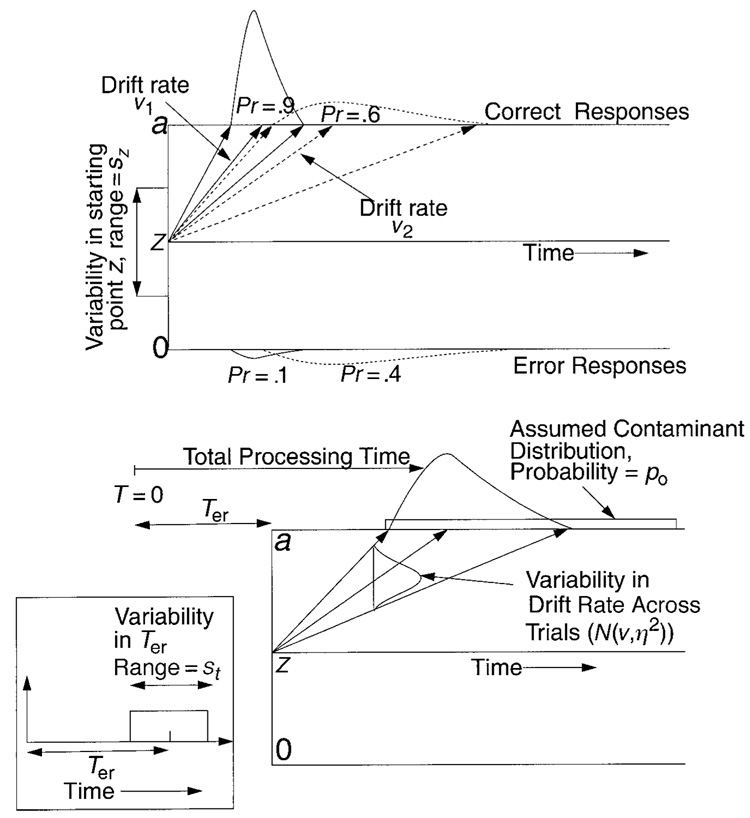
Ratcliff’s (1978) diffusion model is illustrated in Figure 1 in three panels, each showing different aspects of the model. Information is accumulated from a starting point z toward one or the other of the two response boundaries; a response is made when the process hits the upper boundary at a or the lower boundary at zero. The mean rate at which information is accumulated toward a boundary is called the drift rate. During the accumulation of information, drift varies around its mean with a standard deviation of s. Variability is large, and processes wander across a wide range, sometimes reaching the wrong boundary by mistake, which results in an error response. The top panel of the figure shows two processes, one with a drift rate of v₁ (solid arrows) and the other with a drift rate of v₂ (dashed arrows). Variability in drift rate leads to distributions of finishing times (reaction time distributions), one distribution for correct response times (at the top boundary for the processes shown in the figure) and another distribution for error responses (at the bottom boundary in the figure). The spread of the solid arrows shows the reaction time distribution for the process with drift rate v₁, and the spread of the dashed arrows shows the reaction time distribution for the process with drift rate v₂. The geometry of the diffusion process naturally maps out the right-skewed reaction time distributions typically observed in empirical data. The panel also shows how smaller drift rates (e.g., v₂) lead to slower responses, with more chance of reaching the wrong boundary, and so to larger error rates.

Figure 1.

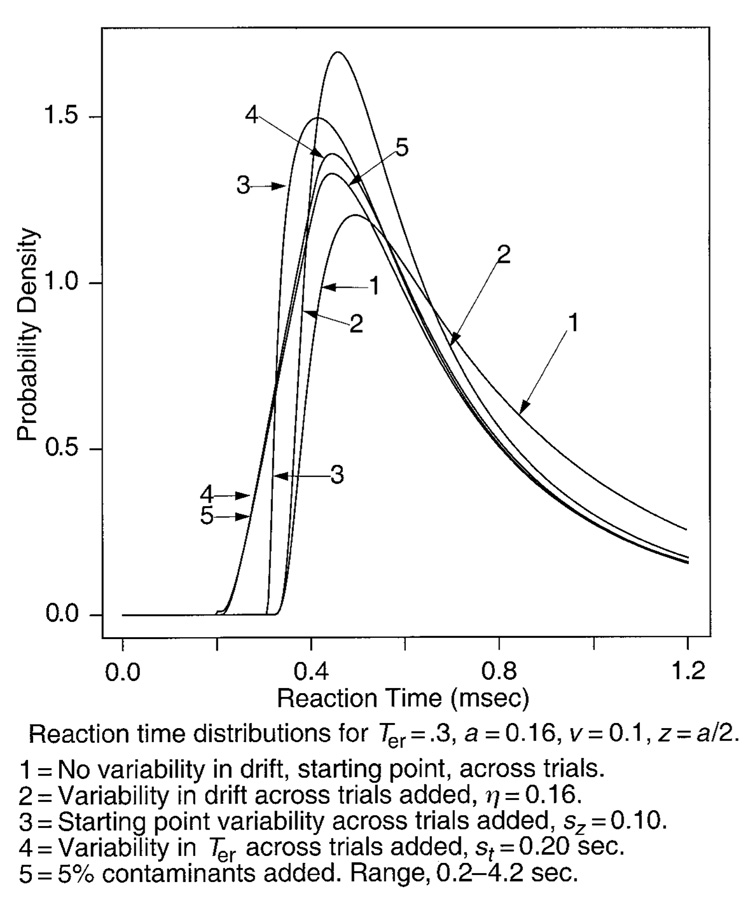
An illustration of the diffusion model and parameters. The top panel shows starting point variability and illustrates how accuracy and reaction time distribution shapes for correct and error responses change as a function of two different drift rates (v₁ and v₂). The bottom right panel illustrates variability in drift across trials (standard deviation η) and the distribution of contaminants. The bottom left panel shows variability in T_er, the nondecision component of reaction time.

The variability in drift rate within a trial, represented by the parameter s, is a scaling parameter; if it were doubled, for example, all the other parameters could be changed to produce predictions identical to those before the change. The s is a fixed, not a free, parameter in fits of the model to data. It would be possible to fix another of the parameters instead—for example, boundary separation. But some empirical manipulations would be expected to affect boundary separation (e.g., speed–accuracy instructions), so that if such a parameter were fixed, the effects of the manipulation would show up in the values of other parameters and interpretation would be difficult. The most natural assumption (and the standard assumption) is to hold within-trial variability in drift constant, assuming that it is a constant value across the whole range of different kinds of decisions in an experiment, from easy to most difficult. We fixed s at 0.1, a value near those used in previous applications of the model (e.g., Ratcliff, 1978).

Variability in Parameters Across Trials

Besides variability in drift rate within each trial, there are several sources of variability across trials. For one, the mean drift rate for a given stimulus varies across trials (because subjects do not encode a stimulus in exactly the same way every time they encounter it). This variability is assumed to be normally distributed with a standard deviation of η, and it is illustrated in the bottom right panel of Figure 1.

Another source of variability is variability across trials in the starting point z (top panel of Figure 1). Variability across trials comes from a subject’s inability to hold the starting point of the accumulation of information constant across trials. The distribution of starting point values is assumed to be rectangular, with s_z as its range. A rectangular distribution was chosen so that the starting point would be restricted to lie within the boundaries of the decision process.¹

Without variability in drift rate and starting point across trials, simple random walk and diffusion models would predict that reaction times will be the same for correct and error responses when the two response boundaries are equidistant from the starting point; this is contrary to data. There has been a number of attempts to account for error reaction times within random walk and accumulator model frameworks (e.g., Laming, 1968; Link & Heath, 1975; Smith & Vickers, 1988), and some of these were moderately successful. But the inability of most models to deal with the full range of effects led to a deemphasis of error reaction times in the literature: Error reaction times have relatively rarely been reported, and there has been relatively little effort to deal with them theoretically until recently.

However, recent work has shown how variability in drift rate and starting point can produce unequal correct and error reaction times (Laming, 1968; Ratcliff, 1978, 1981; Ratcliff et al., 1999; Smith & Vickers, 1988; Van Zandt & Ratcliff, 1995). Ratcliff (1978) showed that variability in drift across trials produces error reaction times that are slower, and Laming (1968) showed that variability in starting point across trials produces error reaction times that are faster. Ratcliff et al. (1999) and Ratcliff and Rouder (1998) showed that the combination of the two types of variability can produce accurate fits to both patterns. Most interestingly, the combination can produce a crossover, so that errors are slower than correct responses when accuracy is low and errors are faster than correct responses when accuracy is high. This crossover has been observed a number of times experimentally (Ratcliff & Rouder, 1998, 2000; Ratcliff et al., 1999; Smith & Vickers, 1988).

The diffusion process is a model of the decision process, and not of the other processes involved in a task, processes such as stimulus encoding, response output, memory access, retrieval cue assembly, and so on. The times required for these other processes are combined into one parameter, T_er (bottom right panel, Figure 1). From a theoretical perspective, it has always been recognized there must be variability in T_er (and it has been used in the simple reaction time literature; cf. Smith, 1990). But it has never been clear what the addition of the extra parameter would buy for the sequential sampling models; it appeared that success or failure of the models was not dependent on it. However, we recently found sets of data for which the diffusion model fits missed badly in some conditions and discovered that this was due to large variability in the .1 quantile reaction times across conditions. Adding variability in T_er to the model corrected the fits (Ratcliff et al., 2002).

For purposes of modeling, T_er is assumed to be uniformly distributed (bottom left panel of Figure 1). The true distribution for T_er might be skewed or normal, but this distribution is convolved with the distribution from the decision process that has a larger standard deviation (by a factor of at least 4). The distribution of the convolution is determined almost completely by the distribution of the decision process, and so the precise shape of the distribution of T_er has little effect on predicted reaction time distribution shape. The standard deviation of the distribution of T_er determines the amount of variability in the .1 quantile reaction times across trials that can be accommodated by the model, and it also determines the size of the separation between the .1 and the .3 quantile reaction times relative to the case with no variability in T_er.

Simulating the Diffusion Process

The first step in an examination of fitting methods is to produce data to be fit. A computer program was written that, given input values for all the diffusion model parameters, generated simulated data from the model. That is, the program generated individual data points, each one a response choice with its associated reaction time. The aim was that the fitting methods should recover the correct parameter values—in other words, the parameter values from which the data were generated.

To produce simulated data from the diffusion process, a random walk approximation was used. Feller (1968, chap. 14) derived the diffusion process from the random walk by using limits in the random walk: As step size becomes small, the number of steps becomes large, and the probability of taking a step toward one boundary approaches .5. Specifically, if the random walk has a probability of q of taking a step down, a step size in time of h, and a step size in space of δ, the random walk approaches the diffusion process when δ→0, h→0, and q→1/2, so that (p − q)δ/h→v and 4pqδ²/h→s², where v and s² are constants and p = 1 − q. If these limits are applied to the expression for reaction time distributions (first-passage times) and response probabilities, the diffusion process expressions are obtained (see Feller, 1968, chap. 14; Ratcliff, 1978).

To scale the random walk approximation so that the diffusion model parameters can be used, the step size and the probability of taking a step up or down need to be scaled, using the step size in time and the standard deviation in drift (s). First, we define the parameter h to be the step size in time (e.g., h might be 0.05 msec). Then, in one time step, the process can move a step size of δ up or down. We set $\delta =s\sqrt{h}$ and the probability of going distance δ to the lower boundary to be $0.5(1-v\sqrt{h/s).}$ The simulation starts from starting point z, and after each unit of time h, it takes a step of size δ until it terminates at 0 or a. With these definitions, as h→0, then δ→0; the mean displacement during time h equals (p − q)δ/h, which approaches drift rate v; the variance of the displacement approaches 4pqδ2/h; and so the random walk approaches the diffusion process.

To implement this random walk approximation to the diffusion process in a computer program, it is more efficient to use integer arithmetic, rescaling distance so that a step is one unit up or down. This is accomplished by dividing a, z, and v by δ. To produce simulated data from the diffusion process, we reduced the step size in the random walk, in accordance with the limits stated above, until the random walk approximated the diffusion process. Steps with a size of 0.05 msec were used, and these produced mean reaction times within 0.1 msec and response probabilities within 0.1% of the values produced by explicit solutions for the diffusion model (see Appendix A).

There are many other ways in which a diffusion process could be simulated (Tuerlinckx, Maris, Ratcliff, & De Boeck, 2001). The advantage of the random walk approximation is generality. There are cases in which the drift rate is assumed to change over position in the process, as in the Ornstein Uhlenbeck diffusion model (Busemeyer & Townsend, 1992, 1993; Smith, 1995), or over time during the process. For example, if a stimulus display was masked before a response had been produced, during processing, the drift rate could be assumed to fall after masking (see Ratcliff & Rouder, 2000). In these cases, exact solutions are usually not available, but it is extremely easy to modify the program that simulates the diffusion process with the random walk.

CONTAMINANT REACTION TIMES

In evaluating the three fitting methods, we addressed the issue of contaminant reaction times. We defined contaminants as responses that come from some process other than the diffusion decision process. One class of contaminants is outliers—response times outside the usual range of responses (either shorter or longer). Outliers are a serious problem in reaction time research. They can cause major problems in data analysis, because they can distort estimates of mean reaction time and standard deviation in reaction time (see Ratcliff, 1979). Also, outliers significantly reduce the power of an analysis of variance (see Ratcliff, 1993; Ulrich & Miller, 1994). The other class of contaminants is reaction times that overlap with the distribution of reaction times from the process being examined. These are also a problem for data analysis, although not as serious as the problem caused by outliers. Contaminants might arise, for example, from a guess or from a momentary distraction that is followed by a fast response.

Fast guesses, one kind of outlier, have in themselves been a topic for modeling. The influential “fast guess” model was developed to account for speed–accuracy tradeoffs when these tradeoffs were accomplished by increasing or decreasing the number of fast guesses (Ollman, 1966; Swensson, 1972; Yellott, 1971). Often, fast error responses are called fast guesses. This is usually not an accurate description. True fast guesses are guesses—that is, their accuracy is chance (Swensson, 1972). So, in a condition in which there are fast error responses, it is necessary to determine whether all fast responses are at chance. If many fast responses are accurate and there are few fast errors, the fast errors are not fast guesses. It cannot be stressed enough that fast errors are not fast guesses unless all responses below some lower cutoff (e.g., the fastest 10%, 5%, or 1% of the responses) are at chance responding. This is the signature that is needed to identify fast guesses and that can be used to eliminate subjects or devise where to place lower cutoffs.

The method we have adopted for dealing with contaminants in data analyses is, first, to eliminate fast and slow outliers, using cutoffs. For fast outliers, we place an upper cutoff at, say, 300 msec and a lower cutoff at zero and examine how many reaction times appear in that range for each subject, examining the accuracy of these responses. If a subject has a significant number of responses (e.g., over 5% or 10%) that are fast and at chance, the subject is a candidate for elimination from the experiment (we occasionally find such noncooperative subjects). We then increase the upper cutoff (to, say, 350 msec) to see whether accuracy begins to rise above chance. Repeating this process with increasingly larger cutoff values allows us to determine a good choice of a cutoff for fast outliers.

The method just described for setting a cutoff for fast outliers is workable in most situations. However, when an experimental task biases one response over the other (e.g., Ratcliff, 1985; Ratcliff et al., 1999), then typically, one response will be faster than the other, sometimes by as much as 100–200 msec in mean reaction time. This means that the shortest reaction times for responses for the biased response will be up to 100 msec shorter than responses for the nonbiased response. In this case, the use of cutoffs will not allow fast guesses of the biased response to be distinguished from genuine responses from the decision process. Examination of the shape of reaction time distributions might be one way of detecting fast outliers. If the leading edge of the distribution has a long rise or reaction times are less than 250 msec, the short reaction times should be viewed with suspicion. Also, if only fast errors occurred in a high-accuracy condition when the correct response was biased against, these fast errors could come from fast guesses of the biased response.

For slow outliers, we set an upper cutoff not by some fixed proportion of responses, but rather by determining a point above which few responses fall. The choice depends on the research goal; the cutoff might be smaller for hypothesis testing than for model fitting (see Ratcliff, 1993, for a discussion of the power of tests).

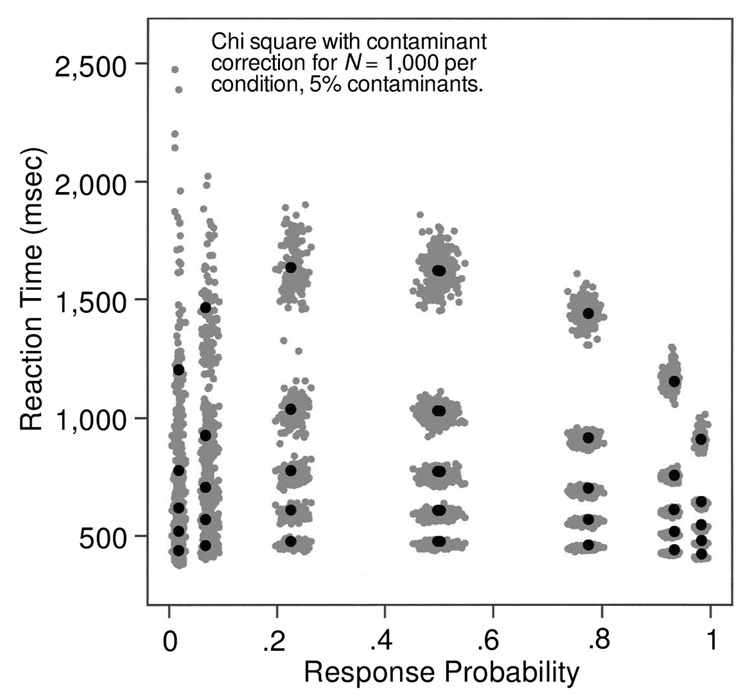
For model fitting, cutoffs can eliminate extremely fast and slow outliers. However, to eliminate all contaminants is impossible. The solution we adopted to deal with these remaining contaminants was to explicitly represent them in the fitting method and estimate their proportion (p_o). For the diffusion model simulations, we assumed that contaminants were generated only by a delay inserted in the usual decision process. Specifically, we assumed that on some proportion of the trials, a random delay was introduced into the response time. Thus, the observed response times in each condition were a mixture of responses from a regular diffusion process (with a probability of 1 − p_o) and contaminant responses (with a probability of p_o; see Figure 1, bottom right panel).

Our assumptions about contaminants are reasonable if subjects are cooperative and if they make errors only as a result of lapses of attention or other short interruptions. If subjects produce contaminants in other ways (e.g., they could guess in difficult conditions), different assumptions could be incorporated into the fitting program. Dealing with contaminants theoretically in this way can easily be extended to fitting summary distributions for reaction time distributions, as in Heathcote et al. (2002), Ratcliff (1979), Ratcliff and Murdock (1976), and Van Zandt (2000).

For clarity, it is worth noting that issues of fitting contaminant reaction times will not be addressed until the methods for fitting the diffusion model have been introduced and evaluated in detail. Issues concerning variability in T_er will be addressed even later in the text.

FITTING THE DIFFUSION MODEL

To fit the diffusion model to a set of data, characteristics of the data have to be compared with the model’s predictions for those characteristics. The three different fitting methods we evaluated each compare different characteristics, and each requires an expression for the model’s predictions. Collectively, the comparisons require the predicted probability densities for individual reaction times, the predicted cumulative probability distribution, and predicted values of accuracy for each of the experimental conditions. The expressions for all of these are given in Appendix B.

Because the expressions do not have closed forms and because some of the parameters’ values vary across trials (starting point, drift rate, and T_er), the predictions must be computed numerically as described in detail in Appendix B. Numerical computation allows the accuracy of the predictions to be adjusted by adjusting the number of terms in infinite series for the reaction time distributions or increasing the number of terms in numerical integration over starting point and drift variability (although the more accuracy desired, the longer the fits take). For the tests of the fitting methods described below, predicted values of reaction time and accuracy were computed to within 0.1 msec and .0001, respectively.

Maximum Likelihood Fitting Method

Given simulated data and expressions for predictions about the data from the diffusion model, we can fit the model to the data to see how well the maximum likelihood method does in recovering parameter values. For the maximum likelihood method, the predicted defective probability density [f (t_i)] for each simulated reaction time (t_i) for each correct and error response is computed. By a defective density, we mean nothing more than one that does not integrate to one (see Feller, 1968); it integrates to the probability of the response. The product of these defective density values is the likelihood [L = Πf (t_i)] that is to be maximized by adjustment of parameter values. Because the product of large numbers of values of densities can exceed the numerical limits of the computers used to compute likelihood, log of the likelihood is used (maximizing the likelihood is achieved with the same parameters as maximizing the log of the likelihood). Also, maximizing log likelihood is the same as minimizing minus the log likelihood, and most routines are designed for minimization.

Ratcliff’s implementation of the maximum likelihood method involves using the predicted defective cumulative distribution function to obtain the defective cumulative probability for each reaction time, F(t_i), and the defective cumulative probability for that reaction time plus an increment, F(t_i + dt), where dt is small (e.g., 0.5 msec). Then, by using f (t) = [F(t + dt) − F(t)]/dt, the predicted defective probability density at point t can be obtained. Summing the logs of the predicted defective probability densities for all the reaction times gives the log likelihood. Again, minus the log likelihood is minimized.

To minimize minus the log likelihood, Ratcliff used the SIMPLEX routine (Nelder & Mead, 1965; see also Appendix B). This routine takes starting values for each parameter, calculates the value of the function to be minimized, then changes the value of one parameter at a time (sometimes more than one) to reduce the value of the objective function. This process is repeated until either the parameters do not change from one iteration to the next by more than some small amount or the value to be minimized does not change by more than some small amount.

Tuerlinckx’s implementation of the maximum likelihood method uses the defective probability density of each reaction time obtained directly from the predictions of the model (rather than through the cumulative distribution function). Drift variance is integrated over explicitly, and so there is one less numerical integration for the density function. (We were unable to integrate over drift variance for the cumulative distribution function, but only for the density, and Ratcliff used his expression for the distribution function—used in the chi-square and weighted least squares programs—to numerically produce the density for use in maximum likelihood partly so that it and Tuerlinckx’s method could be checked against each other.)

To minimize minus the log likelihood, Tuerlinckx used a constrained optimization routine (NPSOL; Gill, Murray, Saunders, & Wright, 1998; implemented in the NAG library) that searches for the minimum of minus the log likelihood function by using finite difference approximations to the first derivatives for the objective or target function. Although the NPSOL computer algorithm allows the user to supply the theoretical partial derivatives (slopes of the function as a function of each of the parameter values), these were not used, because they are very complicated. In general, in this application, the finite difference method is faster than the SIMPLEX method, because it uses more information about the objective function (derivatives). But it is less robust and can lead to problems in numerical instability that cause it to fail to converge on the minimum of the function being minimized. Tuerlinckx’s method is about five times faster than Ratcliff’s method.

Chi-Square Fitting Method

There are several ways of using a chi-square method for fitting the diffusion model to data; the one we chose was designed to maximize the speed of its computer implementation (and it is the method routinely used by Smith, 1995; Smith & Vickers, 1988).

The chi-square method we used works as follows. First, the simulated reaction times are grouped into bins, separately for correct and error responses. The number of bins we chose was six, with the two extreme bins each containing 10% of the observations and the others each containing 20%. We compute the empirical reaction times that divide the data into the six bins, and these are the .1, .3, .5, .7, and .9 quantiles. Inserting the quantile reaction times for the five quantiles for correct responses into the cumulative probability function gives the expected cumulative probability up to that quantile for correct responses. Subtracting the cumulative probabilities for each successive quantile from the next higher quantile gives the proportion of responses expected between each pair of quantiles, and multiplying by the total number of observations (total number of correct responses) gives the expected frequencies in each bin for correct responses. Doing the same thing for the five quantiles for error responses gives the expected frequencies in each of the bins for error responses. (If there were fewer than five errors in an experimental condition, five quantiles could not be computed, and the error reaction times for the condition were excluded from the chi-square computation.) The expected frequencies (E) are compared with the observed frequencies (O). The chi-square statistic to be minimized is the sum over the 12 bins, the 6 correct response bins and the 6 error response bins, of (O − E)²/E (with these sums for each condition summed over conditions). This chi-square statistic is the objective function to be minimized by parameter adjustment.

For each condition, only five evaluations of F(t) are required for correct responses, and five are required for error responses (no matter how many observations in each condition). As compared with Ratcliff’s maximum likelihood method, the program runs 50 times faster with 250 observations per condition and 200 times faster with 1,000 observations per condition (because the distribution function has to be computed twice for each density function).

Weighted Least Squares Fitting Method

In this method, the sum of the squared differences between observed and predicted accuracy values plus the sum of the squared differences between observed and predicted quantile reaction times for correct and error responses is minimized. The expression for the minimized function is the following: the sum over experimental conditions (for correct and error reaction times separately) of 4(pr_th − pr_ex)² + Σ_iwt × pr_ex × [Q_th(i) − Q_ex(i)]², where pr is accuracy, Q(i) is the quantile reaction time in units of seconds, th stands for predicted, ex stands for experimental, and wt was 2 for the .1 and .3 quantiles, 1 for the .5 and .7 quantiles, and 0.5 for the .9 quantile. Just as with the chi-square method, if there were fewer than five errors in a condition, five quantiles could not be computed, and the error reaction time for the condition was excluded from the least squares computation.

The weights were chosen to roughly approximate the relative amounts of variability in the quantiles, weighting more heavily those quantile points for which variability was smaller. For simple linear regression, an appropriate weighting scheme is to divide each data point by its variance. This gives the smallest standard deviations in the estimates of the parameters (for normally distributed residuals). Whether our weights correspond to the relative variabilities of the quantile reaction times can be determined in two ways: by computing the theoretical standard deviations for the quantile points and by computing their standard deviations empirically from experiments. Theoretically, the asymptotic variance of a quantile reaction time at quantile q is q(1 − q)/(Nf²), where N is the number of observations and f is the probability density at the quantile (Kendall & Stuart, 1977, Vol. 1, p. 252). We carried out this computation for two sets of parameter values (the first and sixth rows of Table 1, with drift rates of .3 and .1, respectively), computing the standard deviations in the quantile reaction times. We then divided the .5 quantile standard deviation by each of the others to give relative weights. For the five quantiles .1, .3, .5, .7, and .9, the ratios were 2.4, 1.6, 1.0, 0.7, and 0.3 for the first set of parameter values and 2.3, 1.6, 1.0, 0.6, and 0.3 for the sixth set of parameter values. Thus, the weights we chose are approximately in the ratio of the standard deviations. The problem with this theoretical computation is that the expression for the variance is accurate only asymptotically and our data have too few observations (especially in extreme error conditions) to be asymptotic. So, additional work would be needed to compute expressions for the nonasymptotic case.

Table 1.

Parameter Values for Simulations

Parameter Set	a	Ter	η	sz	v1	v2	v3	v4
A	0.08	0.300	0.08	0.02	0.40	0.25	0.10	0.00
B	0.08	0.300	0.16	0.02	0.40	0.25	0.10	0.00
C	0.16	0.300	0.08	0.02	0.30	0.20	0.10	0.00
D	0.16	0.300	0.16	0.02	0.30	0.20	0.10	0.00
E	0.16	0.300	0.08	0.10	0.30	0.20	0.10	0.00
F	0.16	0.300	0.16	0.10	0.30	0.20	0.10	0.00

Empirically, we calculated the standard deviations in quantile reaction times across subjects for a letter identification experiment (Thapar et al., 2002; see also Ratcliff & Rouder, 2000). Again, to represent the standard deviations as weights, we divided the standard deviation for the .5 quantile by each of the others. For three experimental conditions that spanned the range of accuracy values in the experiment (probability correct of .9 to .6), the ratios were the following: 1.3, 1.2, 1.0, 0.7, 0.4; 1.4, 1.2, 1.0, 0.8, 0.4; and 1.3, 1.1, 1.0, 0.8, 0.6. The squares of these ratios (relative variances) are not far from our selection of weights. Thus, given both the theoretical and the empirical calculations, we conclude that the weights we used (2, 2, 1, 1, and .5) were not unreasonable.

Another issue concerning the optimality of the least squares method is that the data entering each term in the sums of squares should be independent of each other (see, e.g., Seber & Wild, 1989). If the data are not independent, all possible covariances among the quantities should be taken into account (Seber & Wild, 1989). In our case, it is clear that quantile reaction times for correct and error responses and accuracy values all covary. If a single parameter of the model is changed, all the quantile reaction times and accuracy values will change in a systematic way. Some of the covariances are known. For example, the asymptotic covariation between all the reaction time quantiles for one response (correct or error) is given by Kendall and Stuart (1977). But this is an asymptotic expression and would not apply accurately to error reaction times (for which there are few data points). Also, theoretical formulations for the covariations between correct and error reaction time quantiles and accuracy values are not available. It would be very difficult to find expressions for all the covariances required to produce an optimal version of the weighted least squares method. The weighted least squares method we employed should, therefore, be viewed as the kind of ad hoc method that is often used in fitting.

To implement our weighted least squares method, the predicted reaction time for each of the quantiles needs to be computed. To compute these, the whole predicted cumulative reaction time distribution has to be obtained. We used 400 reaction times to obtain cumulative frequencies and then linear interpolation between pairs of values to determine the quantile reaction times. The SIMPLEX routine was used to minimize the weighted least square, and the implementations ran at about the same speed as Ratcliff’s maximum likelihood program—that is, much slower than the chi-square method.

In the weighted least squares method, accuracy is represented explicitly in the sum of squares, but it is not represented explicitly in the maximum likelihood and chi-square methods. In those methods, accuracy is represented by the predicted relative frequencies in the reaction time distributions for correct and error responses. For example, for 250 observations per condition and an accuracy value of .9, the total observed frequency for errors would be 25, and the total frequency for correct responses would be 225. In the fitting process, if the model predicted an accuracy of .8, it would overpredict errors (frequency of 50) and underpredict correct responses (frequency of 200). Then the fitting program would attempt to adjust these frequencies, subject to the other experimental conditions and other constraints.

PARAMETER VALUES

The parameter values were chosen to be representative of real experiments in which subjects are required to decide between two alternatives—for example, word or non-word in lexical decision or bright or dark in brightness discrimination. We simulated data for an experiment with four conditions, the conditions representing four levels of difficulty of a single independent variable, as, for example, in a lexical decision or recognition memory experiment with four levels of word frequency or in a two-choice signal detection experiment with four levels of brightness of the stimulus. We assumed that the levels of the variable are randomly assigned to trials in each experiment, so that subjects cannot anticipate which condition is to occur on any trial (see Ratcliff, 1978, Experiment 1). This means that subjects cannot adjust processing as a function of condition and, therefore, none of the parameters of the model except the parameter representing stimulus difficulty can change across levels of the manipulated variable.

The simulated data were generated from 12 different sets of parameter values, with the values chosen to span the ranges of values that are typical in fits of the diffusion model to real data. For the 6 sets shown in Table 1, the starting point z was symmetric between the two boundaries. The drift rates are all positive because the same results would be obtained with negative drift rates, since the boundaries are symmetric. (We also performed the same analyses with asymmetric boundaries; the results are qualitatively the same as those for the symmetric boundary case, and tables displaying the results can be found on Ratcliff’s or the Psychonomic Society’s Web pages).

T_er, the parameter for the nondecision components of processing, was always set at 0.3 sec. This parameter largely determines the location of the leading edge of the reaction time distribution. When boundary separation is small, the leading edge is a little closer to T_er, and when boundary separation is large, the leading edge is a little further away from T_er. None of the other parameter estimates or standard deviations in parameter estimates are changed by changing the value of T_er, because a change in T_er shifts all the reaction times by the same fixed amount.

Drift rate (v) represents the quality of evidence driving the decision process—that is, the difficulty level of a stimulus. For the four levels of the independent variable, we selected four drift values that span the range from high accuracy (about 95% correct) to low accuracy (about 50% correct). The values for the four drift rates are different for different values of boundary separation because when boundary separation (a) is small, there is more chance that a process will hit the wrong boundary by mistake, and so a higher value of drift rate was used to produce the same high accuracy values as when boundary separation was larger.

We selected two values for variability in drift across trials (η, which is the standard deviation in a normal distribution) and two values for variability in starting point across trials (s_z, which is the range in a uniform distribution), one relatively large and one relatively small, as compared with typical values obtained in fits to real data.

We used two values of a, a = 0.08 and a = 0.16, both with symmetric boundaries and asymmetric boundaries. These values roughly bracket the values of boundary separation typically obtained in fits to real data.

Overall, the selected parameter values cover the range of values we have obtained when fitting the diffusion model to experimental data (Ratcliff, 2002; Ratcliff et al., 2002; Ratcliff & Rouder, 1998, 2000; Ratcliff et al., 2001; Ratcliff et al., 1999; Thapar et al., 2002).

EVALUATING FITTING METHODS

Our evaluation of the fitting methods will start by using models and simulated data with no contaminants or variability in T_er. Then we will introduce contaminants and report their effects on the fitting methods. We will then introduce corrections for contaminants in the fitting methods and will discuss their performance. Finally, we will introduce variability in T_er and will evaluate performance of the models without and then with this explicitly modeled. This also follows our chronological study of these issues.

We evaluated the methods by comparing the parameter values each method recovered from simulated data with the parameter values that were used to generate the data. We examined each method’s ability to recover the correct parameter values, whether the recovered values were biased away from the correct values in some consistent way, and the size of the standard deviations in the parameter values across fits to multiple simulated data sets. The standard deviations in the estimated parameter values are important for determining how much power is available for testing hypotheses about differences in parameter values across experimental conditions or subject populations. Also, the relative sizes of the standard deviations in the estimated parameter values from the different methods provide estimates of the relative efficiencies of the methods.

The diffusion model was used to produce the simulated empirical data as follows: Given a value for each of the diffusion model’s parameters, the model produces responses, each with its response time. For each set of parameter values for the model, 100 sets of simulated data were generated, each data set with either 250 or 1,000 observations for each of the four experimental conditions.

All of the three methods of fitting the model to data involve computing some statistic—that is, some objective function—to represent how well the model fits the data. A minimization routine (see Appendix B) begins with some starting values of the parameters of the model and then adjusts them to maximize or minimize (depending on the method) the objective function until the best fit is obtained between predicted accuracy values and reaction times and simulated accuracy values and reaction times. This process of finding the parameter values that give the best fit of predictions to data was repeated for each of the 100 sets of simulated data, giving 100 sets of best-fitting parameter values, from which we calculated the mean and standard deviation of the 100 estimates for each parameter. This whole process was repeated for each of the three fitting methods, and then it was all repeated again with the 100 sets of data generated from a different set of parameters. Altogether, 12 different sets of parameter values (6 with symmetric boundaries and 6 with asymmetric boundaries which are not reported) were used to span the range of parameter values typical of fits of the diffusion model to data in past studies (Ratcliff, 2002; Ratcliff & Rouder, 1998, 2000; Ratcliff et al., 2001; Ratcliff et al., 1999; Thapar et al., 2002; other unpublished studies).

For all the 100 sets of data for all 12 sets of parameter values, Ratcliff examined the maximum likelihood, chi-square, and the weighted least squares methods, and Tuerlinckx examined the maximum likelihood method. Ratcliff examined the chi-square method with corrections for contaminants and variability in T_er, and Tuerlinckx examined the maximum likelihood method with these corrections.

The mean values of the best-fitting parameters and their standard deviations allow the three fitting methods to be compared on the basis of how well they allow recovery of the parameter values used to generate the simulated data, how variable the parameter estimates are across sets of data, and whether they produce systematic biases away from the true parameter values. For each set of simulations, we will discuss the overall behavior of the methods in terms of the results from the simulations. But only in the more important cases will we present tables of the mean values of the parameter estimates and the standard deviations in the estimates for the 100 sets of simulated data that were generated for each set of parameter values.

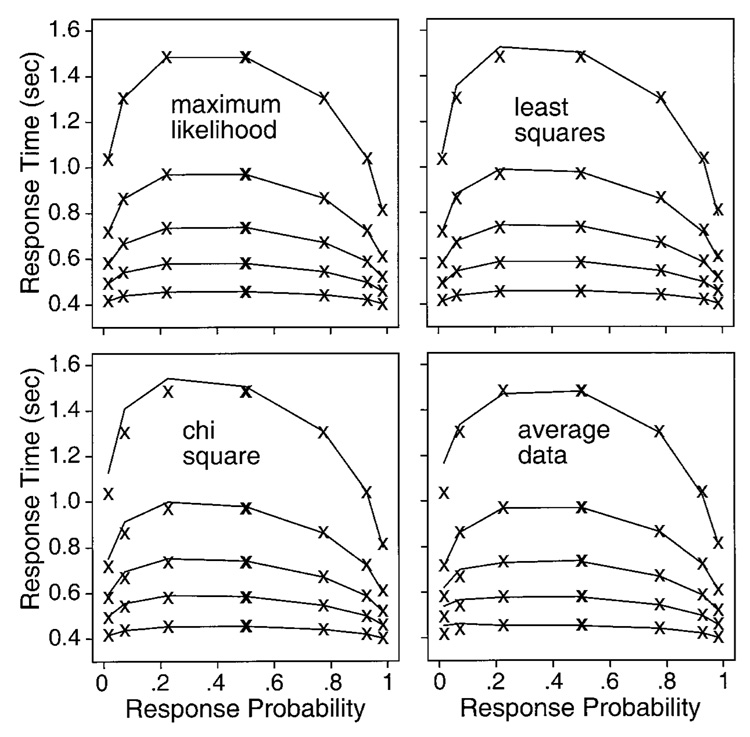
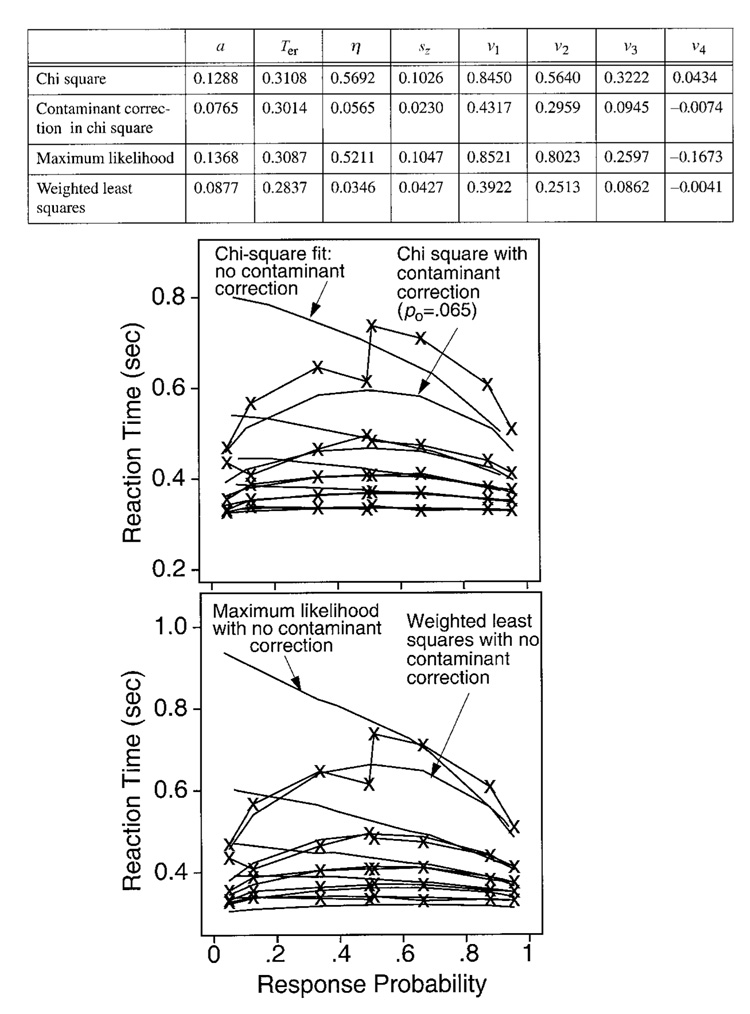
The conclusions of the fitting exercises are complex; each fitting method has advantages and disadvantages. To anticipate, we will list here several main conclusions, but with the caveat that any one set of simulations may have differences from the main results. (1) When the simulated data contained contaminants, as real data often do, we found that the maximum likelihood method was extremely sensitive to the contaminants. Although we developed procedures to correct for some classes of contaminants, the presence of even a few contaminants that could not be corrected for was sufficient to produce poor fits and poor parameter recovery. However, in the absence of contaminants, the maximum likelihood method produced unbiased parameter estimates and had the smallest standard deviations in the estimates of any of the methods. (2) The chi-square method was much more robust than the maximum likelihood method. The presence of a few contaminants for which we did not correct had little effect on the results of fitting: parameters were estimated with only small biases away from the values used to generate the data, and the parameters had standard deviations in their estimated values that were only somewhat larger than those obtained for the maximum likelihood method. In addition, implementations of the chi-square method are much faster than implementations of either the maximum likelihood method or the weighted least squares method. (3) The weighted least squares method produced mean parameter estimates about as biased as those for the chi-square method, but the standard deviations were larger. However, the weighted least squares method was the most robust in the face of contaminants. It was capable of producing reasonable fits even in situations in which the other methods failed dramatically, although the recovered parameters were not the same as those used to generate the diffusion process portion of the data. The weighted least squares method is most useful as a guide to whether the diffusion model is capable of fitting a data set.

QUANTILE PROBABILITY FUNCTIONS

Fits of the diffusion model to data are complicated to display, because the data include two dependent variables—accuracy rates and correct and error reaction times—as well as distributions of reaction time. Traditionally, accuracy, mean reaction time, and reaction time distributions are all presented separately as a function of the conditions of an experiment. Here, we show a method of presenting all the dependent variables on the same plot so that their joint behavior can be better examined.

In earlier research, latency probability functions have been used to display the joint behavior of mean reaction time and accuracy. They are constructed by plotting mean reaction time on the y-axis and probabilities of correct and error responses on the x-axis (Audley & Pike, 1965). Responses with probabilities greater than .5 are typically correct responses, and so, data from correct responses typically fall to the right of the .5 point on the x-axis. Responses with probabilities less than .5 are typically errors and, so, typically fall to the left. Latency probability functions capture the joint behavior of reaction time and response probability, how fast the two change across experimental conditions, and how fast they change relative to each other. However, latency probability functions do not display information about reaction time distributions.

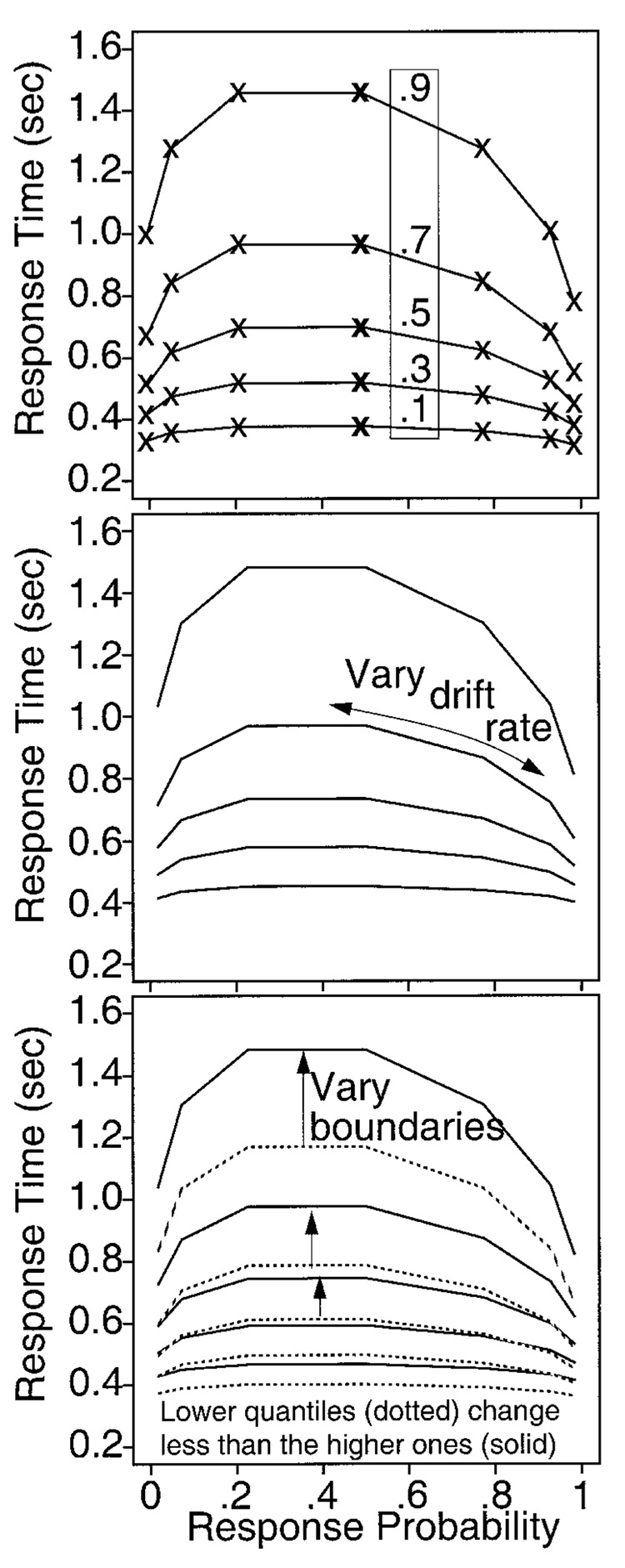
Ratcliff (2001) generalized latency probability functions to quantile probability functions, the method of presenting data that we use in this article. A quantile probability function plots quantiles of the reaction time distribution on the y-axis against probabilities of correct and error responses on the x-axis. In Figure 2, five quantiles are plotted, the .9, .7, .5, .3, and .1 quantiles, as labeled in the vertical rectangle, for four experimental conditions. For a given experimental condition with a probability of correct responses of, say, .8 (to the right of the vertical rectangle), the five quantile points form a vertical line above .8 on the x-axis. The spread among the points shows the shape of the distribution. The lower quantile points map the initial portion of the reaction time distribution, and the higher quantiles map the tail of the distribution. Because reaction time distributions are usually right skewed, the higher quantile points are spread apart more than the lower quantile points. Lines are drawn to connect the quantiles of the experimental conditions, one line to connect the first quantiles of all the experimental conditions, another line to connect the second quantiles, and so on. If, as is usually the case, responses with a probability of greater than .5 are correct responses and responses with a probability of less than .5 are error responses, the mirror image points on the x-axis around the probability of .5 point allow comparisons of the shapes of correct and error response time distributions. In the example presented in Figure 2, in the lowest accuracy condition, both correct and error responses have a probability of .5, and so their quantiles fall on top of each other. Also, comparing the quantile points across different probability values shows how distribution shape changes as a function of experimental condition. For example, if the whole distribution (all quantiles) becomes slower and slower as the difficulty of the experimental conditions increases (and probability of a correct response decreases), this is easily seen as parallel changes in all the quantiles. But if instead, the distribution becomes more skewed as the difficulty increases, the first quantiles for all the conditions will change little across conditions, and the last (longest) quantiles will change most, as is the case in the top panel of Figure 2.

Figure 2.

An illustration of quantile probability plots. The top panel shows quantile probability functions, the middle panel illustrates how the quantiles change as drift rate changes, and the bottom panel illustrates the effect of changing boundary separation.

The parameters of the diffusion model each have a systematic effect on the quantile probability function. Varying drift rate varies left to right position on the quantile probability function. Changes in drift rate can produce only a small change in the lowest quantile and a large change in the highest quantile (Figure 2, middle panel). This corresponds to the distribution’s skewing a lot and shifting its leading edge a little. Increasing boundary separation results in the distribution’s both shifting and skewing. The lowest quantile increases, and the highest quantile increases more (Figure 2, bottom panel).

If starting point variability across trials (s_z) increases, the quantiles to the left of a probability of .5 (typically, errors) decrease, and they decrease most on the extreme left side of the plot. This can lead to errors that are faster than correct responses in the most accurate conditions. If variability in drift rate across trials (η) is increased, the plot becomes more asymmetric. With η = 0, s_z = 0 and z = a/2, the quantile probability function is symmetric. As η is increased, the peak is lowered a little, and it moves to the left as error responses slow relative to correct responses.

When the points plotted on the quantile probability function are from an experiment in which subjects cannot change response criteria or strategies between experimental conditions, as in the experiments simulated here for tests of the fitting methods, then for the diffusion model, the shapes of the lines that connect the quantiles in the quantile probability plot are completely determined by just three parameters: a, η, and s_z. This means that, in fitting the model, only drift rate can vary as a function of condition. The quantile probability function is what is called a parametric plot, with drift rate the parameter of the plot. Thus, besides providing a useful summary of the joint behavior of reaction time distribution shape and accuracy, the quantile probability function provides a stringent visual demonstration of how well the diffusion model fits the data. (For examples of patterns of data the diffusion model cannot fit, illustrated using quantile probability functions, see Ratcliff, 2002.)

Variability in Simulated Data

Quantile probability functions provide a vehicle with which to illustrate variability in the simulated data we used to test the three fitting methods. Variability in the data provides a backdrop for understanding why the variability in estimated parameters that we will present later is as large or as small as it is.

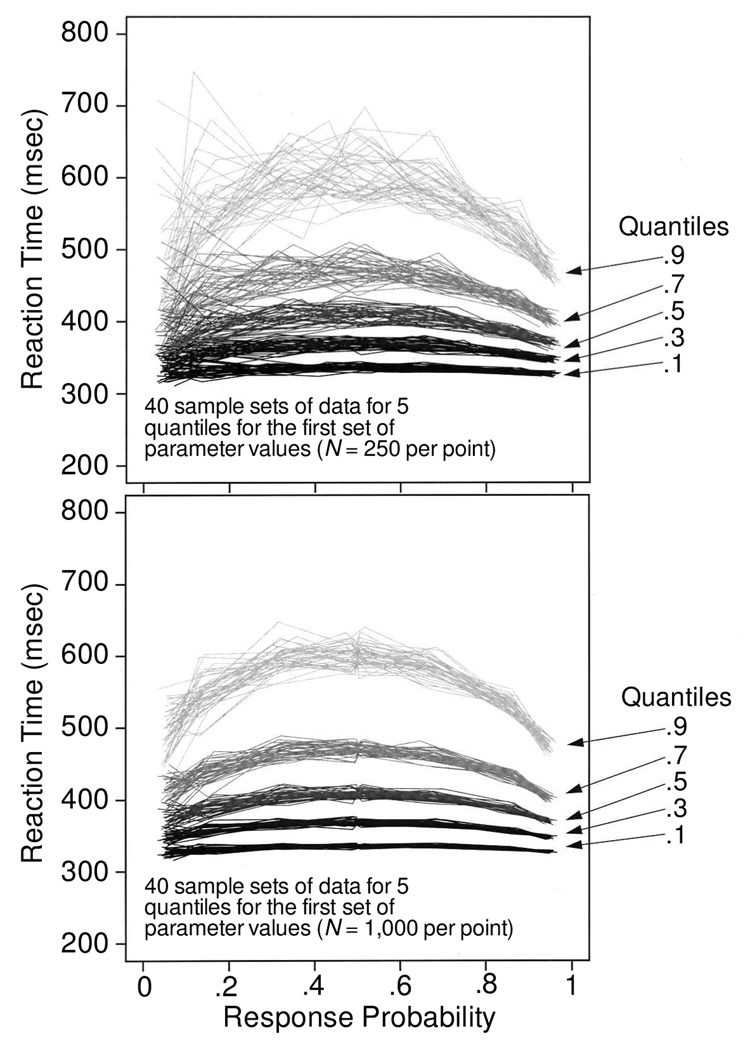
Figure 3 shows quantile probability functions for data simulated with the set of parameters shown in the first line of Table 1. Only the quantile probability functions for 40 sets of data, not the full 100 sets, are shown, in order to reduce clutter. The “smears” on the figure are the 40 overlapping lines at each of five quantiles. The figure shows how much variability there is in the quantile points and that there is more variability when the quantiles are derived from only 250 observations per condition (top panel) as compared with 1,000 observations per condition (bottom panel). (The quantile reaction times scale as a function of the square root of N, so the spread in the bottom panel is half that in the top panel. The figures provide a visualization of the size of the spread for these sample sizes and these values of accuracy.)

Figure 3.

Quantile probability functions for 40 sets of simulated data for 250 observations per condition (top panel) and 1,000 observations per condition (bottom panel). These illustrate the variability in simulated data for the five different quantiles and how the variability changes, going from high-accuracy correct responses (right-hand side of the figure) to errors on the left-hand side of the figure.

With 250 observations per condition, the .9 quantile varies around its mean by as much as 300 msec (for errors at the extreme left of the figure, which come from conditions with high accuracy), and it varies by as much as 100 msec for correct responses from conditions with intermediate accuracy (in the middle of the figure). The .1 quantile varies little across the 40 sets of data, except for errors in the conditions with high accuracy. With 1,000 observations per condition, the location of the quantiles is much tighter, but even so, the .9 quantile for error responses in the high-accuracy conditions varies by as much as 100 msec.

It is possible to understand which parameters have greater or lesser variability associated with them from these figures. T_er and a are determined to a large degree by the position of the .1 quantile. The figures show that the .1 quantile is quite well located without much variability. On the other hand, η and s_z are largely determined by error reaction times, and these have a large amount of variability associated with them. For example, with 250 observations per condition (e.g., Figure 3, top panel), simulated data generated from parameters that should produce slow errors can easily, by chance, produce errors as fast as correct responses. This would produce a fitted value of variability in drift across trials (η) of zero. This means that with 250 observations per condition and η = 0.08, it is easily possible (e.g., 5% or 10% of the time) to obtain a set of data that produces a fitted value of η near zero. Therefore, we expect variability in η to be large when fitting simulated data.

Figure 3 shows the variability that simulated data have associated with them. If the diffusion model is correct—that is, if real data are generated from a diffusion process—the same variability will be associated with real data. This is why we provide the standard deviations in the parameter values we obtain from fitting simulated data. These standard deviations give some reasonable idea of what we can expect from parameter estimates based on real data.

PARAMETER ESTIMATES FROM THE MAXIMUM LIKELIHOOD METHOD

For all three methods of fitting, we will report and discuss results for fitting the simulated data that were generated from the six sets of parameter values for which the starting point is equidistant from the boundaries (Table 1). We will report the means of the parameter estimates across the 100 data sets and the standard deviations in the estimates. In the series of fits described first, results will be shown and discussed for the data sets with 250 observations per condition. It turns out that the standard deviations for 1,000 observations per condition are almost exactly twice as small as those for 250 observations per condition (i.e., the standard deviations change as the square root of the number of observations). Therefore, we will later discuss the results with 1,000 observations per condition only briefly. The next sections will present simulated data and fitting methods with no contaminants and with no variability in T_er.

Means and Standard Deviations of Parameter Estimates

Recall that Ratcliff and Tuerlinckx obtained probability densities for reaction time distributions in different ways and used different fitting algorithms (which provides a check on the accuracy of the methods). The means of their parameter estimates agreed within 1% of each other, except for the variability parameters (η and s_z ), which agreed within 5%. Correlations between Ratcliff’s and Tuerlinckx’s means were computed for each parameter for each of the six sets of parameter values. Averaging across the six sets of correlations for each parameter value, the correlations were about .9, except that, for T_er, the correlation was .72 and for s_z, the correlation was .58. The low values of the correlations for the variability parameters were due mainly to the set of parameters for which η and s_z were both large. Although the correlations for T_er were low, the standard deviations in T_er were small (3–10 msec), so the low correlations do not indicate large differences between Ratcliff’s and Tuerlinckx’s estimates of T_er. Ratcliff’s values will be reported in the tables that immediately follow, and Tuerlinckx’s values will be reported for the investigations of contaminants and variability in T_er that will be presented later.

Table 2 contains the means and standard deviations of the parameter estimates that were recovered from the 100 sets of data simulated for each set of parameters in Table 1, for the data sets with 250 observations per condition. Overall, the means of the parameter estimates are unbiased—that is, they are close to the true values of the parameters with which the simulated data were generated. The standard deviations in the estimates are small, averaging about 4% of the mean for a, 3–10 msec for T_er, about 10% of the mean for drift rates (v), but anywhere from 20% to 70% of the mean for standard deviation in drift across trials (η). When s_z was small (0.02), its standard deviation was about the same size as the mean, but when it was larger, it was about 30% of the mean. The relative sizes of these differences among standard deviations are consistent across all three fitting methods. Below, we will describe the results for each of the parameters in turn.

Table 2.

Means and Standard Deviations of Parameter Values Recovered From the Maximum Likelihood Fitting Method (N = 250 per Condition)

Value	Parameter Set	a	Ter	η	sz	v1	v2	v3	v4
M	A	0.0793	0.3010	0.0859	0.0206	0.4180	0.2612	0.1061	−0.0021
	B	0.0788	0.3009	0.1596	0.0178	0.4057	0.2543	0.0958	0.0032
	C	0.1598	0.3039	0.0794	0.0220	0.3064	0.2024	0.1018	−0.0007
	D	0.1590	0.2998	0.0762	0.1095	0.2963	0.1985	0.1002	−0.0019
	E	0.1618	0.3055	0.1696	0.0319	0.3146	0.2092	0.1039	−0.0007
	F	0.1602	0.3000	0.1605	0.1068	0.3027	0.2008	0.0986	0.0025
SD	A	0.0023	0.0029	0.0519	0.0144	0.0402	0.0292	0.0220	0.0195
	B	0.0029	0.0029	0.0496	0.0159	0.0442	0.0295	0.0218	0.0238
	C	0.0058	0.0080	0.0225	0.0255	0.0269	0.0194	0.0143	0.0104
	D	0.0076	0.0045	0.0291	0.0372	0.0294	0.0229	0.0176	0.0139
	E	0.0078	0.0097	0.0297	0.0313	0.0375	0.0299	0.0204	0.0143
	F	0.0077	0.0060	0.0295	0.0327	0.0325	0.0273	0.0227	0.0153

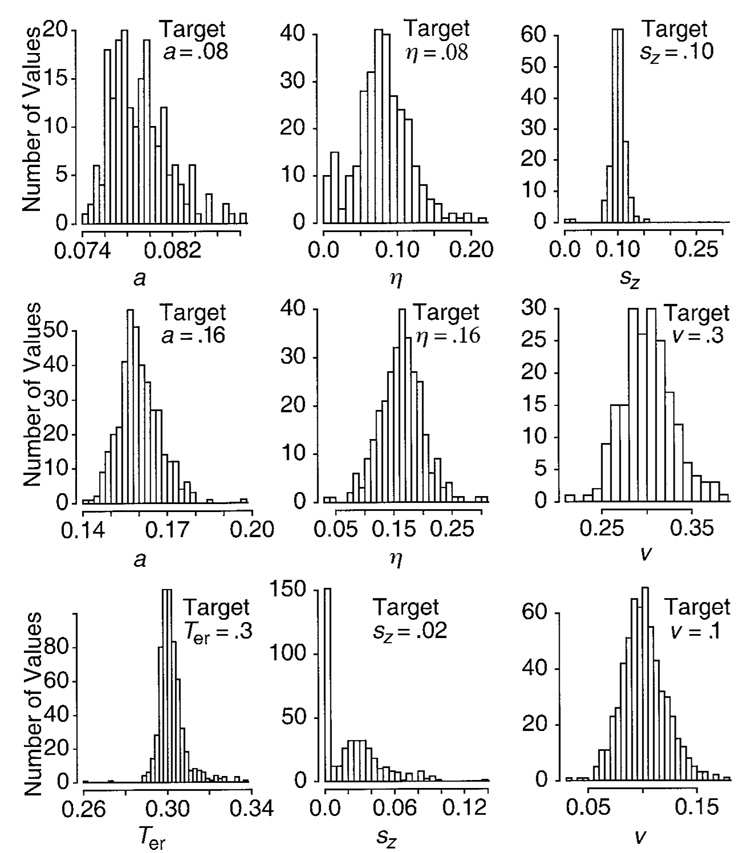
To show how the parameters vary across the random samples (the 100 data sets), Figure 4 presents nine histograms that display the parameter values. For two of the sets of parameter values used to generate the simulated data, a was 0.08. The first histogram (top left) shows all the estimates of a from the data generated with both sets. The next histogram, just below, shows the estimates of a for the data generated from the four sets of parameter values with a = 0.16. Before grouping the two sets of data for which a = 0.08 and the four for which a= 0.16, we made sure that there were no systematic differences among them. We also employed groupings for the histograms for the other parameter values, always first checking that there was no variation as a function of other parameter values.

Figure 4.

Histograms of the parameter values recovered from fits of the diffusion model, using the maximum likelihood method to simulated data (using parameters in Table 1).

For the boundary separation parameter a, all the means of estimates shown in Table 2 are within 4% of the target value (either 0.08 or 0.16), which is within less than one standard deviation. When 0.08 was the target value, the distribution was skewed only a little to the right. When 0.16 was the target value, the distribution was symmetric, roughly normal. Thus, the fitting method is recovering parameter values near the true values, with neither large deviations nor a bias toward one or the other side of the target value.

The means of the estimates for T_er are also near the true value (300 msec). The histogram for the values of T_er (Figure 4, bottom leftmost panel) is symmetric around the true value, although there are a few straggling values in the tail. The standard deviation in the estimates is reasonably small, always less than about 10 msec. The standard deviation is smaller, about 3 msec, when boundary separation (a) is small and somewhat larger, 5–10 msec, when boundary separation is larger. This is because, when a is small, the .1 quantile has a smaller value, closer to the 300-msec value of T_er, and is less variable. Hence, T_er is better located and so has a smaller standard deviation. This same explanation holds for large s_z as opposed to small s_z: With a large s_z, more processes have a value of the .1 quantile near T_er than with a smaller s_z.

The means of the estimates for drift rates are typically within 6% of the true values, with no systematic bias away from the true values, and they do not vary systematically with other parameters of the model (we show histograms for drift rates 0.3 and 0.1 only, because they are representative of all four drift rates). The standard deviations in the estimates of drift rates are about 10% of the mean for high drift rates and about 20% of the mean for low drift rates (disregarding the drift value of zero). The standard deviation in drift rates is larger for the lower value of boundary separation a than for the higher value of boundary separation. This is because the quantile probability function is flatter for the smaller value of a and, so, drift rates are constrained mainly by their position on the x-axis (accuracy) and less by their position on the y-axis (reaction times), because the latter do not vary much across experimental conditions. The standard deviation in drift rates is also larger for larger boundary separation when the variability across trials (η) is larger. This is again because the quantile probability functions are flatter when η is large.

The two variability parameters (η and s_z) are considerably less accurately estimated than the other parameters (this is true for most models that use variability parameters; cf. Ratcliff, 1979). Although there do not appear to be any systematic biases in η away from the true values (0.16 and 0.08), large standard deviations mean that, if there were any systematic bias, it would be hidden in the variability. The standard deviation in the estimate of η varies from about 0.03 to about 0.05, 20%–60% the size of the mean. The reason for large variability in η is that its estimate is based on error reaction times, which themselves have such large variability (see Figure 3) because there are often few of them (see Ratcliff et al., 1999). Thus, for some simulated data sets, the best-fitting value of η is near zero, and for other simulated data sets, the best-fitting value is over twice as large as the true value used to generate the simulated data. This is shown clearly in the histograms in Figure 4. For η = 0.08, there are a number of estimates near zero. These come from simulated data for which boundary separation a is 0.08. For η = 0.16, the distribution of estimates is narrower and more symmetric. The standard deviation varies with boundary separation a. When a is 0.08, the standard deviation is larger, around 0.05, and when a is 0.16, the standard deviation is smaller, around 0.03. Thus, the larger the value of a, the better the estimate of η.

The quality of the estimates of the parameter s_z depends on the true value of the parameter. When the value that was used to generate the data is small, 0.02, two standard deviation intervals include zero and a value twice as large as the true value (see the histogram in Figure 4). This extreme variability in estimates comes about because the size of s_z is determined by error response times in conditions with high accuracy, in which there are relatively few error responses. When the true value of s_z is 0.10, the estimates are near the true values, because the effect of s_z on error reaction times is larger and, so, is less likely to be masked by random variation in the data. The distribution of estimated values for s_z = 0.10 is symmetric (see the histogram in Figure 4), but there are still two values near zero.

In sum, the parameters a, T_er, and drift rates are quite well estimated, within 10% of the mean parameter value. For each of these parameters, the mean of the estimates from the 100 data sets falls close to the true mean, there is no consistent bias toward values larger or smaller than the true mean, and the standard deviation among the estimates is small relative to the size of the estimated value. But the variability parameters, η and s_z, are much more poorly estimated, within 20%–70% of the mean parameter value. If it is necessary to obtain good estimates of these parameters, sample size must be increased by running experiments with many sessions per subject.

Correlations Among Parameter Values

A potentially major problem in recovering parameters for a model is that the value of the estimate for one parameter may be significantly correlated with the value of another. In attempting to find the best-fitting parameter values, given the variability in the data, a fitting method may trade the value of one parameter off against the value of another. Using results from the 100 fits to the simulated data, we can investigate how serious this problem is.

This issue is especially critical when testing for differences among parameter values across experimental conditions. A larger value of a parameter in one condition than in another could be due to random variation, or it could be due to a genuine difference in the values for the two conditions. If other parameters of the model covary with the parameter at issue in a way that is expected from the model and the difference is just barely significant, it is less likely that the observed difference is real than if the other parameters do not covary in this way.

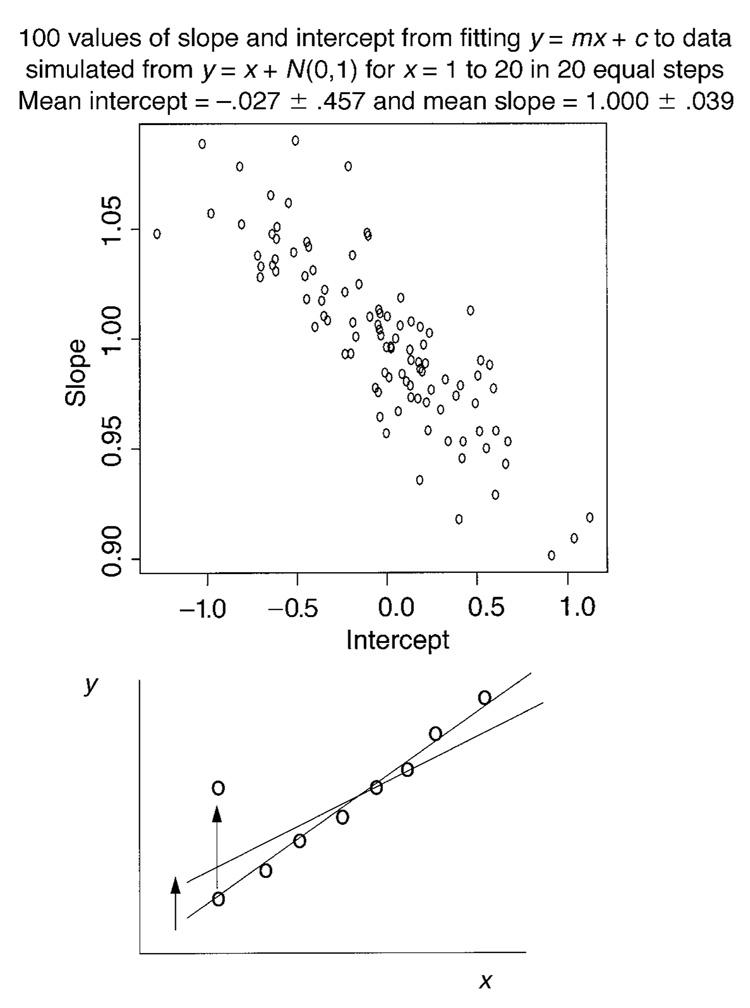
Before taking up the issue of covariation for the diffusion model, we will illustrate covariation between parameters with an example, linear regression (straight line fitting), for which there are only two parameters. Fitting the equation for a straight line, y = mx + c, to data provides estimates of slope m and intercept c. We generated 100 sets of data for a straight line, with 20 points on the line per data set. The 100 sets of data were generated with a slope of 1 and an intercept of zero, and to add variability to the function, each point had a value added to it from a normal distribution with a mean of zero and a standard deviation of 1: y = mx + c + N(0,1). For each data set, a straight line was fitted to it by the least squares method (the standard method for linear regression), giving an estimate of slope and intercept for each data set. The slopes and intercepts are plotted in Figure 5 (top panel).

Figure 5.

An illustration of the covariation between parameter estimates for linear regression. The top panel shows values of slope and intercept from simulated data (falling in an elliptical shape), and the bottom panel shows how moving one data point up (by random variation) would decrease the slope and increase the intercept of the best-fitting straight line.

In linear regression, if the correlation between the slope and the intercept is computed, it usually has a large negative value. The correlation is large if the slope is positive and the range of y values is more than four times greater than the standard deviation in the variability in y. Figure 5, top panel, illustrates this negative correlation. Plotting the slopes versus the intercepts produces a roughly elliptical shape with a negative slope. For the 100 random samples in Figure 5, the correlation between the slopes and the intercepts is −.848.

The explanation for the negative correlation is straightforward. If a data point near either end of the line is moved far from the line, as illustrated in the bottom panel of Figure 5, the slope is raised, and the intercept is lowered (or vice versa). This gives a negative correlation. It is much less likely that the slope and the intercept are both raised in some random set of data (giving a positive correlation), because this would require a change in all the data points in the same direction.

When parameter estimates are evaluated, confidence intervals are often shown for a single parameter without reference to the behavior of other parameters. However, confidence regions can be drawn for the joint behaviors of parameters. For linear regression, the confidence region for the slope and the intercept forms an ellipse with a negative slope for the major axis (e.g., Draper & Smith, 1966, p. 65). In Figure 5, this would be an ellipse around the points in the top panel. Joint confidence intervals can be important, as the following examples show: If the slope for linear regression is higher and the intercept is lower than the hypothesized population values, this can be the result of random variation in the data, but if both the intercept and the slope are higher, the values could be different from the population values. For example, in the top panel of Figure 5, imagine a point at slope = 1.07 and intercept = 0.6. This point would lie inside the individual confidence intervals for both the slope and the intercept (i.e., 1.07 lies within the vertical scatter of points, and 0.6 lies within the horizontal scatter of points). But the point would lie outside the joint confidence region (the ellipse that would contain 95% of the points in the top panel of Figure 5). So an understanding of the joint confidence regions provides additional useful information in testing hypotheses about differences among parameter values.

For linear regression, joint confidence regions can be determined analytically, and hypotheses can be tested about the joint behavior of the slope and the intercept. But for the diffusion model, such analytical results are almost impossible to produce. However, simulation methods can provide information that can be used more informally to determine whether joint behavior of parameter values is something that needs to be examined for a particular set of fits for a particular data set. This will not allow hypotheses to be tested but will provide enough information to determine whether the issue of correlated estimates needs to be considered in drawing conclusions about differences among parameter values across conditions or whether it can be ignored.

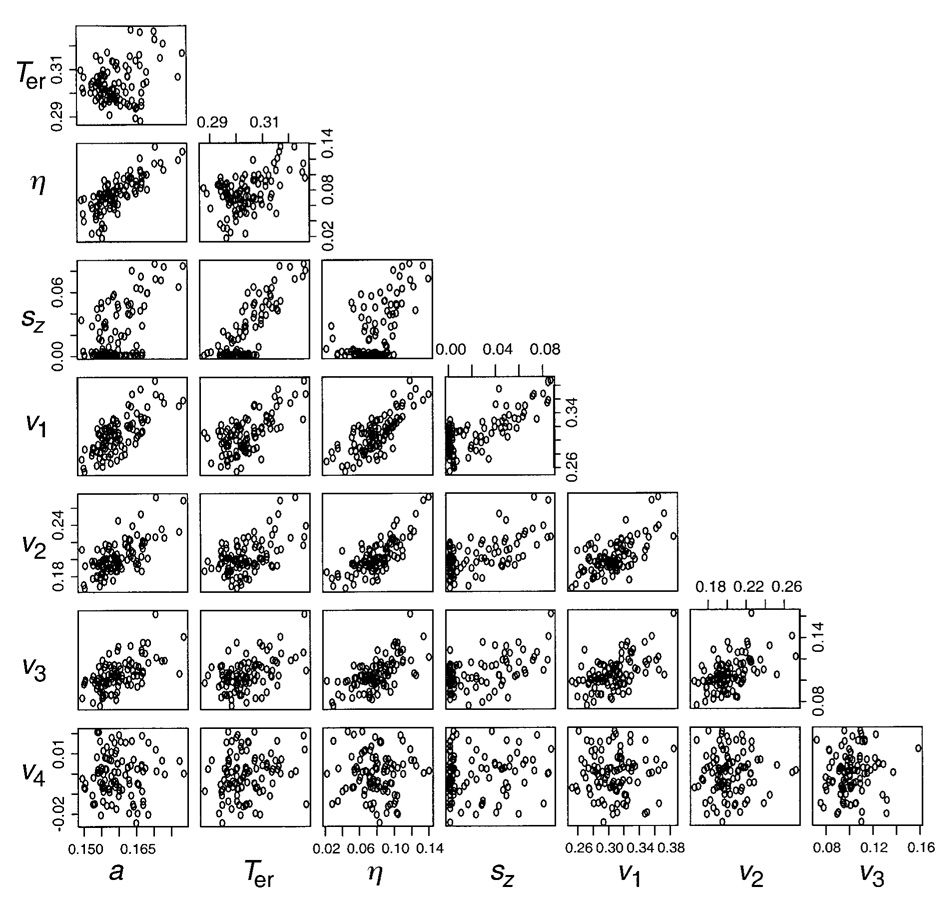
For the diffusion model, Table 3 contains correlations between each pair of parameters for the maximum likelihood fits shown in Table 3. For each of the 100 data sets for each of the 6 sets of parameter values, we computed correlations between each pair of estimated parameters, and Table 3 shows the means of these correlations. Figure 6 shows scatterplots for the 100 parameter estimates for the fits generated from 1 of the 6 sets of parameter values (the 3rd set in Table 1). For the 100 data sets, each scatterplot shows the estimated value of one parameter plotted against the estimated value of another parameter.

Table 3.

Correlations Among Parameter Values for Maximum Likelihood Fits (N = 250 per Condition)

	a	Ter	η	sz	v1	v2	v3	v4
a	1.0000	.3980	.8263	.6238	.7842	.6819	.5000	−.0227
Ter	.3980	1.0000	.4257	.7904	.5295	.4751	.2890	.0355
η	.8263	.4257	1.0000	.5330	.7837	.7129	.5270	.0115
sz	.6238	.7904	.5330	1.0000	.6019	.5233	.3312	.0165
v1	.7842	.5295	.7837	.6019	1.0000	.6534	.4620	−.0432
v2	.6819	.4751	.7129	.5233	.6534	1.0000	.4378	−.0300
v3	.5000	.2890	.5270	.3312	.4620	.4378	1.0000	.0171
v4	−.0227	.0355	.0115	.0165	−.0432	.0300	.0171	1.0000

Figure 6.

Scatterplots among the parameters of the diffusion model for fits to simulated data, using the maximum likelihood method (using parameters from line 3 in Table 1).

Many of the correlations in Table 3 are positive. This comes about because of the effects of extra slow error reaction times. The occurrence by chance of a few, extra slow error reaction times moves the estimates of many of the parameters of the model away from their true values, all in the same direction (the variability parameters η and s_z are moved more as a percentage of their means than are a, T_er, and drift rates), and how they change together is what the correlations show.

To show the effect of slow error response times, we provide a concrete example to illustrate the effect: We took the third set of parameter values from Table 1 and produced predicted values of response probabilities and quantile reaction times from the diffusion model. We then increased the fifth quantile reaction time for errors in the condition with drift = 0.1 by 100 msec. We fit the model to the data with and without this increase. When the original data were fitted using the chi-square method detailed next, the parameters were recovered to within 0.1% of their true values. When the functions with the single increased quantile reaction time were fitted, the estimated values changed by small amounts. The value of a was increased from 0.16 to 0.162, T_er from 0.3 to 0.302, η from 0.08 to 0.086, s_z from 0.02 to 0.030, and the three drift rates that differed from zero increased from 0.300, 0.200, and 0.100 to 0.307, 0.205, and 0.103, respectively. Figure 7 shows the quantile probability functions for the data with one data point moved up and the fitted quantile probability function for the latter. The result is that the fitted quantile probability function is moved up a little, more in the higher quantiles than in the lower quantiles. This is reflected in an increase in the estimated values for all the model’s parameters, as was described above. Making changes in more of the quantiles would magnify the small effect of the change in only the fifth quantile reaction time for errors with drift = 0.1.

Figure 7.

An illustration of what happens to the fit of the diffusion model if one error quantile is increased (cf. the change in one data point in Figure 4).

This increase in all the parameter values is exactly the pattern we see in the correlations and scatterplots in Figure 6 and Table 3. The most common and largest random variation in data is in error reaction times, as is illustrated in Figure 3, especially in the longest quantiles. As the example above shows, this variation is sufficient to produce the positive correlations observed in the parameter values.

The general conclusion for the diffusion model is that random differences among samples of data produce differences in all the parameters’ estimates in the same direction. This means that if the sizes of differences among parameter values are important, correlations must be considered. For example, if there is a significant difference between two values of boundary separation a and if η and drift rates also vary in the same direction as a, the differences in a could be due to random variation in the data. The positive correlations among estimated parameter values come from variability in error reaction times, and so they are also obtained with the chi-square and weighted least squares methods of fitting.

Parameter Estimates for the Maximum Likelihood Method When Boundaries Are Asymmetric

For the case with asymmetric boundary separation (all the parameters were the same as in Table 1, except z = .375a, and drift rates were −.3, −.1, .1, and .3), the standard errors in the recovered parameters were smaller than those for the symmetric case. One of the main reasons for the better estimates is that with the starting point being asymmetric, reaction times for the response with the closer boundary are shorter, which makes both T_er and a better estimated. The correlation matrix for asymmetric boundaries shows the same pattern as that in Table 3, but the correlations are 25% smaller because of better parameter estimation. These same differences between the symmetric and the asymmetric cases are found in most of the fits presented later in this article, so we will discuss the asymmetric case only if the results are different from the symmetric case.

PARAMETER ESTIMATES FROM THE CHI-SQUARE FITTING METHOD

An important advantage of the chi-square method is that the time needed to produce a fit is 25 times shorter per experimental condition than that for the maximum likelihood method with 250 observations per condition and 100 times shorter with 1,000 observations per condition. For example, when the chi-square method is used, a fit to one set of data takes about 25 sec on a 500-MHz Compaq XP1000 with a 21264 Alpha processor and about 14 sec with PC running Linux, using an Intel compiler on a 1.33-GHz Athlon processor. For fitting many sets of data (many individual subjects or many simulated data sets), the chi-square method runs for minutes or hours, whereas the maximum likelihood method runs for days.

Table 4 shows the mean parameter estimates and the standard deviations in the parameter estimates with 250 observations per condition. In order to provide a rough guide for comparison of the three different fitting methods, we will discuss the sizes of the standard deviations in terms of approximate averages. When we want to compare two methods, we compute the ratios in the standard deviations of their parameter estimates and then compute the median across the ratios for each of the parameters. This gives a rough summary of the performance of each method. For example, the standard deviations in the parameter values given by one method might be anywhere from 1 to 2 times larger than those for another method, with a median of about 1.5 times larger. Summary statements like these are only approximate, because the differences in the standard deviations between fitting methods can be different for different parameters.

Table 4.

Means and Standard Deviations of Parameter Values Recovered From the Chi-Square Method (N = 250 per Condition)

Value	Parameter Set	a	Ter	η	sz	v1	v2	v3	v4
M	A	0.0810	0.3010	0.1135	0.0279	0.4346	0.2710	0.1114	−0.0026
	B	0.0808	0.3002	0.1883	0.0249	0.4156	0.2649	0.1009	0.0028
	C	0.1653	0.3067	0.0995	0.0388	0.3296	0.2148	0.1092	−0.0009
	D	0.1588	0.2936	0.0748	0.0951	0.2915	0.1925	0.0977	−0.0016
	E	0.1657	0.3048	0.1786	0.0422	0.3328	0.2130	0.1067	0.0001
	F	0.1603	0.2886	0.1550	0.0918	0.2981	0.1912	0.0944	0.0023
SD	A	0.0039	0.0039	0.0701	0.0155	0.0606	0.0379	0.0281	0.0215
	B	0.0039	0.0042	0.0648	0.0174	0.0625	0.0370	0.0251	0.0258
	C	0.0095	0.0136	0.0359	0.0374	0.0499	0.0382	0.0215	0.0116
	D	0.0090	0.0162	0.0401	0.0280	0.0424	0.0309	0.0217	0.0133
	E	0.0103	0.0121	0.0399	0.0340	0.0485	0.0369	0.0241	0.0164
	F	0.0111	0.0175	0.0453	0.0375	0.0464	0.0412	0.0258	0.0160

The first result of note is that the median standard deviation is 33% larger, on average, for the chi-square method than for the maximum likelihood method. This means that parameters recovered with the chi-square method are likely to be farther away from their true values than those recovered with the maximum likelihood method. Second, there are biases in some of the parameter estimates: in particular, η and the drift rates have estimated values that are larger than their true values by 5%–10%; s_z has estimated values higher than the true value when s_z is 0.02, but when it is 0.10, it is estimated to be a little lower than the true value. However, the means of the estimates for T_er and a are near their true values, with no systematic direction for differences from the true values.

We do not present histograms of the estimated parameter values, because they are qualitatively similar to those shown in Figure 4 for maximum likelihood. In general, they show the same biases for the same parameters. The only major differences are a few more cases in which η is estimated to be zero and some cases in which η is estimated to be larger for the chi-square method than for the maximum likelihood method. The correlation matrix for the chi-square fits shows almost the same patterns as those in Table 3, but with slightly higher correlation values. This is because the maximum likelihood and the chi-square methods produce variation in parameter values in the same way in response to random variations in the simulated data. So, all the conclusions that were presented for the maximum likelihood covariations among parameter values apply equally to correlations among parameter values derived from the chi-square method.

When boundary positions are not symmetric, just as for the maximum likelihood estimates, the standard errors in the estimates are smaller than when the boundaries are symmetric. Also, there is slightly less bias than in the symmetrical case.

In sum, the chi-square method is somewhat worse at recovering accurate parameter estimates, but it is significantly faster than the maximum likelihood method. It also turns out, as will be seen later, that the chi-square method is a little more robust to a small proportion of outliers than is the maximum likelihood method.

PARAMETER ESTIMATES FROM THE WEIGHTED LEAST SQUARES FITTING METHOD

Like the maximum likelihood method, the weighted least squares method suffers from a speed problem. For the weighted least squares method, the whole reaction time distribution has to be estimated for each condition for both correct and error responses, which requires hundreds of points (recall that we used 400 points). If the weighted least squares method turned out to be the best estimation method, it could be speeded up by using search methods to find the quantiles, but it would still be at least 10 times slower than the chi-square method.

Table 5 shows the means and standard deviations in the recovered parameter values. The first thing to notice is that for the lower value of a (true value = 0.08), this method is better than the chi-square method; the recovered estimates of all the parameters are nearer the true values, and standard deviations in them are smaller. But for the higher value of a, the opposite is true. The average across the two values of a of the standard deviations is about 29% larger for the weighted least squares method than for the chi-square method. Overall, the biases in the mean parameter values away from the true values are about the same for the chi-square and the weighted least squares methods, but the weighted least squares method has higher standard deviations overall than does the chi-square value. For both the chi-square and the weighted least squares methods, the estimates are less accurate than the maximum likelihood estimates, and their variability is greater. The average of the standard deviations for the weighted least squares method is about 63% larger than that for the maximum likelihood method.

Table 5.

Means and Standard Deviations of Parameter Values Recovered From the Weighted Least Squares Method (N = 250 per Condition)

Value	Parameter Set	a	Ter	η	sz	v1	v2	v3	v4
M	A	0.0795	0.2955	0.0916	0.0213	0.4251	0.2637	0.1079	−0.0026
	B	0.0789	0.2953	0.1592	0.0191	0.4099	0.2571	0.0957	0.0041
	C	0.1643	0.3086	0.0951	0.0422	0.3353	0.2228	0.1122	0.0001
	D	0.1605	0.2966	0.0813	0.1011	0.3061	0.2069	0.1047	−0.0010
	E	0.1666	0.3082	0.1879	0.0460	0.3422	0.2282	0.1139	−0.0012
	F	0.1632	0.2940	0.1717	0.0998	0.3189	0.2116	0.1055	0.0027
SD	A	0.0031	0.0038	0.0579	0.0144	0.0464	0.0325	0.0232	0.0205
	B	0.0036	0.0037	0.0641	0.0144	0.0566	0.0365	0.0233	0.0265
	C	0.0123	0.0193	0.0462	0.0443	0.0668	0.0501	0.0286	0.0118
	D	0.0138	0.0213	0.0507	0.0364	0.0642	0.0500	0.0283	0.0148
	E	0.0139	0.0201	0.0551	0.0504	0.0737	0.0520	0.0335	0.0175
	F	0.0156	0.0269	0.0635	0.0473	0.0849	0.0640	0.0375	0.0186

The correlations among parameters for the weighted least squares method are a little larger, on average, than those for the chi-square method (they vary between 5% lower and 10% larger, except for zero drift, for which the correlations are near zero). But the correlations all show exactly the same patterns: When one is higher than another in weighted least squares, it is also higher in chi-square and maximum likelihood. This means that all three methods produce correlations among parameters, for the reasons that were discussed above (using the example in Figure 7).

In sum, the parameter estimates from the weighted least squares method are about as biased as those from the chi-square method, but they have larger standard deviations, and the weighted least squares method has a huge deficit in computational speed. Both the weighted least squares and the chi-square methods recover mean parameter values less accurately than does the maximum likelihood method (by about 5%–10%, depending on the parameter), and the standard deviations in the estimates are larger than those with the maximum likelihood method. But the maximum likelihood method is slow relative to the chi-square method and more sensitive to outliers, as will be demonstrated below.

AN EXAMPLE OF THE QUALITY OF THE FITS OF DIFFUSION MODEL TO SIMULATED DATA

As was just pointed out, the parameter estimates for the maximum likelihood method are quite accurate, and for the chi-square and weighted least squares methods, they are reasonably accurate, within about 5%–10% of the true values. The question we raise here is how good the fit of the diffusion model to the simulated data is, given these estimates.

To provide an example of how good the fit is, we chose one representative data set for which the estimated parameter values from all three methods were near to the true parameter values from which the simulated data were generated. The true values were the first set of parameter values in Table 1. Each set of estimated parameter values, one set from each method, was used to generate predicted values of accuracy and reaction time quantiles for each experimental condition. Figure 8 shows the quantile probability functions for the simulated data (the X points) and the quantile probability functions for the predicted values for each method. In general, the fits all look good, and all indicate that the model is fitting the data well. The weighted least squares and the chi-square methods produce fits to the quantile probability functions that are almost identical to each other. The chi-square method produces a larger value of η (50% larger) and a larger value of s_z than does the least squares fit, but the effects of these two larger values lead to only small differences (compared with the weighted least squares method) in the predicted reaction time quantiles in the quantile probability functions. The maximum likelihood method produces f its that do not match the .9 quantiles quite as well as the other two methods (by visual inspection at least), but ignoring the fits from the other two methods, the fit looks quite acceptable. One would be hard-pressed to determine which method produced which of the fits in Figure 8 or to work out which fit was the best or worst simply by looking at the graphical fit of the predicted functions to the data functions. The maximum likelihood method produces parameter estimates slightly closer to the values used to generate the simulated data, but this may not translate into better-looking fits to the quantile probability functions.

Figure 8.

A sample fit of the three methods (maximum likelihood, chi-square, and weighted least squares) to one set of simulated data (the Xs). The parameters are shown at the top, and the parameters used to generate the simulated data are in the column headings of the table. The top theoretical function (for each of the five quantiles) is from the maximum likelihood method, the middle function is from the chi-square method, and the lower function is from the weighted least squares method.

The fits for one representative data set shown in Figure 8 illustrate that all three fitting methods do well. But the three methods do show systematic, although small, differences in their fits. The differences come about because the chi-square and the weighted least squares methods fit data summarized in quantiles, whereas the maximum likelihood method fits all the individual reaction times. We will explain and illustrate this in the next paragraphs.

Figure 9 shows data and fits for the third set of parameter values in Table 1. The lines in the bottom right-hand panel of Figure 9 show the average quantiles for the 100 sets of simulated data generated with these parameter values. The Xs are the predicted values of the quantiles. As the figure shows, the average quantiles from the simulated data do not exactly match the predicted values: For errors that have very low probability (points to the far left), the average quantiles for the data are higher than their predicted values. This is an inherent characteristic of the diffusion model because of the variability in drift rate. As drift rate varies around its mean, some responses will come from slightly higher values of drift rate, and some from slightly lower values. For slightly higher values of drift rate, accuracy will be greater, and so there will be relatively fewer errors. For slightly lower values of drift rate, accuracy will be lower, and there will be relatively more errors. The errors from low values of drift rate are slower, and there are more of them, so averaging across all the responses that have the same mean drift rate gives slower errors than would be expected from the mean alone. Also, for some of the data sets, accuracy in the most accurate experimental conditions may have been so high that there were too few errors to compute quantiles. Drift rate would have been large for these conditions, and so error response times would have been fast. Eliminating these fast errors because there were too few of them to compute quantiles would make the quantiles computed from the simulated data larger than the predicted quantiles.

Figure 9.

Predicted functions from the average parameter values from the fits of the maximum likelihood, chi-square, and weighted least squares methods (third lines of Table 3, Table 6, and Table 9) to the predictions from the diffusion model for input parameters from the third line of Table 1. The curve with Xs represents the theoretical predictions from the input parameters. The bottom right panel shows the average quantiles from the simulated data (the lines).

The chi-square and weighted least squares methods fit data as it is summarized by quantiles. Because the extreme (far left) error quantiles for data are systematically higher than predicted, the chi-square and weighted least squares fits yield parameter estimates that also give slower extreme errors. This is shown in the bottom left and top right panels of Figure 9, where the Xs are the same as in the bottom right panel—that is, they are the quantile values predicted from parameter values that were used to generate the simulated data—and the lines are the quantile values predicted from the means of the parameters estimated from fitting the 100 sets of data. In contrast, the maximum likelihood method fits individual reaction times, so quantiles predicted from the means of the parameters estimated for the 100 data sets with this method do not show the problem with extreme errors. Because the extreme quantiles are higher than the predicted values from the parameters, they are fit with higher values of η, thereby producing slightly slower errors in the most accurate condition. When sample size is increased to 1,000 observations per condition, the bias in η is reduced for the chi-square and weighted least square methods, because the quantile error reaction times in the most accurate condition are better estimated.

If the bias toward estimating higher values of η for the chi-square and weighted least squares methods results from the bias in the data, fits of the chi-square method to the average quantile reaction times should show the same bias. Fits of the chi-square method to the average data are shown in the bottom right panel of Figure 9 (the least squares method shows the same results). Parameter estimates were within a few percent of those in Parameter Set C of Table 4: for example, the values of a = 0.1643, T_er = 0.3091, η = 0.0952, and v₁ = 0.3352 (the other drifts were equally close to the values in Parameter Set C of Table 4). Thus, the biases in the chi-square fits do indeed come from the method’s use of quantile reaction times as summary statistics for the data.

It should be noted that when quantiles computed from single data sets are graphed and compared with quantiles predicted from parameters estimated with the chi-square and weighted least squares methods, the fits will often appear to the eye to be slightly better than quantiles predicted from parameters estimated with the maximum likelihood method. This is because the chi-square and weighted least squares methods capture the same bias toward slow extreme errors, as is exhibited by the quantiles of the data themselves.

In summarizing the quality of the fits of the three methods, we pointed out that the estimated values of parameters for the maximum likelihood method were quite accurate and that the estimated values for the chi-square and weighted least squares methods were about 5%–10% farther away from the true values and about 30%–60% more variable. The bias in the values of the standard deviation in drift across trials (η) for these two methods arose from the fact that error quantile reaction times are biased in the highest accuracy condition. When the chi-square and weighted least squares methods were used to fit predicted quantile reaction times and accuracy rates generated from the model (and not simulated data), the recovered parameter values matched the values used to generate the predicted values quite accurately.

CHANGING THE RANGE OF DRIFT RATES

In the investigations we have reported so far, drift rates spanned a range such that accuracy rates varied widely, from floor to ceiling. In this section, we will show what happens for other ranges of accuracy values. To summarize the conclusions, parameters are recovered about as accurately when the range of accuracy rates is much smaller than floor to ceiling. The only exception occurs when accuracy rates have a small, very high range, with accuracy in all the experimental conditions above about 90% (as would be the case in many lexical decision experiments).

Table 6 shows what happens with the maximum likelihood and chi-square fitting methods when the drift rates used to generate the simulated data are limited in range. (Because weighted least squares provides the same quality of fits as the chi square, it would provide the same results here as the chi square.) The results are qualitatively the same as those obtained when drift rates span the range from ceiling to floor (Table 2 and Table 4). For example, when the chi-square estimator is biased in Table 6, it is also biased in Table 4. For Sets A and B, the standard deviations are about the same as those shown in Table 2 and Table 4, and the biases in the parameters are about the same. For Sets C and D, the standard deviation in T_er is larger, but the other estimates and standard deviations are about the same as those in Table 2 and Table 4. The larger standard deviation in T_er occurs because the .1 quantile and shortest reaction times are larger and more variable than when there are larger drift rates that produce shorter reaction times, which locates T_er better. For Set E, the standard deviations are larger for both maximum likelihood (Table 2) and chi square (Table 4; except for T_er, which is better because the .1 quantile is smaller and less variable than in the lower accuracy conditions).

Table 6.

Maximum Likelihood and Chi-Square Fitting Methods Applied to Samples Where Drift Rates Do Not Span the Range From Low to High (N = 250 per Condition)

Set	Measure	a	Ter	η	sz	v1	v2	v3	v4
High drift rates (A)	Target value	0.0800	0.3000	0.0800	0.0200	0.4000	0.3500	0.3000	0.2500
	MLH mean	0.0790	0.3005	0.0743	0.0164	0.4117	0.3570	0.3052	0.2522
	MLH SD	0.0026	0.0027	0.0467	0.0151	0.0381	0.0359	0.0300	0.0285
	χ2 mean	0.0803	0.3009	0.1103	0.0263	0.4283	0.3689	0.3167	0.2648
	χ2 SD	0.0039	0.0038	0.0552	0.0161	0.0591	0.0506	0.0417	0.0378
High drift rates (B)	Target value	0.1600	0.3000	0.1600	0.0200	0.3000	0.2500	0.2000	0.1500
	MLH mean	0.1618	0.3047	0.1704	0.0243	0.3158	0.2585	0.2096	0.1570
	MLH SD	0.0075	0.0089	0.0271	0.0314	0.0368	0.0338	0.0258	0.0244
	χ2 mean	0.1657	0.3047	0.1832	0.0414	0.3372	0.2678	0.2158	0.1594
	χ2 SD	0.0105	0.0109	0.0380	0.0343	0.0535	0.0410	0.0368	0.0272
Low drift rates (C)	Target value	0.0800	0.3000	0.0800	0.0200	0.1500	0.1000	0.0500	0.0000
	MLH mean	0.0792	0.3011	0.0730	0.0203	0.1558	0.1065	0.0519	−0.0026
	MLH SD	0.0024	0.0032	0.0671	0.0145	0.0246	0.0247	0.0214	0.0184
	χ2 mean	0.0816	0.3018	0.1177	0.0286	0.1651	0.1157	0.0536	−0.0023
	χ2 SD	0.0049	0.0067	0.0953	0.0205	0.0372	0.0337	0.0243	0.0211
Low drift rates (D)	Target value	0.1600	0.3000	0.1600	0.0200	0.1500	0.1000	0.0500	0.0000
	MLH mean	0.1609	0.3061	0.1665	0.0259	0.1553	0.1011	0.0499	0.0004
	MLH SD	0.0072	0.0118	0.0318	0.0315	0.0249	0.0188	0.0175	0.0161
	χ2 mean	0.1638	0.3066	0.1655	0.0414	0.1949	0.1048	0.0515	−0.0008
	χ2 SD	0.0090	0.0180	0.0397	0.0373	0.0716	0.0229	0.0194	0.0152
Very high drift rates (E)	Target value	0.1600	0.3000	0.1600	0.0200	0.4500	0.4000	0.3500	0.3000
	MLH mean	0.1606	0.3030	0.1672	0.0223	0.4692	0.4135	0.3576	0.3046
	MLH SD	0.0076	0.0072	0.0228	0.0265	0.0450	0.0397	0.0324	0.0336
	χ2 mean	0.1669	0.3072	0.1987	0.0492	0.5073	0.4416	0.3829	0.3279
	χ2 SD	0.0173	0.0107	0.0508	0.0366	0.0796	0.0752	0.0668	0.0655

These results show that the best estimates of the parameters of the diffusion model are produced when experimental conditions span a moderately wide range of accuracy values, but not necessarily all the way from ceiling to floor. Only when accuracy is very high (above, say, 90%) for all conditions do the estimates suffer seriously for each of the three methods. Therefore, when collecting data for fitting this model (and probably similar stochastic models), it is important to have conditions that span a moderately wide range of values of accuracy.

CHANGING SAMPLE SIZE: CONSISTENCY OF ESTIMATORS

So far, we have discussed results for simulated data with a sample size of 250 observations per condition. This would be about one session of data per subject (4 × 250 trials × 3 sec per trial = 50 min). The means of the estimated parameter values and their standard deviations (presented in the tables) can be used to construct confidence intervals around the parameter values estimated for a single session for a single subject. For the simulations with 1,000 observations per condition, the results were exactly what would be expected for the behavior of the standard deviations as a function of sample size: They scaled as a function of $1/\sqrt{N}$ (the standard deviation is the square root of the sum of squared differences divided by N). For example, the average standard deviation in the maximum likelihood parameter estimates is decreased by 1.98 (with symmetric boundaries) as N is increased from 250 to 1,000 observations per condition, and for the chi-square estimation method, the standard deviation is decreased by 2.03.

Because the standard deviations scale as expected, tables for standard deviations for a sample size of 1,000 are not necessary. To a good approximation (within 10%), standard deviations for sample size N can be computed from the values in the tables for sample size 250 by multiplying the standard deviations by $\sqrt{(250/N).}$

However, the means of the parameter estimates do change as a function of sample size. They approach the input values from Table 1, so that a value of η (for the chi-square method) of 0.1135 in Table 4 (top row) becomes 0.0951 with N = 1,000. Likewise, a drift rate of 0.4346 in Table 4 (top row) becomes 0.4116 for N = 1,000. For the chi-square and the weighted least squares methods, the mean parameter values were closer to the parameter values that generated the simulated data for 1,000 observations per condition than to those for 250 observations per condition (the maximum likelihood method had parameters that had little bias with both 250 and 1,000 observations per condition). This reduction in bias is due to better estimation of the quantiles for error reactions times in the conditions with few errors.

CONTAMINANTS AND VARIABILITY IN T_er

One of the major problems bedeviling research in which reaction time measures are used is the problem of contaminant reaction times—reaction times that come from some cognitive process other than the one being studied. Contaminants include both reaction times that overlap the distribution of reaction times from the decision process under study and outlier reaction times that are outside the distribution of reaction times from the process being studied.

In this section, we will construct new sets of simulated data for which contaminant reaction times are added to the reaction times generated from the diffusion model. We will show that the chi-square and maximum likelihood methods fail badly with these data. We will also show that the weighted least squares method is robust, although the recovered parameter values are different from those used to generate the diffusion model portion of the data.

Then we will apply a correction for contaminants to the maximum likelihood and chi-square methods (we did not apply the correction to the weighted least squares method, because implementations are slow and it would perform about the same as the chi-square method). With the correction, the chi-square and maximum likelihood methods do a good job of recovering parameter values. Importantly, however, it is not possible to correct for all possible contaminants. If, after correction, there remain a small number of contaminants not represented in the model (e.g., a small number of fast responses in one condition), the chi-square method performs adequately, but the maximum likelihood method does not.

To correct for contaminants, we explicitly represent them in the fitting process and estimate their proportions. The correction leads to an increase in the standard deviations of the estimates of parameter values, because the contaminants reduce the quality of the data and also increase the number of parameters to be estimated.

Besides contaminants, we investigated variability in the parameter T_er, the parameter that encodes the time taken up by processes involved in the task under study other than the decision process itself. In examining how well the diffusion model fitted data from a recognition memory experiment (Ratcliff & Smith, 2002), the weighted least squares fitting method produced good fits (by visual inspection). But the chi-square method failed dramatically (Ratcliff & Smith, 2002). For example, the predicted .9 quantile reaction times missed the data by as much as 200–400 msec across experimental conditions. We noticed that in the data, the .1 quantile was much more variable than was the case in other data sets and was especially more variable than the simulated data examined in this article so far. To accommodate the increased variability in the .1 quantile reaction times, we assumed that T_er was variable across trials. Previously, variability in T_er was never considered a necessary addition to sequential sampling models for two-choice decisions (when it was thought about at all). However, the investigations we will present below indicate that variability in T_er should always be included in models when data are fit.

In the end, the fitting methods we present as optimal are chi-square and maximum likelihood methods that incorporate the correction for contaminants and also have variability in T_er. But we also argue that the weighted least squares method is the most robust of the three methods.

Fast and slow outliers that lie outside the distribution of reaction times from the decision process under investigation can occur for many reasons. For example, fast guesses often occur when subjects anticipate the stimulus and hit the response key by mistake. Or they can occur when subjects become frustrated or bored and start hitting response keys quickly without trying to perform the task (although this behavior can sometimes be eliminated by introducing a time delay after every response time shorter than some value, such as 250 msec). Slow outliers often occur when subjects are momentarily distracted, which leads to a delay in responding.

We treat fast and slow outliers differently. First, fast guesses, as was suggested in the introduction, can be eliminated (in large part) experimentally or with cutoffs on reaction times. Once most fast guesses have been eliminated, some of the remaining fast responses that are not from the decision process under investigation might be subsumed by variation in T_er. If there are spurious fast responses still remaining in the data, but only a few of them, they have relatively small effects on parameter estimates obtained with the chi-square method, because they will have little effect on the .1 quantile reaction time. Slow outliers can be eliminated by cutoffs, as was also mentioned in the introduction. Any remaining contaminants, contaminants that overlap with the distributions of response times from the cognitive processes under investigation, are accommodated by our correction, as we will show below.

Fast Contaminants and Their Consequences for the Three Fitting Methods

Fast contaminants provide a particularly nasty problem for the maximum likelihood method. Because each response time has to have a probability density assigned to it [f(t)], the value of T_er has to be lower than the shortest reaction time. This usually severely distorts the estimates of all the other parameters. The chi-square and the weighted least squares methods avoid this problem to some degree because they group responses into quantiles, so that the precise location of the minimum is lost and not used by the fitting method. But when the proportion of fast contaminants is greater than a few percent, the chi-square method produces poor recovery of parameters, because the .1 quantile is distorted, as we will show below. The weighted least squares method is the most robust to fast contaminants.

To illustrate the dependence of maximum likelihood parameter estimates on the fastest responses, we examined the correlations of estimates of T_er with minimum reaction times for the fits for the simulated data generated from the parameters in Table 1. The average correlation over the six groups of parameter values was about .45. This means that T_er is being determined to a large degree by the minimum reaction time. In contrast, the correlations between T_er and the minimum reaction time for the chi-square and weighted least square estimates averaged about zero, as would be expected because the fitting methods have information only about quantile reaction times.

Slow Outliers and Their Consequences for the Three Fitting Methods

Slow outliers cannot easily be eliminated by cutoffs, except in extreme cases. They can be difficult to detect, because they can hide in the tail of the reaction time distribution (see Ratcliff, 1993; Ulrich & Miller, 1994). They spread out the tail, rather than producing a second mode (as sometimes occurs with fast contaminants; Swensson, 1972). There is always going to be some small number of responses that are slow outliers, so it is important that methods be developed that allow their effects to be reduced or minimized. However, little can be done with really bad data. As a rule of thumb, if more than about 5% of responses are fast guesses or slow outliers, we should consider the data unusable for model fitting. This rule of thumb motivates the choice of 5% as the assumed proportion of contaminants in the simulations presented next.

We examined the dependence of the parameter estimates shown in Table 2, Table 4, and Table 5 on long reaction times for the fits to the simulated data generated from the parameter values from Table 1. The correlations (averaged over fits to the 100 sets of data and over the six groups of parameter values) between the estimated values of the parameters and the smallest .1 quantile and the largest .9 quantile were computed for the three methods. There were small correlations between all the parameter estimates and the .1 quantile for chi square (.1), weighted least squares (.1), and maximum likelihood (−.08), and there were larger correlations (.35 for chi square, .40 for weighted least squares, and .20 for maximum likelihood) between all the parameters and the .9 quantile. This means that random variation in the recovered parameter values across the simulated data sets is determined to some degree by the variation in the largest of the .9 quantiles across the experimental conditions (a condition with a large .9 quantile will often have a large .7 quantile also). This reflects the point made earlier about correlations among parameter values, that if one of the .9 quantiles is increased, most of the estimated parameter values increase. Again, this shows how much the estimated values of the parameters are determined by the tail of the reaction time distribution.

If, as we have just shown, parameter estimates depend significantly on the longest reaction times, then if those reaction times are contaminants, the parameter estimates will be altered, sometimes drastically, away from their true values. We will show this in the next section by explicitly adding contaminants to simulated data.

FITTING THE DIFFUSION MODEL IN THE PRESENCE OF CONTAMINANT RESPONSE TIMES

To examine the behaviors of the three fitting methods when they are applied to simulated data that contain a small proportion of contaminants, we added, with a probability of p_o, a random time of between 0 and 2 sec to reaction times derived from the diffusion model. The value of p_o was set to .05, which means that if there are 250 observations in a condition, on average 12.5 will be contaminants, although sometimes there might be 0 or 25 contaminants. With contaminants in the data, all three methods fail badly to recover reasonable parameter estimates when a = 0.08, and fail, but not as badly, when a = 0.16. In the former case, contaminants occur well out in the tail, where no reaction times occur in the data simulated from the diffusion model. In the latter case, the diffusion model produces reaction time distributions with much longer tails, and so the contaminants overlap much more with the tails. If we were to assume that the range of the contaminant reaction times increased as a increased, then a = 0.16 fits would have failed as much as those in the a = 0.08 case. However, the assumption we made (range from 0 to 2 sec) is about what might be expected in practice in experimental data. The next three sections will detail our results, and then we will go on to discuss corrections for fitting contaminated data.

Maximum Likelihood Method

The maximum likelihood method uses each reaction time in the fitting computation, and each one is weighted equally, so contaminants have a serious effect on parameter estimates. We fitted only a small number of representative data sets, because each fit produced extremely bad estimates of the parameters and each fit took a very long time (hours). In each case we examined with a = 0.08, a was estimated to be about 0.14, η was estimated to be about 0.5, instead of 0.08, and the drift rates were two to four times their correct values.

Figure 10 shows quantile probability functions produced from the parameters estimated from the maximum likelihood method for one representative set of contaminated data. The method attempts to fit correct responses at the expense of error responses, because there are more observations for correct responses (hence, the large misses between the predictions for the error quantiles and the data). We will discuss the issue of poor fits further in the next section, with reference to the chi-square method. The arguments there can be applied equally well to the maximum likelihood method.

Figure 10.

Quantile probability functions for fits of the maximum likelihood, weighted least squares, and the chi-square methods, with and without corrections for contaminants, to one data set with contaminants. The data set was chosen to illustrate some of the worst fits of the models without corrections for contaminants. The top panel shows the parameter values for the fits. The five lines represent the .1, .3, .5, .7, and .9 quantile reaction times.

Chi-Square Method

Table 7 shows the means and standard deviations in the parameter values for the chi-square method applied to the contaminated data. The result is relatively poor recovery of the parameter values. The boundary separation (a) is overestimated in each case by as much as 20%, the drift rates are overestimated by as much as 40% (especially at low values of a), and η is overestimated by a factor of two to three at low values of a. The standard deviations in the parameter values also increased from those for simulated data without contaminants (Table 4), especially at the low value of a. For the conditions with a = 0.16, some of the recovered parameters are quite close to the target values. This is because the contaminants span much the same range as the real data. The average maximum reaction time from the simulated data without contaminants is about 2,500 msec, and the largest maximum contaminant reaction time is about 4,300 msec, but few of the contaminants are this large. The median reaction time from the diffusion model plus the maximum contaminant is about 2,700 msec, and extra long reaction times are possible with and without contaminants being added. In contrast, for small values of a, all long reaction times are contaminants; the average maximum reaction time from the model is less than 1,000 msec, and contaminants have up to 2,000 msec added to the reaction time generated from the model. In practice with real data, some of these reaction times would be trimmed out as outliers, and the problem would not be as severe.

Table 7.

Means and Standard Deviations of Parameter Values Recovered From the Chi-Square Method With No Corrections Applied to Data with 5% Contaminants (N = 250 per Condition)

Value	Parameter Set	a	Ter	η	sz	v1	v2	v3	v4
M	A	0.1024	0.3012	0.2874	0.0556	0.5530	0.3570	0.1570	0.0085
	B	0.1047	0.3018	0.3817	0.0587	0.5653	0.3684	0.1631	−0.0001
	C	0.1866	0.2991	0.1378	0.0630	0.3449	0.2345	0.1217	0.0011
	D	0.1791	0.2896	0.1133	0.1154	0.3073	0.2089	0.1088	0.0004
	E	0.1838	0.2916	0.1992	0.0439	0.3314	0.2184	0.1186	0.0021
	F	0.1770	0.2777	0.1733	0.0977	0.3082	0.1953	0.0982	0.0002
SD	A	0.0159	0.0073	0.1600	0.0317	0.1707	0.1099	0.0691	0.0313
	B	0.0134	0.0065	0.1247	0.0295	0.1513	0.0921	0.0693	0.0455
	C	0.0169	0.0163	0.0462	0.0442	0.0688	0.0457	0.0271	0.0147
	D	0.0166	0.0217	0.0565	0.0384	0.0637	0.0439	0.0299	0.0123
	E	0.0107	0.0123	0.0349	0.0315	0.0405	0.0295	0.0289	0.0173
	F	0.0126	0.0236	0.0467	0.0409	0.0480	0.0381	0.0252	0.0164

Figure 10 shows one of the pathological cases in which the drift rates are estimated to be very high (as compared with the parameters used to generate the diffusion process portion of the data), the variability in drift is estimated to be very high, and the boundary separation is estimated to be high. The method is attempting to fit correct responses at the expense of errors (which are weighted less because there are fewer of them). One reason that the fits are poor for this set of data is that there are contaminants in the four conditions for correct responses but few contaminants in the error responses (because there are only 5% contaminants, on average, in any condition; on a particular simulation, there may be 0%, 5%, or 10% contaminants). The predicted function gets close to the correct responses and to the intermediate accuracy errors and badly misses the extreme errors (to the left-hand side of the top panel).

The key point is that parameter estimates are much larger than the values used to generate the noncontaminant data, because the data set is generated not from a diffusion model with the target parameter values, but from the diffusion process plus contaminants.

Weighted Least Squares Method

As was discussed earlier, in the weighted least squares method, the .9 quantile is weighted less than the lower quantiles. This is because the shorter quantiles have less variability, whereas the longer quantiles have more variability. Because the .9 quantile shows the effects of contaminants most and is weighted least, the weighted least squares method is less affected by contaminants than are the other methods.

The recovered drift rates are quite near their true values (except the highest drift rates for a = 0.08, which may have had cases in which the number of errors was too small to provide quantiles). The parameter a was better estimated than with the chi-square method, but T_er was underestimated, which it was not for the chi-square method. The value of η was overestimated, but by much less than with the chi-square method. The standard deviations in η were less for the chi-square method than for the weighted least squares method, which means that the former produced an incorrect estimate with smaller spread than did the latter. The value of T_er was more overestimated for weighted least squares, but all the other parameters were more overestimated for chi square (on average).

Figure 10 shows the quantile probability functions from the best-fitting parameter values for the weighted least squares method, using the parameter values in Figure 10. Unlike the chi-square and maximum likelihood methods, the data are fit reasonably well, and the speed-up in error reaction times, going from the middle of Figure 10 to the left-hand side, is well captured. The parameter values are much closer to those that generated the diffusion model portion of the data, and the effects of contaminants on the parameter estimates are not large.

We conclude that the weighted least squares method does better than the chi-square and the maximum likelihood methods (without corrections for contaminants) at fitting contaminated data. The fitted quantile probability function comes much closer to all the data for the weighted least squares method than for the chi-square and the maximum likelihood methods (for this single example and for other data sets). This is true especially in cases such as the one presented in Figure 10, where the contaminants affect correct reaction times more than they affect error reaction times. The parameter estimates are biased away from the true parameter values for the diffusion component of the simulated data because of the contaminants. This is a problem if the aim is to recover accurate values of the parameters but is not a problem if the aim is to see whether the model can fit the data. The example in Figure 10 illustrates the point that the weighted least squares method is much more robust than the other two methods to contaminated data.

CORRECTION FOR CONTAMINANTS

In this section, we will examine a correction scheme for the maximum likelihood and chi-square methods. The correction allows recovery of estimates of parameters that are about as good as when the data contain no contaminants but the standard deviations in the estimates are about 10% larger. The quality of the fit is usually similar or somewhat better than that of the weighted least squares method without correction for contaminants.

Contaminants are added to simulated data by adding a random amount of time of between 0 and 2 sec to a reaction time derived from the diffusion model. This assumption about the distribution of contaminants is our best guess about what happens when motivated subjects have occasional distractions. The random amount of time is added to a small proportion of the responses with probability p_o, which we set to .05. This sum produces a combined distribution of contaminated reaction times that is almost a rectangular distribution. It has a rapid rise, a long flat asymptote, and a slow fall in the tail (see Figure 10; Ratcliff, 1993).

In order to take contaminants into account in the fitting methods, it is necessary to make an assumption about what form the distribution of contaminant response times takes, an assumption that entails few additional parameters and is consistent with what we know about contaminants in real experimental data. The assumption we make below in modeling is not identical to the assumption we make in generating the simulated data but is not too different (the assumption in modeling allows contaminants to be random, as well as the result of a random delay added to a regular decision). The assumption we make is that contaminants come from a rectangular distribution with a range determined by the maximum and the minimum reaction times in each experimental condition and that the probability of a contaminant (p_o) is the same in each condition (i.e., is independent of the stimulus). The maximum and minimum reaction times will not determine the true range of contaminants in any particular condition (there may not be any contaminants in some conditions). But our method of fitting all the conditions with the same parameter values gives successful recovery of the parameters of the diffusion process and the proportion of contaminants.

To summarize, to fit the diffusion model to simulated data with the added contaminants, a mixture of two distributions is used. The first component is the distribution of reaction times from the diffusion process weighted with probability 1 − p_o, and the second component is a uniform distribution that ranges from the minimum to the maximum reaction times in each condition, weighted by probability p_o. The probability density for each reaction time is (1 − p_o) f_d(t) from the diffusion model plus p_of_u(t) from the uniform distribution.

We applied the correction method to the maximum likelihood and the chi-square fitting methods. The weighted least squares method is robust, and the contaminant correction method would improve performance about as much as it does for the chi-square method, but implementations would be so slow that it would never be used in practice.

Maximum Likelihood

For the maximum likelihood method, each reaction time is used to compute the probability density [f(t)] for the diffusion process and the probability density for a uniform distribution with a range of maximum reaction time minus minimum reaction time. These are weighted by 1 − p_o and p_o, respectively, and summed to provide the likelihood of that reaction time. In all other respects, the fitting method is the same as without correction.

Generally, the parameters of the diffusion model are recovered a little less accurately than when the uncorrected method is applied to data without contaminants. For all six sets of parameter values, the value of η is overestimated by 10%–20%, and drift rates are overestimated by 5%–10%, as compared with the values used to generate the simulated data (Table 1). For a = 0.08, the proportion of contaminants (p_o) recovered by the fitting program is about .049, close to the true value of .05. For a = 0.16, p_o is estimated to be less than .03, and the value of a is overestimated by about 5%. With a = 0.16, the reaction time distribution is spread more than in the a = 0.08 case, and the fitting method accommodates some proportion of the contaminants as though they were generated from the diffusion process. The standard deviations in the parameter values are increased by approximately 15% relative to fitting the uncontaminated data.

In practice, it is not possible to know whether data do or do not contain contaminants (unless they are extreme enough to be removed by cutoffs). Therefore, it is important to check whether the contaminant correction method recovers parameter values accurately even when there are no contaminants in the data. We applied the corrected maximum likelihood method to the original sets of simulated data that contained no contaminants. The estimated value of p_o was less than .01. The parameters a, η, and s_z were slightly underestimated, and drift rates were underestimated by around 5%. The standard deviations were close to the same as when the method was applied without the correction for contaminants. This means that application of the corrected method to data without contaminants produces results similar to those when the uncorrected method is applied.

The addition of the correction method to maximum likelihood allows it to produce parameter estimates that are close to those used to generate the data, differing from the true values by only about 20% for η and 10% or less for the other parameters. Standard deviations increased by about 15%. Even though the distribution assumed for fitting is not quite the same as the distribution used to generate the simulated data (a diffusion process reaction time plus a uniformly distributed distraction time), the use of the mixture allows the maximum likelihood method to produce good fits, in contrast to its failure with contaminated data when no correction is used. Also, the implementation does not suffer in speed, running at about the same speed as the program without the correction.

Chi Square

Just as for the maximum likelihood method, the chi-square fitting method is corrected with the assumption that the data are a mixture made up of a distribution of reaction times from the diffusion process and a uniform distribution of contaminants. The range between the maximum and the minimum reaction times for each condition provides the range of the rectangular distribution of contaminants, and p_o is the probability density within that distribution of contaminants.

To apply the chi-square method to the mixture distribution, we first obtain the quantile points of the observed reaction time distributions from the data just as for the chi-square method without corrections for contaminants. Then we estimate the proportion of contaminants between the quantiles, and we subtract these away to leave the proportion of responses between the quantiles that arise from the diffusion process. Specifically, the rectangular distribution of contaminants is divided into ranges by the observed quantile reaction times (the sum of the proportions of responses between the quantiles is p_o). Then the proportions of responses between the quantiles (and outside the quantiles) assumed to come from contaminants are subtracted from the observed proportions from the data (which are .1, .2, .2, .2, .2, and .1). The resulting proportions represent the probability densities between the quantiles that come from (and are to be fit by) the diffusion process. (In the computer program used to fit the diffusion model, these proportions are normalized by dividing by 1 − p_o, and the diffusion model is fit as before.)

The correction method gives reasonably good recovery of parameter values. The η parameter is overestimated by 25% or less, and drift rates are overestimated by less than 10%, as compared with the values used to generate the diffusion process portion of the data. The overestimation is about as large as that obtained with the corrected maximum likelihood method applied to contaminated data and about the same, overall, as the uncorrected chi-square method applied to uncontaminated data. The estimated proportion of contaminants from the fitting method is .043 for a = 0.08, near the correct value of .05, but as for the maximum likelihood method, for a = 0.16, the value is less than the true value, about .03 instead of .05. The standard deviations in the parameter values increase by only about 5% over the standard deviations for the chi-square method without corrections applied to uncontaminated data. They are about 38% greater than the standard deviations for the corrected maximum likelihood method applied to contaminated data.

When the chi-square method is applied to data without contaminants, the biases are about the same as those for the chi-square method without the correction for contaminants, and the standard deviations are about 6% smaller. The proportion of contaminants estimated is less than 0.9%.

The chi-square method with the correction for contaminants has biases in recovered parameters about the same as those for the maximum likelihood method with the correction for contaminants, but it has standard deviations, on average, 22% higher than those for the maximum likelihood method. The chi-square method also runs 25–100 times faster.

If there are reasons to believe that a particular task has some other known distribution of contaminants, this could be used instead of the uniform distribution used here.

VARIABILITY IN T_er

As was mentioned above, it has never been considered necessary to add variability in T_er to sequential sampling models; generally, the models fit their target data well without it. However, given the need for it in recent fits of the diffusion model (Ratcliff & Smith, 2002), we will investigate its effects here. We will explicitly model variability in T_er and will examine the effect of the additional parameter and additional variability in data on recovery of all the parameters of the model.

Variability in T_er was modeled by assuming a rectangular distribution of T_er values with range s_t. A rectangular distribution was chosen because it limits the range of values (as compared, for example, with a normal distribution).

The most important consequence of adding variability in T_er is to increase the robustness of the fitting methods to variability in fast responses. Because T_er has a distribution of values, probability density or cumulative probabilities exist for values of time less than T_er. This increases robustness, because now s_t, not T_er alone, is determined by the shortest reaction time (this may also help with fast outliers that are in the range of T_er − s_t/2). However, the assumption of variability in T_er also adds one parameter, which increases the standard deviations in the other parameter estimates. Also, greater variability in the .1 quantile reaction times will reduce the accuracy of the location of T_er, which will increase the variability in all the parameters.

We chose a value of s_t =200 msec (for the uniform distribution with range s_t, the standard deviation is $s_t/\sqrt{12}=58\text{msec}$) for our simulations, because this value was at the high end of those we obtained when fitting experimental data.

Adding variability in the onset of the decision process (T_er) actually changes the predicted quantile reaction times by a relatively small amount, as compared with the case in which there is no variability in T_er. For example, a value of s_t = 200 msec (as compared with s_t= 0 msec) reduces the .1 quantile reaction time by only 10–40 msec, and it reduces the .3 quantile by only 0–10 msec (depending on drift rate). But variability in T_er produces much greater variability in the .1 quantile reaction time across conditions in simulated data sets (and hence, accommodates such variability in fitting data with large variability in the .1quantile reaction time across conditions).

We generated simulated data as in the other simulations, with 5% contaminants and with a range in the distribution of T_er of s_t = 200 msec, using the six sets of parameter values in Table 1. We will present the results for the maximum likelihood method with 250 observations per condition and for the chi-square method with 1,000 observations per condition. The computations for the maximum likelihood method with 1,000 observations per condition would have taken several weeks to run, so we used the results for 250 observations per condition.

We chose to use 1,000 observations per condition for the chi-square method because with 250 observations per condition, the results for the chi-square method were very poor. There were large biases away from the parameter values used to generate the diffusion process reaction times. For example, the estimate of a was 0.094 instead of 0.08, η was 0.19 instead of 0.08, and drift rates were 20% too high (for the values in the first row of Table 1). In the 100 sets of fitted parameter values, there were values of η that were 0.45 instead of 0.08. These large biases are clearly unacceptable. The standard deviations, on the other hand, were exactly what was expected as a function of the number of observations: The average standard deviation for 250 observations per condition was 1.96 the standard deviation for 1,000 observations per condition (i.e., scaling as a function of the square root of N). We attribute the biases in parameter estimates with 250 observations per condition to excessive variability in the estimated quantiles for error reaction times when there was variability in T_er and when there were small numbers of observations. With 1,000 observations per condition, there were only a few cases in which there were serious distortions in parameter estimates, because quantile reaction times were better estimated with this number of observations. For this reason, we present results for the chi-square fits only for 1,000 observations per condition and note that at least 1,000 observations per condition are needed when applying this version of the chi-square method.

Maximum Likelihood Method With Correction for Contaminants and Variability in T_er

To examine the effects of slow contaminants and variability in T_er, we simulated data from the diffusion model with a rectangular distribution for T_er with a range of 200 msec and 5% contaminants from the distribution that was used in earlier simulations (i.e., by adding between 0 and 2,000 msec to a reaction time generated from the diffusion model). In generating simulated data, we first added variability to T_er by adding a random number of between −100 and +100 msec, and then, on 5% of the responses, we added a random number of between 0 and 2,000 msec to produce the contaminant.

The only modification to the fitting program was adding the computation that integrated over values of T_er (with the range of integration of −s_t/2 to +s_t/2). Then we fitted the simulated data with the maximum likelihood method with the correction for contaminants as before and with the assumption of a uniform distribution of values of T_er.

Table 8 presents the means and standard deviations of the estimated parameter values. The standard deviations are about 36% higher than those in Table 2 for the uncorrected method without variability in T_er applied to data without contaminants. There are biases in some of the parameter values. For example, a, the drift rates for some conditions, and the values of the variability parameters (η and s_z) are usually overestimated (by up to 40% for the conditions with a = 0.08). The estimate of the proportion of contaminants is underestimated (.025 instead of .05) at the larger value of boundary separation a. Values of T_er and a are estimated within 5% or 6% of the values used to generate the simulated data. With larger values of the number of observations per condition, these biases would be reduced (but fitting time for 100 data sets would approach weeks).

Table 8.

Means and Standard Deviations of Parameter Values Recovered From the Maximum Likelihood Method With Corrections Applied to Data with 5% Contaminants and Variability in T_er (N = 250 per Condition)

Value	Parameter Set	a	Ter	η	sz	v1	v2	v3	v4	po	st
M	A	0.0806	0.3053	0.1135	0.0337	0.4603	0.2861	0.1136	−0.0020	0.0554	0.2019
	B	0.0794	0.3054	0.1832	0.0307	0.4413	0.2729	0.1083	−0.0029	0.0554	0.2022
	C	0.1708	0.2950	0.0985	0.0273	0.3102	0.2086	0.1051	−0.0002	0.0244	0.1883
	D	0.1707	0.2987	0.1011	0.1134	0.3095	0.2103	0.1101	−0.0023	0.0226	0.1917
	E	0.1709	0.2968	0.1753	0.0275	0.3103	0.2115	0.1035	−0.0025	0.0247	0.1880
	F	0.1702	0.2935	0.1756	0.1063	0.3091	0.2064	0.1029	0.0009	0.0258	0.1875
SD	A	0.0046	0.0063	0.0814	0.0118	0.0805	0.0544	0.0292	0.0220	0.0088	0.0103
	B	0.0050	0.0050	0.0802	0.0070	0.0716	0.0489	0.0338	0.0253	0.0101	0.0099
	C	0.0090	0.0177	0.0271	0.0348	0.0378	0.0251	0.0179	0.0113	0.0145	0.0252
	D	0.0112	0.0175	0.0344	0.0239	0.0436	0.0292	0.0193	0.0124	0.0157	0.0260
	E	0.0106	0.0173	0.0369	0.0386	0.0444	0.0327	0.0214	0.0155	0.0180	0.0280
	F	0.0147	0.0206	0.0488	0.0352	0.0568	0.0390	0.0242	0.0180	0.0195	0.0278

Chi-Square Method With Correction for Contaminants and Variability in T_er

First, we determined that application of the uncorrected chi-square method without variability in T_er to contaminated data with variability in T_er would fail. In the real data set mentioned above, for which the chi-square method failed, we believed that the failure was due to excessive variability in the .1 quantile, and we wanted to check that this was correct. As was expected, there were severe biases in parameter estimates. Boundary separation, a, was overestimated by between 10% and 20%, T_er was underestimated by 30–60 msec, drift rates were underestimated by 10%–30%, η was one quarter its target value when a = 0.08 but close to the correct values when a = 0.16 (probably an overprediction from contaminants was canceled out by underprediction from variability in T_er). Drift rates were underestimated by 40% for a = 0.08 and by 5%–20% for a = 0.16.

We then applied the corrected chi-square method with the correction for contaminants and with variability in T_er to the data sets with contaminants and with variability in T_er. Table 9 presents the results. There are slight biases of 3–15 msec in T_er, and there are biases of about 5% of the mean in a and about 10% of the mean in η, except when η and a are small (the first condition). Drift rates are also within 5% of the target values, except for the first condition. The recovered range in T_er (s_t) is around 180– 200 msec, which is close to the input value of 200 msec, and the estimated proportion of contaminants is between 3% and 4%, smaller than the input value of 5%. The standard deviations in Table 9 are about 50% larger than those for the uncorrected chi-square method without variability in T_er applied to data without contaminants or T_er variability for 1,000 observations per condition. They are also about 45% greater than standard deviations with the corrected maximum likelihood method with variability in T_er (scaled for 1,000 observations per condition).

Table 9.

Means and Standard Deviations of Parameter Values Recovered From the Chi-Square Method With Corrections Applied to Data with 5% Contaminants and Variability in T_er (N = 1,000 per Condition)

Value	Parameter Set	a	Ter	η	sz	v1	v2	v3	v4	po	st
M	A	0.0832	0.2955	0.0972	0.0255	0.4025	0.2543	0.1014	−0.0007	0.0382	0.1962
	B	0.0827	0.2965	0.1714	0.0235	0.4055	0.2538	0.1020	−0.0023	0.0426	0.1979
	C	0.1650	0.2964	0.0896	0.0277	0.3010	0.2036	0.1026	0.0007	0.0369	0.1954
	D	0.1617	0.2888	0.0749	0.0939	0.2811	0.1908	0.0953	−0.0004	0.0375	0.1927
	E	0.1651	0.2970	0.1687	0.0251	0.3080	0.2025	0.1031	−0.0000	0.0418	0.1954
	F	0.1625	0.2849	0.1524	0.0858	0.2865	0.1873	0.0954	−0.0009	0.0379	0.1928
SD	A	0.0048	0.0090	0.0461	0.0158	0.0543	0.0308	0.0166	0.0108	0.0207	0.0095
	B	0.0061	0.0082	0.0671	0.0192	0.0741	0.0475	0.0244	0.0119	0.0209	0.0080
	C	0.0072	0.0095	0.0176	0.0230	0.0201	0.0150	0.0093	0.0052	0.0184	0.0227
	D	0.0087	0.0174	0.0302	0.0268	0.0336	0.0218	0.0121	0.0069	0.0195	0.0343
	E	0.0077	0.0096	0.0215	0.0244	0.0234	0.0196	0.0123	0.0077	0.0171	0.0189
	F	0.0132	0.0197	0.0436	0.0408	0.0450	0.0350	0.0194	0.0091	0.0193	0.0258

These results show that estimates of parameters from the corrected chi-square method with variability in T_er are no more biased (with 1,000 observations per condition) than those for the uncorrected method without variability applied to uncontaminated data without T_er variability. The standard deviations in the parameter values are increased relative to the case with neither contaminants nor T_er variability, but that is to be expected because both contaminants and variability in T_er reduce the quality of the data and because the number of parameters in the model is increased. Applying the method to data without contaminants or T_er variability recovers the parameters of the model as well as does the method that does not have these factors built into the fitting program.

Weighted Least Squares Without Correction Applied to Data With Contaminants and Variability in T_er

To illustrate the robustness of the weighted least squares method, Table 10 shows the results of application of the method to the data set with contaminants and variability in T_er with 1,000 observations per condition. The weighted least squares method is not corrected for slow contaminants, and it does not have variability in T_er represented in the fitting program. The results show large biases in parameter estimates. There is underestimation (by 30–60 msec) of T_er, overestimation of a by up to 20%, underestimation of the variance parameters η (by up to 40%) and s_z, and underestimation of the drift rates by up to 25%.

Table 10.

Means and Standard Deviations of Parameter Values Recovered From the Weighted Least Squares Method (With No Corrections) for Data With Contaminants and Variability in T_er (N = 1,000 per Condition)

Value	Parameter Set	a	Ter	η	sz	v1	v2	v3	v4
M	A	0.0940	0.2507	0.0454	0.0145	0.3175	0.2026	0.0801	−0.0001
	B	0.0933	0.2493	0.0870	0.0134	0.2980	0.1853	0.0736	−0.0016
	C	0.1710	0.2616	0.0730	0.0217	0.2635	0.1820	0.0933	0.0006
	D	0.1688	0.2526	0.0636	0.0896	0.2499	0.1732	0.0872	−0.0002
	E	0.1731	0.2595	0.1428	0.0286	0.2643	0.1785	0.0912	−0.0003
	F	0.1716	0.2571	0.1415	0.0970	0.2613	0.1755	0.0896	−0.0011
SD	A	0.0026	0.0032	0.0351	0.0118	0.0243	0.0176	0.0114	0.0076
	B	0.0018	0.0036	0.0283	0.0127	0.0183	0.0144	0.0091	0.0079
	C	0.0052	0.0097	0.0190	0.0279	0.0219	0.0158	0.0095	0.0046
	D	0.0077	0.0194	0.0313	0.0290	0.0342	0.0257	0.0129	0.0062
	E	0.0078	0.0143	0.0286	0.0349	0.0349	0.0265	0.0172	0.0068
	F	0.0105	0.0206	0.0381	0.0336	0.0455	0.0306	0.0184	0.0085

The standard deviations for the fits for the weighted least squares method without contaminants or variability in T_er, shown in Table 5 (with N = 250 observations per condition), are about twice (94% greater) as large as those for the weighted least squares method applied to data with contaminants and variability in T_er for N = 1,000 observations per condition (Table 10). Because the standard deviations scale as the square root of N, this means that the variability is comparable for the two cases. This means that the weighted least squares method is finding solutions around parameter values that are clustered just as tightly for the cases with and without contaminants and variability in T_er, but with large biases in the former cases.

Although we do not present a figure showing this, the quality of the fits to data (quantile probability functions) are good for the application of the weighted least squares method applied to data with contaminants and variability in T_er. There appear to be no large systematic deviations of the theoretical fits from the data using the average parameter values from fits to the 100 simulated data sets. Thus, the weighted least squares method provides a good method to see whether the diffusion model can fit the data but does not provide accurate parameter estimates if there are contaminants or variability in T_er.

REACTION TIME DISTRIBUTIONS WITH CONTAMINANTS AND VARIABILITY IN T_er

Earlier, we said that adding variability in T_er does not change reaction time distribution shape very much. Here, we show how the various sources of variability and contaminants affect distribution shape. Adding variability in T_er alters the shape of the reaction time distribution, because the leading edge rises more slowly than it does without variability in T_er. But the effect on the shape of the reaction time distribution is relatively small, even though it affects the fitting methods a great deal because it allows a lot of variability in the early quantile reaction times (e.g., the .1 quantile). Figure 11 shows reaction time distributions with the presence and absence of the various sources of variability: variability in drift, starting point, T_er, and contaminants, for one set of parameter values. The first function has no variability in drift or starting point across trials. The second adds variability in drift, the third adds variability in starting point, the fourth adds variability in the nondecision component of reaction time (T_er), and finally, the fifth adds the distribution of contaminants used above. The key differences among these functions are the following. In adding variability in drift across trials, accuracy decreases (dropping from .83 with η = 0 to approximately .69 for the other four functions with η = 0.16), and the distribution becomes more peaked. Adding starting point variability (s_z) shifts the distribution a little to the left, and adding variability in T_er shifts it even further to the left. Adding contaminants changes the last distribution little, raising the extreme right tail a little. In each of these latter four cases, the tail of the distribution changes little, and the shape of the distribution remains about the same.

Figure 11.

Five reaction time distributions for predictions from the diffusion model with the various sources of variability present and absent (see the figure legend).

The changes in quantile reaction times as variability in T_er is added to the model with the parameter values in Figure 11 can be described as follows: The .1 quantile decreases by 14 msec when s_t is 200 msec relative to the case in which s_t is 0. The .3 quantile decreases by about 4 msec, and higher quantiles change by less than 5 msec. The size of the differences is greater at higher drift rates (e.g., the .1 quantile is lowered by 30 msec when the drift rate is 0.4), but generally, changes in drift rate produce what seems to be a shift in the distribution by about 10– 40 msec for the range of parameter values we have considered (those in Table 1). This means that with variability in T_er, high drift rates, and small boundary separations, what would appear to be a shift in the position of the reaction time distribution as a function of moving from an easier to a harder condition (e.g., Balota & Spieler, 1999) could actually be the result of variability in T_er (Ratcliff et al., 2002).

The effect of adding variability in T_er is to add a modest shift in the leading edge of the theoretical reaction time distribution. However, it allows random samples of data to have large differences in the leading edge (e.g., .1 quantile) from data sample to data sample. Adding variability in T_er into the diffusion model allows the chi-square and maximum likelihood methods to accommodate these large differences in the leading edge. This allows the methods to fit experimental data in cases in which they would not fit the data without variability in T_er.

GOODNESS OF FIT: THE GRAPHICAL MONTE CARLO METHOD

Evaluating goodness of fit for the diffusion model has not been mentioned up to this point. This is because the focus is on just this one model. There are no other models that have been shown to fit all the data that are obtained from two-choice reaction time experiments. We see four steps that represent different points in the development and testing of models, and in the reaction time domain, the field is still largely at the first step. The first step is to ask whether there is any model at all that might fit the experimental data. If we are at this point, a graphical Monte Carlo method for displaying goodness of fit is sufficient, as will be presented shortly. Second, do we have more than one model that might fit the data? Then, we can use the graphical Monte Carlo method to determine whether and how well all the models fit the data. Third, if we have more than one model that adequately fits the data, is it possible to devise experiments that differentiate between the models? Do the models make differential predictions, or do the models mimic each other? Fourth, if the models do not mimic each other exactly, but no strong differential predictions can be obtained, standard goodness-of-fit measures can be used to distinguish among them.

When a numerical value to represent the goodness of fit is needed, a chi-square statistic can be used. The use of a chi-square statistic is a standard method for assessing goodness of fit, and the chi-square fitting method would provide it as a by-product of fitting data (it is the objective function being minimized).

The graphical Monte Carlo method offers a visual presentation of the variability associated with predictions from a model for the sample size and conditions in the experiment. The idea is to use the best-fitting parameters to generate random samples of simulated data with the same number of observations per condition as the data. Then the experimental data can be plotted with the simulated data, and for 100 random samples of simulated data, the experimental data should lie within limits established by the middle 95%.

One example of the graphical Monte Carlo method is presented in Figure 12. We chose one of the sets of parameters with symmetric boundaries (the third set in Table 1). From this set of parameters, 100 sets of simulated data were generated with 1,000 observations per condition (we chose 1,000 observations per condition to reduce the overlap between the quantiles; see Figure 2) and with 5% contaminants with no variability in T_er. The diffusion model with correction for contaminants was fitted to the data, using the chi-square method, and the data and the two sets of fits are shown in Figure 12. This example illustrates how well the model with corrections for contaminants fits the simulated data with contaminants.

Figure 12.

Examples of the graphical Monte Carlo method for 100 sets of simulated data with 5% contaminants with parameters from the third line of Table 1. The black dots represent the quantile reaction times from the theoretical fits from the average parameter values for the fits to each data set, and the gray dots represent the Monte Carlo samples.

Both panels of Figure 12 display gray dots (that as groups approximately form ellipses) representing the 100 sets of simulated data. The black points are predictions from the means of the estimated values of the parameters. The means of the parameter values a, T_er, η, s_z, and four drift rates were 0.162, 0.301, 0.086, 0.027, 0.308, 0.210, 0.103, and 0.001, respectively, and the estimated probability of contaminants was .0484. The fits fall in the middle of the range of simulated data points, and there appear to be no systematic deviations between the simulated data sets and predictions. Examples of the use of this method are presented in Ratcliff et al. (2002).

USING THE WEIGHTED LEAST SQUARES METHOD TO EXPLORE THE QUALITY OF THE FIT

In examining how well the diffusion model would fit data from a recognition memory experiment (Ratcliff & Smith, 2002), the weighted least squares fitting method was used, and it produced quite good fits by visual inspection. As was noted earlier, when the chi-square method was used to fit the data, it failed dramatically (see Ratcliff & Smith, 2002); for example, the .9 quantile reaction times missed by as much as 200–400 msec. We noticed that in the data, the .1 quantile was much more variable than in other data sets and was especially more variable than simulated data examined in our simulation. Because the weighted least squares method fitted well, we looked for factors that might have caused the chi-square method to fail, and it was as a result of this search that we added variability in T_er into the chi-square fitting method. The use of the weighted least squares method allowed us to determine that the data could be fit adequately and prompted us to search for problems with the chi-square method. In general, if there are problems with the chi-square method, but the weighted least squares method fits adequately, the chi-square method should be examined for the source of the problems.

If the weighted least squares method does not produce good fits, it is possible to change the weights on the various components of the sum of squares in order to experiment to see whether better fits can be obtained. For example, if the fits to the higher quantile reaction times (e.g., .7 and .9 quantiles) are poor, the .9 quantile could be weighted more and more until the value generated from the parameter values for the fit comes into line with the data. Then the .1 quantile could be weighted more, and accuracy could be weighted less, for example. This might allow the predicted accuracy values to deviate away from their best fits (by a few percent) and bring the reaction time quantiles into better register. The point is that the weighted least squares method allows more flexibility in weighting different components of the data than do the chi-square and the maximum likelihood methods.

The weighted least squares method can be seen as an exploratory tool; the graphical quality of the fits can be manipulated because each component (accuracy and the quantiles for both correct and error reaction time quantiles) can be weighted differently. Although ad hoc weighting schemes are not recommended for final presentation of fits to data, and especially not for model comparison, they can be used to understand where a model is misfitting data and what specific aspects of the data are providing the problems.

At this point in the history of testing reaction time models and evaluating their goodness of fit, we finally have models (e.g., diffusion models, accumulator models, etc.) that appear capable of accounting for the full range of experimental data. The data include two dependent variables for each experimental condition, reaction time and accuracy, as well as reaction time distributions for correct and error responses. In terms of the stages of model testing that were described above, we feel we are about at the stage of trying to determine whether models can handle larger and more comprehensive data sets than they have so far, whether the models are capable of mimicking each other, and whether we can find cases in which the models make differential predictions (e.g., Ratcliff & Smith, 2002).

DISCUSSION

This article has presented the first study aimed at investigating methods for fitting a sequential sampling model, the diffusion model, to experimental data. We evaluated fitting methods, presented examples of parameter estimates and their standard deviations, and examined the properties of the estimators. We conclude that the fitting methods provide reasonable solutions for estimating parameters for the diffusion model even when the data contain contaminants. The results provide measures of bias and standard deviations in the recovered parameter values for ranges of parameter values that match experimental data. The standard deviations can be used as guides to the standard deviations we might expect in parameter values from fits to group data from single experiments or from fits to data from single subjects. The standard deviations can be used in testing hypotheses about differences in parameter values between conditions or groups of subjects—for example, whether one group adopts more conservative response criteria than another. We hope that the work in this article can serve as a prototype for investigations of fitting methods for other models of reaction time and accuracy and for other models more generally.

The method that is usually the first choice for parameter estimation is the maximum likelihood method. It has attractive statistical properties: The parameter estimates are asymptotically unbiased, and the variances in the parameter estimates are the smallest possible for asymptotically normally distributed estimators. We found in application to the diffusion model that the maximum likelihood method provided the smallest standard deviations in parameter estimates and the most unbiased estimates among the methods we studied. The method was very sensitive to contaminated data, and we were able to correct for contaminants that overlapped the reaction time distributions for the simulated data by explicitly representing them in the model. With the correction, the method provided better parameter estimates (estimates with about the same bias but lower variance) than did the other method with the same correction. However, the maximum likelihood method is very sensitive to spurious fast responses and excessive variability in the fastest responses (i.e., more variable than those produced from the model), because it has to place T_er below the shortest reaction time to determine its probability density, f(t). If it is possible that data contain such variability or fast outlier responses and they cannot be eliminated experimentally, the estimated parameters and fits can be severely distorted. To address the issue of excessive variability in the fastest responses, we added assumptions about variability in T_er and found that the maximum likelihood method again produced better estimates than did the other methods. However, the method is not robust: If the assumptions about contaminants or variability in T_er are not reasonably accurate, the method can fail quite badly, even with just a few deviant data points.

The chi-square method with corrections for contaminants and variability in T_er is very fast (25–100 times faster than the maximum likelihood method and runs in minutes, as opposed to hours, on fast workstations). The chi-square method has higher standard deviations in parameter estimates than the maximum likelihood method and will often produce biased estimates of the parameter values. This is the result of biases in the estimates of the quantile reaction times for errors with small numbers of observations. However, the chi-square method is robust to a few fast or slow contaminants, much more robust than the maximum likelihood method.

The weighted least squares method is about 100 times slower than the chi-square method, but it is robust in the face of contaminants and variability in T_er, more robust than either of the other two methods. When the method is applied to data with contaminants or with variability in T_er, as implemented in the studies above, it produces a solution that produces predicted functions near the data. This is very useful because it shows whether or not the model is capable of fitting the data. But the estimated parameters are usually biased away from the parameters used to generate the portion of the data generated by the diffusion model (unless such corrections were introduced into the method). The parameter estimates are about as biased as those for the chi-square method when applied to data without contaminants or variability in T_er, but the standard deviations in parameter values are larger.

Besides being more robust, the weighted least squares method is easier to manipulate (i.e., to experiment with) to determine the source of misses between the model and the data. For example, if there are slow contaminants, the .9 quantile can be weighted less, or if error rates in some conditions are thought to be the result of guessing, accuracy in these conditions can be weighted less. This allows various guesses about distortions in the data to be evaluated using the model, and this could (and did) lead to other assumptions (explicit representation of contaminants and variability in T_er) being added to the chi-square and maximum likelihood methods.

It is also important to note that the three different fitting methods are fitting different objective functions. This means that biases in parameter estimates can be due to the different summaries of the data used in fitting (e.g., biases in quantile reaction times vs. individual reaction times). We showed that in the case of the chi-square and weighted least squares methods, biases in parameter estimates were due to biases in the data summaries used in fitting the model (quantile reaction times for error responses). When the methods are applied to accurate predicted quantile reaction times and accuracy values, the parameters used to produce the predictions are recovered quite accurately.

When a model is to be fit to data, it is important to consider the aim of the project. We listed four aims: (1) to find out if a model can produce fits that are near the experimental data, (2) to competitively test between models on a single data set, (3) to devise manipulations that produce differential testable predictions from the models, and (4) to use goodness-of-fit methods to discriminate between models that make about the same (but identifiably different) predictions. At this point of research using the diffusion model and other models of this class, the usual aim is to determine whether a model can fit experimental data, and the methods we have presented here allow this to be done. We are at the point in this domain of research where comprehensive projects aimed at testing between models and examining mimicking between models are possible. Such projects will require careful consideration of fitting methods, and the methods presented here will provide a good starting point for model comparison.

One important question that is often asked is the following: Can the diffusion model fit any pattern of reaction time and accuracy data, or are there patterns the model is incapable of fitting? The short answer is that there are many patterns the model cannot fit but these rarely occur in experimental data. Some examples of patterns the model cannot fit are the following. First, the model predicts that the reaction time distribution shape is right skewed and that it has about the same qualitative shape across a wide range of drift rates and boundary separations. Data sets from a variety of tasks all show about the same shape for reaction time distributions, which matches the shape predicted from the model. If the shapes of empirical reaction time distributions were considerably more symmetric or more skewed than they are, the model would fail. Second, if drift rate changes across conditions in a within-subjects design in which all other parameters are fixed, the reaction time distribution must skew with only a small change in the shortest quantile, but with a large change in the longest quantile (e.g., Figure 2). If instead the whole distribution shifted (i.e., all quantiles slowed or speeded up equally), the model would fail. Third, if it is assumed that a speed/ accuracy manipulation affects only the boundary separation parameter, this must be reflected in a moderate increase in the .1 quantile (e.g., 100 msec) for the accuracy condition relative to the speed condition and a large increase in the .9 quantile (e.g., 500 msec). If the data showed a large shift in the position of the whole distribution, the model would fail, or it would have to be assumed that some other parameter (e.g., T_er) is affected by the manipulation. For examples of other patterns that cannot be fit by the diffusion model, see Ratcliff (2002).

After working with the sequential sampling class of models for some time, we find that intuition can often be wrong. Sometimes it seems obvious that a pattern of data cannot be accommodated by the model, but after application of the model, it turns out that the data are fit in an unexpected way. Conversely, although a set of data might be qualitatively consistent with the behavior of a model, it is only when the model has been fit to the data that it is possible to say that the model can fit the data. This is because the model may fail to fit quantitatively.

Limitations

In this section, we will present a discussion of the limitations on what this article has accomplished. We will discuss when the tables can be used in assessing standard errors in parameters, what needs to be done when the experiments involve more conditions than are presented above, what happens if the assumptions about contaminants or variability in T_er are not correct, and what patterns of data can make the diffusion model fail.

1. The tables of means and standard deviations presented in this article assume that the number of observations is the same for each condition in an experiment. For cases in which the number of observations per condition is the same across conditions but the number differs from those presented here, the standard deviations can be scaled by the square root of N. However, if numbers of observations differ substantially across conditions, new simulations will be required to compute values of standard deviations.

2. The values of the standard deviations in the tables cannot be used when the experiments deviate a lot from those that are mimicked in our simulations, but there are some generalizations that can be made. In our simulations, each set of fits of the model to Monte Carlo data presented in the tables represents experiments in which four conditions are tested with one set of boundaries, one value of T_er, and one value of the between-trial variance parameters. The four drift rates represent the experimental conditions, which might represent number of repetitions of a stimulus in a memory experiment or several levels of stimulus intensity in a perceptual experiment. But in some experiments, subsets of parameters might be kept constant across blocks of trials, and others might be allowed to vary. For example, if we vary speed-accuracy instructions between blocks of trials, only boundary settings might be expected to change between speed and accuracy conditions, and all other parameters, including T_er and drift rates, might be expected to be the same. For model fitting, it is first necessary to find out what the reasonable hypotheses are and, second, to fit the model to the data, keeping all other parameters constant. The results in the tables for standard deviations cannot be used to provide estimates for the standard deviations for experiments like these. However, from our experience, to a rough approximation, the standard deviations in the tables can be scaled by the total number of observations. So, for instance, if there are N observations per condition for speed trials and N observations for accuracy trials, a rough scaling factor (for drift rates, T_er, and variance parameters) is the square root of 2N instead of N in the first point in this section.

To determine whether speed and accuracy trials can be fit with the same parameter values, allowing only boundary separation to change, we recommend the following procedure (Ratcliff & Rouder, 1998). First, perform separate fits to the data for the speed and accuracy conditions. Make sure that the only parameter that has a large change between speed and accuracy is boundary separation. Then modify the fitting program to fit the model to both speed and accuracy conditions simultaneously, with only boundary separation changing between speed and accuracy conditions. The same process can be carried out for other manipulations, such as varying the probability of the two responses.

3. Our choices of assumptions for contaminants and T_er are designed to mimic what is likely to occur in real data, but slightly different assumptions should not affect the results significantly. The uniform distribution for T_er was selected because it is a simple distribution with two parameters and probability density is spread across the whole range of values. The distribution is bounded so T_er can never be negative. The distribution of contaminants is selected as one that plausibly mimics long contaminants. Usually, fast outliers can be brought under experimental control by punishing subjects with a time delay when they produce a fast outlier (although having a few fast outliers does not affect the chi-square fitting method). But if fast outliers are part of what is being examined in the experiment, different assumptions could be made about contaminants, and they could be explicitly modeled and included as part of the fitting program.

4. There are limitations on the quality of data to be used in fitting the diffusion model. Averaging over subjects or sessions can be a problem, because performance can change from session to session and different subjects can produce different patterns of data. In examining data prior to model fitting, it is necessary to determine whether the patterns of results are different across subjects or across sessions for individual subjects. For example, it would not be a good idea to average data from subjects who are fast and accurate with a small proportion of fast errors together with data from subjects who are slower and inaccurate with a large proportion of slow errors (this pattern occurs in the lexical decision task; see Ratcliff et al., 2002). This would lead to an average that was not representative of either type of subject. If subjects show different patterns from each other, their data can be combined into subgroups that show similar patterns and averaged.

Recommendations

Our recommendation for fitting the diffusion model to data is to use the chi-square method with the corrections for contaminants and variability. In preparing data for fitting, cutoffs for fast and slow responses should be used. This reduces both starting point variability and the proportion of slow outliers. Also, the data from all the subjects should show the same patterns across experimental conditions. If the plots of the quantile probability functions for predictions and data miss each other, the weighted least squares method should be used to see whether an adequate fit can be obtained (keeping in mind that this will generally not produce accurate estimates of the parameter values). If the weighted least squares method produces a reasonable fit, the chi-square method may be failing because some of the assumptions are not correct (e.g., assumptions about contaminants). Then an attempt should be made to modify or add assumptions to the chi-square method to match hypotheses about what kinds of contamination there might be in the data.

A number of issues of general importance emerge from our investigation of fitting methods. We have shown how, from Monte Carlo studies, it can be determined whether estimates are biased, how large their standard deviations are, whether the estimates’ distributions are normally distributed or not, and whether there are tradeoffs (correlations) among parameters. It can be determined whether the accuracy and standard deviations of the estimates vary as a function of sample size and whether data averaging or grouping introduces biases into the estimates. If a model fails to fit experimental data, we have illustrated how investigations can be undertaken to determine whether the miss is the result of contaminants or whether it might be the result of minor misspecification of the model (e.g., in our case, failing to include variability in T_er). If a model fails to fit a set of experimental data, it is necessary to determine whether this is a failure of the fitting method because of violation of assumptions or a failure of the model. If it were a violation of assumptions in the fitting method, it would be necessary to understand how contaminants or misspecifications affect parameter estimation over a range of parameter values. Then a choice could be made about whether to try to model contaminants or eliminate them or to try to modify assumptions to deal with misspecifications. A check on the new model or fitting method would be to generate Monte Carlo data that have no contaminants and no misspecifications, to make sure that the fitting program could recover the parameter values used to generate the Monte Carlo data. It might also be important to compare more than one fitting method for the same data set, because as we have shown here, different fitting methods can have different properties, so that one fails where the other succeeds.

The diffusion model and other stochastic models (the Ornstein Uhlenbeck model, Busemeyer & Townsend, 1993, and Smith, 1995; accumulator models, Smith & Vickers, 1988, and Vickers, 1970) are currently the only models capable of fitting the range of correct and error reaction times, response probabilities, and reaction time distributions (see Ratcliff & Smith, 2002). At this point in the evolution of this class of models, goodness-of-fit and model-fitting methods have taken a back seat to the problem of finding a model that is capable of fitting all aspects of the experimental data. But as the models evolve and are evaluated, fitting methods and goodness-of-fit measures will become important.

APPENDIX

APPENDIX A

Properties of Estimators

In this article, we are concerned with estimating the unknown parameters of a set of statistical distributions produced from the diffusion model (reaction time distributions for correct and error responses for several experimental conditions). Key concepts of statistical estimation theory that underlie our methods are presented here. We draw a distinction between an estimator (the rule or the estimation method used to determine the unknown parameter’s value from a sample) and the estimate (the assigned value that results from applying the estimator). Standard references in the statistical literature on estimation are Kendall and Stuart (1967) and Lehmann (1983). A summary of the basic ideas of estimation theory can also be found in most advanced introductions to mathematical statistics (e.g., Silvey, 1975).

No estimation method succeeds in recovering the true parameter value from any arbitrary sample of a distribution, and therefore, we want estimation methods that are “as good as possible.” To assess the performance of an estimation method, five features need to be considered: (1) unbiasedness, (2) variance, (3) efficiency, (4) consistency, and (5) robustness.

Unbiasedness and variance refer to the performance of an estimator when a sample of the same size is repeatedly drawn and used to estimate the unknown parameter (these are called small-sample properties because they are concerned with properties when the sample size is finite). If the mean of a large number of estimates from the same population coincides with the parameter’s true value, the estimator is said to be unbiased, because on average, the estimator estimates the true value. The variance of the estimates represents how tightly the estimates are clustered around the mean. If we have two estimators that are unbiased, the one with the smallest variance is called the most efficient one of the two.

In simple cases, such as estimating the mean of a normal distribution by using the sample mean, it is straightforward to derive the distribution for the estimator and assess its unbiasedness and variance analytically. However, this is an almost impossible task for the diffusion model, and so we use a Monte Carlo simulation method. We draw a number of samples from the model, estimate the parameters, and determine bias and variance (or standard deviation) in the estimates.

The consistency of an estimator is a large-sample property because it describes how the estimator behaves when the sample size becomes infinitely large. If an estimator is consistent, the estimate it produces should converge to the true parameter value as sample size increases. Consistency has been proved in mathematical statistics for many estimators under rather general assumptions. However, as will be explained later, these assumptions are not valid in the case of the diffusion model, and this is another reason we rely on simulation methods, increasing sample size to assess consistency.

Robustness describes how sensitive an estimator is to contaminated data. Whenever contaminants are likely or even possible, robustness is desirable. Simulation studies allow us to determine the robustness of our estimation methods by introducing contaminants and observing their effects on parameter estimation.

For the three methods we investigated, none of them performs uniformly the best on all five criteria, because they are often involved in tradeoff relations. As an analogy, in estimating the mean of a normal distribution, the mean has lower variance than the median, but the median is more robust to contaminants than the mean. The same applies, but much more complexly, to our fitting methods. Also, although some aspects of our methods have been investigated theoretically in statistics, it has usually been only under restricted conditions, conditions that are not met under the practical considerations of empirical data. In the next paragraphs, we will spell out what aspects of our methods meet the restrictions and what aspects do not.

The use of the maximum likelihood method is usually motivated by three properties of its estimates (under some mild regularity conditions; see Lehmann, 1983). First, although for small samples, maximum likelihood estimates may be biased, they are consistent. Second, maximum likelihood estimates have an asymptotic normal distribution with a parameter’s true value as its mean. Third, maximum likelihood estimates are asymptotically the most efficient estimators, because the asymptotic variance attains a lower bound and no other estimator has a smaller asymptotic variance.

However, for the diffusion model, the standard proofs that these properties hold do not apply. This is because an important regularity condition required to show that the maximum likelihood method has the three properties is that the range of possible values of the data that can be observed under the model (technically, this is called the support of the distribution) is independent of the model’s parameters. For the diffusion model, the lowest possible observable response time is T_er, which is a parameter of the model, and so this violates the regularity condition. This does not mean that it is impossible for the diffusion model parameters to be consistent; it means that other ways of proving the result must be found, but that is generally a difficult task (e.g., such a proof has been achieved for the diffusion model with only one absorbing boundary, the shifted inverse Gaussian distribution; see Cheng & Amin, 1981).

The asymptotic variance for a maximum likelihood estimate can be computed by taking the expectation of the second derivative of minus the log likelihood and inverting the quantity. In practice, the asymptotic variance is often approximated just by evaluating the second derivative at the maximum likelihood solution and inverting it, without considering the expectation. In the multidimensional case (more than one parameter), the second derivatives of minus the log likelihood are taken with respect to all the parameters (including cross terms), and the resulting terms are placed in a matrix that must then be inverted. Because the expressions for the diffusion model have no closed form solutions, numerical methods would have to be used to approximate the second derivatives. This would be a cumbersome task. Therefore, we have chosen instead to use Monte Carlo estimates to approximate the variances.

The other methods used in this article, the minimum chi-square and the weighted least squares methods, both involve grouping reaction time data. This leads to a loss of information, relative to the case in which all individual observations are used (as in maximum likelihood). The chi-square estimation method is consistent and asymptotically as efficient as the maximum likelihood method, and its estimates are normally distributed (Neyman, 1949; Rao, 1973). But the asymptotic efficiency of this estimator is relative to other estimators that use the same degree of grouping of the data (which means that it is asymptotically as efficient as a maximum likelihood method applied to group data, but not to a maximum likelihood method that uses ungrouped data). We show in our Monte Carlo studies that in the diffusion model case, the maximum likelihood estimator that uses ungrouped data has a higher efficiency than the chi-square and weighted least squares methods that use only grouped data.

The weighted least squares method minimizes the squared deviation between empirical and predicted values for reaction time quantiles and response probabilities for each experimental condition. We could find no investigation in the statistical literature of the weighted least squares method applied to quantiles. However, when sample size increases, the sample quantiles converge to their true values, and it is reasonable to assume that the parameters estimated from these quantiles also converge to their true values (note that with 250 observations per condition, the sample was too small for the quantiles to converge to their true values). However, exact results are difficult to obtain, and it is unlikely that the weighted least squares method is as efficient as the other two methods. In our Monte Carlo simulations, the weighted least squares method was a little less efficient than the chi-square method; for some reasons for this, see our discussion of limitations of our implementation of weighted least squares in the body of the article.

There have been some studies of the relative amount of (asymptotic) information (or efficiency) that is lost when going from ungrouped to grouped data (e.g., Haitovsky, 1989; Lindley, 1950). The ratio of the asymptotic variance of an estimate based on the ungrouped data and the asymptotic variance based on grouped data gives the percentage of information loss owing to the grouping. The results from these studies are only marginally relevant for our application, because only simple distributions and, mostly, one-parameter problems have been studied. However, to give an idea of the percentage of increase in the asymptotic variance introduced by grouping, consider the estimation of the mean of a normal distribution with the variance known. In this case, grouping into six classes of equal probability leads to a loss of information of 8%. For an estimate of the variance if the mean is known, the information loss doubles to about 16%. Our results from the diffusion model show a typical information loss of about 50%, owing to grouping in the chi-square and weighted least squares methods, relative to the maximum likelihood method without grouping. Thus, grouping is likely responsible for some of the loss of efficiency of the chi-square and weighted least squares methods, relative to the maximum likelihood method, which uses ungrouped data.

Heathcote et al. (2002) have proposed a maximum likelihood method, the quantile maximum likelihood method, that uses grouping. There is a direct connection between this method and the chi-square method examined in this article. With even moderate size samples (e.g., the same size as in the simulations in this article), the two methods give almost identical results, because maximizing the multinomial likelihood is essentially the same as minimizing a modified chi square. The modified chi square is defined as the sum over (O − E)²/O (note the observed value, O, instead of the expected value, E, for the regular chi square, in the denominator), and the large-sample equivalence of the two methods to each other has been proved in Jeffreys (1961, pp. 196–197). Furthermore, Neyman (1949) showed that the minimization of the modified chi-square function gives the same results as the minimization of the regular chi square in large samples (see also Jeffreys, 1961). We performed fits, using the simulated data generated from the parameter values in Table 1, and found that the regular chi-square and the quantile maximum likelihood methods produced the same parameter values to within 1% for each individual simulated data set.

Perhaps the main conclusion from this discussion of properties of estimators is that we want to use estimators that have the best balance of the five properties that we listed above. Although there are proofs that establish desirable properties in many situations, there appear to be no proofs that establish all of the properties for application of the diffusion model. Even if this was done, it would probably not apply to cases with contaminants. For this reason, we examine the properties of the estimators by using Monte Carlo methods.

APPENDIX B

Fitting the Diffusion Model

The key quantity to be computed in fitting the diffusion model to data is the cumulative distribution (cumulative probability of a response) at any time t. This represents the proportion of processes that have terminated by t. We distinguish between the cumulative distribution (or cumulative probability distribution, or the conditional cumulative distribution), in which as t tends to infinity, the value of the distribution function approaches 1, and the defective cumulative distribution, in which as t tends to infinity, the value of the distribution approaches the probability of the correct or error response, depending on the condition.

From the theoretical defective cumulative distribution, predicted values for the density, the accuracy, and the predicted quantile reaction times can be computed. From the values of quantile reaction times obtained from data, the theoretical cumulative probabilities can be computed at those times, and differences between successive theoretical cumulative probabilities can provide the expected values for the proportion of responses between the quantile reaction times. In our model fitting, the maximum likelihood method requires the theoretical defective probability density, the chi-square method requires the expected proportion of responses between the quantile reaction times, and the weighted least squares method requires predicted accuracy and quantile reaction times.

In what follows, we will show schematically how to build a computer program to produce the defective cumulative distribution function and then will outline how to compute the other quantities that the fitting methods need. We begin with the simplest case with no variability in the parameters across trials and then add variability in the parameters one at a time.

The parameters of the basic model are as follows. The boundary separation is a, the starting point is z, and the drift rate is ξ. The parameter s is what is called a scaling parameter. This means that if it were doubled in size, the other parameters of the model could be adjusted (doubled) to produce exactly the same predicted values. The s is set to 0.1 for consistency with fits of the model to data in other articles. The value of the defective cumulative probability at time t, G(t,ξ,a,z) (see Feller, 1968; Ratcliff, 1978), is given by

$$G(t,\xi ,a,z)=P(\xi ,a,z)-\frac{\pi s^2}{a^2}{e}^{-(\xi z/s^2)}\times {\displaystyle \sum _{k=1}^{\infty }\frac{2k\text{sin}(k\pi z/a)e^{-\frac{1}{2}({\xi }^2/s^2+{\pi }^2{k}^2{s}^2/a^2)t}}{({\xi }^2/s^2+{\pi }^2{k}^2{s}^2/a^2)},}$$ (B1)

where

$$P(\xi ,a,z)=(e^{-(2\xi a/s^2)}-e^{-(2\xi z/s^2)})/e^{-(2\xi a/s^2)}-1)$$ (B2)

and P(ξ,a,z) is the probability of a response at the bottom (zero) boundary in Figure 1. [Note that the cumulative probability distribution equals the defective cumulative distribution, divided by P(ξ,a,z)].

Equation B1 shows the expression for the defective cumulative distribution for no variability in the values of drift rate, starting point, or nondecision component of reaction time. In a computer program, the value of P(ξ,a,z) can be computed in one line, and the value of G(t,ξ,a,z) is computed in a small loop. The first problem to face is that the sum in Equation B1 is an infinite sum and the terms start off large and get smaller as k increases. (As k increases, the exponent of the exponential term becomes a larger negative number, and so the exponential term tends to zero. Also, on the bottom line of the equation, the second term involves k squared, so as k increases, the reciprocal of the term tends to zero.) The standard way to compute such a sum is to compare each term to the previous sum and terminate when the term becomes so small that it and following terms do not change the sum. The major fly in the ointment is the sine term on the top line of the equation. This causes the value of the product to oscillate (and not monotonically decrease), and so any term can be close to zero. Thus, monitoring each term in the sequence and terminating the sum if the term is less than some tolerance (e.g., the current sum multiplied by 10⁻²⁹) may terminate incorrectly, because the sine part of the expression reduces the term to near zero and the next term term may be higher than the tolerance. To avoid this problem, on each iteration of the sum, we checked both the current term and the previous term to see whether they were both less than the tolerance. If they were both less than 10⁻²⁹ times the current sum, we terminated the sum. All the computations in our programs are carried out in double precision.

At this point, we have the defective cumulative probability of the model with fixed values of the parameters across trials. To deal with variability across trials, we need to integrate over distributions of the parameter values (z, ξ, and T_er). This is quite simple using numerical integration subroutines. A numerical integration routine is typically given the function to be integrated and the limits of integration. We first present integration over drift rate, ξ, where drift rate is assumed to be normally distributed across trials, with mean v and standard deviation η:

$$G_1(t,v,a,z,\eta )={\displaystyle \underset{-\infty }{\overset{\infty }{\int }}G(t,\xi ,a,z)\frac{1}{\sqrt{2\pi {\eta }^2}}{e}^{-\left(\frac{{(v-\xi )}^2}{2{\eta }^2}\right)}d\xi .}$$ (B3)

In programming this integration, we first have a subroutine that produces the value of G(t,ξ,a,z), given the input parameters and t (i.e., an implementation of Equation B1). The value of G is multiplied by the normal distribution density (as in Equation B3), and the quantity within the integral (in Equation B3) is provided to the integration routine (we used Gaussian quadrature) along with the limits of integration (we used −4η to + 4η).

The result of this integration is a value of G₁ for input parameter values and t. Next, we integrate over the distribution of the starting point (assumed to be uniform with mean z and range s_z). This can be done in exactly the same way for G₁, using the density for the uniform distribution [f(x) = 1/s_z for z − s_z/2 < x < z + s_z/2 and zero outside this range] instead of the density for the normal distribution. This will produce a value of G₂ given values of the parameters and t [G₂(t, v, a, z, η, s_z)].

The equations for the cumulative distributions so far assume that time begins at zero—that is, T_er equals zero. To introduce a nonzero value for T_er into the expression for Equation B1 (for example), each occurrence of t would be replaced by t − T_er. Then t would refer to reaction times with a nondecision component equal to T_er. The final step is to integrate over the uniform distribution of values of T_er [f(x) = 1/s_t for t − T_er − s_t/2 < x < t − T_er + s_t/2 and zero outside this range]. [When the value of x is less than zero, the value of f(x) is set equal to zero.] This produces a defective cumulative distribution function, F(t,v,a,z, η, s_z, s_t, T_er), which is used for modeling. This provides the basis for generating predictions from the model (e.g., given a best-fitting set of parameter values, generate the mean reaction times, accuracy values, distributions, etc.).

To fit the model to data, a minimization routine is used (Ratcliff used SIMPLEX; Nelder & Mead, 1965), which takes a set of initial parameter values and adjusts them to minimize the objective function (e.g., sum of squares or chi square). The SIMPLEX routine computes the M + 1 values of the function where each value is obtained from parameter values that are slightly different from the input values, where M is the number of parameters. The method finds the largest value of the objective function among the M + 1 and alters the parameters for that objective function to produce a smaller value of the objective function (using simple rules for adjusting parameters). Then the next highest value of the objective function is selected, and the parameters are adjusted for that function. This process continues until an accuracy criterion is reached (e.g., the objective function changes by less than the critical value in 20 iterations) or the parameters do not change (e.g., by less than some fraction of their value in 20 iterations). The minimization routine has an initial set of parameter values input (if these are far away from the best-fitting values, the program can terminate with an error). The value of the objective function is computed in a subroutine given the current set of parameter values in the search, and the value of the objective function is returned to the minimization routine.

For the maximum likelihood method, the density at time t has to be obtained. The defective cumulative distribution F needs to be converted to a cumulative probability distribution (F₁) so that the probability density integrates to 1. This is done by dividing F(t) by P, the probability of a response [computed by integrating P(v,a,z) over drift, starting point, and T_er, as for F above]. A numerical value of the density can be found easily using the approximation f(t) = [F₁(t + dt) − F₁(t)]/dt. In Ratcliff’s programs, a value of 0.5 msec was used for the value of dt.

Tuerlinckx’s approach differs somewhat from Ratcliff’s because it starts from the density function g(t,ξ,a,z), rather than from the cumulative distribution function G(t,ξ,a,z) (Equation B1). The density can be easily obtained by calculating dG(t,ξ,a,z)/dt. Then, g₁(t,v,a,z,η) is found by integrating over the drift rate ξ by completing the square in the exponent term. The explicit integration avoids the numerical integration over the drift rate used by Ratcliff [but we could not obtain an explicitly integrated G(t,ξ,a,z) over drift rate]. We could not find an explicit solution for the integration of g₁ over the distribution of the starting point and T_er; hence, these two integrals were approximated numerically as described above (but with the cumulative distribution function replaced by the density function).

To compute the likelihood, for each reaction time t_i, f(t_i) is computed for the current set of parameter values. For error responses, the parameters are changed so that z = a − z and drift rate v is replaced with drift rate −v (to turn the top boundary into the bottom boundary for computing the distribution function), and f(t_i) is computed in the same way.

For the chi-square method, the value of F₁(t_q) needs to be computed for each of the quantile reaction times t_q for each condition. For the .1, .3, .5, .7, and .9 quantiles (q), the observed cumulative probabilities are .1 (up to the .1 quantile), .2, .2, .2, .2, and .1 (after the .9 quantile). The expected values are F₁(t_.1), F₁(t_.3) − F₁(t_.1),…,1 − F₁(t_.9), which are then multiplied by the theoretical response probability for that condition and the sum of the number of correct and error responses in that condition to give the expected values. These then are entered into the expression for chi square Σ(O − E)²/E (where E = expected value and O = observed value).

For the weighted least squares method, estimates of the quantile reaction times have to be produced. To do this, the cumulative distribution function is generated in 5-msec steps for times starting at T_er and ending at some upper limit, such as 2 sec. Then the quantile reaction times are computed by linear interpolation (for the .1 quantile, the time corresponding to .1 cumulative probability is computed). Because the whole distribution function has to be computed, 300 or 500 evaluations of the cumulative probability have to be performed for each correct and each error response. This is 60–100 times more than the chi-square method and similar to the number of evaluations needed for the maximum likelihood method with N = 300–500 observations per condition.

The following are schematic code fragments that show the logic of a program to fit the diffusion model using the chi-square method. The language actually used is Fortran, so the code fragments are in Fortran-like style.

• subroutine G(outg,t,v,a,z)

• Loop over k

• sum = sum+…*sin(…)*exp(…)     (see Eq. B1)

• check if this term and prior term less than 10⁻²⁹*sum

• end loop over k

• P=(exp(…)−exp(…))/exp(…)−1)     (see Eq. B2)

• outg=P−…*sum   (see Eq. B1)

• end

• function Gv(t,v,a,z,η)

• call G(…)

• Gv=outg*((1/sqrt(…))exp(−…)     (see Eq. B3)

• end

• G1 = integrate-routine(Gv,lowerlimit,upperlimit)

• function Gz(t,v,a,z,η,s_z)

• Gz=G1*(1/s_z)

• end

• G2=integrate-routine(Gz,lowerlimit,upperlimit)

• function Gt(t,v,a,z,η,s_z,s_t,T_er)

• Gt=G2*(1/s_t)

• end

• F(t,v,a,z,η,s_z,s_t,T_er) = integrate-routine(Gt,lowerlimit,upperlimit)

This last line computes the value of the defective cumulative probability, F, as a function of time (t) and the parameters of the model (v, a, z, η, s_z, s_t, T_er).

In these schematic code fragments, subroutine G produces the value G in Equation B1, and the value is placed in variable outg. Function Gv assigns the integrand in Equation B3 (outg times the normal density) to the variable Gv. The integration routine then calls Gv to get values of the integrand and integrates this from the lower to the upper limit (e.g., −4η to 4η) and assigns the value to G1. The function Gz produces the integrand as a function of z, and G2 is the value of the integral over z. The function Gt produces the integrand as a function of T_er, and finally, F is the value of the integral over T_er. F is a defective cumulative distribution function, and the cumulative distribution function, F₁, is given by F/F(t = ∞) [F(t = ∞) is identical to the result of integrating P over drift, starting point, and T_er as for F].

To model contaminants with a probability of p_o and a range of t_min to t_max, the new cumulative probability at time t is given by F_p = (1 − p_o)F₁(t)+p_o(t − t_min)/(t_max − t_min).

The data and the function F are used to produce a value of likelihood, chi square, or weighted least squares, which is then placed in a minimization routine such as SIMPLEX.

The main program has the following core components:

• Initial values of the variables:

• x(1)=a

• x(2)=z

• …

• Simplex criterion=1.0E-10 (plus other control values such as maximum number of iterations)

• …

• call simplex(x,fun,…control…)

• print,x

• (the best fitting parameters.)

• end

Below is the function to return the value of chi square (for example), given the initial parameter values stored in the array x, and given the routine to compute cumulative probabilities F(t) (and given the data: quantile RTs, response probability, number of observations).

• function fun(x,nparams)

• read in data: rtq(i), prob, N for correct and error responses, where rtq is an array of RT quantiles, prob is the response probability for that condition, and N is the number of observations.

• form chi square using F and the data:

• Expected frequency for correct responses between 0 and the .1 quantile

• = F(rtq(1))*N,

• Observed frequency is .1*prob*N

• Expected frequency for correct responses between the .1 and .3 quantiles

• = F(rtq(2))-F(rtq(1))*N,

• Observed frequency is .2*prob*N

• (etc. for the other quantiles)

• chisq5sum((O-E)²/E)

• fun=chisq

• end