Skip to main content
NCBI home page
Proceedings of the National Academy of Sciences of the United States of America logoLink to Proceedings of the National Academy of Sciences of the United States of America
. 2008 Jul 18;105(30):10390–10395. doi: 10.1073/pnas.0802496105

Insights into protein flexibility: The relationship between normal modes and conformational change upon protein–protein docking

Sara E Dobbins 1, Victor I Lesk 1, Michael J E Sternberg 1,*
PMCID: PMC2475499  PMID: 18641126

Abstract

Understanding protein interactions has broad implications for the mechanism of recognition, protein design, and assigning putative functions to uncharacterized proteins. Studying protein flexibility is a key component in the challenge of describing protein interactions. In this work, we characterize the observed conformational change for a set of 20 proteins that undergo large conformational change upon association (>2 Å Cα RMSD) and ask what features of the motion are successfully reproduced by the normal modes of the system. We demonstrate that normal modes can be used to identify mobile regions and, in some proteins, to reproduce the direction of conformational change. In 35% of the proteins studied, a single low-frequency normal mode was found that describes well the direction of the observed conformational change. Finally, we find that for a set of 134 proteins from a docking benchmark that the characteristic frequencies of normal modes can be used to predict reliably the extent of observed conformational change. We discuss the implications of the results for the mechanics of protein recognition.

Keywords: conformational selection, elastic network model, induced fit, protein interactions, protein recognition

Proteins are not static, and many undergo substantial rearrangements upon binding to other molecules (1). Such changes are central to protein function (2). The limitations of our understanding of conformational change impact markedly on our ability to model such changes. A successful approach to modeling protein flexibility, one of the key current challenges in developing protein–protein docking algorithms, would have far-reaching consequences for the fields of drug design and function prediction.

The initial lock-and-key description of protein interaction, first introduced by Fischer in 1894 (3), did not account for conformational change and has since been modified, beginning with Koshland's induced fit hypothesis in 1958 (4). However, a range of studies including molecular dynamics (picosecond–nanosecond time scales), NMR, and single-molecule FRET experiments (microsecond–millisecond time scales) (5–7), have questioned the extent to which conformational change can be considered induced by the binding partner.

An alternative mechanism is conformational selection, where the native state of the protein exists in an ensemble of conformations, with the partner binding selectively to a specific conformation, thus shifting the equilibrium toward the binding conformation (8). An elaboration, proposed by Grunberg et al. (9), describes a three-stage process consisting of (i) independent diffusion of the receptor and ligand each subject to conformational fluctuations, (ii) an encounter between the receptor and ligand leading to a series of microcollisions that may result in the formation of a recognition complex, and (iii) either dissociation of the encounter complex or formation of the bound complex with possible further conformational changes resulting from induced fit. An important question to address is, therefore, to what extent the intrinsic thermal motion, rather than induced fit, is responsible for conformational change.

Here, we use normal modes, which are related to the thermal motion of individual proteins, to gain insights into the nature of conformational change in protein–protein interactions. The model used to calculate the normal modes considers Cα atoms only; thus, the conformational change we predict is associated with backbone, and not side-chain, motion. We explore features of the observed conformational change for a set of proteins and contrast these with features of motion predicted by normal-mode analysis (NMA). Specifically, for a set of 20 protein structures [taken from the protein–protein docking benchmark 2.0 (10)] that are observed to undergo large conformational change upon complexation, we assess the success of normal modes at locating mobile regions and describing the direction of conformational change. Then, for a large benchmark set of proteins with diverse conformational change, we show that normal-mode analysis can provide a powerful guide as to whether a protein will undergo substantial conformational change upon association. This information would be useful to the protein docking community, which at present can consistently predict only the interactions of fairly rigid proteins correctly (11). Our protocol will allow the assessment of whether a rigid-body approach to docking is likely to be successful. Finally, insights gained into the dynamics of proteins are interpreted within the framework for protein recognition.

NMA.

Normal modes of vibration are simple harmonic oscillations characterizing the dynamics of the system around an energy minimum (12). Each mode describes a state of the system where all particles are oscillating with the same characteristic frequency. The dynamic behavior of most systems of physical interest may be approximated by a linear combination of normal modes.

NMA has been used for more than three decades to study protein flexibility, with early work focusing on β-polypeptides (13), glucagon (14), and trypsin inhibitor (15–17). Historically, NMA was hindered by the mathematical form of the Coulombic and van der Waals potentials. However, a framework proposed by Tirion (18), where the standard potential was replaced by a simple pairwise Hookean potential between atoms within a specified connectivity cutoff Rc of each other, has proved accurate in reproducing normal modes. The success of this elastic network model indicates that motions predicted by NMA are robust to the models and force fields used.

NMA has many limitations such as use of the harmonic approximation, neglect of solvent damping, and an inability to model energy barriers and multiple minima (19–21). Furthermore, the trajectory of protein motion will rarely be in a straight line, and therefore an otherwise correctly predicted initial direction of motion might deviate noticeably from the observed conformational change (22). Despite these limitations, many studies have found agreement between features of the motion predicted by NMA and the observed or simulated conformational change of one or a small number of proteins (23–30). A number of large-scale studies have assessed the success of normal modes at describing protein motion as defined by the database of macromolecular movements (31). The database identifies putative motions if two or more substantially different structures are available from the Protein Data Bank (PDB). Tama et al. (32) found that, for half of the 20 proteins studied, there was a single mode, most often one of the lowest three, corresponding substantially with the observed conformational change. Gerstein's group (22, 33) has shown that the observed motion lies most often in the direction of two modes, and that the direction of motion is predicted most accurately for atoms that move the most. A further study has looked specifically at conformational change on association for four protein–protein systems, finding in all cases that the motions predicted by NMA correlate well with the observed conformational change, although in three of the four cases, additional rearrangements, attributed to possible induced fit effects, are required (34).

Recent studies have utilized this agreement between normal modes and observed motion in a number of applications. For example, normal modes have been used in docking refinement, where all six cases in one study showed improvement in RMSD after refinement along 5–10 of the lowest-frequency modes (35) and in flexible docking (36–38), where the success has been more varied. Coarse-grained normal modes have also been shown to be useful for the prediction of functional sites (39).

Theory.

The vectors calculated in NMA describe the direction and relative magnitude of each atom's motion. The overall scale of motion is not defined and depends on the conditions of the system, e.g., temperature. In cases where the range of masses is small, the energetic cost of displacing the system by one unit along its eigenvector depends largely on the frequency of the mode (40). Because each mode is assigned kBT of energy, as dictated by the equipartition theorem, the atomic fluctuations will be greatest for low-energy modes.

The atomic fluctuations are given by:

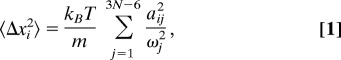graphic file with name zpq03008-3923-m01.jpg

where 〈Δxi2〉 is the time-averaged square displacement of atom i, ωj is the frequency of mode j, aij is the displacement of atom i under mode j, and N is the number of residues (41, 42). All atoms are assigned mass m. Thus, the lower the mode frequency, the larger is its general contribution to the displacement of atoms. This relationship between mode frequency and the range of atomic motion during thermal fluctuations is central to our interpretation.

The RMSD of a protein is taken as the root of the average square displacement over all N Cα atoms. Hypothesizing that conformational change is driven by thermal motion, we can define a measure of predicted RMSD as:

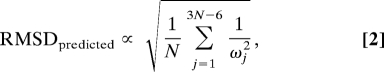graphic file with name zpq03008-3923-m02.jpg

where we have used the normalization condition

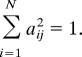graphic file with name zpq03008-3923-m03.jpg

Theoretically, from Eq. 1, the exact magnitude of motion can be defined. However, this would require careful estimation of the spring constant and mass parameters. To avoid this, we consider only relative sizes of mode magnitudes to devise a measure of relative predicted flexibility using the same value for the spring constant for all proteins.

Results

The high-flexibility dataset contains 20 proteins that are observed to undergo large conformational change upon complexation (>2 Å Cα RMSD). Using this dataset, we investigated the extent to which the thermal motion of proteins, as modeled by NMA, could provide insights into the general nature of conformational change.

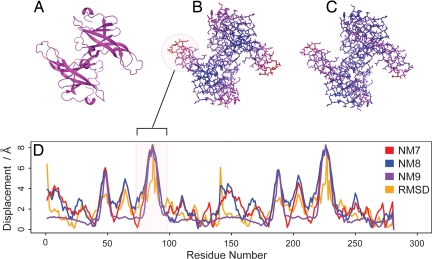
Fig. 1 illustrates the relationship between the observed motion and the motion predicted by NMA for ecotin (1ecz). This profile is typical for a protein where there is good agreement between the low frequency modes and observed conformational change.

Fig. 1.

Fig. 1.

Open in a new tab

Picture of protein inhibitor ecotin (1ecz) as cartoon (A), colored by the amplitude of the lowest frequency mode (with the scale blue to red representing small to large amplitude respectively) (B), colored by extent of observed conformational change upon complexation with trypsin (with the scale blue to red representing small to large displacement, respectively) (C), and amplitude of the three lowest frequency (nontrivial) modes and observed conformational change amplitude along the length of the protein (D).

Global Features of Conformational Change.

The observed RMSD upon complexation for the high-flexibility dataset varies between 2.1 and 14.1 Å, with an average of 3.8 Å. The RMSD measured over the binding-site atoms is, on average, 1.2 times that measured over the entire protein. Ten proteins were characterized by the software DynDom (25, 43) as undergoing dynamic domain deformation implying quasi-rigid body motion between domains. DynDom's definitions often coincided with structural definitions of domains based on interresidue contacts (44). DynDom did not assign domain definitions for the remaining 10 proteins.

The collectivity (K) of observed motion, which reflects the number of atoms moving together, varies from 0.07 to 0.75, with an average value of 0.45. A low collectivity might characterize a small loop movement, compared with large-scale concerted movement for those proteins with high collectivity. A correlation of 0.65 is found between the observed collectivity and that predicted by the lowest frequency mode (P value 0.002). Furthermore, the average values for the observed and predicted collectivity are 0.40 and 0.38, respectively. Thus, the low frequency modes are not overestimating the collective character of observed motion.

Particularly low collectivity for the lowest mode is observed in four proteins. Closer inspection of all four reveals that the predicted motion is localized to weakly connected terminal regions. Excluding these proteins increases the correlation to 0.79. A additional three of the remaining four proteins where the predicted and observed collectivity differ by >40% contain missing residues, which are likely to prejudice the predicted or observed collectivity.

Location of Conformational Change.

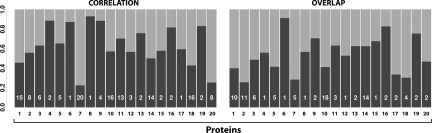
The correlation function Cj measures the agreement between the locations of displacements of the conformational change and the mode j (see Fig. 2). The average Cj for the lowest mode is 0.35, rising to 0.63 if one takes the maximum Cj of the lowest 20 modes for each protein. For 12 proteins, the Cj for the lowest mode is >0.2; assuming normality and independence, a correlation of >0.2 is highly significant for a 200-residue protein (t test).

Fig. 2.

Fig. 2.

Open in a new tab

Plots of maximum correlation (Cj) and overlap (Oj) for the high-flexibility dataset. Both quantities were calculated by using all residues assessing the lowest 20 nontrivial modes only. The mode number (with which the maximum correlation/overlap is found) is printed in the bar for each protein.

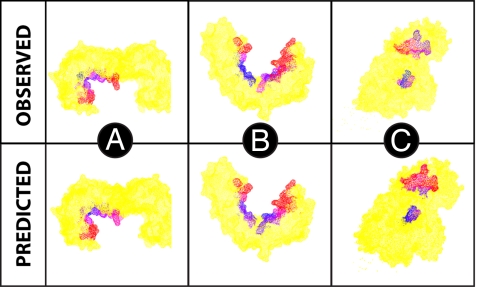
The mobility over the binding site was investigated for both the observed motion and that predicted by normal modes. In many proteins, the binding site was observed to have both rigid and highly flexible regions. Fig. 3 compares the observed motion over the binding with the motion predicted by NMA for three sample proteins. Splitting the binding site into core and periphery residues, we find that for five of the proteins, the observed motion of the peripheral residues is more than twice that of the core, in agreement with other studies (45, 46).

Fig. 3.

Fig. 3.

Open in a new tab

Proteins 14-3-3 protein ζ/δ (A), importin-β-FXFG nucleoporin complex (B), and horse plasma gelsolin (1qjb, 1f59, and 1d0n, respectively) (C). The protein is colored in yellow except for the binding site, which is either colored by observed conformational change or relative amplitude of normal-mode motion. The scale blue to red represents small to large displacement, respectively.

Describing the Direction of Motion.

The overlap Oj measures the agreement between the direction of the conformational change and mode j. The average Oj of the lowest mode is 0.24, rising to 0.54 if one takes the maximum Oj of the lowest 20 modes for each protein. The maximum Oj over the 20 lowest modes is with one of the lowest three modes in 12 proteins. Seven proteins are found to have an Oj of >0.6 with one of the lowest three modes. These results agree with another study (32) that observed a maximum Oj of >0.6 in the lowest three modes in 7 of 20 proteins. We assessed the significance of our results by comparing the maximum Oj of the three lowest-frequency modes to that of three randomly selected higher-frequency modes. For 85% of proteins, the difference in overlaps was found to be statistically significant at the 95% level. Additionally, the mode with the greatest Oj is also found to be the mode with the greatest correlation Cj for eight proteins.

When considering the binding site only, the average Oj of the lowest mode with the conformational change rises to 0.38, with an average of 0.65 for the maximum of the lowest 20 modes.

The unbound protein structures can be optimally perturbed along a single low-frequency mode to produce an altered structure that is closer to the bound coordinates. For proteins with Oj >0.6 in one of the three lowest modes, applying an optimal perturbation gives an average decrease of 37% in the RMSD with the unbound structure. An additional problem for docking applications would be choosing the “correct” mode; although the maximum Oj of the lowest 20 modes for each protein was, on average, 0.54, this is reduced to 0.43 and 0.36 when considered the average of the best two and best three modes, respectively. However, a study of eight complexes has shown that small improvements in RMSDs can lead to limited improvements in docking performance (47).

Predicting the Extent of Motion.

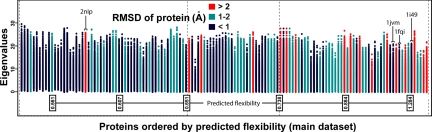
We now focus our attention on the main dataset of 134 proteins and investigate the ability of normal modes to predict the extent of conformational change upon complexation. Fig. 4 shows the full eigenvalue spectrum for each protein in the main dataset plotted in order of increasing predicted flexibility. The striking feature is that the proteins observed as having high flexibility (>2 Å Cα RMSD) are concentrated in the top 40% of the plot. A Wilcoxon rank-sum test shows the predicted flexibilities of the flexible and rigid proteins to be drawn from different populations with a significance value of 0.0003. Thus, we see that low-frequency modes are generally a prerequisite for a protein to undergo a large conformational change. Furthermore, the proteins undergoing substantial conformational change have, on average, a lowest mode whose frequency is 2.5 times lower than those that undergo limited conformational change (<1 Å).

Fig. 4.

Fig. 4.

Open in a new tab

All mode frequencies are shown for each protein in the dataset. Proteins are ranked by predicted flexibility (see Eq. 2). The spectrum for each protein is colored according to extent of conformational change.

This result was found to be robust to varying the connectivity cutoff, with lengths of 8, 10, and 14 Å resulting in similar predictive power. Ranking the proteins by lowest-frequency mode is also highly predictive [see supporting information (SI) Fig. S1].

The cutoffs provided depend on characteristics of the normal mode program, particularly the spring constant. Details of the program and parameters used to produce these plots are given in Materials and Methods. Raw data are supplied in Tables S1–S6.

A correlation might be expected between mode frequency and protein size given that large proteins are more capable of collective motion. In our results, protein size was also predictive of conformational change but less reliably than mode frequency (Wilcoxon test), with proteins undergoing large conformational change found throughout the whole range of possible sizes (Fig. S2). This fact, together with the theoretical basis for mode analysis, has led us to select mode frequencies over protein size for our predictive framework.

An analysis of those proteins with large conformational change shows that there is no significant difference between the distributions of predicted flexibility for those proteins with, and those without, dynamic domains (as defined by DynDom—see Materials and Methods) (Wilcoxon test) i.e., the method is not specifically predicting dynamic domain motion. Although agreement between the conformational change and lowest mode direction (as described by Oj) is better for those proteins with dynamic domains (Wilcoxon test, P value 0.05), no significant difference remains when considering the maximum Oj of the lowest 20 modes.

Three proteins are predicted to be highly flexible but undergo only limited conformational change (<1 Å). For 1jvm (KCSA potassium channel), missing coordinates for some residues in the unbound conformation could have led to over-prediction of mobility. For 1i49 (arfaptin) and 1fqi (regulator of G protein signaling 9), missing coordinates in the bound conformation could have led to an underestimation of true flexibility.

Proteins with multiple interaction partners may display large variation in the extent of conformational change that they undergo with each partner. For example, the RMSD for actin (1ijj), varies between 0.89 and 2.72 for its four interaction partners in the dataset. Because the available repertoire of complexed structures may be incomplete, it is possible that proteins in our dataset that do not follow the trend may follow it in other interactions not included in this dataset.

A single protein with large conformational change, 2nip (nitrogenase iron protein), lies in the lower 40% of the plot for the predicted flexibility. Interestingly the second lowest mode of this protein displays very good agreement with the direction of observed conformational change (Oj = 0.83). This may suggest amplification of the mode during induced fit or even a resonance phenomenon produced by interaction with its large binding partner.

CAPRI Targets.

The critical assessment of prediction of interactions (CAPRI) experiment provides periodic assessment of the protein docking field by using a series of blind targets (48). We apply our method to all suitable CAPRI targets up to target 27. Again, we find that the method is highly predictive with no proteins that undergo large conformational change found in the lowest 45% of the plot (Fig. S3).

Discussion

Our results show that nearly all proteins with observed large conformational change undergo substantial thermal motion in isolation as predicted by NMA. With only one exception, our proteins that have a limited range of thermal motion according to NMA do not undergo substantial conformational change upon association. Thus, large conformational changes, whether due to induced fit or thermal motion, require an appropriate level of intrinsic flexibility.

Our results are consistent with the conformational selection model, which requires proteins that exhibit substantial conformational change upon complexation to be intrinsically flexible. This mechanism is supported by other studies where the unbound protein was found to sample conformations close to the bound form (5–7, 34). However, our analysis shows that for only approximately one-third of the proteins with a large conformational change upon association, do the direction and location of motion along one of the lowest normal modes agree well with the observed conformational change. This suggests that, in the majority of interactions with substantial conformational change, the bound conformation is substantially altered during the final stage of the recognition process.

Our analysis finds that the observed mobility varies over the binding site. This is consistent with work which suggest that the binding site has “dual character” with regard to mobility (49). Other studies have highlighted as relatively immobile catalytic residues (50), hot spots (51), and anchor residues (where certain side chains are found to sample their bound form) (46). Combining these observations, a picture emerges wherein flexible regions that prevent binding due to steric hindrance, traverse recognition-compatible conformations during their low frequency thermal motions. This description suggests a promising avenue for flexible docking by identifying conformational subspaces that are particularly worth searching, namely those traversed by the lowest modes. Furthermore the ability to identify flexible regions allows localized intelligent “softening” of shape complementarity or electrostatic scoring functions.

The results from this work suggest that a composite model is necessary to describe the diversity of conformational change observed during molecular recognition. Here, we provide evidence highlighting the importance of intrinsic thermal motion in the protein recognition problem.

Materials and Methods

Normal Mode Calculation.

The Cα-only elastic network model is implemented with a cutoff of 12 Å by using available software (pdbmat and diagrtb) (52). Details of parameter settings are provided in Tables S1–S6. All point masses are set to the same fixed value (52). The six normal modes that correspond to rigid-body rotations and translations of the system are discarded. Mode vectors are normalized to one.

Definitions.

The binding site is the set of residues containing at least one atom within 5 Å of an atom in the other component in the complex structure. Binding-site residues are split into core and periphery according to relative solvent-accessible area being <10% and ≥10%, respectively.

The conformational change vector Δr is the displacement required to move from the unbound to the bound coordinates after superposing the bound structure on the unbound structure such as to minimize the Cα RMSD.

The correlation Cj of mode j with the observed conformational change is a measure of agreement between the magnitudes of the displacements of the observed conformational change and the mode j (32) and is defined:

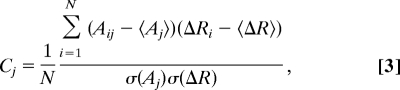graphic file with name zpq03008-3923-m04.jpg

where Aij and ΔRi are the magnitudes of displacement for the ith atom for the jth normal mode and the observed conformational change, respectively. N is the number of atoms. 〈Aj〉 and 〈ΔR〉 represent the average displacements. σ(Aj) and σ(ΔR) represent the corresponding root mean square values.

The overlap Oj describes the similarity between the direction of observed conformational change and the jth normal mode of the protein (29). It is defined:

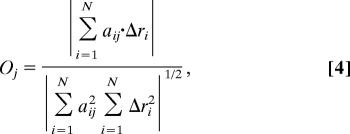graphic file with name zpq03008-3923-m05.jpg

where Δri is the vector describing the observed conformational change between the bound and unbound structures for atom i and aij is the ith atom's displacement in the jth mode. A value of unity means that Δri and aij are in the same direction.

Here, we are comparing a direction valid only in the infinitesimal neighborhood of an energy minimum to one determined by the displacement vector between two experimental structures. For larger conformational changes, errors are likely to be substantial. More sophisticated measures have been developed for considering large rigid-body domain movements where the normal mode vectors are compared with infinitesimal conformational change vectors (53). The conformational changes considered there were, on average, substantially larger than ours, with only 2 of 12 proteins with RMSD <5 Å compared with 17 of 20 in the high-flexibility dataset. Furthermore, their study observed an improvement of <10% for 4 of 12 proteins (cumulative overlap of lowest 12 modes). Because the overlap of only a small number of proteins may therefore have significantly improved, and given the method is applicable only to rigid-body domain motion, we used the simpler methodology.

The collectivity K describes the number of highly mobile atoms for a particular displacement vector and can be calculated for an observed conformational change or as below, to summarize the collective character of a particular mode (54). The collectivity of mode j is defined:

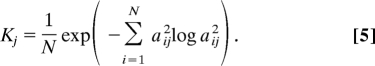graphic file with name zpq03008-3923-m06.jpg

Proteins with Klowest < 0.03 are excluded from the main dataset; the motions associated with these low-collectivity modes are related to weakly connected terminal regions of dubious relevance to the binding process (52).

DynDom.

DynDom requires a set of coordinates and displacement vectors (in this case, calculated by using a least squares best fit of the unbound and bound coordinates). Potential dynamic domains are identified from clusters of rotation vectors; domains are established only if they possess a minimum inter- to intradomain motion ratio (25, 43).

Protein Datasets.

The two datasets of proteins are subsets of protein–protein docking benchmark 2.0 (10). The main dataset is defined as the 134 proteins from the docking benchmark where both unbound and bound structures were available, with those proteins with a very low collectivity mode excluded. The high-flexibility dataset is defined as the 20 benchmark proteins with Cα RMSD >2 Å. This categorization reflects the expected tractability by using current protein–protein docking algorithms (11); specifically, by using an in-house docking program 3D-Garden (55), >80% of proteins with a conformational change >2 Å were not successfully docked (no structure in top 10 of scores within 3.5 Å of theoretically best RMSD). Details of all datasets, along with many results, are found in Tables S1–S6.

The methods presented here are highly sensitive to the quality of the PDB files used in the analysis. We considered excluding proteins with low-quality PDB entries, such as those with missing coordinates in the unbound or bound structures or conflicting biological unit information; ultimately it was too difficult to establish satisfactory inclusion criteria that would leave us with a dataset of sufficient size.

The CAPRI dataset was formulated from all rounds of the CAPRI experiment up to target 27 where the crystal structures have been made publicly available for the bound and unbound structures (excludes target 24). We excluded proteins where the unbound and bound were the same (<0.1 Å RMSD). As before, we excluded those proteins with low collectivity in their lowest-frequency mode.

Supplementary Material

Supporting Information
supp_105_30_10390__index.html (677B, html)

Acknowledgments.

We thank Suhail Islam, Arthur Lesk, and the M.J.E.S. group for insightful comments and suggestions. This work was supported by Wellcome Trust Grant and the Biotechnology and Biological Sciences Research Council.

Footnotes

Conflict of interest statement: M.J.E.S. is a founder director of Equinox Pharma Ltd., holds shares in the company, and has obtained remuneration from the company. Equinox Pharma Ltd. is exploiting computational methods for drug discovery and markets software.

This article is a PNAS Direct Submission.

This article contains supporting information online at www.pnas.org/cgi/content/full/0802496105/DCSupplemental.

References

  • 1.Betts MJ, Sternberg MJE. An analysis of conformational changes on protein–protein association: Implications for predictive docking. Protein Eng. 1999;12:271–283. doi: 10.1093/protein/12.4.271. [DOI] [PubMed] [Google Scholar]
  • 2.Huber R, Bennett WS., Jr Functional significance of flexibility in proteins. Biopolymers. 1983;22:261–279. doi: 10.1002/bip.360220136. [DOI] [PubMed] [Google Scholar]
  • 3.Fischer E. Einfluss der Configuration auf die Wirkung der Enzyme. Ber Dtsch Chem Ges. 1894;27:3189–3232. [Google Scholar]
  • 4.Koshland DE. Application of a theory of enzyme specificity to protein synthesis. Proc Natl Acad Sci USA. 1958;44:98–104. doi: 10.1073/pnas.44.2.98. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 5.Henzler-Wildman KA, et al. A hierarchy of timescales in protein dynamics is linked to enzyme catalysis. Nature. 2007;450:913–916. doi: 10.1038/nature06407. [DOI] [PubMed] [Google Scholar]
  • 6.Gutteridge A, Thornton JM. Conformational changes observed in enzyme crystal structures upon substrate binding. J Mol Biol. 2005;346:21–28. doi: 10.1016/j.jmb.2004.11.013. [DOI] [PubMed] [Google Scholar]
  • 7.Watt ED, Shimada H, Kovrigin EL, Loria JP. The mechanism of rate-limiting motions in enzyme function. Proc Natl Acad Sci USA. 2007;104:11981–11986. doi: 10.1073/pnas.0702551104. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Kumar S, Ma B, Tsai CJ, Sinha N, Nussinov R. Folding and binding cascades: Dynamic landscapes and population shifts. Protein Sci. 2000;9:10–19. doi: 10.1110/ps.9.1.10. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Grunberg R, Nilges M, Leckner J. Flexibility and conformational entropy in protein–protein binding. Structure (London) 2006;14:683–693. doi: 10.1016/j.str.2006.01.014. [DOI] [PubMed] [Google Scholar]
  • 10.Mintseris J, et al. Protein–protein docking benchmark 2.0: An update. Proteins. 2005;60:214–216. doi: 10.1002/prot.20560. [DOI] [PubMed] [Google Scholar]
  • 11.Fernandez-Recio J, Totrov M, Abagyan R. Soft protein-protein docking in internal coordinates. Protein Sci. 2002;11:280–291. doi: 10.1110/ps.19202. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Goldstein H. Classical Mechanics. Reading, MA: Addison–Wesley; 2002. [Google Scholar]
  • 13.Moore WH, Krimm S. Vibrational analysis of peptides, polypeptides, and proteins. II. beta-poly(L-alanine) and beta-poly(L-anaylglycine) Biopolymers. 1976;15:2465–2483. doi: 10.1002/bip.1976.360151211. [DOI] [PubMed] [Google Scholar]
  • 14.Tasumi M, Takeuchi H, Ataka S, Dwivedi AM, Krimm S. Normal vibrations of proteins: glucagon. Biopolymers. 1982;21:711–714. doi: 10.1002/bip.360210318. [DOI] [PubMed] [Google Scholar]
  • 15.Brooks B, Karplus M. Harmonic dynamics of proteins: normal modes and fluctuations in bovine pancreatic trypsin inhibitor. Proc Natl Acad Sci USA. 1983;80:6571–6575. doi: 10.1073/pnas.80.21.6571. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 16.Noguti T, Go N. Collective variable description of small-amplitude conformational fluctuations in a globular protein. Nature. 1982;296:776–778. doi: 10.1038/296776a0. [DOI] [PubMed] [Google Scholar]
  • 17.Levitt M, Sander C, Stern PS. Normal-mode dynamics of a protein: bovine pancreatic trypsin inhibitor. Int J Quant Chem Quant Biol Symp. 1983;10:181–199. [Google Scholar]
  • 18.Tirion MM. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys Rev Lett. 1996;77:1905–1908. doi: 10.1103/PhysRevLett.77.1905. [DOI] [PubMed] [Google Scholar]
  • 19.Elber R, Karplus M. Multiple conformational states of proteins: A molecular dynamics analysis of myoglobin. Science. 1987;235:318–321. doi: 10.1126/science.3798113. [DOI] [PubMed] [Google Scholar]
  • 20.Frauenfelder H, Parak F, Young RD. Conformational substates in proteins. Annu Rev Biophys Biophys Chem. 1988;17:451–479. doi: 10.1146/annurev.bb.17.060188.002315. [DOI] [PubMed] [Google Scholar]
  • 21.Kitao A, Hayward S, Go N. Energy landscape of a native protein: Jumping-among-minima model. Proteins. 1998;33:496–517. doi: 10.1002/(sici)1097-0134(19981201)33:4<496::aid-prot4>3.0.co;2-1. [DOI] [PubMed] [Google Scholar]
  • 22.Alexandrov V, et al. Normal modes for predicting protein motions: A comprehensive database assessment and associated web tool. Protein Sci. 2005;14:633–643. doi: 10.1110/ps.04882105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Hinsen K. Analysis of domain motions by approximate normal mode calculations. Proteins. 1998;33:417–429. doi: 10.1002/(sici)1097-0134(19981115)33:3<417::aid-prot10>3.0.co;2-8. [DOI] [PubMed] [Google Scholar]
  • 24.Delarue M, Sanejouand YH. Simplified normal mode analysis of conformational transitions in DNA-dependent polymerases: the elastic network model. J Mol Biol. 2002;320:1011–1024. doi: 10.1016/s0022-2836(02)00562-4. [DOI] [PubMed] [Google Scholar]
  • 25.Hayward S, Kitao A, Berendsen HJ. Model-free methods of analyzing domain motions in proteins from simulation: a comparison of normal mode analysis and molecular dynamics simulation of lysozyme. Proteins. 1997;27:425–437. doi: 10.1002/(sici)1097-0134(199703)27:3<425::aid-prot10>3.0.co;2-n. [DOI] [PubMed] [Google Scholar]
  • 26.Gibrat JF, Go N. Normal mode analysis of human lysozyme: study of the relative motion of the two domains and characterization of the harmonic motion. Proteins. 1990;8:258–279. doi: 10.1002/prot.340080308. [DOI] [PubMed] [Google Scholar]
  • 27.Kong Y, Ma J, Karplus M, Lipscomb WN. The allosteric mechanism of yeast chorismate mutase: A dynamic analysis. J Mol Biol. 2006;356:237–247. doi: 10.1016/j.jmb.2005.10.064. [DOI] [PubMed] [Google Scholar]
  • 28.Levitt M, Sander C, Stern PS. Protein normal-mode dynamics: Trypsin inhibitor, crambin, ribonuclease and lysozyme. J Mol Biol. 1985;181:423–447. doi: 10.1016/0022-2836(85)90230-x. [DOI] [PubMed] [Google Scholar]
  • 29.Marques O, Sanejouand YH. Hinge-bending motion in citrate synthase arising from normal mode calculations. Proteins. 1995;23:557–560. doi: 10.1002/prot.340230410. [DOI] [PubMed] [Google Scholar]
  • 30.Shrivastava IH, Bahar I. Common mechanism of pore opening shared by five different potassium channels. Biophys J. 2006;90:3929–3940. doi: 10.1529/biophysj.105.080093. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Gerstein M, Krebs W. A database of macromolecular motions. Nucleic Acids Res. 1998;26:4280–4290. doi: 10.1093/nar/26.18.4280. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 32.Tama F, Sanejouand YH. Conformational change of proteins arising from normal mode calculations. Protein Eng. 2001;14:1–6. doi: 10.1093/protein/14.1.1. [DOI] [PubMed] [Google Scholar]
  • 33.Krebs WG, et al. Normal mode analysis of macromolecular motions in a database framework: developing mode concentration as a useful classifying statistic. Proteins. 2002;48:682–695. doi: 10.1002/prot.10168. [DOI] [PubMed] [Google Scholar]
  • 34.Tobi D, Bahar I. Structural changes involved in protein binding correlate with intrinsic motions of proteins in the unbound state. Proc Natl Acad Sci USA. 2005;102:18908–18913. doi: 10.1073/pnas.0507603102. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Lindahl E, Delarue M. Refinement of docked protein–ligand and protein–DNA structures using low frequency normal mode amplitude optimization. Nucleic Acids Res. 2005;33:4496–4506. doi: 10.1093/nar/gki730. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.May A, Zacharias M. Energy minimization in low-frequency normal modes to efficiently allow for global flexibility during systematic protein-protein docking. Proteins. 2008;70:794–809. doi: 10.1002/prot.21579. [DOI] [PubMed] [Google Scholar]
  • 37.Cavasotto CN, Kovacs JA, Abagyan RA. Representing receptor flexibility in ligand docking through relevant normal modes. J Am Chem Soc. 2005;127:9632–9640. doi: 10.1021/ja042260c. [DOI] [PubMed] [Google Scholar]
  • 38.Schneidman-Duhovny D, Inbar Y, Nussinov R, Wolfson HJ. Geometry-based flexible and symmetric protein docking. Proteins. 2005;60:224–231. doi: 10.1002/prot.20562. [DOI] [PubMed] [Google Scholar]
  • 39.Ming D, Cohn JD, Wall ME. Fast dynamics perturbation analysis for prediction of protein functional sites. BMC Struct Biol. 2008;8:5. doi: 10.1186/1472-6807-8-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Cui Q, Bahar I. Normal Mode Analysis: Theory and Applications to Biological and Chemical Systems. London: Chapman & Hall; 2006. [Google Scholar]
  • 41.Brooks B, Janezic D, Karplus M. Harmonic analysis of large systems. I. Methodology. J Comput Chem. 1995;16:1522–1542. [Google Scholar]
  • 42.Califano S. Vibrational States. New York: Wiley Interscience; 1976. [Google Scholar]
  • 43.Hayward S, Berendsen HJ. Systematic analysis of domain motions in proteins from conformational change: New results on citrate synthase and T4 lysozyme. Proteins. 1998;30:144–154. [PubMed] [Google Scholar]
  • 44.Islam SA, Luo J, Sternberg MJE. Identification and analysis of domains in proteins. Protein Eng. 1995;8:513–525. doi: 10.1093/protein/8.6.513. [DOI] [PubMed] [Google Scholar]
  • 45.Smith GR, Sternberg MJE, Bates PA. The relationship between the flexibility of proteins and their conformational states on forming protein-protein complexes with an application to protein–protein docking. J Mol Biol. 2005;347:1077–1101. doi: 10.1016/j.jmb.2005.01.058. [DOI] [PubMed] [Google Scholar]
  • 46.Rajamani D, Thiel S, Vajda S, Camacho CJ. Anchor residues in protein–protein interactions. Proc Natl Acad Sci USA. 2004;101:11287–11292. doi: 10.1073/pnas.0401942101. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 47.Mustard D, Ritchie DW. Docking essential dynamics eigenstructures. Proteins Struct Funct Bioinf. 2005;60:269–274. doi: 10.1002/prot.20569. [DOI] [PubMed] [Google Scholar]
  • 48.Janin J. Welcome to CAPRI: a critical assessment of predicted interactions. Proteins Struct Funct Genetics. 2002;47:257. doi: 10.1002/prot.10381. [DOI] [PubMed] [Google Scholar]
  • 49.Luque I, Freire E. Structural stability of binding sites: Consequences for binding affinity and allosteric effects. Proteins Suppl. 2000;4:63–71. doi: 10.1002/1097-0134(2000)41:4+<63::aid-prot60>3.3.co;2-y. [DOI] [PubMed] [Google Scholar]
  • 50.Yang LW, Bahar I. Coupling between catalytic site and collective dynamics: A requirement for mechanochemical activity of enzymes. Structure (London) 2005;13:893–904. doi: 10.1016/j.str.2005.03.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 51.Li X, Keskin O, Ma B, Nussinov R, Liang J. Protein–protein interactions: Hot spots and structurally conserved residues often locate in complemented pockets that pre-organized in the unbound states: Implications for docking. J Mol Biol. 2004;344:781–795. doi: 10.1016/j.jmb.2004.09.051. [DOI] [PubMed] [Google Scholar]
  • 52.Suhre K, Sanejouand Y-H. ElNemo: A normal mode web server for protein movement analysis and the generation of templates for molecular replacement. Nucleic Acids Res. 2004;32:W610–W614. doi: 10.1093/nar/gkh368. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Song G, Jernigan RL. An enhanced elastic network model to represent the motions of domain-swapped proteins. Proteins. 2006;63:197–209. doi: 10.1002/prot.20836. [DOI] [PubMed] [Google Scholar]
  • 54.Bruschweiler R. Collective protein dynamics and nuclear spin relaxation. J Chem Phys. 1995;102:3396–3403. [Google Scholar]
  • 55.Lesk VI, Sternberg MJE. 3D-Garden: A system for modelling protein–protein complexes based on conformational refinement of ensembles generated with the marching cubes algorithm. Bioinformatics. 2008 doi: 10.1093/bioinformatics/btn093. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_105_30_10390__index.html (677B, html)
0802496105_0802496105SI.pdf (1.3MB, pdf)

Articles from Proceedings of the National Academy of Sciences of the United States of America are provided here courtesy of National Academy of Sciences

RESOURCES