Abstract
Using 13C spin relaxation NMR in combination with molecular dynamic (MD) simulations, we characterized internal motions within double-stranded DNA on the pico- to nano-second time scale. We found that the C–H vectors in all cytosine ribose moieties within the Dickerson–Drew dodecamer (5′-CGCGAATTCGCG-3′) are subject to high amplitude motions, while the other nucleotides are essentially rigid. MD simulations showed that repuckering is a likely motional model for the cytosine ribose moiety. Repuckering occurs with a time constant of around 100 ps. Knowledge of DNA dynamics will contribute to our understanding of the recognition specificity of DNA-binding proteins such as cytosine methyltransferase.
INTRODUCTION
Determination of the sequence dependence of DNA structure and dynamics is crucial for understanding of the recognition of specific DNA sequences by their target proteins such as gene regulators, restriction endonucleases, methylases or other ligands.
Numerous high-resolution structural investigations on DNA, both by NMR and by X-ray crystallography, have provided detailed insight into the structure of these molecules. While the DNA base moiety is usually well reflected by an averaged structure, its ribose moiety exhibits a varying degree of conformational variability. However, since there have been very few experimental studies addressing the internal motions, even of canonical double-stranded DNA, the modes and time scales of internal motions of these molecules have not been determined to date. Thus, although tentative connections have been made between the presence of different ribose pucker conformations and increased internal motions of the ribose moiety (1), the link between structure and dynamics has not been conclusively established.
The furanose ring of nucleic acids is asymmetrically substituted, and therefore the different conformations are weighed unevenly around the pseudorotation cycle. Traditionally, the pseudorotation cycle is divided into four equal-sized quadrants centered around pseudorotation phases (P) of 0°, 90°, 180° and 270°, which are termed the north, east, south and west quadrant, respectively. The south and the north conformation represent energy minima of comparable depth, whereas east and west form energy barriers (2). Ab initio quantum mechanical potential energy calculations in vacuo indicate that for all deoxynucleosides but cytosine, the south conformation is slightly favored by −0.4 to −0.9 kcal/mol, while cytosine prefers the north conformation by −0.3 kcal/mol (3). An east energy barrier of around 4 kcal/mol has been reported (3), which is in agreement with an interconversion across this barrier at room temperature, whereas the west barrier is substantially higher.
Despite the fact that there have been large numbers of NMR studies on different sequences, the sequence dependence of ribose puckering remains elusive. A simplifying two-state conformational equilibrium of the furanose moiety between N (P = 270–90°) and S (P = 90–270°) is assumed in general for the analysis of ribose conformational equilibria from experimental observables such as NMR 3J(H,H) coupling constants (4–8), 13C chemical shifts (9) and H-C residual dipolar coupling (RDC) (10). It is clear that the DNA furanose moiety is predominantly in S, with a higher preference for S for purine nucleotides (>85%) and a larger variation for pyrimidine nucleotides (60–90%) (9). In contrast to this two-state analysis, it has been shown for deoxyribose that a three-state model (north/east/south) is also in agreement with the data (11). Recent molecular dynamic (MD) simulations in explicit solvent demonstrated that solvatization results in (i) the south conformation being the dominant for all four nucleosides, and (ii) reduction of the east barrier to the extent that the east conformation becomes significantly populated for cytosine (12).
Internal motions such as furanose north–south transitions can be studied in great detail by NMR spectroscopy. Carbon spin relaxation experiments provide information on the flexibility of C–H moieties in the picosecond to nanosecond time regime. This technique has only recently been established as a means of studying internal motions of a large number of different C–H sites in nucleic acids (13–17). In order to interpret spin relaxation data in terms of internal motions, they can be subjected to the Modelfree formalism (18,19). This formalism translates spin relaxation data into a parameter for the spatial restriction of the C–H vector, the generalized order parameter S2, and a parameter for the time scale of its reorientation, the internal correlation time τe. Although NMR spectroscopic techniques can thus provide detailed information on amplitudes and time scales of internal motions, it is not possible to characterize the underlying motion. In contrast, MD simulations can generate models of internal motions based on empirical force fields. However, especially for nucleic acids, it is not yet clear how well they are represented in the MD simulations (20). In order to make sure that the models for internal motions extracted from a MD trajectory are physically relevant, it is therefore necessary to link the MD calculations to experimental observables.
In this report, the internal motions in the Dickerson–Drew dodecamer (D3), a palindromic double-stranded dodecamer with the sequence [5′-d(CGCGAATTCGCG)-3′]2, are investigated. Initially, D3 was studied since it contains an EcoR1 restriction site [d(GAATTC)]. In addition, it is composed of two CGCG sequences with a high tendency to form a left-handed Z-helix, which sandwich a Z-incompatible element of the A-tract sequence AATT. The structure of D3 has been investigated in great detail both by X-ray crystallography (21,22) and liquid state NMR spectroscopy (23,24). The molecule forms a regular B-DNA, demonstrating that the 4-nt A-T stretch is sufficient to counteract the Z-DNA propensity of the bracketing CGCG sequences. The fact that D3 has been well-characterized structurally makes it an attractive target for studying sequence-specific dynamics.
MATERIALS AND METHODS
NMR sample preparation
The Dickerson–Drew dodecamer was purchased already synthesized (Invitrogen, Paisley, United Kingdom). A 4.5 mM sample of double-stranded DNA in a volume of 350 μl in 10 mM phosphate buffer, pH 7.0 and 100 mM NaCl was prepared by heating at 95°C for 5 min and subsequent cooling to room temperature. The sample was then lyophilized repeatedly to remove the H2O, and taken up in an appropriate amount of D2O.
NMR spectroscopy
All NMR measurements were performed at 21°C on a DRX600 spectrometer equipped with a 1H, 15N and 13C cryoprobe with a shielded z-gradient. Carbon R1 relaxation rates were measured with a pulse sequence from ref. (25) using a 2.2 s relaxation delay, 44 complex t1 points and 96 scans per free induction decay (FID). Ten R1 delays up to 900 ms were sampled in a total experiment time of 2.5 days. Carbon R1ρ relaxation rates were measured with the pulse sequence described in ref. (26), modified according to ref. (25). All carbon R1ρ spectra were recorded with a relaxation delay of 2.4 s, typically 64 scans per FID and 15 complex t1 points. The carrier frequency of the 13C spin lock of field strength 1445 Hz was placed on the C6, C1′ and C3′, or C5 resonances in separate experiments. Twelve spectra with R1ρ delays up to 55 ms were recorded. In all R1ρ experiments, the energy dissipated in the sample was kept constant by a suitable spin lock applied off-resonance at the beginning of the pulse sequence. The 13C-{1H} nuclear overhauser effect (NOE) was obtained according to ref. (25); the delay for relaxation or H saturation was 4 s, and two spectra each with and without H saturation were recorded in a total time of 34 h.
R1 and R1ρ relaxation rates were obtained by fitting of mono-exponential two-parameter functions to peak heights using programs provided by Palmer and co-workers (27). R2 rates were obtained from the R1ρ and R1 rates as described (15).
Modelfree analysis
R1, R2 and the NOE were subjected to a Modelfree analysis (18,19) using the program Modelfree 4.15 by Palmer and co-workers (28). Separate analyses were carried out for the base (C5, C6 and C8) and the ribose (C1′ and C3′) C–H vectors. Vibrationally averaged effective bond lengths of 1.08 Å (base vectors) and 1.09 Å (ribose vectors) were used. Chemical shift anisotropies of 179 ppm (C6), 134 ppm (C8) and 45 ppm (C1′ and C3′) were used (29). Model selection followed the procedure described in ref. (30). Diffusion parameter optimization for the ribose vectors was carried out during an initial grid search in Modelfree. Analysis of the ribose carbon sites yielded an axially symmetric diffusion model with a diffusion anisotropy of 2.1 and a global rotational correlation time, τc, of 5.0 ns. These results are in good agreement with those of earlier NMR investigations on D3 (diffusion anisotropy of 2.1 ± 0.4) as well as hydrodynamic calculations performed with the program hydronmr 5a (31) (diffusion anisotropy of 1.8, τc of 5.4 ns at 21°C). Due to their biased orientation, the C6–H6 and C8–H8 vectors in the nucleobases are not as sensitive to the diffusion tensor as the ribose vectors. Therefore, the relaxation data of the base moieties were fitted to the diffusion tensor obtained for the ribose data.
MD simulation
A 15 ns simulation was performed with the program CHARMM (32) using the CHARMM27 nucleic acid force field (33,34). A recent NMR structure (pdb identifier: 1NAJ) served as the starting structure for the simulation. Simulations were carried out using periodic boundary conditions in a rhombic dodecahedron cut out of a cube with 70.7 Å side length, filled with pre-equilibrated TIP3P water (35). The system was neutralized with sodium counterions. Non-bonded interactions were smoothly shifted to zero using a 12 Å cutoff. This scheme has been shown to work well in simulations of nucleic acids (36). A pair-list of non-bonded interactions was generated using a 14 Å cut-off, and updated whenever any atom had moved >1 Å since the last list update. Prior to MD runs, the structure was energy-minimized with harmonic positional restraints on the DNA atoms for 50 steps of steepest descent, with a restraint force constant of 100 kcal/mol/Å2, followed by 50 steps of adopted basis-set Newton–Raphson minimization (32) with a force constant of 40 kcal/mol/Å2. The system was then heated from 48 to 298 K during 25 ps followed by equilibration for 500 ps. Trajectory production took place under constant pressure conditions using the Langevin piston method (37), with a check every 4 ps that the average temperature remained within ±5 K of 298 K. Covalent bonds involving hydrogens were constrained with SHAKE (38). Conformations of the system were saved every 0.2 ps for further analysis. Trajectory analysis was performed using CHARMM input scripts. Global rotational and translational motions of the DNA molecule were removed by centering the heavy atoms. C–H order parameters and internal correlation times were obtained from mono- or bi-exponential fits to the first 1 ns of the respective autocorrelation functions. Errors were also obtained from the fitting. In order to improve statistics, averages were formed over the data for identical sites in the two symmetry-related strands of D3. Autocorrelation functions were calculated using the correlation analysis facilities in CHARMM. Order parameters (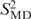 ) were obtained by mono- or bi-exponential fitting of the autocorrelation functions to equations of the form
) were obtained by mono- or bi-exponential fitting of the autocorrelation functions to equations of the form 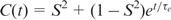 or
or 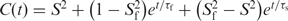 , respectively, using the program Origin.
, respectively, using the program Origin.
RESULTS
NMR-derived generalized order parameters
13C longitudinal (R1) and transversal (R2) relaxation rates and the 13C-{1H} NOE were determined for all C1′, C3′, C6 and C8 sites (Figure 1) in D3, as far as the resonances were resolved (Table S1, Supplementary Material). Order parameters (S2) and the internal correlation times (τe) resulting from the Modelfree analysis are summarized in Table 1. Since D3 is palindromic, only one set of signals is observed for the two identical strands. Under the assumption that each carbon spin forms an isolated I-S spin system together with its directly attached hydrogen, S2-values can be interpreted as spatial restrictions of C–H vector motion on the pico- to nano-second time scale. S2 can adopt values between 0 and 1, with 1 signifying total rigidity, while a value of 0 indicates a totally unrestricted motion of the C–H vector. The τe is the time constant of vector reorientation.
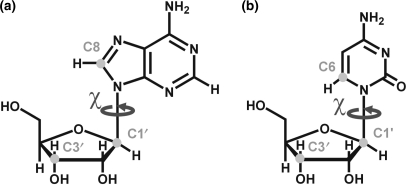
Figure 1.
Carbon sites in purines (a) and pyrimidines (b) that were investigated by 13C spin relaxation measurements, and the angle χ, which is relevant in the analysis of internal motions.
Table 1.
Motional parameters for the C1′, C3′ and C6/C8 sites of D3 at 21°C obtained from 13C relaxation and from the MD trajectory
| Res. | C1′–H1′ |
C3′–H3′ |
C6–H6/C8–H8 |
|||
|---|---|---|---|---|---|---|
| S2 | τe,s | S2 | τe,s | S2 | τe,s | |
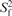 |
τe,f [ps] | 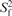 |
τe,f [ps] | 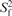 |
τe,f [ps] | |
| C1 | ||||||
| NMR | 0.515 ± 0.016 | 55 ± 4 | 0.385 ± 0.023 | 184 ± 32 | 0.773 ± 0.042 | <10 |
| – | – | 0.673 ± 0.030 | <10 | – | – | |
| MD | 0.525 ± 0.021 | 28 ± 3 | 0.510 ± 0.057 | 26 ± 0 | 0.738 ± 0.020 | 19 ± 6 |
| 0.853 ± 0.033 | 1.5 ± 0.8 | 0.887 ± 0.033 | 1.1 ± 0.8 | – | – | |
| G2 | ||||||
| NMR | 0.781 ± 0.032 | 35 ± 10 | – | – | 0.809 ± 0.067 | <10 |
| MD | 0.835 ± 0.009 | 31 ± 3 | 0.817 ± 0.010 | 52 ± 22 | 0.870 ± 0.007 | 16 ± 2 |
| 0.921 ± 0.000 | 0.3 ± 0.0 | 0.914 ± 0.016 | 1.5 ± 0.9 | – | – | |
| C3 | ||||||
| NMR | 0.741 ± 0.030 | 61 ± 6 | – | – | 0.915 ± 0.038 | <10 |
| MD | 0.637 ± 0.039 | 151 ± 85 | 0.583 ± 0.060 | 110 ± 53 | 0.838 ± 0.025 | 33 ± 13 |
| 0.846 ± 0.041 | 3.9 ± 2.6 | 0.855 ± 0.053 | 4.9 ± 4.2 | – | – | |
| G4 | ||||||
| NMR | 0.879 ± 0.029 | 61 ± 14 | – | – | – | – |
| MD | 0.853 ± 0.002 | 30 ± 9 | 0.845 ± 0.006 | 36 ± 17 | 0.899 ± 0.004 | 27 ± 6 |
| 0.927 ± 0.002 | 0.3 ± 0.1 | 0.936 ± 0.005 | 0.4 ± 0.1 | – | – | |
| A5 | ||||||
| NMR | 0.844 ± 0.026 | 22 ± 7 | 0.897 ± 0.019 | 61 ± 16 | – | |
| MD | 0.896 ± 0.002 | 28 ± 11 | 0.901 ± 0.000 | 27 ± 3 | 0.910 ± 0.001 | 21 ± 6 |
| 0.924 ± 0.009 | 0.5 ± 0.3 | 0.933 ± 0.001 | 0.5 ± 0.1 | – | – | |
| A6 | ||||||
| NMR | – | – | 0.792 ± 0.032 | 20 ± 7 | – | – |
| MD | – | – | – | – | 0.906 ± 0.006 | 21 ± 11 |
| T7 | ||||||
| NMR | 0.916 ± 0.023 | 29 ± 13 | – | – | 0.830 ± 0.018 | <10 |
| MD | – | – | – | – | 0.868 ± 0.003 | 12 ± 2 |
| T8 | ||||||
| NMR | 0.861 ± 0.018 | – | 0.785 ± 0.026 | 24 ± 13 | 0.870 ± 0.040 | |
| MD | 0.855 ± 0.016 | 14 ± 8 | 0.843 ± 0.022 | 36 ± 5 | 0.869 ± 0.002 | 10 ± 4 |
| 0.923 ± 0.012 | 0.3 ± 0.2 | 0.909 ± 0.008 | 1.0 ± 0.2 | – | – | |
| C9 | ||||||
| NMR | 0.676 ± 0.034 | 265 ± 87 | 0.667 ± 0.036 | 255 ± 103 | 0.793 ± 0.064 | <10 |
| 0.821 ± 0.033 | < 10 | 0.837 ± 0.033 | <10 | – | – | |
| MD | 0.724 ± 0.016 | 89 ± 10 | 0.591 ± 0.007 | 109 ± 8 | 0.887 ± 0.002 | 25 ± 0 |
| 0.915 ± 0.009 | 0.5 ± 0.3 | 0.925 ± 0.006 | 0.9 ± 0.4 | – | – | |
| G10 | ||||||
| NMR | 0.848 ± 0.024 | 31 ± 6 | – | – | 0.880 ± 0.040 | <10 |
| MD | 0.852 ± 0.008 | 70 ± 48 | 0.844 ± 0.020 | 172 ± 101 | 0.899 ± 0.002 | 47 ± 15 |
| 0.903 ± 0.022 | 1.0 ± 0.8 | 0.887 ± 0.021 | 3.6 ± 2.0 | – | – | |
| C11 | ||||||
| NMR | 0.708 ± 0.022 | 38 ± 5 | – | – | 0.876 ± 0.036 | <10 |
| MD | 0.735 ± 0.025 | 59 ± 18 | 0.696 ± 0.012 | 65 ± 12 | 0.839 ± 0.003 | 19 ± 5 |
| 0.871 ± 0.031 | 2.7 ± 1.7 | 0.897 ± 0.030 | 2.3 ± 1.9 | – | – | |
| G12 | ||||||
| NMR | – | – | 0.427 ± 0.046 | 40 ± 4 | 0.910 ± 0.077 | <10 |
| MD | 0.772 ± 0.011 | 54 ± 28 | 0.811 ± 0.052 | 93 ± 17 | 0.833 ± 0.017 | 27 ± 8 |
| 0.873 ± 0.035 | 1.9 ± 1.5 | 0.882 ± 0.024 | 2.3 ± 0.6 | – | – | |
The overall correlation time was 5.0 ns and the diffusion anisotropy 2.1. Residues with two sets of order parameters were fitted to a motional model with motions on a slow and a fast time scale: when two order parameters are given, the first one is the overall order parameter of the bond vector S2 and the second the order parameter of the fast motion 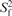 . When two correlation times are given, the first on is the one of the slow (τe,s), the second one the one of the fast motion (τe,f). From NMR relaxation data, only an upper limit of 10 ps can be derived for the fast motion (46). Apart from the parameters listed, fitting of 13C data yielded exchange terms Rex for C1′ of residues G4 and T8, and for C3′ of G12 of 7.1 ± 2.0, 2.8 ± 1.4 and 1.1 ± 1.0 Hz, respectively. For the MD trajectory, S2 and τe-values were extracted from the first 1 ns of the respective autocorrelation functions by mono- or bi-exponential fitting. Average values for S2 (mono-exponential fits) or S2 and
. When two correlation times are given, the first on is the one of the slow (τe,s), the second one the one of the fast motion (τe,f). From NMR relaxation data, only an upper limit of 10 ps can be derived for the fast motion (46). Apart from the parameters listed, fitting of 13C data yielded exchange terms Rex for C1′ of residues G4 and T8, and for C3′ of G12 of 7.1 ± 2.0, 2.8 ± 1.4 and 1.1 ± 1.0 Hz, respectively. For the MD trajectory, S2 and τe-values were extracted from the first 1 ns of the respective autocorrelation functions by mono- or bi-exponential fitting. Average values for S2 (mono-exponential fits) or S2 and 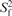 (bi-exponential fits) are given for the two symmetry-related sites in D3; errors are derived from the differences between these sites.
(bi-exponential fits) are given for the two symmetry-related sites in D3; errors are derived from the differences between these sites.
The ribose C–H vectors C1′–H1′ and C3′–H3′ of the two 3′-termini, and also the two 5′-terminal residues, show low-order parameters indicating increased mobility of the ribose moieties at these positions due to their terminal location. Of the eight non-terminal residues, G4, A5, T7, T8 and G10 have high average order parameters of 0.834 ± 0.069 for C1′–H1′ and 0.825 ± 0.094 for C3′–H3′, indicating that these ribose moieties are rigid. In contrast, ribose vector S2-values of the two non-terminal cytosines C3 and C9 are significantly lower than those of the other non-terminal residues (S2 = 0.741 and 0.676 for C1′–H1′ of C3 and C9, respectively, and S2 = 0.667 for C3′–H3′ of C9). For residue C9, both ribose C–H vectors report on internal motions that occur on two time scales that are sufficiently separate that they can be differentiated from each other in the Modelfree analysis. The time scale τe of the slower motion is around 250 ps for both C–H vectors. In contrast, reorientation of the C1′-H1′ vector of residue C3 is considerably faster (61 ps) and comparable to that of the residual motion of the more rigid residues such as A5. This signifies that both cytosines show increased internal motions of their ribose moieties, but on slightly different time scales. In contrast to the C–H vectors in the ribose moieties, all non-terminal base C–H vectors are rigid with an averaged order parameter of 0.853 ± 0.044. While the C6–H6 vector of residue C3 constitutes the most rigid base vector along the sequence, the C6–H6 vector of C9 shows slightly—but not significantly—increased flexibility with an order parameter of 0.793 ± 0.064.
Even within the more rigid non-cytosine residues, a mobility gradient from the base across the ribose to the phosphodiester backbone is observed. Thus, base C–H order parameters of the non-terminal nucleotides are in general slightly higher than the respective C1′–H1′ S2-values, which are in turn higher than the C3′–H3′ S2-values (with average order parameters for all but the terminal residues of 0.853 ± 0.044, 0.806 ± 0.083 and 0.785 ± 0.094 for C6/8–H6/8, C1′–H1′, and C3′–H3′, respectively). Internal correlation times show a similar trend. They are <10 ps for all base C–H vectors, 68 ± 81 ps for C1′–H1′, and 90 ± 111 ps for C3′–H3′. This indicates that even the apparently rigid ribose moieties undergo motions relative to the base moieties. Similar time scales for both ribose C–H vectors suggest that they undergo concerted motions.
MD and comparison with NMR
NMR spin relaxation data indicate increased internal motions of the ribose but not of the base moieties of the non-terminal cytosines C3 and C9 in D3. Although the nature of these internal motions cannot be inferred from the NMR experiments, valid motional models can be obtained from MD simulations as long as the simulation is in agreement with the experimental data. Thus, NMR-derived order parameters (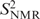 ) were compared to order parameters (
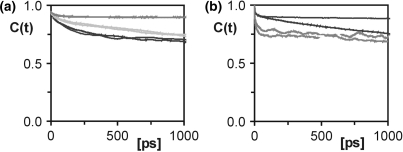
) were compared to order parameters (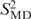 ) extracted from the last 14.5 ns of a 15 ns MD trajectory of D3 (Table 1). NMR spin relaxation is sensitive to motions on the picosecond to nanosecond time scale. Internal motions of isolated interatomic vectors can be separated from overall molecular reorientation, as long as they are at least one order of magnitude faster. Thus, for D3 with a global reorientation time of 5 ns at 21°C internal motions of up to around 500 ps are experimentally relevant. As a rule of thumb, an MD simulation should be at least one order of magnitude longer than the characteristic time of the process of interest. The MD trajectory of D3 is 15 ns long and should therefore provide sufficient sampling to allow study of the internal motions of D3 detected in the experiment. For the majority of the investigated sites, the correlation functions level off to stable plateau values, and similar correlation functions are obtained for the symmetry-related sites on the two identical strands of D3, demonstrating that the MD simulation is converged. Figure 2 shows selected correlation functions obtained for the C1′-H1′ vectors of a number of residues in D3. The resulting order parameters and correlation times are listed individually in Table S2. Averaged S2 and τe values are given in Table 1. In the case of the C1′ of C9, the correlation functions have not decayed to their asymptotic values (Figure 2a), reflecting that a trajectory of limited duration can not cover all possible motions. However, the MD-derived S2 agree between the symmetry-related sites and can therefore be considered an upper limit for the real value of S2. For C3′ of residue C1 and all three investigated sites in residue C3, the agreement between the symmetry-related sites of D3 is slightly poorer than for the other residues (Figure 2a; Table S2). However, the MD data still consistently indicate mobility in the ribose, as opposed to the base and comparison with the NMR results supports this conclusion.
) extracted from the last 14.5 ns of a 15 ns MD trajectory of D3 (Table 1). NMR spin relaxation is sensitive to motions on the picosecond to nanosecond time scale. Internal motions of isolated interatomic vectors can be separated from overall molecular reorientation, as long as they are at least one order of magnitude faster. Thus, for D3 with a global reorientation time of 5 ns at 21°C internal motions of up to around 500 ps are experimentally relevant. As a rule of thumb, an MD simulation should be at least one order of magnitude longer than the characteristic time of the process of interest. The MD trajectory of D3 is 15 ns long and should therefore provide sufficient sampling to allow study of the internal motions of D3 detected in the experiment. For the majority of the investigated sites, the correlation functions level off to stable plateau values, and similar correlation functions are obtained for the symmetry-related sites on the two identical strands of D3, demonstrating that the MD simulation is converged. Figure 2 shows selected correlation functions obtained for the C1′-H1′ vectors of a number of residues in D3. The resulting order parameters and correlation times are listed individually in Table S2. Averaged S2 and τe values are given in Table 1. In the case of the C1′ of C9, the correlation functions have not decayed to their asymptotic values (Figure 2a), reflecting that a trajectory of limited duration can not cover all possible motions. However, the MD-derived S2 agree between the symmetry-related sites and can therefore be considered an upper limit for the real value of S2. For C3′ of residue C1 and all three investigated sites in residue C3, the agreement between the symmetry-related sites of D3 is slightly poorer than for the other residues (Figure 2a; Table S2). However, the MD data still consistently indicate mobility in the ribose, as opposed to the base and comparison with the NMR results supports this conclusion.
Figure 2.
Correlation functions of cytosines compared to other residues. (a) The correlation functions of the C1′–H1′ vector of residues C3 (black), A5 (dark grey) and C9 (light grey). (b) Correlation functions of the non-converged residues A6 (black) and T7 (dark grey). Two correlation functions are given for each vector, one for each of the symmetry-related strands of the palindromic dodecamer.
For residues A6 and T7 in the middle of D3, the correlation functions of the two strands differ substantially, indicating that convergence is not reached for these particular residues (Figure 2b). These two residues have therefore been excluded from further analysis.
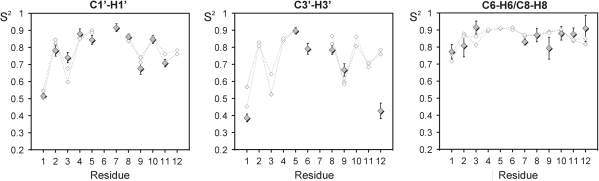
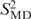 for C1′–H1′, C3′–H3′ and C6/8–H6/8 are shown in Figure 3 for all converged residues, together with the
for C1′–H1′, C3′–H3′ and C6/8–H6/8 are shown in Figure 3 for all converged residues, together with the 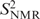 . Very similar
. Very similar 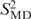 values for the two strands of D3 again demonstrate that the trajectory has converged. The general agreement between
values for the two strands of D3 again demonstrate that the trajectory has converged. The general agreement between 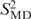 and
and 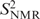 is very good for all carbon sites in the ribose, as well as for the base moieties of all residues apart from the 3′-terminal G12. The very high amplitude of internal motions in the ribose moiety observed experimentally is not reflected in the MD simulation, suggesting that end effects may not be represented satisfactorily in the CHARMM27 force field.
is very good for all carbon sites in the ribose, as well as for the base moieties of all residues apart from the 3′-terminal G12. The very high amplitude of internal motions in the ribose moiety observed experimentally is not reflected in the MD simulation, suggesting that end effects may not be represented satisfactorily in the CHARMM27 force field.
Figure 3.
Comparison between experimental and MD-derived order parameters for D3. Order parameters obtained for C1′, C3′ and C6/8 from the Modelfree analysis of R1, R2: 1,2 as lower index and the heteronuclear NOE are shown as filled diamonds. Order parameters extracted from the MD trajectory for the 10 converged residues are shown as open diamonds. Individual order parameters have been extracted for the two symmetry-related strands of D3.
In agreement with the experimental data, 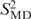 also indicates a general increase in motional amplitudes from the base to the phosphodiester backbone. MD order parameters decrease from an average of 0.882 ± 0.021 for the base to 0.799 ± 0.089 for C1′–H1′, down to 0.765 ± 0.124 for C3′–H3′. In addition, average τe values of non-terminal residues obtained from the trajectory are 11 ± 12 ps, 59 ± 45 ps and 76 ± 50 ps for C6/8–H6/8, C1′–H1′ and C3′–H3′, respectively. This fits well with the experimental data with respect to the larger motional amplitude and longer τe-values of the ribose compared to the base vectors. The only exception is residue T7, for which the C1′-H1′ ribose vector has smaller motional amplitudes than the base vector. Unfortunately, convergence is not reached for this residue in the MD trajectory so that the motional basis for this finding cannot be analysed.
also indicates a general increase in motional amplitudes from the base to the phosphodiester backbone. MD order parameters decrease from an average of 0.882 ± 0.021 for the base to 0.799 ± 0.089 for C1′–H1′, down to 0.765 ± 0.124 for C3′–H3′. In addition, average τe values of non-terminal residues obtained from the trajectory are 11 ± 12 ps, 59 ± 45 ps and 76 ± 50 ps for C6/8–H6/8, C1′–H1′ and C3′–H3′, respectively. This fits well with the experimental data with respect to the larger motional amplitude and longer τe-values of the ribose compared to the base vectors. The only exception is residue T7, for which the C1′-H1′ ribose vector has smaller motional amplitudes than the base vector. Unfortunately, convergence is not reached for this residue in the MD trajectory so that the motional basis for this finding cannot be analysed.
In general, the lower 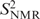 values of the two non-terminal cytosine ribose moieties are reproduced well in the simulation, although the
values of the two non-terminal cytosine ribose moieties are reproduced well in the simulation, although the 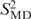 values are slightly lower and internal correlation times are slightly longer for residue C3 than for C9, while the opposite is observed experimentally. These differences are not significant, however. Thus, the overall agreement between the experimental data and the MD simulation for residues 1–5 and 8–11, considering both the amplitudes and the time scales of internal motions, allows extraction of models for the increased internal motions of the cytosine ribose moieties.
values are slightly lower and internal correlation times are slightly longer for residue C3 than for C9, while the opposite is observed experimentally. These differences are not significant, however. Thus, the overall agreement between the experimental data and the MD simulation for residues 1–5 and 8–11, considering both the amplitudes and the time scales of internal motions, allows extraction of models for the increased internal motions of the cytosine ribose moieties.
Internal motions of the cytosine residues
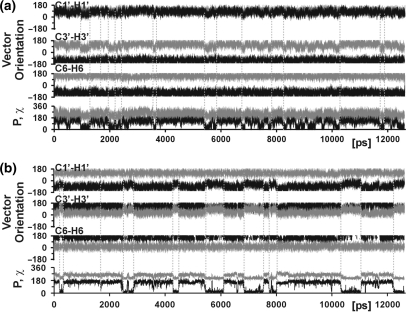
In order to determine the internal motions responsible for the low experimental order parameters of the ribose C–H vectors of the two non-terminal cytosines C3 and C9, C–H vector orientations along the trajectory were correlated to other motional events within these residues (Figure 4). For both residues, reorientation of the C1′–H1′ and the C3′–H3′ vectors occurs in a concerted fashion and in association with repuckering of the ribose moiety. The ribose moiety reorients in a two-state fashion from the south conformation with a sugar pucker phase of around 160° typical of B-form DNA, to the north conformation (P ∼20°), which is associated with the A-form adopted by canonical double-stranded RNA. Apart from south/north repuckering, several short-lived repuckering events to the east conformation (P ∼90°) also occur for residue C3 and less frequently for C9. Reorientation of vectors C1′–H1′ and C3′–H3 is greater upon south/north repuckering than upon south/east repuckering, whereas reorientation of vector C6–H6 is negligible in both cases. This is in agreement with the higher order parameters of the base vector compared to the ribose vectors. The sugar repuckering events are accompanied by changes in the glycosidic torsion, χ (Figure 4), which defines the orientation of the ribose with respect to the base moiety. Upon adoption of the north conformation, χ decreases from 258° to 208°. The χ-angles adopted in the south and north conformation are characteristic for double-stranded nucleic acids in A-form (262°) and B-form (212°), respectively (2). In order to retain a favorable base-stacking arrangement, the flexible ribose moiety rotates around χ by 50° with respect to the rigid nucleobase moiety.
Figure 4.
Analysis of the internal motions that result in lower order parameters for the cytosine ribose moieties. Orientations of the C1′–H1′, C3′–H3′ and C6–H6 vector of residue C3 (a) and residue C9 (b) in polar coordinates relative to the diffusion tensor (θ in black; ϕ in grey) along the last 14.5 ns of the trajectory. The ribose pucker phase (P, in black) and torsion angle χ (in grey) are also shown.
For the more rigid residues, south/north ribose repuckering events are observed only rarely or not at all, indicating that repuckering is in fact responsible for the lower order parameters of the cytosine ribose C–H moieties.
Ribose pucker populations in D3
In the MD simulation, a higher frequency of ribose repuckering could be identified as the source of the increased motion of the C–H vectors of cytosine ribose moieties observed by 13C NMR spin relaxation. Frequency and populations of conformational transitions are unrelated quantities. Consequently, the coincident observation of differences in ribose repuckering frequency and pucker populations can lend additional credibility to the MD simulation. Ribose pucker populations can be determined experimentally from motionally averaged NMR parameters.
Ribose pucker equilibria of D3 have been obtained in earlier investigations from 3J(H,H) coupling constants (4) and also from residual dipolar couplings (RDCs) (10). In these studies, the respective observable has been interpreted in terms of two-state equilibrium. The ribose moiety N populations (as defined in the introduction) reported in these studies are given in Table 2, together with populations obtained from the MD trajectory. Ribose pucker phase histograms extracted from the trajectory are shown in Figure S1 in the Supplementary Material.
Table 2.
Ribose pucker populations in D3
| MD |
RDCa | 3Jb | |||
|---|---|---|---|---|---|
| North (%) | East (%) | N (%) | N (%) | N (%) | |
| C1 | 3 | 51 | 10 | 20 | 22 |
| G2 | 1 | 5 | 1 | 3 | 3 |
| C3 | 16 | 23 | 27 | 32 | 16 |
| G4 | 1 | 8 | 3 | 0 | 1 |
| A5 | 1 | 4 | 1 | 1 | 6 |
| A6 | – | – | – | 4 | 7 |
| T7 | – | – | – | 24 | 15 |
| T8 | 3 | 13 | 6 | 2 | 5 |
| C9 | 24 | 10 | 28 | 22 | 10 |
| G10 | 0 | 8 | 2 | 3 | 7 |
| C11 | 4 | 14 | 7 | 36 | 21 |
| G12 | 1 | 10 | 1 | 33 | 26 |
aWu et al. (10).
bBax and Lerner (4).
North, east and N populations of the ribose moieties from the MD trajectory along the last 14.5 ns, N populations from 3J(H,H) coupling constants (4) and RDCs (10). Populations from coupling constants and RDCs were obtained assuming a two-state equilibrium between N (P = 270–90°) and S (P = 90–270°). North, south and N populations from the MD trajectory were calculated from the fraction of P = 315–45°, P = 45–135° and P = 270–90°, respectively.
Both 3J(H,H)- and RDC-derived N populations are in good qualitative agreement with all converged residues of the MD simulation, in that all non-terminal purine residues and T8 have low N populations between 0% and 7%. 3J(H,H) and RDCs consistently report high N populations of roughly 25% for the 5′-terminal C1 and the two 3′-terminal residues, C11 and G12. In contrast, N populations of these residues are much lower in the MD simulation. This again suggests that terminal residues are not well represented in the CHARMM27 force field. It must be pointed out, however, that although the ribose pucker population does not seem to be well represented by the simulation, the 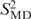 for C–H vectors of ribose in residues C1 and C11 are in good agreement with the respective
for C–H vectors of ribose in residues C1 and C11 are in good agreement with the respective 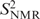 . This observation may be explained by the fact that motional frequencies and populations are unrelated quantities and—for the terminal residues—NMR data and MD results capture different components of these. Thus, the low order parameters observed in the MD trajectory may originate from large-amplitude motion within the south energy minimum, while the NMR results reflect the populations of the N and S conformations.
. This observation may be explained by the fact that motional frequencies and populations are unrelated quantities and—for the terminal residues—NMR data and MD results capture different components of these. Thus, the low order parameters observed in the MD trajectory may originate from large-amplitude motion within the south energy minimum, while the NMR results reflect the populations of the N and S conformations.
Most importantly, in agreement with the data presented here, both 3J(H,H) and RDCs result in elevated N populations for the two non-terminal cytosines C3 and C9. In the MD simulation, 27 and 28% are obtained. From coupling constants, 16 and 10% are obtained for C3 and C9, respectively, whereas N populations are about twice as high in the RDC analysis (32 and 22%). N populations in the MD simulation are closer to the 3J(H,H)-derived value for residue C3, but closer to the RDCs for C9.
As mentioned earlier, the extraction of N populations from 3J(H,H) and RDCs is based on the assumption of a two-state S/N equilibrium. Back-calculation of 3J(H,H) from the N and S populations obtained in the MD trajectory results in a sum of deviations from the measured coupling constants (4) of 28.6 Hz. This includes all 31 measured 3J(H,H) couplings for the nine residues, for which experimental and MD-derived order parameters agree [9 3J(H1′,H2′), 9 3J(H1′,H2″), 9 3J(H3′,H4′) and 4 3J(H2′,H3′)]. No significant improvement is obtained by the three-state model (28.0 Hz) as compared to the two-state N/S equilibrium. The improvement from 28.6 to 28.0 Hz is not significant and while it does not rule out a contribution of the east conformation, it does not add to support it. A possible explanation for the high content of the east conformation for the cytosines in the simulation (Table 2, Figure S1) may be that while the CHARMM27 force field reproduces the relative potential energies of the north and the south conformations, the east potential is underestimated by 1–2 kcal/mol compared to quantum chemical calculations (12).
DISCUSSION
Here, we report the characterization of internal motions in double-stranded DNA on the sub-nanosecond time scale, from a combination of an experimental dynamics technique with atomic resolution and MD simulations. 13C NMR spin relaxation offers the possibility of determining motional amplitudes and time scales of multiple C–H sites within every residue by means of a Modelfree analysis. The agreement between these data and the MD simulation allows extraction of models of internal motion, which have the potential to be physically meaningful.
In our study, there was excellent agreement between the experimental data and the MD trajectory for the major part of the double-stranded dodecamer under investigation, indicating that the energy potentials of deoxynucleotides are well represented in the CHARMM27 force field. Only the 3′-terminal ribose moiety and the two residues in the middle of the molecule are not well represented in the simulation. The deviation in the middle of the sequence is more surprising since both A6 and T7 are located in the middle of the 4-nt A-tract of D3, which is supposed to adopt an ideal B-form DNA conformation.
We have found a general increase in flexibility from the base through the ribose moiety to the phosphodiester backbone. This flexibility gradient is consistently obtained from the experimental data and from the MD simulation with similar absolute and relative order parameters and internal correlation times. Since absolute values of Modelfree parameters depend strongly on the C–H dipole lengths and carbon chemical shift anisotropies incorporated into the analysis, quantitative comparisons between different sites—especially between aliphatic and aromatic sites like base and ribose C–H vectors—can be misleading. However, direct comparison between the MD simulation and the Modelfree analysis validates the parameterization used here (see Materials and methods section).
The analysis of internal motions in D3 shows that all non-terminal base moieties are rigid to the same degree, irrespective of the nucleotide type. Apart from the slight intraresidual flexibility gradient mentioned above, all adenine, guanine and thymine ribose moieties are also rigid, while the ribose moieties of both non-terminal cytosine residues are more flexible. The increased internal motions of the cytosine ribose moiety observed in the NMR relaxation data provide experimental evidence that cytosine is in fact different from the other nucleotides in its ribose pucker potential energy surface in that it favors the north conformation as reported from ab initio calculations (3).
Analysis of the MD trajectory shows that this increased flexibility is in agreement with ribose repuckering between the south and the north conformation. Repuckering occurs with slightly different time scales between around 60 and 250 ps for the two cytosines. This model of internal motions agrees well with a solid-state NMR line shape analysis performed on residue C3 of D3, also indicating substantial motions of the C2′–H2′ bond (39,40), which were in that work interpreted as diffusion of the C2′–H2′ vector on a cone with 80° opening angle. However, the time scale of this motion is about 100 ns, which is substantially slower than in our analysis. In contrast to these earlier results, our data show conclusive evidence that ribose repuckering takes place on the sub-nanosecond time scale in solution. It is obvious that good agreement between the MD simulations and the experimental data does not necessarily mean that the MD-derived motional models are physically relevant. However, an abundance of experimental C–H vectors, providing up to three dynamics probes per residue combined with the agreement between the ribose populations from the trajectory and other NMR techniques such as 3J(H,H) coupling constant (4) and RDC (10) measurements, support the motional models proposed here.
Is increased ribose repuckering a general feature of cytosines or is the extent of repuckering sequence dependent? The two cytosines investigated here are both within the same sequence context; they are located in so-called CpG steps, where a cytosine is followed by a guanine. The number of published experimental dynamics studies on the deoxyribose moiety of DNA in the pico- to nano-second range is very limited to date. However, the few 13C NMR spin relaxation studies that have been published consistently report lower order parameters for the carbon sites of ribose in cytosine compared to ribose moieties of other nucleotides irrespective of the sequence context. Thus, order parameters of cytosine ribose are lower both in other CpG steps (42–44) and in various other sequence contexts (GCTT, TCAA and ACAA) (45). In these previous studies, averaged cytosine C1′ order parameters are 0.69 and thymine order parameters are 0.73, whereas order parameters of purine nucleotides are 0.80. MD simulations of cytosines in other sequence contexts also resulted in north populations of around 15–20% with north/south transition frequencies of around 1010 s−1 (Hart,K., Foloppe,N. and Nilsson,L., unpublished data).
It would be interesting to investigate the biological relevance of increased internal motions in cytosine for molecular recognition. In particular, in the case of CpG steps, it has been reported that methylation in the base abolishes the flexibility of its ribose moiety (39,40).
SUPPLEMENTARY DATA
Supplementary Data are available at NAR Online.
ACKNOWLEDGEMENTS
E.D. and L.N. acknowledge funding from the Swedish Research Council. We are grateful to J. Ferner for carefully reading the article. Funding to pay the Open Access publication charges for this article was provided by Insamlingsstiftelsen at Umeå University.
Conflict of interest statement. None declared.
REFERENCES
- 1.Isaacs RJ, Spielmann HP. NMR evidence for mechanical coupling of phosphate B(I)-B(II) transitions with deoxyribose conformational exchange in DNA. J. Mol. Biol. 2001;311:149–160. doi: 10.1006/jmbi.2001.4855. [DOI] [PubMed] [Google Scholar]
- 2.Sänger W. Principles of Nucleic Acid Structure. New York: Springer; 1984. [Google Scholar]
- 3.Foloppe N, MacKerell AD., Jr Intrinsic conformational properties of deoxyribonucleosides: implicated role for cytosine in the equilibrium among the A, B, and Z forms of DNA. Biophys. J. 1999;76:3206–3218. doi: 10.1016/S0006-3495(99)77472-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bax A, Lerner L. Measurement of 1H-1H coupling constant in DNA fragments by 2D NMR. J. Magn. Res. 1988;79:429–438. [Google Scholar]
- 5.Schmitz U, Zon G, James TL. Deoxyribose conformation in [d(GTATATAC)]2 – evaluation of sugar pucker by simulation of double-quantum-filtered cosy cross-peaks. Biochemistry. 1990;29:2357–2368. doi: 10.1021/bi00461a021. [DOI] [PubMed] [Google Scholar]
- 6.Schmitz U, Kumar A, James TL. Dynamic interpretation of NMR data – molecular-dynamics with weighted time-averaged restraints and ensemble R-factor. J. Am. Chem. Soc. 1992;114:10654–10656. [Google Scholar]
- 7.Rinkel LJ, Altona C. Conformational analysis of the deoxyribofuranose ring in DNA by means of sums of proton-proton coupling constants: a graphical method. J. Biomol. Struct. Dyn. 1987;4:621–649. doi: 10.1080/07391102.1987.10507665. [DOI] [PubMed] [Google Scholar]
- 8.Zhou N, Manogaran S, Zon G, James TL. Deoxyribose ring conformation of [d(GGTATACC)]2 – an analysis of vicinal proton proton coupling-constants from two-dimensional proton nuclear magnetic-resonance. Biochemistry. 1988;27:6013–6020. doi: 10.1021/bi00416a028. [DOI] [PubMed] [Google Scholar]
- 9.LaPlante SR, Zanatta N, Hakkinen A, Wang AH, Borer PN. 13C-NMR of the deoxyribose sugars in four DNA oligonucleotide duplexes: assignment and structural features. Biochemistry. 1994;33:2430–2440. doi: 10.1021/bi00175a011. [DOI] [PubMed] [Google Scholar]
- 10.Wu Z, Delaglio F, Tjandra N, Zhurkin VB, Bax A. Overall structure and sugar dynamics of a DNA dodecamer from homo- and heteronuclear dipolar couplings and 31P chemical shift anisotropy. J. Biomol. NMR. 2003;26:297–315. doi: 10.1023/a:1024047103398. [DOI] [PubMed] [Google Scholar]
- 11.Olson WK. Three-state models of furanose pseudorotation. Nucleic Acids Res. 1981;9:1251–1262. doi: 10.1093/nar/9.5.1251. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Foloppe N, Nilsson L. Toward a full characterization of nucleic acid components in aqueous solution: simulations of nucleosides. J. Phys. Chem. B. 2005;109:9119–9131. doi: 10.1021/jp044513u. [DOI] [PubMed] [Google Scholar]
- 13.Shajani Z, Varani G. 13C NMR relaxation studies of RNA base and ribose nuclei reveal a complex pattern of motions in the RNA binding site for human U1A protein. J. Mol. Biol. 2005;349:699–715. doi: 10.1016/j.jmb.2005.04.012. [DOI] [PubMed] [Google Scholar]
- 14.Vallurupalli P, Kay LE. A suite of 2H NMR spin relaxation experiments for the measurement of RNA dynamics. J. Am. Chem. Soc. 2005;127:6893–6901. doi: 10.1021/ja0427799. [DOI] [PubMed] [Google Scholar]
- 15.Duchardt E, Schwalbe H. Residue specific ribose and nucleobase dynamics of the cUUCGg RNA tetraloop motif by NMR 13C relaxation. J. Biomol. NMR. 2005;32:295–308. doi: 10.1007/s10858-005-0659-x. [DOI] [PubMed] [Google Scholar]
- 16.Petzold K, Duchardt E, Flodell S, Larsson G, Kidd-Ljunggren K, Wijmenga S, Schleucher J. Conserved nucleotides in an RNA essential for hepatitis B virus replication show distinct mobility patterns. Nucleic Acids Res. 2007;35:6854–6861. doi: 10.1093/nar/gkm774. doi:10.1093/nar/gkm774. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Ferner J, Villa A, Duchardt E, Widjajakusuma E, Wohnert J, Stock G, Schwalbe H. NMR and MD studies of the temperature-dependent dynamics of RNA YNMG-tetraloops. Nucleic Acids Res. 2008;36:1928–1940. doi: 10.1093/nar/gkm1183. doi:10.1093/nar/gkm1183. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Lipari G, Szabo A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 1. Theory and range of validity. J. Am. Chem. Soc. 1982;104:4546–4559. [Google Scholar]
- 19.Lipari G, Szabo A. Model-free approach to the interpretation of nuclear magnetic resonance relaxation in macromolecules. 2. Analysis of experimental results. J. Am. Chem. Soc. 1982;104:4559–4570. [Google Scholar]
- 20.Mackerell AD., Jr Empirical force fields for biological macromolecules: overview and issues. J. Comput. Chem. 2004;25:1584–1604. doi: 10.1002/jcc.20082. [DOI] [PubMed] [Google Scholar]
- 21.Wing RM, Drew HR, Takano T, Broka C, Tanaka S, Itakura K, Dickerson RE. Crystal structure analysis of a complete turn of B-DNA. Nature. 1980;287:755–758. doi: 10.1038/287755a0. [DOI] [PubMed] [Google Scholar]
- 22.Minasov G, Tereshko V, Egli M. Atomic-resolution crystal structures of B-DNA reveal specific influences of divalent metal ions on conformation and packing. J. Mol. Biol. 1999;291:83–99. doi: 10.1006/jmbi.1999.2934. [DOI] [PubMed] [Google Scholar]
- 23.Boisbouvier J, Wu ZR, Ono A, Kainosho M, Bax A. Rotational diffusion tensor of nucleic acids from C-13 NMR relaxation. J. Biomol. NMR. 2003;27:133–142. doi: 10.1023/a:1024931619957. [DOI] [PubMed] [Google Scholar]
- 24.Tjandra N, Tate S, Ono A, Kainosho M, Bax A. The NMR structure of a DNA dodecamer in an aqueous dilute liquid crystalline phase. J. Am. Chem. Soc. 2000;122:6190–6200. [Google Scholar]
- 25.Korzhnev DM, Skrynnikov NR, Millet O, Torchia DA, Kay LE. An NMR experiment for the accurate measurement of heteronuclear spin-lock relaxation rates. J. Am. Chem. Soc. 2002;124:10743–10753. doi: 10.1021/ja0204776. [DOI] [PubMed] [Google Scholar]
- 26.Yamazaki T, Muhandiram R, Kay LE. NMR experiments for the measurement of carbon relaxation properties in highly enriched, uniformly 13C, 15N-labeled proteins: application to 13Ca carbons. J. Am. Chem. Soc. 1994;116:8266–8278. [Google Scholar]
- 27.Stone MJ, Fairbrother WJ, Palmer AG, III, Reizer J, Saier MH, Jr, Wright PE. Backbone dynamics of the Bacillus subtilis glucose permease IIA domain determined from 15N NMR relaxation measurements. Biochemistry. 1992;31:4394–4406. doi: 10.1021/bi00133a003. [DOI] [PubMed] [Google Scholar]
- 28.Mandel AM, Akke M, Palmer AG., III Backbone dynamics of Escherichia coli ribonuclease HI: correlations with structure and function in an active enzyme. J. Mol. Biol. 1995;246:144–163. doi: 10.1006/jmbi.1994.0073. [DOI] [PubMed] [Google Scholar]
- 29.Stueber D, Grant DM. (13)C and (15)N chemical shift tensors in adenosine, guanosine dihydrate, 2′-deoxythymidine, and cytidine. J. Am. Chem. Soc. 2002;124:10539–10551. doi: 10.1021/ja012485c. [DOI] [PubMed] [Google Scholar]
- 30.d’Auvergne EJ, Gooley PR. The use of model selection in the model-free analysis of protein dynamics. J. Biomol. NMR. 2003;25:25–39. doi: 10.1023/a:1021902006114. [DOI] [PubMed] [Google Scholar]
- 31.Garcia de la Torre J, Huertas ML, Carrasco B. HYDRONMR: prediction of NMR relaxation of globular proteins from atomic-level structures and hydrodynamic calculations. J. Magn. Reson. 2000;147:138–146. doi: 10.1006/jmre.2000.2170. [DOI] [PubMed] [Google Scholar]
- 32.Brooks AG, Bruccoleri RE, Olafson BD, States DJ, Swaminathan S, Karplus M. CHARMM: a program for macromolecular energy, minimization, and dynamics calculations. J. Comput. Chem. 1983;4:187–217. [Google Scholar]
- 33.Foloppe N, Mackerell AD., Jr All-atom empirical force field for nucleic acids: I. Parameter optimization based on small molecule and condensed phase macromolecular target data. J. Comput. Chem. 2000;21:86–104. [Google Scholar]
- 34.Mackerell AD, Jr, Banavali NK. All-atom empirical force field for nucleic acids: II. Application to molecular dynamics simulations of DNA and RNA in solution. J. Comput. Chem. 2000;21:105–120. [Google Scholar]
- 35.Jorgensen WL, Chandrasekhar J, Madura JD, Impey RW, Klein ML. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 36.Norberg J, Nilsson L. On the truncation of long-range electrostatic interactions in DNA. Biophys. J. 2000;79:1537–1553. doi: 10.1016/S0006-3495(00)76405-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Feller SE, Zhang Y, Pastor RW, Brooks BR. Constant-pressure molecular-dynamics simulation-the Langevin piston method. J. Chem. Phys. 1995;103:4613–4621. [Google Scholar]
- 38.Ryckaert JP, Ciccotti B, Berendsen HJC. Numerical integration of the cartesian equations of motion of a system with constraints: molecular dynamics of n-alkanes. J. Comput. Phys. 1977;23:327–341. [Google Scholar]
- 39.Hatcher ME, Mattiello DL, Meints GA, Orban J, Drobny GP. A solid-state deuterium NMR study of the localized dynamics at the C9pG10 step in the DNA dodecamer [d(CGCCAATTCGCG)](2) J. Am. Chem. Soc. 1998;120:9850–9862. [Google Scholar]
- 40.Meints GA, Karlsson T, Drobny GP. Modeling furanose ring dynamics in DNA. J. Am. Chem. Soc. 2001;123:10030–10038. doi: 10.1021/ja010721d. [DOI] [PubMed] [Google Scholar]
- 41.Boisbouvier J, Wu Z, Ono A, Kainosho M, Bax A. Rotational diffusion tensor of nucleic acids from 13C NMR relaxation. J. Biomol. NMR. 2003;27:133–142. doi: 10.1023/a:1024931619957. [DOI] [PubMed] [Google Scholar]
- 42.Spielmann HP. Dynamics in psoralen-damaged DNA by 1H-detected natural abundance 13C NMR spectroscopy. Biochemistry. 1998;37:5426–5438. doi: 10.1021/bi972536b. [DOI] [PubMed] [Google Scholar]
- 43.Isaacs RJ, Rayens WS, Spielmann HP. Structural differences in the NOE-derived structure of G-T mismatched DNA relative to normal DNA are correlated with differences in (13)C relaxation-based internal dynamics. J. Mol. Biol. 2002;319:191–207. doi: 10.1016/S0022-2836(02)00265-6. [DOI] [PubMed] [Google Scholar]
- 44.Borer PN, LaPlante SR, Kumar A, Zanatta N, Martin A, Hakkinen A, Levy GC. 13C-NMR relaxation in three DNA oligonucleotide duplexes: model-free analysis of internal and overall motion. Biochemistry. 1994;33:2441–2450. doi: 10.1021/bi00175a012. [DOI] [PubMed] [Google Scholar]
- 45.Paquet F, Gaudin F, Lancelot G. Selectively 13C-enriched DNA: evidence from 13 C1′ relaxation rate measurements of an internal dynamics sequence effect in the lac operator. J. Biomol. NMR. 1996;8:252–260. doi: 10.1007/BF00410324. [DOI] [PubMed] [Google Scholar]
- 46.Clore GM, Szabo A, Bax A, Kay LE, Driscoll PC, Gronenborn AM. Deviations from the simple two-parameter model-free approach to the interpretation of the nitrogen-15 nuclear magnetic relaxation of proteins. J. Am. Chem. Soc. 1990;112:4989–4991. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.