Dissection of the Genetic Architecture of Body Weight in Chicken Reveals the Impact of Epistasis on Domestication Traits

Abstract

In this contribution, we study the genetic mechanisms leading to differences in the observed growth patterns of domesticated White Leghorn chickens and their wild ancestor the red jungle fowl. An epistatic QTL analysis for several body-weight measures from hatch to adulthood confirms earlier findings that polymorphisms at >15 loci contribute to body-weight determination in an F₂ intercross between these populations and that many loci are involved in complex genetic interactions. Here, we use a new genetic model to decompose the genetic effects of this multilocus epistatic genetic network. The results show how the functional modeling of genetic effects provides new insights into how genetic interactions in a large set of loci jointly contribute to phenotypic expression. By exploring the functional effects of QTL alleles, we show that some alleles can display temporal shifts in the expression of genetic effects due to their dependencies on the genetic background. Our results demonstrate that the effects of many genes are dependent on genetic interactions with other loci and how their involvement in the domestication process relies on these interactions.

UNDERSTANDING the impact of epistasis on the evolution of multifactorial traits remains a major challenge in complex-trait genetics. Epistasis is more complicated to model, detect, and interpret than marginal (i.e., additive and dominance) genetic effects since the effect of specific alleles at a locus depends on allelic frequencies at other loci. In a population under natural or artificial selection, allele frequencies will change over time and, as a result of this, so will the genetic effects. Explorations of the impact of genetic interactions on phenotypic evolution thus rely on the study of populations in which both genetic and phenotypic information is available. This requires models that are able to decouple the effect of genetic interactions on the displayed genetic variance and to estimate the effect of allele substitutions in different genetic backgrounds.

Domestication of animals and plants provides outstanding examples of rapid evolution. The genetic architecture (i.e., the number of genes and alleles, as well as the nature of interactions among them) that underlies a trait of agricultural interest determines how fast and how far a domesticated species is able to respond to long-term directional selection (Le Rouzic et al. 2007; Le Rouzic and Carlborg 2008). Dissecting the genetic differences between domesticated strains and the corresponding wild populations is a particularly relevant approach to unravel mechanisms involved in the domestication process. Wild and domestic populations normally display large phenotypic differences for a wide range of traits and as domestication has been a rapid process in an evolutionary perspective, a reasonably low number of major genetic factors are expected to contribute to these differences. As wild and domestic populations for agricultural traits produce viable offspring, quantitative trait loci (QTL) detection is a particularly efficient methodology to dissect the genetic architecture involved in domestication (see, e.g., Doebley et al. 1995 and Tanksley et al. 1996 for plants or Andersson et al. 1994 for animals).

The increase in the body weight in farm animals is a good example for which a quantitative trait has been drastically modified during domestication, leading to, e.g., a twofold increase in body size in adult layer-type chickens compared to their wild ancestor. The growth of an animal is a complex process involving the basic genetics of metabolism and health in addition to the general adaptation to a particular environment. Some recent studies aiming to dissect the molecular basis of chicken growth using data from crosses between artificially selected lines or between wild and domesticated strains have found that (i) the genetic architecture of body weight is a polygenic trait (up to 20 loci involved) (Carlborg et al. 2003; Kerje et al. 2003; Jacobsson et al. 2005) and (ii) a significant part of the genetic variation in body weight is due to epistatic effects (Carlborg et al. 2003, 2006).

The history of population-based models of genetic effects for quantitative traits stems from the foundation of quantitative genetics (Fisher 1918) and profited from landmark contributions to incorporate epistasis half a century ago (Cockerham 1954; Kempthorne 1954). More recently, the need for a “physiological” (Cheverud and Routman 1995) or a “functional” (Hansen and Wagner 2001) approach to properly investigate the importance of epistasis in the evolutionary processes has been pointed out, and the theory to integrate this new conceptual scaffold together with the previous statistical framework has been accomplished (Álvarez-Castro and Carlborg 2007). These new developments enable researchers to use the statistical models to properly obtain orthogonal estimates of genetic effects from real data and then to translate them to have a functional meaning—effects of allele substitutions performed in individual genotypes—instead.

In this contribution, we aim to dissect the architecture of the genetic differences in body weight between domesticated and wild chicken. An epistatic QTL analysis was performed in an F₂ population obtained from an intercross between a single male red jungle fowl (“wild”) and several females from a domesticated layer-type chicken population (“White Leghorn”). A subset of eight major loci was selected for further study, and we analyzed the functional effects (i.e., genetic effects estimates that are independent from genotypic frequencies) of Leghorn and jungle fowl QTL alleles in both wild and domesticated multilocus genetic backgrounds.

MATERIALS AND METHODS

Biological material:

We performed genome scans for individual as well as interacting QTL in a red jungle fowl × White Leghorn F₂ intercross. One red jungle fowl male was mated to three White Leghorn females, producing 1046 F₂ offspring in total, 827 of which had measured genotypes. This population has previously been used in QTL mapping for behavior traits (Schütz et al. 2002), egg production (Wright et al. 2006), and morphology (Carlborg et al. 2003; Kerje et al. 2003; Rubin et al. 2007) and a full description of the mapping population can be found in those references.

Previous QTL analyses on this population were based on a linkage map including 94 markers covering 2552 cM on 25 autosomes (Kerje et al. 2003). Here, we use an updated marker map with 439 markers covering 3214 cM on 32 linkage groups (L. Andersson, personal communication).

Phenotypes:

The body weight (BW) of the F₂ chickens was measured five times, at 1, 8, 46, 112, and 200 days of age. As described in Carlborg et al. (2003), four additional phenotypes, corresponding to the difference between consecutive measurements, were used to estimate the growth rates (GR) at different points in life. Among the 827 genotyped chickens, 57 had incomplete growth data (missing points in the time series, most of them being due to death before 200 days) and 5 had a pathological growth (e.g., decrease of the weight between two consecutive points). These individuals were removed from the data set and our analyses were based on the remaining 765 individuals.

To get an analytical description of the shape and the dynamics of the growth over time, a Gompertz growth function was fit to the body-weight time series. The Gompertz function is a particular case of the Richards growth function (Richards 1959) and has been shown to be adequate for chicken growth modeling (Rogers et al. 1987). The function used was

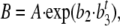where B is the expected body weight, t is the age of the chicken in days, and A, b₂, and b₃ are the three parameters of the Gompertz function. The parameter A (denoted Asym in the rest of this article) has a direct biological meaning; it represents the expected maximum (asymptotic) body weight. Another biologically meaningful parameter, x_mid = −log(b₂)/log(b₃), is the estimate of the age at which the growth rate is maximum (inflection point of the growth curve). The nonlinear regressions were performed with the module “SSgompertz” in the R software (R Development Core Team 2007). The distribution of the regression parameters is provided in supplemental Figure 1.

A principal-components analysis (PCA) over these 13 variables (i.e., five body weights, four growth rates, and four parameters from the Gompertz regression) was performed to extract a smaller number of mutually independent variables for use in the mapping procedure. Our aim was to explore how well the principal components (PCs) capture the variance of QTL affecting growth. Our analysis thus uses the principles of both “functional” approach (Ma et al. 2002; Yang et al. 2006) and dimensional reduction often used in multitrait approaches (see, e.g., Korol et al. 2001).

QTL mapping:

QTL mapping was performed using a three-step strategy. First, QTL were mapped on the basis of their marginal effect (additive and dominance), using a standard least-squares-based method (Haley et al. 1994), with statistical significance assessed by randomization testing (Churchill and Doerge 1994). Significant QTL were successively added to the model as described before (Carlborg and Andersson 2002) to obtain a total model:

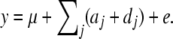Second, a two-locus interaction model, including all epistatic interactions (additive by additive, additive by dominance, dominance by additive, and dominance by dominance), was used to screen for epistatic QTL as described in Carlborg et al. (2003), using the model

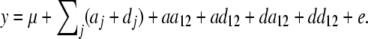Significance for QTL pairs was assessed using empirical significance thresholds (Carlborg and Andersson 2002). Finally, a randomization test was performed to determine which model provides the best fit for all significant QTL detected. For a detailed description of the procedure used, we refer the reader to Carlborg et al. (2003).

Estimation of multilocus genetic effects:

A subset of eight highly significant, unlinked loci was selected for further analysis: loci 1A [chromosome 1, 105 cM (1.105)], 1C (1.481), 3B (3.174), 6A (6.60), 8A (8.65), 11B (11.53), 12A (12.35), and 27A (27.23) (see Table 1), among which all pairwise interactions were considered. The genetic effects of each selected QTL, as well as all pairwise interactions between the eight loci, were computed for all traits, including the principal components, using the regression

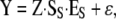where Y is the vector of observed phenotypes, Z is the matrix linking phenotypes to corresponding genotypes, S_S is the genetic-effects design matrix of the statistical formulation of the “NOIA” model (Álvarez-Castro and Carlborg 2007), and ɛ is the vector of random (environmental) effects. The Z matrix is computed from the genotypic probabilities provided by a Haley–Knott regression (Haley et al. 1994), as detailed in Álvarez-Castro et al. (2008). This regression estimates E_S, the vector of statistical genetic effects. To reduce the model to account for only pairwise epistasis, we made the columns of the S matrix corresponding to higher-order epistasis into columns of zeros. The estimates of genetic effects obtained are in this way average effects of allele substitutions in the sample of individuals of the QTL study. From these estimates, “functional” genetic effects E_B, i.e., genetic effects corresponding to allelic substitutions in a given genetic background “B,” can be obtained using the transformation tool

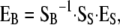where S_B is the genetic-effects designed matrix fitting the desired meaning of the new estimates. Estimates of genotypic values, i.e., the genotype-to-phenotype map G, can be obtained by

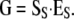These operations (regression and transformation tool) are described in more detail in Álvarez-Castro and Carlborg (2007) and implemented in an R package (Le Rouzic and Álvarez-Castro 2008). In this way, we have obtained estimates of functional effects in two particular genotypes: the homozygous jungle fowl wild genetic background (“1” alleles at the other seven loci) and the homozygous Leghorn “domestic” genetic background (“2” alleles at the other loci).

TABLE 1.

Summary of QTL detected for the 17 analyzed traits

Trait	1A	1B	1C	2A	2B	3A	3B	4A	4B	6A	7A	8A	11A	11B	12A	16A	20A	27A
BW1
BW8	1.107 (3)		(3)			(2)					(2)	8.65 (3)	(1)
BW46	1.105 (2)		1.462 (1)	2.39 (1)			(1)			(1)				11.53 (2)	(3)	16.0
BW112	1.104 (1)		1.480 (2)			(1)	3.161		4.118	6.61 (2)					(4)			27.26 (3)
BW200	1.103 (2)	1.139 (1)	1.484 (3)		2.112 (1)		3.181 (2)			6.61 (2)				(1)	(1)			27.26 (3)
GR18	1.91 (1)	1.138 (3)	(5)			3.91 (2)					7.5 (1)	8.66 (3)
GR846	1.105 (2)		1.462 (1)	2.39			(1)			6.54 (1)				11.44 (2)	(2)	16.0
GR46112	1.104 (1)		1.480 (4)						4.117	6.63					12.23(4)			27.26 (4)
GR112200	1.73	1.139 (1)	1.499 (4)										11.4 (2)
Asym	1.103 (3)	1.139 (1)	1.485 (1)		2.112					(1)				(1)				27.26 (2)
b2	1.105 (3)	(1)	1.452 (3)															(1)
b3
xmid		1.137 (1)											11.0 (1)		12.63		20.35 (1)
PC1	1.104 (2)	1.139	1.485 (2)				3.160 (2)			6.57(2)				11.58 (1)	(2)	16.0	(1)	27.26 (4)
PC2		(1)											11.0 (1)
PC3	1.107 (1)		(1)											(1)				27.21 (1)
PC4								4.8										27.20

BW: body weights at 1, 8, 46, 112, and 200 days. GR: growth rates (increase in body weight between consecutive ages). Asym, b₂, b₃, and x_mid: parameters resulting from the nonlinear regression (Gompertz function). PC1–PC4: the first four principal components. The chromosomal locations refer to the location of the significant QTL peaks in the one-dimensional scan (if any). The numbers in parentheses indicate the number of interactions involving each locus, the genomewide significance level being indicated as follows: underlined, <5%; regular type, <10%; italics, <20%). Underlined column headings are the eight loci selected for the second part of the analysis.

RESULTS

Chicken growth:

There was a high level of correlation among the phenotypic traits (body weights at 1, 8, 46, 112, and 200 days of age, as well as the four growth rates between successive ages) (supplemental Table 1). The correlation between successive body weight measurements for the same individual over time can be modeled using a growth model, in our case the Gompertz growth function. Fitting this model on the data provides estimates for three parameters (Asym, b₂, and b₃) from the five points measured in each series. However, even though the b₂ and b₃ (as well as the age at the inflection point x_mid) parameters bring a longitudinal dimension to the analysis, they are not orthogonal characters since two pairs of parameters (A − b₂ and b₂ − b₃) are substantially correlated (0.48 and −0.53, respectively). Orthogonal scales for the phenotypes were obtained through a principal-components analysis including all 13 previously described phenotypic traits. The four first PCs explain 42.5, 25.0, 15.3, and 8.5% the total phenotypic variance, respectively (91.3% altogether).

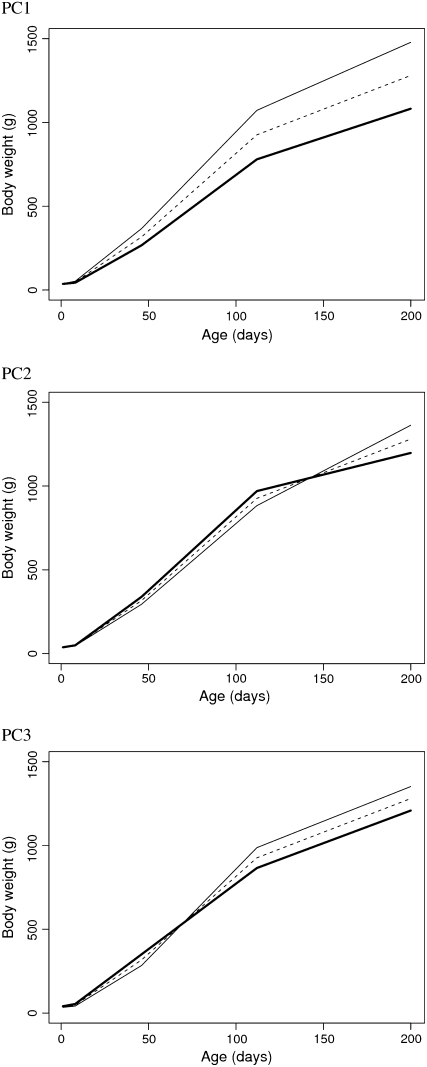
Figure 1 and supplemental Figure 2 illustrate the decomposition of chicken growth according to the three first principal components. PC1 is clearly a total weight variable. It affects the body weight at all measured points in life of the chicken equally. PC2 and PC3 describe “switches” in the growth process, i.e., early fast and late slow growth vs. early slow and late fast growth. This change in growth pattern is late in the case of PC2 and early in the case of PC3. Consequently, PC1 describes the general body-weight trend for an individual, while PC2 and PC3 determine the shape of the growth curve.

Figure 1.—

Graphic illustration of growth pattern features described by the principal components. The mean phenotype of the F₂ population (dotted curve) is taken as a reference to describe the effects of the three first principal components. All PCs are set to 0, except one (top, PC1; middle, PC2; and bottom, PC3) that is varied from −3 (solid thin line) to 3 (solid thick line). The values −3 and 3 roughly represent the maximum and minimum values for the PCs in the population (see supplemental Figure 2).

A network of interacting loci:

Marginal-effect QTL detection was performed for the five raw body-weight measurements, the four growth rates between successive ages, and the four parameters describing the growth curve, as well as for the four first PCs. It revealed 18 genomic regions (QTL) that are significantly associated with at least one of these traits (Table 1, supplemental Data 1). Among these 18 detected loci, 11 are significant (by their marginal and/or interaction effects) at a 5% genomewide significance threshold. Almost all QTL affect several traits, which in some cases can be due to correlations between traits (for instance, BW200, Asym, and PC1 are strongly correlated, supplemental Table 1), but not always. For instance, the QTL located on chromosome 27 affects both PC1 and PC3, which are by definition not correlated. Phenotypes related to the final body weight (BW200, Asym, PC1, and to a lesser extent BW112 and the late growth rates) seem to have a broader genetic basis than the early growth traits, both according to the number of QTL and according to how much of the phenotypic difference between the founder populations they explain. The PCA clearly makes it possible to detect all QTL using fewer genome scans. PC1 alone is the trait for which the largest number of underlying loci was detected.

A two-dimensional genome scan for pairs of interacting QTL using a genetic model accounting for genetic interactions (epistasis) was also performed. Considering all traits together, a total of 41 pairs of interacting loci were significant using a 5% genomewide significance threshold for each trait (supplemental Data 2). When comparing the detected interacting pairs of loci across traits, the loci overlap to a large degree with those of the one-dimensional scan. In particular, the two loci that have the most pronounced effects in the one-dimensional scan (1A and 1C) also show the most epistatic interactions with the other loci (Table 1).

The genetic architecture underlying phenotypic change in body weight during domestication:

Here we focus on studying a network containing the eight loci that have the most pronounced effects in chicken body-weight determination (underlined loci in Table 1). The decomposition of genetic variance is provided in Table 2. By applying the transformation and translation tools of the NOIA model (Álvarez-Castro and Carlborg 2007) to the marginal and epistatic effects estimated for this reduced network, we can predict phenotypic values for all possible multilocus genotypes. These tools are used to compute the effects of allele substitutions performed in domestic and wild reference individual genotypes. In other words, we inspect the functional properties of the genetic network.

TABLE 2.

Decomposition of genetic variance for the 17 analyzed traits

	Var(A)	Var(D)	Var(AA)	Var(AD)	Var(DD)	Var(G)	Var(P)	h2	H2
BW1	0.19	0.24	0.70	1.78	1.05	3.97	13.8	0.01	0.28
BW8	3.50	0.82	1.88	4.13	3.03	13.36	36.64	0.10	0.36
BW46	677.76	32.94	159.79	423.00	165.40	1,458.9	2,973.9	0.23	0.49
BW112	6,848.1	747.8	1,851.5	3,812.4	2,111.7	15,371.6	35,546	0.19	0.43
BW200	13,099	1,490.4	2,835.5	7,574.1	3,655.9	26,655.2	71,090	0.18	0.37
GR18	2.67	0.32	1.80	2.18	1.82	8.78	24.20	0.11	0.36
GR846	602.72	25.77	143.75	412.86	157.43	1,342.54	2,781.6	0.22	0.48
GR46112	3,376.4	569.3	1,300.8	2,222.2	1,409.4	8,878.1	22,977	0.15	0.39
GR112200	1,085.8	255.6	421.3	1,709.9	639.5	4,112.1	13,396	0.08	0.31
Asym	14,954	1,770	3,066	9,401	4247	33,438	87,176	0.17	0.38
b2	0.0077	0.0047	0.0147	0.0185	0.0102	0.0559	0.1868	0.04	0.30
b3 (×10−6)	0.078	0.135	0.498	1.11	0.509	2.33	8.74	0.01	0.27
xmid	1.35	0.89	2.38	8.80	3.50	16.91	65.61	0.02	0.26
PC1	2.66	0.07	0.25	0.50	0.26	3.74	5.53	0.48	0.68
PC2	0.07	0.04	0.18	0.49	0.24	1.00	3.25	0.02	0.31
PC3	0.21	0.02	0.16	0.20	0.09	0.68	1.99	0.11	0.34
PC4	0.01	0.01	0.09	0.15	0.08	0.35	1.11	0.01	0.32

Var(G) is the total of all genetic variances. H² stands for the broad-sense heritability (Var(G)/Var(P)), and h² is the narrow-sense heritability (Var(A)/Var(P)).

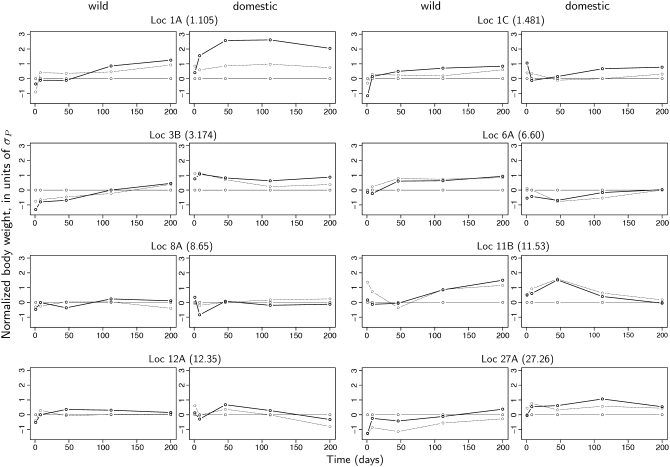
Figure 2 describes the predicted effects of allelic substitutions for the eight major loci on the overall growth pattern in two genetic backgrounds: the wild background (alleles 1 at all other loci) and the domestic background (alleles 2 at all other loci). Most loci display effects that depend on the genotype at other loci, i.e., epistasis, and the epistatic patterns are different for different loci in the network. Locus 1A has a major individual effect on increasing the body weight. The effect is similar in direction in both backgrounds, but appears to be earlier and larger in the wild background. Most loci (3B, 6A, 11B, 12A, and 27A) show background-specific patterns, where the effect on the final weight is often displayed only in either the wild or the domestic background, but not in both at the same time. The domestic allele in 3B and 11B increases growth early in life in a domestic and late in a wild genetic background . Two of the loci (6A and 11B) affect body weight at 200 days only in a wild background, whereas locus 12A changes body weight only in a domestic background (Figure 2).

Figure 2.—

Genetic effects of individual loci in wild and domestic genetic backgrounds. The estimated phenotypic effect of “2” (“Leghorn” or “domestic”) alleles at each of the 8 loci included in the regression analysis in the “wild” (left plots) and “domestic” genetic backgrounds (right plots). The reference is always the “11” (homozygote wild) genotype (solid thin line) in both backgrounds, and plots are scaled according to the residual variance at each age. Additive and dominance effects can be extracted in each plot from the dotted and thick solid lines representing the heterozygote (“12”) and the homozygote domestic (“22”) genotypes, respectively. Epistasis is evident in the comparison of the genetic effects in the alternative genetic backgrounds (if there was no epistasis, right and left plots should be identical). For instance, being 22 instead of 11 at locus 1A increases the body weight at 200 days by ∼1.2σ_P in the “jungle fowl” background (11 genotype at all other loci) and by about 2σ_P in the “Leghorn” background (22 genotype at all other loci).

DISCUSSION

The genetic architecture of chicken growth:

The growth of a complex organism is a quantitative trait, and it is therefore expected that multiple genes are involved in determining the large phenotypic differences between the domesticated White Leghorn chicken and its ancestor the red jungle fowl. The results from the original QTL analysis of this data set (Carlborg et al. 2003) support this as many QTL with both individual effects and loci with large epistatic effects were detected.

Our analysis, which accounts for individual as well as all pairwise epistatic effects in a subset of eight prominent loci, shows a strong trend toward a temporal shift of the allelic effects due to multilocus interactions with the genetic background in which the effects are measured. Alleles that tend to increase late body weight in a wild genetic background display their effects much earlier in life in a domestic background. This trend is only due to complex genetic interactions among these eight loci as no other factors have been included in the analysis. Moreover, the dynamics and robustness of the expression of allelic effects have been evaluated in reduced models, i.e., where each of the eight loci are successively excluded, the effect being then measured in seven-locus networks. The analysis of these seven-locus networks (results not shown) did not indicate that the temporal phenotypic expression was due to any specific interaction with an individual locus; for instance, loci 3B and 11B keep their specific expression pattern (effect on early growth in the domestic background and on late growth in the wild background) even when any of the other loci are excluded from the regression. The epistatic interactions that lead to the temporal shifts are thus due to multilocus interactions in a complex network rather than to a few specific and strong pairwise effects.

Chicken domestication:

The domestication of chickens occurred ∼6000 bc from the red jungle fowl Gallus gallus (Fumihito et al. 1994). The relationships between the different chicken breeds (including egg-, meat-, and fighting-type breeds) are somewhat complicated (Moiseyeva et al. 2003), in particular because they might have resulted from multiple independent domestication events and because late introgressions from the wild species are likely (Liu et al. 2006). Although the White Leghorn is an egg-layer breed, it is likely that during the long domestication process, its ancestors have been subjected to direct or indirect selection for the total weight, as Leghorn chickens are now around twice as large as the wild G. gallus.

One of the main implications of epistatic patterns detected in our analysis is that the effects of the domestic Leghorn alleles (i.e., the alleles that differ between the domesticated egg-layer chickens and the jungle fowl) depend on the genetic state of the population in which they arose by mutation or were introduced by other means. For instance, the domestic alleles in loci 6A and 11B do not increase the adult body weight in the Leghorn background: if these alleles were fixed through artificial selection for larger chickens, they must have been fixed in a background that closely resembles that of the original wild jungle fowl population. In contrast, the domestic alleles in loci 3B and 27A decrease the body weight in a genetic background similar to the jungle fowl. They are thus not expected to be fixed by artificial selection for increased body weight early in domestication. Our results thus strongly suggest that the contribution of the loci detected in this wild × domestic intercross to phenotypic evolution will have changed considerably during the domestication process. It is therefore not expected that the increase in allelic frequency for the loci will have been simultaneous as, e.g., the domestic allele at loci 6A and 11B is more or less neutral in the domesticated chickens, indicating either that the selection on these loci took place early in domestication or that they have a major effect on other selected traits. Locus 27A, on the other hand, has a very low effect in a wild background and is thus expected to have been selected late in the domestication process. The domestic alleles at some loci, e.g., loci 1A and 1C, increase body weight in all genetic backgrounds and these alleles could thus have spread in the population at any time. The domestic alleles at other loci, such as 8A or 12A, appear to have even slightly negative effects on body weight. The fixation of these alleles might be unrelated to artificial selection and due to, e.g., genetic drift or genetic linkage (Hill–Robertson effect). It may also be due to pleiotropic effects on another selected trait (fertility, egg production, muscle–fat ratio, etc.). As the Leghorn breed has not been directly selected in its recent history for increased body weight but rather for increased egg production, pleiotropy appears to be a plausible explanation.

Epistasis, pleiotropy, and the genetic analysis of complex traits:

The potential impact of epistasis on the genetic architecture of quantitative traits has been intensively addressed by theory (e.g., Goodnight 1995; Rice 2000; Hansen and Wagner 2001; Barton and Turelli 2004; Carter et al. 2005; Hansen et al. 2006; Turelli and Barton 2006), and due to important progress in methodological, statistical, and computational issues it has been recently confirmed and generalized from empirical data (e.g., Carlborg and Haley 2004; Malmberg and Mauricio 2005; Zeng et al. 2005). However, despite improvements in the quality and the quantity of tools for detection of epistatic interactions, our ability to interpret the output of these QTL analyses in term of biologically relevant genetic effects is still limited. In particular, the statistical models used for QTL detection are based on the average effects of allelic substitutions (and the corresponding variance) in a population. They are therefore suitable for detection of loci, but as the estimates they provide depend on the genotypic frequencies in the particular population, this so-called “statistical epistasis” (Cheverud and Routman 1995) is of little or no interest for the traditional geneticist. For interpretation, physiological (Cheverud and Routman 1995) or functional (Hansen and Wagner 2001) genetic effects are desirable, i.e., the effects of allelic substitutions in a specific genetic background or genotype to draft a genotype–phenotype map. However, these modeling paradigms have often been intermixed or misunderstood in the literature and only recently a suitable mathematical tool has been developed to transform statistical effects (the output of QTL analysis) into functional effects (Álvarez-Castro and Carlborg 2007).

In a time-series study, the levels and interpretation of epistasis depend on the way the trait is analyzed. A phenotypic measurement, such as the body weight at 46 days of age, considered as an independent trait, has an apparently solid genetic basis with some marginal-effect loci, as well as several significant interaction effects (see also Carlborg et al. 2003). However, the biological significance of the measured genetic effects for the QTL affecting this trait is despite this unclear, as jungle fowl and White Leghorn chickens, as well as their F₂ progeny, are likely to be at different physiological stages 46 days after hatching. Our analyses clearly show that much epistasis detected for individual traits is due to temporal shifts in the genetic effects of loci from interactions with the genetic background. A potential explanation for this could be that individuals with Leghorn alleles at all eight major loci in the genetic network will be at a later physiological stage than individuals with jungle fowl alleles at all loci. This is a very interesting result that indicates the possibility that a common reason for detected statistical epistasis might actually be due to physiological rather than molecular-level interactions. In future studies it would therefore be highly interesting to measure body weights at, e.g., a physiological stage instead of at a particular age to explore this further. This would most likely decrease the differences in the temporal effects of the loci and hence decrease the general levels of statistical epistasis for the studied traits.

The growth of a complex animal, such as a bird, probably involves hundreds or thousands of genes being active at different stages of development, and at one level or another these are likely to interact. Only a subset of these genes (i.e., the polymorphic ones having a strong allele-substitution effect) can be detected as QTL. Here, we analyzed a large number of alternative descriptors of growth (body weights, growth rates, and parameters linked to the shape of the growth curve as well as orthogonal composite descriptors of all the other traits). In spite of the decomposition of this parameter set into principal components, which are by definition not correlated, it has not been possible to distinguish several groups of genes, e.g., being involved specifically in the final body weight or in determining the shape of the growth curve. Virtually all significant QTL affect the first principal component, related to the overall body weight, and there is a surprising lack of genetic support for individual loci affecting the subsequent PCs, despite a nonnegligible part of the total phenotypic variance being associated with these: the QTL analysis was unable to detect any solid genetic factors for PC2, while PC3 has a few weak but significant underlying genetic factors identical to PC1. Consequently, our results do not support the idea that the growth process could be decomposed into genetically independent parts or modules. The detailed analysis of individual gene effects evidences that the same locus can affect different stages of growth depending on the genetic background, generating strong epistatic interactions. However, experimental evidence is lacking to extend these results to other organisms and to assess whether it might be related to the artificially driven evolutionary history of domesticated species.