Detecting Causal Nonlinear Exposure-Response Relations in Epidemiological Data

Abstract

The possibility of hormesis in individual dose-response relations undermines traditional epidemiological criteria and tests for causal relations between exposure and response variables. Non-monotonic exposure-response relations in a large population may lack aggregate consistency, strength, biological gradient, and other hallmarks of traditional causal relations. For example, a u-shaped or n-shaped curve may exhibit zero correlation between dose and response. Thus, possible hormesis requires new ways to detect potentially causal exposure-response relations. This paper introduces information-theoretic criteria for identifying potential causality in epidemiological data that may contain nonmonotonic or threshold dose-response nonlinearities. Roughly, exposure variable X is a potential cause of response variable Y if and only if: (a) X is INFORMATIVE about Y (i.e., the mutual information between X and Y, I(X; Y), measured in bits, is positive. This provides the required generalization of statistical association measures for monotonic relations); (b) UNCONFOUNDED: X provides information about Y that cannot be removed by conditioning on other variables. (c) PREDICTIVE: Past values of X are informative about future values of Y, even after conditioning on past values of Y; (d) CAUSAL ORDERING: Y is conditionally independent of the parents of X, given X. These criteria yield practical algorithms for detecting potential causation in cohort, case-control, and time series data sets. We illustrate them by identifying potential causes of campylobacteriosis, a foodborne bacterial infectious diarrheal illness, in a recent case-control data set. In contrast to previous analyses, our information-theoretic approach identifies a hitherto unnoticed, highly statistically significant, hormetic (U-shaped) relation between recent fast food consumption and women's risk of campylobacteriosis. We also discuss the application of the new information-theoretic criteria in resolving ambiguities and apparent contradictions due to confounding and information redundancy or overlap among variables in epidemiological data sets.

1. INTRODUCTION

This note proposes and illustrates a solution to the problem of detecting and estimating unknown, possibly non-monotonic exposure-response relations in large multivariate epidemiological data sets. This problem is important because existence of a monotonic exposure-response relation has traditionally been regarded as one indication that a statistical association may be causal (Weed and Gorelic, 1996). However, there is no reason that causal exposure-response relations must necessarily be monotonic, and the reality of hormesis in many systems suggests that sometimes they are not. Hence, methods are needed to detect and quantify non-monotonic (e.g., U-shaped, n-shaped, N-shaped, or more complicated) relations in epidemiological data. This statistical challenge is exacerbated by the fact that hormetic effects are often relatively small and may involve interactions among multiple variables, so that searching for them in complex data sets may involve detecting relatively weak signals among a huge number of possibilities.

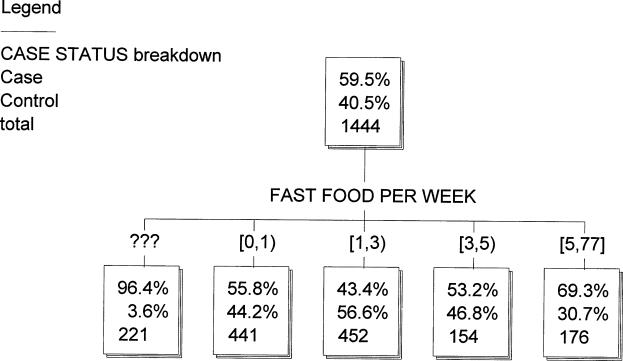
As an example, Figure 1 shows a U-shaped exposure-response relation identified in data from a recent food safety case-control study of campylobacteriosis (Friedman et al., 2004). The data were collected by the Centers for Disease Control and Prevention (CDC) as part of a study of risk factors for sporadic cases of campylobacteriosis, a common foodborne bacterial illness. As described by Friedman et al. (2000),

We enrolled patients with culture-confirmed Campylobacter infections from Foodborne Diseases Active Surveillance Network (FoodNet) sites in California, Georgia, Maryland, Minnesota, New York and Oregon. Information about demographics, clinical illness, and exposures occurring within 7 days before diarrhea onset was collected using a standardized questionnaire. By using random-digit dialing, we interviewed one age-group matched, site-matched community control for each patient. … From January 1, 1998, to March 1, 1999, 1463 patients and 1317 controls were enrolled in the study.

FIGURE 1.

U-Shaped Relation Between Fast Food Consumption and Risk of Foodborne Illness (Campylobacteriosis)

The data set contains one record (with over 800 variables covering demographics, medical information, and recent self-reported food consumption and cooking habits information) for each case and each control. After QA/QC reviews by CDC, it has previously been analyzed by CDC and public health researchers (e.g., Kassenborg et al., 2004). To our knowledge, this data set has not previously been analyzed for evidence of hormesis. The data set was provided to the author as an Excel file by CDC upon request.

In the classification tree notation of this diagram (Lemon et al., 2003), each node in the tree (i.e., each box) indicates the percentages of cases (upper percentage) and controls (lower percentage) for the sub-population described by that box.

The integer at the bottom of each box indicates the total number of subjects described by it. Among 1444 subjects, 59.5% were confirmed campylobacteriosis cases and 40.5% were matched controls, as shown in the top node of Figure 1. (Campylobacteriosis is a food-borne diarrheal illness that typically lasts several days and then, in over 99% of cases, spontaneously resolves itself without need for treatment.) The variable FAST FOOD PER WEEK indicates the number of times that subjects reported eating at a fast food restaurant in the 7 days prior to the onset of campylobacteriosis illness. Thus, this small tree displays basic cross-tab information for case status vs. fast food consumption frequency. (“???” denotes missing data and “77” is a don't know/no answer code.) The methods used to identify the relation in Figure 1 are discussed in the next section.

The classification tree program used to generate Figure 1 (KnowledgeSeeker, marketed by Angoss Software, 2005) automatically partitions the ordinal variable FAST FOOD PER WEEK into the discrete categories shown (i.e., the branches), to create conditional distributions that are statistically significantly different after adjusting for multiple testing bias due to repeated testing with multiple boundary locations. The notation [x, y) on a branch for FAST FOOD PER WEEK indicates the interval x ≤ FAST FOOD PER WEEK < y; thus, the branch labeled [0, 1), for example, denotes people who reported eating at fast food restaurants 0 times in the week prior to illness. These people are at significantly higher risk than people who ate 1 or 2 meals at fast food restaurants (55.8% vs. 34.4%), but risk then increases for more frequent exposures to fast food, reaching a case rate of 69.3% among subjects reporting 5 or more fast food meals per week. The KnowledgeSeeker program is well-suited to this type of analysis as it works with both continuous and discrete variables (including binary and ordered categorical variables) to create highly predictive risk classes without making any specific parametric modeling assumptions (Biggs et al., 1991).

The data display a typical U-shaped (or moderately J-shaped) relation. Such patterns often are not discovered in standard parametric multivariate modeling (e.g., linear or logistic regression with automatic backward or forward stepwise variable selection) even when they exist, since the U shape cannot be expressed by the coefficients in a regression model. (If dummy variables are used to break the domain of the independent variables into downward-sloping and upward-sloping components, then regression methods can be applied successfully, but this requires knowing the correct answer in advance.) The problem is worse when there are hundreds of variables (as in this data set, which has over 800) and many possible interactions: even highly predictive U-shaped relations may be impossible to discover by standard methods in the sea of possible relations.

The following sections develop a possible solution and illustrate it for this data set, building in part on ideas from classification tree analysis, which is designed to detect high-order interactions in models that need not be linear or monotonic.

2. METHODS: INFORMATION-THEORY CRITERIA FOR IDENTIFYING NON-MONOTONIC CAUSAL EXPOSURE-RESPONSE RELATIONS FROM DATA

Traditional epidemiology often begins by seeking non-random associations between potential explanatory variables and response variables of interest, e.g., by using logistic regression modeling to screen for statistically significant predictors of increased risks of adverse health effects (e.g., Lemon et al., 2003). Fully automated variable selection is a notoriously challenging problem, however. On the one hand, “data dredging” (e.g., using automated variable-selection criteria such as the AIC, BIC, or Mallows criteria included in many standard commercial regression software packages) can easily produce false positives (e.g., Raftery et al., 1997). On the other, non-monotonic relations for predictors having both positive and negative relations with risk over different ranges can easily escape detection by these methods, thus producing false negatives. To help overcome these problems, we propose to replace more traditional measures of statistical association between variables, such as correlation coefficients or t-tests of regression coefficients, with mutual information—a measure that also works for arbitrary non-monotonic relations and that is nonparametric, or “model free”, thus reducing the problems of multiple testing bias and model selection bias.

Information Theory Background: Entropy, Mutual Information, and Conditional Independence

Let X and Y be two discrete random variables, e.g., X = level of exposure, Y = level of response. (The following methods can also apply to continuous variables, as in Cover and Thomas, 1991, but we focus on the discrete case, as this is most useful in conjunction with classification trees.) Uncertainty about any discrete random variable X taking values x_i with corresponding probabilities p_i can be quantified by its entropy, defined as:

$$\text{H}(\text{X})=\text{entropy of X}=-{\Sigma }_{\text{i}}{\text{p}}_{\text{i}}{log}_2{\text{p}}_{\text{i}}=\text{E}[{log}_2(1/{\text{p}}_{\text{i}})]\text{bits}$$

H(X) may be interpreted as the average amount of information gained when the value of X is learned. (It is also the expected minimum number of binary yes-no questions with equally likely answers (i.e., Pr(yes) = Pr(no) = 0.5) that one would need to have answered about the value of X to uniquely identify its value.)

The mutual information between any two random variables X and Y, denoted by I(Y ; X), is defined as:

$$\text{I}(\text{Y};\text{X})=\text{H}(\text{Y})-\text{H}(\text{Y}|\text{X}).$$

where H(Y | X) = Σ_xPr(X = x)H(Y | X = x) = E_X[H(Y | X)] is the conditional entropy of Y given X. For any specific observed value of X, say, x, the conditional entropy of Y given that value of X is:

$$\text{H}(\text{Y}|\text{X}=\text{x})=-{\Sigma }_{\text{i}}Pr(\text{Y}={\text{y}}_{\text{i}}|\text{X}=\text{x}){log}_{2}Pr(\text{Y}={\text{y}}_{\text{i}}|\text{X}=\text{x}).$$

Some intuitively appealing properties of entropy H and mutual information, I, include:

1. I(X ; Y) = I(Y ; X), i.e., X and Y provide the same amount of information, or uncertainty reduction, about each other;

2. H(Y | X) ≤ H(Y), i.e., conditioning on (or learning the value of) X never increases the expected uncertainty about Y, but is expected to decrease it unless they are statistically independent.

3. H(X, Y) = H(X) + H(Y | X), i.e., the entropy of the joint distribution of X and Y is the entropy of X plus the entropy of Y given X.

4. I(X ; Y) > 0 if Pr(Y | X = x_i) depends on x_i. For example, if the probability distribution of response variable Y depends on the value of exposure variable X, then the mutual information between them is positive. This allows mutual information to be used in screening for possible exposure-response relations.

5. Let the “causal graph” (also called “Bayesian network”) notation Z → X → Y indicate that the probability distribution of Y depends on the value of X and that the probability distribution of X depends on the value of Z, but the conditional probability distribution of Y given any specific value of X does not depend on the value of Z. In other words, Y is conditionally independent of Z given X. (However, Y is not unconditionally independent of Z, since Z affects Y through X.) Then I(Y ; X) ≥ I(Y : Z), with equality if and only if X is a deterministic, one-to-one function of Z. More generally, in a causal graph, more remote ancestors of a node can never be more informative about it than its direct parents. (In a causal graph, nodes represent variables, and an arrow directed from X to Y indicates that the probability distribution of Y depends on the value of X. Such graphs are required to be acyclic. Each node is conditionally independent of its more remote ancestors, given the values of its parents, i.e., of nodes with arrows pointing into it.)

6. In a causal graph model X – Y – Z (with the arcs oriented in any directions), more remote ancestors can never be more informative that direct parents. Thus, I(X ; Z) ≤ I(X ; Y). Moreover, I(X ; Z | Y) = 0 (i.e., X and Z are conditionally independent given Y) unless both X and Z point into Y.

For these and other aspects of information theory, see Cover and Thomas, 1991.

Classification Trees and Causal Graphs via Information Theory

The above properties suggest that mutual information can be used to help search for potential dose-response relations or exposure-response relations and to identify direct parents of responses in large, multivariate data sets. Two main families of practical data analysis algorithms have exploited this potential: classification tree algorithms and causal graph “learning” algorithms.

A classification tree analysis begins with a specific dependent variable of interest, such as a health response variable in a population, and repeatedly conditions on the “most informative” variables in the data set to calculate its conditional probability distribution, given their values. At any stage in the construction of a tree, each leaf represents a set of values of the variables that have been conditioned on so far. There is a conditional distribution of the values of the dependent variable at each node, given the values of the conditioned-on variables leading to it. At each leaf, the myopically “most informative” variable to condition on next is the one having the highest mutual information with the conditional distribution of the response variable at that leaf. (Less myopic, more CPU-intensive procedures seek the subsets of variables that jointly give the greatest reduction in the entropy of the dependent variable, and then condition on combinations of their values. Continuous variables can be discretized into contiguous ranges as part of this search process by taking either maximum reduction in entropy of the dependent variable or maximal increase in the mutual information of all directly related variables as the goal; see Friedman and Goldsmitz, 1996b). When further conditioning provides no additional useful information about the dependent variable (e.g., as assessed by cross-validation estimation of the true error rate resulting from using the conditional distributions at the current leaf nodes to make predictions about the dependent variable), tree-growing stops.

Like classification trees, causal graphs store conditional distributions at each node. However, the conditional distribution at a node is for the variable represented by that node, rather than for some other dependent variable. Instead of there being a single dependent variable, there is usually a set of variables related by statistical dependence and conditional independence relations that are expressed by the directed arcs (“arrows”) among the variables (nodes). Moreover, the conditional distribution at any node is conditioned only on the values of its parents, i.e., the variables that point into it. This information may be stored in a conditional probability table (CPT) specifying the different conditional probability distributions of that node's variable, for each combination of values of its parents. (Combinations of parent values that lead to the same conditional distribution can be aggregated, e.g., by using ranges of values of the variables to create distinct rows in the CPT.) Several computationally practical algorithms for fitting classification trees and causal graphs to large, multivariate data sets are now available (Murphy, 2001; Tsamardinos et al., 2003)

Classification trees and causal graphs are closely related, as follows. Consider an ideal classification tree algorithm, in which X appears in the tree for Y if I(X ; Y) > 0 (and I(X ; Y | C) > 0 even after conditioning on the other variables, C, in the tree.) For any data set with enough observations, adequate variability in the values of its variables, and redundant variables eliminated (e.g., by replacing any cluster of redundant variables A = B = … = C with any one of them, or more generally by pruning all variables Z satisfying I(X ; Z) = H(X) for some remaining X), the following properties hold (e.g., Frey et al., 2003):

1. All of the parents of a node appear in any mutual information-based classification tree having that node variable as its dependent variable. (This is because, by definition, the conditional distribution of the node depends on the values of its parents.)

2. Once a node's parents (and children, if any) have been included in a classification tree, i.e., conditioned on, no more remote ancestors (or descendants) will enter its classification tree. (By definition, the node's value is conditionally independent of its more remote ancestors, given the values of its parents.)

3. In the causal graph X ← Z → Y, variable Z is called a confounder of the statistical relation between X and Y. It explains away an apparent association between them. Including the parents of a health response variable in its classification tree (i.e., conditioning on them) eliminates all variables that are statistically associated with the response variable only due to confounding. (More generally, X is a parent of Y only if there is no subset of variables C such that I(X ; Y | C) = 0, i.e., only if X provides information about Y that cannot be fully removed by conditioning on any other subset of variables. In the example X ← Z → Y, the tree for Y will include Z but not X. The confounded relation between X and Y is eliminated when the tree conditions on Z.)

4. When a classification tree is grown for a particular node variable, using only its parents as conditioning variables, the leaves of the resulting tree contain the conditional probability table (CPT) information for that node. (The empirical CPT based on the raw data is a maximum-likelihood estimate of the true CPT. It can be used together with a multivariate Dirichlet prior to develop Bayesian posterior estimates of the CPT for purposes of uncertainty analysis; see e.g., Friedman and Goldszmidt, 1996 and Murphy, 2001.)

By property 1, an automated tree-growing procedure based on conditioning on variables having the highest estimated mutual information with the dependent variable tends to create a tree containing the node's parents. In theory, if the dependent variable is a response variable with no children in the data set, the classification tree should consist only of the parents of that node in a causal graph. In practice, it may also include more remote ancestors (and children and descendants, if there are any) since the empirical joint distribution of the variables among the observed cases may contain sampling variability that causes it to differ from the underlying joint distribution determined by the data-generating process. Property 2 can then be used to prune more remote ancestors (and descendants) by testing whether some variables drop out of the tree when others are conditioned on first. In principle, those that cannot be eliminated in this way are the parents and children of a node. To distinguish among parents and children (which are mutually conditionally independent, given the value of the node variable) for variables that have both, it is necessary to orient the arcs.

Health responses are often known a priori to be possible children of exposure-related variables, but not possible parents. Moreover, earlier observations can usually be causes (parents) of later ones but not consequences (children). These properties help to orient the arrows near exposure and response variables in a causal graph. [More generally, if time series information is available on variables, as in many longitudinal epidemiological studies, then X is a potential cause of Y only if the history of X up to and including each time t is informative about the future of Y after t, even after conditioning on the past of Y, i.e.,

$$\text{I}({\text{X}}^{-}(\text{t});{\text{Y}}^{+}(\text{t})|{\text{Y}}^{-}(\text{t}))>0,$$

where X⁻(t) denotes the set of X values at times ≤ t, Y⁻(t) the set of Y values at times ≤ t, and Y⁺(t) the set of Y values after t. This provides an information-theoretic generalization of the concept of Granger causality for multiple time series (e.g., Guatama and Van Hulle, 2003.)]

Property (f) above, which shows that mutual information with a variable Y increases along chains of variables leading to it helps to orient the remaining arcs. The following PC algorithm (Glymour and Cooper, 1999, here modified to use classification trees and mutual information) provides a systematic approach to orienting arcs even without such domain-specific knowledge:

1. Grow a classification tree for each node. Create an undirected arc between each node and every node that appears in its tree (and that cannot be forced to drop out after conditioning on other variables.)

2. Orient any triple of nodes X – Y – Z as X → Y ← Z if and only if I(X ; Z | Y) > 0, i.e., if and only if X and Z are dependent when conditioned on Y.

3. Orient any remaining triple X → Y – Z as X → Y → Z.

4. Orient any pair X – Y with a directed path through X to Y as X → Y. (For example, if X – Y → Z and I(Z; Y) > I(Z ; X) > 0 and I(Z ; X | Y) = 0, then create X → Y.)

5. Repeat steps 3–5 until no more arc directions can be assigned.

A variety of other algorithms are now available for fitting causal graph models even to very large multivariate data sets (Murphy, 2001; Tsamardinos et al., 2003).

We can now summarize our proposed methodology for identifying potential causal exposure-response relations in large data sets, even if the relations are non-monotonic, as follows. First, pre-process the data to remove any redundant variables and to eliminate any variables that occur after the response of interest or that are otherwise known not to be candidates for potential causal variables. (Redundant variables appear as the only nodes in each others' classification trees and satisfy I(X ; Z) = H(X).) Next, identify parents of the response variable in the causal graph for that node. Finally, fit a nonparametric model, such as a classification tree, a non-parametric regression model, or simply the relevant conditional probability table (CPT) (possibly smoothed or approximated by simple regression functions), to the reduced data set consisting of the response variable—which is the dependent variable—and its parents. This approach can be implemented using commercially available classification tree and Bayesian network learning software products, such as KnowledgeSeeker and BayesiaLab, respectively.

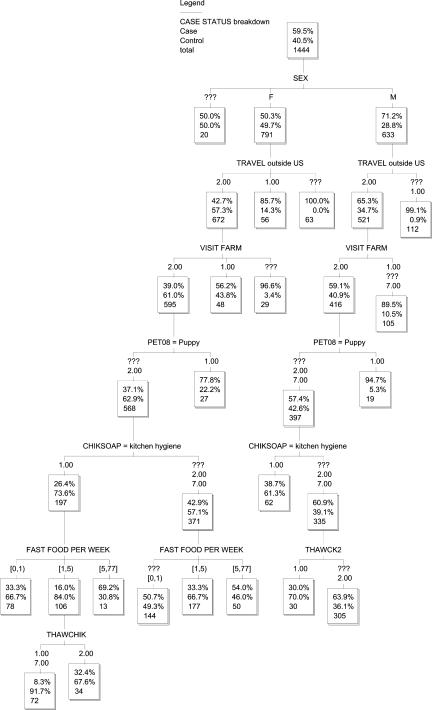
3. RESULTS FOR THE CAMPYLOBACTERIOSIS CASE CONTROL DATA

The cross-tab information in Figure 1 illustrated a single “split” (i.e., conditioning the dependent variable, CASE STATUS, on a single variable, FAST FOOD PER WEEK.) But this is only one of many statistically significant splits, each having positive mutual information with the dependent variable. Figure 2 shows a more fully developed classification tree. All of the variables in this tree are parents of CASE STATUS, in that none can be eliminated by conditioning on other variables. (Potential children and descendants of CASE STATUS, mainly describing duration and treatment of diarrhea, were pruned in the pre-processing step. Throughout the tree, variables are coded so that 1 = Yes, 2 = No, 7 and 77 = don't know/no answer/refused to answer. The KnowledgeSeeker algorithm is computationally efficient, taking on the order of 10 seconds to develop each “split” in the tree when run on a laptop PC.)

FIGURE 2.

Classification Tree for Campylobacteriosis Risk

In this tree, all potential confounding by other variables in the data set has automatically been eliminated, as discussed above. Thus, the statistically significant (but non-monotonic) relation between FAST FOOD PER WEEK and risk (i.e., CASE STATUS) is potentially causal: it cannot be explained away by confounding with other variables in the data set. For example, consider the hypothesis that men, who intrinsically have greater susceptibility to campylobacteriosis, than women also eat at fast food restaurants more frequently, and that this explains the association between fast food dining and risk of campylobacteriosis. This hypothesis can be diagrammed as: FAST FOOD PER WEEK ← SEX → CASE STATUS. It is directly falsified by the classification tree in Figure 2, since the CASE STATUS varies significantly with FAST FOOD PER WEEK even after conditioning on SEX = F, thus proving that I (CASE STATUS; FAST FOOD PER WEEK | SEX) > 0. Other confounding-based explanations for the parents of CASE STATUS shown in Figure 2 are similarly precluded by the data. (A few other variables, including drinking untreated water and having health insurance, were also identified as parents of CASE STATUS for small sub-populations, but were pruned from the bottom of Figure 2, leaving the tree shown. This was done to save space and because they affected only small fractions of the sample and did not appear in multiple parts of the tree, indicating that they had at most only very limited impacts.)

Also interesting is the set of variables that do not appear in the full classification tree for CASE STATUS. For example, it is well known that drinking raw milk is a risk factor for campylobacteriosis. Indeed, the tree-growing program lists it as a significant split, i.e., a variable having significant mutual information (and positive association, by any measure) with CASE STATUS. However, conditioning on VISIT FARM eliminates drinking raw milk as an additional parent of CASE STATUS: they belong to the same cluster of closely associated, partly redundant variables. Similarly, although CHIKSOAP, which records whether subjects reported using soap to wash after handling raw chicken in the kitchen, is a parent of CASE STATUS, buying, handling, thawing, and cooking raw chicken and eating chicken at home all belong to a cluster of tightly inter-related variables that are all associated with reduced risk of being a case. (This cluster of variables is represented by THAWCHICK and THAWCK2 in Figure 2, referring to thawing chicken in any manner and thawing chicken in the refrigerator at home, respectively.) Thus, CHIKSOAP may be a marker for kitchen hygiene in general, rather than specifically for chicken-associated risk.

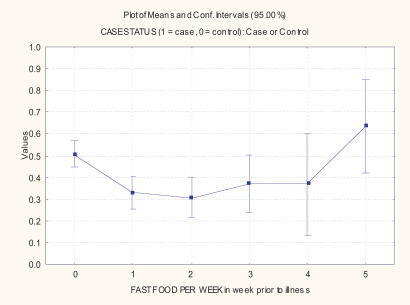
Figure 3 displays the U-shaped exposure-response relation identified in Figure 2 for FAST FOOD PER WEEK and CASE STATUS in a more conventional (interaction plot) format. CASE STATUS has been recoded in Figure 3 so that 1 = case, 0 = control, as this is more usual than the 1 vs. 2 coding used in the original Centers for Disease Control data file. Table 1 summarizes the sizes of the different groups. The reduction in risk between the group exposed to 0 fast food meals per week and the group exposed to fast food once or twice per week is statistically significant (p < 0.05) by all standard tests.

FIGURE 3.

A U-Shaped Exposure-Response Relation for Women

TABLE 1.

Data for Figure 3

Fast Food Meals in Prior Week	Fraction of Exposed Women Who Are Campylobacteriosis Cases	N
0	0.51	276
1	0.33	160
2	0.31	104
3	0.37	54
4	0.37	19
5	0.64	22
All Groups	0.42	650

Although beyond the scope of the data, is tempting to speculate that the increased risk of illness among people with low exposures to fast food may be due to underdeveloped acquired immunity to common pathogens such as Campylobacter, as previously noted for outbreaks associated with raw milk consumption (Blaser et al., 1987).

4. CONCLUSIONS

This paper has proposed and illustrated a general information-theoretic approach to detecting causal non-monotonic exposure-response relations in large epidemiological data sets, based on combining methods from causal graph (or “Bayesian networks”) modeling and classification tree analysis. Applied to a recent food safety case control data set, the new approach successfully discovered a potentially causal (significantly informative, not confounded) U-shaped relation between consumption of fast food by women and resulting risk of a diarrheal illness (campylobacteriosis). This sex-specific non-monotonic relation has not previously been identified in analyses of this data using logistic regression modeling (e.g., Friedman et al., 2004).

In principle, the information-theoretic approach can find arbitrarily shaped causal relations in other large data sets. They essential steps are: (a) Identify informative variables that help to predict the dependent variable (e.g., illness risk) of interest. This can be accomplished via classification tree analysis (even for non-monotonic relations). (b) Eliminate variables (e.g., confounders, redundant variables, variables that follow the effect of interest in time) whose mutual information with the dependent variable is fully explained away by the information contained in other variables or that are inconsistent with the hypothesis of causality. This can be accomplished by conditional independence tests, e.g., using Bayesian network algorithms (including classification tree analysis of individual nodes in a Bayesian network.) (c) Quantify the remaining relation between the dependent variable and its parents using non-parametric methods (e.g., classification trees and conditional probability tables with nonparametric smoothing.) The final relation, even if non-monotonic, reveals the shape of potential causal relations between the dependent variable and a minimal set of predictors (its “parents” in a causal graph.) Current algorithms are practical even for data sets with thousands of records and variables, as run times are on the order of a few minutes on current laptop or desk top machines. Thus, these methods appear to be practical for identifying hormesis (U-shaped) relations and other nonlinearities even in large epidemiological data sets.