Low-Dose Radiation-Induced Protective Process and Implications for Risk Assessment, Cancer Prevention, and Cancer Therapy

Abstract

A low-dose protective apoptosis-mediated (PAM) process is discussed that appears to be turned on by low-dose gamma and X rays but not by low-dose alpha radiation. PAM is a bystander effect that involves cross-talk between genomically compromised [e.g., mutants, neoplastically transformed, micronucleated] cells and nongenomically compromised cells. A novel neoplastic cell transformation model, NEOTRANS₃, is discussed that includes PAM. With NEOTRANS₃, PAM is activated by low doses and inhibited by moderate or high doses and is, therefore, a hormetic process. A low-dose region of suppression of the transformation frequency below the spontaneous frequency relates to the hormetic zone over which PAM is presumed to operate. The magnitude of suppression relates to what is called the hormetic intensity. Both the hormetic intensity and width of the hormetic zone are expected to depend on dose rate, being more pronounced after low dose rates. It is expected that PAM likely had a significant role in the following observations after chronic irradiation: (1) what appears to be a tremendous reduction in the cancer incidence below the spontaneous level for Taiwanese citizens residing for years in cobalt-60 contaminated apartments; and (2) the published reductions in the lung cancer incidence below the spontaneous level in humans after protracted X irradiation and after chronic gamma plus alpha irradiation. Implications of PAM for cancer prevention and low-dose cancer therapy are briefly discussed.

INTRODUCTION

The shape of the dose-response curve for stochastic effects (mutations, neoplastic transformation, and cancer) of exposure to low doses of ionizing radiation or genotoxic chemicals has been the topic of continuous debate (Kondo 1999; Calabrese and Baldwin 2003a,b; Feinendegen et al. 2004; Pollycove 2004; Sykes et al. 2004). The key discussion relates to whether the linear nonthreshold (LNT) model for low-dose extrapolation of cancer risk is valid (Ootsuyama and Tanooka 1993; Azzam et al. 1996; Tanooka 2000; NCRP 2001).

With the LNT hypothesis, any amount of carcinogen exposure increases one's risk of cancer. Now there is growing evidence from epidemiological, experimental, and mathematical modeling studies that does not support the general use of the LNT model for central estimation of cancer risks at low doses of low linear-energy-transfer (LET) radiation (Scott et al. 2003; Scott 2004; Scott et al. 2004). Instead, the results support for adults the existence of hormetic-type, dose-response relationships with low doses and dose rates being protective and high doses causing harm.

Here, a novel approach is used to obtain dose-response functions for cancer relative risk (RR) estimation that allow for hormetic-type dose responses. The approach is based on the previous demonstration of similar dose-response relationships for the RR for cancer induction in humans and for induced neoplastic transformation in vitro (Redpath et al. 2001). The recently introduced, third-generation, neoplastic transformation (NEOTRANS₃) model (Scott 2004) for low-dose, low-LET radiation-induced stochastic effects (genomic instability, mutations, neoplastic transformations) is used to develop RR relationships for neoplastic transformation after single radiation (low- or high-LET) or mixed radiations (low- and high-LET). The RR relationships for neoplastic transformation are then adapted for application to cancer RR estimation in irradiated humans. Implications of the research findings for cancer prevention and low-dose cancer therapy are briefly discussed.

The NEOTRANS₃ model is first introduced, including a description of mathematical relationships associated with radiation-induced neoplastic transformation after brief or protracted exposure to low-LET radiation. RR relationships for neoplastic transformation are then developed for combined exposure to high-LET alpha and low-LET gamma radiation. The RR relationships for neoplastic transformation are then adapted for application to cancer RR in humans for combined, chronic exposure to alpha and gamma radiation. The focus is on characterizing hormetic-type, RR dose-response relationships for specific stochastic effects (neoplastic transformation and cancer).

NEOTRANS₃ MODEL

The NEOTRANS₃ model (Scott 2004) is a refinement of the NEOTRANS₂ model (Scott et al. 2004) which only addressed brief exposures at high rates. In addition to allowing for chronic exposure at low rates, NEOTRANS₃ also allows for varying susceptibilities based on genetic background.

Genomic Instability States

The NEOTRANS₃ model (Figure 1), like its predecessor models NEOTRANS₁ (Scott 1997; Shöllnberger et al. 2001) and NEOTRANS₂ (Scott et al. 2004), links neoplastic transformation potential to the genomic instability status of cells. Such models were given the general name “genomic instability state” models (Scott 1997; Shöllnberger et al. 2001). In addition to a stable genome for resistant cells, NEOTRANS₃ involves three types of genomic instability considered to be important among hypersensitive cells that respond to low radiation doses: (1) normal-minor instability (NMI) associated with normal cell function and normal genome status, (2) transient-problematic instability (TPI) associated with genomic damage that may sometimes be repaired without error but can be misrepaired, and (3) persistent-problematic instability (PPI) that arises from misrepair that yields viable mutants. Thus, PPI can be passed to progeny, increasing their potential for neoplastic transformation. Presently, the model structure does not include a spontaneous transition from the NMI to the TPI state. This is because radiation-associated transitions are assumed to be far more likely over the exposure period considered. The model, however, does allow for spontaneous transition (misrepair related) from the TPI to the PPI state.

FIGURE 1.

NEOTRANS₃ model transitions for hypersensitive cells that respond to low-dose radiation. Genomic instability states NMI, TPI, and PPI are explained in the text. Figure modified from Scott (2004) to clarify normal apoptosis pathway.

For the dose ranges of interest (low doses), it was assumed that hypersensitive cells are much more likely to be impacted than are resistant cells in the target cell population. Thus, newly induced mutants and transformants are much more likely to arise from hypersensitive cells than from resistant cells. Radiation-induced transitions presently relate only to hypersensitive cells.

A key feature of the NEOTRANS₃ model is the inclusion of the previously introduced protective apoptosis-mediated (PAM) process (Scott 2004). PAM is a bystander effect involving cross-talk between genomically compromised (e.g., mutants, transformants, micronucleated cells, etc.) and nongenomically compromised cells leading to intercellular induction of apoptosis among genomically compromised cells. PAM appears to require several hours to be fully activated after a brief low-LET dose and seems to last for at least a day after activation (Scott 2004).

Bauer (2000) has summarized what is known about the intercellular induction of apoptosis among fibroblasts based on numerous studies of his research group (Jürgensmeier et al. 1994; Bauer 1995, 1996; Langer et al. 1996; Hipp and Bauer 1997; Englemann and Bauer 2000). The protective process involves a sophisticated system of interdependencies and interactions of reactive oxygen and nitrogen species. The release of transforming growth factor beta by transformed cells is a key early event. Nontransformed cells, when activated, release a novel peroxidase and nitric oxide. Superoxide anions generated and released by transformed cells participate in the intercellular signaling and also make transformed cells the target for intercellular induction of apoptosis (i.e., transformed cells are selectively removed via apoptosis). The interactions of these molecules result in two currently known major signaling pathways to apoptosis that are based on hypochlorous acid/hydroxyl radicals and on nitric oxide/peroxynitrite. Hydrogen peroxide plays a key role by fostering the hypochlorous acid/hydroxyl radical pathway and by inhibiting the nitric oxide/peroxynitrite pathway.

Several pathways to apoptosis are likely associated with PAM, with the selected path depending on the cell type to be eliminated via apoptosis (mutants, neoplastically transformed cells, micronucleated cells, etc.), its cellular environment, and the nature of the damage to DNA (Scott 2004).

Radiation-associated transitions among hypersensitive cells in NEOTRANS₃ are summarized in Figure 1 for low-LET irradiation. Thus, Figure 1 relates to a hypersensitive sub-fraction, f₁, of cells at risk. Low-LET radiation-induced genomic damage to cells with normal minor instability leads to new cells with TPI. Misrepair and error-free repair, and apoptosis pathways are available for cells with TPI. However, the apoptosis associated with the TPI (called “normal apoptosis”) differs from PAM because PAM is a bystander effect (Scott 2004). Misrepair leads to mutant cells with PPI that have a heightened potential to produce progeny that undergo neoplastic transformation.

Doses above a small stochastic threshold, D_PAM, activate PAM, which then selectively removes precancerous cells (spontaneous and newly emergent transformants) as well as some other genomically compromised cells from the target population. Above a dose-rate-dependent, stochastic, low-LET radiation dose, D_off, PAM is inactivated. Thus, PAM is a hormetic process that takes place in the individual-specific, hormetic zone D_PAM to D_off. Both D_PAM and D_off can vary over in vitro replicates and over different individuals (i.e., in vivo). Thus, they are properly characterized by distributions rather than point estimates. Bayesian analysis methods facilitate obtaining distributions for D_PAM and D_off since the focus of Bayesian analyses is characterization of distributions (called posterior distributions). Conventional regression analysis does not allow addressing stochastic thresholds, although it allows addressing deterministic thresholds when errors in the deterministic quantity are normally distributed.

The parameter α₁ in Figure 1 when multiplied by the radiation dose rate c, accounts for low-dose-induced genomic damage among the hypersensitive cells in the population. The ability of radiation to produce initial damage to DNA is assumed not to depend on genetic background. Rather, genetic background is assumed to influence the DNA damage mitigation process and such influences are accounted for through other model parameters.

The parameter μ₁ governs the rate of commitment of damaged hypersensitive cells to the activated error-free repair pathway. This repair pathway is associated with normal repair, which is presumed to be activated by radiation. The corresponding parameter for the misrepair pathway (which competes with the error-free pathway in normal repair) is η₁. Misrepair leads to a variety of viable mutations (cells with PPI). Activated normal repair includes base excision repair, nucleotide excision repair, recombinational repair (homologous recombination, nonhomologous end joining), and mismatch repair.

The parameter ɸ₁ governs the rate of commitment of newly damaged cells (including lethal mutations) to the normal apoptotic pathway. However, unlike PAM, normal apoptosis is not a bystander effect (Scott 2004). In addition, PAM operates at low doses of low-LET radiation, while normal apoptosis may occur both at low and high doses as well as after high-LET irradiation. PAM appears not to occur after low doses of high-LET alpha irradiation (Scott et al. 2004).

Typical units for α₁ are mGy⁻¹. Typical units for μ₁, η₁, and ɸ₁ are min⁻¹. The parameter f₁ is dimensionless. These parameters are stochastic (i.e., have distributions) but currently are not time dependent.

With the NEOTRANS₃ model PAM, normal apoptosis, and normal repair (error-free component) work together in guarding against genomic instability.

• Normal apoptosis removes damaged cells before mutations arise.

• The error-free component of normal repair eliminates DNA damage but not damaged cells.

• PAM removes mutants, neoplastic transformants, and likely removes other aberrant cells (e.g., micronucleated cells).

Thus, the indicated team of biological protectors provides powerful protection against adverse stochastic effects of exposure to genotoxic agents.

Others (Wolff 1998; Pant et al. 2003) have implied that a novel, possibly error-free DNA repair mechanism rather than PAM may be responsible for low-dose-induced protection against mutations and neoplastic transformation. This hypothetical, essentially error-free repair process, has been called super repair (Scott 2004). The postulated existence of super repair is mainly related to the fact that inhibition of DNA repair inhibits the low-dose-associated protection against stochastic effects. However, it was pointed out (Scott 2004) that inhibition of DNA repair may also inhibit PAM. Further, it was demonstrated (Scott 2004) that the experimental data for neoplastic transformation after inhibition of DNA repair were adequately predicted by the NEOTRANS₃ model when one simply assumed that inhibition of DNA repair also inhibits PAM. It was also pointed out that it is highly unlikely that the clustered DNA damage (e.g., multiple closely spaced double-strand breaks) induced by ionizing radiation can be repaired without any errors and that no new, completely error-free repair processes have been observed. Further, homologous recombination does not operate throughout the cell cycle. In addition, there is an apparent absence of DNA repair after very low doses of low-LET radiation (Rothkamm and Löbrich 2003).

Brief or Protracted Exposure to Low-LET Radiation

For brief exposure to small or moderate doses, D, of low-LET radiation, the expected transformation frequency per surviving cell (TFSC) is given in the context of NEOTRANS₃ by (Scott 2004):

$$\begin{array}{c}TFSC(D)=T_0,forD<D_{PAM},\\ TFSC(D)=(1-f_0)\{T{}_0+[(1-T_0)]k_{T}D\},for{D}_{PAM}\le D<D_{off},\\ TFSC(D)=T_0+[(1-T_0)]k_{T}D,forD\ge D_{off},\end{array}$$ (1)

where the slope parameter k_T is given by:

$$k_T=f_1{\alpha }_1{\eta }_1\Omega /({\mu }_1+{\eta }_1+{ɸ}_1).$$ (2)

The subscript T indicates the endpoint neoplastic transformation, and the parameter f₁ is the fraction of hypersensitive cells. Equation 1 applies to both brief and protracted exposures to low-LET radiation. A similar relationship would apply to mutations.

The parameters ω, μ₁, η₁, and ɸ₁ as well as the efficiency of the PAM process are assumed to be influenced by genetic background. In addition, for in vivo exposure, Ω may differ for different tissues. Thus, k_T depends on genetic background and target tissue in vivo.

The parameter f₀ is the fraction of the spontaneous genomically compromised cells (e.g., spontaneous transformants) removed via radiation-induced PAM and has been given the special name “protection factor” (PROFAC) (Scott et al. 2003). The PROFAC is a measure of the hormetic intensity of the PAM process. For f₀ = 0 (i.e., no PAM), Equation 1 reduces to the LNT model. The PROFAC is expected to increase with decreasing dose rate (e.g., keeping dose constant and increasing the exposure time). A PROFAC also can be used to characterize mutation frequency and cancer incidence (or mortality) dose-response relationships when adaptive responses occur and are associated with hormetic processes.

The currently used data permit estimating k_T only, not the individual parameters on the right-hand side of Equation 2. However, previously it has been shown that with a rich data set (i.e., one with numerous doses over the range of interest and several dose rates), one can indeed estimate basic model parameters (Scott 1997; Schöllnberger et al. 2001).

As already indicated, for in vivo studies of neoplastic transformation or mutations, D_PAM is stochastic. Such stochastic thresholds impact the shape of the dose-response curve for the stochastic effect considered. For in vitro studies, currently available low-dose data place the upper bound for D_PAM below 1 mGy (0.001Gy) (Scott 2004).

For doses below D_PAM, misrepair is currently assumed not to occur (Scott et al. 2004; Scott 2004). For this dose range, damaged cells with TPI are presumed to undergo normal apoptosis. For a dose just above D_PAM and for a specific irradiated individual and target tissue in that individual, the dose-response curve drops down from T₀ to (1 – f₀)T₀ and remains roughly flat for a range of doses; however, for low-dose-rate irradiation, the range over which the dose-response curve remains roughly flat is expected to be extended, possibly to several Gy. Because D_PAM varies in vivo over different individuals (and for in vitro replicates), the dose-response curve for neoplastic transformation derived from averaging over different individuals (or over in vitro replications) will not display the sudden drop indicated but will initially decrease rather smoothly. A similar smooth rise in the dose-response curve also will be associated with the stochastic dose D_off. In addition, f₀ is expected to increase as the time period over which a given dose is delivered increases (i.e., with decreasing dose rate). Thus, f₀ should be considered to depend on low-LET radiation dose rate and on duration of exposure.

Combined Exposure to Low Doses of Alpha and Gamma Radiations

Here RR relationships are first developed for neoplastic transformation induced by combined high-LET alpha and low-LET gamma irradiation. From the relationships for combined exposure, RR relationships for individual radiations can also be expressed. Results obtained for neoplastic transformation facilitate modeling RR for cancer induction in humans.

Currently available data indicate that PAM is not activated (i.e., f₀ = 0) by low doses of high-LET alpha radiation (Scott 2004; Scott et al. 2004). However, for combined exposure to alpha and gamma radiation, it is assumed that PAM could be activated by the gamma-ray component of the dose.

In this section and throughout the remainder of the paper, the subscript H is used for high-LET alpha radiation and the subscript L for low-LET gamma radiation. Thus, for alpha radiation k_T is replaced with k_T,H and for gamma rays k_T is replaced with k_T,L. For the combined alpha and gamma irradiation considered here, it is assumed that the gamma-ray dose is in the hormetic zone (D_PAM < D_L < D_off) so that PAM is activated. Thus, the transformation frequency per surviving cell for the combined exposure is given by:

$$TFSC(D_L,D_H)=(1-f_0)\{T_0+(1-T_0)(k_{T,L}{D}_L+k_{T,H}{D}_H)\}.$$ (3)

The term enclosed within the aggregation signs, {}, is just the joint probability of a spontaneous, gamma-ray-induced, or alpha-radiation-induced transformant among surviving cells. The term (1 – f₀) is just the probability that a transformant arising for any reason will survive activated PAM.

The RR relationship that corresponds to Equation 3 is given by:

$$R{R}_T(D_L,D_H)=(1-PROFA{C}_L)\{T_0+(1-T_0)(k_{T,L}{D}_L+k_{T,H}{D}_H)\}/T_0.$$ (4)

where the hormetic intensity PROFAC_L has replaced f₀. For only low-dose gamma irradiation the RR is given by RR_T(D_L,0). Similarly, for only alpha radiation, the RR is given by RR(0,D_H) but with the PROFAC_L set to zero, which yields the LNT model.

Figure 2 shows results of application (Scott 2004) of Equation 4 to data of Redpath et al. (2001) for gamma-ray-induced neoplastic transformation of HeLa × skin fibroblast human hybrid cells. Bayesian inference methods were used to fit the NEOTRANS₃ model to the data (Scott 2004; Scott et al. 2004). With the Bayesian approach, model parameters are assigned prior distributions which are operated on via a likelihood function that depends on the dose-response model being used and on the observed biological effects data. The outputs are posterior distributions of model parameters (including D_off) that have associated statistics including posterior mean, standard deviation, and specific percentiles. Markov chain Monte Carlo (MCMC) methods have been used to implement the Bayesian analyses (Scott 2004; Scott et al. 2004).

FIGURE 2.

Relative risk (RR) for gamma-ray-induced neoplastic transformation of HeLa × skin fibroblast human hybrid cells based on data of Redpath et al. (2001). The indicated error bars were obtained by dividing the 95% confidence values for the transformation frequency by the mean spontaneous frequency. Thus, uncertainty in the spontaneous frequency is not reflected in the error bars.

The data in Figures 2 did not permit estimating the distribution for D_PAM because of the absence of sufficient data at very low doses (< 1 mGy). All nonzero doses used experimentally were assumed to exceed the maximum for D_PAM. The 5% and 95% values for the posterior distribution for D_off were 155 mGy and 245 mGy, respectively. The associated posterior mean of 200 mGy is essentially the starting value assigned in the MCMC analysis, indicating that a larger data set is needed in order to reliably estimate the mean for the stochastic variable D_off.

For the hormetic zone it is expected that K_T,HD_H >> k_T,LD_L so that a reasonable approximation for Equation 4 is:

$$R{R}_T(D_L,D_H)\approx (1-PROFA{C}_L)\{1+[(1-T_0)/T_0]k{}_{T,H}{D}_H\}.$$ (5)

which depends on the high-LET alpha radiation dose but not on the low-LET gamma ray dose. It is expected that for protracted exposure at low rates, the hormetic zone can be greatly extended possibly with D_off exceeding 1000 mGy (Scott 2004). Thus, Equation 5 is expected to apply to chronic exposure to low, moderate, and possibly higher doses.

It follows from the above that:

$$R{R}_T(D_L,0)\approx 1-PROFA{C}_L,$$ (6)

and

$$R{R}_T(0,D_H)=1+[(1-T_0)/T_0]k_{T,H}{D}_H.$$ (7)

Figure 3 shows results of application of Equation 6 to the low-dose data (0 to 100 mGy) in Figure 2. The horizontal solid line through the data is just the mean of the nonzero dose data (5 points) for RR_T. The dashed lines are the associated 95% confidence region for the indicated mean.

FIGURE 3.

Results of application of the approximation in Equation 6 to the low dose RR data (within hormetic zone) of Redpath et al. (2001) in Figure 2.

In the next section, Equation 5 is used to obtain a similar relationship for RR for cancer induction in humans by combined exposure to alpha and gamma radiation. Justification for this approach to obtaining RR relationships for cancer induction is also provided in the next section.

RELATIVE RISK FOR CANCER INDUCTION IN HUMANS

Redpath and colleagues (2001) have shown that the dose-response relationship for the RR for low-dose, radiation-induced neoplastic transformation in vitro has a similar shape as for the RR for cancer induction in humans. This implies that dose-response functions for RR for neoplastic transformation could be adapted for application to RR for cancer induction in humans, thereby facilitating low-dose risk extrapolation (e.g., into the hormetic zone). This is assumed to be true for gamma radiation, alpha radiation, and for combinations of both. Mathematical relationships obtained for gamma radiation are assumed to also apply to X rays, beta particles, and possibly other forms of low-LET radiation. Whether or not results obtained for alpha radiation apply to neutrons is unclear because neutrons tend to produce secondary gamma rays.

For low-dose induction of cancer in humans by combined chronic gamma plus alpha irradiation, it is assumed that an equation similar in structure to Equation 5 applies based on the above indicated observations by Redpath et al. (2001). Thus, k_T is replaced with a corresponding slope parameter K_C for cancer induction. Throughout this section the subscript C is used to indicate cancer induction. The spontaneous transformation frequency, T₀, is replaced with the baseline cancer incidence, B, for the population considered. Use of PROFAC_L is maintained but with the understanding that here it applies to protection against cancer occurrence and may differ in value from the protection factor associated with protection against neoplastic transformation. For protection against cancer occurrence, immune system stimulation by low-dose radiation may provide added protection (Pollycove 2004; Liu 2004) in addition to PAM.

If follows that for cancer induction by chronic low-dose alpha plus gamma irradiation where gamma-ray doses are in the hormetic zone that:

$$R{R}_C(D_L,D_H)\approx (1-PROFA{C}_L)\left\{1+[(1-B)]/B{K}_{C,H}{D}_H\right\}.$$ (8)

For cancer induction by chronic gamma irradiation within the hormetic zone, the relative risk, RR is just:

$$R{R}_C(D_L,0)\approx 1-PROFA{C}_L.$$ (9)

For chronic exposure to alpha radiation only and assuming PAM is not activated by alpha radiation one gets:

$$R{R}_C(0,D_H)=1+[(1-B)/B]K_{C,H}{D}_H.$$ (10)

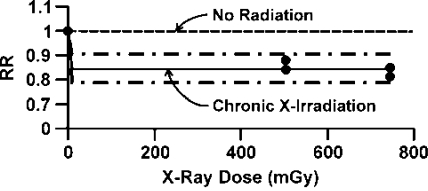
Equation 10 is consistent with the LNT hypothesis and there is no hormetic zone. Figure 4 shows results of the application of Equation 9 to data for the RR for lung cancer mortality among 64,172 Canadian tuberculosis patients (fluoroscopy cohort study) who received fractionated (protracted) exposure to diagnostic X rays. The data were reported by Howe (1995). Only a modest hormetic intensity (PROFAC_L = 0.16 ± 0.03) was implicated against lung cancer. The smooth curve through the data points for D_L > 0 is based on the mean of individual estimates of the difference 1 – PROFAC_L obtained from the four data points occurring between 400 and 800 mGy. The dashed curves surrounding the central curve are 95% confidence values for 1 – PROFAC_L.

FIGURE 4.

Lung cancer mortality relative risk (RR) based on Canadian tuberculosis patients chronically exposed to X rays. Data are from fluoroscopy cohort study of Howe (1995). Equation 9 was used to fit the data.

Equation 8 was applied to RR data (Khokhryakov et al. 1996) for lung cancer in humans (Mayak workers) after chronic exposure over years to alpha plus gamma radiations. The data and modeling results are presented in Table 1. Model fitting was carried out via Bayesian inference conducted with WinBUGS software (Schöllnberger et al. 2001; Scott 2004). The indicated analyses also involved use of MCMC. The prior distribution for PROFAC_L was uniform over the interval (0.7, 1). The prior distribution for K_C,H was uniform over the interval (1.0×10⁻⁵/mGy, 4.0×10⁻⁴/mGy). Baseline incidence rates, B, were fixed at the means reported by Khokhryakov et al. (1996). Because dose groups were used with rather wide dose ranges in some cases, doses were modeled as being uniformly distributed over the dose intervals indicated in Table 1. Thus, analyses were based on only two free parameters K_C,H and PROFAC_L. Cancer cases associated with a specific dose were assumed to have a Poisson distribution.

TABLE 1.

Relative risk (RR) data for lung cancer incidence in Mayak Plutonium Facility workers.

Alpha radiation dose interval (mGy)a	Observed RRC (mean baseline)b	Bayesian posterior mean RRC ± SD	Bayesian posterior 5% value for RRC	Bayesian posterior 95% value for RRC
0–12	0.39 (41 ± 25)b	0.359 ± 0.073	0.246	0.487
12.1 – 50	0.53 (57 ± 41)	0.558 ± 0.092	0.418	0.721
51 – 200	1.58 (76 ± 55)	1.59 ± 0.14	1.36	1.84
201 – 800	4.65 (86 ± 93)	4.66 ± 0.23	4.29	5.05
801 – 3200	28.1 (99 ± 106)	28.1 ± 0.53	27.2	28.9

^aDoses are absorbed doses averaged over the lung.

^bNumbers within parentheses are baseline lung cancer cases per 100,000 persons per year; data are from Khokhryakov et al. (1996).

After carrying out the initial 5000 MCMC iterations, a check was made for the status of autocorrelations to assist in estimating how long a chain needed to be run for convergence. Results indicated that on the order of 500,000 iterations were needed. Instead, 1,000,000 iterations were used with the first 800,000 treated as burn-in (i.e., discarded).

The posterior mean for the slope parameter K_C,H was 1.21×10⁻⁴/mGy (0.121/Gy). The associated standard deviation was 4.0×10⁻⁶/mGy. The posterior mean for PROFAC_L was 0.86 ± 0.07, indicating that about 86% of spontaneous lung cancers (including those associated with smoking) were possibly prevented. Similarly, it appears that about 86% of lung cancer cases that would have occurred with exposure only to alpha radiation were halted (did not occur) because of the chronic gamma irradiation. Thus, the results are consistent with the view that chronic, low-dose-rate gamma irradiation can turn on and prolong the PAM process.

How does the risk coefficient of 0.1 excess lung cancer cases per Gy of alpha radiation compare to results from animal studies? Lundgren et al. (1991) reported a value of 0.11 excess lung cancer cases per Gy for a group of 70 F344/Crl rats that inhaled ²³⁹Pu, when the average dose to the lung (lowest-dose group) was 0.13 Gy. For the next to lowest-dose group (average dose of 0.26 Gy) the corresponding value was 0.16/Gy. In the next to the highest-dose group (average dose 0.76 Gy) the corresponding value was 0.053/Gy. For the highest-dose group (average dose 2.8 Gy), the corresponding value was 0.062/Gy. The average of these four values is:

$$\text{average}=(0.11+\mathrm{0.16.053}+0.062){\text{Gy}}^{-1}/4=0.09625/\text{Gy},$$

which is approximately 0.1/Gy, essentially the same as derived for the Mayak workers!

DISCUSSION

The NEOTRANS₃ model includes the stochastic threshold, D_PAM, and the stochastic dose, D_off, which defined the stochastic width of the individual-specific (or replicate-specific) hormetic zone. Table 2 presents some simulated data for a hypothetical in vitro neoplastic transformation study whereby 10 replicates are used. The hypothetical data presented illustrate the stochastic nature of the width of the replicate-specific hormetic zone. D_PAM was assumed to have a uniform distribution over the interval 0.1 to 1.0 mGy. D_off was assumed to have a uniform distribution over the interval 150 to 250 mGy. For the 10 replicates considered, the replicate-specific width of the hormetic zone ranged from 164 to 226 mGy.

TABLE 2.

Simulated data for width of hormetic zone associated with gamma-ray-induced neoplastic transformation in hypothetical in vitro system.

Replicate	DPAM (mGy)	Doff (mGy)	Width of hormetic zone (mGy)
1	0.42	216	216
2	0.56	226	225
3	0.74	199	198
4	0.75	186	185
5	0.85	227	226
6	0.25	164	164
7	0.84	211	210
8	0.22	202	202
9	0.70	194	193
10	0.98	219	218

The NEOTRANS₃ model was extended to address combined exposure to alpha and gamma radiations. RR relationships developed for neoplastic transformation were adapted for application to cancer induction in humans. Resulting equations were applied to lung cancer induction among Mayak workers exposed over years to alpha and gamma radiations. However, results obtained differed from those obtained by Kreisheimer et al. (2003).

Kreisheimer et al. (2000, 2003) in using internal controls did not find evidence for the existence of a low-dose hormetic zone in their studies of lung cancer but rather concluded that the LNT model adequately described the risk associated with alpha radiation. However, this conclusion is likely due to their choice of using internal controls. For example, had the lowest nonzero dose group in Table 1 been used as controls in the analysis conducted in this paper, the conclusion would have been similar as was arrived at by Kreisheimer et al. (2000, 2003). This is because the RR for the lowest-dose group would have been rescaled from a value close to 1 – PROFAC_L to a value of 1, leading to a much steeper dose-response curve for RR when evaluated based on the LNT model fitted to the full range of doses available. To see the protective impact of PAM, one needs a reference population not having significant low-LET radiation doses. Essentially all of the Mayak workers were exposed to ionizing radiation related to activities that took place at the facility as well as to environmental radionuclide contamination associated with releases from the Mayak facility.

Evidence for a low-dose hormetic zone has been reported for lung cancer induction in association with chronic exposure to ionizing photon radiation. Rossi and Zaider (1997) critically reviewed the literature on radiogenic lung cancer and concluded that, “at radiation doses generally of concern in radiation protection (< 2 Gy), protracted exposure to low-LET radiation (X- or gamma-rays) does not appear to cause lung cancer. There is in fact, indication of a reduction of the natural incidence.”

In a recent publication by Chen et al. (2004) the following is stated related to the approximately 10,000 people who for years occupied cobalt-60 contaminated apartments in Taiwan:

“They did not suffer a higher incidence of cancer mortality, as the LNT theory would predict. On the contrary, the incidence of cancer deaths in this population was greatly reduced—to about 3% of the incidence of spontaneous cancer death in the general Taiwan public. In addition, the incidence of congenital malformations was also reduced—to about 7 percent of the incidence in the general public. These observations appear to be compatible with the radiation hormesis model.”

The indicated results suggest that very high hormetic intensity (PROFAC_L > 0.95) can be associated with chronic exposure of humans at low rates to gamma rays. However, these results should be considered preliminary. Even so, the results are consistent with the view that PROFAC_Lincreases as dose rate decreases and as the exposure time is increased. Further, they suggest that PAM may also provide protection against congenital malformation. However, new research is needed to address this possibility.

The Hanford Thyroid Disease Study did not find evidence of any excess risk for thyroid cancer induction for persons living in the vicinity of the Hanford facility who were exposed to beta radiation from radioactive iodine released from the facility (USDHHS 2002). For doses in the range of 0–100 mGy, risk was not correlated with dose and was less than for the control group based on persons outside what was considered the irradiation zone. In addition, for several health effects, the mean slope of the risk versus dose relationship was negative (indicating a possible low-dose hormetic zone).

Animal data are also consistent with the possible existence of low-dose hormetic zones for cancer induction by low-dose-rate, low-LET radiation (Yamamato et al. 1998; Kondo 1999; Tanooka 2000; Yamamato and Seyama 2000). In addition, Mitchel et al. (2003) have demonstrated that low-dose gamma radiation increases the latency for spontaneous lymphoma formation in cancer-prone Trp53 heterozygous mice, which is consistent with the existence of a low-dose hormetic zone.

Knowledge of the existence of a low-dose hormetic zone associated with low-LET radiation has important implications for cancer prevention and for low-dose cancer therapy (Liu 2004). For populations at high risk for cancer occurrence (e.g., heavy cigarette smokers, persons exposed to high doses of chemical carcinogens, communities ingesting high levels of carcinogens [e.g., aflatoxin] in their diet), the results presented suggest that a little dab of gamma (or X) rays now and then could repeatedly activate PAM and thereby selectively remove precancerous cells from the body. By removing precancerous cells, one would expect the cancer risk to also decrease, possibly leading to extension of the latent period for cancer occurrence in some cases, and possibly preventing cancer occurrences in other cases. The notion that low doses of low-LET radiation (e.g. gamma or X rays) could act as a cancer preventive agent is novel. Each dose of radiation would need to be in the hormetic zone and timing of the doses could be important.

Regarding low-dose therapy for cancer, it is recognized that cancer cells seem to have at least partly lost the ability to undergo apoptosis. This implicates their having a reduced ability to undergo PAM. Knowledge of the molecular changes that prevent cancer cells from undergoing PAM could lead to new molecular tools for reversing the inhibition of PAM, thereby allowing for PAM to operate against existing cancer cells. This could lead to novel low-dose therapy protocols for possibly eliminating cancer without causing severe damage to normal tissue. The currently used high-dose radiation therapy causes severe damage to normal tissue, thereby limiting the success of the therapy.

Arsenic trioxide has been found to sensitize cancer cells to undergoing apoptosis (Miller et al. 2002; Kang et al. 2004). This suggests that novel cancer therapy strategies might involve combined exposure to low dose arsenic trioxide (or other apoptosis sensitizing agents) and low-dose, low-LET radiation. Sensitizing cancer cells to undergo apoptosis and then using low-LET radiation to amplify the PAM process could possibly lead to highly efficient killing of cancer cells while sparing normal tissue from significant injury.

It is important to consider who might not benefit from PAM induction. Should there be members of an at-risk population for radiation exposure, which do not already have significant numbers of genomically compromised cells in their body, then for such persons, PAM activation may not occur and should it occur may not provide any real benefit. For such individuals there may not exist a hormetic zone for low-dose-induced stochastic effects. Possible candidates would be the embryo/ fetus, newborn, young children, and teenagers; as their bodies may not contain significant numbers of genomically compromised cells for PAM to be beneficial.

The existence of a low-dose hormetic zone for low-LET radiation-induced stochastic effects means that low-dose risk extrapolation based on the LNT model can lead to phantom excess risk at low doses; therefore, its use could lead to more harm than benefit to society. Such phantom excess risks could also arise for combined exposure to low- and high-LET radiation in circumstances where PAM is activated by the low-LET component of the dose.

Results presented mainly focused on exposure to alpha or gamma radiation or their combinations. Similar approaches as presented could be used for exposure to a genotoxic chemical, combination of genotoxic chemicals, and to radiation plus genotoxic chemicals. RR relationships could be developed for neoplastic transformation and adapted to application to RR for cancer induction in humans.

CONCLUSIONS

1. Evidence based on the NEOTRANS₃ model was provided for the existence of a low-dose hormetic zone for neoplastic transformation after exposure to low-LET radiation. The zone is explained on the basis of activated PAM.

2. The existence of a low-dose hormetic zone for low-LET radiation-induced stochastic effects means that low-dose risk extrapolation based on the LNT model can lead to phantom excess risk at low doses.

3. While no hormetic zone appears to be associated with low-dose alpha irradiation, combined exposure to low doses of gamma rays and alpha radiation can also be associated with a hormetic zone.

4. The activation of PAM by low doses of radiation makes possible the development of improved protocols for low-dose therapy for cancer as well as for novel cancer prevention strategies for populations already at high risk for cancer development.

5. Not everyone in an at-risk population to radiation exposure may benefit from PAM activation. Persons that may fall into this category include the embryo/fetus, the newborn, young children, and teenagers since they may not possess significant numbers of genomically compromised cells to benefit from PAM.