The Occurrence of Hormesis in Plants and Algae

Abstract

This paper evaluated the frequency, magnitude and dose/concentration range of hormesis in four species: The aquatic plant Lemna minor, the micro-alga Pseudokirchneriella subcapitata and the two terrestrial plants Tripleurospermum inodorum and Stellaria media exposed to nine herbicides and one fungicide and binary mixtures thereof. In total 687 dose-response curves were included in the database. The study showed that both the frequency and the magnitude of the hormetic response depended on the endpoint being measured. Dry weight at harvest showed a higher frequency and a larger hormetic response compared to relative growth rates. Evaluating hormesis for relative growth rates for all species showed that 25% to 76% of the curves for each species had treatments above 105% of the control. Fitting the data with a dose-response model including a parameter for hormesis showed that the average growth increase ranged from 9±1% to 16±16% of the control growth rate, while if measured on a dry weight basis the response increase was 38±13% and 43±23% for the two terrestrial species. Hormesis was found in >70% of the curves with the herbicides glyphosate and metsulfuron-methyl, and in >50% of the curves for acifluorfen and terbuthylazine. The concentration ranges of the hormetic part of the dose-response curves corresponded well with literature values.

INTRODUCTION

Growth stimulatory responses of plants to low doses of chemical stress have been observed by weed scientists for decades. In fact, one of the first herbicides, MCPA, was developed with the purpose of enhancing yield in crops (Allen et al., 1978). Dosing, however, proved to be difficult, and since then the synthetic auxins have mainly been recognized for their deleterious effect on plants at higher doses. As most research on plants and herbicides has been done with the purpose of weed control, focus has been on adverse effects, and hormesis is normally only commented on as outliers relative to the sigmoid dose-response curve (Streibig, 1980). Hormesis in plants has therefore received relatively little attention until recently (Calabrese, 2005a; Calabrese and Blain, 2005). One of the first studies aimed at investigating hormesis in plants was published by Wiedman and Appleby in 1972. They studied the effect of 16 herbicides on oat and cucumber plants and found hormesis on root and shoot dry weight for several photosystem II (PSII) inhibiting herbicides. But the growth increases could not be explained by changes in respiration, photosynthesis or by the content of proteins, free amino acids or soluble carbohydrates (Wiedman and Appleby, 1972). Other studies, however, found that sub-toxic levels of PSII-inhibiting traizine herbicides had hormonal effects (e.g.,Copping et al., 1972) and improve nitrogen metabolism (e.g.,Ries et al., 1967). Since then the mention of hormesis in plants and algae has only been sporadic, until the late 1990'es where general theories concerning the mechanisms behind hormesis started to emerge.

The theories treat the phenomenon of hormesis at different ecological levels. Viewed from an evolutionary perspective, hormesis on plant fitness is not expected (Forbes, 2000). However, trade-off between traits to minimise fitness reduction could be expected. Plants are sessile organisms and can therefore not escape physically from unfavourable conditions. They can however allocate their resources in ways to optimise their growth under stress-full conditions. It is well known that plants allocate root biomass in the soil patches where the environment is favourable in terms of water and nutrients, while avoiding more unfavourable soil patches (Jackson et al., 1990; Wijesinghe and Hutchings, 1999; Kleijn and van Groenendael, 1999). Soil-applied herbicides and allelochemicals can contribute to unfavourable soil conditions, and might therefore affect how resources are allocated both within the root system and between root and shoot.

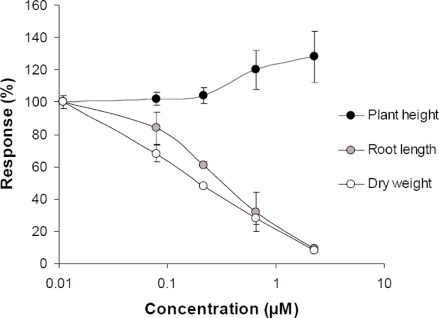
Plant shoots can also change morphology in response to environmental stress. An illustrative example of the result of resource allocation in plants in response to chemical pollutants is given in Figure 1, where both plant dry weight, plant height and root length is measured on the aquatic plant Myriophyllum spicatum exposed to a mixture of tetracyclines (Figure 1). Plant height is stimulated by the tetracyclines, and had the concentration range in the experiment been extended, growth measured as plant height would most probably have formed a typical hormetic dose-response curve. Growth measured on a dry weight basis, however, declined. Hence the apparent hormetic response measured on height was a result of resource allocation within the plant, allocating resources to shoot elongation in response to the light attenuation caused by the brown coloured tetracyclines (Brain et al., 2005). Similar trade-offs between traits have been observed for animal test systems (Forbes, 2000; Fujiwara et al., 2002). It is therefore always important to consider the relative importance of the measured trait for overall fitness of the individual, before evaluating the consequences of a probable hormetic effect.

FIGURE 1.

Relative plants height, root length and plant dry weight of the aquatic macrophyte Myriophyllum spicatum after 28 days growth as a function of the concentration of a tetracycline mixture. The figure is redrawn from figure 2 in Brain et al. (2005).

Viewing hormesis in an ecosystem context, hormetic responses measured on growth can turn out to be a result of altered competition between species. If a competitor, parasite or disease of a species is more susceptible to a certain chemical than the species itself, then the species will experience a relief from a resource-demanding stress factor and hence increase growth at low chemical concentrations. This is the basic principle behind the beneficial effect of pharmaceuticals such as penicillin or vertebrates. An example from the plant world could be the hormetic dose-response curves observed for seven macrophyte species exposed to the herbicide terbuthylazine (Cedergreen et al., 2004; Cedergreen et al., 2005). In this study the epiphytes, which grow on the plant surfaces, were more susceptible to terbuthylazine than the macrophytes. Hence at low concentrations the decrease in light, carbon and nutrient availability caused by the epiphytes was relieved compared to the controls, giving the macrophytes more optimal growth conditions (Cedergreen et al., 2004). This does not exclude that physiological processes inducing hormesis takes place, but changed competition between species was likely to play a considerable role for the observed pattern. Also the relief of density dependent pressure on a population can lead to hormetic responses when measured on individuals (Forbes, 2000). If for example seed germination decrease in a plant population experiencing density dependent growth, then the seeds that do germinate will experience less competition and therefore have better growth conditions. When working with multiple species or multiple individuals of the same species, hormetic growth curves therefore can be a result of altered competition between species or individuals rather that a specific physiological response of the individual.

The physiological and molecular mechanisms behind growth hormesis in plants are not well investigated. Plants have hormones just as animals, and it is possible that some of the hormetic responses stem from induction of plant hormonal systems at low chemical concentrations. This is demonstrated by the synthetic auxins, which have shown to induce hormetic responses in several studies (Morré, 2000; Allender et al., 1997). If low doses of chemicals therefore stimulated the production or activity of natural auxins or other plant hormone systems (Weyers and Paterson, 2001), hormetic responses in some plant traits could be expected. There is a single study suggesting a molecular target at the cell surface enhancing cell enlargement to be responsible for hormesis in plant cells (Morré, 2000), and another study showing that substances affecting the transport of Ca over cell membranes can ameliorate synthetic auxin induced hormesis in cotton and corn (Allender et al., 1997). But apart from these, few studies on molecular mechanisms behind hormesis in plants have been executed.

Finally, it has to be remarked that there are curves which could look like hormetic growth curves which are simply a result of poor test design and data analysis. The most obvious are those where the controls have been deprived of some essential mineral that are then added through the chemical treatment, which eventually results in an initial growth increase. Another cause of apparent hormesis can be an increase in variance of non-normally distributed data when the organisms are stressed, as explained by Forbes (2000).

Despite the many theories concerning the cause of hormesis, few studies have systematically assessed its frequency, magnitude and distribution among different chemicals in photosynthetic organisms on a large number of comparable dose-response curves. The aim of the present study was therefore to examine the frequency, magnitude and dose-range of hormesis in two terrestrial plant species, one aquatic species and an alga species, on the basis of 687 dose-response curves. We also investigated the dependence of the hormetic response on the mode of action of the chemical tested. In total nine herbicides with seven different modes of action were used in these analyses.

MATERIALS AND METHODS

Plants

Dose-response curves from the aquatic plant Lemna minor (lesser duckweed) and the green micro alga Pseudokirchneriella subcapitata were obtained from experiments conducted in the study of Cedergreen et al. (2006a). For L. minor, area specific relative growth rate was the endpoint used, while for P. subcapitata the relative growth rates were based on total chlorophyll content measured three times during the incubation period (Cedergreen et al., 2006a). Dose-response curves from the terrestrial plants Tripleurospermum inodorum (Scentless Mayweed) and Stellaria media (Common Chickweed) were obtained from experiments described in Cedergreen et al., 2006b. The endpoint used was total plant dry weight three to four weeks after treatment.

Pesticides

Nine herbicides and one fungicide were tested in the different test-systems alone and in binary mixtures. In the aquatic test-systems technical compounds were used while in the terrestrial systems formulated compounds were used. Specifications on the herbicides and fungicide, their primary mode of action, purity and source are given in table 1.

TABLE 1.

The primary and intended mode of action of the herbicides, and the one fungicide prochloraz, the purity of the technical compounds, recommended average field rate and specifications of the formulated compounds.

Name	Chemical group	Mode of action	Purity	Field rate (g/ha)	Formulated product	Source
Acifluorfen	Diphenylether	Protoporphyrinogen oxidase inhibitor	40%	400	Blazer (240 g/L)	BASF Corporation
Diquat	Bipyridylium	Photosystem I energy diverter	200 g/L	700 (200 g/L)	Reglone	Syngenta Crop Protection
Glyphosate	Glycine dirivative	EPSPSa inhibitor	95%	1750	Roundup Bio (360 g/L)	Monsanto
MCPA	Aryloxyalkanoic acid	Synthetic auxin	93%	1260	M-750 (750 g/L)	Klarsoe and Co.
Mecoprop	Aryloxyalkanoic acid	Synthetic auxin	89%	1350 (600 g/L)	Duplosan MP	BASF
Mesotrione	Triketone	HPPDb	79%	150	Calisto (100 g/L)	Syngenta Crop Protection
Metsulfuronmethyl	Sulfonylurea	ALSc inhibitor	98.5%	6	Ally (200 g/kg)	DuPont
Prochloraz	Imidazole	Eergosterol biosynthesis inhibitor	97%	500	—	Aventis
Terbuthyla-zine	1,3,5-triazine	Photosystem II inhibitor	>96%	1800	Terbuthyl-azine (500 g/L)	InterTrade
Triasulfuron	Sulfonylurea	ALS inhibitor	97%	7.5	Logran (200 g/kg)	Syngenta Crop Protection

Field rates are given for broad leaf species. Data is from Tomlin (2002).

Statistics

The database contained dose-response data from the above mentioned experiments, giving a total of 687 dose-response curves, which could all be described with a logistic dose-response model. In order to avoid biphasic dose-response curves caused by slow-growing controls, a lowest control growth rate for L. minor and P. subcapitata was selected on the background of the recommendations of the International Standardisation Organisation (International Organization for standardization, 1989; International Organization for standardization, 2004). Hence, L. minor dose-response curves with controls < 0.275 d⁻¹ were not included in the study. For the alga, P. subcapitata, curves with control growth rates < 1.5 d⁻¹ were excluded. For the terrestrial plants no such limit could be drawn, as the plants were grown under varying climatic conditions resulting in varying control growth (Cedergreen et al., 2006b).

The second selection criterion was that the dose-response curves needed to have more than one treatment within or above 105% of the control. The 5% limit was chosen as it represents the lower limit of the hormetic increase which could be detected in an earlier study on L. minor data (Cedergreen et al., 2005). Curves with treatments above 105% of control were fitted to a three parameter logistic model:

$$y=\frac{d}{1+{(x/e)}^b},$$ (1)

where y is the response, d is the maximal response at zero dose, e is the 50% effect dose or effect concentration (ED/EC₅₀) and b is proportional to the slope of the dose-response curve around e. Subsequently the curves were fitted to a model including a term for hormesis (Cedergreen et al., 2005):

$$y=\frac{d+f^{-1/x^{\alpha }}}{1+{(x/e)}^b},$$ (2)

In this model e looses its meaning as ED/EC₅₀, f determines the size of the hormetic response increase, while α gives the rate of increase of the hormetic response. Since the increasing part of the dose-response curve is rarely justified by data, α was pre-set to either 0.25, 0.5 or 1 and the model-fits with the different α-values were compared and the one with the smallest residual sum chosen. The two models (Equation 1 and 2) were then compared with an F-test (Seefeldt et al., 1995) to test if the model including a parameter for hormesis described data better than a monotonic decreasing logistic model. For those dose-response curves where the model including hormesis described data better, the maximal response, the ED/EC₀ and the ED/EC₅₀ were retrieved. ED/EC₀ corresponds to the concentration where the response is equal to the control, also called No Observable Adverse Effect Level (NOAEL) (Calabrese, 2005b). All analyses were done using the free software R (R Development Core Team, 2004) and the add-on package drc (available at: www.bioas-say.dk) (Ritz and Streibig, 2005).

To test the effect of choice of endpoint on the frequency and size of hormesis, all dry weight data from the terrestrial dose-response curves were converted to relative growth rates, assuming a start dry weight of 0.1 gram and a growth period of 25 days (Cedergreen et al., 2006b). The start dry weight was estimated on the background of harvest dry weight of plants receiving a full dose of quickly acting herbicides such as diquat, and the number of days from spray to harvest is the average of the three to four week growth period. Relative growth rates were calculated according to: (ln(DW_T)-ln(DW₀))/T, where DW is the dry weight at the time of spraying (DW₀) and at the harvest time T given in days.

RESULTS

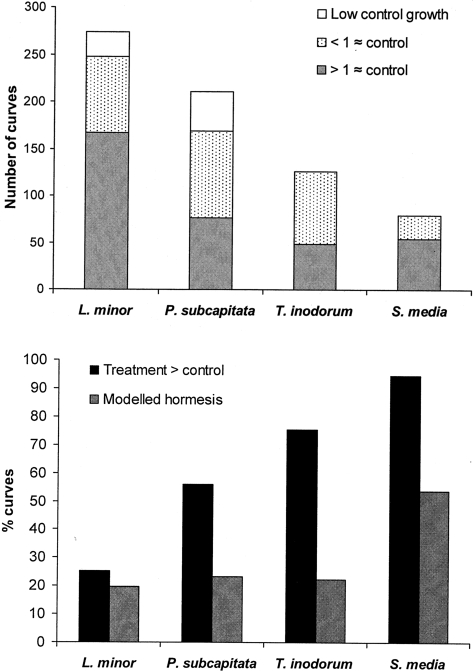
Of the 274 dose-response curves on L. minor, 26 had control levels below the threshold of 0.275 d⁻¹ and another 81 curves had less than one treatment at control level or above (Figure 2). Of the remaining 167 curves, 25% had treatments above the control level and 20% were best described with a model including hormesis. For P. subcapitata there were 211 dose-response curves of which 42 had controls below the threshold of 1.5 d⁻¹ and 91 curves had less than one treatment at control levels or above. Of the remaining 77 curves, 56% had treatments above control levels and 23% was better described with a dose-response model including hormesis (Figure 2). There were 126 curves for the terrestrial plant T. inodorum of which 77 curves had less than one treatment at control levels or above. Of the remaining 49 curves 76% had treatments above the control level and 22% were better described with a dose-response model including hormesis. There were 80 dose-response curves for S. media of which 26 had less than one treatment at control levels or above. Of the remaining 54 curves 94% had treatments above the control and 54% were better described with the model including hormesis (Figure 2). The average maximal response for the curves described with the hormetic model is given in table 2 together with the ED/EC₀, which is the concentration where the response is equal to the control. The distance between the concentration of maximal response and ED/EC₀ is also given as –fold increase in concentration, as this is a parameter also used in other database studies (Calabrese and Blain, 2005).

FIGURE 2.

In the top panel the bars represent the total number of dose-response curves for each of the species represented in the data-base study. The proportion of the curves that were either not included due to low control values, or due to an incomplete dose range in the low dose region are shown in white without and with spots. The grey part of the bars gives the number of curves that passed the entry criteria and were used in the study. The bottom panel shows the proportion of the curves that passed the entry criteria which had treatments above 105% of the control average (black bars), and the proportion which was better described with a model including hormesis (grey bars).

TABLE 2.

The average maximal growth increase relative to the control level of the curves which were best described with a dose-response model including hormesis for the four species included in the study. Also given is the average ED/EC₀, which corresponds to the concentration where the response is equal to the control.

Species	Response increase (%)	ED/EC0 (% of EC50)	Distance between Cmax and ED/EC0	n
L. minor	13 ± 5	28 ± 14	13 ± 16	32
P. subcapitata	16 ± 16	35 ± 18	8 ± 4	18
T. inodorum	38 ± 13	39 ± 17	23 ± 23	11
S. media	43 ± 23	60 ± 28	10 ± 15	29

The ED/EC₀ is given as percent of the ED/EC₅₀. The distance between the concentration of the maximal growth increase (C_max) and the ED/EC₀ is given as –fold increase in concentration.

To test the effect of choice of endpoint on the frequency and size of hormesis, all dry weight data from the terrestrial dose-response curves were converted to approximated relative growth rates. In doing so, the coefficient of variation (CV%) of the controls decreased from 21±8% (n = 26) and 25±10% (n = 10) to 5±3% and 5±2% for T. inodorum and S. media. In comparison the CV% of the controls for L. minor was 7±3% (n = 14) while for P. subcapitata it was 9±5% (n = 12). But also the relative size of the difference between treatments decreased; hence there were fewer curves with a treatment above 105% of the control value when the terrestrial plant data was evaluated on the basis of growth rates. The frequency decreasing from 76% and 94% of the curves included in the test to 35% and 76% of the curves, and the number of curves that was better described with a model including hormesis decreased from 22% and 54% to 8% and 26% of the curves for T. inodorum and S. media respectively. Turning to the size of the hormetic response it decrease from 38±13% and 43±23% of control to 9±1% (n = 4) and 12±5% (n = 14) of control in T. inodorum and S. media.

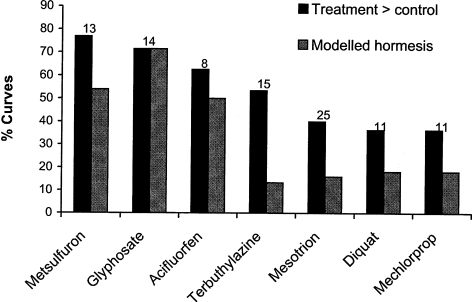
To investigate whether some of the herbicides were more likely to induce hormesis compared to others, all dose-response curves obtained from single chemicals fulfilling the entry criteria were selected. There were 43 curves on L. minor, 20 curves on P. subcapitata, 18 curves on T. inodorum and 20 curves on S. media. To get enough curves representing the different herbicides, curves from all four species were pooled. The results are shown in Figure 3. The figure shows that for all the seven herbicides that could be supported with sufficient dose-response data (more than 5 curves), there were curves that were better described with the hormesis model. Of particular interest, however, is metsulfuron-methyl and glyphosate where more than 70% of the curves included had treatments above the control level. And for glyphosate all of these curves were best described with the hormesis model. For acifluorfen more than 60% of the curves had treatments above control level while for terbuthylazine it was a little above 50% (Figure 3).

FIGURE 3.

Sufficient curves satisfying the entry criteria (> 5) were present to evaluate the pesticide specific frequency of hormesis for seven of the ten pesticides represented in the database. The black columns represent the proportion of the dose-response curves where at least one treatment was above 105% of the control average. The grey column represents the proportion of the curves that were better described by the hormesis model. The total number of curves for each herbicide is given above each column.

DISCUSSION

Frequency of hormesis

Hormetic dose-response curves were found for all four species. For the terrestrial species, hormesis seemed to be the rule rather than the exception when evaluated on a dry matter basis. However, converting the dry matter data to approximate growth rates decreased both the frequency of curves that had treatments above 105% of the control and the number of curves which could be significantly better described with a dose-response model including hormesis. Hence, the high frequency of apparent hormesis in the terrestrial species seems mainly to be caused by the choice of endpoint rather than for example the lack of dismissing low controls, such as was done for the aquatic species. Other differences such as the terrestrial plants being sprayed with formulated herbicides in contrast to the technical compounds used in the aquatic species, or the type of exposure being short term spray exposure for the terrestrial plants in contrast to a long term aquatic exposure might also have influenced the frequency of hormesis. The result emphasizes the importance of recognising the properties of the endpoint. Rates are likely to vary less than the accumulated standing stock, which in this case is biomass. And the longer time a small change in rate occurs the larger the difference in the standing stock.

The data included in this study were single species communities. Hence, it is not likely that the hormetic responses were due to changes in competition within or between species (Forbes, 2000), even though effects on pathogenic microorganisms in principle can not be excluded. The inoculated L. minor plants, however, come from an aseptic culture which makes it unlikely, at least in this test-system, that microbial interactions play a role for the hormetic response. Resource allocation between different plant parts was also suggested as a possible explanation for observed growth hormesis, when only a single plant part was measured (Forbes, 2000), as was the case for the terrestrial plants where only shoots were weighed and for L. minor where only frond surface was measured. But for the alga, population growth rate of whole cells did increase, and laboratory experiments on barley grown hydroponically have shown that the observed growth increase takes place in both roots and shoots independently (Cedergreen, unpublished). Hence, physiological changes such as increasing photosynthetic rates or decreasing respiration must be taking place under the growth conditions giving hormesis.

In should be noted that there are some drawbacks of the approach of counting the number of hormetic curves by counting the number that pass a hypothesis test. One problem is that hypothesis tests are set up asymmetrically in order to limit the probability of falsely rejecting the null hypothesis. Hence, accepting the null hypothesis, in this case that the logistic dose-response model explains data equally well as the model including hormesis, does not necessarily mean that the null hypothesis is true. It might be the case that the null hypothesis is false, but that there is not enough power to reject it. As the experiments included in this database were not set up with the purpose of finding hormesis, they are deficient in the number of low doses tested, and hence the datasets are weak when it comes to test a hypothesis concerning hormesis. As a result, the number of acceptations of the null hypothesis probably undercounts the number of hormetic curves simply because of lack of power of the data.

Magnitude of hormesis

As mentioned, the conversion of dry weight data to relative growth rates decreased the number of curves having treatments above 105% of control. Consequently choice of endpoint and the duration of the experiment, if standing stock is the measured endpoint, therefore also influence the magnitude of hormesis taking place. Looking at relative growth rates, the maximal hormetic response was remarkably consistent being approximately 10–15% above control levels. This is in the low range of the general hormetic increase in plants reported by Calabrese and Blain (2005), which includes 436 dose-response relation-ships of which 36% had a stimulatory response of less than 25% of the control (Calabrese and Blain, 2005). One reason for the relatively low hormetic response observed in this study compared to the literature database is that our estimations of hormetic response are based on model fits and not differences between controls and the maximally responding individual treatment. Curve fits “averages” both high and low hormetic responses and therefore rarely describes the maximal treatments. Another reason is the endpoint being growth rates, which, as discussed, gives lower hormetic effects compared to standing stock endpoints such as dry weight or root or shoot length which is often the measured parameters in the literature (Calabrese and Blain, 2005). Hence, the data from this study is consistent with what has been found generally for plants. The distance between the concentration of the maximal response and the concentration where the response is equal to the control is slightly higher in this study compared to the Calabrese and Blain database study. In the Calabrese and Blain database only 12% of the curves had a more than 10 fold difference, such as was the case for L. minor and T. inodorum (Table 2)(Calabrese and Blain, 2005).

Which chemicals induce hormesis?

Both treatments above 105% of control and significant hormetic dose-response curves were found for all seven herbicides where there were enough curves to evaluate frequency. Hence, in that respect hormesis must be said to be a general phenomenon across different chemical modes of action. However, metsulfuron-methyl and glyphosate, the two herbicides affecting amino acid synthesis (Table 1), were more likely to induce hormetic dose-response curves compared to the other herbicides. Acifluorfen and terbuthylazine were coming in second. Both herbicides affect photosynthesis but in different ways (Figure 3). This could mean that the hormetic response is induced or enhanced either directly or indirectly by some mechanism related to amino acid synthesis, although ALS and EPSPS produce amino acids with quite different metabolic functions, other than in protein synthesis. We plan to examine the mechanisms of hormesis produced by these classes of herbicides, using molecular biology methods.

It is surprising that mechlorprop did not induce hormesis more frequently, as it is a synthetic auxin which has shown to induce both root elongation, increase in specific leaf area and biomass growth at low doses in other studies (Morré, 2000; Allender et al., 1997). It is, however, likely that doses were too high in several of the experiments to convincingly show hormesis, despite the selection criteria of more than one treatment being above or within the range of 105% of control. The frequencies of hormesis in the study are therefore likely to be conservative estimates of the “real” frequency of hormesis, had the experiments been designed to find it.