Abstract
Exercise is well known to cause arterial 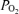 to fall and the alveolar–arterial
to fall and the alveolar–arterial 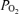 difference (Aa
difference (Aa 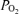 ) to increase. Until recently, the physiological basis for this was considered to be mostly ventilation/perfusion
) to increase. Until recently, the physiological basis for this was considered to be mostly ventilation/perfusion 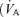 /
/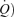 inequality and alveolar–capillary diffusion limitation. Recently, arterio-venous shunting through dilated pulmonary blood vessels has been proposed to explain a significant part of the Aa
inequality and alveolar–capillary diffusion limitation. Recently, arterio-venous shunting through dilated pulmonary blood vessels has been proposed to explain a significant part of the Aa 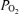 during exercise. To test this hypothesis we determined venous admixture during 5 min of near-maximal, constant-load, exercise in hypoxia (in inspired O2 fraction,
during exercise. To test this hypothesis we determined venous admixture during 5 min of near-maximal, constant-load, exercise in hypoxia (in inspired O2 fraction, 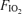 , 0.13), normoxia (
, 0.13), normoxia (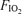 , 0.21) and hyperoxia (
, 0.21) and hyperoxia (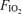 , 1.0) undertaken in balanced order on the same day in seven fit cyclists (
, 1.0) undertaken in balanced order on the same day in seven fit cyclists (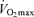 , 61.3 ± 2.4 ml kg−1 min−1; mean ±s.e.m.). Venous admixture reflects three causes of hypoxaemia combined: true shunt, diffusion limitation and
, 61.3 ± 2.4 ml kg−1 min−1; mean ±s.e.m.). Venous admixture reflects three causes of hypoxaemia combined: true shunt, diffusion limitation and 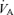 /
/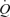 inequality. In hypoxia, venous admixture was 22.8 ± 2.5% of the cardiac output; in normoxia it was 3.5 ± 0.5%; in hyperoxia it was 0.5 ± 0.2%. Since only true shunt accounts for venous admixture while breathing 100% O2, the present study suggests that shunt accounts for only a very small portion of the observed venous admixture, Aa
inequality. In hypoxia, venous admixture was 22.8 ± 2.5% of the cardiac output; in normoxia it was 3.5 ± 0.5%; in hyperoxia it was 0.5 ± 0.2%. Since only true shunt accounts for venous admixture while breathing 100% O2, the present study suggests that shunt accounts for only a very small portion of the observed venous admixture, Aa 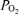 and hypoxaemia during heavy exercise.
and hypoxaemia during heavy exercise.
For many years, heavy endurance exercise has been known to result in a reduction in arterial 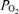 and an increase in the alveolar–arterial
and an increase in the alveolar–arterial 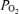 difference (Aa
difference (Aa 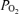 ) in normal subjects (Asmussen & Nielsen, 1960; Whipp & Wasserman, 1969; Dempsey et al. 1984). The physiological basis of this phenomenon has been studied extensively, with a view to understanding the underlying mechanisms (Gledhill et al. 1977; Gale et al. 1985; Torre-Bueno et al. 1985; Rice et al. 1999). Arterial
) in normal subjects (Asmussen & Nielsen, 1960; Whipp & Wasserman, 1969; Dempsey et al. 1984). The physiological basis of this phenomenon has been studied extensively, with a view to understanding the underlying mechanisms (Gledhill et al. 1977; Gale et al. 1985; Torre-Bueno et al. 1985; Rice et al. 1999). Arterial 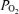 may be reduced by four principal physiological processes (West, 1969): diffusion limitation of O2 exchange across the pulmonary blood : gas barrier, non-uniform distribution of ventilation/perfusion
may be reduced by four principal physiological processes (West, 1969): diffusion limitation of O2 exchange across the pulmonary blood : gas barrier, non-uniform distribution of ventilation/perfusion 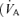 /
/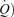 ratios throughout the lungs, hypoventilation, and right-to-left shunt, i.e. venous blood that enters the arterial system without going through ventilated areas of the lung.
ratios throughout the lungs, hypoventilation, and right-to-left shunt, i.e. venous blood that enters the arterial system without going through ventilated areas of the lung.
Diffusion limitation, absent at rest in healthy subjects, may occur during heavy exercise if red cell transit time through the pulmonary microcirculation falls below levels necessary to enable complete equilibration of 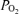 between alveolar gas and capillary blood. Equilibration could be further impaired during exercise if transient pulmonary interstitial fluid accumulation occurs. Evidence suggests that many but not all normal subjects experience diffusion limitation during heavy normoxic exercise, while essentially all normal subjects develop this during hypoxic exercise (Torre-Bueno et al. 1985; Wagner et al. 1986, 1987). Inequality of
between alveolar gas and capillary blood. Equilibration could be further impaired during exercise if transient pulmonary interstitial fluid accumulation occurs. Evidence suggests that many but not all normal subjects experience diffusion limitation during heavy normoxic exercise, while essentially all normal subjects develop this during hypoxic exercise (Torre-Bueno et al. 1985; Wagner et al. 1986, 1987). Inequality of 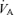 /
/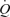 ratios is present to a minor extent even at rest (Wagner et al. 1974a; Gledhill et al. 1977). The degree of inequality could change with exercise as total ventilation and pulmonary blood flow and associated airway and vascular pressures change from resting values. This has indeed been found to occur, with many studies showing modest increases in inequality (Gledhill et al. 1977; Gale et al. 1985; Wagner et al. 1986). In exercise, ventilation of course increases and hypoventilation therefore does not occur. The term is, however, applied to exercise when the relative rise in CO2 elimination by the lungs exceeds the relative rise in alveolar ventilation. If this occurs, arterial
ratios is present to a minor extent even at rest (Wagner et al. 1974a; Gledhill et al. 1977). The degree of inequality could change with exercise as total ventilation and pulmonary blood flow and associated airway and vascular pressures change from resting values. This has indeed been found to occur, with many studies showing modest increases in inequality (Gledhill et al. 1977; Gale et al. 1985; Wagner et al. 1986). In exercise, ventilation of course increases and hypoventilation therefore does not occur. The term is, however, applied to exercise when the relative rise in CO2 elimination by the lungs exceeds the relative rise in alveolar ventilation. If this occurs, arterial 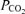 will increase above resting values, and arterial
will increase above resting values, and arterial 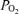 will fall. This may play a role in some subjects (Rice et al. 1999). Right-to-left shunt generally does not occur in normal subjects at rest, but a small degree of venous admixture from bronchial and Thebesian venous drainage into the left side of the circulation may occur on anatomical grounds. In addition, a minority of otherwise normal subjects have a potentially patent foramen ovale in their interatrial wall. This could open during exercise, and if right atrial pressure exceeds left atrial pressure, a right-to-left shunt could occur. This does not usually happen, because left atrial pressures normally exceed those in the right atrium. However, it has been pointed out that even small shunts, functionally irrelevant at rest, may partially explain the fall in arterial
will fall. This may play a role in some subjects (Rice et al. 1999). Right-to-left shunt generally does not occur in normal subjects at rest, but a small degree of venous admixture from bronchial and Thebesian venous drainage into the left side of the circulation may occur on anatomical grounds. In addition, a minority of otherwise normal subjects have a potentially patent foramen ovale in their interatrial wall. This could open during exercise, and if right atrial pressure exceeds left atrial pressure, a right-to-left shunt could occur. This does not usually happen, because left atrial pressures normally exceed those in the right atrium. However, it has been pointed out that even small shunts, functionally irrelevant at rest, may partially explain the fall in arterial 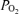 during exercise because their effect is magnified by the much lower
during exercise because their effect is magnified by the much lower 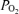 in the venous blood returning from the muscles to the lungs during exercise (Dempsey, 2006).
in the venous blood returning from the muscles to the lungs during exercise (Dempsey, 2006).
More recently, microbubbles injected intravenously have been found to pass through the lungs to the left side of the circulation during exercise, but not at rest (Eldridge et al. 2004; Stickland et al. 2004). Additional studies by this group have shown some transmission of 25 and 50 μm diameter microspheres through the pulmonary circulation (Lovering et al. 2007; Stickland et al. 2007). The authors of these studies have suggested that such bubble/particle transmission indicates the opening of intrapulmonary shunts that might substantially contribute to the fall in arterial 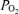 and increase in Aa
and increase in Aa 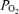 (Stickland et al. 2004). However, the only study from this group that did report quantitative transpulmonary passage of large (25 μm) microspheres during exercise was conducted in dogs and demonstrated a very small shunt that averaged 1.4% of the cardiac output (Stickland et al. 2007). Even then, only three animals were investigated and two had shunts of less than 1% (Stickland et al. 2007). Nevertheless, the link between bubble/particle transmission and hypoxaemia remains in question, as no direct evidence has been presented that supports a cause-and-effect connection between the two. It remains possible that small bubbles may traverse the pulmonary circulation but that the presumed enlargement of pulmonary blood vessels that enables this has no impact on oxygen exchange. Alternatively, bubble/particle transpulmonary passage during heavy exercise may indicate the presence of a shunt.
(Stickland et al. 2004). However, the only study from this group that did report quantitative transpulmonary passage of large (25 μm) microspheres during exercise was conducted in dogs and demonstrated a very small shunt that averaged 1.4% of the cardiac output (Stickland et al. 2007). Even then, only three animals were investigated and two had shunts of less than 1% (Stickland et al. 2007). Nevertheless, the link between bubble/particle transmission and hypoxaemia remains in question, as no direct evidence has been presented that supports a cause-and-effect connection between the two. It remains possible that small bubbles may traverse the pulmonary circulation but that the presumed enlargement of pulmonary blood vessels that enables this has no impact on oxygen exchange. Alternatively, bubble/particle transpulmonary passage during heavy exercise may indicate the presence of a shunt.
Accordingly, the purpose of the present study was to test the hypothesis that during exercise only a very small intrapulmonary shunt is present, and therefore that shunts make only a minor contribution to the fall in arterial 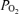 and increase in Aa
and increase in Aa 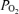 that is seen during heavy normoxic and hypoxic exercise.
that is seen during heavy normoxic and hypoxic exercise.
Methods
Protocol overview
Seven fit, trained cyclists undertook 5 min of heavy, constant-load, cycling exercise in each of three conditions: hypoxia (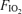 , 0.13), normoxia (
, 0.13), normoxia (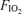 , 0.21) and hyperoxia (
, 0.21) and hyperoxia (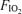 , 1.0), applied in balanced order and each separated by at least an hour of rest, on a single day. A special design aspect was to adjust cycling power outputs as
, 1.0), applied in balanced order and each separated by at least an hour of rest, on a single day. A special design aspect was to adjust cycling power outputs as 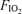 was varied to maintain constant minute ventilation because it is known that venous admixture varies systematically with minute ventilation during heavy exercise (Wagner et al. 1986). It is the arterial oxygenation data across the three
was varied to maintain constant minute ventilation because it is known that venous admixture varies systematically with minute ventilation during heavy exercise (Wagner et al. 1986). It is the arterial oxygenation data across the three 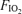 levels that form the basis of the present report.
levels that form the basis of the present report.
Subjects – characteristics and preparation for the study
Seven healthy highly competitive Greek male cyclists were studied. After explaining the approved protocol by the authors’ University Ethics Committee, they volunteered and provided written informed consent. The study was conducted in accordance with the guidelines of the Declaration of Helsinki. Average age was 31 ± 6 years; height was 180 ± 20 cm; weight was 73 ± 2 kg; and maximal normoxic oxygen consumption 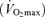 on a standard 30 W min−1 incremental test was 4.66 ± 0.16 l min−1 (61.3 ± 2.4 ml kg−1 min−1) at 374 ± 10 W.
on a standard 30 W min−1 incremental test was 4.66 ± 0.16 l min−1 (61.3 ± 2.4 ml kg−1 min−1) at 374 ± 10 W.
Based on this incremental test to 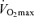 , power outputs of 63 ± 1%, 78 ± 1% and 87 ± 1% of maximal were selected for each subject for the current study as target work loads in hypoxia, normoxia and hyperoxia, respectively. These workloads were chosen to achieve the same minute ventilation across the three
, power outputs of 63 ± 1%, 78 ± 1% and 87 ± 1% of maximal were selected for each subject for the current study as target work loads in hypoxia, normoxia and hyperoxia, respectively. These workloads were chosen to achieve the same minute ventilation across the three 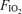 values, based on previous studies (Vogiatzis et al. 2006, 2007). In absolute terms, these were power outputs of 235 ± 6 W in hypoxia, 290 ± 5 W in normoxia and 325 ± 6 W in hyperoxia.
values, based on previous studies (Vogiatzis et al. 2006, 2007). In absolute terms, these were power outputs of 235 ± 6 W in hypoxia, 290 ± 5 W in normoxia and 325 ± 6 W in hyperoxia.
For safety monitoring, subjects were then connected to an ECG (Marquette Max; Marquette Hellige, Germany) and digital pulse oximeter (Nonin 8600; Nonin Medical, USA), and using local anaesthesia (2% lidocaine) and sterile technique, identical catheters were introduced percutaneously into the right femoral artery and right femoral vein about 2 cm below the inguinal ligament, both orientated in the proximal direction. We used 20 cm long 16 gauge flexible catheters (CV-04301; Arrow International, Reading, PA, USA) placed over a 0.1 cm guide wire introduced through an 18 gauge needle. Catheters were secured in place by a 3-O skin suture and additionally by clear adhesive tape.
The catheters were used during the study to collect arterial and femoral venous blood samples and also to inject indocyanine green dye and sample blood after each injection for cardiac output measurements. They were kept patent throughout the study by periodic flushing with heparinized (1 unit ml−1) saline.
Because of the risk of pulmonary arterial catheterization in relation to its benefits in this study, we did not insert a pulmonary artery catheter for direct measurement of mixed venous blood composition and pulmonary artery pressure. However, we used the Fick principle of mass balance to calculate mixed venous O2 concentration from oxygen consumption 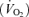 , cardiac output and arterial blood O2 concentration (see below), and extrapolated mean pulmonary artery pressure from current cardiac output measurements and previously published direct measures of pulmonary artery pressure and cardiac output during exercise (Wagner et al. 1986).
, cardiac output and arterial blood O2 concentration (see below), and extrapolated mean pulmonary artery pressure from current cardiac output measurements and previously published direct measures of pulmonary artery pressure and cardiac output during exercise (Wagner et al. 1986).
Exercise protocol
The studies were conducted in Athens, Greece at sea level. After all the above preparations, initial baseline measurements were made, mainly to assure proper functioning of all equipment. Subjects then warmed up by cycling at 180 ± 65 W for 5 min. Without stopping, they were switched to one of three 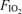 values (0.13, 0.21 or 1.0) using a standard mouthpiece and two-way non-rebreathing valve system and began 5 min of heavy exercise at the power output indicated above for the chosen
values (0.13, 0.21 or 1.0) using a standard mouthpiece and two-way non-rebreathing valve system and began 5 min of heavy exercise at the power output indicated above for the chosen 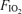 . Between minutes 3 and 5, cardiac output was measured in duplicate by indocyanine green dye dilution, and arterial and femoral venous blood samples were also taken, again in duplicate. At the end of exercise, subjects rested for an hour before the next exercise trial at the second
. Between minutes 3 and 5, cardiac output was measured in duplicate by indocyanine green dye dilution, and arterial and femoral venous blood samples were also taken, again in duplicate. At the end of exercise, subjects rested for an hour before the next exercise trial at the second 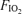 . The protocol for the second exercise trial was identical to that of the first, except for the
. The protocol for the second exercise trial was identical to that of the first, except for the 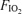 and the workload – the latter adjusted as mentioned to achieve the same minute ventilation across the three
and the workload – the latter adjusted as mentioned to achieve the same minute ventilation across the three 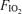 values. The third trial, again using the same protocol, was then undertaken at the third
values. The third trial, again using the same protocol, was then undertaken at the third 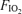 . The order of application of
. The order of application of 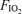 was balanced across subjects 1–6, each of these subjects having their own unique order. Subject 7 repeated the sequence order of subject 1.
was balanced across subjects 1–6, each of these subjects having their own unique order. Subject 7 repeated the sequence order of subject 1.
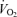 ,
, 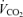 and minute ventilation
and minute ventilation
Standard methods were used to measure 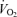 , CO2 production
, CO2 production 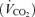 and minute ventilation during exercise. Minute ventilation was measured breath by breath (Vmax 229; Sensor Medics, Anaheim, CA, USA) and expressed as litres per minute (BTPS).
and minute ventilation during exercise. Minute ventilation was measured breath by breath (Vmax 229; Sensor Medics, Anaheim, CA, USA) and expressed as litres per minute (BTPS). 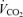 and
and 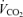 were measured breath by breath in normoxia and hypoxia using the Vmax apparatus, and the results expressed as litres per minute (STPD). During 100% O2 breathing, this system is unable to measure
were measured breath by breath in normoxia and hypoxia using the Vmax apparatus, and the results expressed as litres per minute (STPD). During 100% O2 breathing, this system is unable to measure  , but can still measure
, but can still measure 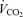 . Based on the similar relative workloads and similar arterial blood lactate levels across the three
. Based on the similar relative workloads and similar arterial blood lactate levels across the three 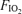 values, we assumed that for each subject the respiratory exchange ratio (R) on 100% O2 was the same as that at the two lower
values, we assumed that for each subject the respiratory exchange ratio (R) on 100% O2 was the same as that at the two lower 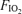 values. Using this estimate of R and the measured value for
values. Using this estimate of R and the measured value for 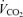 , we calculated
, we calculated 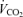 as
as 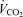 /R. We checked this against the
/R. We checked this against the 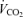 expected by using an increment of 10 ml min−1 W−1 above the normoxic values. Nevertheless, possible errors in
expected by using an increment of 10 ml min−1 W−1 above the normoxic values. Nevertheless, possible errors in 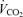 calculated while breathing 100% O2 would have negligible effect on shunt estimation. A 10% error in
calculated while breathing 100% O2 would have negligible effect on shunt estimation. A 10% error in 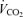 would change calculated shunt by less than 0.1% of the cardiac output.
would change calculated shunt by less than 0.1% of the cardiac output.
Blood gases and their temperature correction
Femoral arterial and venous blood samples were analysed using a calibrated ABL 520 system (Radiometer, Copenhagen, Denmark) operating at 37.0°C. This system provided direct measures of 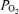 , O2 saturation, haemoglobin concentration,
, O2 saturation, haemoglobin concentration, 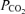 , pH and whole blood lactate concentration. Samples of 2 ml were collected anaerobically in heparinized syringes and any bubbles were immediately expressed. Every arterial sample was analysed within 10 s of collection. Venous samples were placed on ice until arterial samples had been analysed and were then immediately measured. No venous samples sat longer than 5 min in ice before measurements were made.
, pH and whole blood lactate concentration. Samples of 2 ml were collected anaerobically in heparinized syringes and any bubbles were immediately expressed. Every arterial sample was analysed within 10 s of collection. Venous samples were placed on ice until arterial samples had been analysed and were then immediately measured. No venous samples sat longer than 5 min in ice before measurements were made.
We attempted to measure body temperature aurally, but this clearly failed to show systematic increases that always occur with this intensity (85–90% of maximal) and duration (5 min) of cycle exercise. Accordingly, we assumed that body temperature was 37.0°C at rest and 38.0°C when samples were taken during normoxic exercise. As power output was slightly less in hypoxia, we assumed a temperature of 37.8°C during hypoxic exercise, and as power output was slightly higher in hyperoxia, we assumed a temperature of 38.2°C at 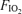 of 1.0. We assessed the importance of these assumptions on outcome variables by a sensitivity analysis. Blood gas values are presented corrected to assumed body temperatures. Systematic and random errors in blood gas analysis were assessed by plotting for all samples in a single subject measured
of 1.0. We assessed the importance of these assumptions on outcome variables by a sensitivity analysis. Blood gas values are presented corrected to assumed body temperatures. Systematic and random errors in blood gas analysis were assessed by plotting for all samples in a single subject measured 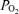 (after correcting to standard conditions of
(after correcting to standard conditions of 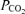 40 mmHg; temperature 37°C; pH 7.40) against measured O2 saturation.
40 mmHg; temperature 37°C; pH 7.40) against measured O2 saturation.
We used a least-squares approach (Wagner et al. 2007) to compute standard PO2 of which hemoglobin saturation is 50%P50 from these data, and examined the residual sum of squares between measured and predicted saturations as an index of total analysis errors. As can be seen from Fig. 1, the analyser displayed very little random error in all subjects, and moreover, the mean standard P50 of 26.6 mmHg is well within established limits, indicating accuracy as well as low error.
Figure 1. Relationship between directly measured blood saturation and blood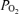 corrected to pH of 7.40,
corrected to pH of 7.40, 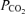 of 40 mmHg and temperature of 37°C for each of the seven subjects.
of 40 mmHg and temperature of 37°C for each of the seven subjects.
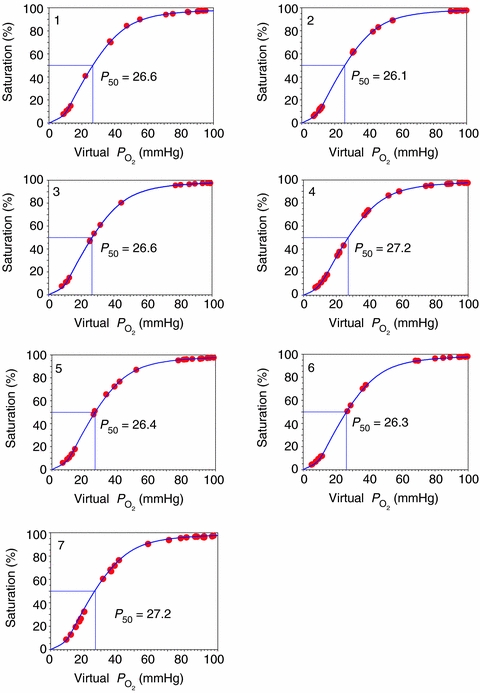
This figure shows that the level of random error in blood gas measurements is low.
Cardiac output
Cardiac output is important in the present paper as a factor in the shunt calculations (see below). We measured cardiac output by a standard indocyanine green (Pulsion ICG; ViCare Medical, Denmark) indicator dilution method (Dow, 1956) using known volumes of dye (usually 1.2 ml at 5 mg ml−1) injected into the femoral venous line with simultaneous arterial sampling by an automated pump (Harvard Apparatus, USA). At the end of each subject's study, individual 3-point dye calibration curves were measured using the subject's own blood. Cardiac output was determined as the ratio of injected mass of dye to the average arterial dye concentration–time curve area (after correcting for recirculation).
Calculations
The alveolar–arterial 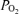 difference (mmHg) was calculated using the standard alveolar gas equation (Rahn & Fenn, 1955) for
difference (mmHg) was calculated using the standard alveolar gas equation (Rahn & Fenn, 1955) for 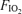 values of 0.13 and 0.21:
values of 0.13 and 0.21:
Here, 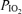 and
and 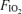 are inspired partial pressure and fractional concentration of O2.
are inspired partial pressure and fractional concentration of O2. 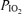 (mmHg) is given by the equation
(mmHg) is given by the equation 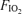 *(PB– SVP), where PB is barometric pressure and SVP saturated water vapor pressure at body temperature (both mmHg).
*(PB– SVP), where PB is barometric pressure and SVP saturated water vapor pressure at body temperature (both mmHg). 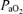 and
and 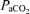 are measured, temperature-corrected arterial
are measured, temperature-corrected arterial 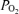 and
and 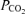 , and R is the measured respiratory exchange ratio.
, and R is the measured respiratory exchange ratio.
While breathing 100% O2, Aa 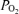 was calculated as:
was calculated as:
Blood O2 concentrations (generically labelled C) were calculated in the standard manner from the sum of Hb-bound and dissolved levels as follows:
Here, the number 1.39 is the millilitres of O2 that can bind to all sites on 1 g of Hb, and 0.003 the solubility of O2 in blood in ml dl−1 mmHg−1. [Hb] is in g dl−1; saturation is in per cent and 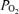 in mmHg, such that C is in ml dl−1.
in mmHg, such that C is in ml dl−1.
At each 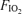 , venous admixture was also calculated. This parameter quantifies the percentage of cardiac output that must be attributed to a shunt in order to explain the observed arterial
, venous admixture was also calculated. This parameter quantifies the percentage of cardiac output that must be attributed to a shunt in order to explain the observed arterial 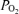 in the absence of any other gas exchange limitation. Because of this assumption, it therefore represents the greatest amount of shunt that could be present. This is a useful parameter in the present study because the focus is on the amount of shunt. The formula for venous admixture is based on mass balance (Riley & Cournand, 1949) and is:
in the absence of any other gas exchange limitation. Because of this assumption, it therefore represents the greatest amount of shunt that could be present. This is a useful parameter in the present study because the focus is on the amount of shunt. The formula for venous admixture is based on mass balance (Riley & Cournand, 1949) and is:
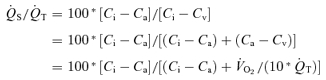 |
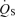 /
/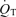 is the shunt
is the shunt 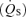 as a percentage of the cardiac output
as a percentage of the cardiac output 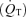 . Ci is the O2 concentration in blood corresponding to the ideal alveolar
. Ci is the O2 concentration in blood corresponding to the ideal alveolar 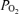 (calculated from the alveolar gas equations above) and is expressed in ml dl−1; Ca and Cv are measured arterial and calculated mixed venous O2 concentrations, respectively, and
(calculated from the alveolar gas equations above) and is expressed in ml dl−1; Ca and Cv are measured arterial and calculated mixed venous O2 concentrations, respectively, and 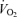 is oxygen consumption (ml min−1) while
is oxygen consumption (ml min−1) while 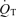 is in l min−1. In the absence of direct measures of mixed venous
is in l min−1. In the absence of direct measures of mixed venous 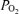 , mixed venous O2 concentration can be calculated from the Fick principle of mass balance as indicated in the above equations, since the Fick principle expresses oxygen consumption as the product of cardiac output and arterio-venous O2 concentration difference, Ca–Cv.
, mixed venous O2 concentration can be calculated from the Fick principle of mass balance as indicated in the above equations, since the Fick principle expresses oxygen consumption as the product of cardiac output and arterio-venous O2 concentration difference, Ca–Cv.
Statistics
Variables during heavy exercise were compared across 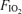 using a repeated measures one-way analysis of variance, with post hoc testing (t tests with Bonferroni correction for multiple comparisons) to establish significant differences from normoxic conditions. Significance was accepted at P < 0.05. Data are expressed as means ±s.e.m. Standard error was used rather than standard deviation because this study is concerned with variance in the means, not variance in the individual measurements.
using a repeated measures one-way analysis of variance, with post hoc testing (t tests with Bonferroni correction for multiple comparisons) to establish significant differences from normoxic conditions. Significance was accepted at P < 0.05. Data are expressed as means ±s.e.m. Standard error was used rather than standard deviation because this study is concerned with variance in the means, not variance in the individual measurements.
Results
Table 1 shows basic exercise data at each 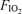 . Power output was significantly increased in hyperoxia and reduced in hypoxia, per experimental design, which was to achieve similar ventilation at each
. Power output was significantly increased in hyperoxia and reduced in hypoxia, per experimental design, which was to achieve similar ventilation at each 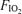 . Exercise intensity approached maximal levels for each
. Exercise intensity approached maximal levels for each 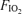 , again by design, with appropriately high R values, arterial blood lactate concentrations and heart rates. Cardiac output was high but not significantly different across the three
, again by design, with appropriately high R values, arterial blood lactate concentrations and heart rates. Cardiac output was high but not significantly different across the three 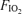 values in spite of the purposefully imposed different absolute work loads.
values in spite of the purposefully imposed different absolute work loads.
Table 1.
Exercise-related variables
| Variable | ||||
|---|---|---|---|---|
| 0.13 | 0.21 | 1.0 | P | |
| Work rate (W) | 235 ± 6 | 290 ± 5 | 325 ± 5 | < 0.001 |
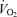 (l min−1) (l min−1) |
3.41 ± 0.05 | 4.29 ± 0.09 | 4.70 ± 0.13** | < 0.001 |
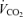 (l min−1) (l min−1) |
4.08 ± 0.14 | 4.65 ± 0.21 | 5.08 ± 0.27 | < 0.001 |
| R | 1.20 ± 0.03 | 1.08 ± 0.03 | 1.08 ± 0.03* | < 0.001 |
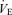 (l min−1) (l min−1) |
124.5 ± 3.5 | 122.5 ± 6.5 | 126.5 ± 7.5 | NS |
| [La] (mmol l−1) | 9.6 ± 1.8 | 9.3 ± 1.4 | 10.3 ± 1.9 | NS |
| HR (beats min−1) | 169 ± 8 | 174 ± 10 | 171 ± 9 | NS |
| CO (l min−1) | 27.6 ± 1.2 | 28.4 ± 2.0 | 27.8 ± 1.6 | NS |
| [Hb] (g dl−1) | 15.3 ± 0.4 | 15.2 ± 0.4 | 15.2 ± 0.5 | NS |
Values are means ± S.E.M. 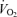 , oxygen consumption;
, oxygen consumption; 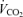 , carbon dioxide production; R, respiratory exchange ratio;
, carbon dioxide production; R, respiratory exchange ratio; 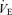 , minute ventilation; [La], arterial lactate concentration; HR, heart rate; CO, cardiac output; [Hb], haemoglobin concentration.
, minute ventilation; [La], arterial lactate concentration; HR, heart rate; CO, cardiac output; [Hb], haemoglobin concentration.
Assumed to be the same as at 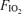 = 0.21.
= 0.21.
Calculated from R at 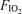 : 0.21 and
: 0.21 and 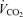 at
at 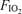 : 1.0.
: 1.0.
Mean haemoglobin concentration was 15.2 g dl−1 and standard P50 was 26.6 mmHg, both well within the usual range for normal subjects.
Table 2 shows the blood gas data expressed at the estimated body temperatures as described above. There were the expected, well-known effects of varying 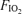 on these variables, with alveolar and arterial
on these variables, with alveolar and arterial 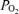 and saturation reflecting the imposed
and saturation reflecting the imposed 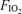 , and with corresponding effects on arterial
, and with corresponding effects on arterial 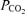 . The normoxic Aa
. The normoxic Aa 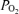 values were typical for normal trained subjects exercising near maximal oxygen consumption, as were the large Aa
values were typical for normal trained subjects exercising near maximal oxygen consumption, as were the large Aa 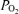 values in hypoxia. In contrast, the values of Aa
values in hypoxia. In contrast, the values of Aa 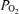 during hyperoxia were small, especially given the sensitivity of arterial
during hyperoxia were small, especially given the sensitivity of arterial 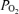 to small changes in arterial oxygenation at these high
to small changes in arterial oxygenation at these high 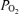 values (because of the very flat nature of the O2 dissociation curve in hyperoxia).
values (because of the very flat nature of the O2 dissociation curve in hyperoxia).
Table 2.
Gas exchange variables during exercise
| Variable | ||||
|---|---|---|---|---|
| 0.13 | 0.21 | 1.00 | P | |
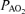 (mmHg) (mmHg) |
63.4 ± 1.4 | 113.1 ± 0.9 | 669.6 ± 0.6 | < 0.001 |
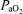 (mmHg) (mmHg) |
42.5 ± 1.1 | 89.4 ± 2.5 | 640.4 ± 10.5 | < 0.001 |
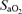 (%) (%) |
73.8 ± 1.6 | 95.3 ± 0.4 | 99.9 ± 0.0 | < 0.001 |
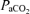 (mmHg) (mmHg) |
33.2 ± 1.2 | 38.0 ± 0.5 | 41.4 ± 0.6 | < 0.001 |
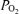 (mmHg) (mmHg) |
21.0 ± 2.3 | 23.8 ± 2.4 | 30.0 ± 9.8 | NS |
Values are means ± S.E.M. 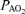 , alveolar
, alveolar 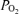 ;
; 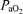 , arterial
, arterial 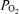 ;
; 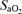 , arterial oxygen saturation;
, arterial oxygen saturation; 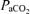 , arterial
, arterial 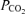 ; Aa
; Aa 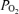 , alveolar–arterial
, alveolar–arterial 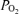 difference.
difference.
Table 3 shows the principal outcome variable of the present manuscript: calculated venous admixture. The values are strikingly different as a function of 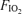 . While large in hypoxia (22.8% (range 9.9–28.9%) of the cardiac output) and modest in normoxia (3.5% (range 1.0–4.9%)), they are very small (0.5% (range 0.0–1.1%)) while subjects breathed 100% O2.
. While large in hypoxia (22.8% (range 9.9–28.9%) of the cardiac output) and modest in normoxia (3.5% (range 1.0–4.9%)), they are very small (0.5% (range 0.0–1.1%)) while subjects breathed 100% O2.
Table 3.
Venous admixture (% of cardiac output)
| Subject | 0.13 | 0.21 | 1.0 |
|---|---|---|---|
| 1 | 28.9 | 4.4 | 0.6 |
| 2 | 18.4 | 1.0 | 0.0 |
| 3 | 9.9 | 3.3 | 1.1 |
| 4 | 26.7 | 4.9 | 0.8 |
| 5 | 24.2 | 3.9 | 1.0 |
| 6 | 26.6 | 3.5 | 0.0 |
| 7 | 25.0 | 3.7 | 0.2 |
| Mean | 22.8 | 3.5 | 0.5 |
| s.d. | 6.6 | 1.2 | 0.5 |
| s.e.m. | 2.5 | 0.5 | 0.2 |
P≤ 0.001 for all pairwise comparisons between the three mean values.
Sensitivity to the assumed blood temperatures is physiologically insignificant because the calculations of shunt use directly measured oxygen saturation values that are temperature insensitive. It is only the very small dissolved component that would change with temperature. As the solubility of O2 is so low, the effects of a 1°C error in temperature are negligible.
Discussion
Data summary and interpretation of the primary outcome of the study
The major finding of this study is that arterial 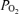 , Aa
, Aa 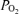 and calculated venous admixture determined during heavy exercise while breathing 100% O2 are inconsistent with substantial right-to-left shunts. This is despite venous admixture reaching substantial levels in hypoxia, and modest levels in normoxia, in the same subjects on the same day, as shown in Table 3.
and calculated venous admixture determined during heavy exercise while breathing 100% O2 are inconsistent with substantial right-to-left shunts. This is despite venous admixture reaching substantial levels in hypoxia, and modest levels in normoxia, in the same subjects on the same day, as shown in Table 3.
Our interpretation of the different effects of 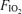 is based on classical concepts of pulmonary gas exchange developed some 60 years ago by Rahn & Fenn (1955) and Riley & Cournand (1949, 1951). In this concept, the only cause of arterial hypoxaemia seen while breathing 21% O2 that will persist while breathing 100% O2 is right-to-left shunting. This is because, with the complete elimination of alveolar N2 by removing it from the inspired gas, alveolar gas
is based on classical concepts of pulmonary gas exchange developed some 60 years ago by Rahn & Fenn (1955) and Riley & Cournand (1949, 1951). In this concept, the only cause of arterial hypoxaemia seen while breathing 21% O2 that will persist while breathing 100% O2 is right-to-left shunting. This is because, with the complete elimination of alveolar N2 by removing it from the inspired gas, alveolar gas 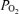 in all regions must rise to the mid-600 mmHg range, no matter how well or poorly ventilated any region may be. This is in turn due to the fact that the sum of the partial pressures of all alveolar gases must equal barometric pressure, which ranged from 754 to 762 mmHg during our study. Since saturated water vapour pressure is about 49 mmHg at 38°C and
in all regions must rise to the mid-600 mmHg range, no matter how well or poorly ventilated any region may be. This is in turn due to the fact that the sum of the partial pressures of all alveolar gases must equal barometric pressure, which ranged from 754 to 762 mmHg during our study. Since saturated water vapour pressure is about 49 mmHg at 38°C and 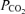 was about 40 mmHg, the rest (about 670 mmHg) must be made up by O2. Accordingly, ventilation/perfusion inequality cannot explain failure of arterial
was about 40 mmHg, the rest (about 670 mmHg) must be made up by O2. Accordingly, ventilation/perfusion inequality cannot explain failure of arterial 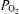 to reach the alveolar levels while breathing 100% O2.
to reach the alveolar levels while breathing 100% O2.
Hypoventilation similarly does not explain any significant failure of arterial 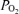 to reach the mid-600 mmHg range. Table 1 shows that ventilation was high and similar under all three
to reach the mid-600 mmHg range. Table 1 shows that ventilation was high and similar under all three 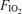 conditions, and Table 2 shows that arterial
conditions, and Table 2 shows that arterial 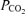 did not increase under any condition, which would have happened had there been inadequate ventilation for the level of exercise undertaken.
did not increase under any condition, which would have happened had there been inadequate ventilation for the level of exercise undertaken.
It is commonly accepted that breathing 100% O2 overcomes any diffusion limitation that may be observed in normoxia. This is because the alveolar to mixed venous 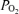 difference at the pulmonary capillary entrance rises from about 100 mmHg (alveolar) to 20 mmHg (mixed venous) in normoxia to about 670 mmHg (alveolar) to 20 mmHg (mixed venous) breathing 100% O2. This difference, increasing from 80 mmHg in normoxia to 650 mmHg in hyperoxia, increases the driving gradient that enables diffusion across the pulmonary blood gas barrier by 8-fold in hyperoxia, overcoming any reasonable abnormalities in lung diffusing capacity or transit time that could occur in normoxia and do occur in hypoxia.
difference at the pulmonary capillary entrance rises from about 100 mmHg (alveolar) to 20 mmHg (mixed venous) in normoxia to about 670 mmHg (alveolar) to 20 mmHg (mixed venous) breathing 100% O2. This difference, increasing from 80 mmHg in normoxia to 650 mmHg in hyperoxia, increases the driving gradient that enables diffusion across the pulmonary blood gas barrier by 8-fold in hyperoxia, overcoming any reasonable abnormalities in lung diffusing capacity or transit time that could occur in normoxia and do occur in hypoxia.
Only shunts can cause arterial 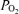 to be lower than alveolar while breathing 100% O2, and as a result, measuring venous admixture under these conditions has become the standard clinical method for measuring shunts in severely ill patients (West, 1969). The effect of shunt is explained by the failure of any alveolar O2 to cross into the bloodstream, or in the case of post-pulmonary shunts (bronchial and Thebesian), the admixture of deoxygenated blood directly into the left side of the circulation.
to be lower than alveolar while breathing 100% O2, and as a result, measuring venous admixture under these conditions has become the standard clinical method for measuring shunts in severely ill patients (West, 1969). The effect of shunt is explained by the failure of any alveolar O2 to cross into the bloodstream, or in the case of post-pulmonary shunts (bronchial and Thebesian), the admixture of deoxygenated blood directly into the left side of the circulation.
Thus, the large venous admixture seen in hypoxia, decreasing in normoxia and essentially vanishing in hyperoxia in our study is best explained mostly by diffusion limitation, which is accentuated in hypoxia. There is also likely to be a (lesser) contribution from ventilation/perfusion inequality, based on prior work (Gledhill et al. 1977; Gale et al. 1985; Wagner et al. 1986). This outcome reproduces what has been observed in normoxia and hypoxia in many earlier studies (Gledhill et al. 1977; Gale et al. 1985; Torre-Bueno et al. 1985; Wagner et al. 1986; Hammond et al. 1986a, b; Bebout et al. 1989; Podolsky et al. 1996) using the multiple inert gas exchange method (MIGET) (Wagner et al. 1974b,c; Evans & Wagner, 1977). The MIGET has the special ability to separately measure the contributions of hypoventilation, diffusion limitation, shunt and ventilation/perfusion inequality to arterial 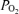 , but has not been used during exercise while breathing 100% O2 to compare any MIGET-derived shunt with the classical O2-derived shunt we report herein. That said, the previous studies referred to have mostly observed very small shunting. Rarely, if ever, has more than 1% shunt been seen during exercise, and the average values are much less (Torre-Bueno et al. 1985; Hammond et al. 1986a). However, these levels of shunt were observed at lower work rate, oxygen consumption and cardiac output values than those achieved by the athletes of the present study. This was an important consideration in our study design, also signifying its novelty, i.e. the inclusion of highly competitive athletes capable of sustaining high work rates and oxygen consumptions. As such we were able to evaluate whether shunt would increase during very intense exercise, or remain at the very low levels found in previous studies (Torre-Bueno et al. 1985; Hammond et al. 1986a).
, but has not been used during exercise while breathing 100% O2 to compare any MIGET-derived shunt with the classical O2-derived shunt we report herein. That said, the previous studies referred to have mostly observed very small shunting. Rarely, if ever, has more than 1% shunt been seen during exercise, and the average values are much less (Torre-Bueno et al. 1985; Hammond et al. 1986a). However, these levels of shunt were observed at lower work rate, oxygen consumption and cardiac output values than those achieved by the athletes of the present study. This was an important consideration in our study design, also signifying its novelty, i.e. the inclusion of highly competitive athletes capable of sustaining high work rates and oxygen consumptions. As such we were able to evaluate whether shunt would increase during very intense exercise, or remain at the very low levels found in previous studies (Torre-Bueno et al. 1985; Hammond et al. 1986a).
In the present study, the observed shunt of 0.5% of the cardiac output measured while breathing 100% O2 could explain only one fiftieth of the 22.8% venous admixture we saw in hypoxia, and only one seventh of the 3.5% venous admixture observed in normoxia, unless one postulated a major change in functional anatomy of the lungs caused by changing 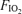 . It seems very unreasonable to claim that the large venous admixture seen during hypoxic exercise is due to a true shunt, which would have to be 22.8% as shown in Table 3, when on the same day only a very small shunt is measured while breathing 100% O2 at similar minute ventilation (by study design), and similar cardiac output (presumably resulting in comparable mean pulmonary artery pressure). Both minute ventilation and mean pulmonary artery pressure may affect venous admixture during heavy exercise (Wagner et al. 1986). Thus, we conclude that shunts are very small during heavy exercise in our normal subjects. Based on our results, shunt accounts for just 2% of the Aa
. It seems very unreasonable to claim that the large venous admixture seen during hypoxic exercise is due to a true shunt, which would have to be 22.8% as shown in Table 3, when on the same day only a very small shunt is measured while breathing 100% O2 at similar minute ventilation (by study design), and similar cardiac output (presumably resulting in comparable mean pulmonary artery pressure). Both minute ventilation and mean pulmonary artery pressure may affect venous admixture during heavy exercise (Wagner et al. 1986). Thus, we conclude that shunts are very small during heavy exercise in our normal subjects. Based on our results, shunt accounts for just 2% of the Aa 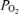 in hypoxia, and only 14% of the Aa
in hypoxia, and only 14% of the Aa 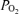 in normoxia.
in normoxia.
Critical issues in measuring 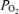 while breathing high O2 concentrations
while breathing high O2 concentrations
We had to assume blood temperature because the aural temperature probe failed to provide reasonable data (no increase in temperature was recorded from rest to exercise). Blood concentrations used to compute venous admixture were however, determined from co-oximeter-measured O2 saturations, which are not affected by electrode temperature differences from body temperature, and thus do not require any temperature correction. On the other hand, the dissolved portion of arterial O2 levels is computed by multiplying solubility by 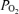 , which is temperature dependent. Solubility is negligibly affected by a 1°C variance in temperature, but
, which is temperature dependent. Solubility is negligibly affected by a 1°C variance in temperature, but 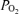 at fixed concentration changes about 6% per degree (Severinghaus, 1966). However, because O2 solubility is so low (0.003 ml dl−1 mmHg−1) the error in venous admixture is negligible as mentioned in the Results.
at fixed concentration changes about 6% per degree (Severinghaus, 1966). However, because O2 solubility is so low (0.003 ml dl−1 mmHg−1) the error in venous admixture is negligible as mentioned in the Results.
On the other hand, issues related to accuracy of measuring arterial 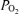 on 100% O2 abound. They relate to the extreme flatness of the O2 dissociation curve when
on 100% O2 abound. They relate to the extreme flatness of the O2 dissociation curve when 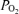 is several hundred millimetres of Hg. One is that heparin in sampling syringes is equilibrated with O2 at room
is several hundred millimetres of Hg. One is that heparin in sampling syringes is equilibrated with O2 at room 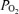 , not 100% O2. Another is that any small gas bubbles in the sampling syringe will also contain O2 at 21%. Another is the diffusion of O2 out of the sample syringe after the sample has been collected, due to the high
, not 100% O2. Another is that any small gas bubbles in the sampling syringe will also contain O2 at 21%. Another is the diffusion of O2 out of the sample syringe after the sample has been collected, due to the high 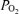 of the blood compared to the much lower
of the blood compared to the much lower 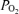 of the surrounding air. Yet another is use of O2 by white blood cells in the sample as the sample sits awaiting analysis. A final concern is consumption of O2 by the electrodes themselves from the sampled blood during the measurement process. It should be noted that every one of these potential problems acts to reduce the
of the surrounding air. Yet another is use of O2 by white blood cells in the sample as the sample sits awaiting analysis. A final concern is consumption of O2 by the electrodes themselves from the sampled blood during the measurement process. It should be noted that every one of these potential problems acts to reduce the 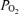 to below its in vivo real value. This means that the recorded
to below its in vivo real value. This means that the recorded 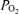 can only be lower than the actual in vivo value, and thus that the shunt values reported in Table 3 would be higher than actual in vivo values. To minimize these sources of potential error, we used minimal volumes of heparin, were careful to express all air bubbles while heparinizing syringes, and most importantly, introduced samples into the analyser within 10 s of collection, because several of the above concerns increase over time between collection and analysis.
can only be lower than the actual in vivo value, and thus that the shunt values reported in Table 3 would be higher than actual in vivo values. To minimize these sources of potential error, we used minimal volumes of heparin, were careful to express all air bubbles while heparinizing syringes, and most importantly, introduced samples into the analyser within 10 s of collection, because several of the above concerns increase over time between collection and analysis.
Absence of pulmonary artery pressure and ultrasound of pulmonary bubble transmission measurements in the present study
Non-invasive measurement of pulmonary artery pressure by echocardiography is not possible during heavy exercise and we did not feel that pulmonary arterial catheterization was justified based on the risk/benefit ratio. However, we were able to estimate pulmonary artery pressure by extrapolation from published data (Wagner et al. 1986) and the cardiac output measurements made in the present study. Based on such extrapolation we would expect mean pulmonary artery pressure to have been ∼40 mmHg in our subjects (Fig. 2).
Figure 2. Relationship between mean pulmonary artery pressure (PAP) and cardiac output during exercise in the study by Wagner et al. (1986), and expected mean PAP in the present study.
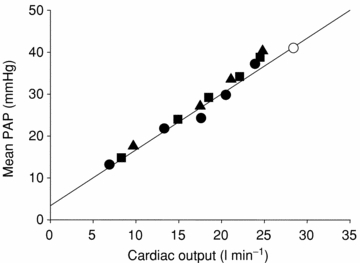
Filled symbols represent mean values obtained during exercise at barometric pressure 752 mmHg (sea level; •), 523 mmHg (▪) and 429 mmHg (▴) in the study by Wagner et al. (1986); line is the correlation line. Open circle represents the expected mean value of mean pulmonary artery pressure in the current study when applying on the diagram the mean value of cardiac output measurements.
In addition, we did not attempt ultrasound measurements of bubble transmission through the pulmonary circulation in the present studies as our subjects were already heavily instrumented. However, recent studies of bubble transmission indicate that essentially all normal subjects undertaking near-maximal exercise exhibit bubble transmission. Thus, 7 of 8 subjects (Stickland et al. 2004) and 21 of 23 subjects (Eldridge et al. 2004) showed bubble transmission during exercise. There is no reason to suspect that our normal subjects were any different in this regard from those used in the above-mentioned studies. Indeed, breathing 100% O2, our subjects reached very high values of oxygen consumption (4.7 l min−1) and cardiac output (28 l min−1), with expected mean pulmonary artery pressure ∼40 mmHg. In the study by Stickland et al. (2004) oxygen consumption was 3.2 l min−1, cardiac output was 25 l min−1 and mean pulmonary artery pressure did not exceed 25 mmHg at stage III (work rate at the ventilatory threshold) when subjects showed bubble passage. In the study by Eldridge et al. (2004) oxygen consumption was only 1.9 l min−1 when bubble transmission was demonstrated during exercise. Therefore, since 28 of 31 (90%) subjects (Eldridge et al. 2004; Stickland et al. 2004; Stickland & Lovering, 2006) showed transpulmonary bubble transmission at lower oxygen consumption, cardiac output and most probably pulmonary artery pressure than in our study, it is highly likely that our subjects would have demonstrated bubble transmission during exercise.
Even if not all our subjects displayed bubble transmission, the reported incidence is so high (90% of 31 subjects) that some undoubtedly would have (probably 6 of the 7 according to the above). It is therefore important to note that not one of the seven subjects showed a shunt greater than 1.1% while breathing 100% O2 and that in most subjects the shunt was much less (Table 3).
Reconciling bubble transmission data with pulmonary gas exchange
Bubble transmission occurring during exercise but not at rest is certainly consistent with an increase in diameter of pulmonary blood vessels during exercise. Distension is indeed an expected outcome of exercise since it is well known to occur in response to elevated pulmonary pressure (al-Tinawi et al. 1991; Hillier et al. 1993; Mehrotra et al. 1993) and because pulmonary artery pressure is equally well known to increase during exercise (Bevegard et al. 1963; Wagner et al. 1986; Groves et al. 1987).
Accordingly, the present results are not to be interpreted as evidence against the enlargement of pulmonary arteries during exercise. They are seen as evidence that any such enlargement does not mean that these vessels must act as important shunts in terms of O2 exchange, in contrast to what has been suggested in prior work (Stickland et al. 2007). It is quite possible that arterial enlargement could have no gas exchange consequence, or that it could alter the distribution of pulmonary blood flow through changing vascular resistance, and that this could promote ventilation/perfusion inequality (which could contribute to arterial hypoxaemia, as it has been well demonstrated before (Gale et al. 1985; Hammond et al. 1986b; Wagner et al. 1986, 1987)). Whether such enlarged arteries could increase alveolar–capillary diffusion limitation by increasing the distance within blood vessels that O2 must travel to reach Hb within red cells, postulated by Stickland & Lovering (2006), is debatable. When cardiac output is some 20–30 l min−1 as in heavy exercise, adequate mixing across the vessel lumen seems likely, but this possibility remains to be specifically tested.
It has been demonstrated that some gas exchange takes place upstream of the capillaries (Conhaim & Staub, 1980), a finding recently invoked by Stickland & Lovering (2006). They suggest that proximal vessel exchange (which occurs by diffusion) favours inert gases over O2 and may on that basis account for the fact that MIGET studies over the years have never found more than a fraction of a per cent of shunt. We would see their argument as implying an additional factor in diffusion limitation for O2 (the others being a limited diffusing capacity and low capillary transit time), but if that is the case, bubble transmission should not be called a shunt because in most circles, a shunt represents blood that by-passes alveolar gas exchange completely. In fact, to the extent that pre-capillary gas exchange occurs, that should only help O2 complete its diffusive exchange compared to a situation in which O2 exchange occurred only in the capillaries.
Stickland et al. (2004) compared bubble transmission to the Aa  in exercising humans. Bubble transmission was associated with heavy exercise, which is when the Aa
in exercising humans. Bubble transmission was associated with heavy exercise, which is when the Aa  is largest (compared to that at rest). This correlation is not questioned, but that does not mean that such a correlation infers cause and effect as the authors suggest. Many exercise-related variables increase in parallel with exercise intensity and would show similar correlations.
is largest (compared to that at rest). This correlation is not questioned, but that does not mean that such a correlation infers cause and effect as the authors suggest. Many exercise-related variables increase in parallel with exercise intensity and would show similar correlations.
Lastly, the magnitude of the so-called shunts, identified by passage of bubbles or microspheres through the lungs, needs discussion. The initial studies (Eldridge et al. 2004; Stickland et al. 2004) used microbubbles detected echocardiographically, and could not quantify the fraction of the cardiac output passing through channels that allowed passage of microbubbles. More recently, isolated human and baboon lungs (Lovering et al. 2007) and dog lungs (Stickland et al. 2007) were tested for microsphere transmission. In those studies, both 25 and 50 μm microspheres passed through the lungs, but it is important to note that the number of microspheres that passed though the lungs was 0.07% (Lovering et al. 2007) and 0.02% (Stickland et al. 2007) of those injected. If that marks the ‘shunt’, then at 0.07% or 0.02% of the cardiac output, it is truly miniscule compared to the values given in Table 3 for venous admixture. This is illustrated in Fig. 3 where the Aa  calculated on the basis of hypothetical shunt values is plotted (continuous line) as a function of shunt fraction for each
calculated on the basis of hypothetical shunt values is plotted (continuous line) as a function of shunt fraction for each 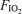 we used, using published computer algorithms (West, 1969). Also indicated in the figure is the measured mean Aa
we used, using published computer algorithms (West, 1969). Also indicated in the figure is the measured mean Aa 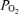 from the present study, and it can be seen that shunts of the magnitude found in isolated lungs (Lovering et al. 2007; Stickland et al. 2007) could account for only a very small fraction of the Aa
from the present study, and it can be seen that shunts of the magnitude found in isolated lungs (Lovering et al. 2007; Stickland et al. 2007) could account for only a very small fraction of the Aa 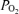 . However, isolated lung data regarding the magnitude of arterio-venous shunts may differ from those obtained during exercise (Stickland et al. 2007), as within the same species the isolated lung has been shown to have less arterio-venous shunts as compared to the exercising animal, possibly due to lower pulmonary blood flow and thus less vascular distension in the isolated lung (Stickland et al. 2007). Indeed, shunt accounts for only 0.02% of the cardiac output in the isolated dog lungs compared to 1.4% in the exercising dogs (Stickland et al. 2007). Regarding this latter study (Stickland et al. 2007), it is hard to say that gas exchange worsened during exercise, as arterial
. However, isolated lung data regarding the magnitude of arterio-venous shunts may differ from those obtained during exercise (Stickland et al. 2007), as within the same species the isolated lung has been shown to have less arterio-venous shunts as compared to the exercising animal, possibly due to lower pulmonary blood flow and thus less vascular distension in the isolated lung (Stickland et al. 2007). Indeed, shunt accounts for only 0.02% of the cardiac output in the isolated dog lungs compared to 1.4% in the exercising dogs (Stickland et al. 2007). Regarding this latter study (Stickland et al. 2007), it is hard to say that gas exchange worsened during exercise, as arterial 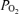 increased by 14 mmHg while arterial
increased by 14 mmHg while arterial 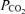 fell by only 5.5 mmHg, changes that do not suggest deterioration of gas exchange. In terms of relevance to human exercise, there is evidence that dogs have lower pulmonary vascular resistance than humans during exercise. Hsia et al. (2007) found that normal dogs exercising at an intensity producing a cardiac output of 350 ml min−1 kg−1 have a mean pulmonary pressure of about 27 mmHg. It has been shown that humans exercising at an intensity resulting in the same cardiac output of 350 ml min−1 kg−1 produce a mean pulmonary artery pressure of 37.2 mmHg (Wagner et al. 1986). This suggests that in the dog, pulmonary arteries are relatively more distensible and might allow passage of more or larger bubbles or microspheres than humans. Nevertheless, even if shunts of the magnitude measured in exercising dogs (Stickland et al. 2007) are present in exercising healthy humans, they are small and can account for only a small fraction of the Aa
fell by only 5.5 mmHg, changes that do not suggest deterioration of gas exchange. In terms of relevance to human exercise, there is evidence that dogs have lower pulmonary vascular resistance than humans during exercise. Hsia et al. (2007) found that normal dogs exercising at an intensity producing a cardiac output of 350 ml min−1 kg−1 have a mean pulmonary pressure of about 27 mmHg. It has been shown that humans exercising at an intensity resulting in the same cardiac output of 350 ml min−1 kg−1 produce a mean pulmonary artery pressure of 37.2 mmHg (Wagner et al. 1986). This suggests that in the dog, pulmonary arteries are relatively more distensible and might allow passage of more or larger bubbles or microspheres than humans. Nevertheless, even if shunts of the magnitude measured in exercising dogs (Stickland et al. 2007) are present in exercising healthy humans, they are small and can account for only a small fraction of the Aa 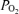 measured during heavy hypoxic and normoxic exercise (Fig. 3).
measured during heavy hypoxic and normoxic exercise (Fig. 3).
Figure 3. Measured alveolar–arterial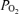 difference (Aa
difference (Aa 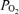 ) at each
) at each 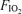 , and calculated relationship between Aa
, and calculated relationship between Aa 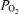 and shunt.
and shunt.
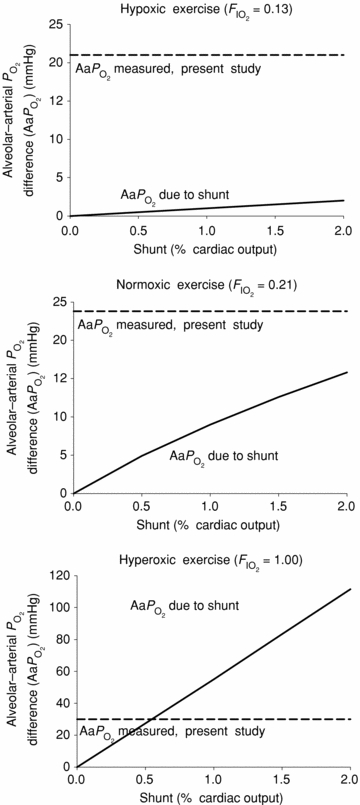
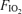 : 0.13 (top),
: 0.13 (top), 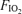 : 0.21 (middle), and
: 0.21 (middle), and 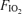 : 1.0 (lower). Horizontal dashed lines are measured mean alveolar–arterial
: 1.0 (lower). Horizontal dashed lines are measured mean alveolar–arterial 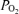 differences, and continuous lines are calculated relationships between Aa
differences, and continuous lines are calculated relationships between Aa 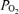 and shunt. The observed mean shunt of 0.5% of the cardiac output measured with
and shunt. The observed mean shunt of 0.5% of the cardiac output measured with 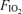 = 1.0 and accounting for 100% of the Aa
= 1.0 and accounting for 100% of the Aa 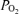 in hyperoxic exercise (lower), indicates that shunt is very small during heavy exercise and accounts for just a small percentage of the measured Aa
in hyperoxic exercise (lower), indicates that shunt is very small during heavy exercise and accounts for just a small percentage of the measured Aa 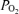 in hypoxic and normoxic exercise (i.e. 2% (top) and 14% (middle), respectively). If flow through dilated pulmonary vessels is less than 0.1% of the cardiac output as estimated by Lovering et al. (2007), it can be seen that even if this flow acts as a shunt, its contribution to the total Aa
in hypoxic and normoxic exercise (i.e. 2% (top) and 14% (middle), respectively). If flow through dilated pulmonary vessels is less than 0.1% of the cardiac output as estimated by Lovering et al. (2007), it can be seen that even if this flow acts as a shunt, its contribution to the total Aa 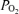 is very small at each
is very small at each 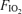 .
.
In conclusion, the present study provides evidence that intrapulmonary shunts even during very heavy exercise are quite small and do not contribute significantly to arterial hypoxaemia during exercise. Our data are consistent with what has been shown previously, i.e. that diffusion limitation and ventilation/perfusion inequality are much more important determinants of arterial 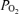 during heavy normoxic (and also hypoxic) exercise in normal humans.
during heavy normoxic (and also hypoxic) exercise in normal humans.
Acknowledgments
This work was supported by the ‘Aliki Perroti’ Visiting Professorship Fund of the Thorax Foundation and NIH HL84281.
References
- al-Tinawi A, Madden JA, Dawson CA, Linehan JH, Harder DR, Rickaby DA. Distensibility of small arteries of the dog lung. J Appl Physiol. 1991;71:1714–1722. doi: 10.1152/jappl.1991.71.5.1714. [DOI] [PubMed] [Google Scholar]
- Asmussen E, Nielsen M. Alveolar-arterial gas exchange at rest and during work at different O2 tensions. Acta Physiol Scand. 1960;50:153–166. doi: 10.1111/j.1748-1716.1960.tb02086.x. [DOI] [PubMed] [Google Scholar]
- Bebout DE, Story D, Roca J, Hogan MC, Poole DC, Gonzales-Camarena R, Ueno O, Haab P, Wagner PD. Effects of altitude acclimatization on pulmonary gas exchange during exercise. J Appl Physiol. 1989;67:2286–2295. doi: 10.1152/jappl.1989.67.6.2286. [DOI] [PubMed] [Google Scholar]
- Bevegard S, Holmgren A, Jonsson B. Circulatory studies in well trained athletes at rest and during heavy exercise with special reference to stroke volume and the influence of body position. Acta Physiol Scand. 1963;57:26–50. doi: 10.1111/j.1748-1716.1963.tb02572.x. [DOI] [PubMed] [Google Scholar]
- Conhaim RL, Staub NC. Reflection spectrophotometric measurement of O2 uptake in pulmonary arterioles of cats. J Appl Physiol. 1980;48:848–856. doi: 10.1152/jappl.1980.48.5.848. [DOI] [PubMed] [Google Scholar]
- Dempsey JA. Challenges for future research in exercise physiology as applied to the respiratory system. Exerc Sports Sci Rev. 2006;34:92–98. doi: 10.1249/00003677-200607000-00002. [DOI] [PubMed] [Google Scholar]
- Dempsey JA, Hanson PG, Henderson KS. Exercise-induced arterial hypoxaemia in healthy human subjects at sea level. J Physiol. 1984;355:161–175. doi: 10.1113/jphysiol.1984.sp015412. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dow P. Estimations of cardiac output and central blood volume by dye dilution. Physiol Rev. 1956;36:77–102. doi: 10.1152/physrev.1956.36.1.77. [DOI] [PubMed] [Google Scholar]
- Eldridge MW, Dempsey JA, Haverkamp HC, Lovering AT, Hokanson JS. Exercise-induced intrapulmonary arteriovenous shunting in healthy humans. J Appl Physiol. 2004;97:797–805. doi: 10.1152/japplphysiol.00137.2004. [DOI] [PubMed] [Google Scholar]
- Evans JW, Wagner PD. Limits on VA/Q distributions from analysis of experimental inert gas elimination. J Appl Physiol. 1977;42:889–898. doi: 10.1152/jappl.1977.42.6.889. [DOI] [PubMed] [Google Scholar]
- Gale GE, Torre-Bueno JR, Moon RE, Saltzman HA, Wagner PD. Ventilation/perfusion inequality in normal humans during exercise at sea level and simulated altitude. J Appl Physiol. 1985;58:978–988. doi: 10.1152/jappl.1985.58.3.978. [DOI] [PubMed] [Google Scholar]
- Gledhill N, Froese AB, Dempsey JA. Ventilation to perfusion distribution during exercise in health. In: Dempsey JA, Reed CE, editors. Muscular Exercise and the Lung. Madison: University of Wisconsin Press; 1977. pp. 325–344. [Google Scholar]
- Groves BM, Reeves JT, Sutton JR, Wagner PD, Cymerman A, Malconian MK, Rock PB, Young PM, Houston CS. Operation Everest II: elevated high-altitude pulmonary resistance unresponsive to oxygen. J Appl Physiol. 1987;63:521–530. doi: 10.1152/jappl.1987.63.2.521. [DOI] [PubMed] [Google Scholar]
- Hammond MD, Gale GE, Kapitan KS, Ries A, Wagner PD. Pulmonary gas exchange in humans during exercise at sea level. J Appl Physiol. 1986a;60:1590–1598. doi: 10.1152/jappl.1986.60.5.1590. [DOI] [PubMed] [Google Scholar]
- Hammond MD, Gale GE, Kapitan KS, Ries A, Wagner PD. Pulmonary gas exchange in humans during normobaric hypoxic exercise. J Appl Physiol. 1986b;61:1749–1757. doi: 10.1152/jappl.1986.61.5.1749. [DOI] [PubMed] [Google Scholar]
- Hillier SC, Godbey PS, Hanger CC, Graham JA, Presson RG, Jr, Okada O, Linehan JH, Dawson CA, Wagner WW., Jr Direct measurement of pulmonary microvascular distensibility. J Appl Physiol. 1993;75:2106–2111. doi: 10.1152/jappl.1993.75.5.2106. [DOI] [PubMed] [Google Scholar]
- Hsia CCW, Johnson RL, Jr, McDonough P, Dane DM, Hurst MD, Fehmel JL, Wagner HE, Wagner PD. Residence at 3,800-m altitude for 5 mo in growing dogs enhances lung diffusing capacity for oxygen that persists at least 2.5 years. J Appl Physiol. 2007;102:1448–1455. doi: 10.1152/japplphysiol.00971.2006. [DOI] [PubMed] [Google Scholar]
- Lovering AT, Stickland MK, Kelso AJ, Eldridge MW. Direct demonstration of 25- and 50-μm arteriovenous pathways in healthy human and baboon lungs. Am J Physiol Heart Circ Physiol. 2007;292:H1777–H1781. doi: 10.1152/ajpheart.01024.2006. [DOI] [PubMed] [Google Scholar]
- Mehrotra PP, Patel DJ, Coleman BR, Tearney RJ, Diggs JA, Cothran LN, Curry CL. Distensibility of small pulmonary blood vessels. J Biomech Eng. 1993;115:286–289. doi: 10.1115/1.2895488. [DOI] [PubMed] [Google Scholar]
- Podolsky A, Eldridge MW, Richardson RS, Knight DR, Johnson EC, Hopkins SR, Johnson DH, Michimata H, Grassi B, Feiner J, Kurdak SS, Bickler PE, Severinghaus JW, Wagner PD. Exercise-induced VA/Q inequality in subjects with prior high altitude pulmonary edema. J Appl Physiol. 1996;81:922–932. doi: 10.1152/jappl.1996.81.2.922. [DOI] [PubMed] [Google Scholar]
- Rahn H, Fenn WO. A Graphical Analysis of the Respiratory Gas Exchange. Washington, D.C: American Physiological Society; 1955. [Google Scholar]
- Rice AJ, Thornton AT, Gore CJ, Scroop GC, Greville HW, Wagner H, Wagner PD, Hopkins SR. Pulmonary gas exchange during exercise in highly trained cyclists with arterial hypoxemia. J Appl Physiol. 1999;87:1802–1812. doi: 10.1152/jappl.1999.87.5.1802. [DOI] [PubMed] [Google Scholar]
- Riley RL, Cournand A. ‘Ideal’ alveolar air and the analysis of ventilation/perfusion relationships in the lung. J Appl Physiol. 1949;1:825–847. doi: 10.1152/jappl.1949.1.12.825. [DOI] [PubMed] [Google Scholar]
- Riley RL, Cournand A. Analysis of factors affecting partial pressures of oxygen and carbon dioxide in gas and blood of lungs: theory. J Appl Physiol. 1951;4:77–101. doi: 10.1152/jappl.1951.4.2.77. [DOI] [PubMed] [Google Scholar]
- Severinghaus JW. Blood gas calculator. J Appl Physiol. 1966;21:1108–1116. doi: 10.1152/jappl.1966.21.3.1108. [DOI] [PubMed] [Google Scholar]
- Stickland MK, Lovering AT. Exercise-induced intrapulmonary arteriovenous shunting and pulmonary gas exchange. Exerc Sports Sci Rev. 2006;34:99–106. doi: 10.1249/00003677-200607000-00003. [DOI] [PubMed] [Google Scholar]
- Stickland MK, Lovering AT, Eldridge MW. Exercise-induced arteriovenous intrapulmonary shunting in dogs. Am J Respir Crit Care Med. 2007;176:300–305. doi: 10.1164/rccm.200702-206OC. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stickland MK, Welsh RC, Haykowsky MJ, Petersen SR, Anderson WD, Taylor DA, Bouffard M, Jones RL. Intra-pulmonary shunt and pulmonary gas exchange during exercise in humans. J Physiol. 2004;561:321–329. doi: 10.1113/jphysiol.2004.069302. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Torre-Bueno J, Wagner PD, Saltzman HA, Gale GE, Moon RE. Diffusion limitation in normal humans during exercise at sea level and simulated altitude. J Appl Physiol. 1985;58:989–995. doi: 10.1152/jappl.1985.58.3.989. [DOI] [PubMed] [Google Scholar]
- Vogiatzis I, Georgiadou O, Giannopoulou I, Koskolou M, Zakynthinos S, Kostikas K, Kosmas E, Wagner H, Peraki E, Koutsoukou A, Koulouris N, Wagner PD, Roussos C. Effects of exercise-induced arterial hypoxaemia and work rate on diaphragmatic fatigue in highly trained endurance athletes. J Physiol. 2006;572:539–549. doi: 10.1113/jphysiol.2005.102442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogiatzis I, Georgiadou O, Koskolou M, Athanasopoulos D, Kostikas K, Golemati S, Wagner H, Roussos C, Wagner PD, Zakynthinos S. Effects of hypoxia on diaphragmatic fatigue in highly trained athletes. J Physiol. 2007;581:299–308. doi: 10.1113/jphysiol.2006.126136. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner PD, Gale GE, Moon RE, Torre-Bueno JR, Stolp WB, Saltzman HA. Pulmonary gas exchange in humans exercising at sea level and simulated altitude. J Appl Physiol. 1986;61:260–270. doi: 10.1152/jappl.1986.61.1.260. [DOI] [PubMed] [Google Scholar]
- Wagner PD, Laravuso RB, Uhl RR, West JB. Continuous distributions of ventilation-perfusion ratios in normal subjects breathing air and 100% O2. J Clin Invest. 1974a;54:54–68. doi: 10.1172/JCI107750. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wagner PD, Naumann PF, Laravuso RB. Simultaneous measurement of eight foreign gases in blood by gas chromatography. J Appl Physiol. 1974b;36:600–605. doi: 10.1152/jappl.1974.36.5.600. [DOI] [PubMed] [Google Scholar]
- Wagner PD, Saltzman HA, West JB. Measurement of continuous distributions of ventilation-perfusion ratios: theory. J Appl Physiol. 1974c;36:588–599. doi: 10.1152/jappl.1974.36.5.588. [DOI] [PubMed] [Google Scholar]
- Wagner PD, Sutton JR, Reeves JT, Cymerman A, Groves BM, Malconian MK. Operation Everest II: pulmonary gas exchange during a simulated ascent of Mt. Everest. J Appl Physiol. 1987;63:2348–2359. doi: 10.1152/jappl.1987.63.6.2348. [DOI] [PubMed] [Google Scholar]
- Wagner PD, Wagner HE, Groves BM, Cymerman A, Houston CS. Hemoglobin P50 during a simulated ascent of Mt. Everest, Operation Everest II. High Alt Med Biol. 2007;8:32–42. doi: 10.1089/ham.2006.1049. [DOI] [PubMed] [Google Scholar]
- West JB. Ventilation/perfusion inequality and overall gas exchange in computer models of the lung. Respir Physiol. 1969;7:88–110. doi: 10.1016/0034-5687(69)90071-1. [DOI] [PubMed] [Google Scholar]
- Whipp BJ, Wasserman K. Alveolar-arterial gas tension differences during graded exercise. J Appl Physiol. 1969;27:361–365. doi: 10.1152/jappl.1969.27.3.361. [DOI] [PubMed] [Google Scholar]


