Actin Polymerization Overshoots and ATP Hydrolysis as Assayed by Pyrene Fluorescence

Abstract

We investigate via stochastic simulation the overshoots observed in the fluorescence intensity of pyrene-labeled actin during rapid polymerization. We show that previous assumptions about pyrene intensity that ignore the intensity differences between subunits in different ATP hydrolysis states are not consistent with experimental data. This strong sensitivity of intensity to hydrolysis state implies that a measured pyrene intensity curve does not immediately reveal the true polymerization kinetics. We show that there is an optimal range of hydrolysis and phosphate release rate combinations simultaneously consistent with measured polymerization data from previously published severing and Arp2/3 complex-induced branching experiments. Within this range, we find that the pyrene intensity curves are described very accurately by the following average relative intensity coefficients: 0.37 for F-ATP actin; 0.55 for F-ADP + P_i actin; and 0.75 for F-ADP actin. Finally, we present an analytic formula, which properly accounts for the sensitivity of the pyrene assay to hydrolysis state, for estimation of the concentration of free barbed ends from pyrene intensity curves.

INTRODUCTION

Actin is a globular protein found in the cytoskeleton of all eukaryotic cells (1). Monomers of actin (G-actin) polymerize into long, polarized filaments (F-actin) that have a rapidly growing barbed end and a slower growing pointed end (2). Filament nucleation and growth is regulated by a large number of actin binding proteins (3). Net filament growth stops when the concentration of monomeric actin drops below the critical concentration (2). As a motile eukaryotic cell constantly reshapes its cytoskeleton via rapid (de)polymerization of actin, understanding the kinetics of actin polymerization is intrinsic to understanding cell motility (4,5). For this reason, numerous measurements of the time-course of in vitro actin polymerization have been performed.

N-(1-pyrenyl)iodoacetamide (henceforth referred to simply as “pyrene”) is a 385-Da fluorophore that preferentially binds to the thiol group of the Cys-374 residue of G-actin monomers (6). It has been shown that the emitted intensity (at 386 nm) of pyrene increases 7–12 fold upon polymerization (7,8) and that this increased intensity is insensitive to filament length (9). Early studies (7,9), which indicated that the addition of the covalently-bound pyrene fluorophore does not alter the thermodynamic properties of actin, recently have been confirmed (10). The process of labeling actin with pyrene is reliable and well known (7). These qualities have allowed the pyrene intensity to become a ubiquitous assay of in vitro actin polymerization.

Actin monomers contain bound nucleotide complexed with a divalent cation such as Mg²⁺ or Ca²⁺ (11). Monomeric actin containing ATP is more rapidly polymerized than actin containing ADP (2). Upon polymerization, the actin subunits undergo a two-step hydrolysis (12). First, the ATP-containing subunits (F-ATP) hydrolyze to a state in which inorganic phosphate remains bound to the nucleotide (F-ADP + P_i). Second, the bound phosphate is released, leaving the subunit in the ADP hydrolysis state (F-ADP). In 1984, Carlier et al. showed that the intensity of pyrene-labeled actin subunits must be different for different hydrolysis states (13). By comparing an independent measurement of the amount of polymerized actin that had completely hydrolyzed (F-ATP→F-ADP) to the timescale of an obvious increase in pyrene intensity, Carlier et al. concluded that completely hydrolyzed subunits (F-ADP) are substantially brighter than unhydrolyzed subunits (F-ATP). In 1985, Enrico Grazi explicitly demonstrated that the fluorescence of the pyrene assay is not linearly proportional to the amount of polymerized actin (14). On this basis he concluded that the pyrene assay detects only the onset of polymerization over short time-courses and, furthermore, that “it cannot provide the experimental basis to the very refined kinetic analysis so far performed by many workers.” It is important to note, however, that the results of both of these experiments were published before the discovery of the intermediate, bound inorganic phosphate hydrolysis state (F-ADP+P_i). Thus, a more complete treatment is needed.

Numerous pyrene fluorescence assays of the rapid polymerization of both yeast and muscle actin clearly indicate an overshoot in the amount of polymerized actin (15–28). Here, we define an overshoot to be a peak in the concentration of polymerized actin followed by a pronounced drop. Thus, the overshoot magnitude is given by the difference between the maximum observed concentration and the minimum concentration that occurs after the maximum. Under most experimentally practical conditions, the minimum concentration after the maximum will be the steady-state concentration. Several mechanisms of accelerating polymerization yield overshoots, including Arp2/3 complex-induced branching, severing via both sonication and ADF/cofilin, and the use of seed filaments. Typical overshoots in similar pyrene-assayed polymerization time-courses found in the literature are shown in Fig. 1. One should note that short lag phases, which imply fast filament nucleation, are not reliable indicators of large overshoot magnitudes. This may be seen from Fig. 1 where the Carlsson et al. (24) (solid) and Goley et al. (27) (dashed) polymerization time-courses exhibit similar lag phases yet have very different overshoot magnitudes.

FIGURE 1.

Typical overshoots in pyrene assayed polymerization time-courses of similar amounts of ATP-actin accelerated by Arp2/3-induced branching. Data were taken from published works. (Solid, Carlsson et al. (24); dot-dashes, Leng et al. (26); dashes, Goley et al. (27); and circles, Tehrani et al. (28) shifted forward in time by 80 s for added clarity.)

In this article, we argue that the overshoots observed in these examples are not artifacts of the pyrene assay, but rather the result of depolymerization occurring at long times due to hydrolysis. A simpler example, schematically illustrated in Fig. 2, in which such an overshoot must occur is the in vitro polymerization of G-ATP actin from a high concentration of spectrin seeds in the absence of excess ATP. Assuming that the initial concentration of G-ATP actin (G_o) is greater than the ATP-actin critical concentration at the barbed end 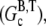the ATP-actin rapidly polymerizes and depletes the G-actin monomer pool to very nearly 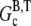(≈0.1 μM (29)). Subsequently, hydrolysis of all subunits occurs leaving only ADP-actin. As the barbed end critical concentration of ADP-actin 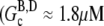(29)) is much higher than that of ATP-actin, the ADP filaments depolymerize until 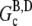is reached. This leaves the steady-state concentration of polymerized actin much less than the maximum concentration. Any accurate assay of actin polymerization would thus indicate an overshoot. If instead we allow an initial concentration of ADP-actin to polymerize, no overshoot will occur as the amount of polymerized actin will increase monotonically until the G-actin pool reaches 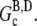Thus, we expect that an overshoot in the polymerization time-course will occur if the time to polymerize most of the actin is less than the time for complete hydrolysis (including phosphate release) and the nucleotide exchange time.

FIGURE 2.

A simple example of an overshoot in the concentration of polymerized actin (solid curve). As described in the text, this overshoot is entirely due to the depolymerization response to the increasing critical concentration that must result from the increasing numbers of completely hydrolyzed monomers (G-ADP) in the monomer pool.

Although precise description of specific experimental conditions may not always be possible, some generalizations can be made about the overshoot magnitude. Under the conditions described above, the maximum overshoot magnitude is 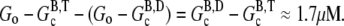Therefore, the magnitude of the overshoot relative to the total polymerized actin will be lower at high actin concentrations. Also, we expect that increasing the concentration of seed filaments (N) will increase the overshoot magnitude until the maximum possible magnitude is achieved. The reason for this is twofold. First, as the net polymerization rate is proportional to N, increasing N means increasing the polymerized actin concentration (F) that has not yet had sufficient time to completely hydrolyze to the F-ADP state. Thus, F at the peak is brought closer to its maximum value of 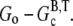Second, as N increases, so does the number of barbed ends available for the rapid depolymerization that occurs when most of subunits have completely hydrolyzed. This second point is important for experiments where excess ATP is present in solution. There, large N implies that the process of nucleotide exchange (G-ADP→G-ATP) can be temporarily overwhelmed by the rapid influx of ADP subunits into the monomer pool. Thus, after sufficient time to hydrolyze the majority of the subunits, F will be brought closer to its minimum value of 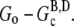These two results of increasing N work cooperatively to increase the magnitude of the overshoot.

If we now take into account the fact that F-ADP pyrene-labeled actin is brighter than F-ATP pyrene-labeled actin (13), any genuine overshoot in polymerization due to a change in critical concentration alone is diminished by the increase in number of brighter F-ADP subunits. In fact, if the actin concentration is high, the effect of the brighter F-ADP subunits can be sufficiently large such that there is no overshoot in the pyrene intensity at all. In both cases, the decay of the polymerization curve from the maximum to the steady state—representing the generation of F-ADP subunits and subsequent net depolymerization—is necessarily different from any decay indicated by the pyrene intensity curve. Thus, the pyrene intensity curve differs in at least two ways from the true kinetics of polymerization.

Considering these differences, independent verification of rapid polymerization time-courses might be attempted via other assays such as NBD fluorescence (13,30,31), intrinsic fluorescence (16,17), or light scattering (13,24). We must point out, however, that direct comparisons between pyrene and light scattering assays are not automatically appropriate. The light scattering intensity is determined by not only the amount of polymerized actin (32,33), but by the structural features of the filaments such as average length (34–36), rigidity (37), and branched-cluster size (38). Since the structure of the filaments changes during polymerization, light scattering does not necessarily measure actin polymerization alone.

It is the purpose of this study to establish how the intensity of polymerized pyrene-labeled actin depends on hydrolysis state, and to describe the implications of this dependence on previous inferences made from pyrene assays of polymerization time-courses. This will be done by the comparison of stochastically simulated intensity curves with published pyrene intensity curves from the rapid polymerization experiments of Carlier et al. (13) and Tehrani et al. (28). The experiment of Tehrani et al. was chosen because it exhibited the most dramatic overshoot of all those we found in the literature. These data are also more complete than similar experiments because they extend to times well beyond the appearance of the overshoot. This allows for thorough investigation of slower processes such as the release of inorganic phosphate from polymerized actin subunits. We sought to contrast these data, representing polymerization accelerated by Arp2/3 complex-induced branching, with data representing a very different mechanism of polymerization stimulation, namely, severing. The Carlier et al. experiment was the only example that we were able to find of severing being continuously applied during polymerization that did not employ the use of ADF/cofilin. The presence of ADF/cofilin complicates the analysis because it may modify the pyrene intensity in unknown ways. The details of the simulation and determination of the individual pyrene intensities are described in the sections that follow.

MODELING METHODS

Stochastic simulation

Rate equations that keep track of the concentrations of G-actin and F-actin alone cannot readily describe processes that alter the distribution of filament lengths such as severing, annealing, or complete depolymerization. Furthermore, such rate equations alone may not adequately model processes in which the hydrolysis state of each subunit must be known, such as debranching and the effects of ATP caps on depolymerization. Therefore, a stochastic simulation code that includes separate subroutines corresponding to the events of spontaneous nucleation, (de)polymerization, (de)branching, severing, annealing, (un)capping, and two-step hydrolysis (including phosphate release) was written in Python v2.4.4, a freely available object-oriented programming language (http://www.python.org). The current simulation differs from similar preceding ones in that the effects of both hydrolysis and annealing events are also included (38,39) and that the physical position of filaments in three-dimensional space is not stored (38,40) because we treat only bulk properties. The probability p of any particular event occurring on a particular filament is given by p = kΔt, where k is the first-order rate of event occurrence and Δt is sufficiently small (Δt = 0.002 s) such that kΔt ≪ 1. This guarantees that, on average, less than one event per filament will occur per time step. Each time an event subroutine is run, a real number is selected from a uniform distribution between zero and unity. If this probability is less than p, the event occurs and the dynamic variables (e.g., number of actin monomers) are updated appropriately. The master set of simulated filaments is stored in memory as strings of characters representing the hydrolysis and branching state of each individual subunit. The left end of the string is always taken to be the pointed end of the filament. For example, the string “ATTPD” represents an Arp2/3 (“A”) induced branched filament consisting of two F-ATP subunits “T,” one F-ADP+P_i subunit “P,” and one F-ADP subunit “D.” To ensure that no residual ordering of the random number generator persists throughout the simulation, the master filament set is shuffled every 125 time steps. Each simulation begins with a single seed trimer, an initial ATP-actin concentration, and, when appropriate, an initial Arp2/3 concentration. To reduce computation time, routines that must parse the entire master set of filament strings, such as that controlling hydrolysis, are skipped a certain number of time steps (N_skip) and then implemented with probability p = kΔtN_skip. As N_skip is chosen for each subroutine such that the time N_skipΔt is still much less than the characteristic time of a given event (1/k), we are confident that this skipping is sound. Table 1 shows the value of N_skip for each subroutine that was skipped. All other subroutines were run every time step.

TABLE 1.

N_skip values

Subroutine	1/rate (per filament)	Nskip × Δt
Hydrolysis	1.3–50 s	50 × 0.002 = 0.1 s
Phosphate release	13–500 s	50 × 0.002 = 0.1 s
Severing	1.5–6.5 s	50 × 0.002 = 0.1 s
Branching	2–14 s	10 × 0.002 = 0.02 s
Debranching	5–50 s	500 × 0.002 = 1 s

To reduce computation time, some routines are skipped a certain of number time steps. Each skip is chosen such that the time N_skipΔt is much less than the characteristic time of a given event (1/k) which ensures that, on average, only one event or less occurs per filament in each run of the subroutine.

Implementation of molecular level processes

A complete summary of all symbols and input parameters described below may be found in Table 2. The densities of free actin monomers, Arp2/3 complex, and capping protein are taken to be spatially uniform (as opposed to being locally depleted near a filament tip). As the actin used in each of the experiments we model included the same divalent cation (Mg²⁺), we did not attempt to model the effects of various cations in our simulation. The most recently available values of monomer association and subunit dissociation rate constants were used (29). The values of both the barbed- and pointed-end off-rates for F-ADP+P_i actin are of particular note. We were unable to find in the literature direct measurements of these off-rates in the absence of saturating inorganic phosphate. We adopted the argument of Bindschadler et al. (41) that since F-ATP and F-ADP+P_i actin subunits have the same barbed-end critical concentration (42) and similar crystal structure (43), the off-rates of F-ADP+P_i subunits should be equivalent to those of F-ATP subunits. We do, however, treat specific cases below where both F-ADP+P_i off-rates were varied by as much as ±50% of the F-ATP value. We conclude that our results are not sensitive to such variations in the F-ADP+P_i off-rates.

TABLE 2.

Symbols and input parameters

Parameter	Symbol	Value	References
Barbed-end G-ATP on-rate.		11.6 μM−1 s−1	(29)
Barbed-end G-ADP+Pi on-rate.		0	See note below.
Barbed-end G-ADP on-rate.		2.9 μM−1 s−1	(29)
Pointed-end G-ATP on-rate.		1.3 μM−1 s−1	(29)
Pointed-end G-ADP+Pi on-rate.		0	See note below.
Pointed-end G-ADP on-rate.		0.13 μM−1 s−1	Calculated. See note below.
Barbed-end F-ATP off-rate.		1.4 s−1	(29)
Barbed-end F-ADP+Pi off-rate.		1.4 s−1	Equivalence with F-ATP.
Barbed-end F-ADP off-rate.		5.4 s−1	(29)
Pointed-end F-ATP off-rate.		0.8 s−1	(29)
Pointed-end F-ADP+Pi off-rate.		0.8 s−1	Equivalence with F-ATP.
Pointed-end F-ADP off-rate.		0.25 s−1	(29)
Pointed-end Arp2/3 uncapping rate.	kun	0	(24)
Filament branching rate per subunit.		0.01 μ−3 s−1	Simulations fit to data.
F-ATP debranching rate.		0.02 s−1	(46)
F-ADP+Pi debranching rate.		0.04 s−1	(46)
F-ADP debranching rate.		0.2 s−1	(46)
Severing rate per subunit.	ksev	5.0 × 10−4	Simulations fit to data.
Filament annealing rate.		300 μM−1 s−1	(50)
G-ATP hydrolysis rate.		0	(41)
G-ADP+Pi inorganic phosphate release rate.		∞	(41)
F-ATP hydrolysis rate.		0.3 s−1	(51)
F-ADP+Pi inorganic phosphate release rate.		0.002 s−1	(12)
F-ATP hydrolysis range.	khyd	0.02–0.78 s−1	Varied in 0.04 s−1 steps.
F-ADP+Pi inorganic phosphate release range.	kphos	0.002–0.078 s−1	Varied in 0.004 s−1 steps.
Nucleotide exchange rate.	kex	0.01 s−1	(45)

Table of all input parameters used in the stochastic simulation. In accordance with the arguments of Bindschadler et al. (41), we assume that inorganic phosphate is instantly released into solution upon depolymerization of an F-ADP+P_i subunit. The F-ADP pointed-end on-rate is calculated such that the critical concentration at the pointed-end is equal to that of the barbed-end.

In the polymerization and depolymerization subroutines, the pointed and barbed ends of each filament string in the master set are first checked for end caps. For example, if a pointed end is capped with an Arp2/3 branch nucleator (“A”), that filament can neither polymerize nor depolymerize at the pointed end. If a filament end is uncapped, polymerization occurs during a time step Δt with probability 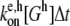and depolymerization occurs with probability 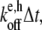where e represents the choice of barbed or pointed end and h represents the monomer hydrolysis state (see Table 2). It is generally accepted that the early lag phase observed during polymerization time-courses is due to the slowness of spontaneous nucleation resulting from the rapid dissociation of actin dimers. More recent measurements suggest that the Arp2/3-actin-actin trimer also dissociates rapidly (19). Thus, in our simulation, a filament is destroyed and its components returned to the monomer pool any time the total filament string length (including caps) is less than three characters.

On the basis of the recent argument of Bindschadler et al. (41), we assume random hydrolysis (F-ATP→F-ADP+P_i), which may occur with equal probability anywhere along the filament at a rate k_hyd per subunit. Subsequent release of inorganic phosphate (F-ADP+P_i→F-ADP) is also assumed to be random (12,44) and occurs at a rate k_phos per subunit. Any F-ADP+P_i subunit that depolymerizes is assumed to instantly release its inorganic phosphate to solution, so that the concentration of G-ADP+P_i is always zero (41). To model experiments in which there is excess ATP in solution, bound nucleotide is exchanged on monomers (G-ADP→G-ATP) at a rate k_ex = 0.01 s⁻¹ (45).

Although the simulation is capable of treating spontaneous nucleation, we ignore this process because the polymerization experiments we treat are dominated by other types of nucleation such as severing via sonication or Arp2/3 complex-induced branching. In our simulation, the branching rate per subunit k_br is given by k_br = 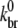[Arp2/3][G]² where [Arp2/3] and [G] are the concentrations of free Arp2/3 complexes and G-actin, respectively. The form proportional to [G]² was found to best fit polymerization data (24). We assume that each subunit has an equal probability of branching at k_br and that nascent branches may comprise actin in any hydrolysis state (46). Upon branch formation, one Arp2/3 complex and two actin monomers are removed from the monomer pool and a new character string is added to the master filament set. Consistent with recent measurements (46), we define an effective debranching rate that is a function of subunit hydrolysis state 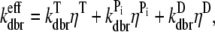where η^T, η^P, and η^D are the probabilities of a subunit being in the ATP, ADP+P_i, or ADP hydrolysis state, respectively. Upon debranching, the nucleating Arp2/3 complex is instantly returned to the pool where it may be reused in new branching events (47,48). If depolymerization beyond a branch point occurs, the Arp2/3 complex detaches from the mother filament yet remains attached to the daughter filament. We do not treat the hydrolysis of Arp2/3 complex (47). All Arp2/3 complexes are always assumed to be in the activated state.

Because use of a previously determined value of 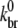(24)—the derivation of which did not include hydrolysis effects—led to a poor fit of experimental data (28), 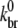is determined by a fit to these data as follows. As indicated by the onset of depolymerization, F-ADP subunits are not present in significant quantity until the peak in the polymerized fraction is reached (which was observed to occur at a time of 37 s). Thus, from the end of the lag phase to the peak polymerization, the pyrene intensity is dominated by the combined intensities of the F-ATP and F-ADP+P_i subunits. We first calculated the least-squares error between the simulated and measured pyrene intensity over a wide range of branching rates for equal brightnesses of these two types of subunits. We found that the minimum error occurred when 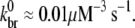As the relative brightnesses of the F-ATP and F-ADP+P_i subunits were themselves in question, we repeated this calculation for several F-ATP brightnesses reduced relative to F-ADP+P_i. We found that 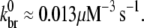To investigate the sensitivity of 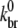to the choice of various parameters, we repeated the above procedure for several combinations of (k_hyd, k_phos) and (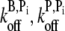) values and found that 0.010 μM⁻³ s⁻¹ < 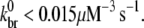We thus conclude that our estimate of 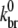is reasonably well constrained.

Sonication is included in our simulation as a severing rate per subunit (k_sev). We assume that severing is independent of filament-filament interactions and that it does not depend on the hydrolysis state of the subunits. Working from the barbed to pointed end, each character (subunit) of a filament string in the master set is parsed and severs with probability k_sevN_skipΔt. If a severing event occurs, the filament string is sliced into two fragments: one remains in the master filament set while the other is stored in a temporary set of new filaments. If either fragment is too short, it is removed from its set and its contents are returned to the monomer pool. Any new fragments created by severing are appended to the master set only after the master set has been parsed completely. To obtain k_sev, the NBD fluorescence data—which are much less sensitive than pyrene fluorescence to the hydrolysis state—published by Carlier et al. (13) for their sonication experiment were compared to simulations run over a range of k_sev values (2.5 × 10⁻⁵ – 1.4 × 10⁻³ s⁻¹; Δk_sev = 1.5 × 10⁻⁴ s⁻¹) while holding all other parameters fixed. The value of k_sev ≈ 5.0 × 10⁻⁴ s⁻¹ yielded a clear minimum (data not shown) in the least-squares error between the data and the simulation and was thus used in subsequent sonication simulations. To ensure that this value of k_sev was insensitive to choice of various parameters, we repeated this procedure for various (k_hyd, k_phos) and (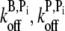) combinations, always recovering the same optimal k_sev value.

At high concentrations of actin under continuous sonication, the effects of annealing could be significant (39). We therefore implement barbed-to-pointed end annealing of filaments with an annealing rate per filament given by 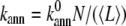as described by Sept et al. (49) and Andrianantoandro et al. (50), where N is the concentration of filaments, and 〈L〉 is the average filament length measured in subunits. In each run of the annealing subroutine, two temporary sets of annealable filaments are constructed, where the left set comprises filaments with an uncapped barbed end, and the right set comprises filaments with an uncapped pointed end. Filaments with both ends uncapped are randomly assigned to either set with equal probability. Each time an annealing event occurs (with probability k_annΔt), one filament string is randomly chosen from each set. These strings are then replaced in the master filament set by a single concatenated filament string.

Validation of code

Extensive integrity checks are included in the computer code to ensure that the total amounts of both actin and Arp2/3 complexes are always conserved and to guard against malformed filaments (e.g., a capping protein character not at the end of a filament string). Simulations of obvious limiting cases where the results are readily calculable—such as when the nucleotide exchange rate is either zero or infinite and when only ADP-actin is available for polymerization—were compared to analytically calculated results and found to agree to within a maximum fractional error of ∼1%. The code also was tested thoroughly for self-consistency via comparison of actual numbers of recorded events to those predicted analytically. For example, the recorded ensemble average number of branching events per unit time should be exactly given by k_br times the recorded ensemble average number of polymerized subunits. Fig. 3 shows the agreement to within a fractional error of ≈4% between the calculated number of branching events per unit time (solid curve) and the actual number of events executed by the code (circles). Confirming this type of prediction for every process over a wide range of parameters offers some assurance that the code implements the model correctly.

FIGURE 3.

Example of a self-consistency check of the computer code. The calculated number of branching events (solid curve) agrees well with the independently recorded ensemble-averaged number of branching events (circles). The peak stems from the initial rise in possible branch sites (F-actin) followed by depletion of the monomer pool (G-actin). The most important feature of the curve is the minimum that occurs at ∼30 s. This time corresponds to the peak in F-actin polymerization (i.e., the onset of depolymerization), which indicates the increasing availability of monomers for the creation of new branches.

COMPARISON TO EXPERIMENTAL DATA

We assume that the pyrene-labeling of actin monomers is random and that the pyrene-label does not interfere with polymerized subunit hydrolysis or phosphate release. Thus, even if labeled subunits tend to cluster together upon polymerization, the distribution of hydrolysis states along the filament remains random. Therefore, in our comparisons below of simulated pyrene intensity curves to those in published experiments, we include the effects of hydrolysis on the pyrene intensity by defining an apparent concentration of polymerized actin as a function of time t. 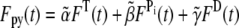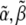This is given by where and 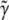are nonnegative, dimensionless intensity coefficients and F^T, 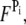and F^D are micromolar actin concentrations of F-ATP, F-ADP+P_i, and F-ADP subunits, respectively. This curve is compared to a normalized pyrene intensity curve D(t) times a scaling prefactor 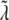to convert intensity to micromolar concentration. This prefactor, which is the parameter that minimizes the least-squares error between the normalized data and the total micromolar concentration of polymerized actin (F(t)), is calculated via the formula

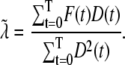(1)

The data for the branching experiment were generously provided by Tehrani et al. (28). In other cases, data were manually digitized from published works (13,51) via ImageJ v1.34s, an image processing program freely distributed by the National Institutes of Health (http://rsb.info.nih.gov/ij/). All data were resampled once every second by an interpolation routine written in MatLab v7.1 (The MathWorks, Natick, MA). A dimensionless fractional error function was then defined as

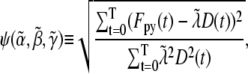(2)

where T is the total time of the experiment. As ψ is a quadratic function of 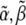and 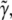the specific set of intensity coefficients that minimizes ψ is readily calculable (see Appendix). Thus, these intensity coefficients are determined directly by the experimental data and simulated data obtained for a given parameter set. To allow for a meaningful comparison between different experiments, we define an intensity unit vector 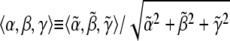such that α, β, and γ are each between zero and unity.

RESULTS

The polymerization experiments of Carlier et al. (13) and Tehrani et al. (28) are henceforth simply referred to as sonication or branching experiments, respectively. The sonication experiment assayed the polymerization of 54 μM actin during continuous sonication. The branching experiment assayed the polymerization of 2.5 μM actin induced by 0.1 μM activated Arp2/3. Both experiments studied polymerization of ATP muscle actin in the presence of excess ATP in solution and employed similar labeling procedures. The sonication experiment displays an increase in brightness long after the steady state of polymerization has been reached, whereas the branching experiment has a typical overshoot in pyrene intensity that appears long before steady-state polymerization is reached. The best values of 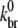and k_sev obtained from fits to experimental data (as earlier described) and the most recently available published values (29,44,51) for all other input parameters were used (Table 2).

Each of the two simulations was run 64 times and the results ensemble-averaged. At first, the intensity unit vector that minimized the error between simulated and real intensity curves was calculated separately for each of the two experiments. The simulated polymerization time-courses (solid curves) are shown in Fig. 4 against the experimental data (circles). In Fig. 4 a, the steady increase seen in the simulated intensity curve does not adequately represent the ultimate leveling of the measured intensity. The opposite problem is seen in Fig. 4 b, where the simulated intensity levels off well before the measured intensity and even begins to increase at long times. In both cases, the simulated intensity at long times exceeds the experimental value. Fig. 5 a shows the components of the intensity unit vectors for the sonication (lighter bars) and branching (darker bars) experiments. In each case, F-ADP subunits are the brightest, F-ATP subunits are the dimmest, and the F-ADP+P_i subunit intensity is in between. Even though the intensity unit vectors independently determined from each experiment are similar, if the intensity unit vector derived from one experiment is imposed upon the other, the fractional error is increased and the quality of fit is substantially worsened. To check for the existence of a single intensity unit vector consistent with both sets of experimental data, we defined the global average error

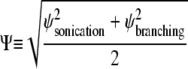(3)

to be the root mean-square of the errors given by Eq. 2 for each experiment. The single intensity unit vector that minimized that global error was calculated and used to generate the polymerization time-courses shown in Fig. 5 b. Of particular note is the exaggerated shoulder in the simulated intensity (dotted curve) relative to the measured intensity (circles) seen early in the sonication experiment and the marked divergence between measured (triangles) and simulated (solid curve) intensities at long times for the branching experiment.

FIGURE 4.

Measured pyrene intensity (circles) and simulated concentration of polymerized actin (solid curves) using only accepted values for input parameters. Note the poor qualitative fit especially at long times. (A) The sonication experiment of Carlier et al. (B) The Arp2/3-induced branching experiment of Tehrani et al. (28).

FIGURE 5.

(A) Bar graph showing the relative intensities of F-actin subunits for the cases of sonication (light bars) and branching (dark bars) obtained from simulation using only accepted values as input parameters. (B) Measured pyrene intensity as functions of time for the sonication (circles) and branching (triangles) experiments are not adequately described by the simulated pyrene intensity (solid curves) using only accepted parameter values as input. Note the poor qualitative fit at long times.

As we could find no single intensity unit vector consistent with both data sets when only accepted parameter values were used, we were motivated to conservatively relax certain parameter values in the hope of finding one parameter set and one intensity unit vector that are consistent with both experiments. As the F-ADP+P_i off-rates have not been directly measured, we varied both off-rates to ≈ ±50% of the values obtained by assumption of equivalence to F-ATP. The barbed-end off-rate was varied between 0.6–2.2 s⁻¹ in steps of 0.2 s⁻¹ while the pointed-end off-rate was varied between 0.4 and 1.2 s⁻¹ in steps of 0.1 s⁻¹. Thus, both sonication and branching simulations were run over an 81-point mesh of (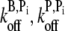) off-rate combinations while holding all other parameters fixed. The global error and the intensity unit vector corresponding to that error were calculated at each mesh point. The value of Ψ at the error-minimizing mesh point was not significantly different from other points in the mesh and the resulting intensity unit vector did not offer any improvement in the fit between simulated and measured polymerization time-courses. Upon observing that this fit was not sensitive to our choice of F-ADP+P_i off-rates, we reset these values to be equivalent with those of F-ATP subunits and sought another parameter to vary.

The original measure of k_hyd ≈ 0.022 s⁻¹ given by Carlier et al. in 1984 (13) differs 14-fold from the currently accepted measure of k_hyd ≈ 0.3 s⁻¹ given by Blanchoin and Pollard in 2002 (51). We therefore ran each simulation holding all other input parameters constant while varying k_hyd over the range 0.02–0.86 s⁻¹ in steps of 0.04 s⁻¹. The global error as a function of k_hyd is shown in Fig. 6 a. A minimum, corresponding to a global error of 3.1%, is observed to occur at k_hyd = 0.22 s⁻¹. The polymerization time-courses simulated at this value of k_hyd are shown in Fig. 6 b. As may be seen in Fig. 6 b, there is a marked difference between the simulated and measured pyrene intensity for each experiment. The simulated pyrene intensity (dotted curve) for the sonication experiment increases steadily whereas experimental data (circles) level off. The simulated pyrene intensity (solid curve) for the branching experiment exhibits clearly diverging long-time behavior not seen in the experimental data (triangles). Thus, variation of k_hyd does not resolve the discrepancies between the simulated and measured pyrene intensities. We note that the similarity of these simulated intensity curves to those of Fig. 5 b illustrates the relative insensitivity of both quantitative error and qualitative fit to k_hyd. If we assume that the G-actin nucleotide exchange rate is constant in time (41,45), it stands to reason that k_phos chiefly determines the long-time composition of actin filaments as it is the slowest rate in the hydrolysis process. We were thus motivated to vary k_phos as well. We varied k_phos over the range 0.002–0.078 s⁻¹ in steps of 0.004 s⁻¹. That is, both simulations were run over a 440-point mesh of (k_hyd, k_phos) values while holding all other parameters fixed. The global error and the intensity unit vector corresponding to that error were calculated at each mesh point. A minimum value of the global error Ψ = 2.3% is obtained at (k_hyd = 0.70 s⁻¹, k_phos = 0.026 s⁻¹) with intensity unit vector 〈0.30, 0.56, 0.77〉. The intensity curves seen in Fig. 7 are simulated using these values and fit the data well, with 1.8% and 2.7% individual fractional error, respectively.

FIGURE 6.

(A) The global fractional error as a function of k_hyd. (B) Measured pyrene intensity for the sonication (circles) and branching (triangles) experiments compared with simulated pyrene intensity (curves) using k_hyd = 0.22 s⁻¹ corresponding to the minimum error and the accepted value of k_phos = 0.002 s⁻¹. Again, note the poor qualitative fit especially at long times.

FIGURE 7.

Measured pyrene intensity (circles), simulated pyrene intensity (solid curves) and simulated amount of polymerized actin (dashed curves) for (A) the sonication experiment and (B) the branching experiment. The insets show the composition of filaments by hydrolysis state (solid, F-ATP; dashes, F-ADP+P_i; dots, F-ADP).

The most important conclusion from the simulations is the large difference, in both experiments, between the simulated polymerization and the polymerization assayed by pyrene intensity. As may be readily seen in Fig. 7, the pyrene assay underestimates polymerization at short times and overestimates polymerization at long times. These differences could lead to erroneous inferences about the rates of various processes. For example, the pyrene assay of the sonication experiment (Fig. 7 a) might lead one to conclude that overall polymerization has not reached the steady state until ∼120 s, when it actually is within 1% of the steady-state value after only 30 s. Additionally, in the branching experiment (Fig. 7 b), the rate of decay from the maximum to the steady-state value of polymerized actin is clearly greater in the simulated polymerization curve than in the pyrene intensity curve.

Figs. 5 b and 6 b show simulated intensity curves (solid curves) for the branching experiment that correspond to global errors within 48% and 33% of the minimum global error, respectively, while still clearly diverging from the measured intensity (triangles) at long times. By visual inspection of numerous simulated polymerization time-courses, we observed the onset of these types of qualitative differences at mesh points corresponding to ≈20% of the minimum global error. We therefore define a mesh point to be consistent with measured data if the global error obtained at that point is within 20% of the minimum value. Fig. 8 a shows the global error Ψ as a function of k_hyd and k_phos after smoothing via convolution with a 5 × 5 Gaussian kernel with standard deviation set to unity. The mesh point at which the minimum error occurs is indicated by a large asterisk. We note that the accepted combination of 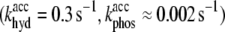(12,44), is far from that mesh point. Because the error varies slowly as a function of k_hyd, we are not able to draw strong conclusions about its value, except that values <0.30 s⁻¹ are inconsistent with the data. The range of k_phos values consistent with the data is 0.014 s⁻¹ to 0.050 s⁻¹.

FIGURE 8.

(A) Global fractional error as a function of k_hyd and k_phos. The location of the minimum error is indicated by the asterisk. (B) Bar graph showing the relative intensities of actin subunits obtained from simulations. Each intensity unit vector component was averaged over the mesh points within 20% of the error-minimizing mesh point. The large error bar in α indicates the relative insensitivity of the global error to the F-ATP intensity component due to rapid hydrolysis.

The average value of the components of the intensity unit vector that minimizes Ψ within the consistent region is shown in Fig. 8 b. Two distinct uncertainties arise in the values of the individual intensity components. First, many mesh points yield simulated intensity curves consistent with measured data, and these mesh points have different values of the intensity coefficients. We describe this variation in terms of standard deviations 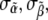and 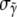of the intensity coefficients evaluated over the consistent region of the k_hydk_phos-plane. The second contribution to the uncertainty reflects the sensitivity of the global error to changes in the coefficients at a single mesh point. For example, as the global error is a quadratic function of 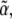the change in that will induce a change of 20% in the global error Ψ is given by

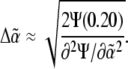(4)

The total uncertainty in 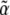is then 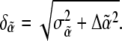The error bars shown in Fig. 8 b represent the uncertainties and 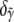propagated through the unit vector normalization described in an earlier section. The large error bar in α indicates the relative insensitivity of the global error to the F-ATP intensity component, due to rapid hydrolysis. We conclude that the pyrene label on an F-ADP actin subunit fluoresces approximately twice as brightly as that of a F-ATP actin subunit, whereas the intermediate F-ADP+P_i pyrene label fluoresces ∼50% more brightly than that of a F-ATP actin subunit.

In an effort to evaluate the validity of our model, we sought to apply our previously determined intensity coefficients to a third rapid polymerization experiment. In 2002, Blanchoin and Pollard published time-courses of the polymerization of pyrene-labeled muscle actin nucleated by unlabeled seed filaments (51). Using the intensity unit vector obtained at the error-minimizing (k_hyd, k_phos) mesh point, we simulated the Blanchoin and Pollard experiment using several different concentrations of free barbed ends (3 nM ≤ N_barb ≤ 40 nM in steps of ≈0.8 nM). A minimum error of <1.1% was obtained when N_barb = 22.4 nM. The results of our simulation (solid curves) are shown in Fig. 9 against the digitized pyrene intensity time-course (circles). The fit to the data is excellent, even though our value of N_barb is higher than that used in the modeling of Blanchoin and Pollard. (51). We believe that the lower concentration of barbed ends reported by Blanchoin and Pollard (51) is a direct result of ignoring the pyrene sensitivity to subunit hydrolysis state. A correction factor, included in an analytic formula for estimation of the concentration of free barbed ends from pyrene intensity curves, is derived in the Discussion.

FIGURE 9.

Measured pyrene intensity (circles), simulated pyrene intensity (solid curve), and simulated amount of polymerized actin (dashed curve) for the seed filament-nucleated polymerization experiment of Blanchoin et al. (51). The insets show the composition of filaments by hydrolysis state (solid, F-ATP; dashes, F-ADP+P_i; dots, F-ADP).

DISCUSSION

Summary

We have described how the polymerization time-course assayed by pyrene intensity differs from the true kinetics of polymerization as estimated by our simulation code. We also have shown that typical published pyrene intensity curves are described well by the following average relative intensity coefficients: 0.37 for F-ATP actin; 0.55 for F-ADP+P_i actin; and 0.75 for F-ADP actin. Although we find that the combination of F-actin hydrolysis and inorganic phosphate release rates of (k_hyd = 0.70 s⁻¹, k_phos = 0.026 s⁻¹) offers the best numerical fit to published pyrene intensity curves, we must stress that many combinations—within the approximate range (0.30 s⁻¹ ≤ k_hyd ≤ 0.70 s⁻¹, 0.014 s⁻¹ ≤ k_phos ≤ 0.050 s⁻¹)—are consistent with those data.

Other possible explanations of the overshoots

Overshoots seen in the pyrene fluorescence have often been assumed to be artifacts of the pyrene assay. However, overshoots are also seen in other assays such as NBD fluorescence (30,31) and turbidimetry (52). Thus, they are not likely to be artifacts of the pyrene assay. Furthermore, as the overshoots can be relatively large in magnitude and occur over a wide range of timescales and assays, photobleaching effects are unlikely to contribute significantly to the overshoots. Taken together, the results of these very different polymerization assays indicate that the overshoot is a genuine feature of many rapid polymerization curves. As the tail of an overshoot curve is, by definition, lower than the peak, less actin must be polymerized at very long times (at steady state) than at short times (near the polymerization peak). The only physically reasonable explanation for the observed depolymerization is an increase in the critical concentration.

One might guess that changing the capping state or the number of free filament ends could cause such a dramatic change in the critical concentration in the absence of hydrolysis. We show that these filament end effects are too small to account for the observed overshoots. From the steady-state polymerization-rate equation, it is straightforward to derive that the critical concentration is the ratio

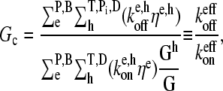(5)

where the superscript eff implies the effective rate, including (de)polymerization at both barbed and pointed ends, resulting from the heterogeneous mix of actin in various hydrolysis states. Here, η^{e, h} is the probability that a subunit at the e end of the filament is in the h hydrolysis state, G^h is the concentration of monomeric actin in the h hydrolysis state, and G is the total monomeric actin concentration. Consider the Arp2/3-induced branching experiment of Tehrani et al. (circles in Fig. 7 b) (28). The maximum possible overshoot due to uncapping of pointed ends is obtained by assuming that at the time of maximum polymerization (t_max) every filament is capped at the pointed end by Arp2/3 and that all pointed ends are later uncapped. In the absence of hydrolysis, G^T = G and G^D = 0 at t_max. Thus, the maximum possible change in G_c due to uncapping alone may be straightforwardly calculated via Eq. 5 (by ignoring the pointed-end terms when the pointed ends are capped) to be ≈0.05 μM. The overshoot observed in the pyrene fluorescence is ≈20% of the maximum, yielding an overshoot magnitude of ≈0.5 μM F-actin. Thus, pointed-end uncapping can only account for ≈10% of the overshoot magnitude. Therefore changes in the pointed-end capping state are insufficient to account for the overshoot observed in this experiment.

Actin polymerization overshoots have been observed in experiments where rapid polymerization was induced by either spectrin-actin or F-actin seeds (15,23,25). Since the number of filaments in these experiments remains relatively constant between the times of peak and steady-state polymerization, a change in the number of exposed filament ends does not explain these overshoots. This was confirmed by our simulations in which various numbers of filaments were held constant during the entire polymerization time-course yet overshoots still appeared (data not shown).

We now argue that the hydrolysis mechanism mentioned in the Introduction is a plausible explanation of rapid polymerization overshoots. As hydrolysis proceeds under conditions of finite nucleotide exchange, some filament ends become transiently capped with F-ADP subunits. As the off-rate for F-ADP actin is much greater than that of F-ATP or F-ADP+P_i actin, even having a relatively small percentage of the filament ends in the F-ADP hydrolysis state can have a large effect on and thus on the critical concentration. Indeed, it has been experimentally confirmed that the rapid polymerization of a nonhydrolyzable actin homolog does not exhibit an overshoot, while ATP actin polymerizing under the same conditions does (53).

Only under conditions of heterogeneous subunit hydrolysis states can a change in the number of filaments—e.g., via debranching, severing, or depolymerization—have large effects on the overshoot. That is, as the number of filaments changes, so can the percentage of filament ends in the F-ADP hydrolysis state, which changes 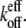For example, the new ends exposed by severing a filament potentially have different hydrolysis states from those of the unsevered filament. 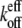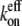Without hydrolysis, changing the number of filament ends alone cannot change or (because all filaments always have the same end state), and thus cannot change the critical concentration. We conclude that hydrolysis is the most likely mechanism to explain overshoots in rapidly polymerized actin. The overshoot magnitude would thus be limited to 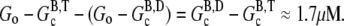This limit is consistent with all overshoots we are aware of in the literature, as well as our own simulations.

Relation to previous work

In the same work (13) from which we obtained the sonication data modeled above, Carlier et al. presented a second, similar sonication experiment in which hydrolysis was independently assayed between a first time-point at onset of steady-state polymerization and a second time-point at onset of steady-state pyrene intensity. Recall that at the time of these experiments, it was not known that the hydrolysis of F-actin is actually a two-step process that includes inorganic phosphate release (F-ATP→F-ADP+P_i→F-ADP). Assuming that one rate of the two-step process is much greater than the other, a measurement of the complete process would give the rate of the slower, rate-limiting process. As it is reasonable to assume that the first step of hydrolysis (F-ATP→F-ADP+P_i) is at least several times faster than the second (F-ADP+P_i→F-ADP) (44,51), one might interpret the original measurement of complete hydrolysis (0.022 s⁻¹) as giving the true phosphate release rate. This is consistent with the results of our simulation of the first sonication experiment. Here, we observed that when steady-state polymerization is reached, the filaments consist predominantly of F-ADP+P_i subunits, whereas at the onset of steady-state pyrene intensity, the filaments consist almost entirely of F-ADP subunits. We estimate the percentage (22%) of completely hydrolyzed subunits (F-ADP) at the first time-point of the second sonication experiment to be the product of the observed rate of change from F-ADP+P_i to F-ADP (0.022 s⁻¹) and the time to achieve that polymerization (≈10 s). Carlier et al. reported that the change in pyrene intensity between the time-points accounted for 27% of the total intensity increase over the entire polymerization time-course. That is, the intensity at the first time-point is 27% less than the steady-state value. Thus, we may use the equation (1 − 0.22)β + 0.22γ ≈ (1 – 0.27)γ to estimate the ratio β/γ ≈ 0.65. This is within ≈10% of the ratio obtained using the averaged coefficients derived from our simulation/error-minimization technique (β/γ = 0.55/0.75 = 0.73). Thus, both our optimal phosphate release rate (k_phos) and ratio of F-ADP+P_i to F-ADP intensity coefficients are consistent with the previously published observations of Carlier et al.

We are puzzled by the discrepancy between our optimal value of k_phos and the values obtained in more recent experiments (12,44). We see no ambiguities in the experimental procedures used to measure k_phos. The fact that the same type of discrepancy (simulation exceeding data at large times) is seen for two very different experiments when the accepted value of k_phos is used means that the effect is unlikely to be an artifact. One possible mechanism which could reconcile the simulations and experiments is a fourth state of the phosphate, between F-ADP+P_i and F-ADP. This could, for example, be a phosphate nonspecifically bound to the actin. The timescale that we deduce from the pyrene assays would correspond to the time required for the phosphate to go from the ADP+P_i state to the fourth state. Although we are unaware of any other evidence for the existence of a fourth hydrolysis state in muscle actin, such a state has been observed recently in yeast actin (54).

Because the evaluation of the concentration of barbed ends from the slope of a pyrene intensity curve is standard procedure in the field, we describe the modifications to this procedure entailed by the difference between the pyrene intensity curve and the amount of polymerized actin. At the onset of polymerization, virtually all of the polymerized actin is in the F-ATP hydrolysis state. Thus, the pyrene intensity is 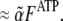The maximum concentration of ATP actin polymerized from seed filaments in the presence of excess ATP is 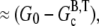where G₀ is the initial concentration of G-ATP actin and is the barbed-end critical concentration of ATP actin. When this peak occurs, the subunits are predominantly F-ADP+P_i. Therefore, 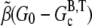serves as a conversion factor between the normalized measured pyrene intensity and actual concentrations of polymerized actin. 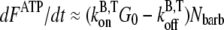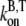The change in polymerized actin in time may be approximated at early times as where and 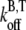are the barbed-end ATP on and off-rates, respectively. Thus, from pyrene intensity data, one can estimate the concentration of free barbed ends via the formula

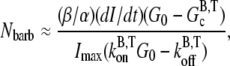(6)

where dI/dt is the short-time slope of the pyrene intensity and I_max is the maximum pyrene intensity obtained from the measured data. We note here that the normalization factors in α and β cancel and thus the ratio β/α may be used. Using Eq. 6 with the published pyrene intensity data (51), we calculate the concentration of free barbed ends to be 22.6 nM, which is in excellent agreement with the value obtained via stochastic simulation (see previous section). Ignoring the differences in relative pyrene intensities would underestimate the concentration of free barbed ends by a factor of β/α ≈ 1.9. We note, however, that there is a large uncertainty in this factor because of the large uncertainty in α.

EXPERIMENTAL PREDICTIONS

We now suggest an experimental means of verifying our estimates of the pyrene intensity coefficients. One must first establish that the pyrene labels are not irreversibly damaged upon hydrolysis. This may be readily done by allowing an amount of labeled ATP-actin to polymerize, and subsequently hydrolyze, until the ADP-actin critical concentration is reached. Addition of excess ATP should then force an increase in the pyrene intensity as the monomer pool drops closer to the ATP-actin critical concentration. The filaments may then be separated from the buffer via centrifugation and dialyzed against an ATP-free buffer so that the filaments are again free to (de)polymerize in the absence of ATP. As long as those procedures, standard to many thiol-reactive fluorophore-labeling protocols, designed to minimize exposure to ambient ultraviolet light, are properly implemented, photobleaching of the pyrene fluorophore should be negligible. Thus, several repetitions of this ATP depletion-addition cycle should place a limit on the extent of the damage due to hydrolysis alone. The relative intensities of the different types of subunits may be measured as follows. First, an amount of pyrene-labeled ADP-actin is allowed to polymerize to the steady state in the absence of ATP. As the critical concentration of ADP-actin is known, the F-ADP intensity coefficient is available immediately. Second, addition of saturating inorganic phosphate to existing capped ADP filaments will establish the F-ADP+P_i intensity coefficient. The F-ATP coefficient may then be independently obtained by fitting stochastically simulated pyrene curves, using the measured coefficients as input parameters, to measured pyrene assays of short-time polymerization of ATP-actin.

APPENDIX: CALCULATION OF THE MINIMUM ERROR

The error function as defined in Eq. 2 can be rewritten in matrix form as

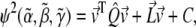(7)

where the matrix 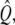the vector 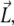and the constant C are obtained from the calculated polymerized actin components, and the intensity vector is defined as

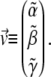(8)

For example, upon algebraic expansion of the error given in Eq. 2, one finds that 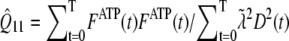and 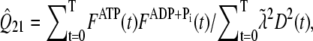where 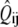is the term in the i^th row and j^th column of the 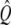matrix. We then wish to find the intensity vector 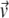that is the solution to the equation 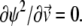Here we make use of the identity

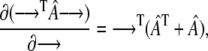(9)

and find that 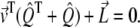As 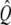is a symmetric matrix, the intensity vector that minimizes the error is

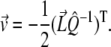(10)

Thus, both the minimum error and minimizing intensity vectors may be calculated analytically without further minimization routines.