Electrostatic Contribution to the Surface Pressure of Charged Monolayers Containing Polyphosphoinositides

Abstract

Structural and functional studies of lateral heterogeneity in biological membranes have underlined the importance of membrane organization in biological function. Most inquiries have focused on steric determinants of membrane organization, such as headgroup size and acyl-chain saturation. This manuscript reports a combination of theory and experiment that shows significant electrostatic contributions to surface pressures in monolayers of phospholipids where the charge spacing is smaller than the Bjerrum length. For molecules with steric cross sections typical of phospholipids in the cell membrane (∼50 Ų), only polyphosphoinositides achieve this threshold. The most abundant such lipid is phosphatidylinositol bisphosphate, which has between three and four charged groups at physiological conditions. Theory and experiment show that surface pressure increases linearly with phosphatidylinositol bisphosphate net charge and reveal crossing of high and low ionic strength pressure-area isotherms, due to opposing effects of ionic strength in compressed and expanded monolayers. Theory and experiment show that electrostatic effects are negligible for monolayers of univalent lipids, emphasizing the unique importance of electrostatic effects for lateral organization of polyphosphoinositides. Quantitative differences between theory and experiment suggest that attractive interactions between polyphosphoinositides, possibly mediated by hydrogen bonding, can lessen the effect of electrostatic repulsions.

INTRODUCTION

Polyphosphoinositide lipids are uniquely important for cellular signaling in part because of their multivalent anionic charge. The vast majority of eukaryotic membrane lipids are either zwitterionic or have a charge of −1 at neutral pH. A small minority of lipids such as phosphatidic acid or polyphosphoinositides that reside on the cytoplasmically facing leaflet of cell membranes bear a net charge of −2 to perhaps as much as −5 depending on factors such as the presence of monovalent and multivalent cations, binding of peripheral membrane proteins, membrane potential, and the local concentration of anionic lipids. The high valence of polyphosphoinositides is essential to their ability to form domains in fluid membranes that are stabilized by electrostatic interactions with cationic protein domains (1,2). Electrostatic attraction of cytoplasmic solutes to the inner membrane leaflet is modeled by calculations of the electric field extending orthogonal to the membrane surface, but the structure of the cell membrane also depends on lateral pressures within the lipid bilayer (3,4). For zwitterionic and monoanionic lipids, surface pressures at physiologically relevant densities are dominated by the length and unsaturation of acyl chains and the size of the headgroup (5), but for more highly charged lipids, a significant surface pressure can arise from electrostatic repulsions between phospholipids (6). Additionally, electrostatic effects become important when considering the interactions of charged lipids with soluble ionic components, such as salts and polyionic macromolecules. While screening of surface charge by soluble counterions is the typically considered mode of interaction, lipid headgroup deprotonation by soluble ions (7) has been shown to be an important determinant of lipid packing (8), phase transitions (9), domain morphology (6), and enzymatic lability (10). Here, we report a theoretical analysis of surface pressures for highly charged lipid systems and compare calculated results to the first experimental observations of pure polyphosphoinositide monolayers.

Pressure/area isotherms of highly charged phospholipid monolayers

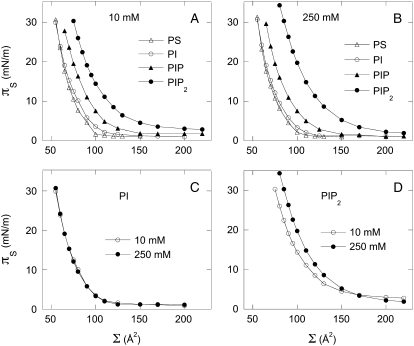
Phospholipids in a cell membrane pack to a density corresponding to an area per molecule of 40–70 Ų, equivalent to a lipid monolayer with surface pressure of ∼30 mN/m (11). At this density the spacing between charges for univalent phospholipids is slightly greater than the Bjerrum length (l_B), the distance at which electrostatic energies are equal to the thermal energy k_BT (∼7.1 Å). As a result, the lipids can be approximated as independent point charges that create a significant field orthogonal to the membrane surface, but only modest repulsive interactions within the plane of the membrane. However, when the valence is >2, as it is for phosphatidylinositol bisphosphate (PIP₂), the most common PPI and one with great biological importance, the charge spacing becomes <l_B leading to significant electrostatic interactions within the plane of the membrane and effects not seen in less highly charged membranes. The magnitude of the electrostatic contribution is shown in Fig. 1, which compares area-pressure isotherms of the anionic lipids phosphatidylserine (PS), phosphatidylinositol (PI), and its mono- and diphosphorylated derivatives PIP and PIP₂. All of these lipids are natural products containing mainly stearoyl and arachidonoyl moieties at their SN1 and SN2 positions, respectively. The unsaturated acyl chains prevent any observable phase transitions from a liquid-condensed phase to a gel phase, hence the differences between the isotherms are the direct effect of the increased charge on PIP and PIP₂, which at neutral pH bear slightly more than two and three charges, respectively. The increased surface pressure of PIP₂ monolayers is not screened out by increasing subphase monovalent salt. Fig. 1 shows that whereas increasing ionic strength from 10 mM to 250 mM has no significant effect on monolayers of PS or PI, it increases the pressure of PIP₂ monolayers over a broad range of molecular areas.

FIGURE 1.

Surface pressure (π_S)-molecular area (Σ) isotherms of naturally derived anionic phospholipids (PS, PI, PIP, and PIP₂) on a buffered subphase with 10 mM (A) and 250 mM (B) subphase NaCl. Isotherms comparing the effect of low (open circles) and high (solid circles) subphase ionic strength on monovalent (PI) (C) and multivalent (PIP₂) (D) acidic phospholipids. All isotherms shown are representative of the average of 5–8 isotherms per condition; choice of buffer did not significantly affect the measured isotherms (data not shown).

Theoretical model of electrostatic contribution to surface pressure

A continuum model can be applied to calculate the electrostatic component of surface pressure when the distance between charged lipids is >Zl_B, where Z is the number of charges per lipid headgroup. In the case of a PIP₂ monolayer, where Z is ∼3–4, Zl_B corresponds to a surface area of ∼160 Ų per molecule. Fig. 1 D shows that at molecular areas higher than Zl_B, where electrostatics are not expected to contribute significantly to lateral pressure, the surface pressure of PIP₂ does not depend strongly on ionic strength. This estimate is also in agreement with the experimental observation (Fig. 1 C) that for PI, which has only one charged group (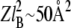), the surface pressure does not show any significant dependence on ionic strength down to 50 Ų per molecule. PIP which has two negatively charged groups does show a small influence of ionic strength <∼80–100 Ų.

If the distance between charged groups is less than defined by the Bjerrum length, then collective effects described by a Gouy-Chapman approach become important to consider. In this case, we describe the monolayer as a charged surface with surface charge density σ. The Poisson-Boltzmann equation for electric potential ϕ distribution near this charged surface reads

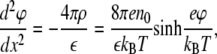(1)

where e is the elementary charge, n₀ is the number density of univalent electrolytes, and ɛ is the dielectric permittivity of water. Solution of the Poisson-Boltzmann equation using the boundary condition at a charged interface

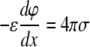(2)

is well known (12). The surface pressure is calculated by evaluation of the variation of the thermodynamic potential Ω due to introducing a charged surface in an electrolyte solution with fixed chemical potentials of ions, which can be found from the charging theorem (13,14):

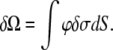(3)

After taking into account Eqs. 1 and 2 and integrating, the change of the thermodynamic potential due to a charged surface can be expressed as

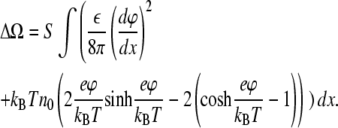(4)

This relation is identical to that used in Chen and Nelson (15) for consideration of charge-reversal instability in mixed bilayer vesicles.

The electrostatic part of the surface pressure can be calculated by differentiating Eq. 4 with respect to the surface area of a monolayer S at fixed charge (variation of the surface charge with surface area is important experimentally and is accounted for by dissociation-association equilibria, as discussed later). Direct calculation of the derivative ∂Ω/∂S from Eq. 4 and the solution of the Poisson-Boltzmann Eq. 1 require several steps. An efficient way to carry it out is to use the identity

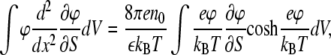(5)

which follows from the Poisson-Boltzmann equation, differentiating it by S, multiplying by φ, and integrating over the volume occupied by electrolyte. As a result, we arrive at

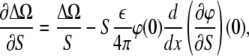(6)

where the first term in Eq. 6 comes from the fact that the thermodynamic potential Eq. 4 is proportional to the area of the monolayer. Since ∂σ/∂S = −σ/S, from the boundary condition Eq. 2, we have

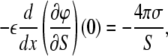and for the surface pressure π_S = – ∂ΔΩ/∂S, we obtain

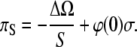Since

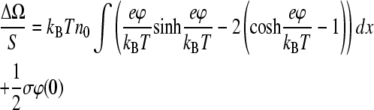and

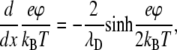it follows from the solution of the Poisson-Boltzmann equation, where λ_D = (8πl_Bn₀)^−1/2 is the Debye screening length, that after integration we obtain

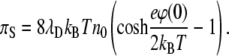(7)

Equation 7 can be rewritten in a more convenient form as

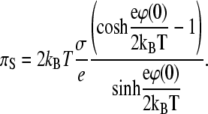(8)

In the limit of large absolute values of the surface potential ϕ(0), Eq. 8 reduces to a very simple form of

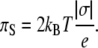(9)

Equation 9 shows that for a highly charged monolayer the electrostatic contribution to the surface pressure is equal to twice the kinetic pressure of a two-dimensional gas, although its physical meaning, of course, is different. The surface potential of a monolayer according to Eq. 2 is found from the expression

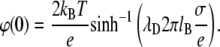(10)

According to Eq. 8, the electrostatic contribution to surface pressure decreases with diminution of the absolute value of the surface potential. According to Eq. 10, this should take place if the ionic strength of the solution increases and the charge of the monolayer is constant.

However, in reality, the charge of the monolayer depends on the dissociation-association equilibrium of the ionic groups of the lipid. In the negatively charged monolayer considered here, a decrease of the surface potential increases the electrochemical potential of the charged lipid headgroups by −eϕ(0), and the dissociation-association equilibrium is shifted. In the condition of equilibrium

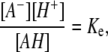the charging of the monolayer can be accounted for by introducing an effective equilibrium constant pK_e, whose value depends on surface potential according to the relation 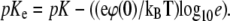The degree of deprotonation dP of the lipid headgroup is then

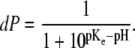(11)

If the absolute value of the surface potential goes down, the effective pK_e goes down as well and the headgroup becomes more deprotonated. This effect of adding more charged groups to the surface can increase the surface pressure (6). If the lipid has several ionic groups which can be deprotonated, then the degree of deprotonation of each of them should be calculated according to Eq. 11.

As a result, we have the following set of equations for the calculation of the electrostatic surface pressure for n lipid headgroups as a function of the ionic strength of the solution

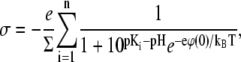(12)

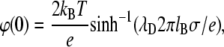(13)

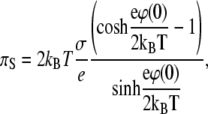(14)

where Σ is the surface area per lipid molecule.

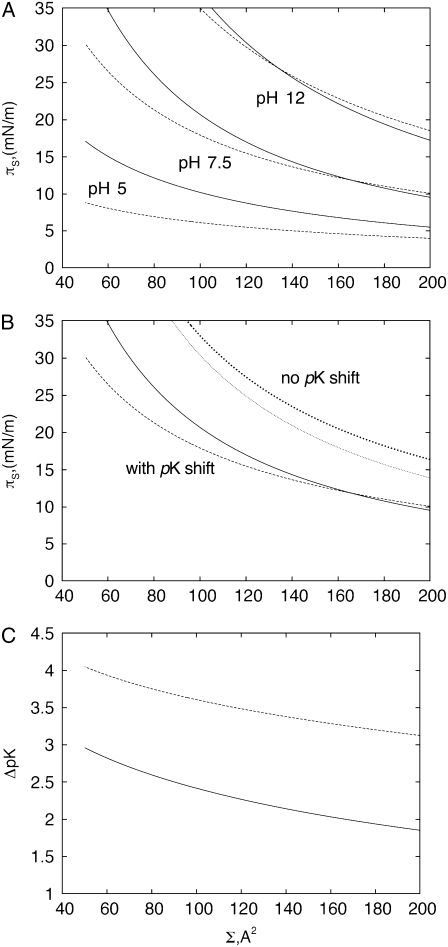
The set of Eqs. 12–14 allows one to draw several important conclusions. The dependence of the electrostatic surface pressure on the surface area per molecule of a lipid like PIP₂ with five ionizable groups and bare pK values of 2, 3, 4, 7, and 7.7 (first ionization pK values from (16); second ionization pK values estimated from pK values of phosphatidic acid (17)) is shown in Fig. 2 A for several pH values at low (c = 10 mM) and high (c = 250 mM) salt concentrations. The theoretical curves have several interesting features, which qualitatively correspond to the experimental data for PIP₂ in Fig. 1 D. In agreement with the experimental data, the surface pressure of compressed monolayers is higher at higher ionic strength, which initially appears counterintuitive due to the increase of screening with ionic strength. The increased surface pressure is due to the increased charge density of the monolayer at higher ionic strength, since high ionic strength diminishes the pK_e value, consistent with previous observations and modeling of less charged amphiphile monolayers (6–8,10). This expansion due to charging of the monolayer with increased subphase ionic strength becomes prevalent when the surface area per lipid molecule reaches a minimal threshold, as seen from the crossing of theoretical isotherms for low and high salt concentrations (Fig. 2 A), in agreement with experimental data (Fig. 1 D). The importance of lipid headgroup deprotonation in the behavior of isotherms is illustrated in Fig. 2 B, where theoretical isotherms for low and high salt concentrations are shown both with and without accounting for the shift of effective pK values as a function of the potential of the monolayer. From these plots, it is clear that if the charge per lipid molecule is fixed, the pressure of the monolayer decreases with increasing ionic strength due to screening. The dependence of the effective pK value on the area per lipid molecule, calculated according to Eqs. 12 and 13 for pH = 7.5 at low (c = 10 mM) and high (c = 250 mM) ionic strengths, is shown in Fig. 2 C. Due to the decrease in pK_e values at higher ionic strength, the charge per lipid molecule increases, which leads to increased surface pressure, as remarked above.

FIGURE 2.

(A) Calculated isotherms of electrostatic surface pressure at low (c = 10 mM; dashed line) and high (c = 250 mM ; solid line) subphase ionic strength at pH = 5,7.5,12. (B) Isotherms of electrostatic pressure with and without accounting for the dependence of effective pK values on the potential of the monolayer. Values: c = 10 mM (dashed line) and c = 250 mM (solid line) accounting for pK shift, c = 10 mM (large dots) and c = 250 mM (small dots) without accounting for pK shift. (C) Variation in pK values (pK_e − pK) as a function of surface area per lipid molecule (Σ) at pH = 7.5 and c = 10 mM (dashed line) or c = 250 mM (solid line).

Equations 12–14 also predict another important property of the system considered here. Calculated at a fixed electrostatic pressure, the dependence of the area per lipid molecule (Σ) on the charge of that lipid is linear with a slope of 2 k_BT/π_s as found from Eq. 9.

METHODS

Natural lipids (bovine liver L-α-phosphatidylinositol, porcine brain L-α-phosphatidylinositol-4-phosphate, porcine brain L-α-phosphatidylserine, and porcine brain L-α-phosphatidylinositol-4,5-bisphosphate) were purchased as 1 mg/ml solutions from Avanti (Alabaster, AL) and stored at −20°C. Concentrations were verified initially by inorganic phosphate analysis, and subsequently by normalizing to measured lipid area per molecule.

For comparisons between different lipids at pH 7.5, monolayer subphases were prepared with 10 mM HEPES, 0.1 mM EDTA, pH 7.4 dissolved in 18.2 MΩ ddH₂O. For varying pH experiments the buffer was 3.3 mM sodium phosphate, 3.3 mM sodium citrate, and 3.3 mM glycine instead of 10 mM HEPES. A quantity of 25–30 mL of subphase solution was filtered through a 0.2-μm syringe filter (Sigma, St. Louis, MO) and introduced to a MicroTroughX Langmuir trough (Kibron, Helsinki, Finland). Approximately seven nmol of lipid was withdrawn through a septum from a container stored at −20°C to prevent solvent evaporation and deposited slowly on the subphase interface. After a 10-min stabilization of the monolayer, the lipids were compressed at 10 Å per molecule per minute by moving the barriers of the trough using a microstepping motor. The monolayer surface pressure was monitored with a surface probe using the Wilhelmy method (18) and the FilmWare software package (Kibron). Both the low amount of lipids and the slow deposition rate were critical parameters for reproducibility of monolayer isotherms. Temperature was maintained at 30°C by a circulating water bath.

DISCUSSION

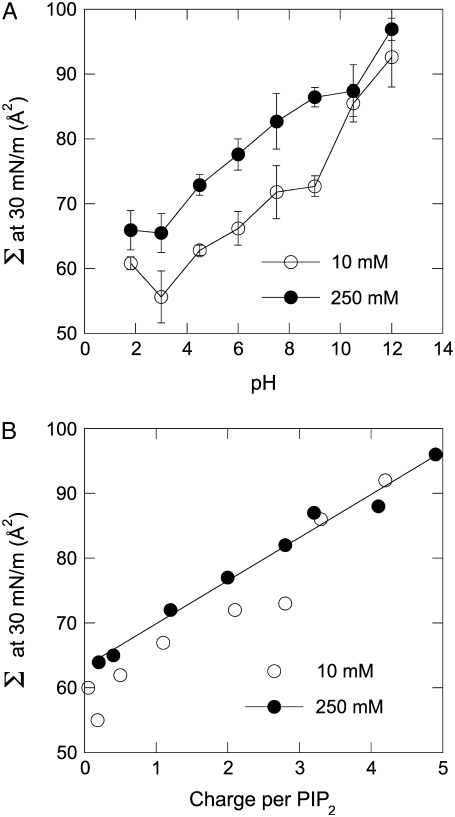
The theory derived above makes several predictions that are verified by experimental data. The linear dependence of the area per lipid molecule on its charge was tested by varying the pH of the aqueous subphase and measuring pressure-area relationships (specifically, area/molecule at π_s = 30 mN/m). Fig. 3 A shows the change in area/molecule of PIP₂ monolayers as a function of pH at high and low ionic strength, and reveals expansion of the monolayer both by increasing ionic strength and increasing pH, both of which lead to increased deprotonation of PIP₂. Equations 12–14 allow calculation of the net charge on PIP₂ at each value of pH and π_S, and the molecular area as a function of net charge is shown in Fig. 3 B. The data at high ionic strength are well fit by a linear relationship over the entire range of charge >−1. The proportionality constant derived from the fit is less than, but within a factor of two from, the simple prediction of 2 k_BT/π_S expected from Eq. 9.

FIGURE 3.

(A) Isobaric (π_S = 30 mN/m) area/molecule (Σ) as a function of measured pH of pure, naturally derived PIP₂ on a buffered subphase with added 10 mM (open circles) or 250 mM (solid circles) NaCl. Points shown are the average ± standard deviation for three trials. (B) Measured area/molecule of PIP₂ as a function of charge/molecule calculated from Eq. 11.

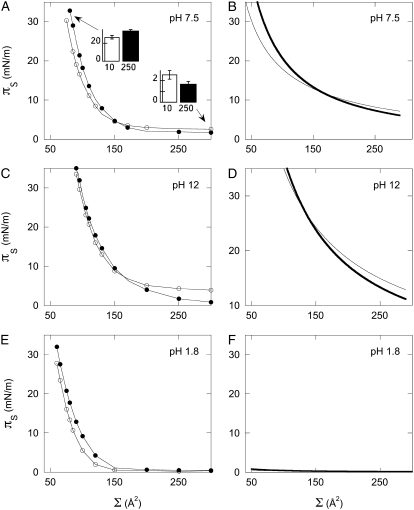
A more detailed comparison of theory and data is shown in Fig. 4, which compares the area-pressure isotherms of PIP₂ at three different pH values where significant differences in charge density are expected. At pH 12, where the charge separation is well below the Bjerrum length and near the minimum value for PIP₂, changing the ionic strength from 10 mM to 250 mM has a small effect over the measurable range of area/molecule (Fig. 4 C). The theoretical curves are similar in shape and magnitude to the experimental data as both theory and experiment show a crossing of the curves at a critical area/molecule where the screening effect of salt on electrostatic repulsions begins to dominate the pK_e lowering effect important at lower molecular areas. At pH 7.5, theory predicts that the crossover occurs in a more expanded monolayer (near 160 Ų, Fig. 4 B), in excellent agreement with the experimental result (Fig. 4 A). The measured differences in pressure of very expanded monolayers are small, but statistically significant (inset, Fig. 4 A). At pH 1.8, where the charge on PIP₂ is near −1, theory predicts a very small effect of electrostatic repulsion on the surface pressure, and the experimentally measured pressure is indistinguishable from zero at areas at >150 Ų/molecule.

FIGURE 4.

Measured isotherms of pure, naturally derived PIP₂ on buffered subphase with added 10 mM (open circles) and 250 mM (solid circles) NaCl at pH 7.5 (A), pH 12 (C), and pH 1.8 (E). Isotherms shown are representative of three trials/condition. (A, inset) Quantification of difference between low and high salt buffer of expanded (300 Ų/molecule) and compressed (80 Ų/molecule) monolayers of PIP₂. Theoretically calculated isotherms for PIP₂ at pH 7.5 (B), pH 12 (D), and pH 1.8 (F) with 10 mM (thin line) and 250 mM (bold line) subphase ionic strength.

The theoretical curves with no adjustable parameters shown here qualitatively agree with the experimental data, suggesting that, unlike PS or PI, polyphosphoinositide membrane surface pressures are strongly affected by electrostatic effects under physiological conditions. However, quantitative differences between theory and experiment suggest the limits of this purely electrostatic model. The theory is not expected to be valid at small molecular areas where steric interactions become significant; correspondingly, at <60 Ų the experimentally measured pressures are systematically larger than theoretical prediction. In contrast, at higher molecular areas (>120 Ų) and pH values, this electrostatic theory predicts significantly larger pressures than are measured (Fig. 4, A–D) and a steeper dependence of molecular area on charge than is observed (Fig. 3 B). The lower pressures measured experimentally compared to the predicted purely electrostatic contribution to lateral pressure suggest that attractive interactions counter the electrostatic repulsions measured and modeled in this study. A likely mechanism of attractive interactions is hydrogen-bonding between lipid headgroups, as suggested in charged phosphatidic acid (19) and zwitterionic phosphatidyl ethanolamine membranes (20), and recently confirmed in bilayers containing phosphoinositides (21,22).

CONCLUSIONS

Unlike univalent charged phospholipids for which charge separation is greater than the Bjerrum length and electrostatic contributions to monolayer surface pressures are negligible compared to steric and dipolar effects, multivalent polyphosphoinositides form monolayers in which electrostatic contributions are significant. A theoretical model is developed to calculate the magnitude of electrostatic contributions to surface pressures for any lipid with known valence and pK_a values. Electrostatic contributions lead to significant surface pressures at molecular areas of greater than four times the steric size of the lipid, and electrostatic screening by increased salt concentration leads to two opposing effects, increased deprotonation and increased surface pressures for compressed monolayers, and decreased repulsions and subsequent lower pressures for highly expanded monolayers. These effects are significant at physiological conditions and perhaps play a role in the unique functionality of polyphosphoinositides in the structure and activity of cell membranes that cannot be reproduced by more abundant, but univalent, anionic lipids such as phosphatidylserine. The value of the theoretical analysis presented here is both its ability to predict many of the observed phenomena, confirming the importance of electrostatics in determining membrane organization, as well as in the prediction of an attractive interaction that would confirm existing experimental results.