Skip to main content
PMC home page
Biophysical Journal logoLink to Biophysical Journal
. 2008 Apr 25;95(3):1474–1486. doi: 10.1529/biophysj.107.128223

Three-Dimensional Microtubule Behavior in Xenopus Egg Extracts Reveals Four Dynamic States and State-Dependent Elastic Properties

Philipp J Keller *, Francesco Pampaloni *, Gianluca Lattanzi †, Ernst H K Stelzer *
PMCID: PMC2479590  PMID: 18441022

Abstract

Although microtubules are key players in many cellular processes, very little is known about their dynamic and mechanical properties in physiological three-dimensional environments. The conventional model of microtubule dynamic instability postulates two dynamic microtubule states, growth and shrinkage. However, several studies have indicated that such a model does not provide a comprehensive quantitative and qualitative description of microtubule behavior. Using three-dimensional laser light-sheet fluorescence microscopy and a three-dimensional sample preparation in spacious Teflon cylinders, we measured microtubule dynamic instability and elasticity in interphase Xenopus laevis egg extracts. Our data are inconsistent with a two-state model of microtubule dynamic instability and favor an extended four-state model with two independent metastable pause states over a three-state model with a single pause state. Moreover, our data on kinetic state transitions rule out a simple GTP cap model as the driving force of microtubule stabilization in egg extracts on timescales of a few seconds or longer. We determined the three-dimensional elastic properties of microtubules as a function of both the contour length and the dynamic state. Our results indicate that pausing microtubules are less flexible than growing microtubules and suggest a growth-speed-dependent persistence length. These data might hint toward mechanisms that enable microtubules to efficiently perform multiple different tasks in the cell and suggest the development of a unified model of microtubule dynamics and microtubule mechanics.

INTRODUCTION

Microtubules are cytoskeletal filaments found in all eukaryotes. They have a fundamental role in cell division (1,2), intracellular trafficking (3,4), coordination of cell movement (5,6), and development and maintenance of cell shape (7,8). Microtubules are regarded as highly dynamic structures that stochastically undergo phases of growth and shrinkage (dynamic instability) (3,9). A third metastable state, usually termed a microtubule pause, in which microtubules apparently neither grow nor shrink, has also been observed, and very recently became the object of detailed research (10,11). Since little is known about the functional role of microtubule pausing in a physiological context, understanding dynamic instability's third state and its associated molecular mechanisms is now considered to be of major importance (10,12).

Recently, we developed a three-dimensional assay (combining three-dimensional preparation and three-dimensional observation) for experiments of microtubule dynamic instability in the physiological system provided by Xenopus laevis egg extracts (13). We demonstrated a significant divergence between microtubule dynamics measured in two and three dimensions and suggested a comprehensive investigation of microtubule dynamics in three dimensions, with a particular focus on microtubule pausing. The differences observed in a three-dimensional environment actually raise the question of whether the conventional kinetic model of microtubule dynamic instability (comprising microtubule growth and shrinkage) provides a correct description of microtubule behavior in this physiologically more relevant context. Moreover, the influence of the experimental environment on the filaments' dynamic properties also suggests an investigation of microtubule elastic properties in an unconstrained three-dimensional set-up. Traditional studies have typically employed buffer systems (14–16), and thus there is still very little known about microtubule elasticity in the physiologically relevant context of Xenopus laevis egg extracts. It is important to note that our new experimental system makes it possible to analyze the dynamic and elastic aspects of microtubule behavior simultaneously in three dimensions. Based on this assay, we obtain and quantify a functional relationship between these two characteristic aspects of microtubule behavior.

MATERIALS AND METHODS

Preparation of fresh interphase Xenopus laevis egg extracts

The experimental results are based on 10 independent experiments that were performed with nine freshly prepared interphase egg extracts.

Undiluted cytoplasmic egg extracts were prepared from Xenopus laevis eggs as described by Murray (17), but with modifications explained below. After dejellying and washing, the eggs were transferred to centrifuge tubes containing CSF-XB plus protease inhibitors and 10 μg/mL cytochalasin D (Sigma-Aldrich, St. Louis, MO). The packing spin was performed for 30 s at 500 rpm, then for 90 s at 2000 rpm and room temperature with a Heraeus Megafuge 1.0R. The centrifuge tubes were then transferred to a Beckman Coulter JS-13.1 rotor at room temperature. The crushing spin was performed for 20 min at 11,000 rpm and 4°C. After collecting the cytoplasmic fraction, we added 10 μg/mL cytochalasin D. The meiotically CSF-arrested extracts were split into 100-μl aliquots, treated with 0.4 mM CaCl2 and 0.7 mM cycloheximide (Sigma-Aldrich) and incubated for 90 min at 20°C to obtain interphase extracts.

Three-dimensional sample preparation

For each experiment, 25 μl of fresh interphase egg extract was gently mixed with 1.5 μl undiluted centrosomes and 1 μl Alexa-488-labeled tubulin (74 ± 1 μM, 38 ± 2% labeling ratio) at 4°C. Thus, assuming an average contribution of 18 μM tubulin from the egg extract (18), 5% of the tubulin was fluorescently labeled. A regenerative oxygen-scavenging system was prepared by mixing 10 μl catalase (10 mg/mL, Sigma-Aldrich), 10 μl glucose oxidase (10 mg/mL, Sigma-Aldrich), 10 μl glucose (1 M) and 3 μl hemoglobin (Sigma-Aldrich) saturated buffer at 4°C. From this system, 1 μl was added to the egg extract, 20 μl were then transferred to a plastic polymer cylinder (19) at 4°C, and 5 μl mineral oil were layered on top of the sample in the plastic polymer cylinder. Before mounting the cylinder in the single plane illumination microscope (SPIM), the mix was equilibrated in the plastic polymer cylinder at 4°C for 3 min. The SPIM imaging chamber was equilibrated to 20°C 1 h before mounting of the cylinder. The imaging chamber's temperature was kept constant at 20°C over the entire course of the experiment.

Three-dimensional imaging

Our observation system for three-dimensional imaging of microtubule dynamics is based on one of EMBL's implementations of light-sheet-based fluorescence microscopy (SPIM) (20,21). Alexa-488 molecules were excited with a Melles Griot (Rochester, NY) argon gas laser at 488 nm. Fluorescence was detected via an Achroplan W 100×/1.0 water dipping lens (Carl Zeiss, Jena, Germany) and a Semrock RazorEdge long-pass filter (>488 nm). Data were recorded with an Orca ER camera (Hamamatsu, Tokyo, Japan) at 2× binning with a temporal resolution of 3.6 s/image stack (29 frames) and a spatial resolution of 0.3 μm laterally and 1.5 μm axially for an imaging volume of 87 × 66 × 20 μm3. The voxel size in the data sets is 129 × 129 × 700 nm3. Data analysis was performed directly on the raw data sets (Supplementary Material, Data S1).

To generate the light sheet, the laser's Gaussian beam profile is first shaped by a set of apertures. The resulting profile is subsequently focused along one dimension by a cylindrical lens (01 LQC 006, Melles Griot). For high-magnification experiments, an additional objective (Epiplan 10×/0.2) is introduced to the microscope's illumination system. Since the illumination objective swaps the focused dimension and the unfocused dimension, the cylindrical lens is tilted by 90° around the optical axis as compared to the orientation in the first implementation of the microscope (20,21). The combination of a cylindrical lens with an illumination objective provides both a sheet-shaped illumination profile (due to the cylindrical lens) and a sufficiently high numerical aperture (due to the illumination objective) to focus the light sheet down to a thickness of 1.5 μm.

Three-dimensional data analysis of microtubule dynamic instability and elasticity

Detailed descriptions of the data analysis and the custom processing algorithms are provided in Data S1.

RESULTS AND DISCUSSION

Evidence for four microtubule states in Xenopus extracts and consequences for the GTP cap model

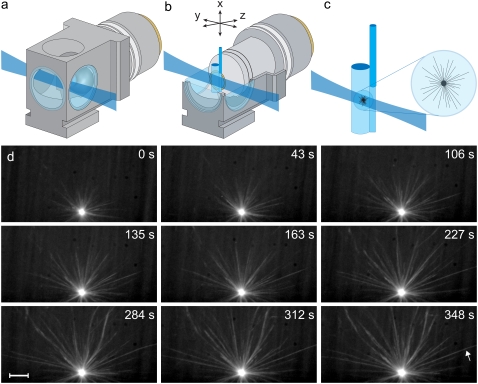
We investigated microtubule dynamic instability in Xenopus laevis egg extracts with our three-dimensional assay (13,19) (Fig. 1, a–c, and Data S1). We employed laser light-sheet fluorescence microscopy for three-dimensional imaging over time (20,21) and a three-dimensional sample preparation of interphase Xenopus laevis egg extracts in spacious cylindrical chambers with 25-μm-thick transparent Teflon walls and a volume of 30 μl. This system facilitates the observation of microtubule dynamics under almost unconstrained three-dimensional conditions (Fig. 1 d) and makes it possible to distinguish between intrinsic and extrinsic events of dynamic instability, the latter triggered by, e.g., microtubule-surface contact.

FIGURE 1.

FIGURE 1

Open in a new tab

Measuring three-dimensional microtubule dynamic instability and elasticity. (a) Illustration (to scale) of the light-sheet imaging arrangement (SPIM). The detection lens in the central SPIM imaging chamber is immersed in water. The light sheet is focused into the chamber from the side and illuminates a single plane of the specimen. (b) The sample cylinder containing the egg extract is attached to a glass capillary and oriented parallel to gravity. The cylinder is located in front of the detection lens and can be moved along three dimensions via a set of linear miniature stages. The detector elements, including the microscope objective lens, are in a horizontal arrangement. Its focal plane is coplanar with the light sheet. The optical sectioning capability introduced by the light sheet profile reduces photobleaching in three-dimensional imaging by a factor of (sample thickness)/(light-sheet thickness) as compared to a conventional microscope, which results in a factor of 20 for experiments of microtubule dynamic instability. (c) The microtubule asters are polymerized in the egg extract inside the Teflon cylinder. The cylinder has a diameter of 2 mm and consists of a Teflon membrane with a thickness of 25 μm (bioFOLIE 25, In Vitro Systems & Services, Germany). The membrane has a high transmittance for visible wavelengths and is refractive-index-matched to water (but not water-permeable). Due to the high viscosity of the egg extract, the polymerized asters can be kept in a stable position anywhere inside the cylinder. The distance between the cylinder's surface and the recorded asters is in the order of 100 μm. Three-dimensional data are recorded by moving the microtubule asters in small z-steps through the light sheet while simultaneously recording images with the CCD camera. (d) Maximum-intensity projections at nine time points of a three-dimensional dynamic instability time-lapse data set, recorded with SPIM. Scale bar, 10 μm. The arrow in the last frame indicates the microtubule that is shown in Fig. 4 a. Tubulin was labeled at a 5% ratio with Alexa-488. Elapsed time is relative to the start time of imaging. For all experiments, imaging starts 1–2 min after the onset of microtubule polymerization. Fluorescence was detected via the Carl Zeiss Achroplan W 100×/1.0 lens.

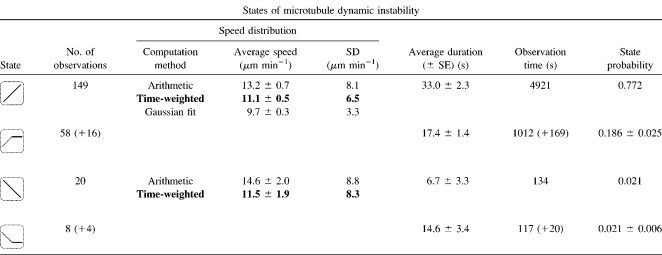
We analyzed three-dimensional microtubule dynamics in 70 microtubules with an average observation period of 91 s/microtubule and obtained 1873 three-dimensional microtubule shapes. Custom automated processing algorithms were employed to classify the microtubule dynamic state (see Methods and Software sections and Fig. S1 in Data S1). We observed 149 phases of growth, 20 phases of shrinkage, and 86 phases of microtubule pause (Tables 1 and 2). To quantify possible differences between microtubule pause after growth and microtubule pause after shrinkage, we considered a maximum of four independent states of microtubule dynamic instability: growth, shrinkage, pause after growth (g-pause), and pause after shrinkage (s-pause). Since the plus-end tips of growing and shrinking microtubules are structurally quite different (22), the associated pauses are not necessarily characterized by the same kinetic parameters. Eight state transitions are theoretically possible and were also experimentally observed (see Fig. 2 for examples). In our data analysis, we consider three models of microtubule dynamic behavior: the conventional two-state model (growth and shrinkage), an extended three-state model (growth, shrinkage, and pause) and a four-state model (growth, shrinkage, g-pause, and s-pause).

TABLE 1.

Experimental results for the states of three-dimensional microtubule dynamic instability

graphic file with name BIO.128223.lw.tbl1.jpg
Open in a new tab

Experimental statistics for the growth, g-pause, shrinkage, and s-pause states (from top to bottom). In total, 86 pause phases were observed. In 66 cases, the preceding dynamic phases were identified, i.e., the pauses could be assigned to either g-pause or s-pause. The numbers in parentheses indicate the statistically most likely phase assignment (g-pause and s-pause) of the 20 remaining unidentified phases, according to the derived state probabilities. The error arising from the unidentified pause phases has been considered in the errors of the state probabilities. Only unambiguously identifiable observations were considered in the calculation of average state durations. The statistics of microtubule shrinkage (n = 20) are too low to apply a Gaussian fit.

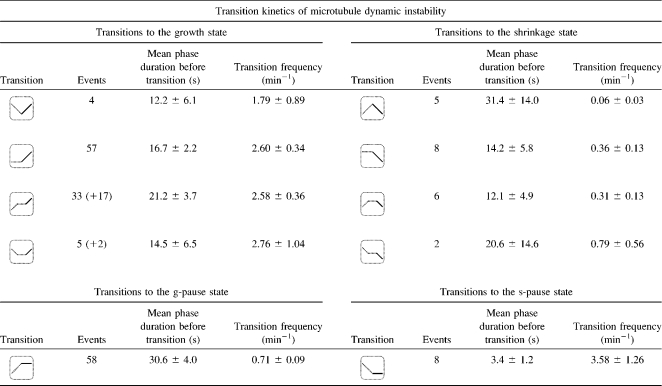
TABLE 2.

Experimental results for the intrinsic transition kinetics of microtubule dynamic instability

graphic file with name BIO.128223.lw.tbl2.jpg
Open in a new tab

The transition symbols show the microtubule's state before the occurrence of the corresponding transition events as a dashed line. The microtubule's state after the transition event is represented by a solid line. For 19 of 57 transitions from pause to growth, the state preceding the pause could not be determined. The statistically most likely phase assignments for these transitions were calculated from the observed state probabilities and are included in brackets. The errors of the phase durations and transition frequencies are computed by dividing the respective parameter by the square root of the number of underlying observation events. Only unambiguously identifiable pause phases were considered in the calculation of the average state durations.

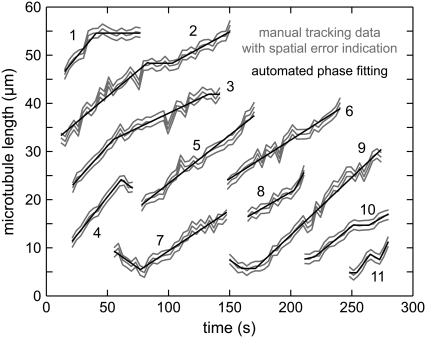
FIGURE 2.

FIGURE 2

Open in a new tab

Automated phase fitting in microtubule length-versus-time diagrams. Manual tracking data of 11 microtubules (gray) and the corresponding dynamic phases automatically computed by the phase-fitting algorithm (black). The spatial error of the length measurements is also indicated in gray. Data set 1 shows a switching from growth to g-pause. Data set 2 illustrates a positive growth contrast with intermediate g-pause. Data set 3 exhibits an example of growth-speed switching. Data set 7 shows a rescue event.

The state probabilities and transition frequencies of the two microtubule pause states were quantified. Only two events out of seven observed transitions leaving the s-pause state resulted in microtubule shrinkage, whereas in the remaining five cases the microtubule started to grow (Table 2, fourth row). The situation in the g-pause state is similarly unbalanced. Of the 39 observed transition events, 6 led to microtubule shrinkage, whereas in 33 cases, the microtubule switched back to microtubule growth (Table 2, third row). These results have implications for the GTP-cap model of microtubule stabilization (23–27). According to this model, a microtubule catastrophe is initiated by hydrolysis of a thin layer of GTP-tubulin at the plus-end of the microtubule (28). In a growing microtubule, the addition of GTP-tubulin subunits to the plus-end tip of the microtubule is fast enough to maintain a stabilizing GTP-tubulin cap. However, if the microtubule switches from growth to a pause, the addition of new GTP-tubulin subunits to the plus-end tip is stopped and a rapid hydrolysis of the remaining GTP-tubulin subunits is expected. Assuming a constant rate of GTP hydrolysis (29) and considering the average pause state duration of 17 s measured in our work (Table 1), hydrolysis of all GTP-tubulin subunits should have occurred by the end of a pause phase. Consequently, assuming that microtubule catastrophes occur in response to the hydrolysis of the cap, microtubules should exhibit a preference for switching from pause to shrinkage rather than from pause to growth. Since the experimental results clearly contradict this situation in the spatiotemporal domain accessible with our light-microscopy-based approach, the GTP cap cannot be the driving force of microtubule stabilization in egg extracts on timescales of a few seconds or longer. Although this result does not rule out a direct or indirect contribution of GTP hydrolysis to microtubule dynamic instability, it indicates that GTP hydrolysis is not the major factor in microtubule destabilization. This finding supports MAP-related studies of microtubule dynamics that provide evidence for a modulation of microtubule stability by associated proteins (10,30–32).

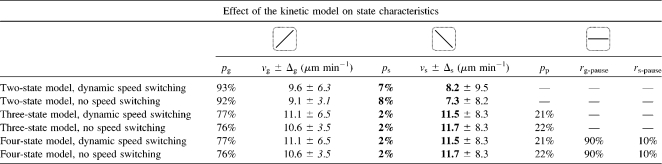
Next, we quantified the parameters for the microtubule states in the proposed different kinetic models. Table 3 shows the state contributions and speed distributions that result from the application of the conventional two-state model and the pause(s)-extended three-state and four-state models. In addition, the possibility of speed changes during growth and shrinkage was considered. Neglecting microtubule pausing (i.e., applying the two-state model) leads to an increase of the microtubule shrinkage state's probability by a factor of 4, whereas the average shrinkage speed is reduced by 30–40% compared with the three-state and four-state models of dynamic instability. The consideration of dynamic speed changes increases the width of the growth-speed distribution by a factor of 2 (Table 3).

TABLE 3.

Analysis of microtubule dynamic instability states using different kinetic models

graphic file with name BIO.128223.lw.tbl3.jpg
Open in a new tab

Overview of the state statistics that result when applying different kinetic models to the data sets. pg is the growth state probability, ps the shrinkage state probability, and pp the probability of microtubule pausing. rg-pause and rs-pause quantify the relative contribution of the g-pause and s-pause states to the total microtubule pausing probability, pp. The shrinkage state contribution and the mean shrinkage speed (bold) are strongly affected by the choice of a two-state or three-/four-state model, respectively (but insensitive to the introduction of dynamic speed switching). The width of the growth speed distribution (italic) is strongly affected by the choice of a model that considers dynamic speed switching (but insensitive to the introduction of the three-/four-state model per se).

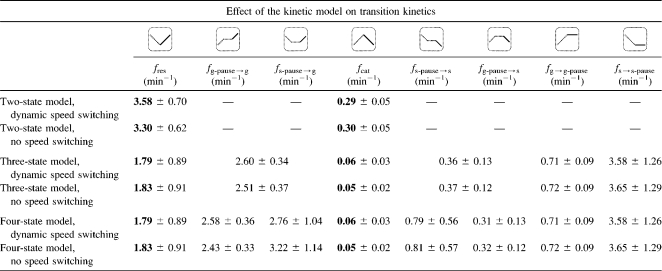
Table 4 shows the effect of the kinetic model on the transition frequencies. As expected, a consideration of speed changes during growth and shrinkage has only a minor effect (<10%) on the transition frequencies. The application of the kinetic two-state model led to an increase of the rescue frequency by a factor of 2 and an increase of the catastrophe frequency by a factor of 5, compared to the experimental results for the three-state and four-state models.

TABLE 4.

Analysis of microtubule dynamic instability transitions using different kinetic models

graphic file with name BIO.128223.lw.tbl4.jpg
Open in a new tab

Overview of the transition statistics that result when applying different kinetic models to the data sets. fres is the conventional rescue frequency, and fcat the conventional catastrophe frequency. All other frequencies are denoted as fx→y, where x is the phase that precedes the event and y the phase that succeeds the event. No transition frequency shows a significant sensitivity to the consideration of dynamic speed switching. However, the rescue and catastrophe frequencies (bold) are strongly affected by the choice of a two-state or three-/four-state model.

In conclusion, the quantitative errors that result from neglecting microtubule pausing are quite large. The most affected parameters are the microtubule shrinkage state probability, the depolymerization speed, the rescue frequency, and the catastrophe frequency. Thus, an extension of the two-state model by at least one pause state is absolutely necessary to obtain quantitatively meaningful data for three-dimensional microtubule dynamic instability. This also raises the question of whether the properties of the pauses after shrinkage differ significantly from those occurring after growth, i.e., whether the theoretical model should be extended by two independent pause states.

A comprehensive four-state kinetic model of three-dimensional microtubule dynamic instability

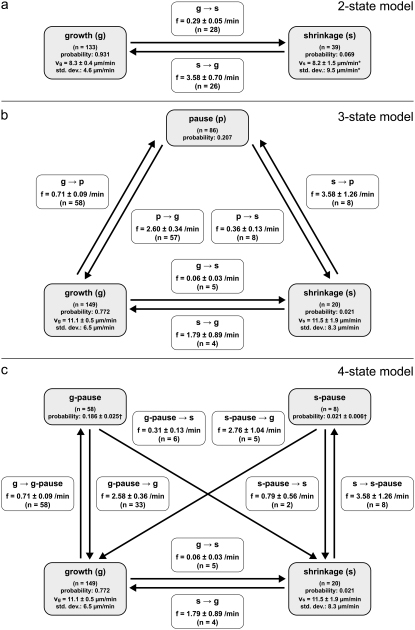
The two-state model (Fig. 3 a), comprising only microtubule growth and microtubule shrinkage, is severely impaired by the following two observations. First, the microtubule pause state is more abundant than microtubule shrinkage by a factor of 10 (21% vs. 2% state probability) and thus cannot be neglected. Second, the model misjudges the characteristic parameters of the two dynamic states (i.e., transition frequencies and (de-)polymerization speeds) by up to a factor of 5.

FIGURE 3.

FIGURE 3

Open in a new tab

The three kinetic models of microtubule dynamic instability. (a) The conventional two-state model of microtubule dynamic instability, introduced by Terrell Hill (34). Parameters resulting for our three-dimensional data are indicated. Microtubule pausing is not considered in this model. (b) The three-state model of microtubule dynamic instability, derived by extending the two-state model by one pause state and introducing four additional state transitions. (c) The four-state model, with two independent pause states, comprising the growth state, the shrinkage state, the pause-after-shrinkage (s-pause) state, and the pause-after-growth (g-pause) state. The four-state model considers transitions that involve at most one of the two pause states. Transitions between the two pause states cannot be determined by observation with conventional microscopy and are therefore not quantified. The errors of the average speeds are standard errors of the mean (SE). The errors of the transition frequencies are calculated by dividing the respective frequency by the square root of the number of underlying observation events. The errors of the pause state probabilities arise from unidentified pause phases, i.e., pauses for which the preceding dynamic phases were not observed.

The necessary extension of the conventional model can be achieved in two ways, i.e., by implementing either one additional pause state (the three-state model (Fig. 3 b)) or two independent pause states considering possible kinetic differences in pausing after shrinkage and pausing after growth (the four-state model (Fig. 3 c)). We tested both models against our experimental data to decide whether the simpler three-state model (which can be seen as a special case of a four-state model) provides a sufficiently accurate description of the microtubules' dynamic behavior. State diagrams and experimental parameters for the two-, three-, and four-state models of microtubule dynamic instability are shown in Fig. 3, a–c.

The conventional two-state model employs a system of two differential equations (Eqs. 1 and 2) that describe the probability densities for microtubules to be in either a shrinkage or a growth state (33,34):

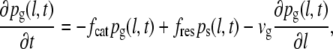graphic file with name M1.gif (1)
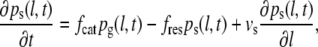graphic file with name M2.gif (2)

where pg(l,t) is the probability density of finding a growing microtubule with length l at time t. Similarly, ps(l,t) is the probability density of the shrinkage state. fcat (catastrophe) is the transition frequency from the growth to the shrinkage state, whereas fres (rescue) is the transition frequency from the shrinkage to the growth state. vg is the microtubule growth speed and vs is the microtubule shrinkage speed.

To obtain the three-state model (Eqs. 3–5), we expand the set of differential equations by one equation for a common pause state. A similar extension of the model was previously suggested (35), but using a framework that does not consider all experimentally possible transitions between growth, shrinkage, and pause. Here, we introduce pp(l,t), the probability density for the pause state, and four transition frequencies: fg→p for transitions from growth to pause, fp→g for transitions from pause to growth, fs→p for transition from shrinkage to pause, and fp→s for transitions from pause to shrinkage.

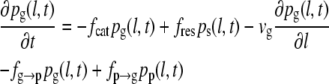graphic file with name M3.gif (3)
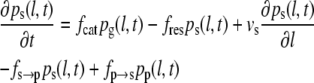graphic file with name M4.gif (4)
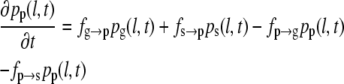graphic file with name M5.gif (5)

In the four-state model, we postulate two pause states: pause after growth (g-pause) and pause after shrinkage (s-pause). The resulting set of differential equations (Eqs. 6–9) includes two additional differential equations that describe the corresponding probability densities pgp(l,t) and psp(l,t), as well as the transition frequencies fg→gp for a transition from growth to g-pause, fgp→g for a transition from g-pause to growth, fgp→s for a transition from g-pause to shrinkage, fs→sp for a transition from shrinkage to s-pause, fsp→s for a transition from s-pause to shrinkage and fsp→g for a transition from s-pause to growth.

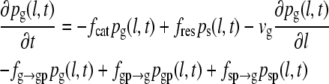graphic file with name M6.gif (6)
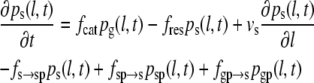graphic file with name M7.gif (7)
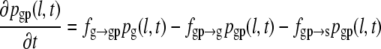graphic file with name M8.gif (8)
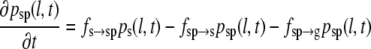graphic file with name M9.gif (9)

The extended three-state and four-state models can be employed to predict transition frequencies in dynamic equilibrium, once the other parameters of microtubule dynamic instability have been measured. We tested both extended models by calculating the transition frequencies associated with the pause states and comparing the obtained values with the measured values in Fig. 3.

First, we define the state probabilities, Px, of the four kinetic states (with x = g, s, gp, sp) as follows:

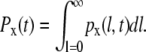graphic file with name M10.gif (10)

Next, we rewrite Eq. 8 for the dynamic equilibrium condition using the state probabilities, Px:

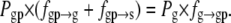graphic file with name M11.gif (11)

The state probabilities, Px, can be expressed by the state observation times Tg, Ts, Tgp, and Tsp:

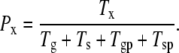graphic file with name M12.gif (12)

Inserting Eq. 12 in Eq. 11, we obtain a relation between the frequencies fg→gp, fgp→g, and fgp→s and the state observation times Tg and Tgp:

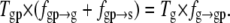graphic file with name M13.gif (13)

Similarly, the relationship between the frequencies fs→sp, fsp→s, and fsp→g and the state observation times Ts and Tsp can be determined from Eq. 9:

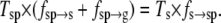graphic file with name M14.gif (14)

Eqs. 13 and 14 can be employed to predict any of the pause-associated transition frequencies of the four-state model, once the other parameters have been measured. A comparison between the predicted and the measured values provides a test for the consistency of the theoretical model with the experimental data, as well as a control for measurements in dynamic equilibrium. A relationship similar to Eqs. 13 and 14 can be obtained for the three-state model from Eq. 5:

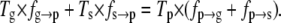graphic file with name M15.gif (15)

An overview of the predicted and measured values for the six pause-associated transition frequencies of the four-state model and the four corresponding frequencies of the three-state model is provided in Table 5. All predicted frequencies are in very good agreement with the experimental data. The average deviation of the four-state model's predictions from the experimental parameters is 6.1%; the average deviation of the three-state model's predictions is 8.6%. In conclusion, both models are in very good quantitative agreement with the three-dimensional data.

TABLE 5.

Prediction of g-/s-pause-related transition frequencies and comparison to the measured parameters

Transition frequency predictions of the four-state model
fg→g-pause (min−1) fg-pause→g (min−1) fg-pause→s (min−1) fs→s-pause (min−1) fs-pause→s (min−1) fs-pause→g (min−1)
Predicted value 0.69 ± 0.13 2.65 ± 0.55 0.38 ± 0.64 3.63 ± 1.28 0.74 ± 1.67 2.71 ± 1.47
Measured value 0.71 ± 0.09 2.58 ± 0.36 0.31 ± 0.13 3.58 ± 1.26 0.79 ± 0.56 2.76 ± 1.04
Transition frequency predictions of the three-state model
fg→p (min−1) fp→g (min−1) fs→p (min−1) fp→s (min−1)
Predicted value 0.70 ± 0.10 2.65 ± 0.38 3.04 ± 4.87 0.41 ± 0.49
Measured value 0.71 ± 0.09 2.60 ± 0.34 3.58 ± 1.26 0.36 ± 0.13
Open in a new tab

Pausing and unpausing frequency predictions were performed as described in the section entitled “A comprehensive four-state model of microtubule dynamic instability.” All frequencies were measured independently (Table 2). All predicted parameters are in agreement with the measured parameters. Since the predictions are only valid for a measurement in dynamic equilibrium, this comparison also serves as a consistency test for the extract conditions.

The classical two-state model was previously shown to describe the kinetics of microtubule dynamic instability in metaphase egg extracts (2). The four-state model (as well as the three-state model) represents a general framework that includes the classical two-state model as a special case. Hence, with this extension, a comprehensive model for the kinetics of both metaphase and interphase microtubule dynamic instability has been established.

Although dynamic instability has been investigated for over two decades (16), most of the underlying molecular mechanisms and structural details are still under debate (3,36,37). The term “pause” has been used by many investigators, for studies both in vitro (11,38,39) and in vivo (40–43). However, our inability to detect either growth or shrinkage at the microtubule's tip during extended periods of time does not imply that the involved structures become inactive (44). It has been shown that the molecular processes underlying microtubule pausing are at least partially controlled by a complex regulatory network of MAPs (10,11,30), which potentially interacts differently with microtubule plus ends that entered the pause after a period of molecular disassembly as compared to a phase of filament elongation. Thus, we determined whether the properties of microtubule pause-after-shrinkage phases differ significantly from those of pause-after-growth phases. Identical time intervals and transition frequencies would suggest a three-state model as the simplest accurate description of intrinsic microtubule dynamic instability in three dimensions. On the other hand, a significant deviation of the kinetic properties would indicate the existence of two independent pause states and would therefore demand a four-state model of dynamic instability.

Three issues need to be considered. First, the ratio of the two state probabilities is ∼9:1, indicating that the g-pause is much more abundant than the s-pause. Second, although the transition frequencies from g-pause and s-pause to growth differ by only 7%, the transition rates to the shrinkage state differ by more than a factor of 2. They do, however, agree within the statistical errors (Table 2). Third, we determined that g-pauses last on average 20% longer than s-pauses, and we obtained a >75% confidence level for nonidentical phase durations (Student's t-test).

These data suggest two conclusions. First, and in agreement with previous studies (33), we conclude that pausing cannot be a mere artifact of observation, i.e., a statistical fluctuation that results from a synchronized succession of catastrophe and rescue events. Although such a phenomenon might lead to a nearly constant filament length and could therefore be observed as a “pause” in a light microscope, it would also demand identical transition frequencies and phase durations for both pause states. Therefore, microtubule pausing cannot be directly linked to microtubule growth and microtubule shrinkage. Second, the statistical differences between the characteristics of the two pause states are sufficiently conclusive to favor an implementation of two independent pause states in the microtubule dynamic instability theoretical framework (i.e., a four-state model).

Microtubule pausing in egg extracts and cells is a phenomenon that should also be carefully addressed on a submicroscopical level. Investigating the structural and biochemical modifications of microtubules during pause phases will shed new light on microtubule dynamics regulation and might elucidate implications for the cell function.

Determination of the microtubule persistence length from three-dimensional fluctuations of clamped microtubules

The influence of the experimental environment on the dynamic properties of microtubules suggests an investigation of other characteristic properties of microtubules, such as the elastic properties of the filaments, in an unconstrained three-dimensional set-up. Since traditional studies have typically employed buffer systems (14–16), very little is known about microtubule elasticity in the physiologically more relevant context of Xenopus laevis egg extracts.

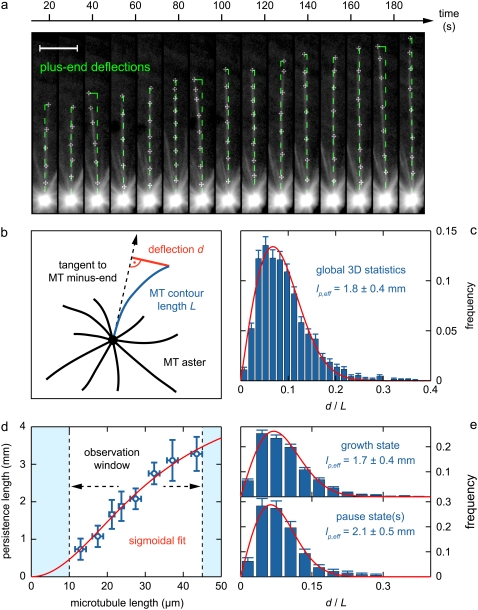
We derived the microtubules' persistence length from three-dimensional measurements and analyzed the relationship between microtubule elasticity and microtubule dynamics. The data set consists of n = 1817 independent three-dimensional microtubule contour measurements (Fig. 4 a), for each of which the microtubule's kinetic state was determined. The filament persistence length lp can be derived from the distribution of microtubule tip deflection ratios, r (the tip deflection d normalized to the contour length L (Fig. 4 b)) (45). The deflection ratio histogram of the entire microtubule population is shown in Fig. 4 c. The histograms in Fig. 4 e, upper and lower, show the subpopulations for microtubule growth (n = 1441) and microtubule pause (n = 321), respectively. All deflection ratio histograms were fitted with a model for three-dimensional tip deflections in clamped filaments.

FIGURE 4.

FIGURE 4

Open in a new tab

Three-dimensional mechanics of dynamic microtubules in interphase egg extracts. (a) Maximum-intensity projections of the three-dimensional contour shape of an unconstrained microtubule at 15 time points of a dynamic instability time-lapse data set (Fig. 1 d, arrow). Microtubule bending is caused by thermal fluctuations. Three-dimensional tip deflections and minus-end tangents (green) (Fig. 4 b) are automatically computed from the microtubule tracing points. Images are rotated such that the minus-end tangents are vertically oriented. Scale bar, 10 μm. (b) Schematic concept of the three-dimensional deflection measurements. The microtubules are “clamped” at their minus ends, which are embedded in the centrosome's matrix. The deflection ratio d/L is a direct measure of the filament's elasticity. (c) The global statistics of deflection ratios, obtained from n = 1817 independent three-dimensional measurements of microtubules with different contour lengths. The red curve indicates the best fit obtained with the one-parameter model (Eq. 18). The resulting effective persistence length, 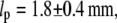Inline graphic characterizes the entire population of microtubules in the length regime L = 10–45 μm. The microtubule length distribution has been considered according to Eq. 2. The frequency errors are introduced by data binning. The numerical error of the persistence length includes the error of the fit and a conservative estimate of the spatial error in the deflection measurements (Data S1). (d) Analysis of the persistence length's filament-length dependency. The total statistics was subdivided into the length intervals 10–15, 15–20, 20–22.5, 22.5–25, 25–30, 30–35, 35–40, and 40–50 μm. The microtubule length error is the standard deviation of the bin size 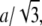Inline graphic with a = 2.5 or 5 μm. The error of the persistence length is calculated as described in Fig. 4 c. (e) Effective persistence lengths for growing (upper, n = 1441) and pausing (lower, n = 321,) microtubules in the microtubule length regime 10–45 μm. Fitting and errors as in Fig. 4 c.

To derive the microtubule persistence length from the three-dimensional fluctuations of the centrosome-attached microtubules, we assume that microtubules can be described as wormlike chains (WLCs) of persistence length 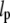Inline graphic(46,47). As already reported in Pampaloni et al. (45), the persistence length of microtubules depends on their total contour length, L. In the following discussion, we will assume that the persistence length is approximately constant over the range explored by a single measurement. Armed with this simplifying hypothesis, we derive the distribution function of length-independent quantities by measuring all lengths in units of the contour length, L.

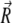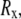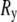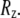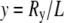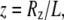We define Inline graphic as the end-to-end vector joining the two ends of the microtubule. The component along the tangent to the clamped end is defined as the x-component Inline graphic and the two perpendicular components as Inline graphic and Inline graphic The WLC model leads to two Gaussian distributions (48) for the dimensionless variables Inline graphic and Inline graphic both of width

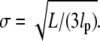graphic file with name M25.gif (16)

The distribution function of the dimensionless variable 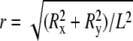Inline graphic can be obtained in a straightforward way by applying the usual transformation laws of probability theory and the properties of the Dirac δ-function:

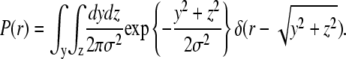graphic file with name M27.gif (17)

By calculating the above integrals, we find

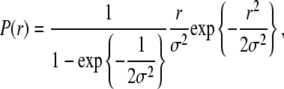graphic file with name M28.gif (18)

where we have inserted a normalization factor to take into account that r is defined in the range [0,1] and not in the range [0,∞], as implicitly assumed by Gaussian distributions. By fitting this distribution function to the experimental data, we obtain an estimate of the parameter 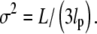Inline graphic Since we are analyzing data corresponding to different lengths, L, this estimate is only an average over the range of lengths spanned by our assay. Assuming again that the persistence length does not vary in the length range examined, and by defining 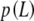Inline graphic as the distribution function of the lengths in our assays, we find:

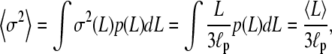graphic file with name M31.gif (19)

which yields

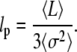graphic file with name M32.gif (20)

This is the formula we used to obtain an estimate of the persistence length 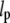Inline graphic from our data.

Microtubule elastic properties are state-dependent in Xenopus laevis egg extracts

Eq. 20 is only strictly valid if lp is independent of the filament length L. Since the statistics underlying Fig. 4, c and e, is based on microtubules with different filament lengths, the persistence lengths that were obtained in these situations represent average values that characterize the entire population of microtubules. Therefore, they can only be employed for a qualitative comparison of microtubule elasticity in different kinetic states.

The analysis of elasticity in the growth state (mean filament length 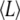Inline graphic = 24.3 ± 0.2 μm) yields an average persistence length lp = 1.7 ± 0.4 mm. The analysis of the g-pause- and s-pause-states (mean filament length 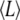Inline graphic = 25.3 ± 0.5 μm) yields an average persistence length lp = 2.1 ± 0.5 mm. The analysis of the filament length dependence on the persistence length (Fig. 4 d) predicts a difference of 0.1 mm in the average persistence lengths due to the shift of 1.0 μm of the centers of the microtubule length distributions. The measured difference of 0.4 mm in the average persistence lengths of growing and pausing microtubules hence suggests an additional dependence of the persistence length on the microtubule kinetic state. To investigate the relationship between elastic and dynamic properties of microtubules in more detail, we performed an analysis of the persistence length of growing microtubules with a categorization of the filaments according to their growth speed (Fig. S2 a in Data S1 for a speed step histogram). Our results indicate an inverse relationship between the persistence length and the microtubule growth speed (Fig. 2 b in Data S1). The persistence length decreases by almost 50% over the growth-speed regime 2–30 μm min−1. The observed trend is quantitatively consistent with the data obtained by Janson and Dogterom (49) for buffer-based in vitro measurements.

Next, we defined contour length intervals of 2.5 μm and 5 μm for a contour-length-resolved analysis of the microtubule's persistence length. The persistence length was then determined for each length interval individually (Fig. 4 d). The length intervals were chosen so that approximately the same number of microtubule contours contributed to each lp evaluation (n ≈ 230 per length interval). Error estimates were assigned conservatively (Data S1). To assess the statistical robustness of our analysis, the statistics of each length interval were reduced by a factor of 2 and the resulting persistence lengths were compared to those that were derived with the full statistics. The mean absolute deviation of persistence lengths between the complete and the control data was 10%, indicating that the analysis of lp was not influenced by artifacts arising from poor statistics (Data S1). The obtained persistence lengths range between lp = 0.7 ± 0.3 mm for a microtubule contour length of L = 13.0 ± 1.4 μm, and lp = 3.3 ± 0.5 mm for a microtubule contour length of L = 43.5 ± 1.4 μm (see also Table S2 in Data S1).

To obtain the persistence length limit for very long microtubules (L > 50 μm), a sigmoidal fit was applied (Fig. 4 d), as previously described (45):

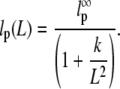graphic file with name M36.gif (21)

The constant k takes into account the microtubules' molecular structure and elastic moduli. The sigmoidal fit yields the persistence length limit lp,∞ = 5.2 ± 1.2 mm.

Previous studies of microtubule stiffness in buffer systems included active elastic deformation by atomic force microscopy (50), optical tweezers (14,51), hydrodynamic flow (15), or osmotic pressure (52); analyzed thermal fluctuations of the shape of microtubules (53,54), or investigated the first bending mode of clamped microtubules (15,45). Notably, the microtubule persistence length values reported in the literature are scattered across a range of 1–8 mm. It has been shown that the average persistence length depends on the assembly kinetics, the polymerization temperature, and the initial tubulin concentration (55), and several authors have provided evidence for an influence of contour length on microtubule stiffness (45,56).

In our study, the elastic properties were measured from the three-dimensional thermal fluctuations of dynamic microtubules in the physiologically relevant context of Xenopus laevis egg extracts. The persistence lengths for different microtubule contour lengths were obtained from the combined contour statistics in small length intervals. The results are in agreement with two-dimensional studies of microtubules in buffer solution (e.g., Pampaloni et al. (45)). The persistence length limit of 5.2 ± 1.2 mm for very long unstabilized microtubules in three dimensions is consistent with values previously reported for taxol-stabilized microtubules in two dimensions (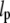Inline graphic = 5.2 ± 0.2 mm (53), 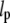Inline graphic = 6.3 ± 0.8 mm (45)).

We measured the microtubule persistence length in different kinetic states as classified by the four-state model and obtained a difference of 24% in the persistence lengths of pausing and growing microtubules. It is important to note that the slight difference in microtubule length distribution in the two subpopulations accounts for only one-fourth of this deviation. The molecular origin of the remaining difference is unknown but could be related to MAP activity, which has also been suggested by other studies of microtubule elasticity (e.g., Felgner et al. (51)). In particular, MAPs have been shown previously to strongly modulate the microtubules' properties by binding to the filaments and thereby altering the free energy stored in the microtubule lattice.

Since our observations indicate a global relationship between microtubule dynamics and microtubule mechanics, it is interesting to speculate on the possible implications in the context of a cell. A reduced stiffness of dynamic microtubules would support a “search-and-capture” process of metaphase microtubules (57,58). Dynamic microtubules would explore a larger volume in the cell not only due to the change in filament length, but also because of an increased flexibility. A brief calculation gives a rough idea of the expected effect: we approximate the small tip deflections as movements on a spherical surface. With a reduction of 19% in the persistence length in the growth state (1.7 mm vs. 2.1 mm), the widths of the Gaussian distributions of the tip's coordinates increase by ∼11% (along both angular dimensions) according to Eq. 16. In conclusion, Eq. 16 predicts an ∼23% total increase of the area on the sphere's surface explored by the plus-end tip.

Complementarily, a larger stiffness of nondynamic microtubules might increase the precision of microtubule-aided transport processes in the cell.

Although we have established three-dimensional experiments that provide insights into the relationship between the mechanics and dynamics of microtubules, further investigations of microtubule elasticity and dynamics in three dimensions are necessary to understand whether and how MAPs might alter microtubule elasticity in cell extracts and in vivo. When we have gained more insight into these mechanisms, it should eventually become possible to set up a unified model of microtubule behavior that describes both kinetic and mechanical properties of the filament.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

Supplementary Material

[Supplement]
107.128223_index.html (761B, html)

Acknowledgments

We thank Klaus Greger for implementing the microscope's subsystem for high-resolution SPIM experiments. We thank Jan Huisken and James Swoger for many helpful comments on SPIM and three-dimensional image processing. We very much appreciate the excellent advice on Xenopus egg extract handling by Maiwen Caudron, Iva Kronja, and Stefanie Kandels-Lewis, and the discussions about microtubule dynamic instability in egg extracts with Eric Karsenti. We thank Henrik Flyvbjerg for discussions and comments on the GTP-cap model of microtubule stabilization. We thank Holger Kress, Damian Brunner, Thomas Surrey, Michael Knop, François Nédélec, and Eric Karsenti for valuable comments on the manuscript.

P.J.K. developed the sample preparation in PTFE cylinders, performed the experiments on microtubule dynamic instability and microtubule elasticity, developed the processing software for three-dimensional microtubule data analysis, elaborated the kinetic four-state model of microtubule dynamic instability, and wrote most parts of this article. F.P. trained P.J.K. in the biochemical aspects of the experiments, contributed to project planning, and participated in manuscript preparation. G.L. developed the theoretical description of microtubule tip deflection distributions in three dimensions and participated in manuscript preparation. E.H.K.S. elaborated, outlined, and supervised the project, and participated in all stages of manuscript preparation.

G.L. acknowledges financial support from the Italian Ministry for University and Research (MIUR) under the scheme PRIN2005 No. 2005027330_002.

Francesco Pampaloni and Gianluca Lattanzi contributed equally to this work.

Editor: Gerard Marriott.

References

  • 1.Luykx, P. 1970. Cellular mechanisms of chromosome distribution. Int. Rev. Cytol. 2:1–173. [PubMed] [Google Scholar]
  • 2.Cohen, W. D., and L. I. Rebhun. 1970. An estimate of the amount of microtubule protein in the isolated mitotic apparatus. J. Cell Sci. 6:159–176. [DOI] [PubMed] [Google Scholar]
  • 3.Desai, A., and T. J. Mitchison. 1997. Microtubule polymerization dynamics. Annu. Rev. Cell Dev. Biol. 13:83–117. [DOI] [PubMed] [Google Scholar]
  • 4.Schliwa, M., and G. Woehlke. 2003. Molecular motors. Nature. 422:759–765. [DOI] [PubMed] [Google Scholar]
  • 5.Wittmann, T., and C. M. Waterman-Storer. 2001. Cell motility: can Rho GTPases and microtubules point the way? J. Cell Sci. 114:3795–3803. [DOI] [PubMed] [Google Scholar]
  • 6.Rodriguez, O. C., A. W. Schaefer, C. A. Mandato, P. Forscher, W. M. Bement, and C. M. Waterman-Storer. 2003. Conserved microtubule-actin interactions in cell movement and morphogenesis. Nat. Cell Biol. 5:599–609. [DOI] [PubMed] [Google Scholar]
  • 7.Tilney, L. G., and J. R. Gibbins. 1969. Microtubules in the formation and development of the primary mesenchyme in Arbacia punctulata. II. An experimental analysis of their role in development and maintenance of cell shape. J. Cell Biol. 41:227–250. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 8.Handel, M. A., and L. E. Roth. 1971. Cell shape and morphology of the neural tube: implications for microtubule function. Dev. Biol. 25:78–95. [DOI] [PubMed] [Google Scholar]
  • 9.Mitchison, T., and M. Kirschner. 1984. Dynamic instability of microtubule growth. Nature. 312:237–242. [DOI] [PubMed] [Google Scholar]
  • 10.Brittle, A. L., and H. Ohkura. 2005. Mini spindles, the XMAP215 homologue, suppresses pausing of interphase microtubules in Drosophila. EMBO J. 24:1387–1396. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Tirnauer, J. S., S. Grego, E. D. Salmon, and T. J. Mitchison. 2002. EB1-microtubule interactions in Xenopus egg extracts: role of EB1 in microtubule stabilization and mechanisms of targeting to microtubules. Mol. Biol. Cell. 13:3614–3626. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Tirnauer, J. S., E. D. Salmon, and T. J. Mitchison. 2004. Microtubule plus-end dynamics in Xenopus egg extract spindles. Mol. Biol. Cell. 15:1776–1784. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 13.Keller, P. J., F. Pampaloni, and E. H. Stelzer. 2007. Three-dimensional preparation and imaging reveal intrinsic microtubule properties. Nat. Methods. 4:843–846. [DOI] [PubMed] [Google Scholar]
  • 14.Felgner, H., R. Frank, and M. Schliwa. 1996. Flexural rigidity of microtubules measured with the use of optical tweezers. J. Cell Sci. 109:509–516. [DOI] [PubMed] [Google Scholar]
  • 15.Venier, P., A. C. Maggs, M. F. Carlier, and D. Pantaloni. 1994. Analysis of microtubule rigidity using hydrodynamic flow and thermal fluctuations. J. Biol. Chem. 269:13353–13360. [PubMed] [Google Scholar]
  • 16.Mickey, B., and J. Howard. 1995. Rigidity of microtubules is increased by stabilizing agents. J. Cell Biol. 130:909–917. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 17.Murray, A. W. 1991. Cell cycle extracts. Methods Cell Biol. 36:581–605. [PubMed] [Google Scholar]
  • 18.Parsons, S. F., and E. D. Salmon. 1997. Microtubule assembly in clarified Xenopus egg extracts. Cell Motil. Cytoskeleton. 36:1–11. [DOI] [PubMed] [Google Scholar]
  • 19.Keller, P. J., F. Pampaloni, and E. H. Stelzer. 2006. Life sciences require the third dimension. Curr. Opin. Cell Biol. 18:117–124. [DOI] [PubMed] [Google Scholar]
  • 20.Huisken, J., J. Swoger, F. Del Bene, J. Wittbrodt, and E. H. Stelzer. 2004. Optical sectioning deep inside live embryos by selective plane illumination microscopy. Science. 305:1007–1009. [DOI] [PubMed] [Google Scholar]
  • 21.Greger, K., J. Swoger, and E. H. Stelzer. 2007. Basic building units and properties of a fluorescence single plane illumination microscope. Rev. Sci. Instrum. 78:023705. [DOI] [PubMed] [Google Scholar]
  • 22.Arnal, I., E. Karsenti, and A. A. Hyman. 2000. Structural transitions at microtubule ends correlate with their dynamic properties in Xenopus egg extracts. J. Cell Biol. 149:767–774. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Mandelkow, E. M., E. Mandelkow, and R. A. Milligan. 1991. Microtubule dynamics and microtubule caps: a time-resolved cryo-electron microscopy study. J. Cell Biol. 114:977–991. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Chretien, D., S. D. Fuller, and E. Karsenti. 1995. Structure of growing microtubule ends: two-dimensional sheets close into tubes at variable rates. J. Cell Biol. 129:1311–1328. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 25.Chretien, D., I. Jainosi, J. C. Taveau, and H. Flyvbjerg. 1999. Microtubule's conformational cap. Cell Struct. Funct. 24:299–303. [DOI] [PubMed] [Google Scholar]
  • 26.Caplow, M., R. Ruhlen, J. Shanks, R. A. Walker, and E. D. Salmon. 1989. Stabilization of microtubules by tubulin-GDP-Pi subunits. Biochemistry. 28:8136–8141. [DOI] [PubMed] [Google Scholar]
  • 27.Caplow, M., and J. Shanks. 1996. Evidence that a single monolayer tubulin-GTP cap is both necessary and sufficient to stabilize microtubules. Mol. Biol. Cell. 7:663–675. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Walker, R. A., N. K. Pryer, and E. D. Salmon. 1991. Dilution of individual microtubules observed in real time in vitro: evidence that cap size is small and independent of elongation rate. J. Cell Biol. 114:73–81. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Davis, A., C. R. Sage, C. A. Dougherty, and K. W. Farrell. 1994. Microtubule dynamics modulated by guanosine triphosphate hydrolysis activity of β-tubulin. Science. 264:839–842. [DOI] [PubMed] [Google Scholar]
  • 30.Tournebize, R., A. Popov, K. Kinoshita, A. J. Ashford, S. Rybina, A. Pozniakovsky, T. U. Mayer, C. E. Walczak, E. Karsenti, and A. A. Hyman. 2000. Control of microtubule dynamics by the antagonistic activities of XMAP215 and XKCM1 in Xenopus egg extracts. Nat. Cell Biol. 2:13–19. [DOI] [PubMed] [Google Scholar]
  • 31.Heald, R. 2000. A dynamic duo of microtubule modulators. Nat. Cell Biol. 2:E11–E12. [DOI] [PubMed] [Google Scholar]
  • 32.Popov, A. V., A. Pozniakovsky, I. Arnal, C. Antony, A. J. Ashford, K. Kinoshita, R. Tournebize, A. A. Hyman, and E. Karsenti. 2001. XMAP215 regulates microtubule dynamics through two distinct domains. EMBO J. 20:397–410. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Verde, F., M. Dogterom, E. Stelzer, E. Karsenti, and S. Leibler. 1992. Control of microtubule dynamics and length by cyclin A- and cyclin B-dependent kinases in Xenopus egg extracts. J. Cell Biol. 118:1097–1108. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 34.Hill, T. L. 1984. Introductory analysis of the GTP-cap phase-change kinetics at the end of a microtubule. Proc. Natl. Acad. Sci. USA. 81:6728–6732. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 35.Tran, P. T., R. A. Walker, and E. D. Salmon. 1997. A metastable intermediate state of microtubule dynamic instability that differs significantly between plus and minus ends. J. Cell Biol. 138:105–117. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 36.Janosi, I. M., D. Chretien, and H. Flyvbjerg. 1998. Modeling elastic properties of microtubule tips and walls. Eur. Biophys. J. 27:501–513. [DOI] [PubMed] [Google Scholar]
  • 37.Nogales, E., S. G. Wolf, and K. H. Downing. 1998. Structure of the αβ tubulin dimer by electron crystallography. Nature. 391:199–203. [DOI] [PubMed] [Google Scholar]
  • 38.Shirasu-Hiza, M., P. Coughlin, and T. Mitchison. 2003. Identification of XMAP215 as a microtubule-destabilizing factor in Xenopus egg extract by biochemical purification. J. Cell Biol. 161:349–358. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 39.Gliksman, N. R., R. V. Skibbens, and E. D. Salmon. 1993. How the transition frequencies of microtubule dynamic instability (nucleation, catastrophe, and rescue) regulate microtubule dynamics in interphase and mitosis: analysis using a Monte Carlo computer simulation. Mol. Biol. Cell. 4:1035–1050. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 40.Komarova, Y. A., I. A. Vorobjev, and G. G. Borisy. 2002. Life cycle of MTs: persistent growth in the cell interior, asymmetric transition frequencies and effects of the cell boundary. J. Cell Sci. 115:3527–3539. [DOI] [PubMed] [Google Scholar]
  • 41.Shelden, E., and P. Wadsworth. 1993. Observation and quantification of individual microtubule behavior in vivo: microtubule dynamics are cell-type specific. J. Cell Biol. 120:935–945. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Tirnauer, J. S., E. O'Toole, L. Berrueta, B. E. Bierer, and D. Pellman. 1999. Yeast Bim1p promotes the G1-specific dynamics of microtubules. J. Cell Biol. 145:993–1007. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 43.Rusan, N. M., C. J. Fagerstrom, A. M. Yvon, and P. Wadsworth. 2001. Cell cycle-dependent changes in microtubule dynamics in living cells expressing green fluorescent protein-α tubulin. Mol. Biol. Cell. 12:971–980. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 44.Schek 3rd, H. T., M. K. Gardner, J. Cheng, D. J. Odde, and A. J. Hunt. 2007. Microtubule assembly dynamics at the nanoscale. Curr. Biol. 17:1445–1455. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 45.Pampaloni, F., G. Lattanzi, A. Jonas, T. Surrey, E. Frey, and E. L. Florin. 2006. Thermal fluctuations of grafted microtubules provide evidence of a length-dependent persistence length. Proc. Natl. Acad. Sci. USA. 103:10248–10253. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 46.Kratky, O., and G. Porod. 1949. X-ray examination of long polymer chains in solution. Recueil des Travaux Chimiques des Pays-Bas. 68:1106–1123. [Google Scholar]
  • 47.Saito, N., K. Takahashi, and Y. Yunoki. 1967. The statistical mechanical theory of stiff chains. J. Phys. Soc. Jpn. 22:219–226. [Google Scholar]
  • 48.Benetatos, P., and E. Frey. 2003. Depinning of semiflexible polymers. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 67:051108. [DOI] [PubMed] [Google Scholar]
  • 49.Janson, M. E., and M. Dogterom. 2004. A bending mode analysis for growing microtubules: evidence for a velocity-dependent rigidity. Biophys. J. 87:2723–2736. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 50.Vinckier, A., C. Dumortier, Y. Engelborghs, and L. Hellemans. 1996. Dynamical and mechanical study of immobilized microtubules with atomic force microscopy. J. Vac. Sci. Technol. B. 14:1427–1431. [Google Scholar]
  • 51.Felgner, H., R. Frank, J. Biernat, E. M. Mandelkow, E. Mandelkow, B. Ludin, A. Matus, and M. Schliwa. 1997. Domains of neuronal microtubule-associated proteins and flexural rigidity of microtubules. J. Cell Biol. 138:1067–1075. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 52.Needleman, D. J., M. A. Ojeda-Lopez, U. Raviv, K. Ewert, H. P. Miller, L. Wilson, and C. R. Safinya. 2005. Radial compression of microtubules and the mechanism of action of taxol and associated proteins. Biophys. J. 89:3410–3423. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 53.Gittes, F., B. Mickey, J. Nettleton, and J. Howard. 1993. Flexural rigidity of microtubules and actin filaments measured from thermal fluctuations in shape. J. Cell Biol. 120:923–934. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 54.Kurz, J. C., and R. C. Williams, Jr. 1995. Microtubule-associated proteins and the flexibility of microtubules. Biochemistry. 34:13374–13380. [DOI] [PubMed] [Google Scholar]
  • 55.Janson, M. E., and M. Dogterom. 2004. Scaling of microtubule force-velocity curves obtained at different tubulin concentrations. Phys. Rev. Lett. 92:248101. [DOI] [PubMed] [Google Scholar]
  • 56.Kis, A., S. Kasas, B. Babic, A. J. Kulik, W. Benoit, G. A. Briggs, C. Schonenberger, S. Catsicas, and L. Forro. 2002. Nanomechanics of microtubules. Phys. Rev. Lett. 89:248101. [DOI] [PubMed] [Google Scholar]
  • 57.Holy, T. E., and S. Leibler. 1994. Dynamic instability of microtubules as an efficient way to search in space. Proc. Natl. Acad. Sci. USA. 91:5682–5685. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 58.Wollman, R., E. N. Cytrynbaum, J. T. Jones, T. Meyer, J. M. Scholey, and A. Mogilner. 2005. Efficient chromosome capture requires a bias in the ‘search-and-capture’ process during mitotic-spindle assembly. Curr. Biol. 15:828–832. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplement]
107.128223_index.html (761B, html)
107.128223_1.pdf (337.9KB, pdf)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES