Developing Polarized Protein-Specific Charges for Protein Dynamics: MD Free Energy Calculation of pK_a Shifts for Asp²⁶/Asp²⁰ in Thioredoxin

Abstract

Ab initio quantum mechanical calculation of protein in solution is carried out to generate polarized protein-specific charge(s) (PPC) for molecular dynamics (MD) stimulation of protein. The quantum calculation of protein is made possible by developing a fragment-based quantum chemistry approach in combination with the implicit continuum solvent model. The computed electron density of protein is utilized to derive PPCs that represent the polarized electrostatic state of protein near the native structure. These PPCs are atom-centered like those in the standard force fields and are thus computationally attractive for molecular dynamics simulation of protein. Extensive MD simulations have been carried out to investigate the effect of electronic polarization on the structure and dynamics of thioredoxin. Our study shows that the dynamics of thioredoxin is stabilized by electronic polarization through explicit comparison between MD results using PPC and AMBER charges. In particular, MD free-energy calculation using PPCs accurately reproduced the experimental value of pK_a shift for ionizable residue Asp²⁶ buried inside thioredoxin, whereas previous calculations using standard force fields overestimated pK_a shift by twice as much. Accurate prediction of pK_a shifts by rigorous MD free energy simulation for ionizable residues buried inside protein has been a significant challenge in computational biology for decades. This study presented strong evidence that electronic polarization of protein plays an important role in protein dynamics.

INTRODUCTION

Molecular dynamics (MD) simulations of biological systems are now routine exercises in computational biology. Such computational advances have had a huge impact on our ability to understand protein structure and dynamics, protein-ligand binding, protein-protein interaction, drug design, etc. These large-scale MD simulations are made possible by the availability of force fields (FFs), which provide simple and fast evaluation of molecular interactions in biological systems. A great deal of progress has been made over the past decades in the development of molecular mechanics FFs for use in biological simulations (1–6). When parameters are extensively fitted to experimental data, accurate models can be produced. However, for the overwhelming majority of important biological applications, only a limited amount of relevant experimental data is available. Applications of the current molecular mechanics force fields have given decent pictures of the details of atomic motions and energetic interactions, but the level of quantitative accuracy is uncertain and in many cases, not adequate for reliable predictive studies.

An important component of the interaction in proteins is the electrostatic interaction, which plays a significant role in protein structure and function (7–11). Processes such as protein folding, protein-ligand binding, protein-protein interaction, electron transfer, proton binding and release, enzyme reaction, etc. are largely driven by electrostatic interactions. In particular, proton binding is a pH-dependent process and is strongly influenced by electrostatic interactions with the protein and the local environment (12–14). It is well known that the electrostatic interaction between protein side chains depends not only on their distances but also on their locations in the protein and their local solvent environment. In proton-binding, the protein and solvent undergo dielectric relaxation involving electronic polarization and displacement of atomic groups. As is understood, the local electrostatic environment inside a protein is inhomogeneous and hydrophobic, which is generally less favorable for ionization (15). Thus, ionizable (or charged) residues in the interior of proteins can have substantial pK_a shifts compared to those on the surfaces of proteins or isolated amino acids in solution (16).

Current standard force fields, e.g., CHARMM and AMBER, are amino-acid-specific and therefore very portable. Despite great success in application of the standard FFs, there are fundamental limitations in their applications. Specifically, these FFs are amino-acid-specific or mean-field-like and therefore fail to give accurate representation of the electrostatics of the specific protein environment which is highly inhomogeneous and protein-specific. For example, two amino acids of the same type in the same or different proteins should have quite different charge status due to their different electrostatic environments. Thus, using the same set of charges for them is obviously inadequate. In summary, the current amino-acid-based FFs are incapable of describing the polarization state of a particular protein structure, e.g., native protein structure. To overcome this fundamental deficiency of the standard FFs, efforts have been made to develop polarizable force-field models for peptides and proteins (17,18). The polarizable FFs are theoretically attractive but their practical application is much more complicated than for the standard FFs. Consequently, simulations of biomolecular systems with polarizable FFs are still uncommon (19) and uncertainties regarding the accuracy and validity of the underlying theoretical models used to derive polarizable FFs remain (20).

In this article, we present an alternative force field containing polarized protein-specific charges for MD study of proteins. The polarized protein-specific charge (PPC) builds protein polarization into the atomic charges and is therefore computationally attractive for standard MD simulation without any dynamical complications. The PPC is not “polarizable” per se, but it is derived from first-principle quantum solvation calculation of protein in the native (or a given) structure. Thus, PPCs correctly represent the electronically polarized state of the protein and therefore provide accurate electrostatic interaction near the native structure. In our approach, the quantum chemistry calculation of protein solvation is made possible by combining a recently developed fragment-based scheme, molecular fractionation with conjugate caps (MFCC), with a continuum-solvent model. In this article, we employ linearized Poisson-Boltzmann method (21,22) to solve the self-consistent reaction-field equation coupled with quantum chemistry calculation of the solute using the MFCC scheme (23–27). The converged electron density of protein fragment (amino acid) is fitted to generate partial charges for every amino acid in the protein using the RESP method (28,29). The resulting fitted atomic partial charges are protein-specific and they correctly represent the polarized electronic state of the protein in the native (or other given) structure. Because the PPC is atom-centered and maintains the same simplicity as the standard charges in AMBER, it can be easily applied in MD simulation without any additional complication. Thus, we expect PPCs to provide much improved electrostatic interactions in MD simulation of protein near its native structure, both in structure and dynamics. For application of the PPC in MD simulation, one simply replaces the standard charges from the AMBER force field by PPC while keeping the rest of the force parameters intact.

To study the possible effect of PPCs in MD simulation of proteins, we carried out a series of MD studies to investigate various structural and dynamical properties of thioredoxin. The new MD results using PPCs are explicitly compared with those obtained from the corresponding MD studies but using the AMBER charges. In particular, MD free-energy simulation is carried out to predict the pK_a shift of thioredoxin for buried Asp²⁶. Previous MD free energy calculations using both AMBER and CHARMM give pK_a shifts that are twice as large as the experimental value (30). To allow direct comparison with those results, we follow faithfully the computational methods and procedures in Simonson et al. (30) to calculate pK_a shifts except that the standard AMBER charges are replaced by our calculated PPC for thioredoxin. This shall eliminate any possible dynamical uncertainties in the comparison of results.

THEORETICAL APPROACH

In the continuum-solvent model, the solute (protein) is represented by a charge distribution ρ(r) embedded in a cavity surrounded by a polarizable medium with dielectric constant ε. The solute charge distribution ρ(r) polarizes the dielectric medium and creates a reaction field which acts back to polarize the solute until equilibrium is reached. The reaction field acting on the solute can be effectively represented by that of induced charges on the cavity surface according to the classical electrostatic theory. By discretizing the induced charges on the surface of the cavity and iteratively solving the quantum chemistry equation for the solute in an external reaction field created by the surface charges, one obtains the popular PCM method (31) as recently generalized to protein solvation (27,32). However, for large proteins, the PCM model requires many discrete surface charges and thus makes the solution of linear equation difficult computationally. In the current approach, we numerically solve the Poisson-Boltzmann (PB) equation to obtain the reaction field as was done before by other researchers (22,34). This avoids the solution of large linear equations and is computationally more attractive for large proteins.

The basic procedures in fitting atomic charges of protein in our approach can be described as follows: First, gas phase calculation of protein is performed with the MFCC approach to obtain initial electron density of the protein for the given structure as described in earlier publications (24). The calculated electron density is used to fit atomic charges using the RESP program (35). The charge-fitting philosophy used here was the same as that used in the AMBER force field and this makes the guarantee that the PPC was consistent with other parameters of the AMBER force field. Solution of the PB equation is then carried out to obtain the reaction field from which to generate discrete surface charges on the cavity surface.

The coupling of MFCC/RESP charge-fitting method for protein with a Poison-Boltzmann continuum solvent should provide accurate estimates of the solvation free energies of proteins in water. Partial charges on each atom of the protein generated from the MFCC/RESP procedure were passed to the PB solver DELPHI (36) to determine the self-consistent reaction field. A set of induced surface charges q^ind on the dielectric boundary was derived that represent reaction field effects of solvent molecules. The dielectric solute/solvent boundary was defined by AMBER van der Waals radii (37) for atoms of solute molecule with a probe radius of 1.4 Å. The internal dielectric constant, denoted as ε_solute, was set to unity, for molecular polarizability is explicitly included in quantum mechanical calculation. The solvent dielectric constant, denoted as ε_solvent, was set to 80. Grid density was set to 4.0 grids/Å. Surface charges were then added as background charges in the next QM calculation for each capped fragment (CF). As mentioned above, partial charges of the protein and the screened surface charges polarize each other until converge was reached. The cycle stops only when the dipole of the protein and the surface charges both converge to within a certain numerical accuracy.

The electrostatic solvation free energy can be divided into two terms: solute polarization energy (G_pol) and polarized reaction field energy (G_es),

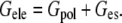(1)

In the DELPHI program, the latter term can be expressed as

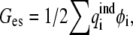(2)

where 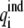is the i^th induced charge on the dielectric boundary, and φ_i is the electrostatic potential on position of i^th induced charge. In the MFCC approximation, the solute polarization energy is given by

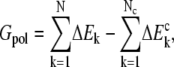(3)

where the polarization energies of individual fragment ΔE_k and conjugate cap 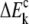are given, respectively, by Mei et al. (27), as

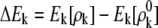(4)

and

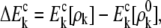(5)

where 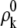and ρ_k stand for electron density distribution of each fragment or conjugate cap in vacuum and in solvent, respectively.

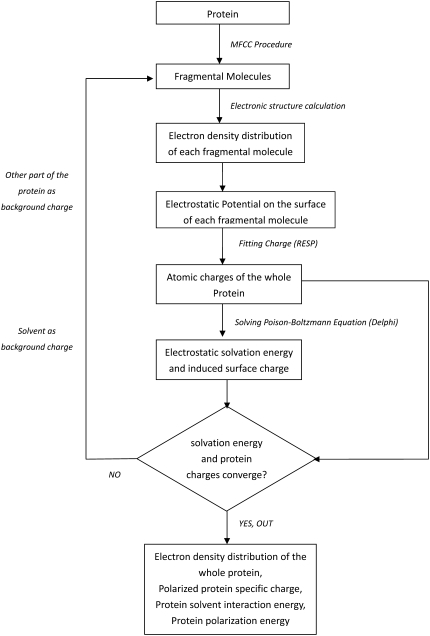
The procedure to generate PPCs can be understood easily from the flow chart in Fig. 1. The quantum chemistry calculation of electron density of individual protein fragment is performed at the level of B3LYP/6-31G* for results reported in this article.

FIGURE 1.

The flow chart of the MFCC-PB computational protocol.

RESULTS AND DISCUSSION

Solvation and polarization of protein

The MFCC-PB computational protocol described in the previous section needs to be extensively tested numerically to validate its efficacy. In particular, we need to examine the effect of protein polarization as represented by PPC on protein solvation. We performed benchmark studies to examine the contribution of electronic polarization on solvation energy for a number of protein systems. The calculated contribution of electrostatic solvation energy for a number of protein systems is listed in Table 1. For comparison, results calculated from the previous calculation using the MFCC-CPCM method were also listed in the table. Different from classical PB or generalized Born (GB) methods, solute polarization energy is quite significant in the calculated electrostatic solvation free energy. Our calculation shows that this term contributes 7 ∼ 19% to the total electrostatic solvation energy as shown in Table 1. This big part of polarization energy indicates that inclusion of the polarization effect in the current force field is needed.

TABLE 1.

Comparison of electrostatic solvation free energies from MFCC-FDPB calculation and MFCC-CPCM (kcal/mol)

		MFCC-FDPB				MFCC-CPCM*
Peptide	PDB ID	Ges	Gpol	Gele†	Gpol/Gele	Ges	Gpol	Gele†
Amyloid	1AMC	−1013.13	163.42	−849.70	19.23%	−991.16	105.15	−886.01
BPTI	1BPI	−1405.71	101.85	−1303.85	7.81%	−1420.23	87.52	−1332.71
Calbindin	1CDN	−2533.75	352.35	−2181.41	16.15%	−2402.94	143.32	−2259.62
Crambin	1CBN	−392.72	47.59	−345.13	13.79%	−406.10	44.58	−361.52
Lysozyme	2BLX	−2112.25	224.06	−1888.19	11.87%	−2034.35	146.64	−1887.71
RP71955	1RPB	−289.25	32.94	−256.30	12.85%	−303.74	36.14	−267.60
Ubiquitin	1UBQ	−1129.00	138.57	−990.44	13.99%	−1091.45	94.43	−997.02

^*See Mei et al. (27).

^†G_ele = G_es + G_pol.

To investigate the effect of protein polarization on various protein properties, we also compare calculated dipole moments of protein in solution calculated from the current PPC with those from AMBER03 force field. Since most proteins have a nonzero net charge, and the calculated dipole moment depends on the placement of a charged entity within the coordinate system, so the protein is first centered to its charge center. 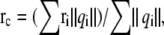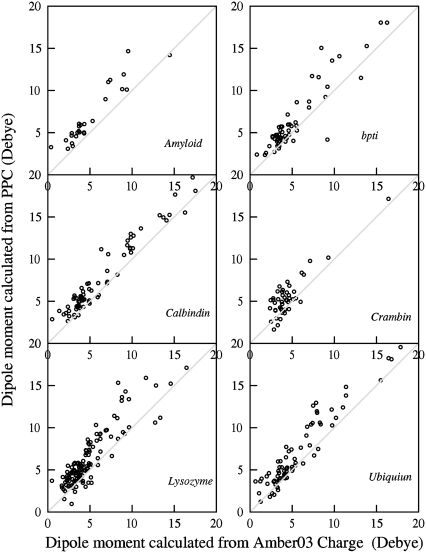The charge center is defined as in which r_i is the original coordinate of the i^th atom in the protein, and q_i is its partial charge. The dipole of the entire protein is then given by 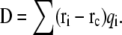To examine more detailed local electrostatic environment, we calculated dipole moments for individual residues of proteins. Fig. 2 shows plots of dipole moment of individual residues calculated from PPC versus that from AMBER03 for a number of protein systems. The comparison shows that dipoles of most residues calculated from PPCs are generally larger than those from the AMBER charges. This may indicate the fact that more polarization of the residues is accounted for in the MFCC-PB charges.

FIGURE 2.

Comparison of dipole moments of individual residues calculated from PPC and those from AMBER03 charge for several protein systems.

Protein-specific atomic charges

Since the MFCC-PB charges correctly describe the electrostatic polarization of the protein, partial charges on the same type of amino acid but in different locations of the protein are generally different as expected. Partial charges on a particular residue are determined by its specific conformation and chemical environment due to other residues of the protein. To illustrate this feature, we listed some partial charges of lysozyme in Table 2. As in lysozyme, we find that charges on the same type of amino acid differ a lot from each other. For examples, the value of atomic charge ranges from −0.083 to −0.642 for backbone atom N in ASP, from −0.727 to −0.556 for backbone atom O in Ser, and from 0.025 to 0.304 for atom CG1 in Ile. This is the most important feature of the PPC, which is different from the standard amino-acid-based force fields with the same fixed atomic charges for a given residue.

TABLE 2.

Some partial charges on lysozyme calculated by MFCC-FDPB

Atom*	Residue	Charge	Atom*	Residue	Charge	Atom*	Residue	Charge
N	Asp18	−0.414	O	Ser24	−0.603	CG1	Ile55	0.024
N	Asp48	−0.082	O	Ser50	−0.727	CG1	Ile58	0.165
N	Asp52	−0.641	O	Ser72	−0.588	CG1	Ile78	0.304
N	Asp66	−0.433	O	Ser85	−0.582	CG1	Ile88	0.024
N	Asp87	−0.309	O	Ser86	−0.604	CG1	Ile98	0.137
N	Asp101	−0.510	O	Ser91	−0.657	CG1	Ile124	0.063
N	Asp119	−0.484	O	Ser100	−0.604
		−0.558†			−0.580†			0.022†

^*Atom name in PDB nomenclature.

^†AMBER03 charge.

Calculations of pK_a shifts for Asp²⁶/Asp²⁰ in thioredoxin

Although standard amino-acid-based partial charge model has worked well in modeling many of the macroscopic properties of proteins in MD simulation, it is expected to have difficulties when simulating properties that are more sensitive to local electrostatic environment. This is because the standard force-field charges are mean-field-like and they do not contain protein polarization and other protein-specific electrostatic information described above. For example, accurate prediction of pK_a shifts for buried residues in proteins is a challenging problem in current MD simulation (30). Accurate calculation of pK_a shifts is crucial for us to understand the mechanism of acid-base catalysis in enzymes. Activity of such enzymes requires that the catalytic residues exist in the appropriate protonation state. A popular approach used in pK_a calculation is based on solving the PB equation in which the solvent is treated as a continuum dielectric medium (38–40). The PB approach is a mean-field theory and can give useful insight for some simple cases. However, the PB approach fails in more complicated situations because it is not a microscopic model and therefore could not account for detailed molecular processes. To accurately predict the pK_a shift, one needs to correctly account for molecular factors affecting the proton-binding process. Thus, microscopic methods in which water molecules are explicitly included are needed to correctly predict pK_a shift from first principles. However, some of the previous attempts using microscopic methods failed to give accurate prediction of pK_a shift (30,41–43).

A recent molecular dynamics free energy (MDFE) study by Simonson et al. to calculate pK_a shift for Asp²⁶ in Thioredoxin demonstrated the problems with the current standard AMBER and CHARMM force fields. The results from the rigorous MDFE simulations with both force fields and from different runs all overestimate the pK_a shift of Asp²⁶ by ∼4–5 kcal/mol (30). The MDFE calculation of pK_a by Simonson et al. is perhaps the most rigorous and extensive study so far and the results can serve as a benchmark for the system being studied. Simonson et al. concluded that the problem must arise in part from systematic errors in the force fields employed (30). In this article, the same rigorous MDFE procedures of Simonson et al. (30) are followed to calculate the pK_a shifts for buried Asp²⁶ and surface-exposed Asp²⁰ but using the new PPC described previously in this article.

In MDFE calculation, the thermodynamic integration approach is employed in which the interaction potential is defined by

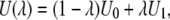(6)

where U₀ and U₁ are energy functions corresponding, respectively, to the protonated and deprotonated states. The parameter λ varies from 0 to 1 representing the system going from the initial (protonated) to the final (deprotonated) state. During the perturbation process, only charges on the residue undergoing titration are changed. The free-energy derivative with respect to parameter λ is given by

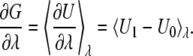(7)

Simulations for a series of values of λ are carried out and the free-energy change is constructed from integration over λ by Gaussian quadrature,

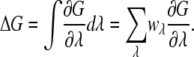(8)

The free energy shift is given by

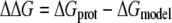(9)

and the corresponding shift of pK_a value is

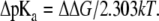(10)

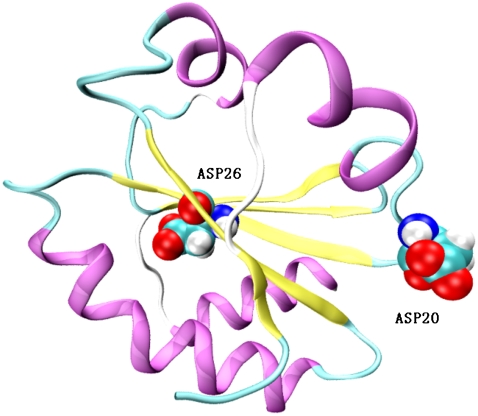
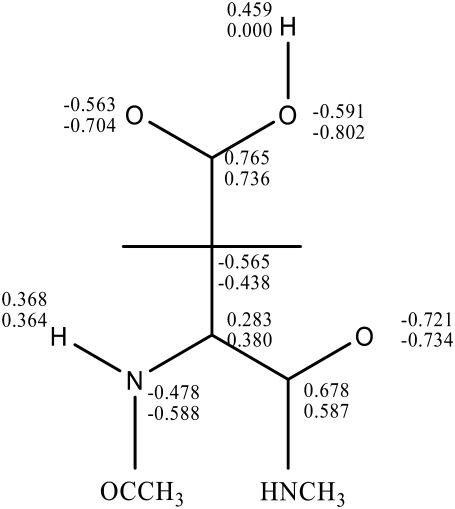
The numerical details of our MDFE simulation closely follow that of Simonson et al. (30). The NMR structure of thioredoxin (Protein Data Bank, i.e., PDB, code 1XOA; and see Fig. 3) is used as the initial structure. The simulations were performed with the AMBER program and explicit water model (TIP3P) with periodic boundary conditions is used. Firstly, the system was equilibrated under NPT ensembles with 500-ps runs at 298 K. The simulation is then continued in the NVE ensemble. SHAKE (44) was used to constrain covalent bonds connected to hydrogens. Long-range electrostatic interactions were treated by the particle-mesh Ewald method. The time step is one femtosecond. The model compound we used is aspartic acid with n-acetyl and n-methylamide blocking groups. Charge distributions in the protonated and ionized states are shown in Fig. 4.

FIGURE 3.

The NMR structure of thioredoxin (PDB code 1XOA) showing buried Asp²⁶ and surface-exposed Asp²⁰.

FIGURE 4.

Partial charges of the model compound (2n-acetyl 1-1 n-methyl-aspartic acid 1-amide) representing change between protonated (upper values) and deprotonated (lower values) states.

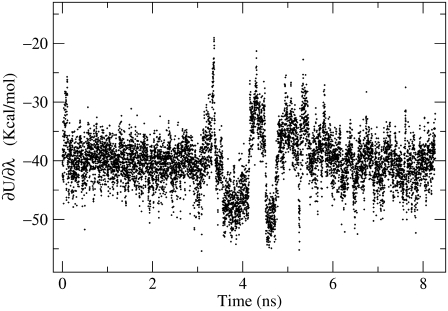
The calculation results for buried Asp²⁶ as well as the surface-exposed Asp²⁰ and the corresponding model system are given in Table 3. Our calculated free-energy shift for deprotonation of Asp²⁶ is 5.0 kcal/mol, which is very close to the experimental value of 4.8 kcal/mol. The simulation went all the way to 18 ns to provide adequate samplings for all the intermediate states of the protein. Fig. 5 shows the energy derivative of the potential with respect to the system parameter λ = 0.5 as a function of simulation time. This corresponds to a fictitious intermediate state between the protonated and d-protonated states of the Asp²⁶. For purpose of verification of our calculation, we also calculated the pK_a shift of Asp²⁰, a surface-exposed residue. Our simulation result gives a free-energy difference of 1.0 kcal/mol, which is in quite reasonable agreement with the experimental value of zero considering the statistical uncertainties of the simulation. Our result shows that using PPC, which correctly describes the polarized electrostatic environment surrounding the charged residue in the protein, can give accurate prediction of pK_a shift from rigorous MDFE simulations from first principles. In contrast, the same numerical simulation but using AMBER and CHARMM charges produced pK_a shifts that are twice as large as the experimental value in Simonson et al. (30).

TABLE 3.

Results from molecular dynamics free energy simulation for shifts of pK_a values of Asp²⁶ and Asp²⁰ in thioredoxin

	Model	Asp26	Asp20
Run length (ns)	6	18	18
∂G/∂λ(λ = 0.11270)	10.1	3.5	12.3
∂G/∂λ(λ = 0.5)	−43.6	−35.5	−42.5
∂G/∂λ(λ = 0.88279)	−101.8	−83.2	−102.3
ΔG	−44.9	−39.8	−43.9
ΔΔG		5.0	1.0
ΔΔG*		9.1	1.7
ΔΔG(expt)		4.8	0.0

All energies are in kcal/mol.

^*Result from Simonson et al. (30) using the AMBER force field.

FIGURE 5.

Time series of the free energy derivative 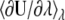with λ = 0.5.

To estimate the statistical error, we performed block averaging analysis in which each trajectory of 6-ns duration is divided into four blocks. The statistical uncertainty of the derivatives is estimated as twice the standard deviation of block averages. As we can see from Table 3, the statistical error of the free energy is ∼1 kcal/mol and the calculated theoretical value is within the statistical error bar from the experimental data for Asp²⁶ and Asp²⁰. Since our MDFE calculation is exactly the same as those in Simonson et al. (30) except that we replaced AMBER atomic charges by PPC while keeping all the other parameters in the force field, the different result must come from the effect of charges. In other words, the polarization effect of the protein contained in the PPC is responsible for the accurate prediction of pK_a shift in Asp²⁶. This result really demonstrated the important role that electronic polarization plays in delicate electrostatic interaction of protein.

The above result implies that the lack of electronic polarization may be a major culprit in some earlier MD free-energy calculations of pK_a shifts for ionizable residues buried in the interiors of proteins. Of course, more such calculations for different protein systems are needed to confirm this conclusion. There are of course other important dynamical effects that have been proposed to explain the failure of MD simulations of pK_a shifts. For example, Kato and Warshel have proposed that a major factor that determines the pK_a values of buried groups are the structural changes that take place when an internal group is ionized (42,45). However, the possibility of large structural reorganization is not easy to study computationally because of problems associated with limited MD samplings. For example, the calculation of pK_a shift for Glu⁶⁶ in staphylococcal nuclease has presented a huge challenge so far. Kato and Warshel developed a special overcharging approach to allow for more structural reorganization and obtained encouraging pKa shift for Glu⁶⁶ in staphylococcal nuclease (45). In reality, we expect that both electronic polarization and structural reorganization should play some roles in determining pK_a shifts for buried residues and they are likely intertwined with each other. We believe that the actual level of contribution from a particular effect will be case-dependent. Clearly, further computational study will be needed to clarify the situation.

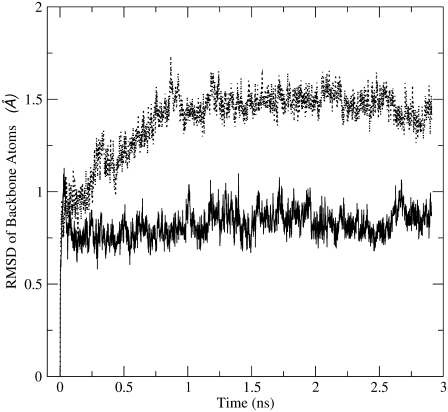
Because the PPC represents the polarized electrostatic state of the protein in a given (native) structure, we expect there will be some difference in structural details of the protein from MD simulations using PPC in comparison to mean-field-like charges as in AMBER. We performed further MD calculations of thioredoxin using both PPC and AMBER charges to compare structural details. First, we examine the characteristics of RMSD from two sets of MD simulations using, respectively, PPC and AMBER03. They obviously exhibit different characteristics as shown in Fig. 6. Since all the other parameters in the force field used in both calculations are the same except the charges, the result in Fig. 6 clearly shows the important effect of protein polarization on detailed protein dynamics, which is electrostatic in nature. Since the formation of internal hydrogen bonds in protein polarize the donors and acceptors, this polarization effect is better represented by PPCs than by AMBER charges. As a result, the hydrogen bonds in protein should generally be more stable during MD calculations using PPC and this may explain the different characteristics of RMSD in MD simulation shown in Fig. 6 for thioredoxin.

FIGURE 6.

RMSD of backbone atoms of thioredoxin as a function of MD simulation time using AMBER03 (upper red curve) and the PPC (lower black curve).

SUMMARY

We presented a new computational protocol for quantum mechanical calculation of protein in solution by combining a linear scaling fragmentation scheme for electronic structure of the protein and continuum dielectric model for the solvent in a self-consistent treatment. The computed electron density of protein in the native structure is employed to produce the polarized protein force field (charges). The derived protein-specific PPC correctly represents the polarized electrostatic state of protein near its native structure and can be easily employed in MD simulation of protein motion. Our computational study from MD simulation for thioredoxin revealed the following properties of PPC.

1. The PPC is protein-specific and thus correctly describes the polarized electrostatic state of the protein near the vicinity of native structure. The charges on the same type of residue are generally different depending on their specific local electrostatic environment. This is in contrast to the amino-acid-based charges that are mean-field-like and remain the same irrespective of the specific position in the protein.

2. By employing PPCs, MD free-energy simulation using thermodynamic integration approach accurately reproduces the experimental pK_a shift for buried Asp²⁶ in thioredoxin while the same calculations employing standard mean-field force fields of CHARMM and AMBER overestimate the pK_a shift by approximately twice as much.

It is also important to point out the limitation of the PPC. Since PPC is based on a given structure (native structure in most cases) of a protein, it may not be appropriate or advantageous to use it to describe structures far off from the given structure. Fortunately, most MD studies of proteins are meant to simulate protein motions near the vicinity of native structures and PPC should be very attractive in such computational studies of proteins.