Lipid Localization in Bacterial Cells through Curvature-Mediated Microphase Separation

Abstract

Although many proteins are known to localize in bacterial cells, for the most part our understanding of how such localization takes place is limited. Recent evidence that the phospholipid cardiolipin localizes to the poles of rod-shaped bacteria suggests that targeting of some proteins may rely on the heterogeneous distribution of membrane lipids. Membrane curvature has been proposed as a factor in the polar localization of high-intrinsic-curvature lipids, but the small size of lipids compared to the dimensions of the cell means that single molecules cannot stably localize. At the other extreme, phase separation of the membrane energetically favors a single domain of such lipids at one pole. We have proposed a physical mechanism in which osmotic pinning of the membrane to the cell wall naturally produces microphase separation, i.e., lipid domains of finite size, whose aggregate sensitivity to cell curvature can support spontaneous and stable localization to both poles. Here, we demonstrate that variations in the strength of pinning of the membrane to the cell wall can also act as a strong localization mechanism, in agreement with observations of cardiolipin relocalization from the poles to the septum during sporulation in the bacterium Bacillus subtilis. In addition, we rigorously determine the relationship between localization and the domain-size distribution including the effects of entropy, and quantify the strength of domain-domain interactions. Our model predicts a critical concentration of cardiolipin below which domains will not form and hence polar localization will not take place. This observation is consistent with recent experiments showing that in Escherichia coli cells with reduced cardiolipin concentrations, cardiolipin and the osmoregulatory protein ProP fail to localize to the poles.

INTRODUCTION

Recent developments in intracellular fluorescence microscopy have led to a new appreciation of protein localization and organization in bacteria. In rod-shaped bacteria, a number of proteins have been found to localize at the poles, such as chemotaxis receptors in Escherichia coli (1), the division proteins MinCD and DivIVA in Bacillus subtilis (2), and the developmental proteins DivJ, PleC, and DivK in Caulobacter crescentus (3,4). The mechanism for such subcellular localization remains unknown for many proteins. The possibility that differences in lipid-membrane architecture might play a role in protein localization has been relatively unexplored (5). Nevertheless, there is growing evidence both of heterogeneities in the composition of bacterial cytoplasmic membranes (6,7) and of preferential binding of some bacterial proteins to particular lipid constituents (8–10). It was recently shown, using the cardiolipin-specific staining agent 10-nonyl acridine orange, that the phospholipid cardiolipin localizes to the polar and septal regions of the cytoplasmic membrane of living cells of E. coli (11,12) and B. subtilis (13). Furthermore, significantly enhanced levels of cardiolipin were found in the membrane of E. coli minicells, which are derived from the cell poles (14), and in the engulfment and forespore membranes of B. subtilis cells during sporulation (13).

In a previous work (5), we proposed that the observed cardiolipin localization is a consequence of microphase separation of the membrane into cardiolipin domains. We postulated that polarly-localized domains of cardiolipin could play a role in targeting proteins to the poles, as specific protein-cardiolipin interactions were well known. For example, membrane targeting of the ATPase MinD, which plays a critical role in bacterial division-site selection, was known to be mediated by a lipid-binding amphipathic helix with a distinct preference in vitro for anionic phospholipids such as cardiolipin (15). Additional recent experimental evidence has supported a direct role of cardiolipin in vivo in polar and septal targeting of the E. coli integral membrane protein ProP, an osmosensory transporter (9,10). These latter studies demonstrated that there is a critical cardiolipin concentration below which both cardiolipin and ProP fail to localize. In this article, we extend our previous model to include the lipid-mixing entropy, which becomes increasingly important at low cardiolipin concentrations, and shifts the distribution of domain sizes toward monomers. Within our model, we show that a continuum mean-field analysis of membrane energetics predicts a critical concentration for cardiolipin microphase separation, in good agreement with the experimentally observed value (9).

In our model, the geometrical constraint of the cytoplasmic membrane by the bacterial cell wall plays an essential role in lipid polar localization. The cell wall is the stress-bearing structure that defines the overall geometry of the cell (16), and typically an osmotic pressure difference pins the cytoplasmic membrane to the surrounding cell wall. However, on a molecular scale, the shape of the cytoplasmic membrane is likely to be influenced by its lipid composition as well. For rod-shaped cells, the difference in curvature between the poles and the cylindrical midcell region has been invoked to explain polar localization of some proteins (17). Similarly, it is natural to expect that, in the inner leaflet of the cytoplasmic membrane, a lipid with a headgroup cross-sectional area significantly smaller than that of its tail will be attracted to the high curvature of the poles (see Fig. 1). Of the three dominant bacterial lipids—phosphatidylethanolamine (∼75% of a typical E. coli membrane), phosphatidylglycerol (∼20%), and cardiolipin (∼5%) (18)—cardiolipin is the most likely to seek high curvature based on a small head/tail ratio (19). Also, preliminary experiments have shown that two-component giant unilamellar vesicles containing cardiolipin frequently adopt morphologies with tubes of submicron diameter indicative of highly curved components (T. Ursell, unpublished data).

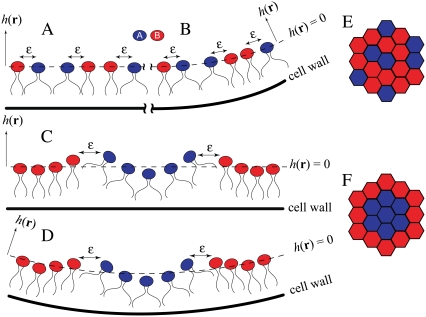
FIGURE 1.

Schematic of lipid clustering in different membrane configurations. (A) A homogeneous mixture (side view) associated with a flat cell wall composed of two lipid components (type A in blue with nonzero intrinsic curvature, type B in red with no intrinsic curvature) has a high energy because of the abundance of unlike nearest-neighbor pairs, each contributing energy ɛ. (B) Same as panel A, except the cell wall has higher curvature; this results in a slight reduction in the energy of lipids of type A. (C) A domain of lipids of type A is accompanied by membrane curvature (∇²h(r)). Though the elastic energy of the membrane increases relative to panel A, the formation of domains eliminates the unlike nearest-neighbor pairs and so reduces the total energy. (D) The same configuration in panel C shifted to a region of cell wall with higher curvature experiences a large reduction in energy, favoring localization of domains of lipid A to the poles. (E and F) Top view of a typical membrane configuration in panel A or C, respectively, where the lipids form a triangular lattice.

However, the difference in length scales between lipid molecules and the radius of curvature of the cell membrane results in ineffectually small polar-targeting energies for single cardiolipin molecules. Consider a patch of membrane containing a lipid, such as cardiolipin, with a high intrinsic curvature γ_lipid and surface area A. The difference in the elastic energy of such a lipid in a flat geometry versus a curved geometry with total curvature γ₀ should be proportional to γ₀, γ_lipid, and A; i.e.,

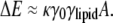(1)

As we show in a later section, the energy scale is set by the membrane bending stiffness κ, with an approximate value of κ ≈ 25 k_BT₀ for T₀ = 300 K (20,21). In a micron-sized bacterium, the difference in cell-wall curvature between the poles and the cylindrical midsection is γ₀ = 1/(500 nm) = 0.002 nm⁻¹, whereas reasonable estimates of the intrinsic radius of curvature and surface area of a single cardiolipin molecule are 10 nm (γ_lipid = 0.1 nm⁻¹) and A = 1 nm², respectively. Therefore, the energy difference in Eq. 1 between polar and nonpolar localization of a single lipid is only ∼0.5% of the thermal energy k_BT₀. In the presence of thermal fluctuations, it is therefore highly unlikely that single lipid molecules will localize preferentially to the poles.

Though single lipids have only a weak energetic preference for the poles, ΔE in Eq. 1 increases linearly with the lipid area A. Therefore, sufficiently large domains of cardiolipin could act as effective large-area molecules with sufficient energetic preference for stable polar localization. Such domain formation is likely to be driven, in part, by short-range interactions between lipid molecules that favor separation of the membrane into distinct phases of cardiolipin and the other lipids. Could cardiolipin localization in bacterial cells be driven by lipid phase separation? Fluorophore-labeled phospholipids have been observed to phase-separate in giant unilamellar vesicles into micron-scale domains, often with distinct curvatures (22–24). However, fundamental differences exist between such large-scale phase separation observed in model membranes and lipid localization in bacteria. Bacteria lack cholesterol, which is typically required for the formation of liquid-ordered domains in model membranes (22). In addition, the experimentally observed bipolar distribution of cardiolipin and rapid repartitioning of cardiolipin to the division site (11–13) and to the engulfment and forespore membranes of B. subtilis (13), would be strongly disfavored if cardiolipin was preferentially segregated in a single, large domain. In the E. coli membrane, such a domain of cardiolipin would cover roughly 5–10% of the bacterial membrane. Therefore, for a 3-μm bacterium with a 1-μm diameter, a single, large cardiolipin domain would not even cover a single pole. Thus, it is unlikely that phase separation alone would lead to the observed approximately equal concentrations of cardiolipin at the two poles.

Instead, we have shown within a quantitative biophysical model that pinning of the cytoplasmic membrane by the cell wall naturally produces stable finite-sized domains of high-intrinsic-curvature lipids (e.g., cardiolipin) which can spontaneously and independently target the two poles of the cell as well as the nascent division site (5). These finite lipid domains target the poles based on their large area, providing sensitivity to small variations in curvature, as implied in Eq. 1. In this work, we employ the methods of statistical mechanics to calculate the distribution of domain sizes and rigorously demonstrate the relationship between domain-size distribution and polar localization. In particular, our prediction of a critical concentration for polar localization of cardiolipin is in good agreement with experimental observations (9). Moreover, we extend our previous Monte Carlo simulations to larger model membranes and examine different lattices to eliminate the possibility of lattice artifacts. The increased size of these simulations allows us to move beyond the approximation of domain independence and investigate domain-domain interactions, which become increasingly important at high cardiolipin concentrations.

MEMBRANE ENERGETICS

To study the in vivo organization of the bacterial membrane, we have developed a simple model for the energetics of a multicomponent lipid bilayer pinned by osmotic pressure to the cell wall. For simplicity, we consider a two-component lipid membrane. We denote the two types of lipids as lipid A and lipid B, where lipid A is taken to have the higher intrinsic curvature (the components could represent, e.g., cardiolipin and phosphatidylethanolamine). Since it is well established in both bacterial membranes and eukaryotic plasma membranes that the lipid composition of the two leaflets of the bilayer can be very different (25,26), we assume that lipids are asymmetrically and independently distributed across the two leaflets of the bilayer. In this study, we focus on lipid composition in the inner leaflet (6,7). We separate the total energy of the membrane into two contributions,

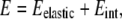(2)

where E_elastic represents the elastic energy of the leaflet and E_int represents the short-range lipid interactions driving phase separation.

The elastic energy is a sum of the bending energy of the leaflet and a pinning potential. The membrane pinning potential arises from the combined outward force of osmotic pressure and inward mechanical force exerted by the cell wall. The total elastic energy can be written as

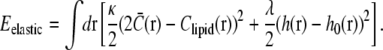(3)

The first term, proportional to the bending stiffness κ, penalizes mismatches in curvature between the total membrane curvature 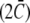and the preferred intrinsic curvature of the lipids (C_lipid). The second term, proportional to the pinning modulus λ, is the pinning potential which penalizes deformation of the membrane away from its minimum energy position with respect to the cell wall. The local mean curvature of the membrane is 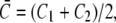with C₁ and C₂ the two principal curvatures of the two-dimensional membrane. C_lipid is the local intrinsic curvature with

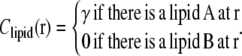(4)

The height perturbation h(r) − h₀(r) is measured as the distance from the unperturbed position h₀(r) of the membrane along the direction normal to a local patch surrounding r, and can be either positive or negative. We adopt the convention that displacement of the membrane away from the cell wall corresponds to negative values of h − h₀. In the Monge representation for small ∇h(r),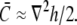

The interaction energy represents the energetic contribution from short-range chemical interactions between lipids that can drive lipid phase separation; these include electrostatic, van der Waals, and hydrophobic interactions (27,28). If the leaflet is represented by a two-dimensional lattice, the interaction energy can be written as

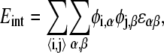(5)

where φ_i,α = 0 or 1 indicates the absence or presence of species α at lattice site i, and α can be either A or B. We consider only nearest-neighbor interactions 〈i, j〉, with ɛ_αβ being the lipid-lipid interaction strengths.

DOMAIN FORMATION IN FLAT GEOMETRIES

As argued above, organization of the membrane into cardiolipin domains of intermediate size is necessary to balance the requirement for sufficiently large polar-localization energy with the requirement for roughly equal partition of cardiolipin to both poles. A lipid mixture under the action of E_int alone can either phase separate or exist as a uniformly mixed state. For a lattice model, phase separation occurs only when

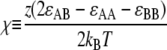(6)

is large enough (χ > 2 within mean-field theory or χ > 3.526 in a physical system with fluctuations), where z is the number of nearest neighbors. Since the behavior of the leaflet depends only on the value of 2ɛ_AB − ɛ_AA − ɛ_BB rather than on ɛ_AA, ɛ_BB, and ɛ_AB separately, we set ɛ_AA = ɛ_BB = 0, and ɛ_AB = ɛ to reduce the number of free parameters. (This choice of a short-range repulsion between unlike lipids is equivalent to a short-range attraction between like lipids, as can be seen from Eq. 6.) In our model, we study a triangular lattice, for which z = 6 and χ = 3ɛ/k_BT. Phase separation mediated by short-range interactions is made kinetically possible by the high diffusibility of lipids in the membrane (D ∼10 μm²/s (29)), and would be expected to result in the formation of one large domain enriched in lipid A. However, as we will see shortly, the combination of membrane elastic energy and lipid interactions can lead to microphase separation, e.g., finite-sized A-rich domains floating in a B-rich background.

How does membrane elasticity affect the phase diagram of a two-component leaflet? If lipid A has significant intrinsic curvature γ_lipid, domain formation due to the short-range interaction is counterbalanced by a longer-range repulsive elastic interaction between lipid A molecules. The short-range interaction lowers the membrane energy by an amount that scales approximately linearly with the number of lipid A molecules in the domain. In contrast, deformation of the membrane away from the cell wall slowly increases the energy as additional high-intrinsic-curvature lipids are added to a domain; for small domains, this increase is proportional to the square of the number of lipid A molecules in the domain. The growth of a small lipid A domain therefore should lead to a decrease in the energy of the membrane until the domain reaches a preferred size determined by the minimum energy per lipid, as shown schematically in Fig. 1, C, D, and F.

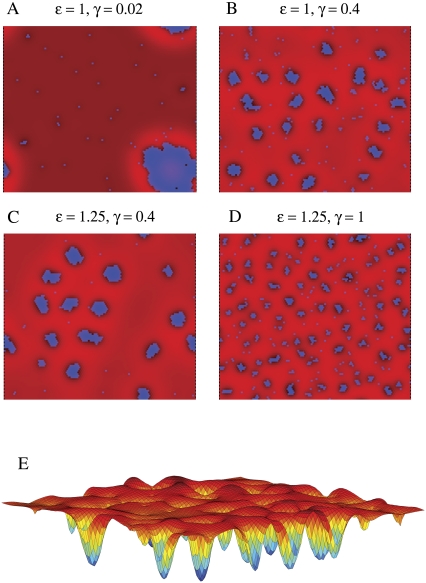
To demonstrate that the energy functional in Eqs. 2–5 can lead to microphase separation, we performed Monte Carlo simulations and studied domain formation in both flat geometries and geometries with spatially varying cell-wall curvature (see Appendix for simulation methodology). In Fig. 2, A–D, we show typical configurations of a membrane represented by a 100 × 100 periodic triangular lattice composed of two types of lipids, A and B, where the intrinsic curvature of the lipids is γ and 0, respectively, and the membrane composition is 7.5% lipid A and 92.5% lipid B. Lipids of type A are shown in blue, and superimposed in shades of red is the height of the membrane h(r) relative to the cell wall, which we initially take to be flat (h₀ = 0). We have assumed a fixed value for the membrane stiffness modulus κ = 28 k_BT₀ that roughly matches measured elastic moduli for lipid-bilayers (20,21) and we have selected a pinning modulus λ = 0.28 k_BT₀/nm⁴ to coordinate lipid domain sizes with the size of the membrane in our simulations.

FIGURE 2.

Lipid domain size as a function of short-range interaction and intrinsic lipid curvature. (A–D) Representative membrane configurations in a mixed membrane of lipids A and B, where lipid A has intrinsic curvature γ, lipid B has no intrinsic curvature, and immediately neighboring lipids of opposite type have an interaction energy ɛ. The stiffness modulus (κ = 28 k_BT₀), pinning modulus (λ = 0.28 k_BT₀/nm⁴), and fraction of lipid A (φ = 0.075) are the same in all panels. Blue indicates the presence of lipid A, whereas brighter shades of red represent greater separation of the membrane away from the cell wall. (A and B) ɛ = 1 k_BT₀ and γ = 0.02 nm⁻¹ and 0.4 nm⁻¹, respectively. (C and D) ɛ = 1.25 k_BT₀ and γ = 0.4 nm⁻¹ and 1.0 nm⁻¹, respectively. (E) The height field of the membrane configuration in panel B.

For fixed values of κ and λ, the lipids phase-separate at large values of the short-range interaction ɛ and small values of intrinsic curvature γ. In Fig. 2 A, due to the small intrinsic curvature of lipid A (γ = 0.02 nm⁻¹), the elastic energy due to curvature and pinning is insignificant compared to the short-range interaction between unlike lipids (ɛ = 1 k_BT₀); thus, the membrane minimizes total energy with a single large domain of lipid A, and the resulting height profile is close to zero (i.e., the membrane is closely pinned to the cell wall). As the intrinsic curvature γ of lipid A increases to 0.4 nm⁻¹ in Fig. 2 B, the single domain of lipid A breaks up into smaller domains. This reduction in domain size can be counteracted by increasing the short-range interaction ɛ to 1.25 k_BT₀ (Fig. 2 C). A further increase in γ to 1.0 nm⁻¹ again reduces the average domain size (Fig. 2 D). We note that with a larger short-range interaction in Fig. 2, C and D, the distribution of domain sizes is narrower, and the domains organize into a semiregular lattice. Unless otherwise noted, we treat the set of elastic and lipid parameters (κ, λ, γ, ɛ) represented in Fig. 2 B as a standard parameter set in the remainder of this work.

A typical height field h(r), for the membrane configuration in Fig. 2 B, is shown in Fig. 2 E. Each lipid A domain corresponds to a region of the membrane with high negative curvature (∇²h < 0) induced by the intrinsic curvature of lipid A, and domains are separated by bands of high positive curvature (∇²h > 0), which keep h small and minimize the pinning energy associated with separation of the membrane from the cell wall.

Continuum theory of lipid domains

How does the distribution of domain sizes as seen in Fig. 2 depend on the parameters describing the short-range interactions and the membrane elasticity? To address this question analytically, we first derive the effective longer-range potential between lipid A molecules due to membrane elasticity.

To derive a course-grained continuum membrane energy, we introduce a field φ(r) that represents the locally averaged fraction of lipid A at position r, so that 〈C_lipid(r)〉_local = γφ(r). The elastic energy, to quadratic order in h, can be written as

We can ignore the constant energy shift 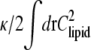and then locally average the fraction of lipid A to obtain

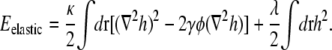The partition function is

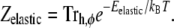(7)

First, we carry out the trace over {h} and obtain an effective Hamiltonian purely as a functional of φ. To achieve this, it is useful to write E_elastic in Fourier space,

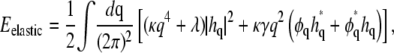where h_q and φ_q are the Fourier transforms of h(r) and φ(r), respectively. Using the relation

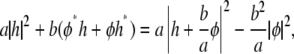we can write

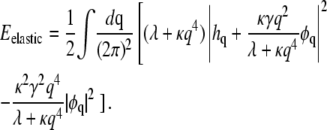(8)

Carrying out the trace over {h}, we are left only with the last term in Eq. 8, which can be written as

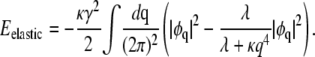(9)

The first term in Eq. 9 can be absorbed into the ɛφ² term in the coarse-grained interaction energy (30)

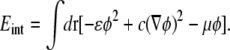Here, μ is the chemical potential that constrains the distributions of domain sizes to conserve φ, as we will demonstrate shortly. The second term in Eq. 9 yields, in Fourier representation,

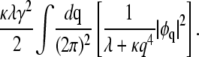In real space, this term takes the form 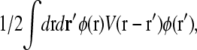where

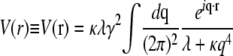is the elastic potential between two lipids separated by a distance r. Defining 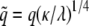and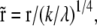

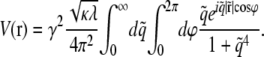(10)

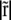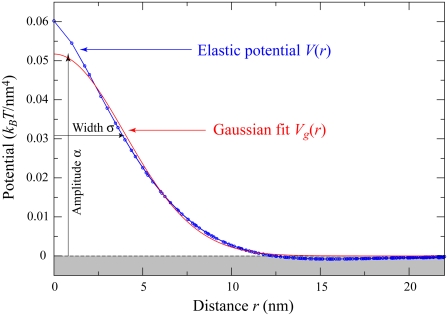
The integrals represent a pure function of with no other parameters and this function can be numerically evaluated as a function of 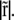We plot V(r) in Fig. 3 on the triangular lattice used in Fig. 2. This elastic potential is longer-ranged than the short-range attraction ɛ, and repulsive at short distances. However, note that V crosses zero when 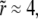corresponding to r ≈ 4(κ/λ)^1/4 = 12.7 nm for the elastic/lipid parameters in Fig. 2. Except at very short distances, V(r) is well fit (R² > 0.99) by a Gaussian,

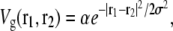(11)

with amplitude α = 0.052 k_BT₀/nm⁴ and standard deviation σ = 4.0 nm. These parameters are determined by the intrinsic curvature γ, stiffness κ, and pinning λ, with 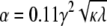and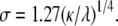

FIGURE 3.

Elastic potential governing domain formation. The elastic potential V(r) between two lipids separated by a distance r (shown in blue) is predominantly repulsive but is weakly attractive for r > 12.7 nm. Shown in red is the least-squares Gaussian fit V_g(r), with amplitude α = 0.052 k_BT₀/nm⁴ and standard deviation σ = 4.0 nm.

Energetically optimal domain size

We can begin to quantitatively account for the domain sizes in Fig. 2 by considering the optimal balance between short-range interactions and the longer-range elastic repulsion in Eq. 10. First, by adding a type A lipid monomer to an existing domain of type A lipids, there is an effective short-range attraction resulting from the elimination of costly interactions between unlike lipids. This short-range interaction tends toward a constant (linearly related to the perimeter of a single lipid) times ɛ as the domain size N grows.

For the triangular lattice used in Fig. 2, consider a domain containing all the neighbors out to the n^th shell around a central lipid. The total number of lipids in the domain is

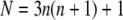(12)

(e.g., N = 7 for all the neighbors out to the first shell, n = 1, as shown in Fig. 1 F), thus the interaction energy per lipid relative to a configuration in which all N type A lipids exist as monomers is

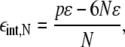where p = 12n + 6 is the perimeter of the domain (measured in units of 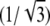nm so that the perimeter of a single lipid is p = 6). Using Eq. 12, we can write 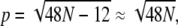giving

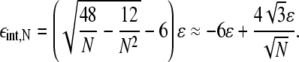(13)

Without the elastic interaction, the energy minimum is always at the maximal domain size. However, at sufficiently low lipid A fractions, entropy will prevent the formation of large domains of lipid A.

Now consider the total energy (elastic and short-range interaction) of a lipid A domain of size N. Denoting the energy per lipid by ε_N, the total energy of the domain is E_N = Nε_N. For domains whose size is smaller than the range of the repulsive potential, we expect that

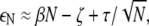(14)

where the first term corresponds to repulsive elastic interactions, and the remaining terms arise from short-range interactions (see Eq. 13). From Eq. 14, we expect ε_N to have a minimum at a finite optimal domain size N = N*, where N* = (τ/2β)^2/3 within the approximation in Eq. 14.

For a more accurate calculation of the energetically optimal domain size N*, we first approximate the elastic energy per lipid, ε_elastic, due to curvature and pinning of the membrane by integrating the Gaussian fit V_g(r) of the elastic potential over a circular lipid domain,

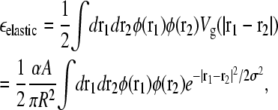where A is the area per lipid, N = πR²/A is the total number of lipids in the domain, and

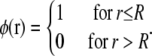In Fourier space, where V_g(q) is the Fourier transform of V_g(r),

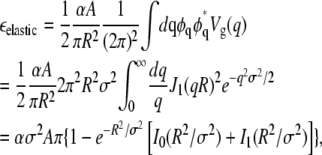(15)

where J₁, I₀, and I₁ are Bessel functions. For R < σ,

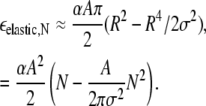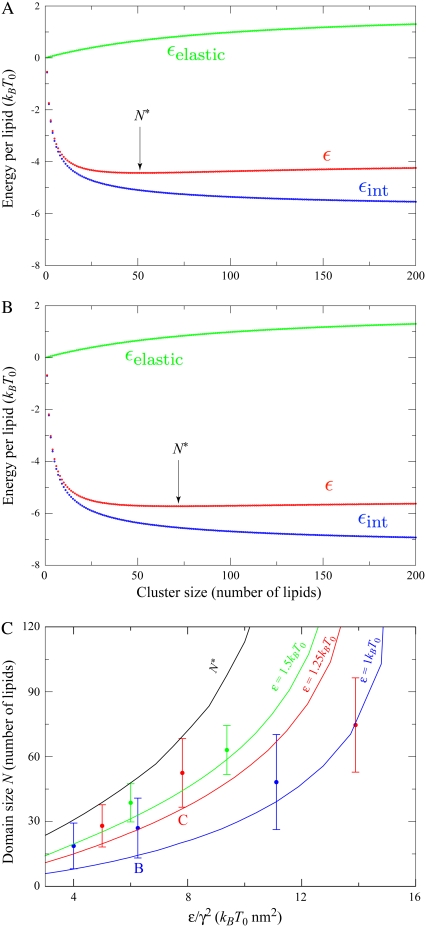
As noted above, the longer-range repulsive elastic energy and the short-range interaction energy grow with different powers of N, and this competition determines an energetically optimal domain size N* that minimizes ε_N = ε_elastic,N + ε_int,N. For the remainder of this work, N* is approximated by minimizing the sum of the estimates for ε_elastic,N and ε_int,N from Eqs. 15 and 13, respectively. In Fig. 4, A and B, these three terms, ε_elastic, ε_int, and ε, are shown as functions of domain size N. Using our standard elastic/lipid parameters from Fig. 2 B, the minimum total energy per lipid in Fig. 4 A occurs at a finite domain size N* = 50, which increases with increasing short-range interaction ɛ and decreasing intrinsic curvature γ (e.g., N* increases to 70 in Fig. 4 B when ɛ is increased to 1.25 k_BT₀). Note that N* does not depend separately on ɛ and γ, but rather is a function of ɛ/γ². By its definition, N* is independent of lipid A fraction φ, and, in the limit T → 0 such that entropy can be ignored and within the approximation V ≈ V_g, all domains will be of size N*.

FIGURE 4.

Energetically optimal domain sizes. The optimal domain size N* is found by minimizing the total energy per lipid ε (shown in red), which is the sum of the elastic and interaction energies per lipid ε_elastic (green) from Eq. 15 and ε_int (blue) from Eq. 13. (A) γ = 0.4 nm⁻¹ and ɛ = 1 k_BT₀, yielding N* = 50. The value N* can be increased by decreasing γ or increasing ɛ. (B) γ = 0.4 nm⁻¹ and ɛ = 1.25 k_BT₀, yielding N* = 70. (C) The energetically optimal domain size N* as a function of ɛ/γ² is shown in black. Distributions of domain sizes from finite-temperature simulations (T = T₀) are shown in blue (ɛ = 1 k_BT₀), red (ɛ = 1.25 k_BT₀), and green (ɛ = 1.5 k_BT₀). Solid blue, red, and green lines are predictions of average domain sizes from Eq. 27, which includes entropic effects. Data labeled B and C correspond to the lipid parameters used in Fig. 2, B and C.

In Fig. 4 C, we plot the predicted energetically optimal domain sizes (see black line marked N*) as a function of ɛ/γ². Also shown are the averages and standard deviations of domain sizes from finite-temperature simulations for several sets of lipid parameters (γ, ɛ), including those used in Fig. 2, B and C. Though the average domain size (circles) trends in the same fashion as the energetically optimal domain size N*, there is clearly significant variability in the observed domain sizes and the average domain size is significantly smaller than N* for large ɛ/γ². This discrepancy is due to the effects of entropy, as we will demonstrate in the following section.

Distribution of domain sizes

In the Monte Carlo simulations in Fig. 2, we observed a distribution of domain sizes peaked well below the energetically optimal domain size. In addition, although the majority of type A lipids are incorporated into domains, a significant number remain as monomers. To obtain an accurate estimate of the distribution of domain sizes, it is necessary to include the effects of entropy.

Within a lattice model in the dilute limit, the number of membrane configurations corresponding to a given distribution of domain sizes {n_N: N = 1, …, ∞} is

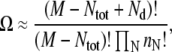where M is the total number of lattice sites, N_tot is the total number of particles (e.g., type A lipids) on the lattice, and N_d is the total number of domains. The entropy per lattice site is given by S = (ln Ω)/M. Using Sterling's approximation, we obtain

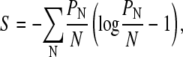(16)

where P_N is the probability that a randomly selected lattice site is occupied by a lipid A molecule that is part of a domain of size N. We note that an equivalent expression for the entropy of micellar size distributions has been given in the literature (31).

The free energy of the membrane per type A lipid is then given by 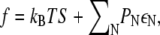which reduces to 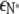as T → 0. To determine the distribution of domain sizes, we minimize f subject to the constraint 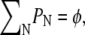where φ is the total lipid A fraction. Specifically, we minimize 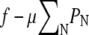with respect to P_N, where μ is a Lagrange multiplier denoting chemical potential. The minimization yields

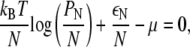which implies

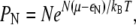(17)

where μ is determined by the constraint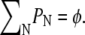

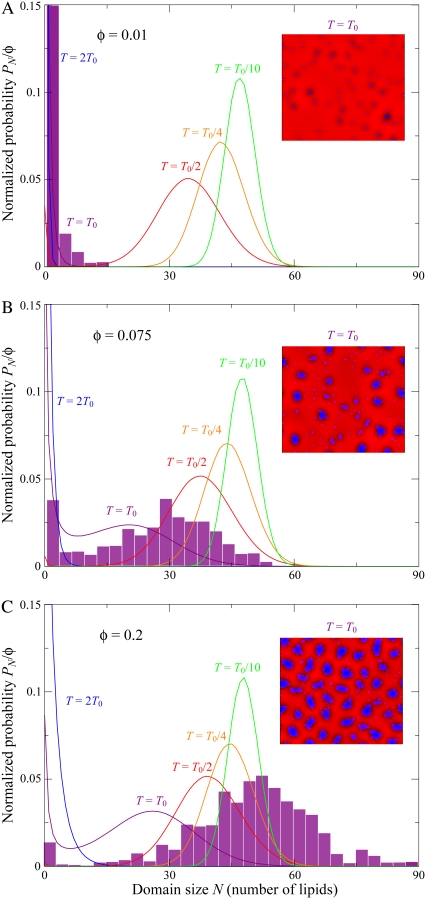
In Fig. 5, we plot the probability distribution of domain sizes (Eq. 17) at different temperatures and lipid A fractions for the same parameters as in Fig. 2 B. In Fig. 5 A (φ = 0.01), the distribution at T = 2T₀ is predominantly made up of monomers and small clusters, but as T decreases, the distribution develops a peak that shifts to larger domain sizes. At T = T₀/10, the distribution is clustered around the energetically optimal size N* = 50. The behavior of the size distribution is qualitatively similar for higher lipid A fractions (φ = 0.075 in Fig. 5 B and φ = 0.2 in Fig. 5 C). We note that although T₀/10 is not a physiologically relevant temperature, scaling T by a factor a is equivalent to scaling the values of κ, λ, and ε by 1/a.

FIGURE 5.

Distribution of domain sizes as a function of membrane composition and temperature. We plot P_N, the probability a lattice site is occupied by a lipid of type A that is part of a domain of size N, from Eq. 17, at temperatures 2T₀ (blue), T₀ (purple), T₀/2 (red), T₀/4 (orange), and T₀/10 (green). Parameters are the same as in Fig. 2 B. In panel A, the lipid A fraction is φ = 0.01; in panel B, φ = 0.075; and in panel C, φ = 0.2. The insets show typical membrane configurations, and the purple histograms show distributions of domain sizes from simulations at T = T₀.

The histograms overlaying Fig. 5 represent the domain-size distribution averaged over 10 Monte Carlo simulations. There is good agreement between the predicted distributions and histograms in Fig. 5, A and B, whereas the histogram in Fig. 5 C is shifted slightly to larger domain sizes. This discrepancy is not surprising given that the derivation of the entropy in Eq. 16 assumes a dilute concentration of lipid A molecules. The discrepancy can also be ascribed in part to domain-domain interactions and a change in domain morphology, which is discussed in later sections.

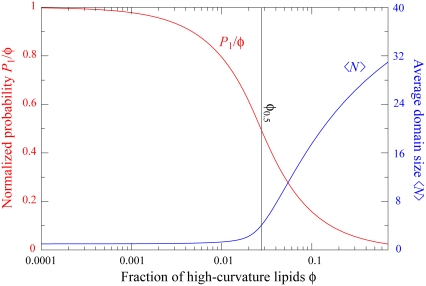
Notice that at T = T₀, the φ = 0.01 distribution is qualitatively different from the φ = 0.075 and φ = 0.2 distributions. The lipids exist mainly as monomers or small clusters and virtually no domains of size comparable to N* are observed. Clearly, there is a transition from lipid A molecules existing mainly as monomers to lipid A domain formation as φ increases from 0.01 to 0.075. In Fig. 6, for T = T₀ we plot the monomer density normalized to the total fraction, as a function of φ, using Eq. 17. The transition point from monomers to domains, φ_0.5, defined as the lipid fraction where monomers make up half of the lipid A population, occurs at φ_0.5 = 0.027. The average domain size

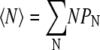(18)

shows a similar transition, increasing rapidly beginning at ∼φ_0.5. Note that 〈N〉 does not reach N* = 50 even for large values of φ, because of the effects of entropy.

FIGURE 6.

Competition between monomers and domains as a function of membrane composition. Using the Gaussian form of the repulsive potential, V_g(r), the probability of finding a lattice site occupied by a lipid A monomer, P₁ (see Eq. 17), normalized by the total fraction, φ, is shown in red. The average domain size 〈N〉 (see Eq. 18) is shown in blue. Parameters are the same as in Fig. 2 B, with T = T₀. The crossover point at which half of the type A lipids are monomers is at φ_0.5 = 0.027 (vertical black line).

We can simply estimate where the crossover from monomers to larger domains occurs as a function of φ, using Eq. 17. Assume that lipid A molecules can only exist as monomers or in domains of size N*, the energetically optimal domain size (an assumption that increases in validity as T decreases). In this case, Eq. 17 simplifies to

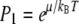where we have made use of ε₁ = 0 for monomers, and

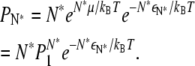We can define a crossover fraction φ_c such that 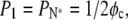yielding

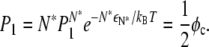(19)

From Eq. 19, it follows that

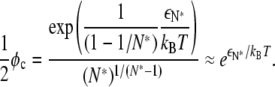(20)

Thus, for φ ≪ φ_c, we expect most lipid A molecules to exist as monomers, whereas for φ ≫ φ_c, we expect most lipid A molecules to join large domains, leaving very few monomers. For the parameters represented in Fig. 6, Eq. 20 predicts a crossover at φ_c ≈ 0.022, which agrees well with our previous estimate φ_0.5 = 0.027.

LOCALIZATION OF LIPID DOMAINS

Domain localization in curved geometries

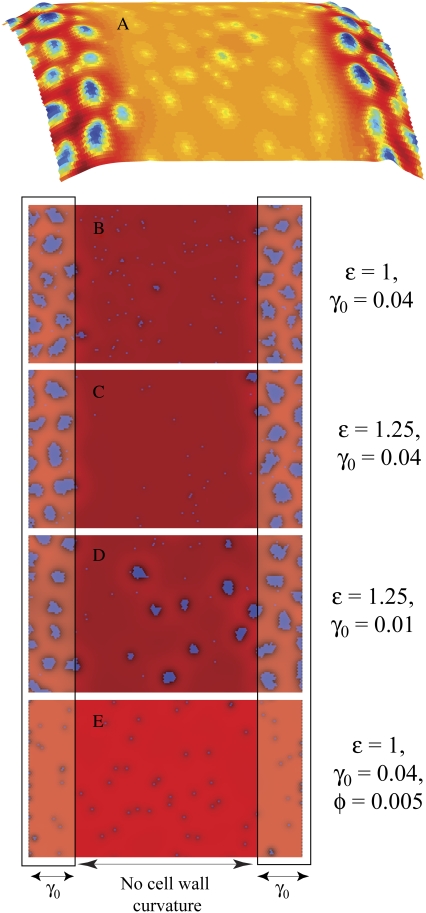
Although the larger curvature at the poles of a bacterial cell cannot stably localize individual lipids due to the mismatch in lipid and cell dimensions, the curvature of the poles may suffice to localize sufficiently large lipid domains. How large must a lipid domain be to spontaneously target the cell poles? In Fig. 7, we show typical membrane configurations in 100 × 150 model cells (periodic in the vertical direction to mimic a cylinder) in which regions of the cell wall on the left and right (the “poles”) have an underlying curvature of γ₀ = 0.04 nm⁻¹ relative to the cylindrical midcell region. The polar regions encompass one-third of the total length of the cell, to mimic the aspect ratio of a 3-μm rod-shaped bacterium with a radius of 0.5 μm.

FIGURE 7.

Polar localization of lipid domains. (A) The membrane height in panel B mapped onto the surface of a capped cylinder. (B) A typical membrane configuration in which the rectangles on the left and right represent the cell poles and have slightly enhanced cell-wall curvature γ₀ = 0.04 nm⁻¹. The color scheme, fraction of lipid A (φ = 0.075), and elastic/lipid parameters κ, λ, γ, and ɛ = 1 k_BT₀ are the same as in Fig. 2 B. (C and D) An increase in ɛ to 1.25 k_BT₀ increases the average domain size, but the degree of localization of the domains depends on the polar cell-wall curvature, which is γ₀ = 0.04 nm⁻¹ in C and γ₀ = 0.01 nm⁻¹ in D. (E) The same as panel B, except the lipid A fraction is lowered to φ = 0.005.

Using our standard elastic/lipid parameters, we show in Fig. 7 B that the difference in cell-wall curvature is sufficient to localize nearly all of the domains of lipid A to the poles of the cell. This localization is critically dependent on domain size. The few lipids in the cylindrical region are all monomers or are part of small clusters. Using the polarly-localized lipid configuration in Fig. 7 B as the initial lipid distribution, we reduced ɛ to 0.5 k_BT₀, and observed that the resulting smaller domains fail to localize to the cell poles but rather spread homogeneously throughout the membrane (5). In contrast, the localization in Fig. 7 C is enhanced by larger ɛ = 1.25 k_BT₀. In Fig. 7 D, we reduced the polar cell-wall curvature to γ₀ = 0.01 nm⁻¹, and found that although the majority of the lipid A domains localize to the poles, the average domain size is smaller and some domains fail to localize. For smaller lipid A fractions φ, the domain size distribution shifts to smaller N, strongly reducing the localization preference of type A lipids. In Fig. 7 E, we reduced φ to 0.005 (<φ_0.5), which leaves many type A lipids as monomers or small clusters that fail to localize.

Although in our simulations in Fig. 7 the polar cell-wall curvature γ₀ is only one-tenth or less of the intrinsic curvature γ of lipids of type A, the observed polar localization of lipid domains can be easily explained within our energetic model. Consider the elastic energy for a membrane patch containing an isolated domain of type A lipids,

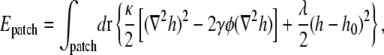where h₀(r) is the local preferred height of the membrane as governed by the curved cell wall. Defining 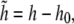we find that

(21)

where γ₀ = ∇²h₀ is the curvature of the cell wall. If γ₀ is a constant, the last term in Eq. 21 is a total derivative, and since 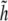approaches zero away from the domain, this term does not contribute to the elastic energy of the patch.

The only contribution of the cell-wall curvature to the energy in Eq. 21 comes from the second to last term, in which the coefficient κγγ₀ can be viewed as an effective curvature-dependent chemical potential for lipid A molecules. Integrating over a patch of 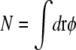lipid A molecules, the energy change ΔE_N for shifting the lipid domain from the lateral cylindrical region of the cell to one of the poles is given by

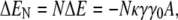where A is the surface area of a lipid A molecule. Our essential conclusion is that although the energy preference of an isolated high-intrinsic-curvature lipid for the poles is only a fraction of the thermal energy k_BT, there exists a critical domain size above which the collective energy change of a domain of such lipids is sufficient to result in stable polar localization.

For the simulations presented in Fig. 7, the polar localization energy of a single lipid A molecule with stiffness modulus κ = 28 k_BT₀, intrinsic curvature γ = 0.4 nm⁻¹ and area A = 0.866 nm² (see Appendix) in a cell with polar cell-wall curvature γ₀ = 0.04 nm⁻¹ is only ΔE = −0.4 k_BT₀. However, for a uniform cell wall with no underlying curvature, the predicted minimum energy per lipid occurs at a domain size of N* = 50 lipids. For this size domain, the total energy is 20 k_BT₀ lower at the cell poles, implying a thermal probability of virtually 100% to find the domain at one of the poles. (In fact, polar localization is even stronger since the energetically optimal domain size grows to 68 lipids at the pole.) If we instead use γ = 0.1 nm⁻¹ and the physiological value of γ₀ = 2 μm⁻¹, ΔE = 0.004 k_BT₀. Thus in the bacterial membrane, effective polar localization requires cardiolipin domains of size N > 250 (corresponding to dimensions of the order of tens of nanometers) so that N|ΔE| > k_BT₀.

Domain localization to regions of low osmotic-pressure difference

The strength of the membrane pinning modulus λ is determined by the balance between the osmotic-pressure difference across the membrane and the inward force exerted by the cell wall. The osmotic-pressure difference is generated by gradients in osmolyte concentrations across the cell membrane. As the osmotic-pressure difference is reduced, the membrane is less constrained by the cell wall, reducing λ, so that it is more likely to contain larger domains of high-curvature lipids. Osmotic pressure can be varied uniformly across the cell wall by changing environmental conditions (32), and certain growth processes can create local variations in the osmotic pressure across the membrane. For example, during cell division, the new septum separates two internal compartments of the cell. These compartments have similar osmolyte concentrations, hence we expect the osmotic-pressure difference across the septal membrane to be small compared to the pressure difference across the rest of the membrane. Similarly, during sporulation in B. subtilis, a new septal membrane and cell wall is created to separate the mother cell from the spore (33,34). In both cases, we expect the osmotic-pressure difference across the division septum to be much smaller than that across the rest of the cell wall, leading to heterogeneity in membrane pinning.

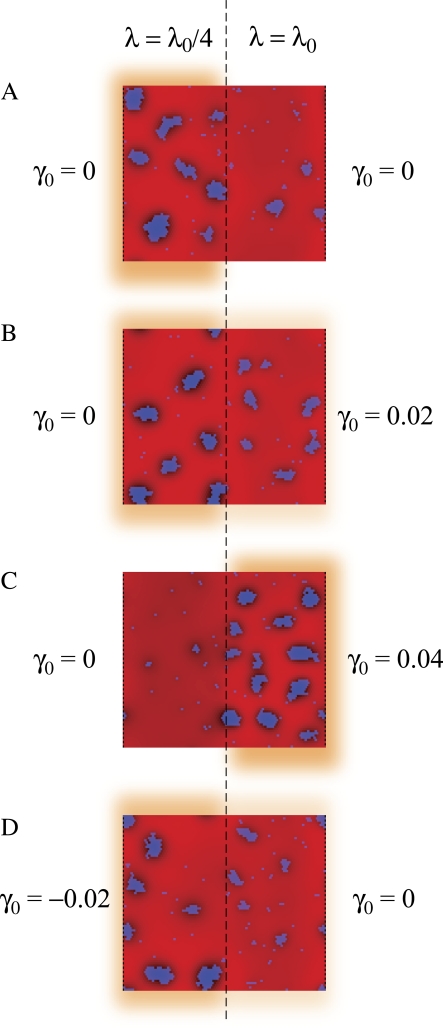
To mimic such a heterogeneity in our simulations, we spatially varied the pinning modulus λ(r) experienced by the membrane. In Fig. 8, A–C, we show typical membrane configurations for 80 × 80 periodic model cells in which the pinning modulus of the left half of the cell is 25% that of the right half of the cell. Using our standard stiffness modulus κ = 28 k_BT₀ and lipid parameters γ = 0.4 nm⁻¹ and ɛ = 1 k_BT₀, we show in Fig. 8 A that in a flat cell with no cell-wall curvature, the fourfold difference in pinning modulus between the two halves of the cell is sufficient to localize all of the domains of lipid A to the region mimicking low osmotic-pressure difference (e.g., the septal/forespore membrane). As with localization due to variation in cell-wall curvature, this pinning-dependent localization is critically dependent on domain size. Using the configuration in Fig. 8 A as the initial lipid distribution, reducing the interaction energy ɛ causes progressive loss of localization as domains shrink (5).

FIGURE 8.

Localization of lipid domains by heterogeneous membrane pinning. (A) The pinning modulus of the left half of the model cell membrane is reduced by a factor of 4 (λ = λ₀/4 = 0.07 k_BT₀/nm⁴) relative to the right half of the cell (λ = λ₀ = 0.28 k_BT₀/nm⁴). The cell-wall curvature is uniform (γ₀ = 0). The color scheme, lipid A fraction, and elastic/lipid parameters are the same as in Fig. 2 B. (B and C) An increase in the cell-wall curvature of the right half of the cell relocalizes lipids to the right (γ₀ = 0.02 nm⁻¹ in B, γ₀ = 0.04 nm⁻¹ in C). (D) Most lipids remain localized on the left half of the cell even when the cell-wall curvature on the left (γ₀ = −0.02 nm⁻¹) is opposite in sign to the lipid A intrinsic curvature.

The localization of lipid domains in Fig. 8 A to regions of low pinning modulus λ can be readily explained within our model. Even a modest decrease in the pinning modulus increases the range and, more importantly, decreases the amplitude of the repulsive elastic potential between lipid A molecules. For example, the fourfold decrease in λ in Fig. 8 leads to an increase in the energetically optimal domain size from 50 to 70 and, more importantly, a decrease in free energy per lipid of ΔE_λ = −0.28 k_BT₀. Therefore, even at the smaller domain size, the total energy of the domain is lowered by >14 k_BT₀ by the fourfold decrease in the pinning modulus.

In Fig. 8 B, we show the results of simulations similar to those in Fig. 8 A, except that the right half of the cell has an underlying cell-wall curvature similar to the polar regions of Fig. 7, γ₀ = 0.02 nm⁻¹. In this case, there is a competition between pinning and curvature for domain localization, and we find a distribution of lipid domains on both sides, with larger domains localizing to the region of low pinning modulus. This localization preference is reversed in Fig. 8 C where γ₀ is increased to 0.04 nm⁻¹. The crossover point between pressure- and curvature-mediated localization occurs approximately when −ΔE_λ = κγγ₀A_lipid, which corresponds to a cell-wall curvature difference of γ₀ ≈ 0.025 nm⁻¹ for our choice of parameters. We conclude that spatial variations in the strength of pinning by the cell wall can serve as a strong localization mechanism. If present, pinning heterogeneity can dominate over curvature, allowing lipid localization in either leaflet of the membrane. For example, in Fig. 8 D the right half of the cell has zero cell-wall curvature, whereas the left half, with lower pinning modulus, has cell-wall curvature γ₀ = −0.02 nm⁻¹ opposite in sign to the lipid A intrinsic curvature. Nevertheless, most lipid A molecules are localized on the left half of the cell. The resulting lipid partition is essentially identical to that in Fig. 8 B, as expected, since curvature-mediated localization depends only on the difference in curvature between two regions of the cell wall, and not on their individual curvatures.

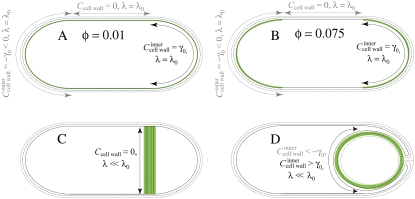
Interestingly, cardiolipin localization to the forespore membrane during sporulation in B. subtilis is accompanied by an apparently complete loss of polar localization (13), as shown schematically in Fig. 9. Though it is unlikely that the curvature of the forespore membrane is significantly higher than that of the poles, there should be little or no osmotic-pressure difference across the forespore membrane. As shown in Fig. 8 A, a modest decrease in osmotic-pressure difference leading to a reduction of the membrane pinning modulus is enough to localize all of the cardiolipin to the region of membrane with low pressure difference (see Fig. 9, C and D). In our model, this effect can dominate over the effect of spatially varying membrane curvature, even allowing cardiolipin localization in the outer leaflet of the forespore-engulfing membrane where the cell-wall curvature is opposite in sign to the cardiolipin intrinsic curvature (see Fig. 8 D). Therefore, our model naturally explains the relocalization of cardiolipin from the poles of the mother cell to the forespore membrane observed experimentally in B. subtilis cells early in sporulation (13). During engulfment of the forespore, the inner leaflet of the mother cell and outer leaflet of the engulfing membrane form a continuous monolayer (34). This allows the relocalization of cardiolipin from the pole of the mother cell first to the forespore septal membranes and thence to the forespore inner membrane and the forespore-engulfing membrane, without requiring flippases to transfer cardiolipin between membrane leaflets (see Fig. 9 D).

FIGURE 9.

Competition between curvature and osmotic localization of lipid domains during cell division and sporulation. (A) During exponential growth, if the fraction of high-intrinsic curvature lipids is too low (e.g., φ = 0.01), no domains form that are large enough to localize to the poles, leading to an approximately uniform lipid distribution across the membrane. (B) At higher fractions (e.g., φ = 0.075), high-intrinsic-curvature lipid domains localize to the poles of the inner leaflet (solid black curve), driven by differences in membrane curvature. Green regions denote cardiolipin localization. All curvatures are measured relative to the curvature in the cylindrical region of the cell. The cell-wall curvature experienced by the outer leaflet of the membrane (solid gray curve) is opposite in sign to the intrinsic lipid curvature. (C) A low osmotic-pressure difference across the septal/forespore-engulfing membranes corresponds to a reduced value of the pinning modulus λ and induces relocalization of the lipid domains to these membranes (see Fig. 8). (D) As the spore is engulfed, the domains of high-intrinsic-curvature lipids can migrate along the continuous leaflet consisting of the inner leaflet of the mother cell and the outer leaflet of the forespore-engulfing membrane to localize around the spore due to the low osmotic-pressure difference.

DOMAIN INTERACTIONS AND PACKING OF DOMAINS

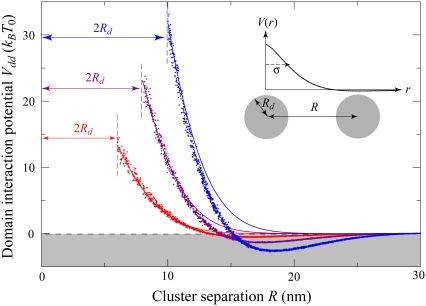
As the fraction of cardiolipin is increased, the fraction at the poles may become high enough that interactions between domains become important for domain packing. As shown in Fig. 3, the elastic potential V(r) between type A lipids is weakly attractive for r > 12 nm, which leads to a small basin of attraction in the elastic interactions between domains. This attractive interaction could be important for domain-packing at intermediate concentrations of cardiolipin. In Fig. 10, we plot the potential V_dd(R, R_d) between two lipid A domains of equal radius R_d, whose centers are separated by a distance R. To avoid lattice artifacts, the centers of the domains were positioned randomly on the lattice, and each domain was defined by the lattice points within a distance R_d of its center. The data points represent V_dd(R, R_d) determined from the true potential between two type A lipids, V(r), shown in Fig. 3. The solid lines are determined by integrating the Gaussian fitting potential, V_g(r), over two circular domains 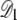and 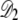to yield

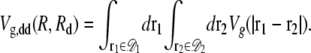V_dd and V_g,dd agree well at short separations, where both are repulsive and monotonically decreasing. However, the true interdomain potential V_dd becomes weakly attractive for edge-to-edge separations of 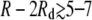nm. For larger domains, of radius comparable to the width of the elastic potential σ = 4 nm, the attractive region of V_dd becomes wider and more negative while shifting to smaller R – 2R_d. This attraction is generated by the increasing fraction of interdomain lipid pairs lying within the basin of attraction in V(r).

FIGURE 10.

Interactions between domains of fixed size. The interaction potential V_dd(R, R_d) between two domains of high-intrinsic-curvature lipids with radius R_d = 3 nm (red), R_d = 4 nm (purple), or R_d = 5 nm (blue) as a function of center-to-center domain separation R. The data points are determined from the true potential, V(r), whereas the solid lines are predictions of V_g,dd(R, R_d) using the Gaussian fit, V_g(r), to the elastic potential. V_dd is repulsive at short separations, but becomes weakly attractive for edge-to-edge separations 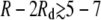nm. The elastic and lipid parameters are the same as in Fig. 2 B.

This attractive region of V_dd has a negligible effect at low lipid A fractions, where the distribution of domain sizes is shifted to small N (Fig. 5 A). At high lipid A fractions, the repulsive portion of the interdomain interaction is likely to influence the packing of lipid domains via excluded-volume effects. Given the relatively low fraction of cardiolipin in a typical E. coli plasma membrane, regions of localization such as the cell poles, division septum, and forespore membrane are likely to contain intermediate concentrations of cardiolipin, where both the repulsive and attractive parts of the domain-domain interaction could promote local patches of short-range order. For example, a local lipid A fraction of 0.15 separated into domains with radius R_d = 4 nm on a hexagonal lattice would correspond to an average domain separation of R = 20 nm.

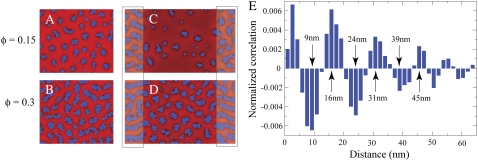
The weak nature of domain-domain interactions relative to the total energy of a lipid domain of size ∼N* implies that the domain size estimates from Fig. 4 should be insensitive to the composition of the membrane as long as the fraction of lipid A is not too large. In Fig. 11 A, as φ is doubled from 0.075 (Fig. 2 B) to 0.15, the average domain size in a 100 × 100 cell increases from 27 ± 14 to 40 ± 15. In addition, the domains are more clearly ordered in a roughly hexagonal lattice. A histogram of the two-body spatial correlation function of lipid A positions is shown in Fig. 11 E. The spatial correlation function of a membrane with randomly chosen lipid A positions (equivalent to κ = ɛ = 0) has been subtracted out, leaving peaks with a periodicity of ∼16 nm. This hexagonal packing arrangement of domains also occurs on a square lattice (not shown) (5), thus it is not an artifact of the hexagonal simulation lattice. As φ is increased further to 0.3, other patterns start to appear. In Fig. 11 B, the type A lipids begin to form long chains or stripes that are typical of domain-forming systems at large filling fraction (35). Similar effects are apparent in simulation cells with polar regions of higher curvature γ₀ = 0.04 nm⁻¹, as shown in Fig. 11, C and D. In both cases, the poles cannot accommodate all of the type A lipids, leading to the overflow of domains into the cylindrical region.

FIGURE 11.

Effect of membrane composition on domain formation. (A) The domains remain approximately the same size when the lipid A fraction is increased from φ = 0.075 (Fig. 2 B) to φ = 0.15. (C) The rectangles on the left and right represent the poles of the cell with slightly higher curvature γ₀ = 0.04 nm⁻¹, as in Fig. 7. (B and D) Identical to panels A and C, respectively, except that φ = 0.3. (E) The two-body spatial correlation function of the configuration in panel A, measured relative to a randomly mixed membrane. The histogram is normalized relative to the total number of lipid pairs.

CONNECTION TO EXPERIMENTS

The lipid-domain sizes considered in previous sections are similar to some estimates of lipid-raft dimensions (36), and although they are certainly below the resolution limit of conventional light microscopy, recent developments in structural illumination (37) and cryo-electron tomography (38) might allow for the observation of domains with radii as small as 50 nm. In addition, we note that we have chosen relatively large values for the intrinsic curvature of lipid A to produce computationally manageable domain sizes. The predicted optimal domain size for our standard values of κ, λ, and ɛ with a lower, more realistic value of intrinsic curvature γ = 0.1 nm⁻¹ is >1000. Since this choice of parameters lies within the range of existing estimates for eukaryotic lipids (20,21), it is reasonable to expect the existence of cardiolipin domains on the order of 100–1000 lipids in bacterial cell membranes.

Regardless of the exact cardiolipin domain size, our model has important general consequences for experimental measurements of cardiolipin localization. First, we predict that at wild-type concentrations, cardiolipin domains in rod-shaped cells will localize to the regions of the cell wall with the highest curvature, namely the cell poles (Fig. 9 B). As a corollary, we predict that spherical bacteria will not exhibit large-scale cardiolipin localization without variations in cell-wall curvature. Our model also explains the experimental observation that cardiolipin localizes to the division site of E. coli and B. subtilis (11–13), a region of higher cell-wall curvature and/or low osmotic-pressure difference, once the septum begins to close. Similarly, our model explains the localization of cardiolipin to the forespore membrane, a region of low osmotic-pressure difference, and predicts that changes in cardiolipin localization as osmotic-pressure difference is varied can be used to probe experimentally the strength of cell-wall pinning. In hypertonic solutions, the membrane may peel away from the cell wall (plasmolysis), which could prove interesting for probing other mechanisms for membrane organization under nonpinning conditions.

Second, we consider the dependence of polar localization on the cardiolipin concentration φ. This dependence can be probed experimentally by varying cardiolipin levels in vivo through inducible expression of the cardiolipin synthase. We predict a critical cellular cardiolipin concentration φ_c ≈ 0.01, below which entropy prevents the formation of domains large enough for stable polar localization. This is in quantitative agreement with the critical concentration of cardiolipin recently observed to be required for polar localization of both cardiolipin and the integral membrane protein ProP (9). The critical concentration is lower in more curved geometries, thus it is possible that domains can form at the poles whereas the cylindrical midcell region contains predominantly monomers. At cardiolipin levels >φ_c, we predict that the number of domains in the cylindrical midcell region should remain low until cardiolipin levels rise high enough that the poles become densely packed with domains. As shown in Fig. 11, C and D, subsequent additions of cardiolipin should produce domains that distribute randomly throughout the cylindrical region.

Third, we predict that cardiolipin domains partition binomially to the poles of rod-shaped cells with a mean separation governed by a weak interaction between nearby domains (see Fig. 10) that can lead, on average, to a semiordered lattice of domains. To further distinguish our model of microphase separation into finite-sized domains from large-scale domain formation driven by complete phase separation, our model predicts that staining specific to at least one of the low-intrinsic-curvature phospholipids should reveal significant levels of fluorescence at the poles and in minicells (overlaying the cardiolipin signal), arising from the interstitial regions between cardiolipin domains in the inner leaflet and throughout the outer leaflet. Indeed, recent experiments using the phosphatidylethanolamine-specific cyclic peptide probe Ro09-0198 have demonstrated that significant levels of phosphatidylethanolamine are present along with cardiolipin at the poles of B. subtilis and E. coli cells (39), though it remains to be determined how much of the signal arises from the inner leaflet.

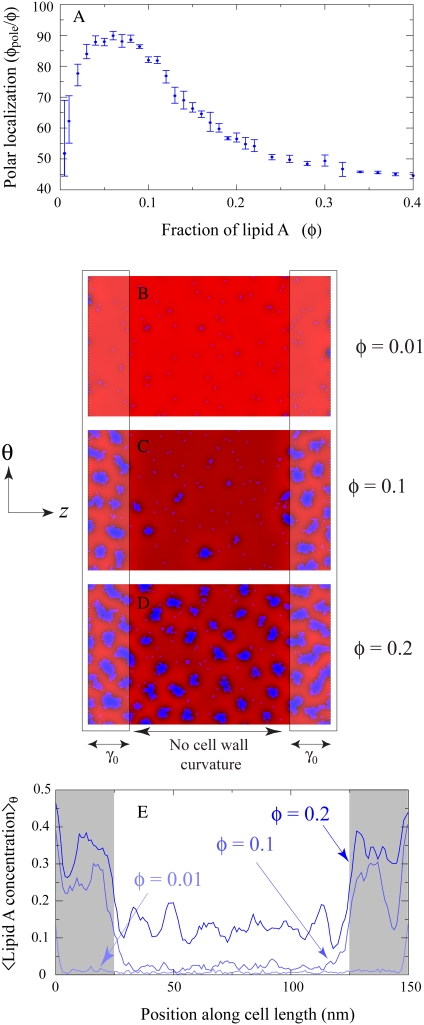
To make these predictions more quantitative, we varied the lipid A fraction from 0.005 to 0.4 in Fig. 12 A in cells with enhanced polar cell-wall curvature γ₀ = 0.04 nm⁻¹ similar to Fig. 7. As discussed previously, at low concentrations the polar localization of lipid A is vastly reduced, and even at φ_c (≈ 0.01), less than two-thirds of the lipid A molecules are polarly localized. The polar localization fraction φ_pole/φ increases with φ and plateaus at ∼90%. Then a transition occurs from nearly complete polar localization to partial midcell localization at ∼φ = 0.1, a value well below the value φ = 0.33 required to fill the poles with lipid A. This midcell localization arises from the repulsion between domains at short length scales shown in Fig. 10, which counteracts the favorable effects of polar curvature and causes domains to overflow into the cylindrical region of the cell.

FIGURE 12.

Change in polar localization as a function of membrane composition. (A) The fraction of polarly-localized type A lipids, φ_pole/φ, in a model cell whose poles have curvature γ₀ = 0.04 nm⁻¹, as a function of the lipid A fraction φ. (B–D) Typical membrane configurations of lipids in a cell with (B) φ = 0.01, (C) φ = 0.1, and (D) φ = 0.2. The color scheme and elastic/lipid parameters are the same as in Fig. 2 B. (E) The lipid A occupancy of the membrane configurations in panels B–D averaged over the θ-direction.

In Fig. 12, B–D, we show typical membrane configurations with φ = 0.01, 0.1, and 0.2, respectively. In Fig. 12 E, we average configurations from 10 simulations with each lipid A fraction in Fig. 12, B–D, and average over the θ-direction. As φ increases from 0.005 to 0.1, there is a characteristic local increase in cardiolipin concentration at the poles, but little population of the midcell region. In contrast, increasing φ from 0.1 to 0.2 results in a uniform increase in cardiolipin concentrations between the poles but little increase at the poles.

These abrupt transitions in localization preference as φ is varied would not be expected if localization was solely determined by the polar positioning of cardiolipin synthase. Instead, in that case we would expect that polar localization would occur even at low concentrations of cardiolipin, and that at higher cardiolipin fractions, the local concentration would increase proportionately in the polar and cylindrical midcell regions. We note, in addition, that the rapid diffusion of lipids in the membrane (D ∼ 10 μm²/s (29)) would likely eliminate any nonuniformities in concentration due solely to synthase localization.

Although our model has been developed in the context of domains in bacterial membranes, the physical mechanisms are general and the calculations presented here could also be relevant for understanding lipid domains observed in eukaryotic cells and in multicomponent supported model membranes (40,41). The lipid-raft model of cholesterol and sphingolipid in the outer leaflet of eukaryotic cell membranes proposes that ordered domains floating in a liquid bilayer act as signaling platforms that couple extracellular events to pathways inside the cell (25,26). Lipid rafts are believed to be ∼10–100 nm in size (25,26), in contrast to the micron-sized domains observed in model lipid membranes (22,23). This discrepancy in sizes is an outstanding mystery. It is interesting to note that in eukaryotic cells the plasma membrane is typically pinned by the actin cortex (or the spectrin-actin membrane skeleton in red blood cells) and spontaneous curvature has previously been associated with lipid rafts (42). Whether a pinning- and curvature-induced mechanism similar to the one proposed here could be relevant for determining the size of lipid rafts remains to be seen.

DISCUSSION

Though anchors are a common source of subcellular protein targeting, ultimately these anchors themselves must be localized by some physical mechanism. Therefore, it may be fruitful to consider possible mechanisms of spontaneous self-organization within cells. Here, we have quantitatively examined a model in which the bacterial cell wall constrains the cytoplasmic membrane to produce finite-sized domains of high-curvature lipids. These domains are large enough to spontaneously and stably localize to the cell poles, and are present in large enough numbers to achieve roughly uniform and equal coverage of both poles. Importantly, these results explain the recent observations of cardiolipin localization to both the poles and division site of rod-shaped bacterial cells, as assayed by 10-nonyl acridine orange fluorescence (see Fig. 9 B).

Extending previous work (5), we have simulated larger model cells and have used a continuum theory to investigate the range of domain sizes and the length scale over which domains interact. In addition, we have derived how entropy leads to a distribution of domain sizes. When the fraction of high-intrinsic-curvature lipid is low or the temperature is high, this distribution differs significantly from the energetically optimal domain size. In these regimes, entropy favors monomers, which cannot stably localize to the poles (see Figs. 7 E and 12 B). These results explain the experimental observation of a critical concentration of cardiolipin for polar localization (9). These results also suggest that regulated changes in cardiolipin concentration could provide a mechanism for regulating protein localization, either by inducing cardiolipin to cross the critical concentration required for localization or by altering the number of domains. In particular, it is possible that the as-yet unexplained upregulation of cardiolipin during sporulation in B. subtilis cells with disruptions in all three candidate alleles coding for cardiolipin synthase (13) may reflect such a mechanism for regulating localization of proteins to the forespore and forespore-engulfing membranes.

Our model of cell-wall-mediated domain formation provides a robust, equilibrium mechanism for localizing and partitioning high-intrinsic-curvature lipids in equal amounts to both poles, and suggests that, similar to lipid rafts, the polar localization of cardiolipin may provide an anchor for polar targeting of proteins such as ProP (9). Although curvature cannot mediate stable polar localization of individual proteins for the same reason of length-scale mismatch given above for lipids, our model also suggests that some proteins, such as the chemotaxis receptors (1), may be localized to the poles via the aggregate curvature of large domains. Our analytical and computational treatment of domain sizes and interactions suggests the possibility of a more quantitative link between theory and future experiments addressing bacterial membrane organization.

APPENDIX: SIMULATION METHODOLOGY

We represent the membrane as a two-dimensional lattice, fully occupied by lipids of types A and B, where lipid A has the higher intrinsic curvature (e.g., cardiolipin). The lattice is hexagonal, except where noted, with lattice spacing a = 1 nm. The intrinsic curvature of the lipids and their positions determine a curvature function C_lipid(r) (see Eq. 4). In the lattice model, the membrane energy can be written as E = E_elastic + E_int (see Eqs. 3 and 5), where

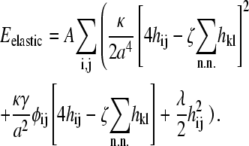(22)

Here, h_ij is the height of the membrane at lattice site (i, j), and φ_ij = 1 if there is a lipid of type A at site (i, j), whereas φ_ij = 0 otherwise. The innermost sums are over the nearest neighbors (k, l) of the lattice site (i, j), and the prefactor ζ is 2/3 for a hexagonal lattice and 1 for a square lattice. For a hexagonal lattice, the area per lipid is 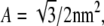whereas for a square lattice A = 1 nm². We assume that the lipid-lipid interaction energy E_int involves only nearest-neighbor pairs (see Eq. 5).By recasting the matrix h_ij as a vector h_n, where the label n represents the sites (i, j), we can write the membrane elastic energy as

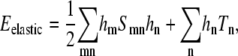(23)

where S is a real, symmetric matrix that does not depend on the lipid type variables, φ_n ≡ φ_ij, and

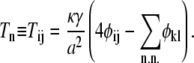(24)

(Small modifications to Eqs. 22 and 24 must be made at the boundaries of a nonperiodic simulation cell.) In Dirac notation, we can rewrite Eq. 23 as

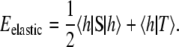(25)

In our simulations, we first minimize the membrane energy with respect to the height field h_n, which gives Equivalently, in Dirac notation, S|h〉 = − |T〉 ⇒ |h〉 = − S⁻¹|T〉, thus

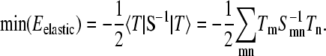(26)

Since the matrix S does not depend on the type variables φ_ij, S⁻¹ need only be calculated once, whereas T must be updated every time φ_ij changes. Therefore, the minimization of E_elastic for a given membrane configuration requires only a single matrix multiplication.We then use a Metropolis Monte Carlo algorithm to minimize the total energy of the membrane. Randomly selected pairs of unlike lipids are exchanged with probability where E_i and E_f are the total membrane energy before and after the move, respectively, until the distribution of lipid domain sizes reaches steady state.