Solubility of Lysozyme in Polyethylene Glycol-Electrolyte Mixtures: The Depletion Interaction and Ion-Specific Effects

Abstract

The solubility of aqueous solutions of lysozyme in the presence of polyethylene glycol and various alkaline salts was studied experimentally. The protein-electrolyte mixture was titrated with polyethylene glycol, and when precipitation of the protein occurred, a strong increase of the absorbance at 340 nm was observed. The solubility data were obtained as a function of experimental variables such as protein and electrolyte concentrations, electrolyte type, degree of polymerization of polyethylene glycol, and pH of the solution; the last defines the net charge of the lysozyme. The results indicate that the solubility of lysozyme decreases with the addition of polyethylene glycol; the solubility is lower for a polyethylene glycol with a higher degree of polymerization. Further, the logarithm of the protein solubility is a linear function of the polyethylene glycol concentration. The process is reversible and the protein remains in its native form. An increase of the electrolyte (NaCl) concentration decreases the solubility of lysozyme in the presence and absence of polyethylene glycol. The effect can be explained by the screening of the charged amino residues of the protein. The solubility experiments were performed at two different pH values (pH = 4.0 and 6.0), where the lysozyme net charge was +11 and +8, respectively. Ion-specific effects were systematically investigated. Anions such as Br⁻, Cl⁻, F⁻, and 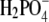(all in combination with Na⁺), when acting as counterions to a protein with positive net charge, exhibit a strong effect on the lysozyme solubility. The differences in protein solubility for chloride solutions with different cations Cs⁺, K⁺, and Na⁺ (coions) were much smaller. The results at pH = 4.0 show that anions decrease the lysozyme solubility in the order 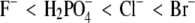(the inverse Hofmeister series), whereas cations follow the direct Hofmeister series (Cs⁺ < K⁺ < Na⁺) in this situation.

INTRODUCTION

Proteins are essential components of organisms and participate in many processes within living cells. They are composed of amino acids joined by peptide groups. Proteins are constructed from amino acids that contain both amine 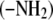and carboxyl 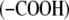groups which may ionize in water and therefore carry positive and/or negative charges. These charges are responsible for the long-range electrostatic interaction. Due to the complex structure of protein molecules, as well as complicated water-mediated protein-protein and protein-electrolyte interactions, a quantitative understanding of the properties of these solutions is still emerging.

Studies of protein separation are motivated by an increasing demand for pure proteins in the pharmaceutical and related industries (1). The precipitation of proteins can be achieved by the addition of a salt or of a neutral component, for example, a nonadsorbing polymer. It is generally accepted that the addition of a simple electrolyte screens the electrostatic repulsion between charged proteins, whereas the addition of a polymer gives rise to the so-called depletion interaction. These two effects decrease the protein solubility, which may eventually precipitate. For the selective separation of biological macromolecules from mixtures, both methods of precipitation can be used. Hoskins et al. (2), for example, studied the separation of proteins in bovine serum albumin-globulin and bovine serum albumin-lysozyme mixtures by controlling the pH of solution and by varying the low molecular electrolyte and dextran concentrations.

The addition of an uncharged polymer to a solution of a protein (or suspension of colloidal particles) induces effective attraction between proteins (colloids), which is known as the depletion interaction, first proposed theoretically by Asakura and Oosawa (3). In a situation where protein molecules or colloidal particles normally repel each other, their interaction may become attractive in the presence of a sufficient amount of nonadsorbing polymer. The attraction is caused by the polymer segments being excluded from the zone between the two proteins, also called the depletion zone. An overlap of the depletion zones favors an increase in the volume accessible to the polymers and in this way increases the entropy of the system. This interaction results in aggregation of protein molecules, which is sufficiently gentle for the proteins not to denature. Many studies have been reported, both experimental and theoretical, to elucidate this interaction (4–11).

Monte Carlo simulations, based on simplified models, have contributed significantly toward the better understanding of the depletion interaction (4–6). Such simulations correctly predict how the depletion interaction depends on the degree of polymerization and concentration of polymer. In some cases, even a quantitative agreement between experimental data and theory was obtained (7–9). Other research has shown that the influence of polymer addition may not always be attractive; in solutions diluted with respect to polyethylene glycol (PEG), a repulsion interaction between proteins was observed (10,11).

To predict the optimal conditions for phase separation, experimental information about the ternary system containing a protein, an aqueous solution of a low molecular weight electrolyte, and a polymer is needed. Despite this fact, there seem to be only a few such studies published so far (12–14). Among these, we should mention the work of Atha and Ingham (12), who determined solubility curves for several proteins, using PEGs of various degrees of polymerization and at varying pH in the solution. These authors showed that the amount of PEG needed for aggregation depends on the protein net charge and on the degree of polymerization of the polymer. It was found empirically (12) that the logarithm of the protein solubility varies linearly with the mass fraction of the polymer in solution.

Precipitation of proteins by the addition of a salt was studied in a large number of publications, and it is impossible to list all the important contributions here. Experimental and theoretical data related to our investigation can be found (15–24). The properties of protein solutions were studied as a function of the electrolyte concentration and for several pH values by Prausnitz and his group, using a variety of physicochemical methods (17,18,21). Effects of pH, protein, and salt concentration were examined theoretically using the Monte Carlo (22,23) and molecular dynamics (24) approaches. The conclusion of these and other studies is that the addition of a low molecular weight electrolyte screens the long-range repulsive forces between equally charged proteins, which may eventually result in protein precipitation.

The nonspecific electrolyte effect (electrostatic screening) described above is only part of the story. For example, two different +1:−1 electrolytes at the same concentration may produce different effects on protein solubility. This phenomenon has long been known; in 1888 Hofmeister (25) reported how different salts in water affect the solubility of proteins. In this work, we think of the Hofmeister series as a list of ions ranked in terms of how efficient they are in precipitating nonpolar solutes, such as benzene (26).

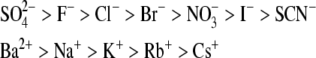(1)

As evident, the 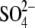and Ba²⁺ ions are the most, and SCN⁻ and Cs⁺ ions the least efficient in this respect. This ordering is called the direct Hofmeister series. Many different theories have been proposed to explain these effects. It is generally believed that water, through water-ion interactions, plays a dominant role in creating such a series. Small ions with large electron density order the water structure (kosmotropes) and therefore have more water molecules in their hydration shells, whereas bigger ions break the water structure and are called chaotropes. Solvation effects are reflected in properties of electrolytes and can be qualitatively explained by simple water models (27,28).

In mixtures of biological macromolecules and low molecular weight electrolytes, the ion-specific effects are the largest in cases where the anions act as counterions. Collins (28) suggested that such effects are due to the distribution of electron density in the water molecule. Anions of a more hydrophobic nature (chaotropes), such as 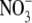and SCN⁻, can penetrate deeper into the protein region and decrease the net charge more efficiently. Other authors have emphasized the role of dispersion forces (29–32). For example, in a study by Finet et al. (33) the scattering curves for α− and γ-crystallin solutions at two different pHs were determined. At low pH, where the net charge of the protein is positive, the authors found an inverse Hofmeister series for anions, whereas at higher pH, where the net charge is negative, the reversed Hofmeister series was obtained. One explanation for this effect, suggested on the basis of experimental data (30), is that the screening ability of an ion is related to its degree of hydration. A short review of current thought in this field is presented in Kunz (34) and the references cited therein.

Lysozyme is one of the most studied proteins (35–37). Riès-Kautt et al. (35,36) have determined solubility curves of lysozyme for various types and ionic strengths of added electrolyte and for different pH values of the solution. These authors concluded that the protein's solubility can change enormously by replacing one electrolyte with another. Chodankar and Aswal (37) found the inverse Hofmeister series (an order opposite to that shown in Eq. 1) for F⁻, Cl⁻, and Br⁻ in lysozyme solution when performing small angle neutron scattering measurements.

In this work ternary mixtures of protein, polymer, and a simple electrolyte were investigated. We were interested in the combined effect of a low molecular weight electrolyte and a nonadsorbing polymer on the solubility of lysozyme in water. To get a clearer picture about the factors determining the stability of lysozyme, we systematically examined the variations in solubility caused by a number of experimental parameters. Lysozyme was dissolved in aqueous solutions of NaCl, NaBr, NaF, NaH₂PO₄, KCl, and CsCl at pH = 4.0 (net charge on lysozyme +11) and then titrated with a solution of PEG. The effect of the degree of polymerization was examined by using PEG of three different (relative) molar masses: M₂ = 3000, 10,000, and 20,000. The effect of the protein net charge was studied for pH values of 4.0 and 6.0 (net charge +8), all in the presence of a 0.20 M solution of NaCl. The influence of the electrolyte concentration was investigated for pH = 4.0, varying the NaCl concentration from 0.20, (0.25) to 0.30 M. Finally, ion-specific effects were examined at pH = 4.0 by varying the type of anion (the cation was Na⁺), starting with F⁻ (NaF), Cl⁻, Br⁻ to 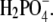In the next set of experiments we varied the cations, from Na⁺ (NaCl), K⁺, to Cs⁺, whereas the anion (Cl⁻) was the same in all cases. The results are presented in the form of solubility curves for ternary mixtures containing lysozyme, PEG, and the aforementioned electrolytes. The focus of this research is the ion-specific effect, as reflected in the ordering of ions, on the solubility of lysozyme. The systematic examination of this effect presented here should contribute toward a better understanding of lysozyme interactions in ternary systems with PEG and various electrolytes. To the best of our knowledge this is the first such study.

Theoretical analysis

The experimental data necessarily apply to definite state points within the limited range of concentrations. To be able to efficiently interpolate between the measured points, or even to predict the solution's properties outside this range, we need a theoretical analysis. In this study we follow the analysis proposed by Atha and Ingham (12). Their approach is designed to treat the effects of the addition of PEG to protein-electrolyte mixtures. According to these authors the chemical potential of protein (μ₃; component 3) in such systems can be expressed as (12)

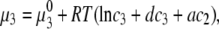(2)

where polymer (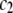) and protein (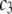) concentrations have units of mol/L and the term 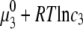refers to the ideal state of pure protein (12). The terms ac₂ and dc₃, therefore, define the deviations from ideality due to interaction between various species. The coefficients a and d refer to the protein-PEG and protein-protein interactions, respectively. Coefficients that are higher than second-order in virial expansion are neglected in this analysis (12). According to this approach, the protein-electrolyte mixture in water is treated as an effective two-component system, with only two explicit components: PEG and protein. All the effects of electrolyte and water are subsumed in the interaction parameter d; in absence of PEG the approach resembles the effective one-component model, which has been used many times before. The chemical potential of the protein under conditions of saturation in the absence 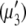and presence 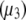of PEG is written as

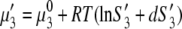(3a)

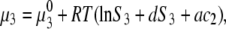(3b)

where S₃ and S₃′ denote the solubility of protein in the presence and absence of polymer. Note that Eqs. 3a and 3b apply to the equal concentration of the particular electrolyte. As the concentration of PEG increases, the chemical potential of the protein increases, and when it eventually exceeds the chemical potential of the solid phase, μ₃(solid), precipitation occurs. For μ₃(solution) = μ₃(solid), we can equate Eqs. 3a and 3b to obtain

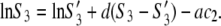(4)

Our measurements were performed at relatively high initial lysozyme concentrations and for electrolyte concentrations of 0.20 M or higher; strong screening of the protein-protein interaction is expected under these conditions. Numerical analysis based on Eq. 4 indicates that the quality of the agreement between experimental and calculated values does not depend on the value of parameter d. Considering this we can assume that the second term on the right-hand side of the expression above is small. In such a case, Eq. 4 can further be simplified to yield

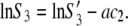(5)

The resulting function predicts a linear dependence of the logarithm of protein solubility with respect to the PEG concentration c₂. Values of constants S₃′ and a depend on the electrolyte type and concentration. The highest solubility (S₃′) is obtained in the absence of PEG.

MATERIALS AND METHODS

Materials

Lysozyme was purchased from Merck (Darmstadt, Germany), product No. 105281, lot K35888481 709. Alkaline salts (>99%, NaF, NaCl, NaH₂PO₄, KCl, and CsCl) were also from Merck, and NaBr was obtained from Kemika (>99%; Zagreb, Croatia). PEGs (peroxides < 0.001%) were purchased from Merck PEG-3000 (M₂ = 2700–3300), PEG-10,000 (M₂ = 8500–11,500), and PEG-20,000 (M₂ = 16,000–24,000).

Methods

The lysozyme concentration was determined using a Cary 1 (Varian, Palo Alto, CA) two-beam spectrophotometer, which uses a Peltier block for temperature regulation. The same spectrophotometer was also used as a turbidity meter. Circular dichroism (CD) spectra were taken to check for possible conformational changes during precipitation. For this purpose we used an AVIV 62A DS CD spectrometer (Lakewood, NJ). pH was measured by an Iskra pH meter (Ljubljana, Slovenia), model MA5740, using a combined glass microelectrode of type InLab 423 from Mettler Toledo (Columbus, OH).

Experimental procedure

The salts were dried at T = 130°C for 2 h in the presence of P₂O₅. Demineralized water was distilled twice in a quartz bidistillation apparatus (Destamat Bi 18E; Heraeus, Hanau, Germany). Aqueous solutions of various salts (NaF, NaCl, NaBr, NaH₂PO₄, KCl, and CsCl) at concentrations of 0.20 M, 0.25 M, and 0.30 M were prepared gravimetrically. The concentration of chlorides was checked with titration by AgNO₃. A chloride electrode was used as an indicator electrode, and an antimony electrode served as a reference. PEG was weighed and dissolved in electrolyte solutions. Three different concentrations of PEG were prepared: c₂ = 0.60 g/mL for PEG-3000, c₂ = 0.45 g/mL for PEG-10,000, and c₂ = 0.30 g/mL for PEG-20,000. All PEG solutions were filtered through a 1.2 μm filter.

Lysozyme was checked for the presence of various ionic species; a small amount of chloride ion was detected. Note that most of our experiments were performed in the presence of excess chloride ions stemming from various alkaline chlorides. Accordingly, lysozyme was in most cases (see also the subsection “Ion-specific effects in the case of simple +1:−1 electrolytes”) used without further purification, dissolved in the same salt solution as PEG, and filtered through a 0.45 μm filter. The protein concentration was measured spectrophotometrically at λ = 280 nm, using the extinction coefficient ɛ = 2.635 dm³/(g·cm) (38). pH values of both PEG and lysozyme mixtures with electrolyte were adjusted with a small amount of acid or base to pH = 4.0. HCl and NaOH solutions were used for pH adjustment in the case of PEG (or protein) mixtures with NaCl. A similar procedure was applied for other electrolytes and concentrations. The majority of experiments were performed at pH = 4.0 ± 0.1; a few others were performed at pH = 6.0. Protein solutions were always used immediately after preparation to avoid any conformational or pH changes.

Experiments were performed at T = (25.0°C ± 0.1°C); temperature regulation was important since lysozyme solubility depends on temperature (39). A total of 600 μL of lysozyme solution was placed in a cuvette and titrated with a solution of PEG. The reference cuvette contained a solution of simple electrolyte (no lysozyme present), which was titrated with PEG solution of the same concentration. The difference between the absorbance of the sample and reference was monitored by the spectrophotometer. After every addition of PEG, the sample was thoroughly mixed. The advent of protein aggregation was detected by an increase in solution absorbance at a wavelength of λ = 340 nm, being sensitive only to the presence of precipitate (40). This experimental procedure was previously used by De Young et al. (40).

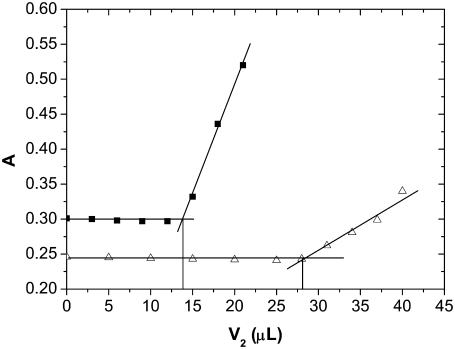
An example of a titration curve is given in Fig. 1. The curve shows the absorbance at λ = 340 nm, monitored during the titration of a lysozyme-electrolyte mixture with PEG. Examples are presented for two different initial concentrations of protein: i), c₃ = 190 g/L (solid symbols); and ii), c₃ = 160 g/L (open symbols), both in 0.20 M NaCl and titrated with PEG-20,000 at a concentration of c₂ = 0.30 g/mL. When conditions for protein aggregation are fulfilled, the absorbance sharply increases due to the precipitate present in the solution, as clearly seen in Fig. 1. During the titration with PEG, solution became more and more viscous. At the end, solution became completely turbid but the precipitated (crystalline-like) protein could be isolated by centrifuge and dissolved again. For a lysozyme concentration equal to 190 g/L, this happened when V₂ = 15 μL of PEG was added to the system, whereas in the case of the lower protein concentration (c₃ = 160 g/L) more PEG was needed; V₂ was 31 μL in this case. The volume of PEG needed for protein aggregation, as shown in Fig. 1, was determined as the intersection of two straight lines. The concentration of protein and PEG at the solubility point was calculated by assuming the additivity of volumes. One may argue that the increased absorbance of the mixture could be due to PEG itself. For this reason we measured absorbance (again at λ = 340 nm) of PEG-20,000 at the concentration c₂ = 0.30 g/mL in 0.20 M NaCl. The resulting absorbance was so small, A = 0.032, that it could be ignored. pH was checked before titration and at the end of it. The maximum deviations from the starting pH were only about ±0.1. Note that no buffer was added to the solution.

FIGURE 1.

Absorbance (λ = 340 nm; T = 25.0°C) during the PEG titration of lysozyme solution at pH = 4.0. Examples are shown for an initial protein solution c₃ = 190 g/L (solid symbols) and c₃ = 160 g/L (open symbols) in 0.20 M NaCl titrated with c₂ = 0.30 g/mL PEG-20,000.

RESULTS AND DISCUSSION

Precipitation by the addition of a nonadsorbing polymer and precipitation by a low molecular weight electrolyte are two of the most common methods of protein precipitation. To study these two effects combined, we utilized the experimental method described in the previous section. Experimental results for lysozyme as a representative protein are shown in Figs. 2–6. In the ternary system containing protein, PEG, and a low molecular weight electrolyte, a number of experimental parameters can be varied. First, it is possible to vary the concentrations of the components present in the system. Second, the pH of the solution can be adjusted to obtain the desired protein net charge. Third, the molecular weight (degree of polymerization) of PEG is another variable that influences the solubility of protein. Finally, it is the salt type, i.e., the cation and anion combination present in the system, which has a strong influence on the solubility of proteins. In what follows, we systematically examine the influence of these parameters.

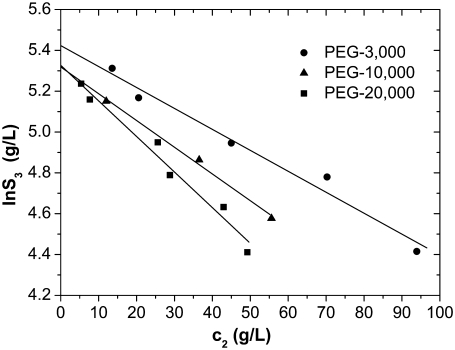
FIGURE 2.

Solubility curves of lysozyme at pH = 4.0 in 0.20 M NaCl, obtained by titration with c₂ = 0.60 g/mL PEG-3000 (circles), c₂ = 0.45 g/mL PEG-10,000 (triangles), and c₂ = 0.30 g/mL PEG-20,000 (squares). Lines represent the results of least squares fit of experimental data by Eq. 5.

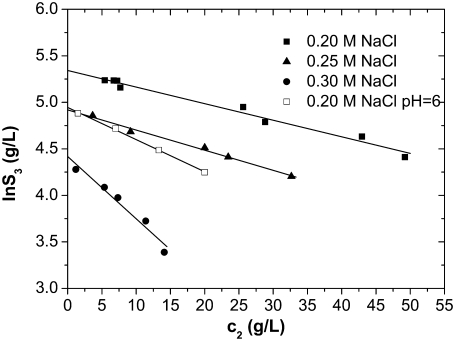
FIGURE 3.

Solubility curves of lysozyme at pH = 4.0 and 6.0 as obtained after titration with c₂ = 0.30 g/mL PEG-20,000 at various NaCl concentrations: 0.20 M (squares), 0.25 M (triangles), and 0.30 M (circles). Solid symbols correspond to pH = 4.0 and open to pH = 6.0. Lines are as for Fig. 2.

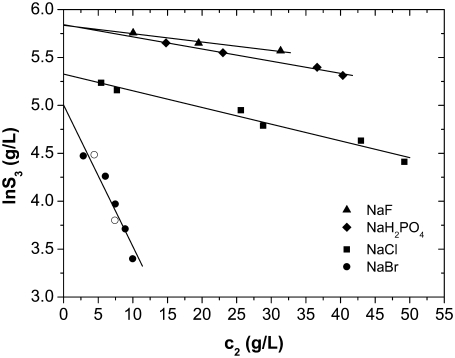
FIGURE 4.

Solubility curves of lysozyme at pH = 4.0 in 0.20 M NaCl (squares), NaBr (circles, open circles after dialysis; see text), NaH₂PO₄ (diamonds), and NaF (triangles) obtained by titration with c₂ = 0.30 g/mL PEG-20,000. Lines are as for Fig. 2.

FIGURE 5.

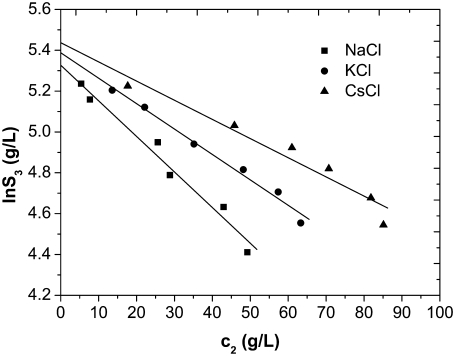
Solubility curves of lysozyme at pH = 4.0 in 0.20 M NaCl (squares), KCl (circles), and CsCl (triangles) obtained after titration with c₂ = 0.30 g/mL PEG-20,000. Lines are as for Fig. 2.

FIGURE 6.

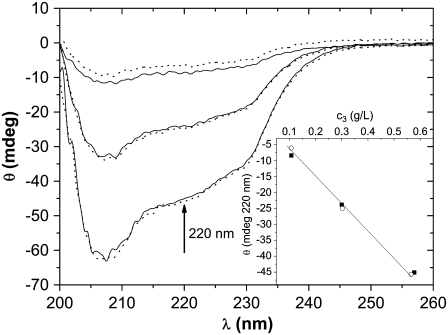
CD spectra before (solid line) and after (dotted line) precipitation of lysozyme for various protein concentrations (c₃). (From bottom to top) 0.57 g/L, 0.30 g/L, and 0.11 g/L. (Inset) ellipticity θ versus protein concentration at λ = 220 nm. Solid symbols correspond to ellipticity before and open after aggregation. The experiment was performed at pH = 4.0 in 0.20 M NaCl and PEG-20,000 (c₂ = 0.30 g/mL).

Effect of degree of polymerization of PEG

We start our discussion by investigating the effect of the degree of polymerization of PEG on the solubility of lysozyme. These kinds of studies are rare: one similar examination was described by Atha and Ingham (12). These authors determined the solubility of human serum albumin as a function of the molecular weight of PEG, varied in the range M₂ = 400–20,000.

In this work we examined the effect of the degree of polymerization, N, of PEG for a ternary system where lysozyme was dissolved in 0.20 M NaCl and the pH of the solution was adjusted to 4.0, where the net charge of lysozyme is +11 (41). The protein solution was stable under these conditions; the stability was checked by monitoring the absorbance at λ = 340 nm. PEGs of different molar mass were used: PEG-3000, PEG-10,000, and PEG-20,000, the number indicating the relative molar mass. The molecular mass of the monomer unit is 44 g/mol, which means that in the case of PEG-3000, the degree of polymerization N is ∼68, for PEG-10,000, the degree of polymerization N ≈ 227, and for PEG-20,000, the degree of polymerization N is ∼445. Since the polymer was polydisperse, we can only speak of an average value of N. Before titration the PEGs were dissolved in 0.20 M NaCl at pH = 4.0.

In Fig. 2 the solubility curves for lysozyme in the presence of PEG with different degrees of polymerization are presented. Circles refer to PEG-3000, triangles to PEG-10,000, and squares to PEG-20,000. Notice that the solubility of pure PEG in water depends on the degree of polymerization and is ∼50 weight %. Different concentrations of PEG were needed to achieve lysozyme precipitation. For PEG-3000 this concentration was c₂ = 0.60 g/mL, for PEG-10,000 it was c₂ = 0.45 g/mL, and for PEG-20,000, only 0.30 g/mL of PEG was needed for the protein to precipitate. As indicated in Fig. 2, only a minute amount of PEG was needed to trigger precipitation at high protein concentration. The experimental data were fitted to Eq. 5, and these results are shown in Fig. 2 by lines. Within experimental uncertainty we obtained a linear dependence between the logarithm of the protein solubility and the PEG concentration, exactly as suggested by Eq. 5. In Table 1 we present the values of S₃′, that is, the solubility of lysozyme in the absence of PEG, and values of the protein-PEG interaction coefficient a, which yield good agreement with the experimental data for these three cases.

TABLE 1.

Lysozyme solubility in the absence of PEG, S₃′, and protein-PEG interaction coefficient a as obtained from a least squares fit of the experimental data by Eq. 5

	S3′ (g/L)	a (L/g)	a (L/mol)
PEG-3000	230	0.010	31
PEG-10,000	200	0.013	130
PEG-20,000	210	0.018	360

pH = 4.0 and for 0.20 M NaCl. The number of significant figures is defined by the mean value of the standard deviation.

The coefficient a given in Table 1 in units of L/g and L/mol determines the slope of the line. By extrapolation to zero PEG concentration we obtained the solubility of lysozyme in 0.20 M NaCl as S₃′ = ∼210 g/L for both PEG-10,000 and PEG-20,000. A similar extrapolation performed for the PEG-3000 results gave a somewhat higher value. As seen from Table 1, the values of S₃′ calculated from these measurements are within 10%. This consistency yields some confidence in the accuracy of our experiments. Despite an intensive literature search, we were not able to find any information about lysozyme solubility under these experimental conditions (0.20 M NaCl, no buffer present, 25.0°C). For this reason, and to examine the accuracy of our results further, we performed a separate experiment in which the solubility of lysozyme in a mixture with electrolyte (PEG-free solution) was determined. The solubility of lysozyme in 0.20 M NaCl was found to be S₃′ = 230 g/L at 25.0°C, which is close to the average value obtained from extrapolation to zero PEG concentration for the PEG samples examined here (Table 1).

Depletion precipitation is an entropy-driven process. The number of possible polymer conformations increases with chain length, so the entropy loss in the zone between two proteins becomes larger. PEG with a higher degree of polymerization is therefore expected to be more efficient in protein precipitation; lysozyme should reach the solubility point at a lower PEG concentration. The amount of PEG needed to precipitate lysozyme decreases in the order PEG-3000 > PEG-10,000 > PEG-20,000. This finding is in agreement with the conclusions reported in Atha and Ingham (12), as well as with theoretical predictions (6) based on a simplified model. Under the conditions studied here, the differences between PEG-10,000 and PEG-20,000 are smaller than those between the PEG-3000 and PEG-10,000.

Effect of the electrolyte concentration

The solubility of proteins in aqueous solutions depends on the concentration of electrolyte present in such mixtures, and most often it decreases with increasing electrolyte concentration. The effect is ascribed to the screening of the charges on proteins (16,17,20,35,36). A good measure of nonspecific electrolyte influence is provided by the Debye screening length

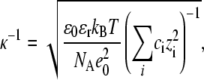(6)

where c_i and z_i are the concentration and the valence of the electrolyte i, 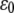and 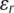the dielectric constants of a vacuum and pure solvent ( 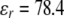at T = 298 K), respectively, k_B is the Boltzmann constant, and N_A is Avogadro's number.

The solubility experiments were performed for 0.20 M, 0.25 M, and 0.30 M solutions of NaCl in water, using c₂ = 0.30 g/mL PEG-20,000. In Fig. 3 we present solubility curves for lysozyme solution at pH = 4.0 for different concentrations of NaCl: 0.20 M as squares, 0.25 M as triangles, and 0.30 M as circles. The Debye length is 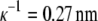for 0.20 M NaCl, 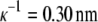for 0.25 M NaCl, and for 0.30 M NaCl. As seen from Fig. 3, by increasing the electrolyte concentration from 0.20 M to 0.25 M, it is possible to decrease the solubility of lysozyme. Constants S₃′ and a, obtained from fitting the experimental data to Eq. 5, are given in Table 2. The lysozyme solubility in the absence of PEG (S₃′) in 0.20 M NaCl, as mentioned before, was found to be ∼210 g/L. For lysozyme in 0.25 M NaCl this value was ∼140 g/L, and in 0.30 M NaCl it was only ∼80 g/L. It is obvious that small differences in screening lengths result in large differences in solubility.

TABLE 2.

Coefficients S₃′ and a as obtained from the least squares fit of the experimental data by Eq. 5

	S3′ (g/L)	a (L/g)	a (L/mol)
0.20 M NaCl; pH = 6.0	140	0.035	690
0.25 M NaCl	140	0.022	430
0.30 M NaCl	83	0.067	1300

pH = 4.0 (unless otherwise specified) and PEG-20,000 (c₂ = 0.30 g/mL) for various NaCl concentrations.

There are some experimental limitations which we wish to mention here. For various reasons, it is difficult to determine the solubility, S₃, at low protein concentrations. One limitation is the sensitivity of the spectrophotometer. Another is the fact that by adding a substantial amount of PEG (or PEG with a higher degree of polymerization) the solution becomes very viscous and difficult to stir. To estimate the uncertainties in the determination of solubility S₃, we performed three independent titrations with PEG. For each experiment, salt, protein, and PEG solutions were freshly prepared. The measurements were performed for initial protein concentrations of c₃ = ∼190 g/L. The results are shown in Fig. 3 (solid squares), and we can see that the errors in solubility determinations are relatively small. The error is larger at lower protein concentration because the difference in signal before and after aggregation is smaller in such situations (Fig. 1).

Effect of the pH of solution

The pH of solution determines the ionization of amino acids and therefore the protein net charge in solution. To explore how the net charge of lysozyme affects its solubility, we performed the PEG titrations not only for pH = 4.0 (lysozyme net charge is +11) but also for pH = 6.0 (net charge is +8). The experiments were performed for a 0.20 M solution of NaCl in water, using c₂ = 0.30 g/mL PEG-20,000. In Fig. 3 the results for solutions with pH = 6.0 are represented by open squares. In this case considerably smaller amounts of PEG were needed to aggregate the protein. For example, only 5 g/L of PEG was needed to precipitate the protein (S₃ = 100 g/L) at pH = 6.0 and 33 g/L at pH = 4.0. From Eq. 5 we calculated the solubility in this case to be S₃′ = 140 g/L (Table 2). We also attempted to obtain the solubility curve for pH = 8.0, where the net charge is further reduced to +7. A strong decrease in solubility was observed in this case, and we estimated S₃′ to be ∼10 g/L. Shih et al. (16) report the same pH dependence of lysozyme solubility in a mixture with various electrolytes (no PEG present) but for higher ionic strengths than studied here.

Ion-specific effects in the case of simple +1:−1 electrolytes

At pH = 4.0, where the net charge is +11, the lysozyme molecules are expected to repel each other due to Coulomb repulsion. When a simple salt is added to such a system, the additional ions screen the charged amino acid residues and the repulsion between the proteins is reduced. As a consequence the proteins can approach each other, and short-range forces should become more important (15,21,23,24). To investigate the ion-specific effects in lysozyme solution, i) we performed experiments by varying the anion (from F⁻, Cl⁻, Br⁻ to 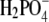), keeping the same cation (Na⁺) in all cases; and ii) in separate experiments, we studied various chlorides: the cations were varied from Na⁺, K⁺ to Cs⁺. The solubility curves presented in Figs. 4 and 5 were obtained by titration of the protein with PEG-20,000 (c₂ = 0.30 g/mL) in the presence of electrolyte with a concentration of 0.20 M.

First, we discuss the situation where we vary the anions; note that anions (net charge of the lysozyme molecule is positive) are counterions here. The results for F⁻ in Fig. 4 are represented by triangles, for 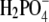by diamonds, for Cl⁻ by squares, and for Br⁻ ions by circles. Fig. 4 (cf. also Table 3) shows significant differences in the solubility of lysozyme obtained by varying the anion. In the case of Br⁻ (in NaBr), the solubility of lysozyme in the absence of PEG, S₃′, as obtained from extrapolation on the basis of Eq. 5, is ∼140 g/L. For Cl⁻ (NaCl), this value is 210 g/L, and for the F⁻ and 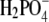ion as a counterion (NaF, NaH₂PO₄), the value of S₃′ increases to 340 g/L. It should be mentioned that the pK_a of hydrofluoric acid is ∼3 and that at pH = 4.0, the concentration of F⁻ could be a bit lower than 0.20 M. This could be a reason for very high solubility of lysozyme in NaF. Further, we found coefficient a to be much higher for Br⁻ than for the Cl⁻, F⁻, and 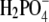counterions at this electrolyte concentration (0.20 M). It is worth mentioning that we found the solubility of lysozyme in a 0.20 M solution of I⁻ ions (NaI) and 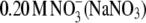to be very low, i.e., S₃′ = ∼5 g/L. As mentioned, lysozyme solubilities were determined for various electrolytes in buffer solutions (34). It seems that the addition of buffer decreases the solubility but does not change the lysozyme-electrolyte interactions.

TABLE 3.

Coefficients S₃′ and a as obtained from the least squares fit of the experimental data by Eq. 5

	S3′ (g/L)	a (L/g)	a (L/mol)
NaF	340	0.0087	170
NaH2PO4	340	0.013	250
NaBr	140	0.14	2900
KCl	220	0.013	250
CsCl	230	0.0094	190

pH = 4.0 and PEG-20,000 (c₂ = 0.30 g/mL) for 0.20 M solutions of various electrolytes.

To check for possible interference of chloride ions emanated from protein itself (see section “Experimental procedure”), we performed separate experiments, where protein was dissolved in 0.20 M NaBr solution at pH = 4.0. To substitute chloride ions with Br⁻, the solution was dialyzed against 0.20 M NaBr at pH = 4.0. A dialysis cassette Slide-A-Lyser (Pierce, Rockford, IL), with a 3500 Da cutoff was used for this purpose. After the dialysis, the protein solution was processed as usual. These new results are shown in Fig. 4 with open circles. It is easy to see that the new results agree within experimental uncertainties with those obtained without dialysis (solid circles). We can therefore conclude that the presence of chloride ions emanated from proteins does not influence the results.

Halide anions studied were chosen to vary systematically in ionic crystal size, from the smallest F⁻ to the largest Br⁻ (due to the low solubility, no results for I⁻ are reported here). It is generally accepted that the F⁻ ion orders the water structure and as such is a typical representative of the kosmotropes. The same applies to the 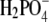ion, which is, due to its structure, also classified as a kosmotrope. The Cl⁻ ion is found to have a marginal effect on water structure, whereas Br⁻ breaks the water structure and is a typical chaotrope (27,28,42). The F⁻ ion is more strongly hydrated than the other ions; their sizes when hydrated increase in the order 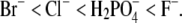Strongly hydrated anions are unable to “screen” the protein charges as efficiently as weakly hydrated ones: the latter can approach closer to the protein charges (28,43,44). The results presented in Fig. 4 and the results published in Shih (16) and Riès-Kautt and Ducruix (35) support the idea of protein solubility being related to the screening efficiency of the counterions present in solution. The same conclusion has also been arrived at in other studies, most recently in a molecular dynamics study of short ionene molecules with F⁻, Cl⁻, Br⁻, and I⁻ ions as counterions (45).

In Fig. 5 we show the solubility data for the case of different chlorides; the results for the Na⁺ ion (NaCl) are represented by squares, for K⁺ by circles, and for the Cs⁺ ion by triangles. These results reveal that varying the coion has less effect on protein solubility. Fig. 5 shows that the amount of PEG needed to solubilize the protein is the largest in the presence of Cs⁺ (CsCl) and the smallest in the presence of Na⁺ (NaCl) ions in the system. Our analysis, based on Eq. 5 (results are presented in Table 3), indicates that solubility in the absence of PEG (S₃′) increases in order from NaCl through KCl to CsCl.

Notice that not all experimental methods reveal differences in effects produced by the different cations (even if they act as counterions) present in solution. When x-ray measurements were performed in lysozyme salt solutions (I = 0.15), no differences in the results obtained for various cations were found, even at scattering vectors lower than 0.05 (46). On the other hand, Grigsby et al. (47) studied lysozyme solubility in various electrolyte solutions at pH = 4.0 by performing cloud point measurements. Considerable differences in the results for different cations were observed, and the solubilities followed the direct Hofmeister series.

It seems interesting to discuss the results for cations in relation to their ability to order water molecules. Among these ions Na⁺ is a typical kosmotrope, being the most disruptive of water hydrogen bonding. The potassium ion in this case is in the middle of the series, and Cs⁺ is generally accepted to be a chaotrope (27). The ion sizes when hydrated increase in the order Cs⁺ < K⁺ < Na⁺. Considering that cations are coions in this situation, they are expected to be distributed away from the positively charged proteins. The actual situation may not be that simple. The positive net charge of the lysozyme molecule is a result of the subtraction of the positive and negative charges. In other words, besides positively charged groups there are also negatively charged ones present on proteins. Weakly hydrated ions, such as Cs⁺, are expected to screen the patches of negative charges more efficiently than more strongly hydrated ions. There is, however, another effect which should not be ignored. When strongly hydrated ions, such as Na⁺, compete for water with a protein, they decrease the hydration of a protein and consequently its solubility (48). Both effects would predict the correct ordering of coions with respect to the solubility decrease (Fig. 5).

Lysozyme denatures under conditions where the net charge on the molecule is negative. We can therefore only speculate about the ionic series for the hypothetical case when the lysozyme net charge is negative. In such a situation, cations are counterions and anions coions. Sodium as a kosmotrope is expected to have a weaker effect on screening than a strong chaotrope (Cs⁺), and the cations would probably follow the inverse Hofmeister series. In a situation where the anions (coions) are varied in the salt, the direct Hofmeister series is expected. Such an ordering for anions was determined in solutions of α-crystallin using the x-ray diffraction technique (33).

Circular dichroism spectra

To check for protein stability, we recorded CD spectra before and after the precipitation process. CD spectra were taken in the wavelength range λ = 260–200 nm (T = 25.0°C), where the CD signal is sensitive to changes in secondary and ternary structure. The wavelength step was 0.5 nm and the average measuring time 3 s. The aggregation process was monitored for the initial lysozyme concentration c₃ = 190 g/L at pH = 4.0 in 0.20 M NaCl with c₂ = 0.30 g/mL PEG-20,000. First the CD spectrum of the initial protein-electrolyte mixture was recorded. After precipitation the precipitate was dissolved in 0.20 M NaCl salt solution and diluted to a concentration appropriate for CD measurements. Fig. 6 shows the CD spectra before (solid line) and after (dotted line) aggregation. The inset shows the linear dependence of ellipticity, θ, as a function of the protein concentration c₃ at λ = 220 nm. The results confirm that the protein retains (or perhaps regains) its native form upon subsequent dilution and that precipitation under these conditions is reversible. This finding is important because isolation of proteins is useful only if the isolated protein preserves its structure.

CONCLUSIONS

The solubility of lysozyme in a mixture with PEG and various salts was determined under different experimental conditions. As a result the solubility curves were obtained as a function of variables such as the pH of solution, electrolyte concentration, electrolyte type, and degree of polymerization of PEG. All experiments were performed at 25.0°C and for pH values 4.0 and 6.0, where the net charge of lysozyme was +11 and +8, respectively.

The solubility of lysozyme, titrated with PEG in the presence of various low molecular weight electrolytes, was measured by monitoring the absorbance at 340 nm. The precipitated protein could be dissolved again and was found to be in the native state, as indicated by CD spectra measurements. The results show that the solubility of lysozyme decreases with the addition of PEG for all the electrolyte concentrations and types studied here. The solubility decrease depends on the degree of polymerization of PEG: it is larger in the presence of polymer with a higher degree of polymerization. This conclusion is in agreement with the findings of other researchers and is valid for both binary (polymer-colloid or polymer-protein) and ternary (12) (polymer-protein-electrolyte) systems.

Our investigation of salt effects in the presence of PEG confirmed previous observations, for example, Riès-Kautt and Ducruix (35), that the solubility of lysozyme decreases with increasing electrolyte concentration in the mixture. This is valid for all salt types studied here. The pH dependence of the protein solubility was also examined. When the pH of lysozyme solution was increased from pH = 4.0 (net charge +11) to 6.0 (net charge +8), under otherwise identical experimental conditions, a substantial decrease in solubility was observed. In other words, less PEG was needed to precipitate lysozyme at pH = 6.0. This effect can be ascribed to the reduction of the protein net charge from +11 to +8 and has been reported (16) for binary protein-electrolyte mixtures.

For all the systems investigated in this work, the logarithm of the protein solubility was a linear function of the PEG concentration. The experimental data were analyzed using the thermodynamic approach developed in Atha and Ingham (12), which allows determination of the lysozyme solubility in the absence of PEG. The protein-protein interaction coefficient was found to be small under the conditions studied in this work. This finding can be ascribed to the electrostatic screening caused by added salt.

Ion-specific effects were studied by systematically varying the cations and anions in the electrolytes present in the mixture. Anions, acting as counterions, have a large effect on the lysozyme solubility, whereas the influence of cations (serving as coions) is smaller. We may expect this result on the basis of electrostatic considerations; the probability of finding a counterion next to a protein molecule is much higher than it is for a coion. The results show that the anions (in combination with the Na⁺ ion), when ordered by their power to decrease the lysozyme solubility, follow the series 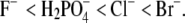In other words, the anions studied here follow the inverse Hofmeister series (Eq. 1). On the other hand, the cations (when in combination with the Cl⁻ ion) follow the order Cs⁺ < K⁺ < Na⁺ (direct Hofmeister series). In summary, to induce lysozyme precipitation, more PEG is needed in the presence of CsCl than in the presence of NaCl. The same ordering of anions was previously observed in PEG-free solutions by the scattering technique (37) and for cations by cloud point measurements (47). Ion-specific effects influencing protein solubility seem to be due to water-mediated interactions between ions and charged groups on the protein molecule. This effect can be correlated with the hydration strength of various ions.

The conclusions emerging from this study are in agreement with previous experimental and theoretical studies of binary protein-electrolyte and protein-polymer systems. It seems that the addition of a nonadsorbing polymer (PEG in this case) does not qualitatively change the lysozyme-electrolyte interaction. This finding includes ion-specific effects. We found this conclusion encouraging; it suggests that, at least qualitatively, the behavior of a ternary system can be predicted on the basis of information about relevant binary systems. This is perhaps the most important conclusion of this work, in which the combined effects of the depletion interaction caused by the presence of PEG and ion-specific effects were systematically examined.