More Gating Charges are Needed to Open a Shaker K⁺ Channel than are Needed to Open an rBIIA Na⁺ Channel

Abstract

This study presents what is, to our knowledge, a novel technique by means of which the ratio of the single gating charges of voltage-gated rat brain IIA (rBIIA) sodium and Shaker potassium ion channels was estimated. In the experiment, multiple tandems of enhanced green fluorescent protein were constructed and inserted into the C-terminals of Na⁺ and K⁺ ion channels. cRNA of Na⁺ and K⁺ ion channels was injected and expressed in Xenopus laevis oocytes. The two electrode voltage-clamp technique allowed us to determine the total gating charge of sodium and potassium ion channels, while a relative measure of the amount of expressed channels could be established on the basis of the quantification of the fluorescence intensity of membrane-bound channels marked by enhanced green fluorescent proteins. As a result, gating charge and fluorescence intensity were found to be positively correlated. A relative comparison of the single gating charges of voltage-gated sodium and potassium ion channels could thus be established: the ratio of the single gating charges of the Shaker potassium channel and the rBIIA sodium channel was found to be 2.5 ± 0.4. Assuming the single channel gating charge of the Shaker K⁺ channel to be ∼13 elementary charges (well supported by other studies), this leads to approximately six elementary charges for the rBIIA sodium channel, which includes a fraction of gating charge that is missed during inactivation.

INTRODUCTION

Voltage-gated ion channels are the elementary units underlying the generation and propagation of biological electrical signals. The voltage sensitivity of voltage-gated ion channels depends mainly on the number of gating charges that move along the electric field of the membrane. Estimation and comparison of the number of gating charges of different voltage-gated ion channels were of interest in many articles. Hodgkin and Huxley (1) had originally proposed that at least 4.5–6 elementary charges fully move across the membrane electric field to open a sodium channel. More recent methods give values at ∼13 elementary charges for the Shaker K⁺ channel and 5–16 for different types of Na⁺ channels.

Among these voltage-gated channels, the K⁺ channels which, due to their simpler structure and kinetics are more easily studied, received most attention. Many studies estimated the number of ion channels in a given sample and correlated it with the total gating charge to determine how many charges move per channel during the gating process. Different techniques were used to measure the number of channels. Aggarwal and MacKinnon (2) expressed Shaker K⁺ channels in Xenopus laevis oocytes and used a radiolabeled α-KTx scorpion toxin that blocks the channel pore with a stoichiometry of 1:1. Division of the total radioactivity by the specific activity of the radiolabeled toxin allowed them to estimate the number of channels. They correlated this number with the total gating charge measured by the two-electrode voltage-clamp technique from the same oocyte, and thus calculated the number of gating charges per channel, which was found to be 13.6 elementary charges. Noceti et al. (3) estimated the number of gating charges per channel by using the limiting slope analysis of the conductance-voltage relationship and by variance analysis. They found that 13 elementary charges are involved in the gating process of the Shaker K⁺ channel and 8.6 elementary charges in the Ca²⁺ channel. Using the same method, Zagotta et al. (4) estimated 12–16 elementary charges for the Shaker K⁺ channel, whereas Schoppa et al. (5) and Islas and Sigworth (6) estimated this number to be 12.5.

Na⁺ channels are less often studied and the presently available data show a large spread for the estimated single gating charge. Conti and Stühmer (7) found that the activation of a single rBIIA sodium channel occurs in two-to-three brief packets, each carrying an equivalent of ≃2.3 elementary charges. This is still in the range of the original figure given by Hodgkin and Huxley (1). Sheets and Hanck (8) estimated the lower limit of the gating charge per channel of the human cardiac Na⁺ channel hH1a to be 5.2 elementary charges. Single channel recordings of the skeletal muscle Na⁺ channel enabled Hirschberg et al. (9) to estimate that at least 12 elementary charges are involved in the gating process. They measured the open probability as a function of membrane potential, which gave them a quantitative indication of the number of gating charges that move through the electric field when the channel switches from the closed to the open state. The measurements done by Kuzmenkin et al. (10) have indicated that the bacterial sodium channel NaChBac needs 16 elementary charges for activation.

The aim of this study is the direct comparison of the single channel gating charge of the Shaker K⁺ and the rBIIA Na⁺ channels and to derive an estimate for the single channel gating charge from the better known K⁺ to the Na⁺ channels by a new approach. To do so, enhanced green fluorescent protein (eGFP) was inserted into the C-terminal of K⁺ and Na⁺ channels on the cDNA level and the resulting channels were studied in Xenopus laevis oocytes. Because the K⁺ channel is a homotetramer, it has four identical nonlinked subunits, each with one C-terminal, whereas the Na⁺ channel has four homologous and covalently linked domains (DI–DIV) and only one C-terminal. As a consequence, insertion of the coding sequence of one eGFP molecule into the C-terminal coding sequence of a K⁺ channel will result in the expression of four eGFP molecules per K⁺ channel (one per each domain), whereas the analogous insertion into the Na⁺ channel will lead to the expression of only one eGFP molecule per channel (see Fig. 1). Multiple eGFP tandems were constructed and inserted into the C-terminal of the Na⁺ and K⁺ channels. The fluorescence intensity of the incorporated eGFP molecules was measured and correlated with the gating charge obtained from the same oocyte. This correlation allows for the comparison of the relative size of the single gating charge between Shaker K⁺ and rBIIA Na⁺ channels. Preliminary work has been done and presented in the literature (11–13).

FIGURE 1.

(A) K⁺ channel construct with one eGFP molecule at the C-terminal of each domain (KG1). The eGFP is inserted at the existing SpeI site (AA 503/4). (B) Na⁺ channel construct with one eGFP molecule at the C-terminal (NaG1). The eGFP is inserted at a newly created SpeI site, which was introduced after AA 1970 by changing the next bases T,C at 5910/11 to A,G. The charge symbols do not reflect the actual number of positive charges in each S4, but the approximate proportional distribution instead.

METHODS

Molecular biology

The cDNA coding for the nonconducting (W434F) Shaker K⁺ channel with normal inactivation and for the rBIIA Na⁺ channel was used. All were embedded in the high expression vector pBSTA providing flanking Xenopus β-globin and a T7 RNA promoter (14). The cDNA coding for the eGFP constructs was introduced into the C-terminal, for the K⁺ channel at the existing SpeI-site at amino-acid (AA) 503/4 (following (15)), and for the Na⁺ channel a new SpeI-site was introduced after AA1970 by changing the next bases T,C at 5910/11 to A,G. For expression in Xenopus oocytes, cRNA was obtained from linearized cDNA (NotI) by in vitro transcription and capping using T7-polymerase (mMessage mMachine Kit, Ambion, Austin, TX). The RNA concentration was checked spectroscopically and the integrity by RNase-free agarose gel electrophoresis.

For the construction of multiple tandem repeats of eGFP, the following strategy was developed and used. The basic cDNA for eGFP was obtained from a commercially available vector (Genbank # U76561, Clontech Laboratories, Mountain View, CA), which was modified by changing the start and end to SpeI-sites (5′-a/ctagtgtgag- - - -eGFP- - - -gtaca/ctagt-3′), i.e., adding 717 basepairs (bps) when inserted into a host frame. A special 14-AA linker was used to join multiple tandem eGFPs with a protease-resistant AA sequence (RHGTGSTGSGSSGS, based on information for a 12 AA linker from (16)), where the 5′-end was an XbaI overhang (CTAGA, AGA coding for the R) and the 3′-end was an XbaI overhang (TCTAG, TCT coding for the last S). In addition, the XbaI site on the 3′-end was capped by a short stretch of bases with a blunt end, such that, in the next ligation step, the linker would only bind with its 5′-end to eGFP; this cap was removed later by XbaI. This linker was ligated to the 3′-end of the eGFP, generating a hybrid SpeI/XbaI connection; this was achieved by mass ligation of eGFP and linker DNA (the linker not phosphorylated). Then the resulting dimers (linker-eGFP-eGFP-linker) were separated from a preparative gel and cut with SpeI, which resulted in an eGFP-linker pool where 50% had the correct orientation. These fragments (759 bps) were inserted into a vector, and from the clones, the correct combination was identified by sequencing, and used as the element for the multiple tandem ligations, as follows. The elements were mass-ligated, and then cut by SpeI and XbaI. Only the desired hybrid connections of the linker 3′-end XbaI to the next eGFP 5′-end SpeI were preserved, and the unwanted SpeI or XbaI connections cut. Fig. 2 shows the preparative gel with the mono-, di-, tri-, etc., tandem repeats of the eGFP-linker as well as the ring forms of the mono- and probably the di-sequence. The tandems were stored in a bluescript vector prepared with SpeI and XbaI for later use in the channel cDNA. (For further verification of the tandem inserts in the channel cDNA, see Results.)

FIGURE 2.

(A) Preparative agarose gel and analysis of the multiple tandem repeats of the element /SpeI-eGFP-SpeI//XbaI-Linker-XbaI/ after mass ligation of this element and recutting by SpeI and XbaI: Linear forms G1–G4 were prepared for later use; ring forms and larger tandems were discarded. (B) Plot of running distances of G1–G4 measured in pixels from the gel photo versus the number of ligated tandem repeats. The solid line is a power fit to the data.

Oocyte extraction and RNA microinjection

Large frogs (Nasco, Fort Atkinson, WI) were anesthetized in 2 g/l MS-222 (ethyl 3-aminobenzoate methanesulfonate salt; cat. No. A5040-100G, Sigma, St. Louis, MO) for 10–15 min and then operated to extract the oocytes. The extracted stage V–VI oocytes were put into calcium-free OR II (2 mM KCl, 1 mM MgCl₂, 82.5 mM NaCl, 20.0 mM HEPES, and titrated with 0.5 M Tris base to reach pH 7.3) to which 50 μg/ml gentamicine sulfate and 5 μg/ml doxycycline hydrochloride were added. The oocytes stayed there for ≃30 min until the end of the operation. To remove follicular cells, the oocytes were then put in a solution of calcium-free OR II and collagenase (No. C-9891, 2 mg/ml, Sigma) until approximately half of the follicular cells were digested (after ≃60 min). To remove all of the leftover collagenase after defolliculation, oocytes were washed two times in OR II and two times in modified Barth's solution (MBS: 88 mM NaCl, 1 mM KCl, 2.4 mM NaHCO₃, 0.82 mM MgSO₄, 0.33 mM Ca(NO₃)₂, 0.41 mM CaCl₂, 20.0 mM HEPES and titrated with 0.5 M Tris base to reach pH 7.3) to which 50 μg/ml gentamicine sulfate and 5 μg/ml doxycycline hydrochloride were added. Oocytes were then kept in MBS at 18°C. Twenty-four hours later, each oocyte was microinjected with 50 nl solution, which contained 30–50 ng cRNA. After injection, oocytes were kept at 18°C in MBS, which was changed daily. In this way, the oocytes stayed intact for 10–14 days.

Gating charge measurements

Five-to-ten days past injection, gating currents were recorded using two-electrode voltage-clamp (DAGAN CA-1, Minneapolis, MN and Turbo-Tec05, NPI-Electronics, Tamm, Germany), and filtered at 5 kHz with an eight-pole Bessel filter. Intracellular agarose cushion electrodes (17) were filled with 3 M KCl solution, and had a resistance between 100 and 200 kΩ. To measure K⁺ gating currents, oocytes were clamped to a holding potential of −100 mV at temperatures ranging from 12 to 15°C in MBS (pH 7.3). A pulse protocol was applied to the clamped oocytes as follows: Depolarizing pulses from −100 to +60 mV in steps of 20 mV and a hyperpolarizing pulse from −150 to −180 mV. Na⁺ gating currents were measured by clamping the oocyte to −100 mV. Depolarizing pulses ranged from −100 to +60 mV and the hyperpolarizing pulse went from −120 to −150 mV. For measurements on K⁺ as well as on Na⁺ channels, the hyperpolarizing pulses had the same duration as the depolarizing pulses. Linear capacitance and linear leak currents were removed by subtracting scaled-up versions of the currents that resulted from the hyperpolarizing pulses from the currents that resulted from the depolarizing pulses as described earlier (14).

In case of measuring Na⁺ gating currents, suppression of ionic currents was achieved by adding tetrodotoxin to the bath solution to reach a concentration of 2 μM. Examples of measured gating currents of different constructs are shown in Fig. 3. Note that even the K⁺ channel construct with 12 eGFP molecules per channel shows normal gating currents, indicating that the functionality of the channel protein is kept intact despite the inserted eGFP molecules.

FIGURE 3.

Gating currents of various channel constructs. (A) Gating current of a K⁺ channel with four eGFP molecules per channel (KG1) and a Na⁺ channel with three eGFP molecules per channel. Because of the higher expression level of K⁺ channels, the corresponding gating current is approximately six times larger in amplitude than that of the Na⁺ channel. Considering the slower kinetics of K⁺ channels, the charge is ≃20 times larger. Pulse protocols: For KG1, holding potential is −100 mV; depolarizing pulse is from −100 to + 60 mV; and hyperpolarizing pulse is from −150 to −180 mV. For NaG3, holding potential is −100 mV; depolarizing pulse is from −100 to + 65 mV; and hyperpolarizing pulse is from −120 to −150 mV. (B) Gating currents of K⁺ channels with eight and twelve eGFP molecules per channel (KG2 and KG3). Both channel constructs are still fully functional despite the insertion of eight and twelve eGFP molecules per channel, respectively. Pulse protocols were for both KG2 and KG3: Holding potential is −100 mV, depolarizing pulse is from −100 to + 60 mV, and hyperpolarizing pulse is from −150 to −180 mV. All applied pulses are sufficient to collect the full gating charge.

Fluorescence microscopy setup

To get a relative measure of the number of ion channels that were incorporated in the membrane of the oocyte, the intensity of eGFP emission was quantified. Two conventional fluorescence microscopy setups with filter blocks optimized for eGFP were used for all fluorescence measurements:

• Setup 1. Model No. IX71 with a UPlanFI 4× objective (NA = 0.13), from Olympus, Tokyo, Japan; and filter set model No. 41017 (excitation bandpass of 450–488 nm, transition wavelength of dichroic mirror of 498 nm; emission bandpass of 501–547 nm), from Chroma Technology, Rockingham, VT.

• Setup 2. Model No. IM 35 with a Plan 6.3× objective (NA = 0.16), from Zeiss, Jena, Germany; a custom made lens at the camera port to demagnify the image; and filter set model No. XF100 (excitation bandpass: 456–489 nm, transition wavelength of dichroic mirror: 500 nm, emission bandpass: 519–560 nm) from Omega Optical, Brattleboro, VT.

The illumination source was a 100 W mercury lamp.

Images were acquired with a 12-bit charge-coupled device (CCD) camera (model No. A102f, Basler, Ahrensburg, Germany) with a pixel size of 6.45 × 6.45 μm² and an internal gain, which was controlled by a self-developed software to enable exposure times in a range from 1 ms to 4 s in steps of 1 ms. The internal gain was held as low as possible to maximize the signal/noise ratio. The camera offset was ≃17 counts. All data are offset-corrected. The background was determined for every image and subtracted from the pixel counts.

RESULTS

Verification of tandem constructs

As mentioned in Methods, the single element of the eGFP-linker construct inserted into a bluescript vector was fully sequenced. For the multiple repeat tandems, sequencing is not easily possible, since a good sequencing run covers up to ∼900 bps and the sequencing primer has to be outside the tandem region to prime only once. Thus, the following two tests were done for checking the multiple repeats for correct number and direction of insertion, although the way of construction already optimized the outcome.

Fig. 4 A shows one test for the plasmids pG1 to pG4 containing the tandem repeats and also the K⁺ channel constructs KG1 to KG3. These constructs were cut with BsrGI, which cuts near the 3′-end of eGFP at position 712 from 759. It can easily be seen that pG1 and KG1 would just be linearized giving the long band of 3711 or 5944, respectively (seen in the gel of Fig. 4 A). For higher tandems pGn or KGn, additional bands of 759 bps appeared with an intensity growing relative to the long band in proportion n − 1. Note that an inverted eGFP would create bands of 2 × 47 and 2 × 712. Fig. 4 B shows clearly that the intensity ratios increase linearly as expected and more steeply for pGn than for KGn. For this test, the intensities of the bands have been measured from a photo of the gel taken with the Basler CCD camera, which provided a linear range over 12-bit resolution. Fig. 4 C shows a second test on a gel for the NaG1–NaG4 constructs. The cDNA was cut with SpeI and SacII close to either side of the tandem repeat. The lengths of the inserts were as expected. As shown in Fig. 4 D, the running distance increased according to the expected length of fragments, which confirms the number of tandem repeats.

FIGURE 4.

Gel analysis of plasmid- and channel-cDNA containing multiple tandem repeats inserted. (A and B) Gel and analysis of pG1–pG4 and KG1–KG3, as indicated (for KG2, two preparations of the same clone were tested; for KG3, two clones produced in parallel were tested which gave superimposing crosses in panel B; for NaG3, results from two subclones are shown). The constructs were cut with BsrGI and analyzed as described in the text. Note that the gel shown was taken with a CCD camera with γ = 0.5, which enhances the weak bands, but the gel was also photographed with the Basler camera providing a linear (γ = 1) 12-bit resolution for the quantitative analysis shown in panel B. (C and D) Gel and analysis of NaG1–NaG4. DNA was cut with SpeI and SacII, which cut close to either end of the tandem repeats. The expected lengths for the fragments with the insert are 1537, 2296, 3055, and 3814 bps for G1–G4 and for the remaining fragment 8882 bps; the last band is a linearized K⁺ channel plasmid used for comparison (marker, 5185 bps). The solid line is a power fit to the data.

Fluorescence intensity measurements

Two intrinsic properties of the oocytes potentially make these measurements difficult: The oocytes show a strong cytoplasmic autofluorescence; and the distribution of channels over the surface is inhomogeneous.

Autofluorescence

Autofluorescence is mainly caused by flavins within the cytoplasm (18). One-half of the oocyte is naturally covered with a dark pigment layer, which lies underneath the cellular membrane and masks the autofluorescence to a large extent (animal pole). On the other half of the oocyte, which is not pigmented (vegetative pole), autofluorescence is so high that it can hardly be distinguished from eGFP emission (see Fig. 5). However, a comparison of the intensity profiles of images of a noninjected control cell and an oocyte injected with Na⁺ channel cRNA shows that, in the detection region, the cytoplasmatic contribution to the fluorescence signal is small in comparison to the signal originating from membrane-bound eGFP molecules. The difference is most striking on the animal pole, where the fluorescence signal in the border region of the control cell is as low as the background. In contrast to this, the fluorescence signal of the Na⁺-injected oocyte shows a sharp peak. In the border region of the vegetative pole, the difference is not as obvious, but still substantial (see inset of Fig. 5).

FIGURE 5.

Comparison between a noninjected control oocyte and an oocyte injected with Na⁺ channel cRNA (NaG4). The length of one pixel on the image corresponds to a length of ≃1.6 μm on the sample. (A) The animal pole of the control oocyte (left side of the oocyte), which is covered with a dark pigment layer shows no fluorescence whereas the vegetative pole (right side of the oocyte) shows strong autofluorescence. (B) On the vegetative pole (right side of the oocyte), the autofluorescence intensity of the Na⁺ injected oocyte is similar to the one of the control oocyte. At the edge of the animal pole (left side of the oocyte), however, a strong peak appears, which indicates the presence of channels in the cellular membrane. The insets show the border region of the two oocytes on the vegetative side. The two lines specify the width of the ring which is used for data analysis. The fluorescence intensity of membrane-bound channels leads to a sharp rise on top of the autofluorescence of the cytoplasm that disappears toward the border of the oocyte. Oocytes were placed on a glass slide into which a hole with a diameter of ≃0.8 mm was drilled. This allowed for precise positioning of the oocytes. The edge of the hole can be seen as a circular shape in the inner part of the oocyte. Images are normalized to account for different illumination and imaging conditions. Normalization allows for a direct quantitative comparison between the two images.

Assuming a uniform distribution of fluorophores over the surface of the oocyte, the intensity of the fluorescence signal will be highest near the outermost part of the oocyte and decrease toward the center. The reason for this lies in the curvature of the oocyte: in an area near the circumference of the oocyte (see Fig. 6), a larger fraction of the surface will be projected onto a unit area of the CCD chip than it will be the case in an area near the center. Even though the cells have a nearly spherical shape, on the micrometer scale, the cellular membrane is characterized by a microvilous structure that extends toward the outside of the cell. Various studies report the length of these microvilli to be ∼1 μm (19,20), 3–4 μm (21), and up to 10 μm (22,23). The confocal image in Fig. 6 clearly shows that the fluorescing region extends over a length of ≃13 μm (full width at half-maximum). Therefore, a method based on a MatLab routine (The MathWorks, Natick, MA) was developed that detects the circumference of the oocyte and analyzes the fluorescence signal in a concentric ring of a width of 13 μm. This corresponds to a length of ≃8.1 pixels on the Olympus microscope and to a length of ≃6.6 pixels on the Zeiss microscope. This concentric ring is the projection of a spherical layer onto the CCD chip. Thereby the detectable signal originating from eGFP molecules bound to ion channels is maximized, while the contribution from autofluorescence is minimized (see Fig. 6 for details). With the diameter D of the oocyte, the surface A of this spherical layer can be calculated ( where d is the width of the concentric ring). With a typical diameter of 1.2 mm, this amounts to ≃10% of the whole cell surface. Based on this fraction of the cell surface, the total of the measured pixel counts was extrapolated to the whole cell surface to allow for a quantitative comparison between oocytes. Note that for the relative comparison of the fluorescence intensity of two cells, it is not necessary to calculate the cell surface absolutely (including the enlargement by microvilli), but rather to ensure that all fluorescence originating from the marked ion channels is collected and reflects a relative measure of the total fluorescence intensity.

FIGURE 6.

Data analysis of images of channel expressing oocytes. (A) Illustration of the projection of a small band along the circumference of an oocyte onto the CCD chip. (B) Image of an oocyte expressing K⁺ channels. Only fluorescence light originating from the area in-between the two concentric rings is taken into account for data analysis. (C) Between successive images, the oocyte is rotated by 120°. (D) Confocal image of the membrane of an oocyte. The membrane shows fluorescence over a width of ≃13 μm (full width at half-maximum).

Inhomogeneous distribution of channels

Because the distribution of channels over the surface of the oocyte is inhomogeneous, fluorescence intensities differ very much depending on the imaged area. To quantify the fluorescence from the whole cell—and thus get a relative measure of the number of expressed channels—the oocyte has to be imaged from several sides. With a ring width of 13 μm, the cell would have to be rotated by 24° between successive images to allow for the coverage of the whole cell surface, adding up to a total of 15 images per oocyte. Because the handling of the oocytes is quite delicate and because it is hard to achieve rotation in a precise and reproducible way, it is preferable to make as few images as possible while still getting a measure of the fluorescence intensity from the whole cell. Furthermore, because the exposure time of each image is between 0.5 and 4 s (depending on the expression level), photobleaching increasingly becomes an issue as more pictures are taken.

Various tests were made taking three, four, five or seven pictures per oocyte, rotating them by 120°, 90°, 72°, and 52° in-between images, respectively (see Fig. 6). For each set of images, the mean pixel count per image was calculated. When the same set of images was evaluated repeatedly, the measured mean pixel counts did not vary >10–15%, regardless of how many pictures were taken. For even numbers, the images can be reordered in such a way, that they are pairs of images taken from opposite sides (the second picture of each pair is taken after a rotation of 180°). Because these pairs image a similar area of the oocyte, it is advisable to take an odd number of images. As it turned out, taking only three images is better than taking four pictures, and the fluctuation of the mean pixel counts is ∼10% (three images) as opposed to 15% (four images).

Fluorescence intensity was therefore quantified by taking three pictures per oocyte with a rotation of 120° in-between successive images for all subsequent measurements. These three images cover ≃30% of the whole cell surface.

Illumination and detection properties

To account for a slow change in power of the Hg lamp, the lamp power at 488 nm was measured before each image acquisition. Images were then corrected for changes in illumination intensity. Furthermore, the properties of the CCD camera were characterized with respect to the shutter time and the internal gain. This allowed for a normalization of each image to a shutter time of 1 s and an internal camera gain of one. All data points were normalized in this way.

Because two setups were used for measuring the fluorescence intensity, an additional normalization factor was introduced. To account for the different optics (objectives, filters and optical path), ≃10 oocytes were imaged and their fluorescence intensity was measured on both setups. This comparison revealed that the Olympus setup yields 1.5 ± 0.2 times more counts than the Zeiss setup for an identical sample. All following data are normalized by this factor.

Capturing the total gating charge

To be able to compare the gating charge per channel of Na⁺ and K⁺ ion channels, capturing the total gating charge of these channels was of prime importance. One method to measure gating charge is by integrating the total displacement current that results from applied pulses (see (2)). This yields a charge versus voltage (Q–V) plot which shows the linear (capacitive) and nonlinear (gating) components of the displaced charges (see Fig. 7). The nonlinear component of this plot is the gating charge. The voltage at which the charge starts to deviate from linearity indicates the beginning of gating charge movement. To find the potential at which this deviation occurs, many linear fittings were made in different voltage ranges at hyperpolarized potentials. Investigation of the residuals of these fittings lead to the conclusion that, in the voltage range from −150 to −200 mV, the charge movement for K⁺ channels is purely capacitive and linear, without any contribution from gating charges.

FIGURE 7.

Displacement charge (capacitive and gating charge) as a function of applied voltage steps of a K⁺ channel. The holding potential was at −100 mV. A fit illustrates the linearity in the region from −200 to −150 mV (lower dashed line). The extrapolation of the fit in the region from −150 to + 60 mV shows the deviation from linearity (i.e., movement of gating charges). The distance between the two dashed lines corresponds to the total gating charge Q.

On the basis of these findings, a conventional pulse protocol used for gating current experiments was adapted to the appropriate region of the hyperpolarizing pulse. The holding potential was set at −100 mV and pulses ranged from −100 to +60 mV in steps of 20 mV. Hyperpolarizing pulses ranged from −100 to −130 mV in a first experiment, from −130 to −160 mV in a second one and from −150 to −180 mV in a final experiment. Current traces resulting from the hyperpolarizing pulses were inverted, scaled-up according to the pulse height of the depolarizing pulses and subtracted from the current traces that resulted from depolarizing pulses. The difference trace is then due only to the movement of gating charges and integration reveals the total gating charge.

Compared to the first method, the measured gating charge was 10% lower with a hyperpolarizing pulse from −100 to −130 mV and 5% lower with a hyperpolarizing pulse from −130 to −160 mV. As expected, the gating charge was the same when a hyperpolarizing pulse from −150 to −180 mV was applied, because, in this region, charge movement is purely linear. This pulse protocol with a hyperpolarizing pulse from −150 to −180 mV was used for all subsequent measurements of K⁺ channel gating currents.

For the Na⁺ channels, a hyperpolarizing pulse from −120 to −150 mV was sufficient, because Na⁺ channels do not show voltage-dependent steps at these hyperpolarizing potentials. Holding the membrane at −120 mV for 20 min was adequate to bring all voltage sensors down to the resting state position and to recover all channels from the slow inactivation known for Na⁺ channels (see, for example, (24)).

Correlation of gating charge and fluorescence intensity

The plots in Fig. 8 show the fluorescence intensity as a function of the gating charge. For all constructs, fluorescence intensity and gating charge are positively correlated. When normalized to the slope of KG1, the slope of KG2 is approximately twice as high and the slope of KG3 is three times as high as the slope of KG1 (), as can be expected. The slope of NaG4 is only ≃1.1 times higher than that of NaG3.

FIGURE 8.

Fluorescence intensity as a function of gating charge for all channel constructs. In each of the graphs (A–E), the straight line represents the best fit to the data. The first data point in each graph corresponds to a noninjected control cell. These data points are included in the fit, but the fit is not forced to coincide with these points. (A–C) Fluorescence intensity as a function of gating charge for K⁺ channel constructs with four (KG1), eight (KG2), and twelve (KG3) eGFP molecules per channel. (D–E) Fluorescence intensity as a function of gating charge for Na⁺ channel constructs with three (NaG3) and four (NaG4) eGFP molecules per channel. The linear fits of all K⁺ and Na⁺ channel constructs only show a small deviation from linearity. (F) Fluorescence intensity as a function of gating charge for K⁺ (triangles) and Na⁺ (circles) channel constructs without eGFP molecules. Autofluorescence remains constant over time and expression level (at ≃0.07 for KG0 and at ≃0.04 for NaG0, which is in good agreement with the autofluorescence of the noninjected control cells). All data are normalized to the same illumination and detection properties to allow for a direct quantitative comparison.

Further analysis of these data was based on the following assumptions. The fluorescence intensity F is proportional to the total number of channels N times the number of eGFP molecules per channel of the construct # eGFP_{K, Na}, and the total gating charge Q is equal to the total number of channels N times the single gating charge q_{K, Na},

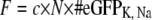(1)

where the proportionality factor c depends only on the illumination and detection properties of the setup (and not on the specific channel construct). For this reason, the change of the slope from one construct to another reflects the change in fluorescence intensity due to the presence of different numbers of eGFP molecules per channel in each construct. All linear fits to the data intersect the y axis at the same point which coincides with the autofluorescence found for control cells without eGFP (KG0 and NaG0). Therefore, after rearrangement of Eq. 1, the ratio of the single gating charges can be expressed as

(2)

where S_K = F_K/Q_K and S_Na = F_Na/Q_Na are the slopes of the correlations.

The ratios between the number of eGFP molecules and the correlation slopes are summarized for all channel constructs in Table 1.

TABLE 1.

Ratio of the number of eGFP molecules to the slope of the correlations

Channel		Weighted mean*
KG1	28.6 ± 2.0	27.8 ± 1.4
KG2	25.0 ± 3.1
KG3	28.6 ± 2.7
NaG3	10.0 ± 1.0	11.0 ± 0.7
NaG4	12.1 ± 1.1

^*Weighted means are from KG1 to KG3 and from NaG3, NaG4, respectively.

With these numbers and Eq. 2, the ratio of the single gating charges between K⁺ and Na⁺ channels was obtained as

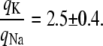DISCUSSION

The initial motive behind this study was to examine Na⁺ channels marked with eGFP fluorophores and expressed in Xenopus oocytes. However, when marked with just one eGFP in the C-terminal, their fluorescence is very weak. To improve on this, multiple tandem repeats of eGFP were constructed and tested in K⁺ channels. These channels have several advantages: 1), ∼5–10 times higher expression in oocytes; and 2), Due to their four independent domains—each having a C-terminal—automatically four times more fluorescence was obtained per channel. As shown in this article, it became clear that the channels operate normally even with higher multiples of the fluorophore. The method of obtaining a reliable estimate for the total fluorescence by rotating the oocytes and averaging the integrated fluorescence from tangential sections was developed. And, as shown in this study, the so-obtained fluorescence was strictly proportional to the gating charge and to the number of incorporated eGFP molecules. Furthermore, the contamination by autofluorescence of the cytoplasm was shown to be negligible in this tangential section.

These studies also paved the way for applying the method to the more-difficult Na⁺ channels. In the course of the study, it became obvious that the results obtained could be used for a new approach to estimate the single gating charge of the Na⁺ channels. As outlined in the Introduction, in the present literature there are many more estimates of the single gating charge for the Shaker K⁺ channel with figures at ∼12–14 elementary charges, but only little is published for the Na⁺ channel. As shown in this study, the new data provide a ratio between the two single gating charges and, therefore, an estimate from the better-known K⁺ channels to the less-known Na⁺ channels. Before discussing this in more detail, some critical points about the method used shall be discussed here.

Submembranous channels

Most critical is a possible contamination of the fluorescence by submembranous channels which would not produce gating current but fluorescence. These could be channels which are expressed and traveling toward the membrane and are not yet incorporated, or channels which have left the membrane by endocytosis with the eGFP molecules still functioning. Fig. 8 illustrates clearly, that a substantial and changing amount of submembranous channels can be excluded. The data points are close to the linear fit, i.e., in a constant proportion to the number of the membrane-bound channels which produce gating charge. If over the time of the 3–14 days of channel expression the amount of channels resting under the membrane would change substantially, a nonconstant relation to the incorporated channels should be present. However, the two special cases where such contaminating channels would be present in either a constant amount or in a constant percentage relative to the membrane-bound channels shall be discussed in the following.

In the ideal uncontaminated case, the correlation can be described by the equation F_n(Q_n) = s_nQ_n + b_n, where F_n is the fluorescence signal, s_n the slope of the correlation, Q_n the gating charge, and b_n the contribution of autofluorescence. The index n denotes the number of incorporated eGFP molecules of the construct under investigation. It seems reasonable to assume that neither the gating charge nor the level of autofluorescence depends on the number of inserted eGFP molecules, which means Q_n = Q and b_n = b. The correlation can then be rewritten as

(3)

The constant b is the intercept of the correlations with the y axis (see Fig. 8).

Constant amount of submembranous channels

Assuming a constant amount of submembranous channels, there would be a contribution c_n to the fluorescence signal, which would be constant over time. Equation 3 would then change to F_n(Q) = s_nQ + b + c_n. The c_n values are dependent on and proportional to the number of eGFP molecules of the construct, i.e., c_n = k₁n, where k₁ is the same constant factor for all channel constructs. If this were the case, all correlations would be shifted by c_n, which would grow with n. As can be seen in Fig. 8, A–E, all correlations intercept the y axis—within the error—at the same position (at 0.06 for K⁺ channels and at ≃0.10 for Na⁺ channels; see Fig. 8). Measurements on channel constructs without eGFP show fluorescence intensity values which coincide with the intercept of the correlations (see Fig. 8 F). Therefore, this type of submembranous channel is either not present, or, if present, its contribution to the fluorescence signal is so low that its effect is not detectable by the presented method.

Constant percentage of submembranous channels

If the channels under the membrane, within the 13-μm ring of the evaluated tangential section, would be of a relevant constant percentage relative to the membrane-bound channels, the slope of the correlation would increase. An additional factor d_n, which would change the slope of the correlation, would have to be introduced. Equation 3 would be modified as

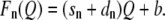(4)

Again, the s_n and d_n values are proportional to the number of eGFP molecules per channel of the construct under investigation. Therefore, s_n = k₂n and d_n = k₃n, where k₂ and k₃ are the same constant factors for all channel constructs. With Eq. 4 follows

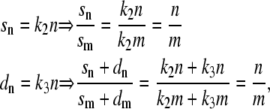where s_m is the F/Q slope of a channel construct with m eGFP molecules per channel. The ratio of the slopes of two different channel constructs is therefore independent of the presence of this type of submembranous channel, and Eq. 2 can be applied without modification.

Since such a contamination would still result in a linear relation between F and Q, it cannot be safely excluded by our data. However, since the different constructs KG1 to KG3 show slopes which increase according to the number of eGFPs in each construct, it is very likely that such contamination would be of constant percentage across all constructs. Most likely, this argument is valid also for the Na⁺ channels and then it would not change the obtained ratio of q_K/q_Na. If this argument does not apply to the Na⁺ channels, the ratio of submembranous to membrane-bound channels would be greater for Na⁺ channels than for K⁺ channels, because the Na⁺ channel is four times larger and does not express as well in the membrane as the K⁺ channel. Then the fluorescence intensity of the Na⁺ channels were overestimated and the real q_Na would be larger (see Eq. 1 and 2). Thus, the obtained ratio q_K/q_Na represents an upper limit.

Quenching

Fluorophore-fluorophore quenching can result either from the interaction of eGFP molecules of neighboring channels or from eGFP molecules within the same channel.

The number of expressed channels is ∼10¹⁰ per oocyte. The diameter of a typical oocyte is ≃1.2 mm and thus has a spherical surface area of ≃4.5 mm². Because the surface of the oocyte is not flat but enlarged by microvilli, its effective surface is approximately four times larger. This leads to a channel density of ≃550 channels/μm² and thus to a mean distance of ≃40 nm between neighboring channels. Quenching can only occur when the fluorophore and the quencher (which, in this case, is another eGFP molecule) are in close vicinity. Typical distances for quenching to occur are ∼0.2 nm (25). Therefore, fluorophore-fluorophore quenching between eGFP molecules of neighboring channels is very unlikely to occur. Furthermore, fluorescence intensity and gating charge would not be linearly dependent from each other, because fluorescence intensity would be reduced as more channels are expressed. This stands in contradiction to our findings.

Fig. 9 shows a plot of the slopes that were found in the correlation measurements on K⁺ channels as a function of the number of eGFP molecules per channel. The three data points correspond to K⁺ channels with 4, 8, and 12 eGFP molecules per channel and are close to the linear fit. If fluorophore-fluorophore quenching between eGFP molecules from within an individual channel were present, a reduced fluorescence intensity would be expected as more eGFP molecules per channel are introduced, i.e., the slopes of the correlations as a function of the number of eGFP molecules per channel would decrease for higher multiples of eGFP, which is not the case. This is in accordance with a study from Chen et al. (26), who measured the fluorescence intensity of oligomerized eGFP molecules and found quenching not to be present for tandem eGFP molecules. For further confirmation, see Saffarian et al. (27).

FIGURE 9.

Slopes of the correlations of fluorescence intensity versus gating charge (see Fig. 8) of the three K⁺ channel constructs (KG1, KG2, and KG3) as a function of the number of eGFP molecules per channel. The straight line represents the best fit to the data (see Discussion).

Concluding remarks

Taking the ratio of q_K/q_Na of 2.5 ± 0.4 and a figure for q_K of ∼13 elementary charges which is supported by the many studies quoted in the Introduction, it follows that the single gating charge for activation of the rBIIA Na⁺ channel would be ∼5.2 elementary charges. It has also to be mentioned that the integration for the Na⁺ gating charge covers the main gating current, which ends shortly after the activation peak. Therefore, it does not include all of the gating charge related to inactivation. Greeff and Forster (28) were able to detect the slow component of the gating current during the inactivation phase of the macroscopic sodium current. They estimated a number of 1.21 elementary charges to be correlated with inactivation. These open-inactivated transitions might have occurred in ∼50% of all channels during the integration time for the total gating charge Q used in this study. Thus, ∼0.6 elementary charges should be added, resulting in 5.8 elementary charges for q_Na, including inactivation.

This number is supported by the work of Conti and Stühmer (7), who estimated a value of six-to-eight elementary charges for the rBIIA Na⁺ channel. Furthermore, Sheets and Hanck (8) estimated a lower limit of the single gating charge of the human cardiac hH1a Na⁺ channel to be 5.2 elementary charges. In this context, it is also worthwhile to quote the study by Noceti et al. (3). They found 13 elementary charges for the single gating charge of the Shaker K⁺ channel and 8.6 for the Ca²⁺ channel, which has a very similar molecular structure as the Na⁺ channel. They determined the single gating charges of the Shaker K⁺ channel and the Ca²⁺ channel by using the same method.

At present, it is well accepted that, from the four domains in the Na⁺ channel, DI and DII are responsible for activation but the function of DIII is under dispute (29) and DIV is related to inactivation (14,30). With respect to the study by Hirschberg et al. (9) that gives a figure of at least 12 elementary charges for q_Na, it has to be mentioned that it concerned muscle Na⁺ channels in contrast to the rat brain IIA sodium channels of this study. As a further point, it may be considered that Na⁺ channels in nerve might be optimized for speed. Such an optimization has been proposed by Hodgkin in 1975 for the propagation speed of the action potential in squid (31); for optimal speed the gating charge should be rather smaller and the single ionic current rather larger. In this context, a recent study by Angelino and Brenner (32) analyzes the presently known Na⁺ channels with respect to the propagation of the action potential and shows clear differences between the nerve and muscle Na⁺ channels. Therefore, a figure at approximately six elementary charges for the Na⁺ channel activation in nerve seems reasonable.