Abstract
The electrocardiogram (ECG) is a measure of the collective electrical behavior of the heart based on body surface measurements. With computational models or tissue preparations, various methods have been used to compute the pseudo-ECG (pECG) of bipolar and unipolar leads that can be given clinical interpretation. When spatial maps of transmembrane potential (Vm) are available, pECG can be derived from a weighted sum of the spatial gradients of Vm. The concept of a lead field can be used to define sensitivity curves for different bipolar and unipolar leads and to determine an effective operating height for the bipolar lead position for a two-dimensional sheet of heart cells. The pseudo-vectorcardiogram (pVCG) is computed from orthogonal bipolar lead voltages, which are derived in this study from optical voltage maps of cultured monolayers of cardiac cells. Rate and propagation direction for paced activity, rotation frequency for reentrant activity, direction of the common pathway for figure-eight reentry, and transitions from paced activity to reentry can all be distinguished using the pVCG. In contrast, the unipolar pECG does not clearly distinguish among many of the different types of electrical activity. We also show that pECG can be rapidly computed by two geometrically weighted sums of Vm, one that is summed over the area of the cell sheet and the other over the perimeter of the cell sheet. Our results are compared with those of an ad hoc difference method used in the past that consists of a simple difference of the sum of transmembrane potentials on one side of a tissue sheet and that of the other.
INTRODUCTION
The electrical activity of the heart produces electric potentials that can be measured at the body surface. Potential differences between points on the body surface provide the electrocardiogram (ECG), a time-dependent signal that encompasses the collective electrical behavior of the heart. The ECG is used clinically to distinguish among different conduction patterns such as sinus rhythm, tachycardia, and fibrillation (1). For in silico, in vitro, or ex vivo cardiac model systems, the pseudo-ECG (pECG) provides a measure of the collective electrical behavior of the system. It has been applied to one- and two-dimensional computational models and two-dimensional slices or sheets of cardiac tissue. The value of the pECG, as evidenced by its usage in the literature, is its representation of tissue-level effects as a clinical-like waveform even though the waveform contains less information than complete maps of Vm. In doing so, results obtained from simplified experimental systems can be interpreted and understood from a clinical perspective. Furthermore, like the ECG, the presence of beat-to-beat variations in activation and/or repolarization patterns at a global level become apparent.
Experimentally, pECG has been measured in ex vivo preparations by bipolar electrodes placed on or around the tissue (2–4). However, when such recordings are unavailable or unfeasible to make, pECG can be computed from spatial maps of transmembrane potential (Vm). One approach that has been used is an ad hoc, difference method, which subtracts the average Vm from one-half of a myocardial tissue layer from the average of the other half, as was done for thin ventricular epicardial slices and atrial tissue (5–8).
An alternative method used a theoretical approach to compute the extracellular potential at a particular point in space (i.e., for a unipolar lead), based on the model's spatial distribution of Vm, (9). A unipolar lead voltage was computed at a certain distance from the end of a one-dimensional multicellular fiber of coupled cardiac cells meant to represent the transmural heterogeneities in the ventricles. A unipolar lead has also been utilized in two-dimensional computation models (10,11).
In this study, we theoretically derive the bipolar and unipolar pECGs for any desired lead location from optical recordings of Vm in a two-dimensional isotropic monolayer of cardiac cells. Further, we demonstrate that our expressions simplify to a weighted sum of Vm, scaled by two geometric functions. We then discuss the relative strengths and weaknesses of bipolar and unipolar pECGs, through examples of different patterns of electrical propagation in cultured cardiac cell monolayers. We show that computation of the pseudo-vectorcardiogram (pVCG), based on an orthogonal pair of bipolar leads, clearly illustrates the collective electrical behavior of the cells and can be used to distinguish among different types of electrical activity.
METHODS
Theoretical considerations
Bipolar pECG: ad hoc difference method
A computationally simple pECG can be obtained by subtracting the average of Vm from one-half of a cell sheet from that of the other half (6,12), which we refer to as the difference method. The pseudo-lead voltages along the x and y axes, 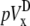 and
and 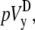 are defined as
are defined as
 |
(1) |
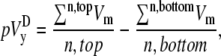 |
(2) |
where n is the number of recorded sites in each half of the monolayer. The values 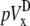 and
and 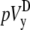 will be compared in the next section with the theoretically derived pseudo-lead voltages, pVx and pVy.
will be compared in the next section with the theoretically derived pseudo-lead voltages, pVx and pVy.
Bipolar pECG: theoretical approach
We previously used the concept of a lead field to compute a bipolar pECG for cell monolayer experiments (13,14). Here, we generalize our approach and determine the pECG for any desired placement of lead electrodes. Let the cardiac cells occupy U, a circular two-dimensional area of radius R lying on the bottom of a semiinfinite bath. A bipolar lead is placed in the x direction, with electrodes at (a,0,h) and (−a,0,h), respectively (Fig. 1, A and B). We define the pseudo-lead voltage, pVx, as
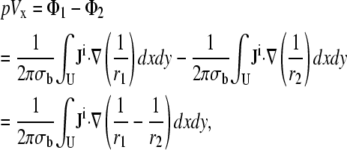 |
(3) |
where Eq. 3 is obtained as the superposition of dipole potentials (15). Ji is the area density of bioelectric dipole current sources contained within U, 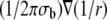 is the dipole potential field, σb is the conductivity of the bath, and
is the dipole potential field, σb is the conductivity of the bath, and
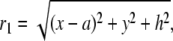 |
(4) |
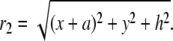 |
(5) |
Ji is the area density of the sum of dipole current sources directed along the x and y axes. Current sources that are directed along the x axis give rise to the x component of Ji, and assuming that the cell sheet is isotropic with uniform intracellular surface conductivity gi (equal to the intracellular conductivity σi times the sheet thickness), 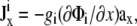 where Φi is the intracellular potential, and ax is the unit vector in the x direction (15). A similar expression can be written for the y component of Ji. Because Vm is equal to Φi–Φe, and because the cell monolayer lies in a conductive, semiinfinite bath (so that the extracellular potential Φe is ≪Φi), gradients in Φi are approximately equal to gradients in Vm. Accounting for the possibility that sources can be randomly oriented,
where Φi is the intracellular potential, and ax is the unit vector in the x direction (15). A similar expression can be written for the y component of Ji. Because Vm is equal to Φi–Φe, and because the cell monolayer lies in a conductive, semiinfinite bath (so that the extracellular potential Φe is ≪Φi), gradients in Φi are approximately equal to gradients in Vm. Accounting for the possibility that sources can be randomly oriented,
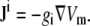 |
(6) |
In the general case where intracellular conductivity is anisotropic, gi would be replaced by an intracellular surface conductivity tensor. From Eq. 3 we can define a lead field, L12,
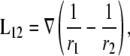 |
(7) |
where L12 is the sensitivity of the lead voltage to the sources Ji located at different x,y positions. (Note that, from the reciprocity theorem, L12 can be interpreted as the electric field that would be produced in the x,y plane at point (x,y,0) for a unit current injected into the lead electrode at (−a,0,h) and withdrawn from the lead electrode at (a,0,h) (16).) Combining Eqs. 3 and 6,
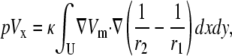 |
(8) |
where
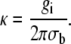 |
(9) |
Expanding the integrand, Eq. 8 becomes
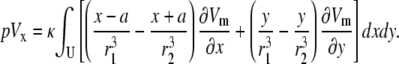 |
(10) |
Experimentally, Vm was recorded at 253 discrete sites over a 17-mm-diameter area in confluent cell monolayers (17,18). The gradients are converted to differences in Vm interpolated between adjacent sites in the x,y plane, and the integral operation is replaced by a summation.
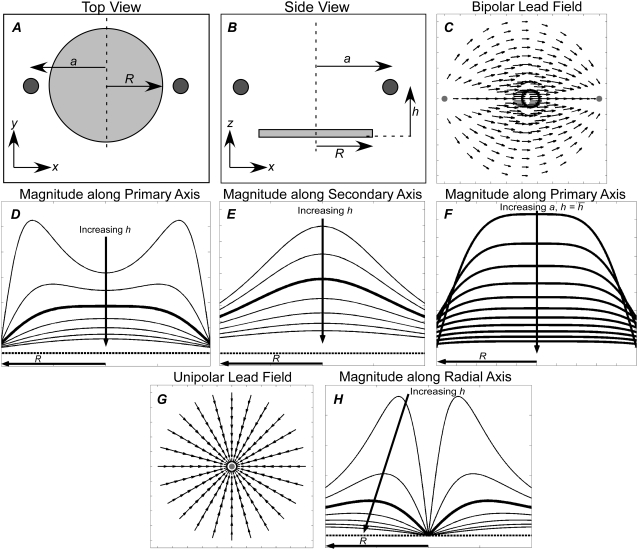
FIGURE 1.
(A) Top view of monolayer and (B) side view of monolayer and bipolar lead electrode position. (C) Bipolar lead field, (D) lead field magnitude along primary axis (x axis in A), and (E) secondary axis (y axis in A) of bipolar lead field for increasing h (at a = R). (F) Lead field magnitude along primary axis for increasing a at height 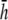 (a ≥ R). (G) Unipolar lead field. (H) Lead field magnitude along radial axis of unipolar lead field for increasing h (at a = R). For panels D–H, h is plotted from
(a ≥ R). (G) Unipolar lead field. (H) Lead field magnitude along radial axis of unipolar lead field for increasing h (at a = R). For panels D–H, h is plotted from 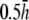 to
to 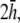 in steps of
in steps of 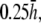 with
with 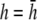 shown as the bold trace. The case of
shown as the bold trace. The case of 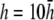 is also plotted as the dashed trace. For panel F, a is plotted from R to 2R, in steps of 0.1R.
is also plotted as the dashed trace. For panel F, a is plotted from R to 2R, in steps of 0.1R.
The method outlined above can be generalized to any placement of electrode leads. For example, a bipolar lead oriented in the y direction and situated a distance h above the monolayer, with electrodes a radial distance of a from the center, would have a pseudo-lead voltage of
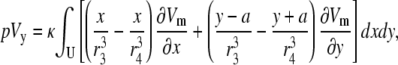 |
(11) |
and r3 and r4 are defined as
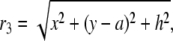 |
(12) |
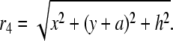 |
(13) |
An important factor to consider is the location of the lead electrodes. Assuming that they are symmetrically placed about the center of the monolayer, the two variables are the electrode displacement from the center of the monolayer, a, and the height above the monolayer, h (Fig. 1, A and B). L12 (Eq. 7, Fig. 1 C) represents the sensitivity of the bipolar pECG to the negative transmembrane potential gradient at different locations in space. To quantify the lead sensitivity, the magnitude of L12 along the primary (parallel to the axis of the lead) and secondary (perpendicular) axes was plotted with variation of h or a. Along both axes, the lead sensitivity decreases for increasing h (Fig. 1, D and E) as expected. Near the edge of the monolayer, directly below either of the lead electrodes, the sensitivity is at a minimum for all h. For small h, there is a near-edge region with heightened sensitivity along the primary axis, seen by the prominent side lobes in the sensitivity curve (Fig. 1 D). As h increases, both the sensitivity and the variation in sensitivity decrease over the monolayer. Ideally, the lead field is one that is as flat as possible. If we define the x axis as the primary axis, the lead sensitivity curve along the x axis as 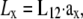 and the effective operating height
and the effective operating height 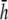 as the case where Lx is flat at the center of the monolayer (i.e.,
as the case where Lx is flat at the center of the monolayer (i.e., 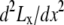 at x = 0), then
at x = 0), then
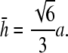 |
(14) |
The lead sensitivity curves at 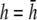 are shown as bold traces in Fig. 1, D and E, and are plotted in Fig. 1 F for increasing a. The width of the flat region can be defined to be that portion of the sensitivity curve along the primary axis that falls within 5% of the value in the center, in which case the width increases as h increases from 0 to just under
are shown as bold traces in Fig. 1, D and E, and are plotted in Fig. 1 F for increasing a. The width of the flat region can be defined to be that portion of the sensitivity curve along the primary axis that falls within 5% of the value in the center, in which case the width increases as h increases from 0 to just under 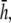 then decreases as h increases to a value of
then decreases as h increases to a value of 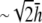 and then increases again with further increases in h (not shown). Thus, measurement of the bipolar pECG becomes a compromise between the magnitude and uniformity of the lead sensitivity with an effective operating height at
and then increases again with further increases in h (not shown). Thus, measurement of the bipolar pECG becomes a compromise between the magnitude and uniformity of the lead sensitivity with an effective operating height at 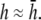 At
At 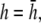 as a increases, the lead electrodes are farther from the monolayer and the width of the central region of uniform sensitivity increases, but sensitivity decreases (Fig. 1 F). For all bipolar pECGs, we used the parameters a = R and
as a increases, the lead electrodes are farther from the monolayer and the width of the central region of uniform sensitivity increases, but sensitivity decreases (Fig. 1 F). For all bipolar pECGs, we used the parameters a = R and 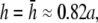 and in our experiments, a = 8.5 mm. By comparison, in previous experimental studies we used the parameters a = R and
and in our experiments, a = 8.5 mm. By comparison, in previous experimental studies we used the parameters a = R and 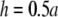 (13,14).
(13,14).
To facilitate their calculation, pVx and pVy can be expressed as integrals of Vm rather than integrals of derivatives of Vm. Green's first identity for the divergence theorem in two dimensions (for any two continuous functions, φ and ψ) is
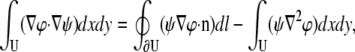 |
(15) |
where ∂U is the boundary of U, n is the unit outer normal to the boundary, and dl is a differential element along the boundary. Setting ψ = Vm and 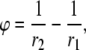 and substituting Eq. 15 into Eq. 8,
and substituting Eq. 15 into Eq. 8,
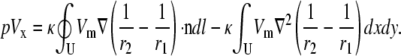 |
(16) |
Since U is a circular area with radius R, Eq. 16 simplifies to
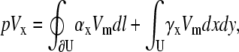 |
(17) |
where
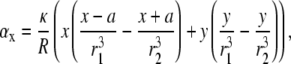 |
(18) |
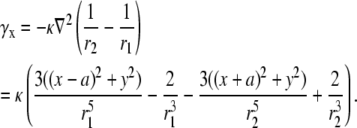 |
(19) |
Using a similar derivation, the voltage for a bipolar lead in the y direction for a circular cell monolayer with radius R is
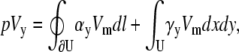 |
(20) |
where αy and γy are the geometric weighting functions,
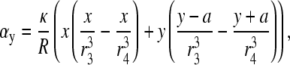 |
(21) |
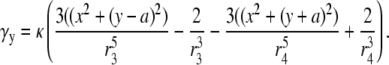 |
(22) |
The lead voltage is the sum of two terms: a boundary term (a weighted sum along the perimeter of the monolayer) and an area term (a weighted sum over the monolayer area). There can be significant differences in calculation times for the lead voltages, depending on the computational method used. Implementing Eq. 10 requires computation of a numerical gradient, which may necessitate signal processing such as spatial filtering or interpolation to reduce error. Implementing Eq. 17 does not require further processing, because the transmembrane potential values are used directly in the computation. For a two-second optical recording at 1-ms time resolution with 253 recording sites in our cell monolayers, using Eq. 10 requires interpolation of our hexagonal recording array and takes ∼1 min to compute, whereas using Eq. 17 takes <1 s to compute (on an Intel Pentium M 1.6 GHz processor). We confirmed the equivalency of Eqs. 10 and 17 for all of the examples presented in this study, and found negligible differences between the ensuing lead voltages except for some occasional minor baseline offsets that we attribute to discretization errors.
The ad hoc bipolar lead voltages (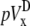 and
and 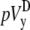 ) are also integrals (sums) of Vm (see Eqs. 1 and 2) but have different weighting functions for Vm (
) are also integrals (sums) of Vm (see Eqs. 1 and 2) but have different weighting functions for Vm (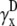 and
and 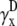 ) compared with γx and γy, and do not include a boundary term at the perimeter of the monolayer (first term of Eq. 17). The value
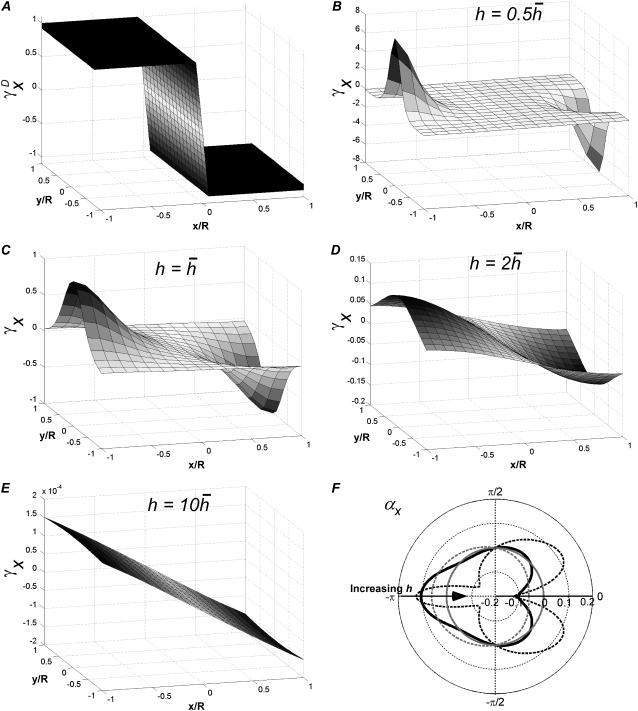
) compared with γx and γy, and do not include a boundary term at the perimeter of the monolayer (first term of Eq. 17). The value 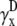 is a two-dimensional sign function, positive on one-half of the cell sheet and negative on the other half (Fig. 2 A). It is a coarse approximation of γx (see Eq. 19) at
is a two-dimensional sign function, positive on one-half of the cell sheet and negative on the other half (Fig. 2 A). It is a coarse approximation of γx (see Eq. 19) at 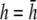 (Fig. 2 C). The value γx is also shown at other values of h (normalized to the maximum of γx at
(Fig. 2 C). The value γx is also shown at other values of h (normalized to the maximum of γx at 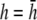 ). It increases sharply near the electrodes at
). It increases sharply near the electrodes at 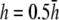 (Fig. 2 B) and becomes much flatter and linear in shape at
(Fig. 2 B) and becomes much flatter and linear in shape at 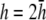 (Fig. 2 D). At large h
(Fig. 2 D). At large h 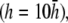 γx approaches a flat plane tilted around the y axis (Fig. 2 E). The value αx has a maximum amplitude directly below the electrodes, at θ = 0 and π, and is zero in the y direction at θ = π/2 and −π/2 (Fig. 2 F). At
γx approaches a flat plane tilted around the y axis (Fig. 2 E). The value αx has a maximum amplitude directly below the electrodes, at θ = 0 and π, and is zero in the y direction at θ = π/2 and −π/2 (Fig. 2 F). At 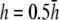 (Fig. 2 F, dashed black trace), αx has sharper peaks and a larger amplitude below the electrodes, compared with
(Fig. 2 F, dashed black trace), αx has sharper peaks and a larger amplitude below the electrodes, compared with 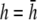 (Fig. 2 D, solid black trace). At
(Fig. 2 D, solid black trace). At 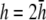 (Fig. 2 F, dashed shaded trace), αx has a flatter angular dependence and a lower amplitude under the electrodes. At
(Fig. 2 F, dashed shaded trace), αx has a flatter angular dependence and a lower amplitude under the electrodes. At 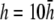 (Fig. 2 F, solid shaded trace), αx is near zero at all locations. The amplitude of αx has been scaled by the ratio of the monolayer circumference to area (and normalized to the maximum of γx at
(Fig. 2 F, solid shaded trace), αx is near zero at all locations. The amplitude of αx has been scaled by the ratio of the monolayer circumference to area (and normalized to the maximum of γx at 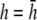 ) to allow comparison with γx. At
) to allow comparison with γx. At 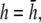 the maximum value of αx is <10% of γx. For increasing h, the amplitude of γx decreases at a faster rate than that of αx and therefore the relative weight of the boundary term increases.
the maximum value of αx is <10% of γx. For increasing h, the amplitude of γx decreases at a faster rate than that of αx and therefore the relative weight of the boundary term increases.
FIGURE 2.
Weighting functions for bipolar pECGs. The value γx, computed by (A) difference method 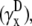 and (B–E) theoretical method. For panels B–E,
and (B–E) theoretical method. For panels B–E, 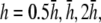 and
and 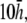 respectively. (F) The value αx, computed by theoretical method is shown on a polar plot, with radial axis ranging from −0.2 to 0.2. For panel F,
respectively. (F) The value αx, computed by theoretical method is shown on a polar plot, with radial axis ranging from −0.2 to 0.2. For panel F, 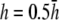 (dashed black trace),
(dashed black trace), 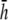 (solid black trace),
(solid black trace), 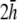 (dashed shaded trace), and
(dashed shaded trace), and 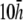 (shaded trace).
(shaded trace).
Pseudo-vectorcardiogram (pVCG)
The pseudo-vectorcardiogram (pVCG) is obtained by plotting pVy against pVx. For comparison, the pseudo-vectorcardiogram (pVCGD) is also obtained by plotting 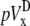 against
against 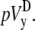
Unipolar pECG: theoretical approach
A unipolar (single electrode) lead, placed at (a,b,h) with reference at infinity, can be used for pECG measurements instead of the bipolar leads. The derivation of the unipolar lead voltage pV0 closely follows that of the bipolar lead voltage. The unipolar lead was placed over the center of the monolayer (a = 0, b = 0) unless otherwise stated. The unipolar lead field, L0, is assumed to be for the case where the reference electrode is at infinity, and is given by
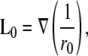 |
(23) |
where
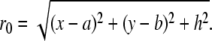 |
(24) |
L0 differs significantly from that of the bipolar lead. Instead of being primarily oriented along and sensitive to the x or y axis, the sensitivity of the unipolar lead is oriented radially outward from the electrode location (Fig. 1 G). The lead field is zero directly below the electrode, and therefore, the lead voltage is completely insensitive to electrical sources located there. The sensitivity rises sharply around the electrode location, becomes maximal at 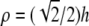 (where ρ is the radial distance from (a,b,0)), and then drops off with increasing ρ (Fig. 1 H). As h increases, the overall lead sensitivity decreases, and the peak moves radially outward. For comparison with the bipolar lead, h was taken to be
(where ρ is the radial distance from (a,b,0)), and then drops off with increasing ρ (Fig. 1 H). As h increases, the overall lead sensitivity decreases, and the peak moves radially outward. For comparison with the bipolar lead, h was taken to be 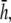 for which the concavity of the sensitivity curve changes sign at the edge of the monolayer, at radius R (Fig. 1 H, bold trace).
for which the concavity of the sensitivity curve changes sign at the edge of the monolayer, at radius R (Fig. 1 H, bold trace).
The unipolar lead voltage, pV0, is given by
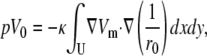 |
(25) |
which can be expanded as
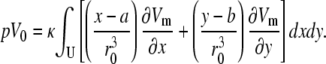 |
(26) |
Alternatively, the lead voltage can be obtained as an integral of Vm,
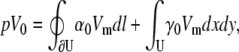 |
(27) |
where
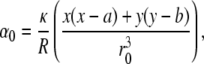 |
(28) |
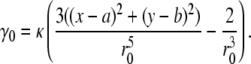 |
(29) |
Experimental methods
Cell monolayer
Our cell culture procedure to create cell monolayers has been previously described (11,12). Briefly, neonatal rat ventricular myocytes were dissociated from two-day-old Sprague-Dawley rat hearts with the use of the enzymes, trypsin, and collagenase. The resulting cell suspension was plated at high density onto plastic coverslips to form monolayers that became confluent after 3–4 days of culture. Experiments were performed on days 4–9 after plating. The data for each example presented is from a different cell monolayer.
Optical mapping
Our method of optical mapping of cell monolayers has been previously described (17,18). Briefly, maps of transmembrane potential were recorded by placing the cell monolayer directly on top of a bundle of 253 optical fibers 1-mm in diameter, arranged in a tightly packed, 17-mm-diameter hexagonal array. During experiments, the cell monolayers were stained with 10 μM di-4-ANEPPS, a fluorescent voltage-sensitive dye, and continually superfused with warmed (36 ± 0.5°C) oxygenated Tyrode's solution (in mmol/L: 135 NaCl, 5.4 KCl, 1.8 CaCl2, 1 MgCl2, 0.33 NaH2PO4, 5 HEPES, 5 glucose). The fluorescent dye signal was relayed by the optical fiber bundle to an array of photodetectors and amplifiers, processed by custom-written software and converted into pseudo-colored maps of Vm.
Data analysis
To compare pVCGs calculated using the difference and theoretically derived methods, we first centered each pVCG at the origin by subtracting from Vx and Vy their respective mean values. We then determined the maximum excursion of the pVCG from the origin and normalized the radial distance of each pVCG point to that value. In this way, the pVCG lay within a unit circle. Using Eq. 30, we computed the root mean-square difference (RMSD) by taking the square root of the mean of the square of the difference (in percent) of the two traces at each time point,
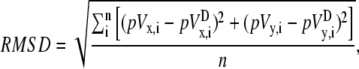 |
(30) |
where i is the index of the data points at time ti and n is the total number of time points.
RESULTS
Planar wave propagation
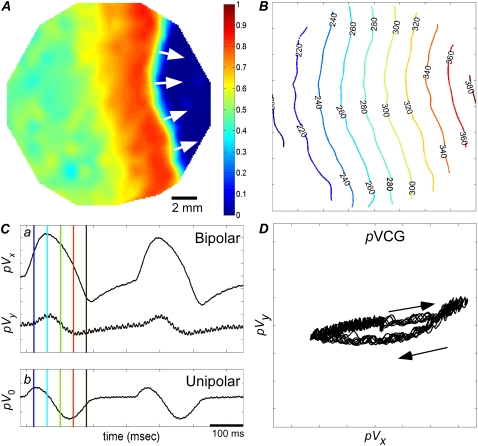
We show an example in Fig. 3 of a planar wave propagating across the monolayer that was initiated from a line electrode on the left side. The voltage map and isochrone map are shown in Fig. 3, A and B, respectively. The wave is propagating across the monolayer primarily in the positive x direction, with a small component in the positive y direction. Both pVx and pVy are initially zero (Fig. 3 C a) and become positive (or negative) when the wavefront (or waveback) propagates across the monolayer. pVx and pVy are periodic at the pacing rate, larger during wavefront than waveback propagation (because of the larger transmembrane potential gradient), and approximately in phase with the same sign. It is possible for pVx and pVy to have opposite sign if the direction of propagation is toward the upper left or lower right (second or fourth quadrants) so that pVx is negative while pVy is positive, or vice versa. pVCG also reflects the direction of propagation and is oriented primarily in the x direction with a small component in the y direction (Fig. 3 D). The unipolar lead voltage pV0 (Fig. 3 C b) captures the general activity of planar wave propagation because there exists a component of the unipolar lead field (Fig. 1 H) that is oriented along the direction of propagation. However, pV0 does not indicate what the direction of propagation is, and it has a similar appearance for a wave propagating along any other direction across the monolayer.
FIGURE 3.
(A) Normalized voltage map for planar propagation. The color bar on the right indicates the relative amplitude of Vm (scaled from 0 to 1). (B) Isochrone map. (C) (a) Bipolar pECGs (pVx and pVy) and (b) unipolar pECG (pV0). The colored vertical lines in panel C correspond to isochrones in the isochrone map in panel B. (D) pVCG. Arrows indicate the direction of pVCG with time.
Radial wave propagation
We show a radial wave propagating outwardly from a point stimulus in Fig. 4 A. The position of the stimulus is slightly off-center by ∼1 mm, toward the upper-left quadrant of the monolayer. Propagation terminates slightly sooner in the upper-left region, as seen in the isochrone map (Fig. 4 B). Because of the earlier termination of propagation in the upper-left region, residual propagation persists for a short time with an average direction toward the lower-right region. The x component (or y component) of the bipolar lead field is oriented in the same (or opposite) direction as the x (or y) component of the residual wave. Therefore, pVx (or pVy) shows positive (or negative) deflections during depolarization and negative (or positive) deflections during repolarization. pVx and pVy are approximately in phase with one another but have opposite signs (Fig. 4 C a, solid traces). The residual activity vector leads to large deflections in the pVCG in the lower right direction during depolarization and small deflections in the upper left direction during repolarization (Fig. 4 D, solid trace). To compute more balanced pECGs and pVCG, we can shift the lead placement so that the stimulus site is centered and then equalize the amount of tissue on all sides by taking an appropriate subset of optical recording sites. With this adjustment, the morphologies of pVx and pVy are altered (Fig. 4 C a, shaded traces), and pVCG remains close to the origin during wavefront propagation (Fig. 4 D, shaded trace). However, because the monolayer repolarizes nonuniformly in this example, the waveback propagates more slowly in the lower-right direction. This results in a pVCG that retains a small deflection in the upper-left direction (Fig. 4 D, shaded trace). pV0 measured with the lead placed over the middle of the monolayer (Fig. 4 C b, solid trace) or centered over the stimulus site (Fig. 4 C b, shaded trace) measures the radial component of propagation, and the two are nearly identical. In the latter case, the unipolar lead field (Fig. 1 G) is completely aligned with the direction of propagation.
FIGURE 4.
(A) Normalized voltage map for radial propagation. (B) Isochrone map. (C) (a) Bipolar pECGs (pVx and pVy) for leads placed asymmetrically around (solid traces) or centered on (shaded traces) the stimulus site, and (b) unipolar pECG (pV0) for lead offset from (solid trace) or centered on (shaded trace) the stimulus site. The shaded trace is covered by the solid trace at nearly all points and is difficult to see. (D) pVCG for bipolar leads placed asymmetrically (solid trace) or symmetrically (shaded trace) around the stimulus site. Different colors for the isochrones in panel B correspond to the instants of time shown in panel C.
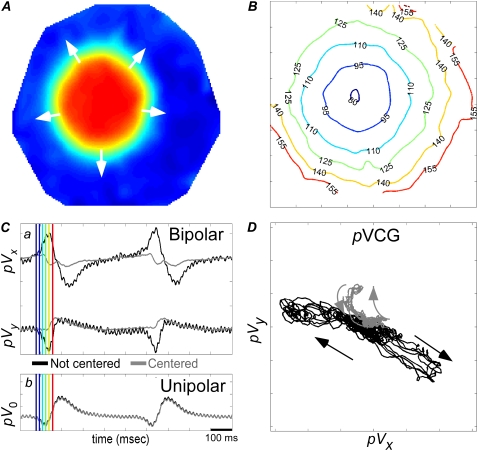
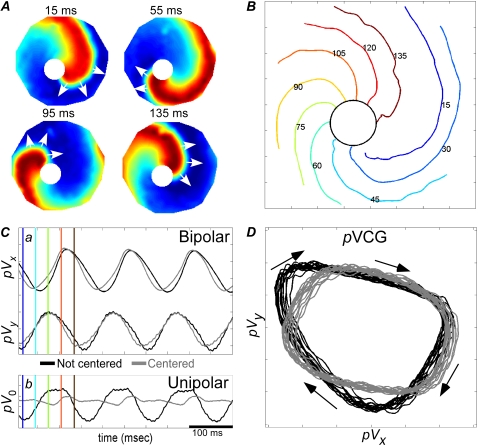
Anchored spiral wave
In Fig. 5, a spiral wave is pinned to and propagating around a 3.5-mm-diameter hole near the center of the monolayer. pVx and pVy are periodic (at the rotation frequency of the spiral wave), sinusoidal, roughly equal in magnitude, and have an ∼90° phase difference (Fig. 5 C a, solid traces). pVCG is roughly circular (Fig. 5 D, solid trace), although with distinct bends because the hole is off-center and the amount of tissue differs on opposite sides of the hole. With a shift in the lead placement so that the hole is centered with equal amounts of tissue on all sides (like in the case of point stimulation), pVx and pVy are shifted slightly in time (Fig. 5 C a, shaded traces), and pVCG is more circular in shape (Fig. 5 D, shaded trace). Plotting pVCG in time (not shown) also reveals the direction of rotation (clockwise for this example). Slight variations in pVx and pVy amplitude and pVCG shape over successive cycles are due to small variations of the relative timing of the wavefront and waveback from cycle to cycle. With a unipolar lead placed directly above the center of the monolayer, a periodic waveform similar to albeit less sinusoidal than that obtained with the bipolar leads is observed (Fig. 5 C b, solid trace). Although the spiral wave moves primarily in a tangential direction perpendicular to the radially oriented unipolar lead field (Fig. 1 G), pV0 oscillates at the spiral wave period because of the offset position of the unipolar lead from the center of the hole, which renders components of the lead field to be more sensitive to the wave movement. However, if the lead position is shifted so that it lies over the center of the hole, the lead field is relatively insensitive to wavefront propagation. pV0 acquires a low-amplitude, harmonic component (Fig. 5 C b, shaded trace) at twice the reentry rate, which is a typical observation at the core of a spiral wave (6). Regardless of lead placement, pV0 does not contain information regarding the direction of rotation.
FIGURE 5.
(A) Normalized voltage maps of spiral wave anchored to 3.5-mm-diameter hole. (B) Isochrone map. (C) (a) Bipolar pECGs (pVx and pVy) for leads placed asymmetrically (solid traces) or symmetrically (shaded traces) around hole, and (b) unipolar pECG (pV0) for lead offset from (solid trace) or centered on (shaded trace) the hole. (D) pVCG for bipolar leads placed asymmetrically (solid trace) or symmetrically (shaded trace) around the hole. Different colors for the isochrones in panel B correspond to the instants of time shown in panel C.
Figure-eight reentry
A figure-eight reentry was initiated by rapid pacing followed by a premature stimulus. The reentry wave consists of a pair of entrained spiral waves that rotate in opposite directions and merge during part of the cycle along a common pathway. In the example shown in Fig. 6 A, the axis of the common pathway (the open line delineating the collision site of the two spiral wave bands) happens to slowly rotate in the clockwise direction with successive cycles. The lead voltages are periodic at the rotation frequency of the reentry, and the phase difference between pVx and pVy varies during each cycle and from cycle to cycle (cycles shown with different colors, Fig. 6 B a). pVCG is elliptical in shape, with the primary axis parallel to the common pathway (Fig. 6 C). The primary axis of the ellipse rotates in the clockwise direction with successive cycles. pV0 is a noisy, irregular trace with varying frequency and amplitude, and information concerning the rotation frequency or common pathway of the reentry is absent (Fig. 6 B b).
FIGURE 6.
(A) Normalized voltage maps of rotating figure-eight reentry. (B) (a) Bipolar pECGs (pVx and pVy) and (b) unipolar pECG (pV0). (C) pVCG. Different colors for the times in panel A correspond to different cycles and are the same as in panels B and C.
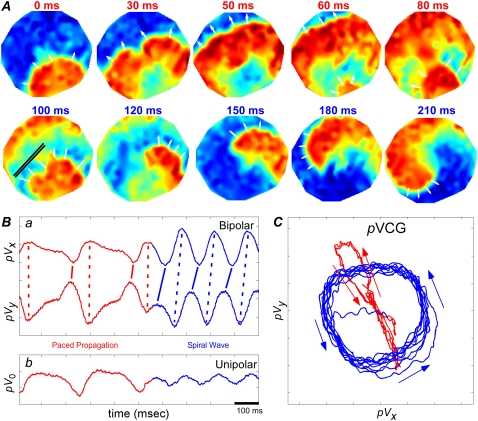
Transition 1: transition from paced propagation to spiral wave
In Fig. 7 A, point stimulation near the edge produces a wave propagating mostly in the positive y direction, with a small component in the negative x direction (0–60 ms). The wave moves through a heterogeneous region in the center of the monolayer, where conduction velocity is slower. The next stimulated wave breaks (80–100 ms) and forms a spiral wave anchored to the heterogeneous region (120–210 ms). pVx and pVy have broad deflections during paced propagation and appear sinusoidal during spiral wave propagation (Fig. 7 B a). pVCG mirrors the direction of paced propagation−pVx is increasingly negative and pVy is increasingly positive during wavefront propagation, leading to a deflection in the upper-left direction. pVx, pVy, and pVCG all demonstrate the transition from paced propagation to a spiral wave and is clearest for pVCG (Fig. 7 B a and C). The transition is also apparent in the phase difference between the two lead voltages, changing from ∼0° (with opposite sign) to ∼90°, as indicated by the decreased tilts of the vertical timing marks (compare blue versus corresponding red marks). Like pVx and pVy, the value pV0 shows a change in morphology upon the transition, with sharp deflections during paced propagation and a sinusoidal shape during the spiral wave (Fig. 7 B b).
FIGURE 7.
(A) Normalized voltage maps during transition from paced wave to spiral wave. (B) (a) Bipolar pECGs (pVx and pVy) and (b) unipolar pECG (pV0). Vertical bars have been added to mark the relative timing of the peaks and valleys. (C) pVCG. Different colors in the times in panel A correspond to different propagation patterns and are the same as in panels B and C.
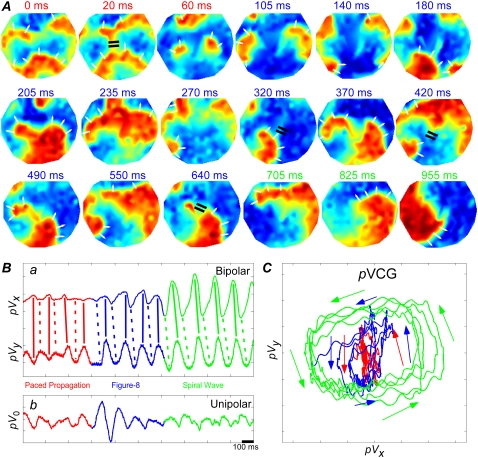
Transition 2: a complex transition
A more complex transition between electrical behaviors is illustrated in Fig. 8. As shown in Fig. 8 A, the monolayer was initially paced from a point stimulus electrode near the edge (0 ms). A heterogeneous region in the center of the monolayer caused wavebreak (20 ms), leading to a figure-eight reentry after pacing ended (60–235 ms). The figure-eight reentrant wave eventually transitioned into a single spiral wave rotating around the center region (705–955 ms). For clarification, the times are colored differently during the three propagation patterns. The bipolar lead voltages transition from single deflections to sinusoids, as behavior changes from paced propagation to reentry (Fig. 8 B). The lead voltages are in phase with opposite sign during paced propagation and are on average ∼90° out of phase during spiral wave propagation, as shown by the decreased tilts of the vertical timing marks. The phase difference varies during figure-eight reentry. Both transitions are difficult to identify from a single lead voltage trace. However, pVCG differentiates the three behaviors clearly (Fig. 8 C). The initial pacing is illustrated by a fairly linear pVCG (red trace), which becomes elliptical for the figure-eight reentry (blue trace) and circular for the single spiral wave (green trace). Regarding pV0, it is not clear from this signal alone what type of propagation is initially present, although some kind of transition is evident by the large jump in amplitude after ∼600 ms that is followed by a more sinusoidal shape. The transition from figure-eight reentry to single spiral wave also cannot be specifically identified, although some kind of transition is apparent by the appearance of a high frequency component during the last 700 ms of the trace (Fig. 8 B b).
FIGURE 8.
(A) Normalized voltage maps during transition from paced wave to figure-eight to spiral wave. (B) (a) Bipolar pECGs (pVx and pVy) and (b) unipolar pECG (pV0). Vertical bars have been added to mark the relative timing of the peaks and valleys. (C) pVCG. Different colors in the times in panel A correspond to different propagation patterns and are the same as in panels B and C.
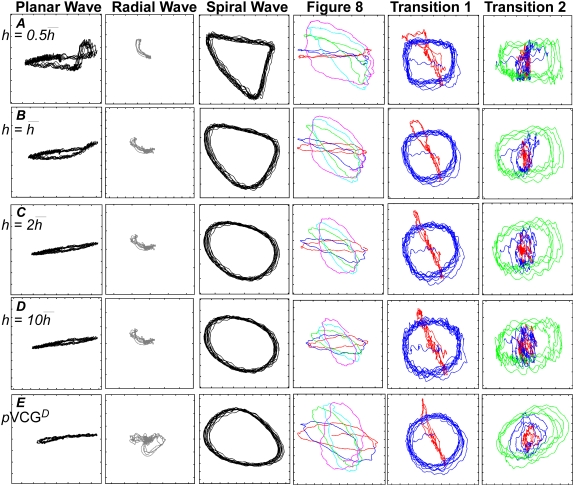
Bipolar lead vectorcardiogram—dependence on height parameter h
For comparison, pVCG was computed at other heights (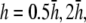 and
and 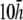 ) for the six examples presented earlier. pVCGs at
) for the six examples presented earlier. pVCGs at 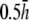 (Fig. 9 A) are distorted from the pVCGs at
(Fig. 9 A) are distorted from the pVCGs at 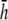 (Fig. 9 B). For the planar wave, pVCG loses its linear shape. The spiral wave pVCG is less circular and has sharper corners. The figure-eight pVCG does not have a distinctly elliptical shape. The transition from paced propagation to spiral wave reentry (Transition 1) is identifiable, since the pVCG shape remains very different for the two behaviors. However, both the linear and circular shaped regions are distorted from their shapes at
(Fig. 9 B). For the planar wave, pVCG loses its linear shape. The spiral wave pVCG is less circular and has sharper corners. The figure-eight pVCG does not have a distinctly elliptical shape. The transition from paced propagation to spiral wave reentry (Transition 1) is identifiable, since the pVCG shape remains very different for the two behaviors. However, both the linear and circular shaped regions are distorted from their shapes at 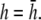 Finally, the transition from paced propagation to figure-eight reentry (Transition 2) is not discernible. pVCGs at
Finally, the transition from paced propagation to figure-eight reentry (Transition 2) is not discernible. pVCGs at 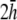 and
and 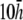 (Fig. 9, C and D) are similar in all cases to pVCGs at
(Fig. 9, C and D) are similar in all cases to pVCGs at 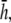 although with lower amplitudes. Hence, we conclude that
although with lower amplitudes. Hence, we conclude that 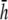 is an effective operating height for the bipolar lead that yields lead signals that represent the global electrical behavior of the cell sheet in a manner akin to those of remote bipolar leads, while at the same time maintaining the amplitude of the signals (Fig. 1).
is an effective operating height for the bipolar lead that yields lead signals that represent the global electrical behavior of the cell sheet in a manner akin to those of remote bipolar leads, while at the same time maintaining the amplitude of the signals (Fig. 1).
FIGURE 9.
pVCGs calculated at (A) 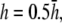 (B)
(B) 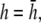 (C)
(C) 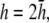 (D)
(D) 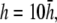 and pVCGD (E) for six cases of wavefront propagation. The example for the radial wave has been centered. Each plot has been normalized to its own peak amplitude. pVCGs computed at
and pVCGD (E) for six cases of wavefront propagation. The example for the radial wave has been centered. Each plot has been normalized to its own peak amplitude. pVCGs computed at 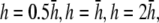 and
and 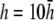 have unnormalized relative amplitudes of ∼2.5, 1, 0.3, and 0.0042, respectively.
have unnormalized relative amplitudes of ∼2.5, 1, 0.3, and 0.0042, respectively.
Comparison of pVCGs using difference and theoretically derived methods
pVCGD values calculated using the difference method are shown in Fig. 9 E for the six examples presented earlier using the theoretical approach. For the most part, pVCGD is similar to pVCG at 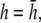 with some notable differences. For the example of radial propagation, pVCGD does not show the small deflection found in pVCG owing to nonuniform repolarization, and for the anchored spiral wave, pVCGD is rotated relative to pVCG. For Transition 2, pVCGD is not as linear as pVCG during paced propagation, is more circular during the figure-eight reentry, and does not have as distinct a transition between figure-eight and single spiral wave reentry. We computed the root mean-square difference between normalized pVCG at
with some notable differences. For the example of radial propagation, pVCGD does not show the small deflection found in pVCG owing to nonuniform repolarization, and for the anchored spiral wave, pVCGD is rotated relative to pVCG. For Transition 2, pVCGD is not as linear as pVCG during paced propagation, is more circular during the figure-eight reentry, and does not have as distinct a transition between figure-eight and single spiral wave reentry. We computed the root mean-square difference between normalized pVCG at 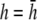 and normalized pVCGD, and the average percent error was 10.5% for all examples, with the largest differences for the radial (19.6%) and spiral (12.4%) waves.
and normalized pVCGD, and the average percent error was 10.5% for all examples, with the largest differences for the radial (19.6%) and spiral (12.4%) waves.
DISCUSSION
Although not in prevalent use today (19), the VCG has been used clinically to provide morphological interpretation of the electrical phenomena of the heart and continues to have diagnostic advantages over the ECG in certain situations (20). The VCG was first constructed in the frontal plane, based on the Einthoven limb leads (21). Since then the VCG was expanded to three dimensions (22), and compound lead systems were proposed to generate a set of orthogonal, corrected leads that compensated for internal inhomogeneities in torso conductance and geometry (23–25). Lead field analysis of the commonly used VCG systems quantified the uniformity and sensitivity of the leads in each dimension (26). Although the two-dimensional sheet lying in a bath is much simpler compared with the whole heart lying in the torso, lead field analysis has not been applied in this context and can be used to determine the sensitivity of the recording leads for the pseudo-ECG to the underlying cellular transmembrane potentials.
In this article, we present a formulation of bipolar pECG and pVCG measurements of a two-dimensional cardiac sheet (cell monolayer) and analyze their dependence on lead placement. Further, we determine a mathematical relation for an effective operating height for the bipolar lead placed over opposite edges of the cell monolayer. Lead placement at half the effective height provides a pVCG that overweights the contribution of cells near the lead electrodes (Fig. 1), whereas pVCGs for bipolar leads at twice or 10-times 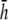 is similar to that at
is similar to that at 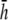 (Fig. 9) but with lower amplitude. Therefore,
(Fig. 9) but with lower amplitude. Therefore, 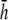 can serve as the operating height that balances global sensitivity and amplitude for pECG and pVCG computation.
can serve as the operating height that balances global sensitivity and amplitude for pECG and pVCG computation.
Numerically calculated bipolar and unipolar leads have been used previously to approximate the clinical ECG for one- and two-dimensional studies (9–11,13). The numerical bipolar leads are analogous to the Einthoven limb leads, which measure the global activity of the heart. The numerical unipolar lead is analogous to the precordial leads, V1–V6 of the 12-lead system, that are placed on the chest to detect localized activity in the region of the heart closest to the lead (27,28). We find that for the case of a unipolar lead situated above a cardiac cell sheet, the unipolar pECG is most sensitive to activity near the electrode, but importantly, it is insensitive to activity at the point directly underneath the electrode (Fig. 1 H). This is because at that location, electrical propagation is perpendicular to the three-dimensional lead field. However, in the three-dimensional heart, electrical activity can propagate parallel to the lead field, and therefore, the precordial leads are most sensitive to activity directly underneath that is propagating toward (or away from) the electrode.
There is growing use of monolayers as an in vitro system for investigating cardiac electrical behavior (29,30), and optical maps of transmembrane potential have enabled the study of different patterns of electrical propagation, as well as transitions between them in the context of arrhythmia (31). Electrical recordings of the VCG would be a valuable adjunct to optical maps because of their succinct representation of the electrical behavior, but are technically very difficult to obtain, owing to the extremely small extracellular potentials generated by a monolayer of cells in a bath. If we consider a 17-mm-diameter cardiac monolayer with intracellular conductivity σi = 2.5 mS/cm (32), a monolayer thickness of 10 μm (33), placed in a bath with conductivity σb = 20 mS/cm (34), and assume an action potential amplitude of 100 mV (35), a maximum transmembrane voltage upstroke velocity, (dVm/dt)max, of 125 V/s (36), and a conduction velocity of 25 cm/s (37), an ECG measurement would have a peak value of ∼4 μV. Instead, pECG (and pVCG) can be determined from the optical maps of Vm using the methodology described in this study. Further, Iravanian and Christini have recently shown that it is possible to process optical signals for real-time control capability (38). Since pECG is a weighted sum of Vm values, it can also be computed in real-time.
For two-dimensional propagation in cardiac cell monolayers, we have shown that the bipolar pVCG capably represents electrical propagation associated with plane waves, radial waves, reentrant spiral waves, figure-eight spiral waves, and transitions between them. Transitions from normal pacing behavior to a reentrant wave, or from a reentrant wave to multiple waves, are crucial cardiac events related to arrhythmia, and their detection is important. Plane waves appear as linear trajectories, radial waves as trajectories localized to the origin, single spiral waves as circles, and figure-eight spiral waves as ellipses. Phase differences between the bipolar lead voltages can also help to identify propagation patterns. The phase difference is ∼0° during paced propagation, 90° during spiral wave propagation, and variable during figure-eight reentries. In contrast, the unipolar pECG does not represent some of these electrical activities well nor the transition between them. Key information such as direction of propagation or frequency of reentry is missing or may be distorted.
Finally, with the advent of optical mapping of Vm from tissue surfaces, bipolar pECGs (lead voltages 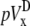 and
and 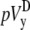 ) were calculated in previous studies by using an ad hoc method that subtracts the sum of Vm on one-half of the mapped area from the sum of the other half (5–8,12). However, we have shown that two sets of geometric functions are necessary to correctly sum Vm for circular cardiac cell monolayers (sheets)—one set (γx and γy) that is applied over the area of the monolayer and the other set (αx and αy) that is applied over the perimeter of the monolayer. Their usage produces bipolar lead voltages pVx and pVy that are biophysically based, and also fast to compute, compared with alternative calculations based on the gradients of Vm.
) were calculated in previous studies by using an ad hoc method that subtracts the sum of Vm on one-half of the mapped area from the sum of the other half (5–8,12). However, we have shown that two sets of geometric functions are necessary to correctly sum Vm for circular cardiac cell monolayers (sheets)—one set (γx and γy) that is applied over the area of the monolayer and the other set (αx and αy) that is applied over the perimeter of the monolayer. Their usage produces bipolar lead voltages pVx and pVy that are biophysically based, and also fast to compute, compared with alternative calculations based on the gradients of Vm.
Acknowledgments
We thank Josh Cysyk, Joyce Lin, and Elizabeth Lipke for providing experimental data.
Funding for this work was provided by National Institutes of Health grants No. R01 HL66239, No. R21 RR017073, and No. R21 EB006171.
Editor: Arthur Sherman.
References
- 1.Alexander, R. W., J. W. Hurst, and R. C. Schlant. 1994. The Heart, Arteries and Veins. McGraw-Hill, Health Professions Division, New York.
- 2.Burashnikov, A., and C. Antzelevitch. 2003. Reinduction of atrial fibrillation immediately after termination of the arrhythmia is mediated by late phase 3 early afterdepolarization-induced triggered activity. Circulation. 107:2355–2360. [DOI] [PubMed] [Google Scholar]
- 3.Wu, T. J., S. F. Lin, J. N. Weiss, C. T. Ting, and P. S. Chen. 2002. Two types of ventricular fibrillation in isolated rabbit hearts: importance of excitability and action potential duration restitution. Circulation. 106:1859–1866. [DOI] [PubMed] [Google Scholar]
- 4.Extramiana, F., and C. Antzelevitch. 2004. Amplified transmural dispersion of repolarization as the basis for arrhythmogenesis in a canine ventricular-wedge model of short-QT syndrome. Circulation. 110:3661–3666. [DOI] [PubMed] [Google Scholar]
- 5.Skanes, A. C., R. Mandapati, O. Berenfeld, J. M. Davidenko, and J. Jalife. 1998. Spatiotemporal periodicity during atrial fibrillation in the isolated sheep heart. Circulation. 98:1236–1248. [DOI] [PubMed] [Google Scholar]
- 6.Pertsov, A. M., J. M. Davidenko, R. Salomonsz, W. T. Baxter, and J. Jalife. 1993. Spiral waves of excitation underlie reentrant activity in isolated cardiac muscle. Circ. Res. 72:631–650. [DOI] [PubMed] [Google Scholar]
- 7.Gray, R. A., J. Jalife, A. Panfilov, W. T. Baxter, C. Cabo, J. M. Davidenko, and A. M. Pertsov. 1995. Nonstationary vortexlike reentrant activity as a mechanism of polymorphic ventricular tachycardia in the isolated rabbit heart. Circulation. 91:2454–2469. [DOI] [PubMed] [Google Scholar]
- 8.Gray, R. A., A. M. Pertsov, and J. Jalife. 1996. Incomplete reentry and epicardial breakthrough patterns during atrial fibrillation in the sheep heart. Circulation. 94:2649–2661. [DOI] [PubMed] [Google Scholar]
- 9.Gima, K., and Y. Rudy. 2002. Ionic current basis of electrocardiographic waveforms: a model study. Circ. Res. 90:889–896. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Baher, A., Z. Qu, A. Hayatdavoudi, S. T. Lamp, M. J. Yang, F. Xie, S. Turner, A. Garfinkel, and J. N. Weiss. 2007. Short-term cardiac memory and mother rotor fibrillation. Am. J. Physiol. Heart Circ. Physiol. 292:H180–H189. [DOI] [PubMed] [Google Scholar]
- 11.Bernus, O., C. W. Zemlin, R. M. Zaritsky, S. F. Mironov, and A. M. Pertsov. 2005. Alternating conduction in the ischemic border zone as precursor of reentrant arrhythmias: a simulation study. Europace. 7(Suppl 2):93–104. [DOI] [PubMed] [Google Scholar]
- 12.Davidenko, J. M. 1993. Spiral wave activity: a possible common mechanism for polymorphic and monomorphic ventricular tachycardias. J. Cardiovasc. Electrophysiol. 4:730–746. [DOI] [PubMed] [Google Scholar]
- 13.Iravanian, S., Y. Nabutovsky, C. R. Kong, S. Saha, N. Bursac, and L. Tung. 2003. Functional reentry in cultured monolayers of neonatal rat cardiac cells. Am. J. Physiol. Heart Circ. Physiol. 285:H449–H456. [DOI] [PubMed] [Google Scholar]
- 14.Tung, L., and J. Cysyk. 2007. Imaging fibrillation/defibrillation in a dish. J. Electrocardiol. 40:S62–S65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Plonsey, R., and R. C. Barr. 2007. Bioelectricity: A Quantitative Approach. Springer, New York.
- 16.Plonsey, R. 1963. Reciprocity applied to volume conductors and the ECG. IEEE Trans. Biomed. Eng. 10:9–12. [DOI] [PubMed] [Google Scholar]
- 17.Lim, Z. Y., B. Maskara, F. Aguel, R. Emokpae, Jr., and L. Tung. 2006. Spiral wave attachment to millimeter-sized obstacles. Circulation. 114:2113–2121. [DOI] [PubMed] [Google Scholar]
- 18.Entcheva, E., S. N. Lu, R. H. Troppman, V. Sharma, and L. Tung. 2000. Contact fluorescence imaging of reentry in monolayers of cultured neonatal rat ventricular myocytes. J. Cardiovasc. Electrophysiol. 11:665–676. [DOI] [PubMed] [Google Scholar]
- 19.Rautaharju, P. M. 1988. A hundred years of progress in electrocardiography. 2: The rise and decline of vectorcardiography. Can. J. Cardiol. 4:60–71. [PubMed] [Google Scholar]
- 20.Perez Riera, A. R., A. H. Uchida, C. F. Filho, A. Meneghini, C. Ferreira, E. Schapacknik, S. Dubner, and P. Moffa. 2007. Significance of vectorcardiogram in the cardiological diagnosis of the 21st century. Clin. Cardiol. 30:319–323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Mann, H. 1920. A method of analyzing the electrocardiogram. Arch. Intern. Med. 25:283–294. [Google Scholar]
- 22.Wilson, F. N., F. D. Johnston, and C. E. Kossmann. 1947. The substitution of a tetrahedron for the Einthoven triangle. Am. Heart J. 33:594–603. [DOI] [PubMed] [Google Scholar]
- 23.Frank, E. 1954. The image surface of a homogeneous torso. Am. Heart J. 47:757–768. [DOI] [PubMed] [Google Scholar]
- 24.McFee, R., and A. Parungao. 1961. An orthogonal lead system for clinical electrocardiography. Am. Heart J. 62:93–100. [Google Scholar]
- 25.Schmitt, O. H., and E. Simonson. 1955. The present status of vectorcardiography. AMA Arch. Intern. Med. 96:574–590. [PubMed] [Google Scholar]
- 26.Brody, D. A., and R. C. Arzbaecher. 1964. A comparative analysis of several corrected vectorcardiographic leads. Circulation. 29:S533–S545. [DOI] [PubMed] [Google Scholar]
- 27.Malmivuo, J., and R. Plonsey. 1995. Bioelectromagnetism: Principles and Applications of Bioelectric and Biomagnetic Fields. Oxford University Press, New York.
- 28.Kligfield, P., L. S. Gettes, J. J. Bailey, R. Childers, B. J. Deal, E. W. Hancock, G. van Herpen, J. A. Kors, P. Macfarlane, D. M. Mirvis, O. Pahlm, P. Rautaharju, G. S. Wagner, M. Josephson, J. W. Mason, P. Okin, B. Surawicz, and H. Wellens. 2007. Recommendations for the standardization and interpretation of the electrocardiogram. Part I: The electrocardiogram and its technology: a scientific statement from the American Heart Association Electrocardiography and Arrhythmias Committee, Council on Clinical Cardiology; the American College of Cardiology Foundation; and the Heart Rhythm Society: endorsed by the International Society for Computerized Electrocardiology. Circulation. 115:1306–1324. [DOI] [PubMed] [Google Scholar]
- 29.Rohr, S., A. G. Kleber, and J. P. Kucera. 1999. Optical recording of impulse propagation in designer cultures. Cardiac tissue architectures inducing ultra-slow conduction. Trends Cardiovasc. Med. 9:173–179. [DOI] [PubMed] [Google Scholar]
- 30.Tung, L., and Y. Zhang. 2006. Optical imaging of arrhythmias in tissue culture. J. Electrocardiol. 39:S2–S6. [DOI] [PubMed] [Google Scholar]
- 31.Bursac, N., F. Aguel, and L. Tung. 2004. Multiarm spirals in a two-dimensional cardiac substrate. Proc. Natl. Acad. Sci. USA. 101:15530–15534. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Roth, B. J. 1997. Electrical conductivity values used with the bidomain model of cardiac tissue. IEEE Trans. Biomed. Eng. 44:326–328. [DOI] [PubMed] [Google Scholar]
- 33.Entcheva, E., and H. Bien. 2006. Macroscopic optical mapping of excitation in cardiac cell networks with ultra-high spatiotemporal resolution. Prog. Biophys. Mol. Biol. 92:232–257. [DOI] [PubMed] [Google Scholar]
- 34.Trayanova, N. A., B. J. Roth, and L. J. Malden. 1993. The response of a spherical heart to a uniform electric field: a bidomain analysis of cardiac stimulation. IEEE Trans. Biomed. Eng. 40:899–908. [DOI] [PubMed] [Google Scholar]
- 35.Rohr, S., D. M. Scholly, and A. G. Kleber. 1991. Patterned growth of neonatal rat heart cells in culture. Morphological and electrophysiological characterization. Circ. Res. 68:114–130. [DOI] [PubMed] [Google Scholar]
- 36.Zhuang, J., K. A. Yamada, J. E. Saffitz, and A. G. Kleber. 2000. Pulsatile stretch remodels cell-to-cell communication in cultured myocytes. Circ. Res. 87:316–322. [DOI] [PubMed] [Google Scholar]
- 37.Bursac, N., K. K. Parker, S. Iravanian, and L. Tung. 2002. Cardiomyocyte cultures with controlled macroscopic anisotropy: a model for functional electrophysiological studies of cardiac muscle. Circ. Res. 91:e45–e54. [DOI] [PubMed] [Google Scholar]
- 38.Iravanian, S., and D. J. Christini. 2007. Optical mapping system with real-time control capability. Am. J. Physiol. Heart Circ. Physiol. 293:H2605–H2611. [DOI] [PubMed] [Google Scholar]