A Fluorescence-Based Technique to Construct Size Distributions from Single-Object Measurements: Application to the Extrusion of Lipid Vesicles

Abstract

We report a novel approach to quantitatively determine complete size distributions of surface-bound objects using fluorescence microscopy. We measure the integrated intensity of single particles and relate it to their size by taking into account the object geometry and the illumination profile of the microscope, here a confocal laser scanning microscope. Polydisperse (as well as monodisperse) size distributions containing objects both below and above the optical resolution of the microscope are recorded and analyzed. The data is collected online within minutes, which allows the user to correlate the size of an object with the response from any given fluorescence-based biochemical assay. We measured the mean diameter of extruded fluorescently labeled lipid vesicles using the proposed method, dynamic light scattering, and cryogenic transmission electron microscopy. The three techniques were in excellent agreement, measuring the same values within 7–9%. Furthermore we demonstrated here, for the first time that we know of, the ability to determine the full size distribution of polydisperse samples of nonextruded lipid vesicles. Knowledge of the vesicle size distribution before and after extrusion allowed us to propose an empirical model to account for the effect of extrusion on the complete size distribution of vesicle samples.

INTRODUCTION

Lipid vesicles have been studied extensively for the past 30 years (1–8). As a model system of biological membranes, they have provided comprehensive insight into the fundamental physiochemical properties of biomembranes (9,10). As uniquely suited systems for the reconstitution of transmembrane proteins, they have greatly contributed to our understanding of protein structure and function (11–15).

To guarantee the reproducibility of vesicle samples, the research community has put significant effort into controlling and characterizing the size distributions of vesicles (16,2,17–19). To control the size of vesicles, different techniques, such as sonication, extrusion, and alternating electric fields, have been used (2,17,20,19). Characterization of the resulting size distribution has attracted similar attention, and today dynamic light scattering (DLS) (21,22) and transmission electron microscopy at cryogenic temperatures (cryoTEM) (18) are the most frequently used techniques (23,24). DLS provides ensemble-averaged information of vesicle size distributions in a fast and rather straightforward manner, whereas cryoTEM resolves shape and size at the single-vesicle level. However, despite their merits, both techniques have difficulty handling polydisperse samples (25,26).

Rehydration of dried lipid powder/films (16,27,28,17), probably the most commonly used vesicle preparation method, results in polydisperse size distributions. The polydispersity of these samples has so far prevented recording of their size distribution by either cryoTEM or DLS, so its dependence on lipid composition or any other parameter is not known. Furthermore, with the initial state as an unknown, the exact mechanism by which all vesicle-processing methods (e.g., sonication, extrusion, or freeze-thawing) operate on size distribution has remained unclear. Here, we address these issues by establishing a simple and accurate technique to record the size distribution of polydisperse vesicle samples.

We use surfaces to immobilize fluorescently labeled vesicles at low densities (29,30). Single vesicles are then imaged with fluorescence microscopy (31,32) and their size (above and below the optical resolution) is calculated from their integrated intensity (33). The technique described here is of value for objects at or below the optical resolution limit. The size of objects several times above the optical resolution can be imaged directly. Typical images contained up to a thousand particles, allowing the creation of statistically reliable histograms. Since the approach is based on single-particle counting, ensemble averaging does not skew the distributions. Furthermore, the large dynamic range of fluorescence imaging instrumentation and the fact that the static/immobilized samples can be imaged sequentially at different detector gains makes possible the accurate recording of widely polydisperse populations. A large number of recent experiments addressing single-vesicle behavior make such a fluorescence-microscopy-based technique even more relevant (34–38,33,39–42).

The aforementioned direct relationship between the size of labeled vesicles and their total fluorescence intensity breaks down when the vesicle size becomes comparable to the depth of field of an optical microscope. This is a critical issue in the recording of polydisperse samples with diameters ranging from, for example, 20 nm to a few microns. Here, we quantify the relation between recorded intensity, object size, and depth of field, and in addition we provide a simple method to correct for the convolution effects related to the illumination and collection profiles of wide-field, confocal, or total internal reflection microscopes.

We first applied the technique to a sample of colloidal beads of known dimension as a control. From these experiments, we verified our calculation of the effect of a finite depth of field: under confocal imaging conditions, a solid sphere 1 μm in diameter will appear ∼25% smaller than it is. Second, we prepared lipid vesicles under different conditions to determine the size distribution of extruded and nonextruded (polydisperse) samples. We chose phospholipid vesicles consisting primarily of the zwitterionic lipid 1,2-dioleoyl-sn-glycero-3-phosphocholine (DOPC). The lipid composition also included 2.0 mol % biotinylated lipid to couple the vesicles on a streptavidin functionalized surface. The size distribution of vesicles extruded through pore diameters of 100 nm and 200 nm obtained using our method was found to be identical to ensemble DLS and size distributions extracted from cryoTEM data.

The ability to characterize polydisperse and extruded vesicle samples under their respective preparation conditions (physiological ionic strength and pH) allowed us to formulate and test an empirical model of the extrusion process. In this scheme, a vesicle redistribution profile is assigned to each extrusion filter. We established Gaussian filter profiles for polycarbonate membranes with filter pore diameters of 100 and 200 nm and compared the theoretical with the measured distributions. A previous description of the extrusion process predicted successfully the ensemble average diameter of an extruded vesicle population (22). By taking into account the conservation of lipid mass upon fragmentation, our model is able to predict the full shape of the size distribution for vesicles extruded through 100- and 200-nm filters. The model also was able to account for the presence of an intrinsic subpopulation of small vesicles, i.e., diameters below the filter size.

SIZE DETERMINATION

Theory

This section will describe a fast and easy single-particle scheme to convert integrated intensity into physical dimensions of fluorescent objects, both above and below optical resolution. Intensity distributions have previously been used to reveal the size of such subresolution objects as colloidal beads (43,44) and even human genes (45), but these procedures have required specialized microscope setups. We present here a general method readily applicable to all objects with a defined geometry. We address the case of spherical symmetry.

Consider a sphere with diameter D stained uniformly throughout the full volume, V = V(x, y, z). The fluorescent sphere is attached to a planar surface at z = 0, where z denotes the position along the optical axis. Upon spatial uniform illumination, the total integrated fluorescence intensity of the sphere is thus proportional to the volume, and scales as D³. Fluorescence confocal laser scanning microscopy (CLSM) measurements yield only a fraction of this intensity, since object detection is constrained by the confocal volume given by the microscope point spread function, P(x, y, z, λ), which depends on the lateral coordinates x and y and the excitation wavelength, λ. P is a convolution of the laser-illumination—and pinhole-detection—profile and can be determined in one of two ways: 1), by theoretical calculation using microscope specifications; or 2), by direct spatial measurement of a subresolution fluorescent object. In the following derivations, it is assumed that P(x, y, z, λ) is known. Applying the normalized point spread function, p(x, y, z, λ), as the weight function, integration of the sphere gives the acquired fluorescence, F.

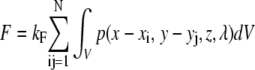(1)

The constant, k_F, holds information about the applied settings of the microscope (i.e., laser power, signal amplification, scanning rate, etc.) and the intrinsic photochemical properties of the fluorophore (i.e., quantum yield, amount of quenching, etc.). N is the number of pixels in each direction of a quadratic image, and λ is the wavelength of the excitation source. This expression can be simplified when the microscope is operated in a manner such that the pixel size is smaller than the diffraction-limited resolution, fulfilling Eq. 2, with A_P and NA the pixel area and numerical aperture, respectively, of the objective.

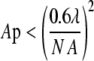(2)

This criterion makes it possible to approximate the xy sum over all point spread functions in Eq. 1 with one confocal slice extending homogeneously throughout the entire xy plane and possessing the axial dependency of the original point spread function. With Eq. 2 satisfied, the emitted fluorescence signal can be expressed with a single integral along the optical axis (Eq. 3) containing the geometrical characteristics G(D, z) of a solid sphere or a spherical shell (Eq. 4).

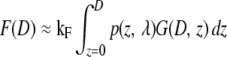(3)

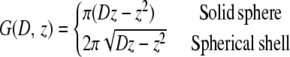(4)

The function describing the fluorescence can now be readily calculated numerically and will depend only on the diameter of the shell/sphere for a fixed microscope setting, i.e., F = F(D). To calculate F(D), it is necessary to have a calibration standard, which grants knowledge of k_F, i.e., it allows conversion from arbitrary intensity units to physical size in, for example, nanometers. Measurement of fluorescence, F_R = F(D_R), from an object with known diameter D_R, allows Eq. 4 to be recast into its final form.

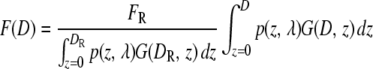(5)

Calibration

There exist a variety of ways to obtain the proportionality factor between acquired fluorescence intensity and physical object size. In this study, we have used two different approaches, 1), fluorescently labeled colloidal beads of known diameter, and 2), cryogenic transmission electron micrographs of a fluorescence-labeled vesicle population. The fluorescence intensities of beads and vesicles are recorded and correlated to their physical dimensions as stated by the manufacturer or measured with cryoTEM.

Step-by-step scheme

To summarize, we have divided the size correlation process into four separate stages outlined below and sketched in Fig. 1.

1. Setup. Choose an object geometry G(D, z) (in this study, solid spheres and spherical shells).

2. Imaging. Determine the axial dependency of the microscope point spread function. This is most easily achieved by measuring pinhole profiles with an xz stack of images in reflection mode. Localize objects in the focus plane and acquire micrographs. Integrate object intensities.

3. Confocal correction. Determine F_R and D_R from a reference sample and calculate the conversion function, F(D), from Eq. 5.

4. Results. Generate size-distribution histograms from converted object intensities.

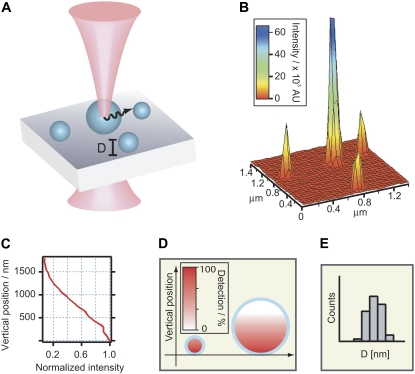
FIGURE 1.

Sketch of intensity-based size mapping. (A) Fluorescently labeled objects with a well defined geometry are imaged with a confocal laser scanning microscope exhibiting an axial decaying illumination/collection profile. (B) Micrograph (intensity surface plot) of lipid vesicles labeled in the bilayer and immobilized on a glass slide through receptor-ligand binding of streptavidin-biotin. (C) The axial part of the microscope point spread function (PSF) determines to what degree an object is illuminated and emitted light is collected. The axial intensity profile of the focused beam along the optical axis (i.e., axial dependence of the PSF) displayed here was measured from an x,y,z image stack of a reflecting surface. (D) Objects comparable in size to the depth of field will exhibit less intensity per volume compared to particles within the field, as indicated by the color table. (E) Knowledge of the PSF, along with the total integrated particle intensities, obtained from micrographs, allow the construction of the physical size distribution of e.g., polydisperse vesicles consisting of vesicles both below and above the optical resolution.

To convert fluorescence into object size, numerical aperture of the objective, excitation wavelength, and pixel size must be known, to ensure that Eq. 2 is satisfied. Finally, identical imaging conditions must be applied, since Eq. 5 is related to the same set of microscope characteristics.

VESICLE SIZE DISTRIBUTIONS

We find the ability to record the shape of polydisperse vesicle size distributions very interesting, since it is now possible to extend previous theoretical and experimental work with vesicle sizes above the diffraction-limited resolution (46–49,25). Attention has previously been directed to full size distributions of vesicles produced through chemical equilibrium or by fragmentation with ultrasound. Vesicles produced through equilibrium have been predicted and verified to have narrow size distributions (radii ranging between 15 and 50 nm) shaped like stretched Gaussian or approximate log-normal distributions (50,48,25). Vesicle populations produced by fragmentation by either ultrasound (47) or extrusion (49) have experimentally been shown to assume the shape of Weibull extremal probability distributions. However, the shapes of vesicle size distributions produced by thin film rehydration, the most common preparation procedure, still remain unknown.

After rehydration, the shape of the initial size distribution can be perturbed by a variety of techniques, e.g., mechanical extrusion, ultrasonication, or freeze thawing. Consequently, knowledge of characteristic parameters describing the initial population is a prerequisite for making any quantitative predictions on the resulting population.

EXTRUSION MODEL

We formulate here an empirical approach to account for the effect of extrusion on a polydisperse lipid vesicle preparation. In the extrusion process, a distribution of lipid vesicles of various sizes are forced through a polycarbonate membrane filter with a defined pore size by applying external pressure. Vesicles with a diameter comparable to or larger than the filter pore diameter will be affected by this treatment and are fragmented into smaller sizes, thus shifting the initial population toward lower diameters. Vesicles cannot exist below a certain critical diameter, D₀, which we define as a lower limit to the filter-induced fragmentation. To describe this process, we assign a vesicle redistribution profile, f(D), to each polycarbonate membrane filter.

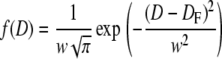(6)

We define the profile by a Gaussian distribution, with D_F the mean filter pore diameter and the width, w, defined as 0.6D_F. We estimated w on the basis of extrusion experiments described in Results and Analysis; for more details, consult Supplementary Material, Data S1. The vesicle redistribution profile is applied on the initial nonextruded polydisperse vesicle distribution, P(D), to obtain the distribution of vesicles created by fragmentation, T(D), and the distribution of vesicles, S(D), that are removed from P(D) by fragmentation. Thus, the new population resulting from extrusion P_E(D) is given by adding T(D) and subtracting S(D) from P(D).

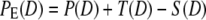(7)

The distribution T(D) is determined by converting a fraction of the total lipid mass from vesicles with diameters 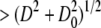into vesicles of diameter D.

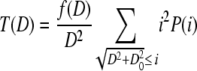(8)

The distribution S(D) is obtained by summing all lipid mass fractions from vesicles with diameter D, which are converted into smaller-diameter vesicles.

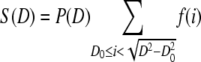(9)

We recognize that this is a simplified sketch of the extrusion process in the sense that the only physical parameter entering the vesicle redistribution profiles is the filter pore diameter. Nevertheless, this approach is able to account for the changes in population characteristics that we observe upon extrusion (see Results and Analysis). We find the simplicity of this approach attractive, and envision that theoretical vesicle redistribution profiles can be computed based on physical parameters, e.g., membrane bending modulus, lipid geometry, extrusion pressure, mean filter pore diameter, and thickness.

MATERIALS AND METHODS

Materials

TetraSpeck fluorescent microspheres with nominal diameters of 100 nm, 210 nm, 500 nm, and 1000 nm were purchased from Invitrogen (Taastrup, Denmark). The fluorescent microspheres were polystyrene beads stained throughout the volume with four distinct dyes having excitation/emission maxima at 365/430 nm, 505/515 nm, 560/580 nm, and 660/680 nm. DOPC, 1,2–Dioleoyl-sn-glycero-3-[phospho-rac-(1-glycerol)] (sodium salt) (DOPG), 1,2-distearoyl-sn-glycero-3-phosphoethanolamine-N-[biotinyl(polyethylene glycol)2000] (ammonium salt) (DSPE-PEG₂₀₀₀-biotin) were all purchased from Avanti Polar Lipids (Alabaster, AL) as chloroform solutions. 3,3′-Dioctadecyloxacarbocyanine perchlorate (C₁₈-DiO) and streptavidin were purchased from Invitrogen. Bovine serum albumin (BSA) and biotinylated bovine serum albumin (BSA-biotin) were purchased from Sigma Aldrich (Brøndby, Denmark).

Sample preparation

TetraSpeck fluorescent microspheres

Samples of fluorescent colloidal beads were prepared according to information supplied by Molecular Probes. Briefly, aliquots of TetraSpeck fluorescent microspheres were dispersed on clean glass slides. The cleaning was performed by sonicating and rinsing in 2% (v/v) hellmanex in millipore water. The solvent medium was left to evaporate at elevated temperatures (∼40°C) to minimize colloid aggregation. The physisorbed colloidal beads were encapsulated in glycerol between two glass slides and were used for fluorescence microscopy. Two different samples were prepared, which contained mixtures of beads with diameters of 100 nm and 210 nm (sample 1) and 210 nm, 500 nm, and 1000 nm (sample 2). Fluorescence spectra of each bead population were recorded on a Perkin Elmer (Waltham, MA) fluorometer spectrograph. This enabled a calculation of the dye density for each population. Normalizing all other populations to the 210-nm sample compensated for differences in dye density (Data S1).

Vesicle preparation

Small unilamellar vesicles (SUV) (DOPC/DOPG/DSPE-PEG₂₀₀₀-biotin/C₁₈-DiO, 87:10:2:1) and polydisperse unilamellar vesicles (PUV) (DOPC/DOPG/DSPE-PEG₂₀₀₀-biotin/C₁₈-DiO, 87:10:2:1) were prepared by mixing the appropiate lipids in a 5-ml round-bottomed flask. Chloroform was evaporated under nitrogen flow and lipid films were rehydrated in 200 mM D-sorbitol solution to a total lipid concentration of 1.0 g/L. The SUV sample was vortexed and preextruded once through a polycarbonate membrane filter (pore size 400 nm) and subjected to several freeze/thaw cycles according to previous published protocols (22). The sample was divided into two separate populations, which were extruded 11 times through a polycarbonate membrane filter with pore size 100 nm (SUV₁₀₀) and 200 nm (SUV₂₀₀) at pressures of 200 psi and 100 psi, respectively. Multilamellarity of the vesicle preparations was assayed using cryoTEM and yielded 8% of total preparation. The PUV sample was left to rehydrate at 37°C overnight and subjected to 15 freeze/thaw cycles, i.e., immersion in liquid nitrogen and thawing at 45°C in a waterbath, to minimize multilamellarity.

Surface functionalization

Surface functionalization and vesicle tethering was performed according to previous protocols (36). Glass slides, cleaned with 2% (v/v) Hellmanex and millipore water, were mounted in a microscope chamber and incubated with a mixture of 0.1 g/L BSA/BSA-biotin, 10:1, in millipore water for 10 min. Excess protein was removed by gently flushing the surface with phosphate-buffered saline (100 mM NaCl, pH 7.4) and subsequently incubated for 10 min with 0.025 g/L streptavidin. The surface was gently rinsed with phosphate-buffered saline, and small amounts of vesicle suspension were added to each surface, generating a total lipid concentration of ∼1 mg/L.

Confocal laser scanning microscopy

All micrographs were acquired with an inverted confocal microscope (TCS SP5, Leica, Solms, Germany) using an oil immersion objective HCX PL APO, 100× magnification and numerical aperture 1.4. All micrographs were prefocused at the oil/glass substrate interface with the microscope operating in reflection mode.

Microspheres were imaged upon excitation with the 488-nm laserline. A set of identical microscope settings was applied for all micrographs acquired on sample 1. Another set was used for recording micrographs on sample 2. Two sets were used to exploit the full dynamic range of the microscope photomultiplier tubes. Beads with 210-nm diameters present on both samples were used to convert measured intensities from one sample to the other by linear scaling. This procedure enabled a broader range of illumination conditions available for optimizing image quality.

Vesicle populations were excited with the 488-nm laserline and imaged after 30 min of incubation to ensure a faithful reconstruction of the vesicle population in solution. An image resolution of 2048 × 2048 pixels, physical pixel area of 70 × 70 nm², and bit depth of 16 was applied on all samples.

Image treatment and size conversion

Micrographs were treated with ImageJ Analysis Software version 1.34S (National Institutes of Health, Bethesda, MD). Particles were located and sorted according to the magnitude of integrated fluorescence intensity. Briefly, we chose a threshold intensity value to define the area of particles. The threshold intensity was adjusted manually to be slightly greater than the background intensity. The same threshold value was applied on all processed micrographs, and only particles >100 pixels were accepted. The elongations of all particles were evaluated as the ratio of elliptical minor axis to major axis, and we used this ratio to accept only circular objects. All particle intensities were subtracted from the background intensity value which was ∼0.7% of the entire dynamic range. Intensity histograms were plotted and converted to physical diameter using a custom designed Igor Pro v. 5.01 routine (Wavemetrics, Lake Oswego, OR). The calibration was performed separately for beads and vesicles. Mean integrated fluorescence intensity, F_R, from the 210-nm colloid bead population was recorded using CLSM, and mean diameter, D_R, was obtained from manufacturer specifications. The vesicle calibration was based on a reference population (SUV₁₀₀). An iterative scheme was applied in which F_R (CLSM on SUV₁₀₀) and D_R (cryoTEM on SUV₁₀₀) were used to calculate an initial conversion function F(D)⁰. F(D)⁰ was then used to convert the reference population intensities into diameters, to obtain the mean diameter 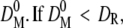then a new conversion function F(D)¹ was calculated by decrementing the initial diameter. If 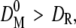the initial diameter was incremented. Every new conversion function was reapplied on the reference population to obtain new mean diameters 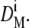After the ith iteration, 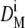converged with D_R after applying F(D)ⁱ. The final conversion function, F(D)ⁱ, was then applied on SUV₂₀₀ and the polydisperse sample.

Dynamic light scattering

Dynamic light scattering was performed using an ALV-5000 Correlator equipped with a 633-nm laserline. The vesicle size distribution was measured at 90° and the scattered intensity was measured for 10 × 30 s. To ensure that the evaluated peaks were related to translational diffusion, angle-dependent measurements were conducted at 70°, 90°, 110°, and 130°. The scattered intensity was measured for 3 × 10 s at each angle. All data was collected at 20°C. The vesicles were diluted to a final concentration of 0.01% (w/v) in 0.02 μm filtered buffer.

The correlation function was translated into the number-weighted size distribution using the dls 2g(t) regularized fit routine implemented in the ALV correlator software. The formfactor of vesicles with a membrane thickness of 4.5 nm was applied to all data.

Cryogenic transmission electron microscopy

Transmission electron microscopy was performed at Biomikroskopienheten, Materialkemi, Kemi Centrum, University of Lund, Sweden using a Philips CM120 (BioTWIN Cryo) equipped with a GATAN CCD camera (1024 × 1024 pixels).

Samples were prepared by applying 5 μl vesicles on a carbon grid where the excess buffer was removed by tissue. The grid was immediately frozen to −180°C according to the plunging method and kept at this temperature during imaging. Several regions of at least two separate grids were inspected to ensure representative data collection.

RESULTS AND ANALYSIS

Colloidal beads

We used fluorescent microspheres with a known mean diameter as a control sample to compare theoretical/calculated and measured particle intensities. Using the geometry and size of the TetraSpeck fluorescent microspheres as an initial parameter, we were able to measure the effect of the decaying illumination profile on sampled particle intensities (i.e., the axial dependence of the point spread function), and test the validity of Eq. 5.

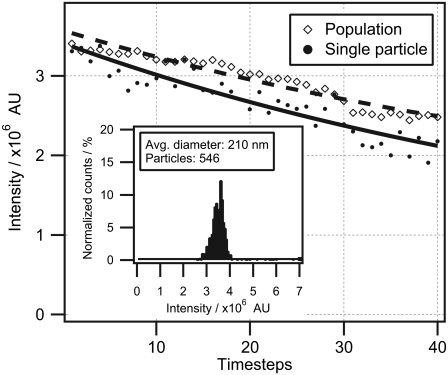
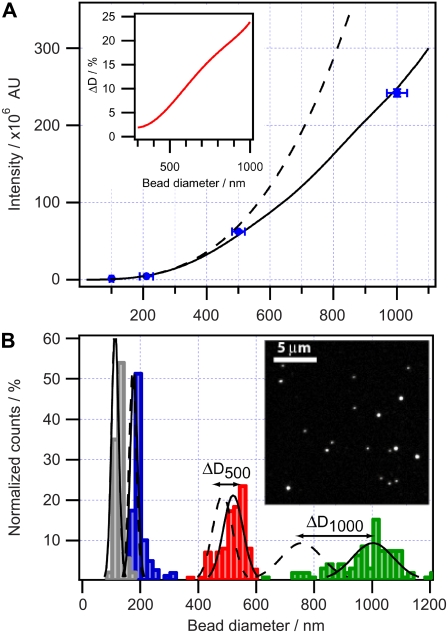
First, we measured the errors associated with recording the mean intensity of a single particle. We collected fluorescence micrographs from several hundreds of particles and applied image analysis to evaluate the mean particle intensity (I_MI) and standard deviation (δ_I). Initially, we measured δ_I by imaging the same particle 40 times and monitored the decrease in I_MI (Fig. 2, solid symbols). I_MI was fitted to a single exponential decay function, yielding a δ_I value of 5.1%. All particles within the 210-nm population were then recorded. The mean integrated intensity of the full population was measured and fitted to a single exponential decay function (as in the case of a single particle), resulting in a δ_I of 2.8% (Fig. 2, open symbols). The periodic nature of the variations in both curves of Fig. 2 suggests that δ_I is not dominated by random errors but rather by periodic fluctuations in, for example, z drift or PMT sensitivity. A histogram of I_MI was constructed and found to follow a Gaussian shape, suggesting a single population of particles (Fig. 2 inset).Mean integrated intensities were thereafter collected from four particle populations and plotted versus the nominal bead diameter (Fig. 3 A, blue dots). We also plotted in Fig. 3 A an ideal D³ tendency (dashed line) that deviates significantly from the data and the solid line, which is the predicted intensity for confocal acquisition. The predicted curve was obtained by numerically calculating integrated fluorescence intensity applying Eq. 5 with solid-sphere geometry. We used a correlation parameter, F_R = F(D_R) = 210 nm (we chose the 210-nm population for calibration because of its presence in both samples, and thus avoided accumulating error during size conversion), with F_R corresponding to I_MI from >500 particles having a nominal diameter of 210 nm. The obtained function was applied to convert all data sets. Indeed, the I_MIs of all four bead populations overlap perfectly with the confocal-illumination solid line. The effect of confocal illumination becomes more pronounced as the size of the object increases, since a smaller portion is within the optical depth of field. The error in percentages is plotted in the inset of Fig. 3 A. We see that for these typical confocal illumination conditions, the deviation for smaller spheres (diameter <300 nm) is within 2%. The deviation in percentages becomes significant (∼25%) for particles >1 μm in diameter.

FIGURE 2.

Evaluation of the signal/noise ratio of a single colloidal particle. The solid line represents the bleaching curve of a single 210-nm particle imaged 40 consecutive times and fitted to an exponential decay. Fluctuations in the integrated intensity are calculated as the standard deviation (δ_I) of each point from the fit. This yielded a deviation value of δ_I = 5.1%. The dashed line indicates the mean integrated intensity of the full population imaged 40 consecutive times and fitted to an exponential decay. This yielded a deviation value of δ_I = 2.8%. (Inset) Intensity histogram of the full population constructed from the first micrograph in the time series.

FIGURE 3.

Influence of a confocal depth of field on the measured intensity of fluorescent objects of various sizes. (A) Measured mean intensity of dye-labeled bead populations with specified diameters (blue dots). Acquired intensity calculated using the measured pinhole profile of the microscope (solid line) compared with calculated total intensity of a fluorescent solid sphere (dashed line). Error bars in the x direction correspond to manufacturer specifications, whereas error bars in the y direction (typically <3% of the mean) are deviations from the mean measured intensity. (Inset) The fractional error as a function of bead diameter. (B) Histograms of four fluorescent colloidal bead populations with nominal diameters of 100 nm (gray), 210 nm (blue), 500 nm (red), and 1000 nm (green), with Gaussian fits to confocal-corrected populations (solid lines) and to noncorrected populations (dashed lines). The double arrows indicate the error ΔD in the mean diameter between corrected and noncorrected populations. (Inset) A representative micrograph of the beads.

To characterize the shape of the supplied distributions, we constructed a sample containing a mixed population of beads with nominal diameters of 100 and 210 nm and another composed of beads with nominal diameters of 210, 500, and 1000 nm. We acquired several micrographs on each sample to establish a statistical significance of the measured intensity distributions. Integrated intensities from >4000 particles were collected from micrographs (Fig. 3 B, inset).

The size distribution histogram of the entire mixed population showed four distinct subpopulations, as expected (Fig. 3 B). To quantify the size histograms, we fitted each subpopulation to a Gaussian distribution characterized by distinct amplitude, baseline offset, mean diameter D₀, halfwidth w, and mean diameter displacement ΔD₀. We defined ΔD₀ as the difference between the mean diameter measured under confocal conditions and that calculated under homogeneous illumination. The obtained values of D₀, w, and ΔD₀ are summarized in Table 1. We observed an almost identical fractional polydispersity of 10–15% for all populations (defined as the ratio of Gaussian halfwidth to Gaussian mean diameter). This characteristic quantity is an intrasample property and is not stated in the bead specifications.

TABLE 1.

Quantification of colloidal bead populations with CLSM

Nominal diameter as stated by manufacturer (nm)	Measured mean diameter, DM (nm)	Gaussian mean diameter, D0 (nm)	Gaussian halfwidth, w (nm)	Mean diameter displacement, ΔD0 (nm)
100 ± 6	123	113 ± 1	17 ± 0	0
210 ± 21	209	178 ± 1	21 ± 1	4
500 ± 20	515	521 ± 2	53 ± 3	37
1000 ± 32	977	1002 ± 6	99 ± 7	243

Comparison of labeled colloidal bead specifications with measured values. From the left, the first column displays the nominal bead diameter and intersample variations of the mean as stated by the manufacturer. Columns 2–5 show measured mean diameter, D_M, Gaussian mean diameter, D₀, Gaussian halfwidth of population, w, and mean diameter displacement, ΔD₀. The quantities D₀, w, and ΔD₀ are quantities resulting from the Gaussian fit of the populations in Fig. 3 B, whereas D_M is the mean value of all converted beads. The mean diameter displacement, ΔD₀,_, is calculated as the difference between homogeneous and confocal illumination graphs in Fig. 3 A.

Lipid vesicles

Lipid vesicles were tethered to a streptavidin functionalized substrate using a biotinylated poly(ethylene glycol) lipid conjugate. This created a polymer foundation that minimized surface-induced vesicle deformation. Immobilization was performed by incubating the functionalized surfaces with dilute bulk concentrations of vesicles, thus minimizing aggregation in solution during experiments. Under these conditions, vesicles from the solution were depleted, ensuring an effective transfer of the bulk population onto the surface.

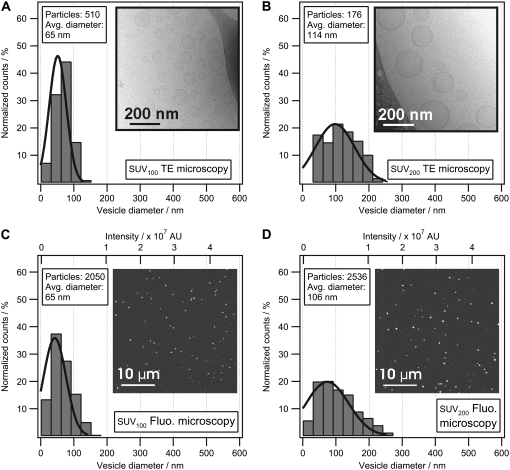
Vesicle populations extruded through filters with diameters of 100 nm and 200 nm were investigated with CLSM, cryoTEM, and DLS. Fig. 4 shows the size-distribution histograms and micrographs of lipid vesicles determined by cryoTEM (Fig. 4, A and B) and CLSM (Fig. 4, C and D). The conversion from fluorescence intensity to physical size was performed using the mean integrated intensity and the mean diameter of the SUV₁₀₀ vesicle population obtained from CLSM and cryoTEM, respectively (see Image treatment and size conversion).

FIGURE 4.

Comparison of vesicle size distributions measured with cryoTEM and CLSM. Size-distribution histograms of extruded vesicles (SUV₁₀₀ extruded using a filter diameter of 100 nm and SUV₂₀₀ extruded using a filter diameter of 200 nm) were measured with cryoTEM and CLSM. Vesicles from SUV₁₀₀ (A) and SUV₂₀₀ (B) were trapped in an amorphous ice film and recorded with cryoTEM to construct histograms of vesicle sizes. Integrated fluorescence-intensity histograms of SUV₁₀₀ (C) and SUV₂₀₀ (D) immobilized on a glass surface and recorded with CLSM. To convert the integrated intensity histogram (C) to a physical size histogram, the mean diameter from the distribution in A was used to convert the abscissa of C to nanometers. Using SUV₁₀₀ as the reference sample, the physical size distribution of SUV₂₀₀ (D) could now be determined from the integrated intensity distribution. Comparing B and D, our model reproduces the mean peak of the physical size distribution obtained from cryoTEM within 7%. The shapes of the histograms obtained from cryoTEM and CLSM were found to be identical, thereby confirming that cryoTEM and CLSM reconstruct the vesicle populations in a similar way. Insets show representative micrographs. The brightness and contrast of the images has been optimized for visual purposes.

The shape of the histograms acquired with cryoTEM is seen to be similar to the histograms acquired with CLSM. This indicates that both techniques faithfully reconstruct the vesicle population. A Gaussian fit to the histograms was applied and, as expected, the width of the distribution is larger for vesicles extruded through a 200-nm filter compared to vesicles extruded through a 100-nm filter. The morphology of vesicles investigated with cryoTEM was found to be spherical (Data S1).

Table 2 compares data from the SUV₂₀₀ population, obtained using the three techniques mentioned previously. The mean diameter of these vesicles was found to be 106 nm using the converted CLSM data, 114 nm using cryoTEM, and 116 nm using DLS. Comparing size distribution polydispersity, defined as the standard deviation of the population, using the three investigated methods, DLS yields the largest polydispersity and cryoTEM the smallest.

TABLE 2.

Characterization of an extruded vesicle sample (SUV₂₀₀) with CLSM, cryoTEM, and DLS

Method	Mean diameter of distribution (nm)	SD of mean diameter (nm)	SD of population (polydispersity) (nm)
CLSM	106	12	61
CryoTEM	114	23	50
DLS	116	7	80

The size distribution of vesicles extruded at 200 nm was determined using the CLSM model and compared to the cryoTEM and DLS models. Standard deviation (SD) of the mean diameter was calculated in the case of CLSM and cryoTEM using several individual micrographs from each sample. In the case of DLS, the standard deviation of the mean was obtained from the average value from 10 measurements.

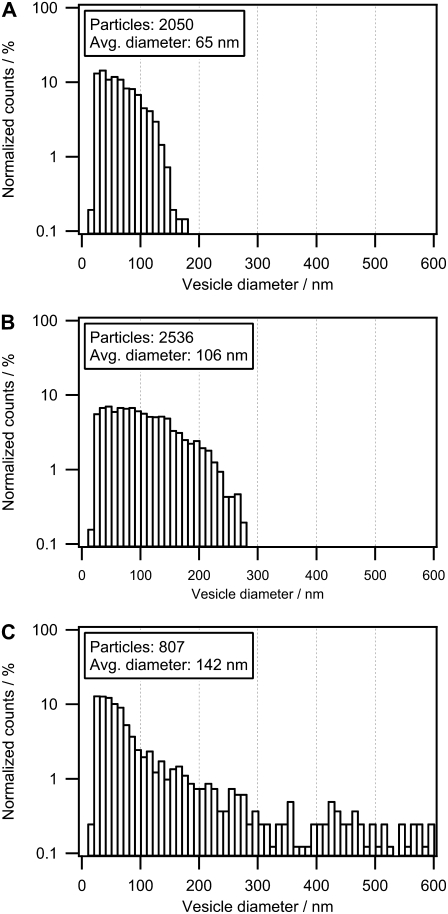
Taking advantage of the wide dynamic range of the intensity-based method, we were able to examine a nonextruded lipid vesicle sample. Fig. 5 shows a replot of the size histograms in Fig. 4, C and D, with reduced binning width and a logarithmic y scale for vesicle populations SUV₁₀₀, SUV₂₀₀, and a nonextruded vesicle sample. The reduced binning width allows discrimination of the histogram fine structure and of differences between samples. Comparison of the histograms (Fig. 5, A–C) reveals that a subpopulation of small vesicles is present at D ≈ 30 nm in all three samples. In this case, the main effect of the extrusion process is to generate an upper size limit of the vesicles; hence, distributions become broader with increasing filter size.

FIGURE 5.

Influence of extrusion on the size distribution of polydisperse vesicle samples. We compare here extruded samples SUV₁₀₀ (A) and SUV₂₀₀ (B) with a nonextruded (polydisperse) vesicle population (C). Histograms based on CLSM contain ∼5–10 times more vesicles than those based on cryoTEM, which allows for reduced histogram bin width and, hence, access to the fine structure of the vesicle size distribution. The polydisperse vesicles consist of a broad size distribution compared to the extruded vesicles. By comparing the three populations, a subpopulation at D = 30 nm was observed in all samples, which indicates an intrinsic subpopulation independent of the extrusion process. Using a lipid composition favoring smaller vesicles, the effect of extrusion is merely to apply an upper size cutoff. The histograms are plotted with a logarithmic scale to visualize the effect of this cutoff.

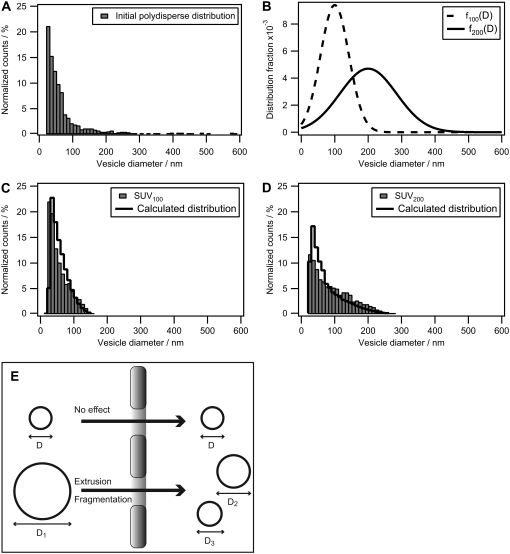
We chose to use the size distribution obtained from the polydisperse unilamellar vesicle preparation to test the ability of vesicle redistribution profiles to predict the outcome of an extrusion. To do this, we applied Eq. 6 to calculate f₁₀₀(D) and f₂₀₀(D) with subscripts denoting the filter pore diameter. Fig. 6 A shows the size distribution of the polydisperse vesicle preparation on a linear y scale, thus making the vesicle population at D ≈ 30 nm more visible compared to Fig. 5 C. The calculated plots of f₁₀₀(D) and f₂₀₀(D) are shown in Fig. 6 B; an increased profile broadening is exhibited with increasing filter pore diameter. We applied both profiles on the initial polydisperse population to obtain calculated values of the extruded vesicle size distribution. In this manner, we constructed the new populations by applying the vesicle redistribution profiles twice on the initial distribution. The measured distribution of lipid vesicles extruded through 100-nm and 200-nm filter pore diameters are shown in Fig. 6, C and D, respectively, along with the calculated populations. The redistributed populations exhibit the same upper-diameter cutoff behavior as their measured counterparts and there is a good agreement in the distribution shape.

FIGURE 6.

Calculation of the influence of extrusion on the size distribution of polydisperse vesicle samples. (A) Plot of the polydisperse nonextruded vesicle population from Fig. 5 C using a linear y axis. It is evident that small unilamellar vesicles dominate the population and only a few large (D > 200 nm) vesicles are observed. (B) Vesicle redistribution profiles calculated for an extrusion filter with pore diameters of 100 nm (dashed line) and 200 nm (solid line). (C and D) Comparison of measured size distributions of small unilamellar vesicles extruded through either 100-nm or 200-nm pores (bars) with calculated distributions (solid line). The calculated histograms are obtained by applying the respective vesicle redistribution profiles twice on the initial polydisperse population. (E) Sketch of the extrusion process. Vesicles with a diameter, D, less than that of the pore pass unaffected, whereas a vesicle with a diameter greater than the pore diameter undergoes fragmentation.

DISCUSSION

Model

We have described here a simple method that allows the calculation of the size of subresolution objects through a measurement of their integrated fluorescence intensities. Using uniformly labeled colloidal particles we demonstrated the need to take the confocal illumination profile into account to convert the measured particle fluorescence intensity to a diameter. The model is straightforward to apply, requiring only a measured illumination profile, calibration reference, and knowledge of particle geometry. Neglecting the confocal illumination/acquisition generates errors up to 25% in the particle diameter (for D ≈ 1 μm) (see Fig. 3 A, inset). The extent of this error depends critically on the microscope optics, particularly the illumination along the optical axis.

Using typical confocal imaging conditions, the fluctuations in the mean integrated fluorescence intensity of a population of 210-nm beads was determined to be 2.8% (standard deviation), which is about one-third of the standard deviation (10%) in the nominal bead diameter as stated by the manufacturer. The absolute value of measured size depends on the chosen calibration reference. Introducing errors in this value will offset the measured particle distributions; however, no additional error will be accumulated in the measurements.

Colloidal beads

Histograms of the diameter of colloidal bead populations revealed distinct Gaussian distributions. Values of measured mean diameter, D_M, and Gaussian fitted diameter, D₀, for each bead population are in good agreement with the nominal diameters as stated by the manufacturer (Table 1). The Gaussian fits depend on the chosen bin width of the histograms, and D₀ thus deviates from nonfitted mean diameters, D_M. The population of 100-nm beads exhibits a discrepancy between the specified mean diameter and the recorded nonfitted mean diameter, which cannot be accounted for by the stated intersample variation of 6 nm and may be due to colloidal aggregation. The presented method for converting fluorescence intensity from throughout stained colloidal particles provides the sensitivity necessary to distinguish not only between populations with different average diameters but also between single particles within the same population. The diameter of single particles was typically measured with an accuracy of ∼5.1%, which corresponds to an error of ∼11 nm. However, this accuracy is related to laser stability and photodetector quality and, for weakly fluorescing monodisperse samples, could provide an overestimate of the population polydispersity. In the described experiments, we find that the signal/noise ratios allow us to accurately resolve the polydispersity of each bead population.

Lipid vesicles

Experiments performed on extruded lipid vesicles showed that size distributions obtained with CLSM compare directly with those from cryoTEM. Comparison of the mean peak position of the Gaussian fit to the SUV₂₀₀ histograms obtained with CLSM and cryoTEM gave a mean diameter deviation of 7%, which is within the experimental error (Table 2). CLSM and cryoTEM provide single-vesicle information, as opposed to the ensemble average measured with DLS, thus enabling a faithful reconstruction of size-distribution histograms representing the entire population. Comparison of SUV₂₀₀ histograms obtained by CLSM with DLS ensemble measurements yielded a mean diameter deviation of 9%.

An important advantage of CLSM over cryoTEM is that it offers the possibility of investigating polydisperse vesicle samples with diameters ranging from 40 to 1000 nm, as demonstrated in Fig. 5 C. In addition, the imaging conditions allow the investigation of a large number of particles, thus enabling improved statistics (Fig. 4, C and D, inset). The total number of vesicles investigated and the precision with which the diameter can be measured determine to what degree the fine structure of a vesicle distribution can be resolved. We demonstrate the improved fine structure here by decreasing the binning width of the lipid vesicle size-distribution histograms of SUV₁₀₀ and SUV₂₀₀ (Fig. 4, C and D) and replotting the histograms (Fig. 5, A and B) together with a polydisperse sample (Fig. 5 C). This revealed a subpopulation of lipid vesicles (D = 30 nm) in all examined samples. This subpopulation remained unaffected by extrusion, as depicted in Fig. 6 E. Indeed, this is to be expected if the chosen lipid composition favors the formation of small unilamellar vesicles with a spontaneous radius below the extrusion filter size.

Our observation is in good agreement with previous theoretical work on the self-assembly process of amphiphilic compounds (50,51), where reported values of the thermodynamically favored vesicle diameter ranged from 20 to 40 nm. We measure two distinct subpopulations within the polydisperse unilamellar vesicle sample: 1), a narrow monodisperse population centered at D = 30 nm, and 2), a broad polydisperse population ranging up to D = 600 nm. The narrow population comprises the majority of vesicles and resembles vesicles formed through thermodynamical equilibrium. Consequently, we speculate that soluble lipid molecules, generated at some point during the preparation process, are allowed to self-assemble into small unilamellar vesicles. Although SUVs dominate the size distribution in numbers, they only make up ∼10% of the total lipid mass. Still, this number is too high considering the partition coefficient of lipids into water. The polydisperse population (diameters >100 nm) dominates the size distribution in terms of mass. We attribute their origin to a nonequilibrium process, i.e., thin-film rehydration. During the rehydration process, bilayer stacks swell and will eventually bud off from the surface to form vesicles. This process is influenced by many factors, such as bending rigidity of the bilayer, bilayer surface area, substrate adhesion, and roughness, in contrast to the equilibrium self-assembly, which is only dominated by lipid (geometrical and chemical) properties.

Our data suggest that a large number of thermodynamically stable SUVs is an intrinsic feature of this vesicle preparation technique. Since we applied extrusion filters with pore diameters >40 nm, we were unable to influence the intrinsic vesicle population composed of small vesicles, which has been noted in previous work also (22). The fact that we were able to reconstruct both SUV₁₀₀ and SUV₂₀₀ histograms only by redistributing lipid mass from a nonextruded polydisperse population supports this view, in the sense that vesicle sizes become shifted only “downward” and not “upward” by this approach.

Other studies of vesicle extrusion and preparation (16,28) suggest that the initial vesicle sizes are shifted both upward and downward to generate a well-defined population with mean diameters comparable to the filter pores. We note that direct comparison of our data to those of previous studies is not possible due to 1), nonidentical lipid composition, and 2), different data representation. Vesicle distribution histograms presented previously were plotted in units of volume percentage as a function of vesicle size (16). This representation alters the shape of the size distribution compared to a y axis in units of normalized counts, as in our case.

We conclude that even though the lipid mass of an initial vesicle population is biased toward large vesicles (D > 100–200 nm), the intrinsic subpopulation of thermodynamically stable vesicles will still dominate the total distribution after extrusion. In the case of DOPC/DOPG vesicles, which we used here, the mass/mass ratio between different parts of the population was M_D>100/M_D<100 = 8.3, where M_D>100 and M_D<100 are the lipid mass values from vesicles with diameters above and below 100 nm, respectively. This implies that the main part, although not all, of the lipid material partitions into metastable configurational states with large radii upon swelling/rehydration of the dried lipid film. The effect of extrusion will thus be most pronounced, i.e., generate Gaussian size distributions, if the following conditions are met: 1), the filter diameter is chosen in a manner such that the majority of lipid material is located in vesicles with diameters greater than the filter diameter; and 2), the broadness of the vesicle redistribution profile is small compared to the broadness of the initial size distribution.

CONCLUSION

In this work, we report a straightforward approach to accurately determine the size of fluorescently labeled objects, as demonstrated here using colloidal beads and lipid vesicles. This approach, the first of its kind that we know of, enabled us to quantify the size distribution of a polydisperse lipid vesicle population at the single-object level and under physiological conditions. The mean diameter of an extruded (200-nm filter) lipid vesicle sample was measured to be 106 nm with CLSM and 114 nm with cryoTEM. Thus, the two methods provide comparable results, differing by only 7%. Furthermore, we were able to study in great detail the response of a lipid vesicle population to extrusion.

The knowledge obtained regarding the shape of the initial vesicle population allowed us to quantify the extrusion process, as well as to track back to the initial preparation the existence of a subpopulation of small, thermodynamically stable vesicles. This finding in turn confirmed some of the early theoretical work done in the field of amphiphile self-assembly that predicted an optimal value of vesicle radius. We acknowledge that there exist a wide variety of parameters that can be regulated to induce changes to the starting vesicle population, i.e., ionic strength, temperature, amphiphile concentration, and pH, and these studies warrant further attention. Thus, our size determination method is indeed suited for monitoring changes in vesicle size distribution characteristics, since samples can be recorded in the same conditions under which they were prepared.

Due to the wide availability of fluorescence microscopy platforms, we find the approach presented here readily applicable to investigation of size-related properties of vesicles, e.g., membrane permeability (52,33), or the size-dependent adsorption of amphipathic helices (53) and BAR (Bin/amphiphysin/Rvs) domains (54,55). We envision that future ensemble-based assays investigating vesicle-size-related effects will benefit from the ability to perform accurate measurements in real time on a great number of single objects.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.