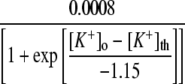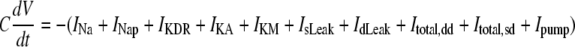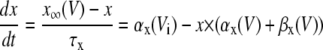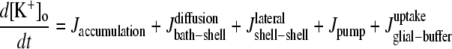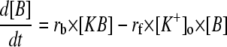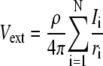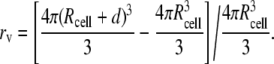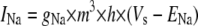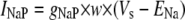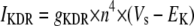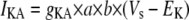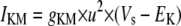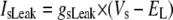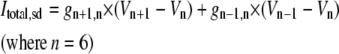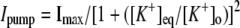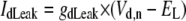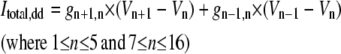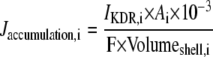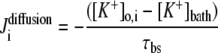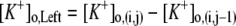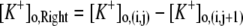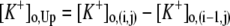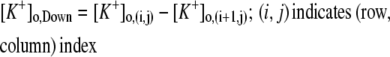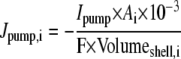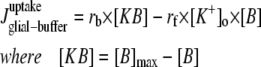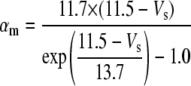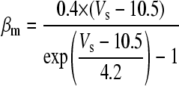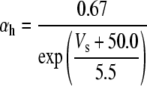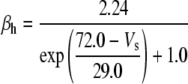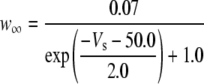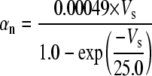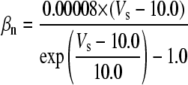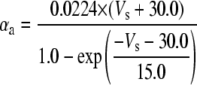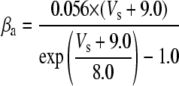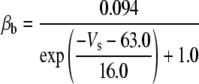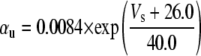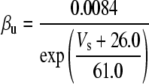Abstract
Diffusive coupling (nearest-neighbor coupling) is the most common type of coupling present in many systems. Previous experimental and theoretical studies have shown that potassium lateral diffusion coupling (i.e., diffusive coupling) can be responsible for synchronization of neuronal activity. Recent in vivo experiments carried out with anesthetized rat hippocampus suggested that the extracellular potassium could play an important role in the generation of a novel type of epileptiform nonsynaptic activity. Yet, the role of potassium in the generation of seizures remains controversial. We tested the hypothesis that potassium lateral diffusion coupling is responsible for the coupling mechanisms for network periodicity in a nonsynaptic model of epilepsy in vivo using a CA1 pyramidal neuron network model The simulation results show that 1), potassium lateral diffusion coupling is crucial for establishing epileptiform activity similar to that generated experimentally; and 2), there exists a scaling relation between the critical coupling strength and the number of cells in the network. The results not only agree with the theoretical prediction, but strongly suggest that potassium lateral diffusion coupling, a physiological realization of the concept of diffusive coupling, can play an important role in entraining periodicity in a nonsynaptic neural network.
INTRODUCTION
Synchronization, one of the most universal phenomena to describe the behavior of two or more interacting systems, has been extensively studied in various areas such as physics, biology, chemistry, and neuroscience (1,2). Synchronization is commonly understood as adjustment of rhythms due to an interaction between two or more oscillators, and therefore it does not necessarily require complete temporal coincidence of signals. Throughout this study, synchronization is specifically understood in terms of phase locking among neurons. Normally, phase-locking can be understood as the nonzero constant phase shift and small fluctuations of the phase difference, and not as equality of phases (2).
A key mechanism of synchronization is a mutual interaction due to the coupling between oscillatory systems. One of well-understood coupling mechanisms is global coupling (or all-to-all coupling) through which each oscillator interacts with equal strength with all of the other oscillators in the system. This type of coupling has been extensively studied (see Okuda (3) and references therein). Lesser attention has been paid to another type of coupling, local coupling, equally termed as nearest-neighbor coupling or diffusive coupling. This diffusive coupling has been introduced initially based on a diffusion like process (4). Unlike global coupling that generates a mean field in the ensemble of oscillators, diffusive coupling produces a local interaction only between each component of the network and its nearest neighbors. Several theoretical studies on diffusive coupling have appeared in the literature in recent years. Some of them concentrate on mathematical theory (5–8) and others include physiological aspects (9–11). Although diffusive coupling is more common and realistic in many physical systems (12–14), it is neither well understood nor widely studied compared to the global coupling (12,13,15).
It is known that global coupling can be implemented by embedding the individual elements of the network in an homogeneous common medium (2,16). In previous studies with diffusion as a coupling method, the coupling strength was proportional to the concentration difference between the bath and the extracellular areas very closely surrounding cell bodies. This type of coupling is, in fact, global coupling because each cell is coupled with all other cells in the network through the same bath. To the best of our knowledge, the physiological realization of local diffusion as coupling between one cell and its nearest neighbor cells through substance movement driven by concentration difference has not yet been reported. Yet this type of coupling, i.e., diffusive coupling seems more likely in neural tissue where ions and neurotransmitters are known to diffuse in the extracellular space and affect their neighbor cells more significantly than the remote cells such as in experiments with zero-calcium solutions.
In vitro experiments, with zero-Ca2+-induced nonsynaptic epileptiform activity have shown that synchronization could take place across a complete mechanical cut in the rat CA1 hippocampal slice (17). Gap junction coupling and ephaptic field effects were excluded as a possible mechanism of synchronization. The underlying synchronization mechanism was attributed to extracellular potassium diffusion. This conclusion was derived from the fact that a transient increase in [K+]o accompanying each epileptiform event was detected and local pressure ejection of KCl was able to evoke epileptiform events propagating across the lesion. Therefore, the synchronized epileptiform activity could explained by lateral diffusion coupling to the nearest neighbor cells through [K+]o (or simply potassium lateral diffusion). Consistent with the experimental data, simulation studies by using a two-cell model have also shown that the potassium lateral diffusion could play an important role in the synchronization of nonsynaptic epileptiform activity (18).
In vivo experiments with anesthetized rat also suggest that extracellular potassium concentration can be a critical causative factor in the generation of nonsynaptic epileptiform activity (19). The experimental results showed that an increase of [K+]o from 6 to 12 mM caused a transformation from a typical nonsynaptic burst with a frequency of 0.34 ± 0.14 Hz into a regular type of epileptiform activity with a frequency of 3.77 ± 1.28 Hz. The physiological properties of the activity such as duration (>30 min) and frequency (2.5 ∼5 Hz) are consistent with those of status epilepticus (SE) reported in the literature (20). The mechanisms underlying the specific activity are not clear. Because synaptic transmission was blocked by lowering Ca2+ concentration, these results could be explained by a nonsynaptic mechanism such as potassium lateral diffusion.
In the in vivo experimental configuration considered in this study, the global coupling (potassium dispersion mechanism) and the diffusive coupling (potassium lateral diffusion mechanism) are thought to coexist. This is because CA1 hippocampal pyramidal cells are embedded in the same bath and at the same time, the cells are aligned and packed so a direct cell-to-cell coupling is highly plausible. Generally, it is impossible to separate these couplings experimentally, and therefore, computer modeling can play an essential role in investigating the effects of the coupling on the synchronization of the activity. Using computer simulations, in this study, we tested the hypothesis that diffusive coupling expressed as potassium lateral diffusion can promote network periodicity under low-calcium nonsynaptic condition in an in-vivo rat preparation. If this hypothesis is correct, the following questions can be also answered: Is it possible to reproduce some temporal characteristics of nonsynaptic activity observed in in vivo experiments with intermediate size of the network? If so, can the diffusive coupling, not the global coupling, be responsible for synchronization?
Because this study focuses not on reproducing the detailed waveform of nonsynaptic activity, but on investigating the temporal aspect of the activity, i.e., the emergence of periodic activity, an intermediate size network was used for modeling. Computer simulations were performed with diffusively coupled 16 zero-Ca2+ CA1 pyramidal neurons that are arranged in two-dimensional array.
METHODS
Throughout this study, we will use the terms “lateral diffusion” mechanism and “diffusive coupling” interchangeably. In general, the term “diffusive coupling” is used for describing a coupling type, i.e., how the elements in the network are coupled with each other, and therefore, the use of this concept is not limited to the actual diffusion process. Also, we will use the terms “dispersion” mechanism and “global coupling” interchangeably. To avoid confusion, throughout this study, we will use “potassium dispersion” instead of “potassium diffusion.”
In vivo experiments
All surgical procedures were approved by the Institutional Animal Care and Use Committee, Case Western Reserve University, Cleveland. Surgical procedures were similar to those in Feng and Durand (19). Briefly, adult Sprague-Dawley rats were anesthetized with urethane (1.25–1.5 g/kg, intraperitoneal) and placed in a stereotaxic apparatus. Body temperature was maintained at 37°C with a heating pad. The skull over the left cortex was opened and the neocortex overlying the dorsal hippocampus was removed. Artificial cerebrospinal fluid (ACSF) was warmed to ∼37°C and perfused over the surface of the exposed dorsal hippocampus. Solutions and drugs used for the experiments can be found in Feng and Durand (19). Calcium chelator ethyleneglycol–bis (β-aminoethyl ether)N,N,N,N-tetraacetic acid (EGTA), 5 mM, was added in CaCl2-free ACSF to reduce [Ca2+]o and to suppress the synaptic transmission in the CA1 region in vivo. Picrotoxin (0.4 mM) was used to induce epileptic bursts by blocking the γ –aminobutyric acid receptor. Extracellular field potentials recorded in the CA1 pyramidal cell body layer were used. The suppression of synaptic transmission was evaluated by a significant decrease in the orthodromically-evoked population spikes.
Computer model
Lateral diffusion-coupled network
In the neuronal network, 16 neurons arranged in a 4 × 4 were coupled through the diffusion of the potassium (Fig. 1). To implement the diffusion process, the three-compartment diffusion model developed previously was used (18). For some simulations, the number of neurons was varied. Each model neuron consisted of 16 compartments: 10 compartments for apical dendrites, five compartments for basal dendrites, and one single compartment for soma. This 16-compartment CA1 pyramidal model exposed to zero-Ca2+ solution was developed previously for simulating nonsynaptic epileptiform activity (21). The single cell kinetics for all channels was constructed based on the previous model designed for low calcium solution (21). The additional modifications to the kinetics were made to incorporate interstitial space (K+ shell) around each neuron (18).
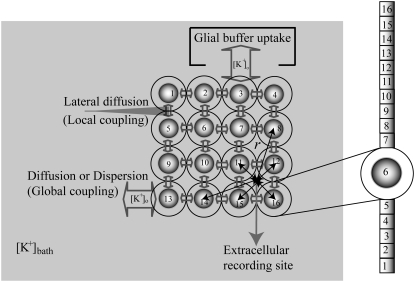
FIGURE 1.
Schematic diagram of three compartment lateral-diffusion-coupled network model. One compartment is assigned for the cell, one for the interstitial space and one for the bath. Dispersion (diffusion to the bath) and lateral diffusion (diffusion between the interstitial spaces of neighboring cells) were included in the model. For the cell, the 16-compartment zero-Ca2+ CA1 pyramidal cells were used and they were arranged in an array. For [K+]o regulation mechanisms, K+ pump and glial buffer uptake were used. With the cell radius of 8.9 μm and the volume ratio of 0.15, the outer diameter of each sphere was estimated as 18.64 μm. All cells with respect to a (virtual) extracellular recording site (solid circle) were used for the calculation of field potential. ‘r’ indicates a distance between the recording location and the center of a cell-body.
Only passive channels were located in dendrite compartments, whereas five active ionic channels were included in the soma compartment. Because an accumulation of potassium ions is more intense in the somatic than in dendritic layers, for simplicity, the interstitial space was assumed to surround only the soma compartments (22–25). The dendrites (basal and apical branch) were assumed to be positioned vertically with respect to a horizontal array of soma compartments. Therefore, the three compartment diffusion model was implemented in the horizontal plane where the soma compartments were placed: one compartment for the soma, one for the K+ shell around the soma, and one for the bath (18). For the potassium lateral diffusion coupling between neurons, four-nearest-neighbor coupling method was applied in the soma plane. The interstitial [K+]o released from the neurons during neuronal firing could diffuse to the bath and to the surrounding interstitial space of the adjacent cell. For the interstitial [K+]o removal mechanisms, K+-pump and glial buffer were used (22,26–30).
A reduced ion pump function (10% reduction with respect to a full pump function) was used to generate spontaneous neuronal activity. This compromised function of the pump was simulated by decreasing the maximum pump rate. The value of the maximum pump current Imax, 73.5 (μA/cm2) for the model was chosen to compensate a leakage of potassium ions at resting state (30) (see Table 4). This reduction is based on the recent experimental findings: a reduction of Na+/K+ ATPase expression in experimental epilepsy (27) and an impaired astrocytes buffering mechanism in both human temporal lobe epilepsy (29) and experimental epilepsy (28) have been observed.
TABLE 4.
Parameter values used for zero-Ca2+ pyramidal neuron (18)
| Parameters | Names | Values | Source* | |
|---|---|---|---|---|
| R | Radius of cell | 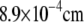 |
a | |
| A | Soma surface area (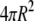 ) ) |
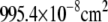 |
b | |
| F | Faraday's constant | 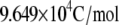 |
c | |
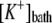 |
Potassium concentration in the bath | 7.6 mM | g | |
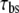 |
Diffusion time constant | 1000 ms | d | |
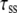 |
Lateral diffusion time constant | Varied from 5 to 500 ms | d | |
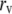 |
Volume ratio | 0.15 | e, f | |
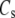 |
Soma capacitance | 1.0 μA/cm2 | a, d | |
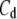 |
Dendrite capacitance | 1.88 μA/cm2 | a, d | |
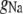 |
Fast Na+ conductance | 20.5 mS/cm2 | a, d | |
 |
Persistence Na+ conductance | 0.24 mS/cm2 | a, d | |
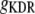 |
Delayed-rectifier K+ conductance | 19.7 mS/cm2 | a, d | |
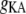 |
A-type transient K+ conductance | 3.0 mS/cm2 | a, d | |
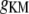 |
Muscarinic K+ conductance | 3.0 mS/cm2 | a, d | |
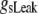 |
Soma leakage conductance | 1.8 mS/cm2 | a, d | |
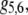 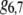
|
Conductance between soma and dendrite | 6.3 mS/cm2 | a, d | |
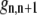 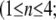 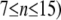
|
Conductance between dendrites | 3.67 mS/cm2 | a, d | |
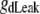 |
Dendrite leakage conductance | 0.0292 mS/cm2 | a, d | |
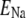 |
Sodium reversal potential | 67.0 mV | a, d | |
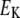 |
Potassium reversal potential | 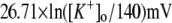 |
a, d | |
 |
Leakage reversal potential | −60.0 mV | a, d | |
 |
Pump maximal current | 73.5 μA/cm2 | d, e | |
Impairment: 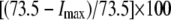
|
10% | d | ||
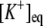 |
Equilibrium potassium concentration | Set equal to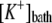
|
d, e | |
| [KB] | K+ bound to buffer | [B]max − [B] | e, f | |
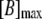 |
Maximal buffer capacity | 265 mM | d, e | |
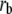 |
Backward rate of buffer mechanism | 0.0008 | e, f | |
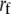 |
Forward rate of buffer mechanism |
|
d, e | |
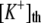 |
Threshold 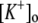 for glial buffer for glial buffer |
15 mM | e |
Equations, currents, variables, and the values of parameters used in these simulations are given in Tables 1, 2, 3, and 4, respectively. A Runge-Kutta fourth order algorithm was used for integrating the set of differential equations with the time step of 0.01 ms. The initial conditions were randomly chosen within a physiological range. The initial buffer size ([B]) for all neurons was assumed to start with the same value.
TABLE 1.
Equations used in the simulation
| Equations | Source* | |
|---|---|---|
| For each zero Ca2+ pyramidal neuron | ||
|
a | |
|
b | |
|
c | |
|
d | |
| For external field potential (extracellular recording) | ||
|
e | |
1. ρ: the extracellular resistivity was set to 375 (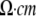 ) (32). ) (32). |
||
| 2. N: the estimated number of neurons used for calculating field potential. | ||
| 3. I: the total currents coming into and out from the soma measured at the recording site. | ||
| 4. r: a distance between the recording site and the center of each soma compartments respectively. The radius of cell was calculated as the volume ratio varied.The equation for the calculation of the radius of cell as the volume ratio changes can be described as: | ||
|
TABLE 2.
Currents and potassium flux in a zero-Ca2+ pyramidal neuron (18)
| Currents (μA/cm2) | Source* | |
|---|---|---|
| Soma compartment | ||
|
a | |
|
a | |
|
a | |
|
a | |
|
a | |
|
a | |
|
a | |
|
b | |
| Dendrite compartments | ||
|
a | |
|
a | |
| Potassium flux (mM/ms) | ||
|
c | |
|
c | |
|
c | |
| where | ||
|
||
|
||
|
||
|
||
|
c | |
|
b |
TABLE 3.
Gating functions for zero-Ca2+ CA1 pyramidal neuron (18)
| Gating variable | Rate coefficients (ms−1) | Source* | |||
|---|---|---|---|---|---|
| Fast Na+ current activation (m) |
|
|
a | ||
| Fast Na+ current inactivation (h) |
|
|
a | ||
| Persistent Na+ current activation (w) |
|
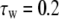 |
b | ||
| Delayed-rectifier K+ current activation (n) |
|
|
a | ||
| A-type transient K+ current activation (a) |
|
|
a | ||
| A-type transient K+ current inactivation (b) |
|
|
a | ||
| Muscarinic K+ current activation (u) |
|
|
a |
Because this model study focuses on the effect of lateral diffusion coupling on synchronization, other types of nonsynaptic mechanisms such as field effects and gap junctions were not included in the model, i.e., neurons are coupled only through diffusion.
Coupling strength
Because a coupling signal generated by potassium lateral diffusion mediates mutual interaction between cells, the lateral diffusion time constant (τss) modulates the coupling strength. The coupling strength ɛc can be expressed as: ɛc ∝ 1/τss (ms). This is due to the fact that the faster movement of potassium ions can increase a mutual interaction between cells. A previous simulation study has confirmed that both the coupling strength and the synchrony level decrease as τss increases (18).
Heterogeneity
Simulation studies based on a model of a CA1 pyramidal neuron in zero-calcium solution (21) show that a variation of one of the potassium or sodium conductance values (gKDR, gKA, gKM, gNa, and gNaP) can change the frequency of the neuronal activity. Two parameters, potassium delayed-rectifier conductance (gKDR) and sodium conductance (gNa) were varied to induce heterogeneity between the cells. For all simulations, the heterogeneity degree was set to 0.2% with respect to a baseline value 19.7 for gKDR and 20.5 for gNa (mS/cm2). Note that “x% heterogeneity of the network” can be described as “x% difference with respect to a preset value y” and the value was within a range of 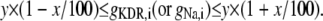 The values of the conductance were randomly assigned to each neuron of the network. With this level of heterogeneity, the mean frequency of neurons of the network varied between 3.97 and 4.03 Hz (experimental mean value: 4.0 Hz).
The values of the conductance were randomly assigned to each neuron of the network. With this level of heterogeneity, the mean frequency of neurons of the network varied between 3.97 and 4.03 Hz (experimental mean value: 4.0 Hz).
Synchrony index
To quantify synchronization, the synchrony index (γ) of intracellular activity between each pair of cells in the network was calculated by using relative phases. Relative phases (Ψ) were calculated from the spike times obtained by threshold crossing (see Fig. 5 a in Park and Durand (18) for the details). The threshold value was chosen to be 20 mV. Using the relative phases, the synchrony index is described as: 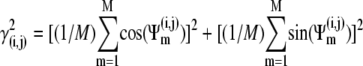 (2,18,31), where
(2,18,31), where 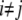 (i and j indicate i-th cell in a row and j-th cell in a column of the 4 × 4 array, respectively). M is the number of firing events that was used for the average. The values of γ lie between 0, which indicates no synchrony, and 1, which indicates perfect synchrony. For the network synchrony analysis, the relative phases were calculated between one cell (e.g., cell A) and its neighboring cells. The number of neighboring cells of the cell A is determined by the location of the cell A in the array (i.e., two neighboring cells for the corner, three for the edge, and four for the middle of the array). By using the relative phases, the values of the synchrony index between one cell and its adjacent cells were calculated and averaged over the number of neighboring cells. Because the firing was periodic and low frequency, several hundreds of firing events were sufficient to estimate the level of synchrony. Due to the randomness introduced through the initial conditions, all measures in these simulations were averaged over the number of realizations. For all simulations, 10 realizations were used. In this study, 〈γ〉 indicates the synchrony index averaged over 10 realizations.
(i and j indicate i-th cell in a row and j-th cell in a column of the 4 × 4 array, respectively). M is the number of firing events that was used for the average. The values of γ lie between 0, which indicates no synchrony, and 1, which indicates perfect synchrony. For the network synchrony analysis, the relative phases were calculated between one cell (e.g., cell A) and its neighboring cells. The number of neighboring cells of the cell A is determined by the location of the cell A in the array (i.e., two neighboring cells for the corner, three for the edge, and four for the middle of the array). By using the relative phases, the values of the synchrony index between one cell and its adjacent cells were calculated and averaged over the number of neighboring cells. Because the firing was periodic and low frequency, several hundreds of firing events were sufficient to estimate the level of synchrony. Due to the randomness introduced through the initial conditions, all measures in these simulations were averaged over the number of realizations. For all simulations, 10 realizations were used. In this study, 〈γ〉 indicates the synchrony index averaged over 10 realizations.
FIGURE 5.
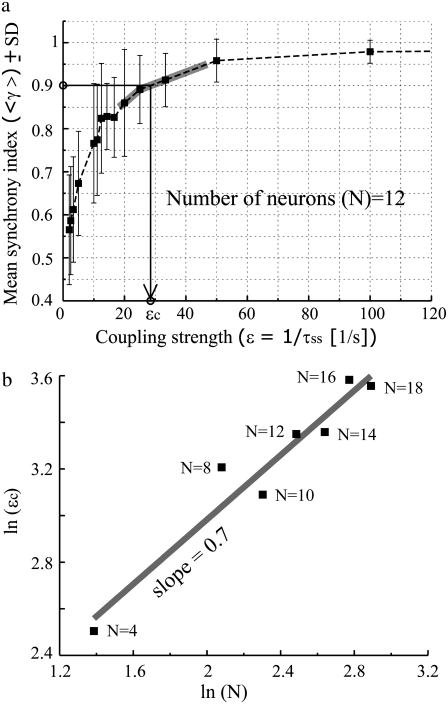
Relation between synchrony index and coupling strength and scaling behavior between the number of neurons in the network and critical coupling strength. (a) The ensemble average synchrony index 〈γ〉 as a function of coupling strength (ɛ) for N = 12 is shown. The critical coupling strength ɛc is determined at the value where 〈γ〉 = 0.9. Solid gray line along the curve indicates interpolated values. (b) The algebraic scaling between ln ɛc and ln N; ln ɛc = α × ln N is plotted. The scaling exponent “a” was 0.7 ± 0.08.
Field potential estimation
With a point current source approximation, extracellular field potential (Vext) can be described as 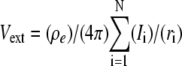 (32), where ρe is the extracellular resistivity with a value up to 375 (Ω · cm) that is three times greater than the intracellular resistivity (125 Ω · cm) (33). N is the estimated number of neurons used for calculating field potential. I indicates the total currents coming into and out from the one soma membrane, and r represents the distance between the recording site and the center of each soma compartments (Fig. 1).
(32), where ρe is the extracellular resistivity with a value up to 375 (Ω · cm) that is three times greater than the intracellular resistivity (125 Ω · cm) (33). N is the estimated number of neurons used for calculating field potential. I indicates the total currents coming into and out from the one soma membrane, and r represents the distance between the recording site and the center of each soma compartments (Fig. 1).
Interevent intervals
To show a periodicity of extracellularly recorded field potential activity obtained from both in vivo experiments (19) and simulations, a histogram of interevent intervals was obtained. The interevent interval was defined as the time difference between two consecutive maximum peaks of the spontaneous bursting activity, which exhibits doublet or multiplet waveform. The duration between two consecutive spikes within a single bursting event, was excluded throughout this study.
Cyclic relative phase distribution
The distribution of the cyclic relative phase can be used as a method to detect phase synchronization in noisy systems (2,34,35). The term “noise” includes both random and purely deterministic perturbations to phases. Phase synchronization can be shown in a statistical sense by the existence of preferred phase values in the distribution regardless of the difference among the mean frequencies of the oscillators. In these simulations carried out with a deterministic system, random initial conditions and 0.2% heterogeneity could provide randomness as an initial perturbation to phases. Once the relative phases between each pair of neurons of the network were obtained, the cyclic relative phase distribution was used to detect synchronization measured by phase locking state of the neuronal activities.
RESULTS
Periodic epileptiform activity in in vivo experiments and in computer simulations
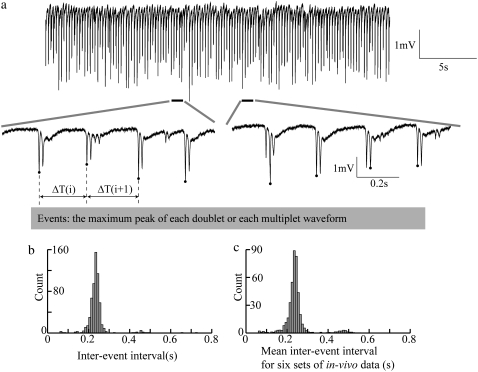
A typical nonsynaptic SE-like activity recorded extracellularly in in vivo experiments is shown in Fig. 2 a. A distribution of interevent intervals was used to reveal temporal periodicity of in vivo SE-like activity and plotted in Fig. 2 b. The interevent interval (ΔT) was estimated by the time difference between the maximum peaks of two consecutive spontaneous bursting events. The amplitudes of the maximum peaks were typically >1 mV. The intervals between the peaks within a bursting were not considered in this study. For the data set shown in Fig. 2 b, 606 events were detected in the duration of 144 s. The mean frequency in this case is therefore 4.21 Hz. The largest number of intervals falls within the 0.23–0.24 s time bin (bin width = 0.01 s). The corresponding frequency to the maximum peak in the histogram was 4.17–4.35 Hz. For all six data sets, 422 events (averaged over six data sets) were estimated in the averaged duration of 103 s, providing ∼4 Hz of the mean frequency. A histogram of the mean intervals for six other in vivo data sets further shows that the structure of distribution is quite stable (Fig. 2 c).
FIGURE 2.
In vivo SE-like activity and distribution of interevent intervals. (a) Thirty seconds long in vivo SE-like activity obtained in the rat hippocampus exposed to a medium with EGTA, zero Ca2+, and high K+. The onset times of consecutive two events provide time intervals ΔT shown in enlargements. (b) The distribution of inter event intervals calculated from ∼140 s long recording associated with SE-like activity shown in (a). A local maximum around 0.25 s is consistent with a frequency of ∼4 Hz. (c) Statistical sensitivity analysis of the distribution of interevent intervals obtained from six separate in vivo data sets. Each data set was recorded for 1– 2 min with the data sampling rate of 20 KHz after 60, 65, 70, 75, 80, 85 min use of EGTA.
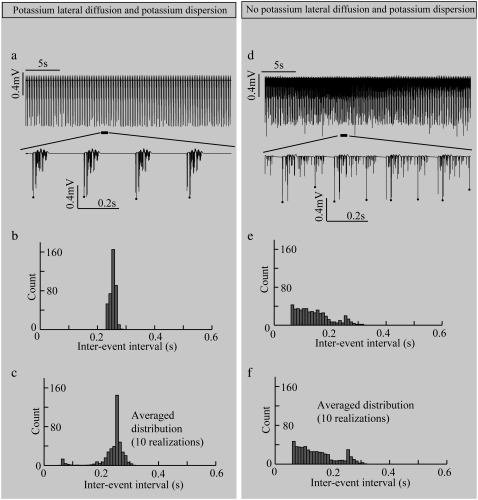
Computer simulations were able to generate similar extracellular periodic neural activity with a network lacking synaptic transmission and using higher K+ bath concentration of 7.6 mM (Table 4) compared to normal values ranging from 3 to 5.5 mM (19,36). With lateral diffusion coupling, the simulated field potential activity clearly exhibited a periodic pattern (Fig. 3 a). To investigate the effect of the potassium lateral diffusion (diffusive coupling) on the network activity, the lateral diffusion paths were removed. As a result, only potassium dispersion (global coupling) was present in the network. As shown in Fig. 3 d, without potassium lateral diffusion coupling, the network generated field potential activity without any noticeable periodicity, i.e., the periodicity was lost. The distribution of interevent intervals for the coupled model is tightly localized around a mean value of 0.25 s (Fig. 3 b) consistent with the in vivo experimental data, whereas the uncoupled model is not (Fig. 3 e). To examine the stability of the distribution, 10 separate realizations (100 s long for each realization) were simulated and the numbers falling into each bin of the histogram were averaged for all the trials (Fig. 3, c and f). The distributions shown in Fig. 3, c and f, confirm that the emergence of periodic activity is robust.
FIGURE 3.
Contribution of the diffusive coupling to extracellular field potential activity. Simulation results obtained from coupled and uncoupled networks are plotted in (a–c) and (d–f), respectively. With potassium lateral diffusion coupling, (a) simulated field potential activity shows a periodic pattern; (b) the interevent interval distribution shows a clear local maximum around 0.25 s and (c) a similar local maximum is shown in the average interevent interval distribution for 10 realizations. Without diffusive coupling, (d) no periodicity can be detected from simulated field potential activity; (e) no clear peak can be observed in the interevent interval distribution (for one realization) and (f) the same flatness can be shown in the average interevent interval distribution for 10 different realizations. For the simulations, the parameter values used were: τss = 5 ms and N = 16.
Synchronization as phase locking of intracellular activity: periodicity
To understand the underlying mechanism of extracellular periodic activity appearing with potassium lateral diffusion, the effect of diffusive coupling on the synchronization of intracellular activity was examined. It has been shown that, for regular simple periodic oscillators, either phase locking criterion or frequency locking criterion can be used equivalently to identify synchronization. However, for complex oscillators (e.g., systems with noise and/or randomness), both criteria are needed to be examined and especially the distribution of the relative phase is critical to correctly determine synchronization (34). Schäfer et al. (34) have shown that when the natural frequencies of two uncoupled systems are almost the same, a coincidence of mean frequencies exhibited between coupled and uncoupled systems can be accurately separated as synchronized state and desynchronized state only when the phase distribution is examined. The authors have also shown that the distribution of the relative phase can be used successfully to determine synchronization for the case when phase locking without frequency locking (or vice versa) takes place. The spatial heterogeneity in the scale of the network and 25 dimensions in the scale of each single neuron (i.e., the number of dimensions necessary to govern the dynamics of single neuron activity) add significant complexity to this network model. Therefore, both phase and frequency of intracellular neuronal activity were examined to determine synchronization.
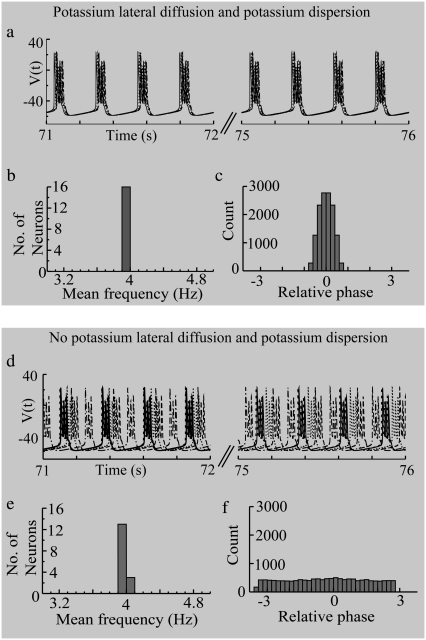
The intracellular activity of both the diffusively coupled and the diffusively uncoupled networks are shown in Fig. 4, a and d. The spike times of neuronal activity in the uncoupled network are broadly distributed compared to those in the coupled network. To reproduce the in vivo epileptiform activity with the mean frequency of 4 Hz, the individual frequencies of the cells were distributed in relatively narrow range of 3.97–4.03 Hz. Therefore, the histogram of mean frequency values for both the diffusively coupled system (Fig. 4 b) and the diffusively uncoupled system (Fig. 4 e) show about the same frequency distribution with a local maximum around 4 Hz. In this particular case, when the individual frequencies of the elements of the network are only slightly different, synchrony could be shown by the distribution of the relative phase (34). A local maximum around a preferred phase in the distribution of the relative phase was used as an indication for detecting synchronization as phase locking (2,34). As shown in Fig. 4 c, synchronization was detected in the diffusively coupled network as expected. However, even with a presence of global coupling, desynchronization could be shown when the diffusive coupling was removed (Fig. 4 f). The results show that the lateral diffusion coupling is responsible for establishing temporal periodicity due to phase locking of the network activity.
FIGURE 4.
Effect of potassium diffusive coupling on the synchronization of intracellular neuronal activity. With potassium lateral coupling, (a) phases of neuronal firings (activities of five neurons out of 16 are shown here) are locked and (b) the mean frequencies of the cells fall within a very narrow range (3.97∼4.04 Hz) given the parameter values used for this simulation (τss = 5 ms; other parameters can be found in Table 4.) (c) The preferred phases are shown in the cyclic relative phase distribution. Without lateral diffusion coupling, (d) phases of neuronal firings keep slipping, and (e) the histogram of mean frequency values shows a pronounced peak around 4 Hz. (f) The relative phase distribution shows no local maximum around preferred phase value. For this simulation, 5 ms lateral time constant (τss) and 16 cells (N) were used. The different types of lines indicate neuronal activity from different cells.
Effect of the number of cells on critical coupling in a lateral diffusion-coupled network
Theoretical analysis of diffusive coupling has shown that the existence of a scaling exponent between the coupling and the number of elements in the network. To determine if such a relationship exists for the potassium diffusion neuronal model, the synchronization of networks with various numbers of elements was analyzed. For potassium lateral diffusion, the coupling strength (ɛ) is inversely related to the lateral diffusion time constant (τss): ɛ ∝ 1/τss (ms), and one would expect that the synchrony index should increase with the coupling strength. The mean value of the synchrony index for a network with 12 elements is plotted together with the standard deviation (SD) versus the coupling strength ɛ in Fig. 5 a. As expected, the synchrony increases toward the maximum value of 1 as the coupling strength increases. Similar results for other network sizes were obtained.
A critical coupling strength (ɛc) for synchronization was defined as the value of ɛ for which 90% of the coupled network system is phase locked (mean value of synchrony index (γ) is equal to 0.9) A primary indication for synchronization as phase locking in a statistical sense is an existence of a pronounced local maximum around a certain preferred phase value in the distribution of the cyclic relative phase (34,37). Therefore, the criterion (〈γ〉 = 0.9) is reasonable and sufficient to expect the local maximum around the preferred phase value.
The average value of the synchrony index of 10 realizations 〈γ〉 as a function of coupling strength (ɛ) for the different size of networks (N = 4, 8, 10, 12, 14, 16, 18) was calculated. The relation between the critical coupling strength (ɛc) and the number of elements N is then plotted in Fig. 5 b. The result shows a linear relation between the logarithmic coupling strength (ln ɛc) and logarithmic number of neurons (ln N) with a slope (i.e., scaling exponent) equal to 0.7 ± 0.08. This scaling relation found in this study is consistent with the previous theoretical analysis of diffusive coupling of nonlinear oscillators in that there exists an algebraic scaling relation between the critical coupling strength (ɛc) for phase synchronized state and the number of oscillators (N): ɛc ∼ Nα (α = scaling exponent) (5).
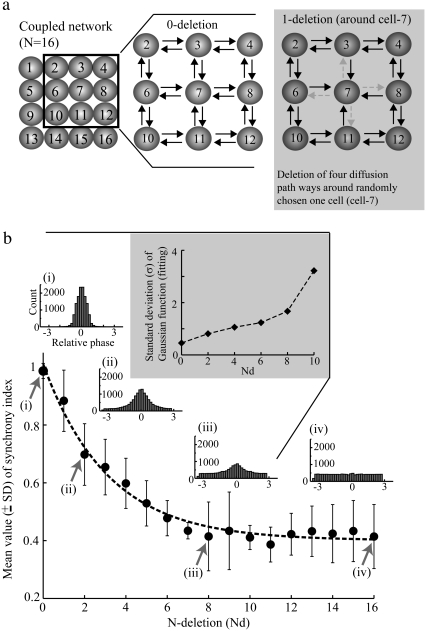
Effect of loss of diffusion paths on periodicity
To further determine whether the lateral diffusion coupling is required for establishing periodicity of neuronal activity, the effect of removing various diffusion paths in the network on the synchronization was examined by measuring the average synchrony index 〈γ〉 (Fig. 6 a). With an intact network (i.e., 0-deletion), the lateral diffusion is characterized by mutual coupling between nearest neighbors. For 1-deletion, four diffusion paths from one randomly chosen cell (e.g., cell 7 in Fig. 6 a) were removed. As the number of diffusion paths is decreased, the value of synchrony index, 〈γ〉 is significantly decreased (Fig. 6 b), and the distribution of the relative phase is transformed from Gaussian to a flat distribution (Fig. 6 b, inset) indicating the complete loss of synchronization. The SD of the phase distribution estimated from Gaussian functions fitted to the histograms increases with the number of deleted coupling paths (indicated by Nd; Fig. 6 b, inset), meaning that the distribution becomes flatter as lateral diffusion paths are removed. These results show clearly that intact lateral diffusion coupling is required for the generation of a phase locked state in the whole intermediate size of the network, which in turn plays a role in sustaining of the periodic behavior. This result is consistent with the relation between the coupling strength (ɛ) estimated by taking inverse of the lateral diffusion time constant (i.e., 1/τss) and the space constant evaluating the complexity of diffusion path (see Appendix B in Park and Durand (18) for the derivation). The loss of diffusion paths suggests that the path-length and therefore the space constant for one cell to the next increases, leading to a decrease in the coupling strength and a loss of synchrony.
FIGURE 6.
Diffusive coupling and periodicity in extracellular activity. (a) Schematic diagram illustrating how each diffusion path was deleted. (b) The mean synchrony index is plotted as a function of the number of active connections through potassium diffusion. The horizontal axis indicates the number of cells around which four diffusion directions toward their nearest neighbor are blocked. With an intact diffusive coupling ((i) 0-deletion), the local maximum around preferred phases are clearly shown in the distribution, whereas with completely blocked diffusion paths ((iv) 16-deletion), only a flatness is shown, i.e., no phase synchronization takes place. In between situation ((ii) 2-deletion and (iii) 8-deletion), a gradual decrease of the maximum peak of the distribution is illustrated as the number of diffusion path deletions increases.
DISCUSSION
The results in this model study show that periodicity zero-calcium induced epileptiform activity observed in in vivo experiments in the absence of synaptic transmission can be explained by a diffusive coupling model of a neural network (or specifically, a model of potassium lateral diffusion coupled network). These in vivo experiments could serve as a suitable physiological test bed to examine a role of diffusive coupling in the mechanism of periodicity of SE-like activity.
Model validation and robustness
To validate this network model, computer simulations were carried out in conditions similar to those in the in vivo experiments: no synaptic coupling and high potassium extracellular concentration. The distributions of the interevent intervals obtained from in vivo neural activity and simulated extracellular field potential activity were compared (Figs. 2 c and 3 c). The averaged maximum peak values and the SD of the average in the histograms from six in vivo data sets are nearly identical to the values obtained from the simulations with the diffusion coupled network model. These results indicate that the model can successfully simulate the in vivo network and that the periodicity of in vivo SE-like activity can be explained by diffusive coupling. In addition, the results show a scaling relation between the critical coupling strengths required for synchronization and the number of neurons of the network. This result is consistent with an existing theory described in Liu et al. (5) where the authors showed a scaling relation between diffusive coupling strength and the number of nonidentical oscillators. It has been also shown from a theoretical prediction that the globally coupled network can be completely synchronized if the number of elements is large enough, whereas the diffusively coupled network cannot be fully synchronized if the number of elements is sufficiently large (8). Therefore, this prediction is consistent with our result in that full synchronization could be achieved in a diffusively coupled intermediate size of the network. The above consistencies not only validate this model but show a role of diffusive coupling in the mechanism of periodic behavior of SE-like activity.
The random removal of diffusion paths indicated that the conclusion concerning the role of potassium diffusion is also robust. Although reducing the number of diffusion paths decreases the peak of the distribution of the relative phase (i.e., the degree of periodicity), still the unimodal pattern persists (Fig. 6 b, inset). Therefore, the synchronization in the diffusion coupled network is a robust phenomenon that remains even when single cell kinetics for each element in the network are different. This robustness also confirms that the effect of diffusion on synchronization is critical to the generation of the periodic synchronized activity.
The synchronized state is determined by the relationship between the coupling strength and the distribution of natural frequencies of individual elements of the ensemble (2). In this study, a narrow distribution of natural frequencies was used to not only reproduce 4 Hz experimental activity but also implement a situation where a false sense of synchronization can occur. Based on (34), a narrow range of frequency distribution may cause a false sense of synchronization, meaning that one can identify uncoupled state as a synchronized state simply because individual frequencies of the elements in the network are similar. For this particular case, one can clearly distinguish between a false sense of synchronization and true synchronization by using the distribution of the relative phase. However, the effect of the range of frequencies of the different cells could affect the effect of the diffusion coupling. Therefore, one would expect that the number of cells synchronized would decrease with an increasing range of frequencies of each element. This suggests that the size of the network that can be synchronized through lateral diffusion decrease with the heterogeneity of cells.
Relation between the coupling strength and the number of neurons, and its physiological relevance
Recently, it has been shown that diffusively coupled nonlinear oscillators could be characterized by an existence of algebraic scaling relation between the coupling strength necessary for achieving phase synchronization and the number of oscillators and the values of scaling exponents were model dependent (5). Consistent with the theory, the results in this model study have confirmed the existence of the scaling relation in diffusively coupled network by potassium diffusion. The scaling behavior indicates that the value of critical coupling strength for synchronization increases with the number of oscillators, i.e., a larger network needs higher coupling strength for the network to be fully synchronized. Therefore, it can be predicted that complete synchronization of a large neuronal network in a living tissue seems unlikely.
The results suggest that lateral diffusion coupling may play an important role in synchronizing neurons when the number and spatial distribution of synapses are absent or suppressed by low extracellular Ca2+ concentration (19). For a neural network with relatively dense synaptic connections, however, the effects of lateral diffusion coupling on synchronization may be negligible, compared to those of synaptic coupling. In agreement with the scaling behavior discussed above, larger networks require a stronger lateral diffusion coupling to synchronize the neurons within that network.
Relevance of the lateral diffusion coupling as a nonsynaptic mechanism
These computational studies have shown that synchronization, as phase-locking mediated by potassium lateral diffusion coupling, can explain the periodicity of SE-like extracellular activity observed in low-calcium in vivo experiments carried out with the rat hippocampus. Whether or not a nonsynaptic mechanism such as diffusion could play an important role in the mechanism underlying periodicity observed in clinical findings is yet to be investigated. However, recent experimental studies by using buccal ganglia of Helix pomatia have shown that mechanism of epileptiform activity is nonsynaptic and synchronization is mediated through diffusion between dendrites of cells (38). Unlike other nonsynaptic mechanisms, such as gap junctions and ephaptic field effects, extracellular potassium was a critical component in generating in vivo nonsynaptic epileptiform activity. Therefore, potassium diffusion mechanism was employed as an important synchronization mechanism in this model study. Other diffusive agents such as Ca2+ (39) and nitric oxide (NO) (40) have been reported to mediate diffusive coupling in the brain. Diffusion-mediated periodicity has been observed in hippocampal brain slices in zero-calcium solution and in the olfactory bulb. Zero-calcium solutions generate periodic activity in the range of 1 Hz (17,41–45). Potassium is known to diffuse through the slice and can mediate synchronization (17). In the olfactory bulb, low frequency oscillations ∼2 Hz are generated by the diffusive coupling of glutamate between synapses (46). These results, taken together, suggest that diffusive coupling can play a significant role in the synchronization of neural activity. The relative importance of this diffusion mechanism to that of synaptic transmission is a question that remains to be investigated.
CONCLUSION
The results of simulations have shown that: 1), potassium lateral diffusion coupling (or diffusive coupling) can be responsible for establishing a periodicity of neuronal firing in a small neuronal network; 2), the mechanism of potassium lateral diffusion can explain the in vivo nonsynaptic epileptiform activity in low-[Ca2+]o–high-[K+]o experiments; and 3), there exists an algebraic scaling between the critical coupling strength required for synchronization and the number of cells in the network. This scaling relation agrees with the theoretical prediction obtained from diffusively coupled nonlinear oscillators. Finally, potassium lateral diffusion could be a real physiological implementation of diffusive coupling in neural networks.
Acknowledgments
The authors thank the Ohio Supercomputer Center (OSC) for providing their computer facilities.
This work was supported by the National Institutes of Health (NS40785-03).
Dr. Eun-Hyoung Park's present address is Department of Neurosurgery, Children's Hospital Boston, Harvard Medical School, Boston, MA 02115.
Editor: Arthur Sherman.
References
- 1.Park, E. H., E. Barreto, B. J. Gluckman, S. J. Schiff, and P. So. 2005. A model of the effects of applied electric fields on neuronal synchronization. J. Comput. Neurosci. 19:53–70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Pikovsky, A. S., M. G. Rosenblum, and J. Kurths. 2001. Synchronization. A Universal Concept in Nonlinear Sciences. Cambridge University Press, Springer, Berlin.
- 3.Okuda, K. 1993. Variety and generality of clustering in globally coupled oscillators. Physica D. 63:424–436. [Google Scholar]
- 4.Bar-Eli, K. 1985. On the stability of coupled chemical oscillators. Physica D. 14:242–252. [Google Scholar]
- 5.Liu, Z., Y. C. Lai, and F. C. Hoppensteadt. 2001. Phase clustering and transition to phase synchronization in a large number of coupled nonlinear oscillators. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 63:055201. [DOI] [PubMed] [Google Scholar]
- 6.Ostborn, P. 2004. Frequency entrainment in long chains of oscillators with random natural frequencies in the weak coupling limit. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 70:016120. [DOI] [PubMed] [Google Scholar]
- 7.Ostborn, P., S. Aberg, and G. Ohlen. 2003. Phase transitions towards frequency entrainment in large oscillator lattices. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 68:015104. [DOI] [PubMed] [Google Scholar]
- 8.Wang, X. F., and G. Chen. 2002. Synchronization in small-world dynamical networks. Int. J. Bifurcat. Chaos. 12:187–192. [Google Scholar]
- 9.Larter, R., B. Speelman, and R. M. Worth. 1999. A coupled ordinary differential equation lattice model for the simulation of epileptic seizures. Chaos. 9:795–804. [DOI] [PubMed] [Google Scholar]
- 10.Postnov, D. E., L. S. Ryazanova, E. Mosekilde, and O. V. Sosnovtseva. 2006. Neural synchronization via potassium signaling. Int. J. Neural Syst. 16:99–109. [DOI] [PubMed] [Google Scholar]
- 11.Stokes, C. L., and J. Rinzel. 1993. Diffusion of extracellular K+ can synchronize bursting oscillations in a model islet of Langerhans. Biophys. J. 65:597–607. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Casagrande, V. 2006. Synchronization, Waves, and Turbulence in Systems of Interacting Chemical Oscillators. Institute for Theoretical Physics of the Technical University of Berlin, Berlin.
- 13.Hong, H., H. Park, and M. Y. Choi. 2005. Collective synchronization in spatially extended systems of coupled oscillators with random frequencies. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 72:036217. [DOI] [PubMed] [Google Scholar]
- 14.Kapral, R., and K. Showalter, editors. 1995. Chemical Waves and Patterns. Kluwer, Dordrecht.
- 15.Kuramoto, Y. 1984. Chemical Oscillations, Waves, and Turbulence. Berlin, New York, Springer-Verlag.
- 16.De Monte, S. 2004. Collective Dynamics in Populations with Microscopic Variability. Department of Physics, The Technical University of Denmark, Lyngby.
- 17.Lian, J., M. Bikson, J. Shuai, and D. M. Durand. 2001. Propagation of nonsynaptic epileptiform activity across a lesion in rat hippocampal slices. J. Physiol. 537:191–199. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Park, E. H., and D. M. Durand. 2006. Role of potassium lateral diffusion in nonsynaptic epilepsy: A computational study. J. Theor. Biol. 238:666–682. [DOI] [PubMed] [Google Scholar]
- 19.Feng, Z., and D. M. Durand. 2006. Effects of potassium concentration on firing patterns of low-calcium epileptiform activity in anesthetized rat hippocampus: inducing of persistent spike activity. Epilepsia. 47:727–736. [DOI] [PubMed] [Google Scholar]
- 20.Coulter, D. A., and R. J. DeLorenzo. 1999. Basic mechanisms of status epilepticus. Adv. Neurol. 79:725–733. [PubMed] [Google Scholar]
- 21.Shuai, J., M. Bikson, P. J. Hahn, J. Lian, and D. M. Durand. 2003. Ionic mechanisms underlying spontaneous CA1 neuronal firing in Ca2+-free solution. Biophys. J. 84:2099–2111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Kager, H., W. J. Wadman, and G. G. Somjen. 2000. Simulated seizures and spreading depression in a neuron model incorporating interstitial space and ion concentrations. J. Neurophysiol. 84:495–512. [DOI] [PubMed] [Google Scholar]
- 23.Nelken, I., and Y. Yaari. 1987. The role of interstitial potassium in the generation of low-calcium hippocampal seizures. Isr. J. Med. Sci. 23:124–131. [PubMed] [Google Scholar]
- 24.Somjen, G. G., P. G. Aitken, J. L. Giacchino, and J. O. McNamara. 1985. Sustained potential shifts and paroxysmal discharges in hippocampal formation. J. Neurophysiol. 53:1079–1097. [DOI] [PubMed] [Google Scholar]
- 25.Somjen, G. G., and J. L. Giacchino. 1985. Potassium and calcium concentrations in interstitial fluid of hippocampal formation during paroxysmal responses. J. Neurophysiol. 53:1098–1108. [DOI] [PubMed] [Google Scholar]
- 26.Tuckwell, H. C., and R. M. Miura. 1978. A mathematical model for spreading cortical depression. Biophys. J. 23:257–276. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Anderson, W. R., J. E. Franck, W. L. Stahl, and A. A. Maki. 1994. Na,K-ATPase is decreased in hippocampus of kainate-lesioned rats. Epilepsy Res. 17:221–231. [DOI] [PubMed] [Google Scholar]
- 28.Gabriel, S., A. Eilers, A. Kivi, R. Kovacs, K. Schulze, T. N. Lehmann, and U. Heinemann. 1998. Effects of barium on stimulus induced changes in extracellular potassium concentration in area CA1 of hippocampal slices from normal and pilocarpine-treated epileptic rats. Neurosci. Lett. 242:9–12. [DOI] [PubMed] [Google Scholar]
- 29.Kivi, A., T. N. Lehmann, R. Kovacs, A. Eilers, R. Jauch, H. J. Meencke, A. von Deimling, U. Heinemann, and S. Gabriel. 2000. Effects of barium on stimulus-induced rises of K+o in human epileptic non-sclerotic and sclerotic hippocampal area CA1. Eur. J. Neurosci. 12:2039–2048. [DOI] [PubMed] [Google Scholar]
- 30.Bazhenov, M., I. Timofeev, M. Steriade, and T. J. Sejnowski. 2004. Potassium model for slow (2–3 Hz) in vivo neocortical paroxysmal oscillations. J. Neurophysiol. 92:1116–1132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Rosenblum, M. G., A. S. Pikovsky, J. Kurths, C. Schäfer, and P. Tass. 2001. Phase synchronization: from theory to data analysis. In Handbook of Biological Physics, Vol. 4. F. G. Moss, editor. Elsevier Science, New York. 279–321.
- 32.Malmivuo, J., and R. Plonsey. 1995. Bioelectromagnetism: Principles and Applications of Bioelectric and Biomagnetic Fields. Oxford University Press, New York.
- 33.Traub, R. D., and R. Miles. 1991. Neuronal Networks of the Hippocampus. Cambridge University Press, New York.
- 34.Schäfer, C., M. G. Rosenblum, H. H. Abel, and J. Kurths. 1999. Synchronization in the human cardiorespiratory system. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 60:857–870. [DOI] [PubMed] [Google Scholar]
- 35.Tass, P., M. G. Rosenblum, J. Weule, J. Kurths, A. Pikovsky, J. Volkmann, A. Schnitzler, and H.-J. Freund. 1998. Detection of nm phase locking from noisy data: application to magnetoencephalography. Phys. Rev. Lett. 81:3291–3294. [Google Scholar]
- 36.Somjen, G. G. 2004. Ions in the Brain. Normal Function, Seizures, and Stroke. Oxford University Press, New York.
- 37.Stratonovich, R. L. 1963. Topics in the Theory of Random Noise. Gordon and Breach, New York.
- 38.Altrup, U. 2004. Epileptogenicity and epileptic activity: mechanisms in an invertebrate model nervous system. Curr. Drug Targets. 5:473–484. [DOI] [PubMed] [Google Scholar]
- 39.Kepseu, W. D., and P. Woafo. 2006. Intercellular waves propagation in an array of cells coupled through paracrine signaling: a computer simulation study. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 73:041912. [DOI] [PubMed] [Google Scholar]
- 40.Garthwaite, J. 1991. Glutamate, nitric oxide and cell-cell signaling in the nervous system. Trends Neurosci. 14:60–67. [DOI] [PubMed] [Google Scholar]
- 41.Bikson, M., R. S. Ghai, S. C. Baraban, and D. M. Durand. 1999. Modulation of burst frequency, duration, and amplitude in the zero-Ca2+ model of epileptiform activity. J. Neurophysiol. 82:2262–2270. [DOI] [PubMed] [Google Scholar]
- 42.Jefferys, J. G. 1995. Nonsynaptic modulation of neuronal activity in the brain: electric currents and extracellular ions. Physiol. Rev. 75:689–723. [DOI] [PubMed] [Google Scholar]
- 43.Jefferys, J. G., and H. L. Haas. 1982. Synchronized bursting of CA1 hippocampal pyramidal cells in the absence of synaptic transmission. Nature. 300:448–450. [DOI] [PubMed] [Google Scholar]
- 44.Taylor, C. P., and F. E. Dudek. 1982. Synchronous neural afterdischarges in rat hippocampal slices without active chemical synapses. Science. 218:810–812. [DOI] [PubMed] [Google Scholar]
- 45.Yaari, Y., A. Konnerth, and U. Heinemann. 1983. Spontaneous epileptiform activity of CA1 hippocampal neurons in low extracellular calcium solutions. Exp. Brain Res. 51:153–156. [DOI] [PubMed] [Google Scholar]
- 46.Schoppa, N. E., and G. L. Westbrook. 2001. Glomerulus-specific synchronization of mitral cells in the olfactory bulb. Neuron. 31:639–651. [DOI] [PubMed] [Google Scholar]
- 47.Yamada, K. A. 1998. Multiple channels and calcium dynamics. In Methods in Neuronal Modeling: From Ions to Networks. C. Koch, Segev, I., editors. MIT Press, Cambridge. 153–154.
- 48.Coulombe, A., and E. Coraboeuf. 1983. Simulation of potassium accumulation in clefts of Purkinje fibers: effect on membrane electrical activity. J. Theor. Biol. 104:211–229. [DOI] [PubMed] [Google Scholar]
- 49.Alzheimer, C., P. C. Schwindt, and W. E. Crill. 1993. Modal gating of Na+ channels as a mechanism of persistent Na+ current in pyramidal neurons from rat and cat sensorimotor cortex. J. Neurosci. 13:660–673. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Buehrer, K. L., S. C. Baraban, and D. M. Durand. 2003. Effects of Furosemide on [K+]o Dynamics and Glial Cell Function in Rat Hippocampal Slice Seizure Models. Society for Neuroscience 33rd Annual Meeting, New Orleans, LA.