Skip to main content
NCBI home page
Biophysical Journal logoLink to Biophysical Journal
. 2008 Feb 29;94(11):4570–4576. doi: 10.1529/biophysj.107.125203

Sound-Evoked Deflections of Outer Hair Cell Stereocilia Arise from Tectorial Membrane Anisotropy

R Gueta *, D Barlam †, R Z Shneck ‡, I Rousso *
PMCID: PMC2480654  PMID: 18310237

Abstract

The exceptional performance of mammalian hearing is due to the cochlea's amplification of sound-induced mechanical stimuli. During acoustic stimulation, the vertical motion of the outer hair cells relative to the tectorial membrane (TM) is converted into the lateral motion of their stereocilia. The actual mode of this conversion, which represents a fundamental step in hearing, remains enigmatic, as it is unclear why the stereocilia are deflected when pressed against the TM, rather than penetrating it. In this study we show that deflection of the stereocilia is a direct outcome of the anisotropic material properties of the TM. Using force spectroscopy, we find that the vertical stiffness of the TM is significantly larger than its lateral stiffness. As a result, the TM is more resistant to the vertical motion of stereocilia than to their lateral motion, and so they are deflected laterally when pushed against the TM. Our findings are confirmed by finite element simulations of the mechanical interaction between the TM and stereocilia, which show that the vertical outer hair cells motion is converted into lateral stereocilia motion when the experimentally determined stiffness values are incorporated into the model. Our results thus show that the material properties of the TM play a central and previously unknown role in mammalian hearing.

INTRODUCTION

Mammalian hearing's exquisite sensitivity and frequency selectivity are achieved by an active amplification mechanism of the cochlea (1–3), and occur through an orchestrated cascade of events. During acoustic stimulation, pressure waves inside the cochlea induces transverse displacement of an elastic connective tissue called the basilar membrane (BM) (4,5). This displacement results in the outer hair cells (OHCs; one of the two auditory sensory cell types of the ear) moving against the tectorial membrane (TM; a highly hydrated matrix containing collagen fibrils and situated over the hair cells) (6) (Fig. 1). During this motion, the stereocilium bundles situated at the surface of the OHCs facing the TM must be laterally deflected as they are pushed against the TM, and only then the shearing motion between adjacent stereocilia will cause the mechanosensitive ion channels at their tips to open. The resulting influx of cations changes the polarization of the OHCs (7), which then exert mechanical force through an electromechanical transduction process (1,8). This force is fed back into the BM motion and amplifies the initial mechanical input. A fundamental question associated with this process is why stereocilia, which are more than 4 orders of magnitude stiffer than the TM (∼3 GPa (9) compared with 30–300 kPa (10,11)), are deflected by it, rather than piercing it.

FIGURE 1.

FIGURE 1

Open in a new tab

Schematic representation of the organ of Corti, showing the location of the TM with respect to the basilar membrane, outer and inner hair cells. The longitudinal and radial directions of the TM are correspondingly shown with double-headed arrows. The relative orientations of the normal (Ez) and lateral stiffness moduli (Ex, and Ey) are shown.

A possible reason for deflection is that the mechanical properties of the TM are not spatially uniform but differ along different axes (12). We propose a “mechanical guiding” model by which lateral deflection of the stereocilia is governed by the anisotropic properties of the TM. Specifically, we submit that the stiffness normal to the membrane surface of the TM (represented as the normal Young's modulus, Ez) is higher than its lateral stiffness (Ex, Ey) (Fig. 1). On stimulation, the properties of the TM coupled with the orientation of the stereocilia restrict their vertical more than their lateral motion, and thus the vertical movement of the OHCs is lateralized at the stereocilia. This model is supported by structural analysis studies that show that the collagen fibers of the TM are not distributed randomly within it, but are rather oriented along its radial direction (13–20).

In this study, the normal and lateral stiffness values of TM samples isolated from mice were analyzed through indentation type and lateral force experiments conducted with an atomic force microscope (AFM) tip. We find that the vertical stiffness of the TM is significantly larger than its lateral stiffness. This difference in stiffness directs the lateral movement of the stereocilia. Incorporating the experimentally determined stiffness values of the TM into a finite element model, the deflection of the stereocilia during acoustic stimulation was emulated. The results of this study show the role of the TM material properties in the micromechanical process that couples basilar membrane motion to hair-bundles deflection motion—a central process in mammalian hearing.

MATERIALS AND METHODS

Sample preparation

TM samples were isolated from a total of 28 adult mice at approximately two months of age using techniques reported previously (12). Isolated TM samples were classified according to three longitudinal regions: apical, midturn, and basal, based on their corresponding position along the cochlea. TM classification was further supported by analysis of sample dimensions. Narrow and thin samples were considered to be associated with the basal region of the cochlea, whereas wider and thicker samples were considered to be taken from the apical end. Samples that could not easily be assigned to either end were considered to be associated with the midturn region. TM samples were attached to Cell-Tak-coated glass slides. A petri dish served as a mold for the PDMS elastomer (polydimethyl siloxane, Sylgard-184, Dow-Corning, Midland, MI). Bubbles in the solution were removed by degassing under low vacuum. Curing was obtained at 65°C for 4 h.

AFM measurements

All atomic force microscopy (AFM) experiments were carried out using a Bioscope with a Nanoscope IV controller (Veeco, Santa Barbara, CA) mounted on an inverted optical microscope (IX70, Olympus). Force measurements were carried out by borosilicate spherical probes with a radius of ∼1 μm (Bioforce, Ames, IA) attached to silicon nitride cantilevers (DNP, Veeco, and CSC12, Micromasch, Tallin, Estonia). Cantilever spring constants (∼0.06 N/m) were determined experimentally by measuring their thermal fluctuations (21). The stiffness normal to the TM surface was determined from indentation type measurements, as described previously (10).

Lateral force measurements

Before each lateral force measurement, a force–distance curve was generated to determine the indentation of the sample at any given normal loading force. We then oscillated the AFM probe perpendicular to the long axis of the cantilever by driving the piezo scanner using a triangular wave signal from an external function generator (Agilent, Santa Clara, CA). The lateral movement scale was precalibrated with a calibration grid. To measure the lateral stiffness values along the radial orientation of the TM, the sample was rotated until the long axis of the cantilever was aligned perpendicular to the TM radial fibers. To measure the lateral stiffness along the perpendicular orientations, the TM sample was rotated by 90°. Orientation of the sample relative to the cantilever's long axis was determined by transmission light microscopy. Cantilever torsion and driving signals were recorded on a computer running LabView by a data acquisition card (National Instruments). The acquired torsion signal was fragmented and then grouped to lateral “load” and “unload” according to the driving signal slope, and the signals within each group were averaged using MatLab (The MathWorks, Natick, MA). The acquisition time for each measurement was ∼60 s, which corresponds to the averaging of ∼60 lateral force curves. Finally, to convert the torsion signal from volts to units of force (nN), we used the calibration method described by Ruan and Bhushan (22). Briefly, a cantilever is scanned over a clean glass slide, along its long axis under different loading forces. The friction coefficient of the glass substrate is the slope of the linear function that best fits the height versus loading force plot. Next, the scanning direction is rotated by 90° (perpendicular to the long axis of the cantilever), and the torsion of the cantilever is recorded as a function of the loading force. Similarly to the above, the friction coefficient is the slope of the linear correlation between the torsion signal and the loading force. Because the two coefficients obtained using the above methods must be identical, it is now possible to calculate the conversion factor from volts to nN for each cantilever torsion signal.

Finite element simulation

Modeling lateral force measurements

To estimate the lateral mechanical properties of the TM we simulated the lateral force experiments using the finite-element method. The TM was modeled as a three-dimensional (3D) plate, resting on a flat rigid surface and loaded by an absolutely rigid 2 μm spherical indenter. Coulomb-Amonton friction was assumed between the flat substrate and the TM model and between the indenter and the TM so giving rise to mechanical nonlinearity. The presence of large displacements creates a geometric nonlinearity. Therefore the numerical model considers large displacements by nonlinear geometric kinematics but linear elastic behavior of the material as the available approximation. Loading was simulated by prescribing the downward movement of the rigid indenter, calculated in 25 consecutive increments. Next, during maximal indentation, the indenter was laterally displaced in 100 consecutive increments. The magnitudes of the simulated lateral displacement and indentation are similar to their experimental counterparts.

Modeling TM–stereocilia mechanical interactions

To simulate the interactions between the TM and a stereocilium, the TM was simulated as a 3D plate as in the previous simulation. The stereocilium was modeled as a nondeformable rod capped by a sphere. The diameter of the stereocilium was 300 nm. It was oriented at a 20° angle with respect to the TM surface, and its tip was embedded 100 nm inside the TM. To simulate the displacement of the stereocilium, it was pushed against the TM, pressure being exerted through its base along its longitudinal axis according to its initial position. The amplitude of the motion was 200 nm. During this movement, the rotational movement of the rod was unconstrained. Two scenarios were simulated. In the control simulation, the TM was considered as an isotropic material with all three Young's moduli being equal (Ex = Ey = Ez). In the second scenario, the experimentally derived moduli of the specific TM portion under consideration (basilar, midturn or apical) were incorporated into the TM model. These problems were solved by MSC.MARC software, and the results were rendered by HyperView (Altair Engineering, Troy, MI).

RESULTS AND DISCUSSION

To test our “mechanical guiding” model, the material properties of the TM were measured using normal-indentation and lateral force spectroscopy conducted by an atomic force microscope (AFM). For each position on the TM, we derived the normal Young's modulus by analyzing the force distance (FD) curve using a modified Hertz model (23). From the FD curve we also determined the depth to which the TM was indented by a given normal loading force (Fig. 2 A). Subsequently, we carried out a lateral force measurement at the same TM position (Fig. 2 B) for a specific TM indentation depth (achieved by applying the appropriate normal loading force, as determined from the FD curve). Measuring lateral force curves with the loading forces shown in Fig. 2 from all TM samples was technically impossible. The cantilevers used for this study were too soft to indent the stiff basal TM samples to a depth of >200 nm, whereas they were too stiff to produce lateral force curves of sufficient quality for the soft apical TM samples during indentation to depths of <100 nm. However, the cantilevers were well suited to measuring lateral force curves at indentation depth of 150–200 nm, and therefore such curves were obtained and analyzed for all TM samples at that depth. Moreover, this level of indentation is similar to the initial depth (∼100 nm) at which stereocilia are naturally embedded within the TM, as determined by cryo-electron microscopy (24).

FIGURE 2.

FIGURE 2

Open in a new tab

Normal and lateral force spectroscopy. (A) An averaged force-distance curve for a TM sample (solid line) and the corresponding cantilever deflection (dashed line). Double-headed arrows indicate the depth (nm) to which the TM is indented by each of five different normal loading forces (3, 9, 16, 26, and 36 nN). (B) Averaged lateral force versus lateral displacement curves acquired at the same TM position as was used for the force–distance curve (B) under five different normal loading forces denoted adjacent to the curves. The lateral force grows as the normal loading force and, consequently, the indentation depth increases.

In a previous study, we measured the normal mechanical properties of the TM (10). The results indicated that TM stiffness in the apical region (the low frequency response region of the cochlea) is one order of magnitude lower than in the basal region (the high frequency response region). Fig. 3 shows the averaged lateral stiffness of the TM, measured along the radial (x) and longitudinal (y) axes of the TM. Similarly to our normal force results (10), we find a gradual increase in the lateral stiffness of the TM going from the apical to the basal region of the cochlea, independent of radial orientation. Student's t-test showed that the difference in lateral stiffness values along the longitudinal direction is significant (p < 0.0001 at 99.9% confidence level). The lateral stiffness of the TM at its apical end (parallel: 1.9 ± 0.2 N/m, n = 18; perpendicular: 2.4 ± 0.2 N/m, n = 27) is only ∼20% of its stiffness at its basal end (parallel: 10.5 ± 1.1 N/m, n = 19; perpendicular: 12.4 ± 1.0 N/m, n = 36). In the midturn region of the cochlea, the lateral stiffness of the TM is 4.4 ± 0.3 N/m (n = 36) for an orientation parallel to the radial direction, and 4.8 ± 0.3 N/m (n = 34) for an orientation perpendicular to it. The differences in lateral stiffness values between the parallel and perpendicular orientations are statistically insignificant. Earlier material property measurements made using magnetic beads attached to the surface of the TM found it to be threefold stiffer in the radial (x) direction than in the longitudinal (y) direction (12). However, we find the TM to be slightly (10–20%) softer along its radial direction compared with the longitudinal direction, with the observed differences probably arising from the arrangement of the TM collagen fibers along its radial direction (20). This discrepancy between the findings of the two research groups may point to differences between the properties of the TM surface (as measured in the earlier study) and its bulk properties (as assessed using our constant indentation approach). Alternatively, it may result from the different measurement methods applied.

FIGURE 3.

FIGURE 3

Open in a new tab

The longitudinal distributions of the TM lateral stiffness. Measurements were localized to the radial zone above the hair cells, which is probably the most functionally relevant region of the TM. Results are grouped into three longitudinal regions: apical, midturn, and basal. Each longitudinal position is subdivided based on the direction of the measurement: along the radial (gray bars) or longitudinal axes (black bars) of the TM. The TM indentation depth was 150–200 nm in all measurements. The bars represent the SE, and the number of samples analyzed is indicated by the number shown in each column.

To evaluate the interrelations between the mechanical properties of the TM along its different axes, the corresponding Young's moduli, Ex, Ey (parallel and perpendicular to the radial direction, respectively) and Ez, should be compared. The normal Young's modulus (Ez) can be obtained reliably by analyzing the indentation experiments using the well established Hertz model. However, no model is available to describe lateral force measurements, which prevents their being used to directly estimate lateral moduli.

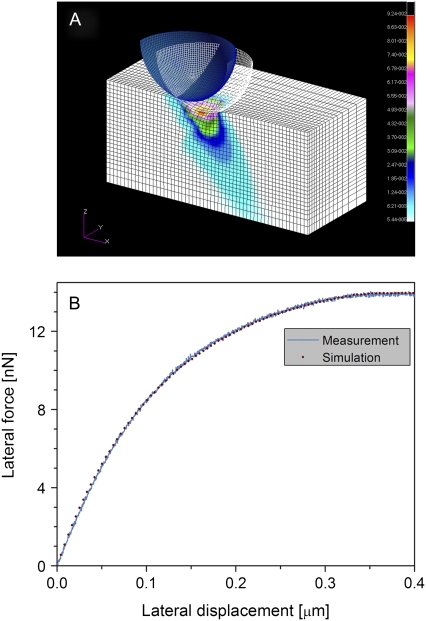
To obtain these moduli, we simulate our lateral force measurements in the framework of continuum mechanics using the finite element (FE) method (Fig. 4 A). The TM is modeled as an anisotropic material characterized by three independent Young's moduli (Ex, Ey, and Ez). Although Ex, and Ey are free parameters, Ez is a constant that is determined experimentally from the normal FD curve. At the end of the FE calculation, the simulated lateral force curve is superimposed over the experimental curve. The differences between the two curves are minimized by optimizing the Ex and Ey values of the modeled TM. The model properties that best fit our force measurements are considered the estimated TM lateral moduli (Fig. 4 B). To evaluate the robustness of the model and the sensitivity of the estimated Young's moduli, we analyzed a series of lateral force curves acquired from a single TM position, at different indentation depths ranging between 100–200 nm. The variance of the FE analysis results was 22% for the entire range and 7% for the indentation range used in this study (150–200 nm).

FIGURE 4.

FIGURE 4

Open in a new tab

Estimating the lateral mechanical properties of the TM by finite element analysis and lateral force spectroscopy. (A) The finite element analysis model. The indentation depth, lateral displacement, as well as the indenter size and shape are similar to their experimental counterparts. In this model, a 2-μm spherical indenter located 150 nm inside the TM is displaced laterally from its starting position (blue) to a 0.5-μm distant final position (white wireframe). Colors represent the total stress distribution in the TM model after the displacement. The size of the TM model was sufficiently large to exclude edge effects even under maximal strain. (B) Simulated (dots) versus experimental (solid line) lateral force curves for the TM. The experimental lateral force curve was measured on a TM sample isolated from the basal region of the cochlea. A normal Young's modulus of 300 kPa was obtained from an indentation-type experiment. Best fit was achieved after optimization of the lateral mechanical properties of the model TM.

According to our FE analysis (Table 1), the TM is ∼1.5-fold stiffer along the axis that is perpendicular to its radial direction (Ey) than along its radial axis (Ex). Lateral stiffness measurements indicate that the difference between the parallel and perpendicular orientations is smaller and statistically insignificant (Fig. 3). This apparent discrepancy arises from a limitation in our lateral force measurements. To switch from measuring the lateral stiffness values along the radial (x) direction to measuring them along the perpendicular (y) direction, the TM sample must be rotated by 90°. This technical limitation makes measurements of the lateral stiffness along both orientations from a single position impossible. As a result, the averaged lateral stiffness values shown in Fig. 3 represent independent sets of data acquired from different locations and often from several TM samples. By contrast, the FE models are optimized to fit lateral force curves that represent a set of material properties representing a single position. To resolve this inconsistency, we calculated a probability distribution function of perpendicular to parallel lateral force ratios for each of the three measured longitudinal regions (Supplementary Material, Fig. S1). In support with our FE analysis results, we find that the probability of obtaining a measured stiffness ratio of above 1.2 is >50%. More importantly, the FE analysis results indicate that, along the entire length of the TM, both lateral moduli (Ex, Ey) are significantly lower than the normal modulus (Ez). The lateral modulus Ex (parallel to the TM radial direction) is ∼6.7, 4, and 2.5 times lower than the normal modulus in the basal, midturn, and apical regions, respectively.

TABLE 1.

Summary of the mechanical properties of the TM

Longitudinal position Young's modulus (kPa)
Ex Ey Ez
Apical 11 16 28
Midturn 18 31 73
Basal 45 75 300
Open in a new tab

The lateral Young's moduli, Ex and Ey, are obtained by optimizing the finite element model for lateral force spectroscopy to the experimental measurements. The normal Young's modulus, Ez, is derived from the normal indentation experiment by fitting a modified Hertz model.

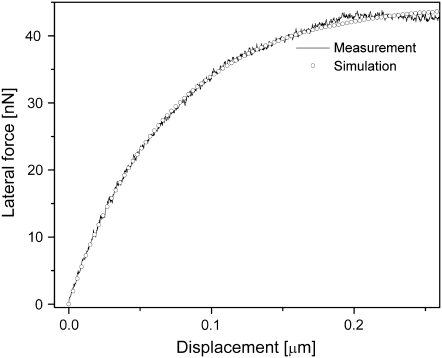
It is possible, however, that the observed differences in stiffness between the lateral and normal directions are affected by the fact that different experimental methods were used to obtain them (indentation versus lateral force). To exclude this possibility, we characterized the mechanical properties of a series of polydimethyl siloxane (PDMS) samples with different stiffness values using both experimental methods (Fig. 5 shows one example). The isotropic material properties of the samples were confirmed by a tensile tester. Normal modulus values obtained by AFM indentation experiments perfectly agreed with those obtained from the tensile test. Analysis of the lateral moduli showed that, for all samples, the FE-model-derived Ex was equal to Ey, and they were both slightly larger than the Hertz-model-derived Ez by a factor ranging from 1.1 to 1.7.

FIGURE 5.

FIGURE 5

Open in a new tab

Estimating the mechanical properties in the lateral direction of an isotropic PDMS sample by lateral force spectroscopy and finite-element analysis. Experimental lateral force measurements (solid line) were then obtained at an indentation of 150 nm. Thereafter, a simulation of the lateral force measurements (open circles) was carried out using the finite element method, with the PDMS mold being modeled as an anisotropic material characterized by three independent Young's moduli (Ex, Ey, and Ez), where Ez is set at the experimentally determined value of 420 kPa. Best fit between the experimental and simulated lateral force curves was achieved when the lateral stiffness moduli of the simulation model were set at Ex = Ey = 700 kPa (this being only 1.7 times the value of Ez).

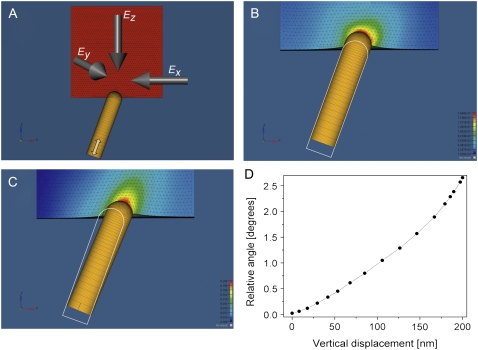
Finally, we simulated the mechanical interactions between the TM and embedded stereocilia using the FE method. The TM was modeled as an elastic 3D plate. Given that a stereocilium is markedly stiffer than the TM, it was modeled as a nondeformable rod (Fig. 6, A–C). The diameter of the stereocilium (300 nm), its initial position inside the TM (100 nm), and angle relative to the TM surface (20°) were obtained from electron microscopy and histological data (24,25). To simulate in vivo motion, the stereocilium was pushed against the TM along its longitudinal axis (Fig. 6 A, white double-headed arrow), whereas rotational movements were unconstrained. In the control simulation, the TM is modeled as an isotropic material. As the stereocilium is pushed against the isotropic TM, it pierces it while maintaining its initial orientation (Fig. 6 B, and Movie S1). By contrast, when the TM is modeled as an anisotropic material that has mechanical properties as per the findings of this study (Table 1), the vertical motion of the base of the stereocilium is converted into a lateral deflection of its tip (Fig. 6 C, D, and Movie S2). The mechanosensitive ion channels at the stereocilia tips open in response to the shearing motion of adjacent stereocilia. This motion depends on the lateral movement of the stereocilium tip rather than on its deflection angle. The length of the stereocilia is smallest at the basal end of the cochlea, and it gradually increases along the length of the cochlea until it is maximized at the apex (26). If the stereocilia deflection angle were constant throughout the entire length of the cochlea, the resulting lateral displacements of their tips would be smallest at the basal end and largest at the apex. We find that when maximally deflected, the stereocilium is tilted by an angle of 1.3°, 1.75°, and 2.6° relative to its initial position in the apical, midturn, and basal regions, respectively. Strikingly, these deflection angles perfectly match the corresponding stereocilium length (26), such that the resulting lateral movement of the stereocilium tip is kept constant (∼114 nm) along the entire length of the cochlea. The lateral movement and the deflection angle of the stereocilium predicted by our model agree extremely well with the experimental observations (27).

FIGURE 6.

FIGURE 6

Open in a new tab

Finite element simulation for the mechanical interactions between the TM and stereocilia. (A) The TM is modeled as an elastic 3D plate made of anisotropic homogenous material. The stereocilium is modeled as a nondeformable rod (150 nm in diameter) capped by a sphere at its tip, implanted 100 nm into the TM. The base of the stereocilium is moved vertically along its longitudinal axes (double-headed white arrow). (B) The penetration of the stereocilium as it is pushed against an isotropic TM model with Ex = Ey = Ez = 300 kPa. (C) The deflection of the stereocilium as it is pushed against an anisotropic TM model with Ex = 45, Ey = 75, and Ez = 300 kPa. The white outline shows the contour of the initial stereocilium orientation. (D) The relative angle of the stereocilium as a function of the vertical displacement of its base.

Several studies suggest that deflection of outer hair cell stereocilia is stimulated by viscous fluid forces in the cochlea (28–30). Our results suggest that the deflection motion is a direct outcome of the anisotropic material properties of the TM. This finding does not contradict the hypothesis according to which fluid plays a role in stereocilia deflection motion. In fact, the coexistence of these two mechanisms may enhance the conversion efficiency of OHC transverse motion into the lateral motion of their stereocilia.

The functional significance of the results obtained in this study becomes apparent in light of a recent study (31), which indicated that the mechanosensitive ion channels of hair cells function more efficiently when the stereocilium bundles deflect in concert in the same direction. Our results indicate that the motion of the stereocilium is controlled by the anisotropic properties of the TM. Because the material properties of the TM are fairly consistent within the area of a single bundle, our model predicts that the bundle will simultaneously move in a unidirectional manner.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.

Supplementary Material

[Supplement]
biophysj_107.125203_index.html (899B, html)

Acknowledgments

We thank S. Cohen, A. Minsky, Z. Reich, H. Sohmer, D. Wagner, and S. Weiner for their comments. I.R. is the incumbent of the Robert Edwards and Roselyn Rich Manson Career Development Chair.

This work was supported in part by the Israel Science Foundation, the Minerva Foundation with funding from the Federal German Ministry of Education and Research, a grant from the Jean-Jacques Brunschwig Fund for the Molecular Genetics of Cancer, the Kimmelman Center for Macromolecular Assemblies, and the Helen and Martin Kimmel Center for Nanoscale Science.

Editor: Thomas Schmidt.

References

  • 1.Brownell, W. E., C. R. Bader, D. Bertrand, and Y. de Ribaupierre. 1985. Evoked mechanical responses of isolated cochlear outer hair cells. Science. 227:194–196. [DOI] [PubMed] [Google Scholar]
  • 2.Hudspeth, A. J. 2005. How the ear's works work: mechanoelectrical transduction and amplification by hair cells. C. R. Biol. 328:155–162. [DOI] [PubMed] [Google Scholar]
  • 3.Gummer, A. W., J. Meyer, G. Frank, M. P. Scherer, and S. Preyer. 2002. Mechanical transduction in outer hair cells. Audiol. Neurootol. 7:13–16. [DOI] [PubMed] [Google Scholar]
  • 4.Mammano, F., and J. F. Ashmore. 1993. Reverse transduction measured in the isolated cochlea by laser Michelson interferometry. Nature. 365:838–841. [DOI] [PubMed] [Google Scholar]
  • 5.Gummer, A. W., W. Hemmert, and H. P. Zenner. 1996. Resonant tectorial membrane motion in the inner ear: its crucial role in frequency tuning. Proc. Natl. Acad. Sci. USA. 93:8727–8732. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 6.Thalmann, I., K. Machiki, A. Calabro, V. C. Hascall, and R. Thalmann. 1993. Uronic acid-containing glycosaminoglycans and keratan sulfate are present in the tectorial membrane of the inner ear: functional implications. Arch. Biochem. Biophys. 307:391–396. [DOI] [PubMed] [Google Scholar]
  • 7.Hudspeth, A. J. 1989. How the ear's works work. Nature. 341:397–404. [DOI] [PubMed] [Google Scholar]
  • 8.Brownell, W. E. 1990. Outer hair cell electromotility and otoacoustic emissions. Ear Hear. 11:82–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 9.Duncan, R. K., and J. W. Grant. 1997. A finite-element model of inner ear hair bundle micromechanics. Hear. Res. 104:15–26. [DOI] [PubMed] [Google Scholar]
  • 10.Gueta, R., D. Barlam, R. Z. Shneck, and I. Rousso. 2006. Measurement of the mechanical properties of isolated tectorial membrane using atomic force microscopy. Proc. Natl. Acad. Sci. USA. 103:14790–14795. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 11.Ghaffari, R., A. J. Aranyosi, and D. M. Freeman. 2007. Longitudinally propagating traveling waves of the mammalian tectorial membrane. Proc. Natl. Acad. Sci. USA. 104:16510–16515. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Abnet, C. C., and D. M. Freeman. 2000. Deformations of the isolated mouse tectorial membrane produced by oscillatory forces. Hear. Res. 144:29–46. [DOI] [PubMed] [Google Scholar]
  • 13.Thalmann, I., G. Thallinger, E. C. Crouch, T. H. Comegys, N. Barrett, and R. Thalmann. 1987. Composition and supramolecular organization of the tectorial membrane. Laryngoscope. 97:357–367. [PubMed] [Google Scholar]
  • 14.Hasko, J. A., and G. P. Richardson. 1988. The ultrastructural organization and properties of the mouse tectorial membrane matrix. Hear. Res. 35:21–38. [DOI] [PubMed] [Google Scholar]
  • 15.Arima, T., D. J. Lim, H. Kawaguchi, Y. Shibata, and T. Uemura. 1990. An ultrastructural study of the guinea pig tectorial membrane ‘type A’ protofibril. Hear. Res. 46:289–292. [DOI] [PubMed] [Google Scholar]
  • 16.Slepecky, N. B., J. E. Savage, L. K. Cefaratti, and T. J. Yoo. 1992. Electron-microscopic localization of type II, IX, and V collagen in the organ of Corti of the gerbil. Cell Tissue Res. 267:413–418. [DOI] [PubMed] [Google Scholar]
  • 17.Weaver, S. P., and L. Schweitzer. 1994. A radial gradient of fibril density in the gerbil tectorial membrane. Hear. Res. 76:1–6. [DOI] [PubMed] [Google Scholar]
  • 18.Tsuprun, V., and P. Santi. 1997. Ultrastructural organization of proteoglycans and fibrillar matrix of the tectorial membrane. Hear. Res. 110:107–118. [DOI] [PubMed] [Google Scholar]
  • 19.Glueckert, R., K. Pfaller, A. Kinnefors, A. Schrott-Fischer, and H. Rask-Andersen. 2005. High resolution scanning electron microscopy of the human organ of Corti. A study using freshly fixed surgical specimens. Hear. Res. 199:40–56. [DOI] [PubMed] [Google Scholar]
  • 20.Gueta, R., E. Tal, Y. Silberberg, and I. Rousso. 2007. The 3D structure of the tectorial membrane determined by second-harmonic imaging microscopy. J. Struct. Biol. 159:103–110. [DOI] [PubMed] [Google Scholar]
  • 21.Hutter, J., and J. Bechheoffer. 1993. Calibration of atomic-force microscope tips. Rev. Sci. Instrum. 64:1868–1873. [Google Scholar]
  • 22.Ruan, J. A., and B. Bhushan. 1994. Atomic-scale friction measurements using friction force microscopy 0.1. General principles and new measurement techniques. J. Tribol. 116:378–388. [Google Scholar]
  • 23.Vinckier, A., and G. Semenza. 1998. Measuring elasticity of biological materials by atomic force microscopy. FEBS Lett. 430:12–16. [DOI] [PubMed] [Google Scholar]
  • 24.Tsuprun, V., and P. Santi. 1998. Structure of outer hair cell stereocilia links in the chinchilla. J. Neurocytol. 27:517–528. [DOI] [PubMed] [Google Scholar]
  • 25.Bohnke, F., J. von Mikusch-Buchberg, and W. Arnold. 1999. Active nonlinear mechanics of the organ of Corti including the stereocilia-tectorial membrane complex. ORL J. Otorhinolaryngol. Relat. Spec. 61:311–317. [DOI] [PubMed] [Google Scholar]
  • 26.Wright, A. 1984. Dimensions of the cochlear stereocilia in man and the guinea-pig. Hear. Res. 13:89–98. [DOI] [PubMed] [Google Scholar]
  • 27.Fridberger, A., I. Tomo, and J. B. de Monvel. 2006. Imaging hair cell transduction at the speed of sound: Dynamic behavior of mammalian stereocilia. Proc. Natl. Acad. Sci. USA. 103:1918–1923. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 28.Cai, H. X., B. Shoelson, and R. S. Chadwick. 2004. Evidence of tectorial membrane radial motion in a propagating mode of a complex cochlear model. Proc. Natl. Acad. Sci. USA. 101:6243–6248. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 29.Fukazawa, T., K. Ishida, and Y. Murai. 1999. A micromechanical model of the cochlea with radial movement of the tectorial membrane. Hear. Res. 137:59–67. [DOI] [PubMed] [Google Scholar]
  • 30.Karavitaki, K. D., and D. C. Mountain. 2007. Evidence for outer hair cell driven oscillatory fluid flow in the tunnel of corti. Biophys. J. 92:3284–3293. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 31.Kozlov, A., T. Risler, and A. Hudspeth. 2007. Coherent motion of stereocilia assures the concerted gating of hair-cell transduction channels. Nat. Neurosci. 10:87–92. [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

[Supplement]
biophysj_107.125203_index.html (899B, html)
biophysj_107.125203_1.pdf (10.6KB, pdf)
biophysj_107.125203_125203anisotropic_TM.gif (2.8MB, gif)
biophysj_107.125203_125203isotropic.gif (1.6MB, gif)

Articles from Biophysical Journal are provided here courtesy of The Biophysical Society

RESOURCES