Abstract
By using multiple molecular dynamics trajectories of photolyzed carbon monoxide (CO) within crystallized myoglobin, a quantitative description of CO diffusion and corresponding kinetics was obtained. Molecular dynamics results allowed us to construct a detailed kinetic model of the migration process, shedding light on the kinetic mechanism and relevant steps of CO migration and remarkably-well reproducing the available experimental data as provided by time-resolved Laue x-ray diffraction.
INTRODUCTION
Myoglobin (Mb) is an oxygen-binding heme protein present in muscles that has long served as a model system for investigating the dynamics of ligand binding and conformational relaxation in proteins (1). Many of these investigations exploit the light-sensitivity of Mb complex with carbon monoxide (CO). The exposure of the MbCO adduct to a monochromatic light pulse breaks the iron-CO bond, initiating a series of spectroscopic and structural changes which may be monitored using different experimental techniques. Kinetic measures showed that xenon, bound to Mb, controls the rate of ligand recombination after photolysis (2), and the four hydrophobic cavities in Mb, identified by host xenon and called Xe1-Xe4 (3), are involved in the formation of transiently forming hydrophobic channels used by CO to migrate from the active site to the protein matrix and eventually escape into the solvent.
In the last few years, several quantitative analyses concerning the structural dynamics of Mb and ligand diffusion, with picosecond-to-millisecond time resolution, have been provided from time-resolved Laue diffraction experiments. Since the pioneering work on wild-type sperm whale Mb (wt-swMb) carried out at room temperature (4,5), molecular movies have been produced with high spatial resolution and wide temporal sampling on a series of Mb mutants at various experimental conditions (6–10).
In the case of wild-type Mb crystal at room temperature (5), the photodissociated CO resides initially in the distal pocket at the primary docking site, where CO is found upon photolysis at low temperature (11–13). Then it tends to migrate to the Xe1 cavity, on the proximal side of the heme, reaching the occupancy peak at ∼0.1 μs, before decaying with a half-life of several microseconds. The experiments carried out on different single mutants, containing an aromatic residue at position B10 (7–10), and on a triple mutant (6), called YQR-Mb (L29Y, H64Q, T67R), are also consistent, indicating that initially CO populates the Xe4 cavity and subsequently migrates to the Xe1 site, with a occupancy peak at time ranging from 0.1 to 0.5 μs. Therefore, the photolyzed ligand migrates inside the protein following a pathway that leads from the distal side to the proximal side through a series of connected cavities.
In a previous article (14), we reported an extended molecular dynamics (MD) simulation (90 ns) regarding the migration of dissociated carbon monoxide in wild-type swMb. In that trajectory, carried out in solution, we observed the CO, starting from the distal pocket, populating progressively the secondary binding sites located in the protein matrix. In particular, the CO reached Xe1 and Xe2 cavities via a pathway involving Xe4 and Xe3 sites and other two minor cavities which were not detected by previous crystallographic studies (14,15). Such a simulation, in agreement with the available experimental and computational data (5,7,9,16–18), provided a clear indication of the CO migration pathway and structural changes associated to the protein relaxation.
In this article, we report the results of a theoretical/computational investigation on the kinetics of CO diffusion in wild-type swMb crystal. MbCO crystal MD simulations provided 32 essentially independent trajectories (25-ns long) of the CO migration in the protein. The time dependence of cavities occupancy, as obtained by MD simulations, was used to construct an explicit kinetic model allowing us to obtain the kinetics of the entire CO migration process within the nanoseconds time range. Finally, the obtained microscopic rate constants and corresponding kinetic relaxation were compared to experimental time-dependent Laue crystallographic data.
METHODS
A total of four simulations of quadruple-unit crystal cells of sperm whale myoglobin (swMb) with photodissociated carbon monoxide were performed.
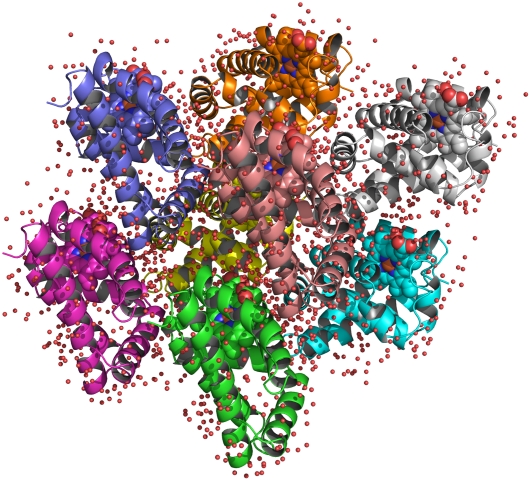
Initial coordinates were taken from the 1.15 Å resolution crystal structure of the CO-bound swMb (PDB entry 1BZR) (16). To simulate photodissociated CO in Mb, we replaced the CO-Fe bond with an unliganded interaction. The carboxy Mb (MbCO) crystal belonged to P21 (P1211) space group, with the following monoclinic cell parameters: a = 3.491 nm, b = 3.104 nm, c = 6.473 nm, and β = 105.53° (16). The P21 crystal unit cell contains two symmetry-related molecules. The starting coordinates of the crystal unit cell were obtained by applying the P21 symmetry transformation; afterwards the starting configuration for the quadruple unit cell was generated by shifting the entire box along the x axis and/or y axis, resulting in a monoclinic simulation box containing eight protein molecules with edges of 6.982, 6.208, and 6.473 nm (Fig. 1). The use of the quadruple unit cell as simulation box shows some advantages with respect to the use of a single unit cell. In fact, the use of the periodic boundary conditions for a crystal cell with a limited number of protein molecules may generate spurious coupling between the motion of the protein and its periodic images modifying the protein modes of motion. Furthermore, when using lattice-sum methods, any protein molecule in the reference unit cell interacts with an infinite number of regularly spaced and identically oriented periodic copies of the protein molecules. This treatment enforces long-range correlations that, in a real crystal, would be reduced by the presence of static and dynamic disorder. The use of a multiple unit cell as simulation box has then the aim to reduce unreal long-range correlations.
FIGURE 1.
Crystallographic structure of a quadruple unit cell of sperm whale myoglobin. The spheres represent the crystallographic position of the water molecules.
The simulations were performed with the GROMACS software package (19) using the GROMOS96 force field (20), Ver. No. 43A1. The CO molecules were modeled with the three-site “quadrupolar” CO model (21).
Since the experimental crystal structure corresponds to pH 6, the residues Glu and Asp, as the heme prosthetic group, were taken to be deprotonated while the residues Lys and Arg were taken to be protonated, leading to a zero net charge. The histidine side chains were modeled as nonprotonated. According to the previous theoretical and experimental results (22–25), the His64(E7) side chain was modeled with hydrogen at the ɛ-position.
The eight proteins were hydrated by placing 1648 SPC water molecules (26) at crystallographic sites and 1896 at noncrystallographic sites. The solvent box has been generated by three different solvent additions, each followed by a solvent relaxation session. Such a procedure provided a homogenously distributed solvent outside the protein, with a box density close to the experimental crystallographic one. The solvent was relaxed by energy minimization followed by 100-ps MD at 300 K, while restraining protein and CO atomic positions with a harmonic potential. The system was then energy-minimized without restraints and its temperature brought to 293 K in a stepwise manner: 10-ps MD runs at 50, 100, 150, 200, and 250 K and 2 ns MD run at 293 K were carried out before starting the production runs. During all equilibration runs, carbon monoxide molecules were coupled separately from the rest of the system to a heat bath at 50 K to avoid diffusion into the protein matrix. Therefore, the initial conditions of the production runs correspond to configurations with CO molecules in the distal pocket close to the heme mimicking CO positional distribution just after photolysis.
Simulations used for subsequent analysis were carried out at 293 K, using the isothermal temperature coupling (27), within a constant volume box and using periodic boundary conditions. Initial velocities were taken randomly from a Maxwell distribution. The bond lengths were constrained by using the LINCS algorithm (28). A time step of 2 fs was used in all simulations.
The particle-mesh Ewald method (29) was used for the calculation of the long-range interactions with a grid-spacing of 0.12 nm combined with a fourth-order B-spline interpolation to compute the potential and forces in between grid points. A nonbonded pair-list cutoff of 9 Å was used for short-range interactions and the pair-list was updated every five time steps.
Note that equilibration runs provided the equilibrium pressure condition of the simulation box as indicated by the pressure tensor providing almost identical diagonal elements (each ∼1000 bars) and virtually null off-diagonal elements (<20 bars). Note that in NVT ensemble MD simulations, equilibrium pressure is usually higher than the experimental one as a consequence of limited box dimension and force-field parameterization, based on structural and energetic data rather than pressure-density correlation.
Starting from two different initial configurations, we have performed four independent MD simulations of the quadruple crystal cell, each 25-ns long, for a total of 32 MD simulations of photodissociated CO in swMb.
RESULTS
During the MD simulations the CO molecules, starting from the distal pocket, migrated toward the proximal side through a pathway that involves the other Mb cavities (packing defects).
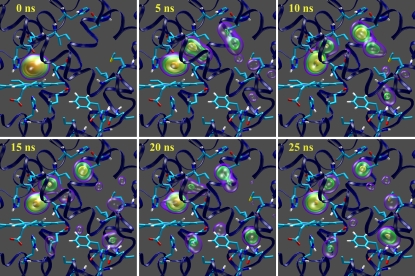
In Fig. 2, the migration of the CO molecules from distal pocket to proximal sites are depicted in terms of density maps. Clearly the CO migrates from distal pocket and reaches the Xe1 cavity following a pathway, which involves the Xe4 and Xe3 cavities and the other two minor cavities, called phantom1 (Ph1, connected to Xe4) and phantom2 (Ph2, connected to Xe3), detected in previous computational studies (14,15). To simplify the kinetic model to be used, we considered Ph1 and Ph2 as included into the Xe4 and Xe3 cavities, respectively, and given the fact that the contiguous Xe1 and Xe2 proximal cavities are both accessed only from Xe3, we also considered them as a single proximal site (Xep). Within such a definition of CO sites, MD data provided the kinetic scheme
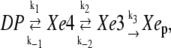 |
(Scheme 1) |
where distal pocket (DP) is the distal pocket and the absence of the reverse rate for Xe3 to Xep step is motivated by the fact that within the time range considered (25 ns), virtually no Xep→Xe3 transitions were observed. Note that, in the previous scheme, no CO exit from Mb is considered, as such a transition was not observed within the MD time range either (clearly, for the larger time range, beyond 100 ns, both Xep→Xe3 transition and CO escape from Mb should be considered in the kinetic scheme).
FIGURE 2.
Density maps of CO migration within myoglobin. The CO probability density at each time is expressed by colored isosurfaces. The heme and the residues His64(E7), His93(F8), Ile28(B9), Leu29(B10), Ile107(G8), Leu104(G5), Phe138(H14), Ile142(H18), Leu137(H13), His82(EF5), Leu76(E19), Met131(H7), Val17(A15), and His24(B5) are depicted in sticks.
According to Scheme 1, we set the system of linear differential equations, parametrically dependent on the five microscopic rate constants, whose solution provides the complete kinetic relaxation as described in detail in the Appendix. Solving the system of equations for different sets of the five rate constants, in a proper range as estimated by a preliminary kinetic analysis, we were able to evaluate their values which best reproduce the kinetic trace provided by MD simulations. Such estimated microscopic rate constants (k1 = 8.70 × 10−1 ns−1, k−1 = 8.47 × 10−1 ns−1, k2 = 8.24 × 10−2 ns−1, k−2 = 7.67 × 10−2 ns−1, and k3 = 5.20 × 10−2 ns−1) were then considered as the true kinetic constants for the CO migration in the simulated MbCO crystal system, providing a kinetic relaxation for the occupancy of the four CO sites determined by three kinetic eigenvalues (λ1= −1.76 ns−1, λ2 = −1.54 × 10−1 ns−1, and λ3 = −1.38 × 10−2 ns−1).
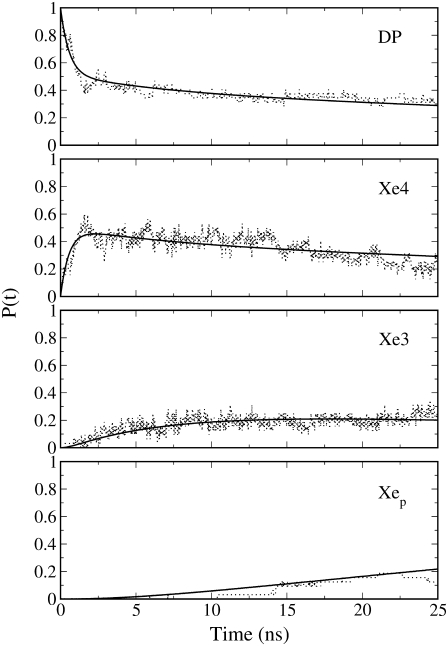
In Fig. 3 we report the time course of the CO occupancy, i.e., probabilities, of the cavities (DP, Xe4, Xe3, Xep) as obtained by MD simulations and evaluated by the theoretical kinetic model defined by the estimated eigenvalues. The accuracy of the model kinetics to reproduce MD data for all CO sites demonstrates the reliability of the sequential kinetic Scheme 1 and the good convergence of the time-dependent occupancies provided by the 32 MD trajectories.
FIGURE 3.
Kinetic trace of photolyzed CO occupancy (probability) in the four sites considered in the kinetic Scheme 1: MD data (dotted lines), and kinetic model (solid lines).
Interestingly, from Fig. 3, distal pocket (DP) occupancy decreases to ∼0.5 within 1 ns, in good agreement with the experimentally detected 0.45 fraction of photodissociated CO in DP after 1 ns (5). However, in that article, the missing 55% of the photolyzed CO electron density, not detected by time-resolved diffraction, is ascribed to positional disorder of the CO molecules in the distal pocket rather than to their distribution in other cavities. Instead, our data show fast forward and backward transitions (mean lives of ∼1 ns) between the adjacent distal and Xe4 cavities, which would not affect considerably the overall rate of ligand rebinding to heme and the slow migration toward the proximal site (characteristic time −1/λ3 of ∼70 ns). The fast ligand interchange between distal and Xe4 sites generates, after a few nanoseconds, a preequilibrium condition characterized by almost the same equilibrium ligand occupancy. Therefore the two cavities might be thought as forming a single kinetic site, after the first relaxation. It is worthwhile to note that the mean residence time in the distal pocket (1/k1 ∼1 ns), as obtained by MbCO crystal simulations, is smaller than the corresponding estimated value (4–5 ns) as provided by MbCO simulations in solution (30). Such a discrepancy suggests a possible difference of CO diffusion kinetics for the solution and crystallized systems, which might be worthwhile to investigate further.
The reliability of our MD simulation data and related kinetic model seems confirmed by the good reproduction of the experimental kinetic data (5) within the time range (<100 ns) where slow processes such as CO escape from Mb, the Xep→Xe3 CO transition, and CO rebinding to heme, may be disregarded, and hence our model may be reliable and accurate.
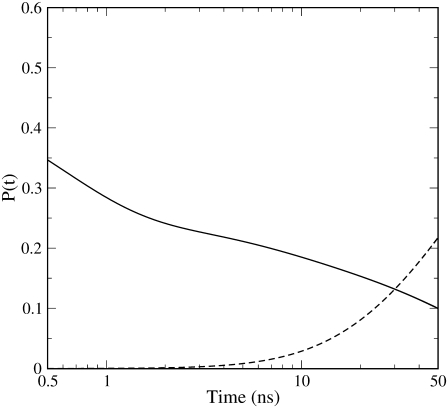
In fact, rescaling the occupancies provided by the kinetic model (Fig. 3), equivalent to the probabilities of the photolyzed CO in each site, by the experimental fraction of photolyzed CO molecules (5), we were able to reconstruct the time dependence of DP and Xep fractions (see Fig. 4) equivalent to the experimental data shown in Fig. 9 of Srajer et al. (5), i.e., fractions of total CO molecules and not only of photolyzed CO molecules. Note that we consider our Xep fraction, obtained by summing Xe1 and Xe2 occupancies, to be essentially equivalent to the experimental Xe1 fraction reported by Srajer et al. (5). This is motivated by the fact that, given the contiguity of Xe1 and Xe2 cavities, a slight variation of the definition of Xe1-Xe2 border may affect CO assignment in each of these proximal cavities—therefore making it difficult to distinguish Xe1 and Xe2 occupancies in comparison with experimental data. Moreover, from our MD simulations it was found that Xe1 provides ∼75% of the total Xep occupancy implying that, within our definition of the two proximal cavities, Xe2 contributes only marginally to the Xep curves reported in Figs. 3 and 4. In Fig. 4, where we consider the proper time range (50 ns) for our model to be reliable and the time is in logarithmic scale, the curves reported not only reproduce rather well the trends of the corresponding experimental curves, but also quantitatively reproduce their crossing occurring at ∼30 ns with an occupancy value of ∼0.15 (5) (the corresponding values as provided by our kinetic model are ∼30 ns and ∼0.13). Interestingly, at ∼100 ns where the experimental data show the maximum proximal occupancy followed by a slow decay due to the slower processes neglected in Scheme 1, our kinetic model still provides a proximal fraction (∼0.35) reasonably close to the experimental one (∼0.25). This clearly indicates that the characteristic time we obtained for the CO flux toward the proximal site (∼70 ns) matches rather well the corresponding experimental value. It is worth noting that the relatively fast DP→Xep CO transition, as provided by Srajer et al. data (5) and our MD simulations, is in contrast with another time-resolved Laue diffraction study (10), providing a qualitative description of CO distribution in Mb, showing no CO occupancy in Xe1 cavity up to ∼32 ns. Such a discrepancy, not discussed in the latter article (10), points out a possible intrinsic variability in time-resolved diffraction data that is probably due to the difficulty of accurately detecting spatially distributed ligands within proteins, as also discussed in Srajer et al. (5).
FIGURE 4.
Kinetic trace of total CO occupancy (probability) for distal pocket (DP, solid line) and proximal site (Xep, dashed line).
CONCLUSIONS
By using 32 essentially independent MD trajectories of CO migration in crystallized Mb at room temperature (293 K), we were able to construct a detailed kinetic model (see Scheme 1) of ligand transitions among the possible CO sites in the protein, for the nanoseconds time range. Results show that a fast distal pocket-Xe4 transition is followed by a slower and, within tens of ns, essentially irreversible flux toward the proximal site, characterized by an overall relaxation time of ∼70 ns. Moreover, MD data indicate that CO escape from crystallized Mb occurs at much longer time (microseconds time range), well-matching the available quantitative experimental data (5). A detailed comparison of our kinetic model results with such time-resolved Laue x-ray diffraction data (5) clearly shows that our model reproduces well the experimental behavior in the nanoseconds time range (within the first 50 ns), where the approximations used in Scheme 1 are accurate, although it suggests an alternative interpretation of the initial fast decay of distal pocket CO population. This points out the good quality of the atomistic force field used and the power of combining theoretical-computational results with experimental data to address mechanistically complex biophysical-biochemical processes.
Acknowledgments
We acknowledge Prof. M. Brunori for stimulating discussions.
This work was supported by grants from Ministero dell'Istruzione, dell'Università e della Ricerca (Progetto di Ricerca di Rilevante Interesse Nazionale).
APPENDIX
According to the kinetic Scheme 1 (see Results) we may set the system of differential rate equations providing the kinetics (probability time dependence) of the three sites: distal pocket (DP), Xe4, and Xe3,
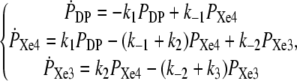 |
(1) |
with PDP, PXe4, and PXe3 the probabilities of finding the CO in each site, which may be expressed by the more compact matrix equation 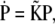 where
where
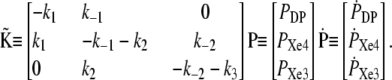 |
Introducing the linear transformation 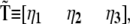 which diagonalizes the kinetic matrix
which diagonalizes the kinetic matrix 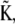 defined by the eigenvectors of
defined by the eigenvectors of 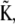 we may readily obtain
we may readily obtain
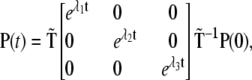 |
(2) |
where λ1, λ2, and λ3 are the kinetic matrix eigenvalues. Therefore, from Eq. 2 and using 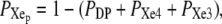 we can obtain the probability time dependence for each kinetic site of Scheme 1.
we can obtain the probability time dependence for each kinetic site of Scheme 1.
Editor: Ron Elber.
References
- 1.Austin, R. H., K. W. Beeson, L. Eisenstein, H. Frauenfelder, and I. C. Gunsalus. 1975. Dynamics of ligand binding to myoglobin. Biochemistry. 14:5355–5373. [DOI] [PubMed] [Google Scholar]
- 2.Scott, E. E., Q. H. Gibson, and J. S. Olson. 2001. Mapping the pathways for O2 entry into and exit from myoglobin. J. Biol. Chem. 276:5177–5188. [DOI] [PubMed] [Google Scholar]
- 3.Tilton, R. F., Jr., I. D. Kuntz, Jr., and G. A. Petsko. 1984. Cavities in proteins: structure of a metmyoglobin-xenon complex solved to 1.9 Å. Biochemistry. 23:2849–2857. [DOI] [PubMed] [Google Scholar]
- 4.Srajer, V., T. Teng, T. Ursby, C. Pradervand, Z. Ren, S. Adachi, W. Schildkamp, D. Bourgeois, M. Wulff, and K. Moffat. 1996. Photolysis of the carbon monoxide complex of myoglobin: nanosecond time-resolved crystallography. Science. 274:1726–1729. [DOI] [PubMed] [Google Scholar]
- 5.Srajer, V., Z. Ren, T. Y. Teng, M. Schmidt, T. Ursby, D. Bourgeois, C. Pradervand, W. Schildkamp, M. Wulff, and K. Moffat. 2001. Protein conformational relaxation and ligand migration in myoglobin: a nanosecond to millisecond molecular movie from time-resolved Laue x-ray diffraction. Biochemistry. 40:13802–13815. [DOI] [PubMed] [Google Scholar]
- 6.Bourgeois, D., B. Vallone, A. Arcovito, G. Sciara, F. Schotte, P. A. Anfinrud, and M. Brunori. 2006. Extended subnanosecond structural dynamics of myoglobin revealed by Laue crystallography. Proc. Natl. Acad. Sci. USA. 103:4924–4929. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Bourgeois, D., B. Vallone, F. Schotte, A. Arcovito, A. E. Miele, G. Sciara, M. Wulff, P. Anfinrud, and M. Brunori. 2003. Complex landscape of protein structural dynamics unveiled by nanosecond Laue crystallography. Proc. Natl. Acad. Sci. USA. 100:8704–8709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Schmidt, M., K. Nienhaus, R. Pahl, A. Krasselt, S. Anderson, F. Parak, G. U. Nienhaus, and V. Srajer. 2005. Ligand migration pathway and protein dynamics in myoglobin: a time-resolved crystallographic study on L29W MbCO. Proc. Natl. Acad. Sci. USA. 102:11704–11709. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Schotte, F., M. Lim, T. A. Jackson, A. V. Smirnov, J. Soman, J. S. Olson, G. N. Phillips, Jr., M. Wulff, and P. A. Anfinrud. 2003. Watching a protein as it functions with 150-ps time-resolved x-ray crystallography. Science. 300:1944–1947. [DOI] [PubMed] [Google Scholar]
- 10.Schotte, F., J. Soman, J. S. Olson, M. Wulff, and P. A. Anfinrud. 2004. Picosecond time-resolved x-ray crystallography: probing protein function in real time. J. Struct. Biol. 147:235–246. [DOI] [PubMed] [Google Scholar]
- 11.Teng, T. Y., V. Srajer, and K. Moffat. 1994. Photolysis-induced structural changes in single crystals of carbonmonoxy myoglobin at 40 K. Nat. Struct. Biol. 1:701–705. [DOI] [PubMed] [Google Scholar]
- 12.Teng, T. Y., V. Srajer, and K. Moffat. 1997. Initial trajectory of carbon monoxide after photodissociation from myoglobin at cryogenic temperatures. Biochemistry. 36:12087–12100. [DOI] [PubMed] [Google Scholar]
- 13.Chu, K., J. Vojtchovsky, B. H. McMahon, R. M. Sweet, J. Berendzen, and I. Schlichting. 2000. Structure of a ligand-binding intermediate in wild-type carbonmonoxy myoglobin. Nature. 403:921–923. [DOI] [PubMed] [Google Scholar]
- 14.Bossa, C., M. Anselmi, D. Roccatano, A. Amadei, B. Vallone, M. Brunori, and A. Di Nola. 2004. Extended molecular dynamics simulation of the carbon monoxide migration in sperm whale myoglobin. Biophys. J. 86:3855–3862. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Bossa, C., A. Amadei, I. Daidone, M. Anselmi, B. Vallone, M. Brunori, and A. Di Nola. 2005. Molecular dynamics simulation of sperm whale myoglobin: effects of mutations and trapped CO on the structure and dynamics of cavities. Biophys. J. 89:465–474. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kachalova, G. S., A. N. Popov, and H. D. Bartunik. 1999. A steric mechanism for inhibition of CO binding to heme proteins. Science. 284:473–476. [DOI] [PubMed] [Google Scholar]
- 17.Cohen, J., A. Arkhipov, R. Braun, and K. Schulten. 2006. Imaging the migration pathways for O2, CO, NO, and Xe inside myoglobin. Biophys. J. 91:1844–1857. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hummer, G., F. Schotte, and P. A. Anfinrud. 2004. Unveiling functional protein motions with picosecond x-ray crystallography and molecular dynamics simulations. Proc. Natl. Acad. Sci. USA. 101:15330–15334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Berendsen, H. J. C., D. van der Spoel, and R. van Drunen. 1995. GROMACS: a message-passing parallel molecular dynamics implementation. Comput. Phys. Commun. 91:43–56. [Google Scholar]
- 20.van Gunsteren, W. F., S. Billeter, A. Eising, P. Hunenberger, P. Kruger, A. E. Mark, W. Scott, and I. Tironi. 1996. Biomolecular Simulations: The GROMOS96 Manual and User Guide. BIOMOS bv, Zurich, Groningen.
- 21.Straub, J. E., and M. Karplus. 1991. Molecular dynamics study of the photodissociation of carbon monoxide from myoglobin: ligand dynamics in the first 10 ps. Chem. Phys. 158:221–248. [Google Scholar]
- 22.De Angelis, F., A. A. Jarzecki, R. Car, and T. G. Spiro. 2005. Quantum chemical evaluation of protein control over heme ligation: CO/O2 discrimination in myoglobin. J. Phys. Chem. B. 109:3065–3070. [DOI] [PubMed] [Google Scholar]
- 23.Merchant, K. A., D. E. Thompson, Q.-H. Xu, R. B. Williams, R. F. Loring, and M. D. Fayer. 2002. Myoglobin-CO conformational substate dynamics: 2D vibrational echoes and MD simulations. Biophys. J. 82:3277–3288. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Nienhaus, K., J. S. Olson, S. Franzen, and G. U. Nienhaus. 2005. The origin of stark splitting in the initial photoproduct state of MbCO. J. Am. Chem. Soc. 127:40–41. [DOI] [PubMed] [Google Scholar]
- 25.Sagnella, D. E., and J. E. Straub. 1999. A study of vibrational relaxation of B-state carbon monoxide in the heme pocket of photolyzed carboxymyoglobin. Biophys. J. 77:70–84. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, and J. Hermans. 1981. Interaction models for water in relation to protein hydration. In Intermolecular Forces. B. Pullman, editor. D. Reidel Publishing, Dordrecht, The Netherlands.
- 27.Evans, D. J., and G. P. Morriss. 1990. Statistical Mechanics of Nonequilibrium Liquids. Academic Press, London, UK.
- 28.Hess, B., H. Bekker, H. J. C. Berendsen, and J. G. E. M. Fraaije. 1997. LINCS: a linear constraint solver for molecular simulations. J. Comput. Chem. 18:1463–1472. [Google Scholar]
- 29.Essmann, U., L. Perera, M. L. Berkowitz, T. Darden, H. Lee, and L. G. Pedersen. 1995. A smooth particle mesh Ewald method. J. Chem. Phys. 103:8577–8593. [Google Scholar]
- 30.Anselmi, M., M. Aschi, A. Di Nola, and A. Amadei. 2007. Theoretical characterization of carbon monoxide vibrational spectrum in sperm whale myoglobin distal pocket. Biophys. J. 92:3442–3447. [DOI] [PMC free article] [PubMed] [Google Scholar]