Abstract
A phylloquinone molecule (2-methyl, 3-phytyl, 1, 4-naphthoquinone) occupies the A1 binding site in photosystem 1 particles from Synechocystis sp. 6803. In menB mutant photosystem 1 particles from the same species, plastoquinone-9 occupies the A1 binding site. By incubation of menB mutant photosystem 1 particles in the presence of phylloquinone, it was shown in another study that phylloquinone will displace plastoquinone-9 in the A1 binding site. We describe the reconstitution of unlabeled (16O) and 18O-labeled phylloquinone back into the A1 binding site in menB photosystem 1 particles. We then produce time-resolved  Fourier transform infrared (FTIR) difference spectra for these menB photosystem 1 particles that contain unlabeled and 18O-labeled phylloquinone. By specifically labeling only the phylloquinone oxygen atoms we are able to identify bands in
Fourier transform infrared (FTIR) difference spectra for these menB photosystem 1 particles that contain unlabeled and 18O-labeled phylloquinone. By specifically labeling only the phylloquinone oxygen atoms we are able to identify bands in  FTIR difference spectra that are due to the carbonyl (C=O) modes of neutral and reduced phylloquinone. A positive band at 1494 cm−1 in the
FTIR difference spectra that are due to the carbonyl (C=O) modes of neutral and reduced phylloquinone. A positive band at 1494 cm−1 in the  FTIR difference spectrum is found to downshift 14 cm−1 and decreases in intensity on 18O labeling. Vibrational mode frequency calculations predict that an antisymmetric vibration of both C=O groups of the phylloquinone anion should display exactly this behavior. In addition, phylloquinone that has asymmetrically hydrogen bonded carbonyl groups is also predicted to display this behavior. The positive band at 1494 cm−1 in the
FTIR difference spectrum is found to downshift 14 cm−1 and decreases in intensity on 18O labeling. Vibrational mode frequency calculations predict that an antisymmetric vibration of both C=O groups of the phylloquinone anion should display exactly this behavior. In addition, phylloquinone that has asymmetrically hydrogen bonded carbonyl groups is also predicted to display this behavior. The positive band at 1494 cm−1 in the  FTIR difference spectrum is therefore due to the antisymmetric vibration of both C=O groups of one electron reduced phylloquinone. Part of a negative band at 1654 cm−1 in the
FTIR difference spectrum is therefore due to the antisymmetric vibration of both C=O groups of one electron reduced phylloquinone. Part of a negative band at 1654 cm−1 in the 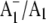 FTIR difference spectrum downshifts 28 cm−1 on 18O labeling. Again, vibrational mode frequency calculations predict this behavior for a C=O mode of neutral phylloquinone. The negative band at 1654 cm−1 in the
FTIR difference spectrum downshifts 28 cm−1 on 18O labeling. Again, vibrational mode frequency calculations predict this behavior for a C=O mode of neutral phylloquinone. The negative band at 1654 cm−1 in the 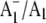 FTIR difference spectrum is therefore due to a C=O mode of neutral phylloquinone. More specifically, calculations on a phylloquinone model molecule with the C4=O group hydrogen bonded predict that the 1654 cm−1 band is due to the non hydrogen bonded C1=O mode of neutral phylloquinone.
FTIR difference spectrum is therefore due to a C=O mode of neutral phylloquinone. More specifically, calculations on a phylloquinone model molecule with the C4=O group hydrogen bonded predict that the 1654 cm−1 band is due to the non hydrogen bonded C1=O mode of neutral phylloquinone.
INTRODUCTION
In photosynthetic oxygen evolving organisms, two photosystems called photosystem 1 (PS1) and photosystem 2 (PS2) capture and convert solar energy independently (but cooperatively) (1,2). PS2 uses light to catalyze the oxidation of water, with the subsequent liberation of molecular oxygen (3). The solar conversion processes in PS2 are responsible for the earth's oxygen rich atmosphere. PS1 uses light to catalyze the formation of reducing products (NADPH) that are ultimately used to assimilate carbon dioxide into larger complex organic molecules (glucose).
PS1 is an enzyme that uses light energy to catalyze the transfer of electrons, via a series of acceptors, across a membrane from plastocyanin to ferredoxin (4). In PS1, light energy is captured and transferred rapidly to a centralized pigment molecule called P700. P700 is a dimeric chlorophyll-a species. Excitation of P700 results in transfer of an electron from P700 to a nearby acceptor called A0 (A0 is also a chlorophyll-a species). In <30 ps, the reduced acceptor,  transfers the electron to a secondary electron acceptor called A1. In this way the photogenerated radical pair state is stabilized.
transfers the electron to a secondary electron acceptor called A1. In this way the photogenerated radical pair state is stabilized.
A1 is a phylloquinone (PhQ) molecule (2-methyl, 3-phytyl, 1,4-naphthoquinone) (5). This PhQ molecule has a midpoint close to −800 mV (6–8). This makes the A1 PhQ one of the most reducing quinones in biology. This unprecedented redox potential is in part a result of interactions of PhQ with the surrounding protein environment. The crystal structure of PS1 at 2.5 Å provides a detailed view of the amino acids surrounding the PhQ cofactor, and suggests several possible pigment-protein interactions (9,10). Fig. 1 shows a view of the PhQ molecule bound to psaA (denoted A1-A) and several of the surrounding amino acids. The B-side is very similar. The indole ring of TrpA697 (Synechococcus elongatus numbering scheme) is π-stacked with the PhQ ring plane. The hydroxyl side chain of SerA692 could be hydrogen (H)-bonded to the backbone oxygen of MetA688, whereas the indole NH group of TrpA697 could be H-bonded to the hydroxyl oxygen of SerA692. The crystal structure (Fig. 1) suggests that the C1=O group of PhQ is probably not H-bonded whereas the C4=O of PhQ is H-bonded to the backbone NH group of LeuA722. MetA688 also ligates the central magnesium atom of the A0 chlorophyll-a (see Fig. 1 in (11) for further details).
FIGURE 1.
A view of A1-A and its environment. Possible H-bonds are shown as dashed lines. The B-side binding site is very similar. The carbonyl oxygen atoms of A1-A are labeled 1 and 4. The various oxygen and nitrogen atoms of the protein backbone and amino acid side chains are also labeled. Figure generated using Swiss PDBViewer (35) from the crystallographic coordinates of PS1 at 2.5 Å resolution (9) (PDB file accession number 1JB0).
The 2.5 Å crystal structure provides a view of PS1 in the ground state. It is likely that some of the molecular groups detailed in Fig. 1 are modified on 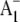 formation. X-ray crystallography provides no information on this excited radical state, however. A molecular specific probe of the radical (anion) state is therefore required. Fourier transform infrared (FTIR) difference spectroscopy (DS) is such a probe (12–14), and, when undertaken in a time-resolved manner,
formation. X-ray crystallography provides no information on this excited radical state, however. A molecular specific probe of the radical (anion) state is therefore required. Fourier transform infrared (FTIR) difference spectroscopy (DS) is such a probe (12–14), and, when undertaken in a time-resolved manner, 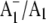 FTIR DS can be obtained (11,15,16).
FTIR DS can be obtained (11,15,16).
We have been using time-resolved step-scan FTIR DS recently to produce  FTIR DS for unlabeled and isotope labeled PS1 particles at 77 K (11). Experiments at 77 K were necessary to slow the
FTIR DS for unlabeled and isotope labeled PS1 particles at 77 K (11). Experiments at 77 K were necessary to slow the  recombination reaction into the hundreds of microseconds regime (17). Recent magnetic spectroscopy experiments on PS1 particles from Chlamydomonas reinhardtii may indicate that under these conditions (77 K) that we are only able to study the PhQ electron acceptor on the psaA side of the reaction center, because the psaA is suggested to be the only active branch at 77 K (18).
recombination reaction into the hundreds of microseconds regime (17). Recent magnetic spectroscopy experiments on PS1 particles from Chlamydomonas reinhardtii may indicate that under these conditions (77 K) that we are only able to study the PhQ electron acceptor on the psaA side of the reaction center, because the psaA is suggested to be the only active branch at 77 K (18).
We have also obtained time-resolved 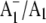 FTIR DS for PS1 particles that have a modified PhQ species occupying the A1 binding site (19), or contain a completely different quinone species (plastoquinone 9 (PQ9)) in the binding site (20). These later studies were undertaken using the so-called menB mutant PS1 particles from Synechocystis sp. 6803 (21). Using menB PS1 particles, it has been shown that it is possible to replace PQ9 in the A1 site with PhQ, by incubating the isolated particles in a large molar excess of PhQ (20,22). PhQ clearly has a much higher affinity for the binding site than PQ9. We have shown that
FTIR DS for PS1 particles that have a modified PhQ species occupying the A1 binding site (19), or contain a completely different quinone species (plastoquinone 9 (PQ9)) in the binding site (20). These later studies were undertaken using the so-called menB mutant PS1 particles from Synechocystis sp. 6803 (21). Using menB PS1 particles, it has been shown that it is possible to replace PQ9 in the A1 site with PhQ, by incubating the isolated particles in a large molar excess of PhQ (20,22). PhQ clearly has a much higher affinity for the binding site than PQ9. We have shown that 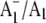 FTIR DS obtained using PhQ reconstituted menB PS1 particles are very similar to that obtained using wild-type PS1 particles, suggesting that the introduced PhQ is incorporated into virtually all of the reaction centers, completely displacing PQ9 (20). This conclusion was also reached in recent EPR experiments (20,22).
FTIR DS obtained using PhQ reconstituted menB PS1 particles are very similar to that obtained using wild-type PS1 particles, suggesting that the introduced PhQ is incorporated into virtually all of the reaction centers, completely displacing PQ9 (20). This conclusion was also reached in recent EPR experiments (20,22).
Based on the 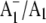 FTIR DS we have obtained for PS1 particles under a variety of conditions, we have been able to propose assignments for several of the bands in the spectra. However, there are still lingering doubts and ambiguities concerning the assignment of bands in the FTIR DS. This is not uncommon in FTIR DS of photosynthetic systems (12).
FTIR DS we have obtained for PS1 particles under a variety of conditions, we have been able to propose assignments for several of the bands in the spectra. However, there are still lingering doubts and ambiguities concerning the assignment of bands in the FTIR DS. This is not uncommon in FTIR DS of photosynthetic systems (12).
To discriminate between bands that are associated with PhQ in the A1 binding site, or bands that are associated with other pigments or protein amino acids, it is desirable to compare FTIR DS obtained on PS1 particles that contain unlabeled and specifically labeled PhQ. Such an approach has been used to gain a detailed understanding of 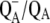 and
and  FTIR DS obtained using purple bacterial reaction centers, in which the native quinone is swapped for one that has specifically labeled oxygen or carbon atoms (23–26). Using menB PS1 particles allows us to incorporate labeled PhQ into the A1 binding site and therefore provides us with a means to distinguish protein bands from pigment bands in
FTIR DS obtained using purple bacterial reaction centers, in which the native quinone is swapped for one that has specifically labeled oxygen or carbon atoms (23–26). Using menB PS1 particles allows us to incorporate labeled PhQ into the A1 binding site and therefore provides us with a means to distinguish protein bands from pigment bands in 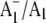 FTIR DS.
FTIR DS.
To help understand spin polarized transient EPR data associated with 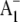 formation, Pushkar et al. (22) have also used menB PS1 particles in which specifically 13C labeled 2-methyl naphthoquinones were incorporated into the A1 binding site. The studies of Pushkar et al. (22) showed that the incorporated 2-methyl naphthoquinone is asymmetrically hydrogen bonded. This result is considered explicitly in our density functional theory (DFT) calculations outlined below, where we calculate the vibrational properties of a PhQ model that has only one of the carbonyl oxygen atoms hydrogen bonded.
formation, Pushkar et al. (22) have also used menB PS1 particles in which specifically 13C labeled 2-methyl naphthoquinones were incorporated into the A1 binding site. The studies of Pushkar et al. (22) showed that the incorporated 2-methyl naphthoquinone is asymmetrically hydrogen bonded. This result is considered explicitly in our density functional theory (DFT) calculations outlined below, where we calculate the vibrational properties of a PhQ model that has only one of the carbonyl oxygen atoms hydrogen bonded.
In this study, we describe the preparation of 18O-labeled PhQ and its incorporation into menB PS1. We then present 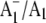 FTIR DS obtained using these PS1 particles containing 18O-labeled PhQ. Difference bands that are impacted by the labeling are most likely associated with modes of PhQ/PhQ−, or amino acid groups that can hydrogen (H) bond to the quinone oxygen. In this way we can unambiguously distinguish bands associated with these modes from all others. A priori, it is not at all obvious how bands will shift, and how their intensity will change, on 18O labeling of PhQ. With this in mind we have used DFT to calculate the harmonic vibrational mode frequencies of unlabeled and 18O-labeled PhQ and PhQ− model systems. We show that the calculated isotope induced band shifts and intensity changes match the experimentally observed changes very well.
FTIR DS obtained using these PS1 particles containing 18O-labeled PhQ. Difference bands that are impacted by the labeling are most likely associated with modes of PhQ/PhQ−, or amino acid groups that can hydrogen (H) bond to the quinone oxygen. In this way we can unambiguously distinguish bands associated with these modes from all others. A priori, it is not at all obvious how bands will shift, and how their intensity will change, on 18O labeling of PhQ. With this in mind we have used DFT to calculate the harmonic vibrational mode frequencies of unlabeled and 18O-labeled PhQ and PhQ− model systems. We show that the calculated isotope induced band shifts and intensity changes match the experimentally observed changes very well.
MATERIALS AND METHODS
Preparation of 18O-labeled PhQ
18O-labeled PhQ was prepared as described previously (25). Briefly, 20 mg of vitamin K1 was mixed with 500 μL of a solution containing 70% tetrahydrofuran (THF) (HPLC grade), 12% trifluoroacetic acid, and 18% 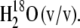 Vitamin K1, tetrahydrofuran, and trifluoroacetic acid were from Sigma-Aldrich (St. Louis, MO) and were used as received.
Vitamin K1, tetrahydrofuran, and trifluoroacetic acid were from Sigma-Aldrich (St. Louis, MO) and were used as received. 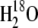 with an isotopic purity >98% was obtained from Cambridge Isotope Laboratories (Andover, MA). The mixture was incubated under argon at 4°C for 14 days. After this incubation period, samples were dried under a flow of nitrogen gas at room temperature. Dried samples were resuspended in THF and used immediately or stored in ethanol at −83°C until further use. 18O-isotopic incorporation into PhQ was estimated from FTIR absorption spectra of labeled and unlabeled PhQ in THF (see below). Such FTIR measurements have been directly correlated with mass spectroscopic analysis in the past (25).
with an isotopic purity >98% was obtained from Cambridge Isotope Laboratories (Andover, MA). The mixture was incubated under argon at 4°C for 14 days. After this incubation period, samples were dried under a flow of nitrogen gas at room temperature. Dried samples were resuspended in THF and used immediately or stored in ethanol at −83°C until further use. 18O-isotopic incorporation into PhQ was estimated from FTIR absorption spectra of labeled and unlabeled PhQ in THF (see below). Such FTIR measurements have been directly correlated with mass spectroscopic analysis in the past (25).
Preparation of PS I particles and incorporation of PhQ into PS I
MenB mutant trimeric PS1 particles were prepared using standard procedures (27). To incorporate PhQ back into the A1 binding site, menB mutant PS1 particles were incubated in the presence of a large molar excess of unlabeled or labeled PhQ (dissolved in ethanol) as described previously (20).
FTIR absorption spectra of labeled and unlabeled PhQ
For FTIR absorption measurements of PhQ in THF, PhQ was first dried under nitrogen and resuspended in THF. This sample was then partially dried to decrease the intensity of THF bands in the acquired spectrum. The thickness of the sample was also adjusted so that the band at 1662/1634 cm−1 in the unlabeled/labeled spectrum has an optical density of ∼0.7. A spectrum of pure THF was used to interactively subtract the well known THF bands present in the PhQ spectrum. In this was a spectrum of pure PhQ was obtained.
Static (light-induced) FTIR procedures
Before time-resolved measurements were undertaken, light-induced P700+/P700 FTIR DS were recorded. For these measurements, a 20 mW, helium-neon laser was used for light excitation. Sixty-four interferograms were collected before, during, and after light excitation. The spectra collected before illumination were ratioed directly against the spectra collected during illumination, as described by Wang and colleagues (28). There was usually a delay of ∼60 min between static and time-resolved measurements at 77 K, in which the helium-neon laser is removed and a YAG laser is incorporated, and the system is realigned.
Time-resolved FTIR procedures
Time-resolved step-scan FTIR experiments with 5 μs time resolution, at 77 K, were undertaken as described previously (11). Briefly, 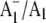 FTIR DS were constructed by subtracting photo-accumulated P700+/P700 FTIR DS (at 77 K) from time-resolved
FTIR DS were constructed by subtracting photo-accumulated P700+/P700 FTIR DS (at 77 K) from time-resolved  FTIR DS collected between 0–45 μs after a laser flash at 77 K (11) (see Supplementary Material, Data S1, for more details).
FTIR DS collected between 0–45 μs after a laser flash at 77 K (11) (see Supplementary Material, Data S1, for more details).
Density functional theory based vibrational frequency calculations
Molecular geometry optimizations and harmonic vibrational mode frequency calculations were carried out using hybrid DFT methods, using the B3LYP functional and the 6–31+G(d) method within Gaussian 03 (Gaussian, Wallingford, CT) (29). Such methods have been shown to accurately model the vibrational properties (and other physical properties) of neutral and reduced quinones (30).
Assignment of calculated vibrational frequencies to molecular groups is somewhat subjective, as modes are assigned by visual identification of the molecular groups that most prominently contribute to the vibration. This visual identification is carried out using the software GaussView 3 (Gaussian), in which the atomic motions associated with each of the vibrational modes can be displayed (30).
Calculated normal mode frequencies presented here have been scaled by 0.965. Such a scaling is appropriate for calculations at this level (31). Such a scaling is used purely for convenience so that the calculated and experimentally derived frequencies are similar. However, we are primarily interested in vibrational frequency changes that occur on isotope labeling, or on radical anion formation. We have shown previously that these frequency differences are accurately calculated without scaling (30,32), presumably because the same errors are inherent in both calculations, and cancel when the difference is taken. The scaling of calculated frequencies is of no consequence as far as the work presented here is concerned, and is used purely for convenient comparison of experimental and calculated frequencies.
Normal mode frequencies and intensities are calculated. With both the frequency and intensity information infrared “stick” spectra can be constructed. By convolving these stick spectra with a Gaussian function of 4 cm−1 bandwidth, more realistic-looking spectra are obtained, which we will call absorption spectra.
RESULTS AND DISCUSSION
Experimental and calculated IR absorption spectra for unlabeled and 18O-labeled PhQ
Fig. 2 A shows experimental FTIR absorption spectra obtained for unlabeled (marked as 16O) and 18O-labeled PhQ in THF. The bands at 1462 and 1377 cm−1 are due to δCH2 and δCH3 modes of the phytyl chain. The 16O and 18O spectra support this assignment as they show that the 1462 and 1377 cm−1 bands are not impacted by 18O labeling. Therefore, the two bands at 1462 and 1377 cm−1 were used for normalization of the labeled and unlabeled spectra. For unlabeled PhQ the three bands at 1662, 1619, and 1597 cm−1 are due to the antisymmetric C=O stretching of both C=O groups, the C2=C3 stretching (see inset in Fig. 2 for numbering), and C=C stretching of the aromatic part of the naphthoquinone ring, respectively (30). In Fig. 2 A it can be seen that a band is still found at 1661 cm−1 after 18O labeling. This band is reduced in intensity by ∼70% compared to the 1662 cm−1 band in the unlabeled spectrum. Virtually identical IR absorption spectra were also reported previously for unlabeled and 18O-labeled PhQ (25). By subtracting ∼30% of the unlabeled spectrum from the labeled spectrum, we derive a pure spectrum for 18O-labeled PhQ. This spectrum is shown in Fig. 2 B (solid line). The unlabeled PhQ absorption spectrum is shown overlaid (dotted line) for comparison. The 1662, 1619, and 1597 cm−1 bands in the unlabeled PhQ absorption spectrum downshift 28, 8, and 4 cm−1 on 18O labeling, respectively (Fig. 2, A and B).
FIGURE 2.
(A) FTIR absorption spectra for unlabeled (16O) (dotted) and 18O-labeled PhQ (solid) in THF. The spectra are scaled so that the intensity of the broad bands below 1500 cm−1 are similar. The ratio of the intensity of the 1662 cm−1 band in the two spectra is 0.30. Based on this assay we conclude that ∼70% of the PhQ carbonyl oxygen atoms are 18O-labeled. (B) 18O spectrum from A with 30% of the 16O spectrum subtracted from it. The resulting spectrum was then divided by 0.7 so that the bands below 1500 cm−1 were again of the same intensity. The ratio of the intensities of the two bands at 1662 and 1634 cm−1 indicate that 18O labeling leads to an ∼24% decrease in intensity of the C=O band of PhQ. (C) Calculated IR spectra obtained from DFT calculations using PhQ model shown in the inset. The absorbance scale does not apply to the calculated spectra in C. The calculated intensities are in km/mol and the 1661 cm−1 mode has an intensity of 369 km/mol (30). The frequency axis for the spectra in (C) have been scaled by 0.965, which is normal for calculations using the B3LYP functional and the 6-31G+(d) basis (31).
A small derivative feature is still observed at ∼1666(−)/1656(+) cm−1 in the “corrected” 18O-labeled spectrum (Fig. 2 B). Such a feature has been observed previously in IR spectra derived from unlabeled and 18O-labeled dimethyl naphthoquinone (DMNQ) (33). DMNQ is the same as PhQ except that the phytyl chain is replaced with a methyl group. The same behavior was also observed for PhQ (33). This 1666/1656 cm−1 derivative feature in the corrected 18O-labeled spectrum in Fig. 2 B arises from a portion of PhQ molecules that bear an 18O label on only one of the two carbonyl groups (33). From mass spectroscopic analysis of DMNQ it is found that the 18O labeling procedure used here results in 54% of the quinones bearing an 18O label on both carbonyls, 38% bearing an 18O label on only one carbonyl, and 8% of the molecules have both carbonyls unlabeled (33). In summary, our labeling procedure results in ∼72% of the carbonyl groups being 18O labeled. The 1662 cm−1 band in the spectrum for unlabeled PhQ is due to the asymmetric vibration of both C=O groups (30). The 1661 cm−1 band left after 18O labeling is due in part to the C=O mode of PhQ molecules that carry no label (8%), and partly to the unlabeled C=O in PhQ molecules bearing a single label. The 1634 cm−1 band in the 18O-labeled spectrum is therefore due to PhQ molecules that have both carbonyls 18O labeled, and to the 18O-labeled C=O mode in molecules that bear a label on only one of the carbonyl groups.
Calculated spectra for an unlabeled (16O) and 18O-labeled PhQ model molecule (Fig. 2, inset) are shown in Fig. 2 C. As described in Materials and Methods, these spectra were constructed from calculated stick spectra that were convolved with a Gaussian function of 4 cm−1 bandwidth, as described previously (30). The calculated spectra in Fig. 2 C are very similar to the experimental spectra in Fig. 2 B. Calculated 18O labeling induced downshifts of the three most intense bands are 28, 7, and 3 cm−1 (Table 1 and Fig. 2 C). These calculations agree extremely well with experimental observations (Fig. 2 B) (notice that in the simple harmonic oscillator approximation, a C=O mode at 1662 cm−1 is predicted to downshift 40 cm−1 on 18O labeling, rather than 28 cm−1). For better comparison of the calculated and experimental spectra, the frequency axis of the calculated spectra in Fig. 2 C was scaled by a factor of 0.965. As pointed out above, however, the actual scaling factor is unimportant. We are specifically interested in isotope induced frequency shifts and anion minus neutral frequency shifts, and these shifts are accurately calculated without scaling. For the unlabeled PhQ spectrum in Fig. 2 C the 1661 cm−1 band is due to the combined antisymmetric vibration of the C1=O and C4=O groups. The calculated 1661 cm−1 mode has an intensity of 369 km/mol (stick intensity) (30). On 18O labeling the C=O vibrations uncouple. Both have about the same frequency (1632 cm−1) with the C1=O/C4=O mode having an intensity of 183/119 km/mol, respectively. The combined intensity is 302 km/mol, which is an 18% intensity decrease for the original combined antisymmetric C=O vibration (Table 1).
TABLE 1.
Mode frequencies and intensities and their assignments for unlabeled (16O) and 18O-labeled PhQ and PhQ−
| PhQ
| ||||||
|---|---|---|---|---|---|---|
|
16O
|
18O
|
Δν (cm−1)
|
ΔI (%)
|
|||
| Mode | Observed ν (cm−1)* | Observed* | Calculated† | Observed* (%) | Calculated† (%) | |
| ν(C=O) | 1662 | 1634 | −28 | −29 | −24 | −18 |
| ν(C=C)q | 1619 | 1611 | −8 | −7 | +18 | +17 |
| ν(C=C)a | 1597 | 1593 | −4 | −3 | +58 | +70 |
| PhQ−
| ||||||
|
16O
|
18O
|
Δν (cm−1)
|
ΔI (%)
|
|||
| Mode
|
Calculated ν (intensity)
|
Observed‡
|
Calculated
|
Observed
|
Calculated
|
|
| ν(C⋯C)q | 1502 (31) | 1500 (31) | −2 | 0 | ||
| ν(C⋯O) | 1480 (395) | 1466 (265) | −15 | −14 | −33 | |
| ν(C⋯C)a | 1431 (46) | 1428 (48) | −3 | +4 | ||
Mode frequencies have been scaled by 0.965. The subscripts a and q refer to the aromatic and quinonic part of the naphthoquinone ring. Some of the mode intensities (from stick spectra) are shown in parenthesis in units of km/mol.
Estimated from the data in Fig. 2 B.
See Fig. 2 C and text.
From Bauscher and Mantele (34), the actual data is for ubiquinone-10.
The calculations outlined in Fig. 2 C predict that the antisymmetric C=O mode of PhQ will decrease in intensity (by ∼18%), whereas the quinonic and aromatic C=C modes of PhQ will increase in intensity by 17% and 70% on 18O labeling, respectively (Table 1). From the spectra in Fig. 2 B we see that the antisymmetric C=O mode intensity decreases by ∼24% while the quinonic and aromatic C=C modes increase in intensity by ∼18% and ∼58%. Clearly, our gas phase calculations reproduce well the experimentally observed isotope induced band intensity changes for PhQ in THF (Table 1, this is also obvious from comparison of the spectra in Fig. 2, B and C). In particular, our calculations predict opposite isotope-induced intensity changes for the C=O and C=C modes of neutral PhQ. This prediction could be of high diagnostic value. Why there are opposite changes in intensity of different modes is not a trivial question. It should be pointed out, however, that we are considering complex vibrations of several atoms (all atoms in the molecule contribute to each mode to some degree), and assigning this complex vibration to a single molecular group that contributes most (30). In addition, the actual mode composition for any mode in the unlabeled and labeled calculations is not identical. Clearly, normal mode analysis of complex molecules is considerably more sophisticated than the consideration of a set of isolated group frequencies, which is how we try to summarize the data.
The calculated spectra in Fig. 2 C describe the experimental data for PhQ in solution very well. However, Fig. 1 suggests asymmetry in the H-bonding environment of the C=O groups of PhQ in the A1 binding site in PS1. Such an asymmetry has also been suggested from magnetic resonance experiments (22). In an attempt to model this asymmetric environment we have calculated the vibrational properties of the quinone-amino acid model system shown in the inset in Fig. 3. In this model the peptide backbone NH group of a truncated leucine residue is H-bonded to the C4=O group of PhQ. The H-atom is 2.15 Å from the carbonyl oxygen atom. The calculated unlabeled spectrum in Fig. 3 shows that the neutral state C=O vibrations are no longer asymmetrically coupled, but are separated with the non H-bonded C1=O vibration being 20 cm−1 higher in frequency (Table 2). On 18O labeling the C1=O mode downshifts 29 cm−1 and decreases in intensity by 41%. On 18O labeling the C4=O mode downshifts 22 cm−1 and increases in intensity by 11% (Table 2).
FIGURE 3.
Calculated IR spectra obtained from DFT calculations using PhQ model shown in the inset, with the C4=O H-bonded to the NH group of the peptide backbone of a truncated leucine residue. As in Fig. 2, frequencies have been scaled by 0.965 cm−1. Part of the IUPAC numbering scheme of PhQ is also shown in the inset. Intensity scale is km/mol.
TABLE 2.
Calculated harmonic vibrational mode frequencies (scaled by 0.965) and intensities with their assignments for the unlabeled (16O) and 18O-labeled PhQ and PhQ− (in the presence of a peptide group that can H-bond to the C4=O group)
| PhQ + Leu
| ||||||
|---|---|---|---|---|---|---|
|
16O
|
18O
|
Frequency shift Δν (cm−1)
|
ΔI (%)
|
|||
| Mode | Calculated frequency (intensity) | Observed* | Calculated | Observed* | Calculated† | |
| ν(C1=O) | 1660 (259) | 1631 (153) | −28 | −29 | −24 | −41 |
| ν(C4=O) | 1640 (176) | 1618 (195) | −28 | −22 | −24 | +11 |
| ν(C=C)q | 1602 (47) | 1595 (60) | −8 | −7 | +18 | +27 |
| ν(C=C)a | 1576 (103) | 1572 (171) | −4 | −4 | +58 | +66 |
| PhQ− + Leu
| ||||||
|
16O
|
18O
|
Δν (cm−1)
|
ΔI (%)
|
|||
| Mode
|
Calculated ν (I)
|
Observed‡
|
Calculated§
|
Observed
|
Calculated§
|
|
| ν(C⋯C)q | 1505 (19) | 1500 (21) | −5 | +10 | ||
| ν(C⋯O) | 1482 (408) | 1467 (268) | −15 | −15 | −34 | |
Calculated IR spectra for labeled and unlabeled PhQ−
IR absorption spectra for one electron reduced PhQ (PhQ−) in solution have not been reported. Calculation of such spectra is straightforward, however, and Fig. 4 A shows calculated IR spectra obtained for PhQ− that is unlabeled and 18O labeled (insets show the model molecule). The highest intensity band at 1480 cm−1 in the unlabeled spectrum is due to the antisymmetric stretching of both semiquinone carbonyl (C⋯O) groups of PhQ−. On 18O labeling the C⋯O mode of PhQ− downshifts 14 cm−1 (Fig. 4 A and Table 1). This is half that calculated for the neutral state (28 cm−1). Experimental data are not available to test this prediction concerning the 18O-induced downshift of the C⋯O mode of PhQ−. However, for neutral ubiquinone-10, the antisymmetric C=O mode was found to downshift 30 cm−1 On 18O labeling, whereas for the ubiquinone-10 anion, the same mode was found to downshift only 15 cm−1 on 18O labeling (34) (Table 1). Our calculated results therefore agree well with these experimental data for ubiquinone-10. What was not reported in these (electrochemical) experiments (34) was how the C⋯O band of the ubiquinone-10 anion changed in intensity on 18O labeling. Vibrational mode frequencies and intensities, their assignments, and how the frequencies and intensities are modified on 18O labeling for PhQ− are outlined in Table 1 (bottom). Table 1 shows that the C⋯O mode of PhQ− decreases in intensity (by 33%) on 18O labeling.
FIGURE 4.
(A) Calculated IR spectra for unlabeled (16O) (dotted) and 18O-labeled (solid) PhQ−. (B) Calculated IR spectra for unlabeled (16O) (dotted) and 18O-labeled PhQ− (solid) in the presence of a truncated leucine residue. The one electron reduced form of the molecular models shown in the insets were used. Calculated frequencies have been scaled by a factor of 0.965. The calculated (18O–16O) double difference spectra for both molecular models (with or without H-bond) are also shown (middle). The central idea is that the band at 1480–1482 cm−1 in the unlabeled spectra corresponds to the band at ∼1495 cm−1 in the unlabeled experimental spectrum in Fig. 5 below. In addition, the band at 1466–1467 cm−1 in the calculated 18O-labeled spectra corresponds to the band at ∼1480 cm−1 in the 18O-labeled experimental spectrum in Fig. 5 (or Fig. 6).
The other bands in the spectra in Fig. 4 A correspond to very complicated vibrations, involving many molecular groups. The band near 1430 cm−1 in both the 16O and 18O spectrum of PhQ− is due to C⋯C stretching modes of both rings of PhQ, coupled to C-H bending modes of the aromatic part of the PhQ ring. This 1430 cm−1 mode involves very little C⋯O stretching. As would then be expected, the 1430 cm−1 band shifts little on 18O labeling. The band near 1419 cm−1 in the 16O spectrum of PhQ− downshifts 5 cm−1, and increases in intensity by ∼45% on 18O labeling. The band near 1419 cm−1 in the 16O spectrum of PhQ− is due to C⋯C stretching modes of both rings of PhQ, coupled to C-H bending and CH2 wagging modes. In addition a significant contribution to the 1419 cm−1 band comes from the antisymmetric vibration of both C⋯O groups of PhQ.
Fig. 4 B shows calculated IR spectra obtained for PhQ− that is unlabeled and 18O labeled, in the presence of leucine residue that can H-bond via the peptide backbone. The band at 1482 cm−1 in the unlabeled spectrum is due to the antisymmetric stretching of both C=O groups of PhQ−. On 18O labeling the C⋯O mode of PhQ− downshifts 15 cm−1 (Fig. 4 B and Table 2, bottom), and decreases in intensity by ∼34%. This is virtually the same as the 18O-induced changes that occur for the same mode in the PhQ model that is not H-bonded. Unlike the situation found for the neutral state, asymmetric H-bonding does not uncouple the two C=O modes in the anion state, and only a single high intensity antisymmetric vibration of both C=O groups is found for the anion state.
In the unlabeled spectrum in Fig. 4 B an intense band is found near 1417 cm−1 (there are actually two bands close in frequency that are both due to quite similar modes) that downshifts ∼6 cm−1 on 18O labeling. This band corresponds roughly to the band at 1419 cm−1 found in Fig. 4 A.
A1−/A1 FTIR difference spectra for PS1 particles containing labeled and unlabeled PhQ
Fig. 5 shows 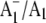 FTIR DS obtained using menB mutant PS1 particles that have been reconstituted with unlabeled (A, solid line) and 18O-labeled (B, dotted line) PhQ. The spectrum for PS1 particles containing unlabeled PhQ is very similar to that obtained using regular wild-type PS1 particles (20), indicating that PhQ is reconstituted into nearly all of the PS1 reaction centers. Using unreconstituted menB PS1 particles, we showed previously that when the A1 binding site is empty a time-resolved 3P700 FTIR DS is obtained (20). This 3P700 spectrum is very different from the time-resolved spectrum obtained when PhQ has been reconstituted. For example, the triplet spectrum displays an intense difference band that is negative at 1635 cm−1 and positive at 1595 cm−1. For PhQ reconstituted particles no such difference band is observed in the time-resolved spectrum. Rather, it was shown that the regular
FTIR DS obtained using menB mutant PS1 particles that have been reconstituted with unlabeled (A, solid line) and 18O-labeled (B, dotted line) PhQ. The spectrum for PS1 particles containing unlabeled PhQ is very similar to that obtained using regular wild-type PS1 particles (20), indicating that PhQ is reconstituted into nearly all of the PS1 reaction centers. Using unreconstituted menB PS1 particles, we showed previously that when the A1 binding site is empty a time-resolved 3P700 FTIR DS is obtained (20). This 3P700 spectrum is very different from the time-resolved spectrum obtained when PhQ has been reconstituted. For example, the triplet spectrum displays an intense difference band that is negative at 1635 cm−1 and positive at 1595 cm−1. For PhQ reconstituted particles no such difference band is observed in the time-resolved spectrum. Rather, it was shown that the regular 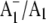 FTIR DS was recovered, with bands of similar intensity to that found using wild-type PS1 particles, when PhQ was added to menB PS1 particles (20). From these observations we concluded that PhQ is reincorporated back into menB PS1 at a very high level.
FTIR DS was recovered, with bands of similar intensity to that found using wild-type PS1 particles, when PhQ was added to menB PS1 particles (20). From these observations we concluded that PhQ is reincorporated back into menB PS1 at a very high level.
FIGURE 5.
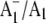 FTIR DS obtained using menB mutant PS1 particles reconstituted with (A) unlabeled (16O) (solid) and (B) 18O-labeled (dotted) PhQ. (C) (18O–16O) FTIR double difference spectrum. (D) Time-resolved spectrum collected before the laser flash (for the sample containing 18O-labeled PhQ). Spectrum D is the average of 9 spectra collected in 5 μs increments before the laser flash. It was collected in a manner identical to that described previously (11), and gives a measure of the noise level in the experiment. The spectra in A/B are the average of three/two measurements on different samples, respectively. Spectrum E/F shows the SD of the three/two spectra used to obtain spectra A/B, respectively. These SD spectra give a true measure of the noise in the FTIR DS.
FTIR DS obtained using menB mutant PS1 particles reconstituted with (A) unlabeled (16O) (solid) and (B) 18O-labeled (dotted) PhQ. (C) (18O–16O) FTIR double difference spectrum. (D) Time-resolved spectrum collected before the laser flash (for the sample containing 18O-labeled PhQ). Spectrum D is the average of 9 spectra collected in 5 μs increments before the laser flash. It was collected in a manner identical to that described previously (11), and gives a measure of the noise level in the experiment. The spectra in A/B are the average of three/two measurements on different samples, respectively. Spectrum E/F shows the SD of the three/two spectra used to obtain spectra A/B, respectively. These SD spectra give a true measure of the noise in the FTIR DS.
Furthermore, in unreconstituted menB PS1 particles, plastoquinone-9 (PQ9) occupies the A1 binding site in a portion of the particles (20). We showed that on  formation a band is observed at 1487 cm−1. On PhQ− formation a similar band is observed at 1495 cm−1 (20). When PhQ is reconstituted into PS1 we observe no band at 1487 cm−1, indicating that PhQ has displaced PQ9.
formation a band is observed at 1487 cm−1. On PhQ− formation a similar band is observed at 1495 cm−1 (20). When PhQ is reconstituted into PS1 we observe no band at 1487 cm−1, indicating that PhQ has displaced PQ9.
It is difficult to quantitate precisely the level of reincorporation of PhQ back into menB PS1 from the 3P700 triplet bands or the PhQ and PQ9 anion bands. However, from magnetic spectroscopy experiments on PhQ reconstituted menB PS1 particles, it was shown that PhQ was reincorporated into at least 95% of the particles, this limit being set by the noise level in the experiment (22). Our FTIR data do not seem to disagree with this result, as we cannot detect any light induced 3P700 state or  states in PhQ reconstituted PS1 particles.
states in PhQ reconstituted PS1 particles.
The (18O–16O) FTIR double difference spectrum (DDS) is shown in Fig. 5 C, and was obtained by subtracting the spectrum in Fig. 5 B from the spectrum in Fig. 5 A. The (18O–16O) FTIR DDS below ∼1500 cm−1 should be compared to the calculated DDS in Fig. 4. Both spectra in Fig. 5, A and B have had a static (P700+–P700) FTIR DS subtracted (the procedures for production of 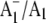 FTIR DS here are identical to that described previously (11)). However, by directly subtracting the time-resolved spectra obtained using 18O- and 16O-labeled particles, an (18O–16O) FTIR DDS can also be obtained. Such a DDS is virtually identical to that shown in Fig. 5 C (a comparison of the FTIR DDS obtained using both approaches is shown in Data S1). This indicates that (P700+–P700) FTIR DS obtained using PS1 with labeled and unlabeled PhQ incorporated are essentially the same. This comparison also removes any doubt concerning the validity of subtracting a static spectrum (relaxed species) from a time-resolved spectrum (unrelaxed species).
FTIR DS here are identical to that described previously (11)). However, by directly subtracting the time-resolved spectra obtained using 18O- and 16O-labeled particles, an (18O–16O) FTIR DDS can also be obtained. Such a DDS is virtually identical to that shown in Fig. 5 C (a comparison of the FTIR DDS obtained using both approaches is shown in Data S1). This indicates that (P700+–P700) FTIR DS obtained using PS1 with labeled and unlabeled PhQ incorporated are essentially the same. This comparison also removes any doubt concerning the validity of subtracting a static spectrum (relaxed species) from a time-resolved spectrum (unrelaxed species).
Fig. 5 D shows a time-resolved spectrum collected before the laser flash for samples containing 18O-labeled PhQ. The spectrum in Fig. 5 D is the average of 9 spectra collected in 5-μs increments before the laser flash. This spectrum gives one measure of the noise level in the experiment. A better measure of spectral variability is to consider the standard deviation (SD) spectrum, which can be calculated from the spectra obtained in independent measurements. We have reconstituted PhQ into three different batches of menB PS1 particles. Fig. 5 A shows the average of three spectra obtained from experiments on each PS1 sample. The SD of the three spectra is shown in Fig. 5 E. Similarly, we have reconstituted 18O-labeled PhQ into two different batches of menB PS1 particles, and spectrum B in Fig. 5 is the average of two spectra. The SD of the two spectra is shown in Fig. 5 F.
Above ∼1660 cm−1 the two spectra in Fig. 5, A and B are virtually identical, with no significant frequency shifts or intensity changes. This indicates that none of the difference bands above 1660 cm−1 are likely to be associated with modes of PhQ.
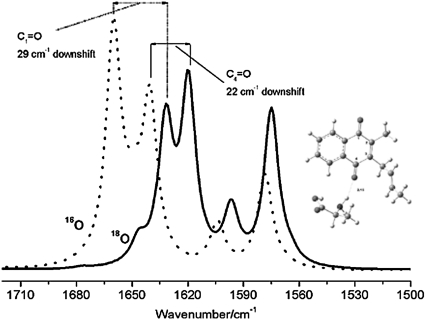
There are two prominent differences between the spectra in Fig. 5, A and B. First, on 18O labeling, a negative band near 1654 cm−1 decreases in intensity whereas a negative band near 1626 cm−1 increases in intensity. This gives rise to the 1654(+)/1626(−) cm−1 feature in the (18O–16O) FTIR DDS. Second, a positive band at 1494 cm−1 decreases in intensity on 18O labeling, whereas a new positive band appears at 1480 cm−1. This gives rise to the 1494(−)/1480(+) cm−1 feature in the (18O–16O) FTIR DDS.
A negative band near 1552 cm−1 seems to increase in intensity on 18O labeling. However, the considerable noise in Fig. 5 F in the 1550 cm−1 region indicates that this latter feature is probably artifactual. Based on this, we will not discuss this feature further.
Importantly, for the two sets of 18O-induced features discussed above, in either the FTIR DS or DDS, the magnitude of the isotope induced changes in the spectra, as shown in Fig. 5, A–C, are all larger than the features found in the noise level spectra in Fig. 5, D–F. To emphasize this point further, an expanded view of the spectra in Fig. 5, in the 1505–1470 cm−1 region, is shown in Fig. 6. The estimated experimental error in the experiment in the 1505–1470 cm−1 region is ∼ ±1.5 × 10−5, which is considerably below the amplitude of the lowest intensity band discussed. Clearly, the difference bands are well resolved in our experiments.
FIGURE 6.
Same spectra as in Fig. 5 but on an expanded scale in the 1505–1470 cm−1 region. (Top) Unlabeled (solid line) and 18O-labeled (dotted line) 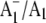 FTIR DS. (Middle) The three measures of the noise level (D–F). (Bottom) (18O–16O) FTIR double difference spectrum. The length of the four thick vertical bars represents absorption difference amplitudes. Clearly, the amplitude of the bands at 1494 and 1480 cm−1 in the 16O and 18O-labeled spectra, respectively, are at least a factor of two above all three measures of the noise level, and the derivative feature in the double difference spectrum is three to four times above the noise level.
FTIR DS. (Middle) The three measures of the noise level (D–F). (Bottom) (18O–16O) FTIR double difference spectrum. The length of the four thick vertical bars represents absorption difference amplitudes. Clearly, the amplitude of the bands at 1494 and 1480 cm−1 in the 16O and 18O-labeled spectra, respectively, are at least a factor of two above all three measures of the noise level, and the derivative feature in the double difference spectrum is three to four times above the noise level.
Origin of the 1494 cm−1 band in A1−/A1 FTIR DS
We have suggested previously that the positive band at 1494 cm−1 in 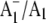 FTIR DS is due to a C⋯O mode of PhQ− (19). On 18O labeling we find that a large part of the 1494 cm−1 band is lost, leaving a residual band at ∼1493 cm−1. In addition, a new band appears at ∼1480 cm−1. The residual band at 1493 cm−1 could be due to unlabeled PhQ−. Remember that in our experiments only ∼70% of the PhQ oxygen atoms are 18O labeled. The band that appears at 1480 cm−1 is lower in intensity than the intensity that is lost at 1494 cm−1 (Fig. 6). From the calculations outlined in Fig. 4 and Tables 1 and 2, a C⋯O mode of PhQ− is predicted to downshift ∼14 cm−1, with a ∼33% decrease in intensity of the mode. This is independent of whether the C4=O mode is H-bonded. Within the noise level, our experiments support the hypothesis that the band appearing at 1480 cm−1 is ∼33% less intense than the band intensity lost at 1494 cm−1. Thus our calculations and specific isotope labeling data together both support the hypothesis that the 1494 cm−1 band is due to a C⋯O mode of PhQ−. More specifically, the 1494 cm−1 band is due to the antisymmetric vibration of both C=O groups. Most of the other bands in the 1520–1400 cm−1 region in Fig. 5, A and B are near the noise level (as quantified by the spectra in Fig. 5 F), and should therefore not be interpreted.
FTIR DS is due to a C⋯O mode of PhQ− (19). On 18O labeling we find that a large part of the 1494 cm−1 band is lost, leaving a residual band at ∼1493 cm−1. In addition, a new band appears at ∼1480 cm−1. The residual band at 1493 cm−1 could be due to unlabeled PhQ−. Remember that in our experiments only ∼70% of the PhQ oxygen atoms are 18O labeled. The band that appears at 1480 cm−1 is lower in intensity than the intensity that is lost at 1494 cm−1 (Fig. 6). From the calculations outlined in Fig. 4 and Tables 1 and 2, a C⋯O mode of PhQ− is predicted to downshift ∼14 cm−1, with a ∼33% decrease in intensity of the mode. This is independent of whether the C4=O mode is H-bonded. Within the noise level, our experiments support the hypothesis that the band appearing at 1480 cm−1 is ∼33% less intense than the band intensity lost at 1494 cm−1. Thus our calculations and specific isotope labeling data together both support the hypothesis that the 1494 cm−1 band is due to a C⋯O mode of PhQ−. More specifically, the 1494 cm−1 band is due to the antisymmetric vibration of both C=O groups. Most of the other bands in the 1520–1400 cm−1 region in Fig. 5, A and B are near the noise level (as quantified by the spectra in Fig. 5 F), and should therefore not be interpreted.
Bands due to C=O modes of PhQ in A1−/A1 FTIR DS?
We have suggested previously that the negative band near 1654 cm−1 in 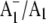 FTIR DS contains contributions from a C=O mode of PhQ (11). On 18O labeling we find that part of the 1654 cm−1 band disappears. In addition, there seems to be an increase in intensity of a band near 1626 cm−1. We propose that the negative feature at 1654 cm−1 is due to a C=O mode of neutral PhQ occupying the A1 binding site in menB reconstituted PS1 particles. On 18O labeling the band that is left at 1654 cm−1 could be due to the portion of PhQ molecules that are unlabeled (as only 70% of the PhQ oxygen atoms are labeled), as well as other species. Because a new negative feature appears near 1626 cm−1 in the spectrum for the 18O-labeled samples we suggest that this band is due to a C=O mode of 18O-labeled PhQ. The C=O mode therefore downshifts ∼28 cm−1 on 18O labeling. Such a downshift is exactly as our calculations predict for the antisymmetric C=O vibration of a PhQ molecule that is free from H-bonding (Fig. 2 C and Table 1). In the (18O–16O) FTIR DDS in Fig. 5 C it seems that the positive 1654 cm−1 band is slightly more intense than the negative 1626 cm−1 band. This suggests a small isotope induced intensity decrease in bands associated with C=O modes. Such an observation is in agreement with the calculated data, although it is difficult to quantify the experimental spectra directly. The calculated spectra for non H-bonded PhQ in Fig. 2 C suggest an intensity decrease of ∼18% (Table 1). The calculated spectra for H-bonded PhQ in Fig. 3 also suggest an overall isotope induced intensity decrease of bands associated with the C=O modes. However, in this latter case, the decrease is more difficult to specify because there are two C=O modes at different frequencies (Table 2); one increases in intensity by 11% whereas the other decreases in intensity by 41% (Table 2). In Fig. 3, the overall trend is clearly an overall isotope induced loss in intensity of bands associated with the C=O modes. Such a calculated result is at least compatible with the isotope induced intensity decrease recognized in Fig. 5 C.
FTIR DS contains contributions from a C=O mode of PhQ (11). On 18O labeling we find that part of the 1654 cm−1 band disappears. In addition, there seems to be an increase in intensity of a band near 1626 cm−1. We propose that the negative feature at 1654 cm−1 is due to a C=O mode of neutral PhQ occupying the A1 binding site in menB reconstituted PS1 particles. On 18O labeling the band that is left at 1654 cm−1 could be due to the portion of PhQ molecules that are unlabeled (as only 70% of the PhQ oxygen atoms are labeled), as well as other species. Because a new negative feature appears near 1626 cm−1 in the spectrum for the 18O-labeled samples we suggest that this band is due to a C=O mode of 18O-labeled PhQ. The C=O mode therefore downshifts ∼28 cm−1 on 18O labeling. Such a downshift is exactly as our calculations predict for the antisymmetric C=O vibration of a PhQ molecule that is free from H-bonding (Fig. 2 C and Table 1). In the (18O–16O) FTIR DDS in Fig. 5 C it seems that the positive 1654 cm−1 band is slightly more intense than the negative 1626 cm−1 band. This suggests a small isotope induced intensity decrease in bands associated with C=O modes. Such an observation is in agreement with the calculated data, although it is difficult to quantify the experimental spectra directly. The calculated spectra for non H-bonded PhQ in Fig. 2 C suggest an intensity decrease of ∼18% (Table 1). The calculated spectra for H-bonded PhQ in Fig. 3 also suggest an overall isotope induced intensity decrease of bands associated with the C=O modes. However, in this latter case, the decrease is more difficult to specify because there are two C=O modes at different frequencies (Table 2); one increases in intensity by 11% whereas the other decreases in intensity by 41% (Table 2). In Fig. 3, the overall trend is clearly an overall isotope induced loss in intensity of bands associated with the C=O modes. Such a calculated result is at least compatible with the isotope induced intensity decrease recognized in Fig. 5 C.
For a PhQ molecule that is asymmetrically H-bonded our calculations predict that the non H-bonded C1=O mode will downshift 29 cm−1 on anion formation (Fig. 3 and Table 2), and decrease in intensity. In this case, we suggest that the 1654 cm−1 feature in the unlabeled spectrum in Fig. 2 A is due to the C1=O mode of PhQ, which downshifts ∼28 cm−1 on 18O labeling. Furthermore, our calculations suggest that the C4=O mode should absorb ∼20 cm−1 lower in frequency (near 1634 cm−1), and downshift ∼22 cm−1 (to near 1612 cm−1) on anion formation. Although a small negative feature is observed near 1612 cm−1 in Fig. 5 C we do not have sufficient sensitivity or spectral resolution to quantify this hypothesis further at this time. However, we have provided strong evidence supporting the hypothesis that a band at 1654 cm−1 in the unlabeled spectrum is due to a PhQ C=O mode, and that this mode is probably the higher intensity C1=O mode of an asymmetrically H-bonded PhQ molecule.
CONCLUSIONS
We have incorporated unlabeled and 18O-labeled PhQ back into the A1 binding site in menB mutant PS1 particles. Using these PS1 particles we have identified bands in 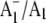 FTIR DS that are specifically impacted by the 18O label. Coupling this experimental work with density functional based vibrational mode frequency calculations of unlabeled and labeled PhQ model molecules allowed the unambiguous identification of bands in the difference spectra that are associated with the C=O modes of neutral and reduced PhQ that occupies the A1 binding site in PS1. Specifically, a C1=O mode of neutral PhQ occurs at 1654 cm−1. The C4=O mode is not well resolved. On anion formation the C=O modes of PhQ are no longer separate, and a distinct mode due to the antisymmetric vibration of both C=O groups is found at 1494 cm−1.
FTIR DS that are specifically impacted by the 18O label. Coupling this experimental work with density functional based vibrational mode frequency calculations of unlabeled and labeled PhQ model molecules allowed the unambiguous identification of bands in the difference spectra that are associated with the C=O modes of neutral and reduced PhQ that occupies the A1 binding site in PS1. Specifically, a C1=O mode of neutral PhQ occurs at 1654 cm−1. The C4=O mode is not well resolved. On anion formation the C=O modes of PhQ are no longer separate, and a distinct mode due to the antisymmetric vibration of both C=O groups is found at 1494 cm−1.
SUPPLEMENTARY MATERIAL
To view all of the supplemental files associated with this article, visit www.biophysj.org.
Supplementary Material
Acknowledgments
This work was supported by the National Research Initiative of the U.S. Department of Agriculture Cooperative State Research Education and Extension Service (2004-35318-14889) to G.H.
Editor: Edward H. Egelman.
References
- 1.Barber, J. 1992. The Photosystems: Structure, Function, and Molecular Biology. Elsevier Science, Amsterdam.
- 2.Walker, D. 1993. Energy, Plants and Man. Oxygraphics, Mill Valley, CA.
- 3.Ke, B. 2001. Photosynthesis: Photobiochemistry and Photobiophysics. Kluwer Academic Publishers, Boston, MA.
- 4.Golbeck, J. 2006. Photosystem I The Light Driven Plastocyanin:Ferridoxin Oxidoreductase. Springer, Dordrecht, The Netherlands.
- 5.Golbeck, J. H., and D. Bryant. 1991. Photosystem I. In Current Topics in Bioenergetics. Academic Press, New York. 83–175.
- 6.Itoh, S., M. Iwaki, and I. Ikegami. 2001. Modification of photosystem I reaction center by the extraction and exchange of chlorophylls and quinones. Biochim. Biophys. Acta. 1507:115–138. [DOI] [PubMed] [Google Scholar]
- 7.Semenov, A. Y., I. R. Vassiliev, A. van Der Est, M. D. Mamedov, B. Zybailov, G. Shen, D. Stehlik, B. A. Diner, P. R. Chitnis, and J. H. Golbeck. 2000. Recruitment of a foreign quinone into the A1 site of photosystem I. Altered kinetics of electron transfer in phylloquinone biosynthetic pathway mutants studied by time-resolved optical, EPR, and electrometric techniques. J. Biol. Chem. 275:23429–23438. [DOI] [PubMed] [Google Scholar]
- 8.Vos, M., and H. van Gorkom. 1988. Thermodynamics of photosystem I studied by electric field stimulated charge recombination. Biochim. Biophys. Acta. 934:293–302. [Google Scholar]
- 9.Jordan, P., P. Fromme, H. T. Witt, O. Klukas, W. Saenger, and N. Krauss. 2001. Three-dimensional structure of cyanobacterial photosystem I at 2.5 angstrom resolution. Nature. 411:909–917. [DOI] [PubMed] [Google Scholar]
- 10.Fromme, P., P. Jordan, and N. Krauss. 2001. Structure of photosystem I. Biochim. Biophys. Acta. 1507:5–31. [DOI] [PubMed] [Google Scholar]
- 11.Sivakumar, V., R. Wang, and G. Hastings. 2005. A1 reduction in intact cyanobacterial photosystem I particles studied by time-resolved step-scan Fourier transform infrared difference spectroscopy and isotope labeling. Biochemistry. 44:1880–1893. [DOI] [PubMed] [Google Scholar]
- 12.Mäntele, W. 1993. Infrared vibrational spectroscopy of photosynthetic reaction centers. In The Photosynthetic Reaction Center. J. Deisenhofer and J. Norris, editors. Academic Press, San Diego, CA. 239–283.
- 13.Mäntele, W. 1995. Infrared vibrational spectroscopy of reaction centers. In Anoxygenic Photosynthetic Bacteria. R. E. Blankenship, M. T. Madigan, and C. E. Bauer, editors. Kluwer Academic Publishers, Boston, MA. 627–647.
- 14.Nabedryk, E. 1996. Light-induced Fourier transform infrared difference spectroscopy of the primary electron donor in photosynthetic reaction centers. In Infrared Spectroscopy of Biomolecules. H. H. Mantsch and D. Chapman, editors. Wiley-Liss, New York. 39–81.
- 15.Hastings, G. 2006. FTIR studies of the intermediate electron acceptor A1. In Photosystem I: The Light Driven Plastocyanin:Ferredoxin Oxidoreductase. J. Golbeck, editor. Springer, Dordrecht, The Netherlands. 301–318.
- 16.Remy, A., and K. Gerwert. 2003. Coupling of light-induced electron transfer to proton uptake in photosynthesis. Nat. Struct. Biol. 10:637–644. [DOI] [PubMed] [Google Scholar]
-
17.Schlodder, E., K. Falkenberg, M. Gergeleit, and K. Brettel. 1998. Temperature dependence of forward and reverse electron transfer from
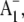 the reduced secondary electron acceptor in photosystem I. Biochemistry. 37:9466–9476. [DOI] [PubMed] [Google Scholar]
the reduced secondary electron acceptor in photosystem I. Biochemistry. 37:9466–9476. [DOI] [PubMed] [Google Scholar] - 18.Santabarbara, S., I. Kuprov, P. J. Hore, A. Casal, P. Heathcote, and M. C. Evans. 2006. Analysis of the spin-polarized electron spin echo of the [P700+ A1-] radical pair of photosystem I indicates that both reaction center subunits are competent in electron transfer in cyanobacteria, green algae, and higher plants. Biochemistry. 45:7389–7403. [DOI] [PubMed] [Google Scholar]
- 19.Bandaranayake, K. M., R. Wang, and G. Hastings. 2006. Modification of the phylloquinone in the A1 binding site in photosystem I studied using time-resolved FTIR difference spectroscopy and density functional theory. Biochemistry. 45:4121–4127. [DOI] [PubMed] [Google Scholar]
- 20.Bandaranayake, K. M., R. Wang, T. W. Johnson, and G. Hastings. 2006. Time-resolved FTIR difference spectroscopy for the study of photosystem I particles with plastoquinone-9 occupying the A1 binding site. Biochemistry. 45:12733–12740. [DOI] [PubMed] [Google Scholar]
- 21.Johnson, T. W., G. Shen, B. Zybailov, D. Kolling, R. Reategui, S. Beauparlant, I. R. Vassiliev, D. A. Bryant, A. D. Jones, J. H. Golbeck, and P. R. Chitnis. 2000. Recruitment of a foreign quinone into the A1 site of photosystem I. I. Genetic and physiological characterization of phylloquinone biosynthetic pathway mutants in Synechocystis sp. pcc 6803. J. Biol. Chem. 275:8523–8530. [DOI] [PubMed] [Google Scholar]
- 22.Pushkar, Y. N., J. H. Golbeck, D. Stehlik, and H. Zimmermann. 2004. Asymmetric hydrogen-bonding of the quinone cofactor in photosystem I probed by C-13-labeled naphthoquinones. J. Phys. Chem. B. 108:9439–9448. [Google Scholar]
- 23.Breton, J., C. Boullais, J. R. Burie, E. Nabedryk, and C. Mioskowski. 1994. Binding sites of quinones in photosynthetic bacterial reaction centers investigated by light-induced FTIR difference spectroscopy: assignment of the interactions of each carbonyl of QA in Rhodobacter sphaeroides using site-specific 13C-labeled ubiquinone. Biochemistry. 33:14378–14386. [DOI] [PubMed] [Google Scholar]
- 24.Brudler, R., H. J. de Groot, W. B. van Liemt, W. F. Steggerda, R. Esmeijer, P. Gast, A. J. Hoff, J. Lugtenburg, and K. Gerwert. 1994. Asymmetric binding of the 1- and 4-C=O groups of QA in Rhodobacter sphaeroides R26 reaction centres monitored by Fourier transform infra-red spectroscopy using site-specific isotopically labeled ubiquinone-10. EMBO J. 13:5523–5530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Breton, J., J. R. Burie, C. Berthomieu, G. Berger, and E. Nabedryk. 1994. The binding sites of quinones in photosynthetic bacterial reaction centers investigated by light-induced FTIR difference spectroscopy: assignment of the QA vibrations in Rhodobacter sphaeroides using 18O- or 13C-labeled ubiquinone and vitamin K1. Biochemistry. 33:4953–4965. [DOI] [PubMed] [Google Scholar]
- 26.Brudler, R., H. J. de Groot, W. B. van Liemt, P. Gast, A. J. Hoff, J. Lugtenburg, and K. Gerwert. 1995. FTIR spectroscopy shows weak symmetric hydrogen bonding of the QB carbonyl groups in Rhodobacter sphaeroides R26 reaction centres. FEBS Lett. 370:88–92. [DOI] [PubMed] [Google Scholar]
- 27.Johnson, T. W., B. Zybailov, A. D. Jones, R. Bittl, S. Zech, D. Stehlik, J. H. Golbeck, and P. R. Chitnis. 2001. Recruitment of a foreign quinone into the A1 site of photosystem I. In vivo replacement of plastoquinone-9 by media-supplemented naphthoquinones in phylloquinone biosynthetic pathway mutants of Synechocystis sp. PCC 6803. J. Biol. Chem. 276:39512–39521. [DOI] [PubMed] [Google Scholar]
- 28.Wang, R., V. Sivakumar, T. W. Johnson, and G. Hastings. 2004. FTIR difference spectroscopy in combination with isotope labeling for identification of the carbonyl modes of P700 and P700+ in photosystem I. Biophys. J. 86:1061–1073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Frisch, M. J., G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, J. R. Cheeseman, J. J. A. Montgomery, T. Vreven, K. N. Kudin, J. C. Burant, J. M. Millam, S. S. Iyengar, J. Tomasi, V. Barone, B. Mennucci, M. Cossi, G. Scalmani, N. Rega, G. A. Petersson, H. Nakatsuji, M. Hada, M. Ehara, K. Toyota, R. Fukuda, J. Hasegawa, M. Ishida, T. Nakajima, Y. Honda, O. Kitao, H. Nakai, M. L. Klene, X., J. E. Knox, H. P. Hratchian, J. B. B. Cross, V. Adamo, C. Jaramillo, J. Gomperts, R. Stratmann, R. E. Yazyev, O. Austin, A. J. Cammi, R. Pomelli, C. Ochterski, J. W. Ayala, P. Y. Morokuma, K. Voth, G. A. Salvador, P. Dannenberg, J. J. Zakrzewski, V. G. Dapprich, S. Daniels, A. D. Strain, M. C. Farkas, O. Malick, D. K. Rabuck, A. D. Raghavachari, K. Foresman, J. B. Ortiz, J. V. Cui, Q. Baboul, A. G. Clifford, S. Cioslowski, J. Stefanov, B. B. Liu, G. Liashenko, A. Piskorz, P. Komaromi, I. Martin, R. L. Fox, D. J. Keith, T. Al-Laham, M. A. Peng, C. Y. Nanayakkara, A. Challacombe, M. Gill, P. M. W. Johnson, B. Chen, W. Wong, M. W. Gonzalez, C. and Pople, J. A. 2004. Gaussian 03, Revision C.02. Gaussian, Wallingford, CT.
- 30.Bandaranayake, K., V. Sivakumar, R. Wang, and G. Hastings. 2006. Modeling the A[1] binding site in photosystem. I. Density functional theory for the calculation of “anion - neutral” FTIR difference spectra of phylloquinone. Vib. Spectrosc. 42:78–87. [Google Scholar]
- 31.Foresman, J., and A. Frisch. 1996. Exploring Chemistry with Electronic Structure Methods, 2nd ed. Gaussian, Pittsburgh, PA.
- 32.Wang, R., S. Parameswaran, and G. Hastings. 2007. Density functional theory based calculations of the vibrational properties of chlorophyll-a. Vib. Spectrosc. 44:357–368. [Google Scholar]
- 33.Breton, J., J. R. Burie, C. Boullais, G. Berger, and E. Nabedryk. 1994. Binding sites of quinones in photosynthetic bacterial reaction centers investigated by light-induced FTIR difference spectroscopy: binding of chainless symmetrical quinones to the QA site of Rhodobacter sphaeroides. Biochemistry. 33:12405–12415. [DOI] [PubMed] [Google Scholar]
- 34.Bauscher, M., and W. Mantele. 1992. Electrochemical and infrared-spectroscopic characterization of redox reactions of p-quinones. J. Phys. Chem. 96:11101–11108. [Google Scholar]
- 35.Geux, N., and M. C. Peitsch. 1997. SWISS-MODEL and the Swiss-PDBViewer: an environment for comparative protein modeling. Electrophoresis. 18:2714–2723. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.