Determination of ζ-Potential in Rat Organotypic Hippocampal Cultures

Abstract

ζ-potentials of entities such as cells and synaptosomes have been determined, but ζ of brain tissue has never been measured. Electroosmotic flow, and the resulting transport of neuroactive substances, would result from naturally occurring and experimentally or clinically induced electric fields if ζ is significant. We have developed a simple method for determining ζ in tissue. An electric field applied across a rat organotypic hippocampal slice culture (OHSC) drives fluorescent molecules through the tissue by both electroosmotic flow and electrophoresis. Fluorescence microscopy is used to determine each molecule's velocity. Independently, capillary electrophoresis is used to measure the molecules' electrophoretic mobilities. The experiment yields ζ-potential and average tissue tortuosity. The ζ-potential of OHSCs is −22 ± 2 mV, and the average tortuosity is 1.83 ± 0.06. In a refined experiment, ζ-potential is measured in various subregions. The ζ-potentials of the CA1 stratum pyramidale, CA3 stratum pyramidal, and dentate gyrus are −25.1 ± 1.6 mV, −20.3 ± 1.7 mV, and −25.4 ± 1.0 mV, respectively. Simple dimensional arguments show that electroosmotic flow is potentially as important as diffusion in molecular transport.

INTRODUCTION

An understanding of brain function, especially extracellular transport, requires a quantitative understanding of the physicochemical properties of the extracellular space. Diffusion in the extracellular space of the brain and slice preparations is fairly well understood. Nicholson (1,2) and Sykova (3) measured the transport of tetramethylammonium ion (TMA⁺) and polymers to reveal the details of extracellular diffusion. Other methods such as cortical surface photobleaching (4), magnetic resonance (5–8), integrative optical imaging (9), and dual-probe microdialysis (10,11) have been used to evaluate the diffusive transport of markers and biomolecules as well as water in living brain tissue. A detailed understanding of variations in diffusion caused by changes in the extracellular volume fraction has led to applications of these techniques in assessing, e.g., edema (4). The dimensions of the intercellular space have been determined by measuring particle diffusion rates (12). Tortuosity has a large effect on transport rates in heterogeneous media. Tortuosities vary depending on the local geometry of the tissue (13,14). In addition, certain brain regions are anisotropic (15), leading to a valuable method in magnetic resonance imaging called “diffusion tensor imaging” (5,8). We conclude that there is a rather firm understanding of diffusive transport in the brain, which is critical for understanding extrasynaptic (paracrine or volume) transmission (16,17) and neuronal development (18) as well as for making inferences from measurements (19,20).

On the other hand, there is less known about electrically mediated transport in the brain. Electric fields and currents in heterogeneous media create a fluid flow, called electroosmotic (EO) flow, by virtue of the field's motivating force on the mobile counterions to fixed charges on surfaces or immobile macromolecules in the extracellular space. The fixed charges create a ζ-potential, the potential at the shear plane between a charged surface and a moving electrolyte solution (21). The magnitude of the ζ-potential controls the magnitude of the EO flow. The ζ-potential in brain tissue is a consequence of cell-surface functional groups, such as phospholipids, proteins, and carbohydrates, as well as fixed components of the extracellular matrix.

The focus of this work is to create and apply a method for the determination of the ζ-potential in nervous tissue. In the paragraphs below, we justify the need to understand this currently undetermined parameter of brain tissue and demonstrate how a method similar to electrophoresis can be used.

Certainly, electric fields occur naturally in brain. Recently, Savtchenko et al. showed how the electrical field created in the synapse during ion-channel opening can influence molecular transport in the synapse, normally viewed as occurring by diffusion (22). Several clinical techniques, such as transcranial direct current stimulation (23–26) and magnetic stimulation (27–30), also create electric fields in brain (31). These treatments are effective in depression (25,28), stroke (24), and other diseases. Electric fields are also used in seizure control (32). In research laboratories, electric fields are applied to brain tissue to direct neuronal growth (33), to perform iontophoresis in the brain (34), to carry out electroporation in brain (35) and embryos (36,37), and for transnasal delivery of a charged peptide (by an electric field created between the nasal cavity and the back of the head (38)). As far as we are aware, EO flow is largely overlooked in these endeavors.

EO flow and/or ζ-potential have been measured in some biologically relevant matrices by a variety of techniques. EO flow is knowingly created in transdermal iontophoresis (39–45). EO dewatering of tumors also depends on the existence of a ζ-potential within tissues (33,46). Outside the fields of transdermal iontophoresis and transdermal sampling (reverse iontophoresis (44,47)), measurements of ζ-potential, or EO mobility, are rare in biological systems. Values of ζ-potential have been reported for isolated cells using electrophoresis (48), microelectrophoresis (49), and microcapillary electrophoresis on a chip (50). Electrophoretic methods have also been applied to bone particles (51) as well as isolated nuclei (52), vesicles (53), and synaptosomes (54) from brain tissue. Measurements of transport through tissue, such as skin that can act as a film separating two liquid phases, are based on quantitative determination of the flux of a solute from a “source” phase to a “receiving” phase. Similarly, EO mobility in plant tissues (55) can be made this way. Alternative measurements using an oscillating electric potential (56) or scanning electrochemical microscopy on individual skin pores are also used (45). None of these methods is suited to whole brain, acute brain slices, or slice cultures.

At a more fundamental level, knowing the ζ-potential in intact tissue is vital to understanding molecular movement between cells. Electroosmosis has been proposed as a contributor to learning and memory (57). Even local electric fields, such as those that materialize during epileptic seizures, may generate fluid motion. In tissues other than brain, i.e., lung (58) and epithelial tissue (59), naturally occurring potential gradients are thought to drive fluid flow. A mathematical theory, including double layer overlap and coupling of mechanical and electrical forces, has been applied to glycogen-containing cartilage models (60).

We conclude that EO phenomena have been studied in tissues where it clearly must contribute to the observed phenomena, e.g., skin (iontophoretic drug delivery and sampling) and bone (stimulated bone growth). However, there is virtually no understanding qualitatively and certainly no understanding quantitatively of the ζ-potential in nervous tissue.

We have developed a method to measure EO mobility and thus ζ-potential as well as average tortuosity in organotypic slice cultures of the rat (61). The velocities of fluorescent molecules are measured in the cultured tissue under an applied field. Data analysis is guided by simple theory, shown below.

THEORY

Consider a set of fluorescent molecules with various electrophoretic mobilities. A spot consisting of a single fluorophore is placed in an OHSC. In an electric field, the fluorophore will move at an observed velocity, v_obs, as given in Eq. 1, which can be inferred from Boyack and Giddings (62) and Rathore et al. (63) (λ_e = tortuosity; v_eo = EO velocity; v_ep = electrophoretic velocity):

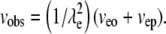(1)

We assume that v_eo and v_ep experience the same tortuosity. Note that the definition of tortuosity is consistent with Boyack and Giddings (62) and Rathore et al. (63). We denote that the tortuosity influences an electrokinetic process with the subscript “e”. This tortuosity may not be the same as the ratio of free and effective diffusion coefficients (see Discussion for more detail). Equations 2 and 3 (21,63) define the velocities as the products of mobilities, μ, and a field, E.

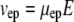(2)

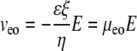(3)

Equation 3 shows that μ_eo is a function of ζ, the ζ-potential, the medium's viscosity (η), and permittivity (ɛ). Values of μ_ep can be determined for each fluorophore independently in HBSS by CE; thus they are known quantities. The observed mobility, μ_obs, can be defined as Eq. 4 for an individual fluorescent species. If the tortuosity is not dependent on the fluorophore, a plot of μ_obs versus μ_ep will yield a straight line with a slope of 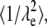where the brackets indicate “average”. The intercept provides μ_eo, and thus ζ.

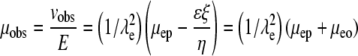(4)

Another approach involves the use of two molecules simultaneously (molecule 1 and molecule 2). Each molecule is independently described by Eq. 5. Thus the term 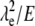can be eliminated, as shown in Eqs. 6 and 7 (subscripts 1 and 2 refer to individual molecules).

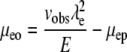(5)

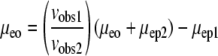(6)

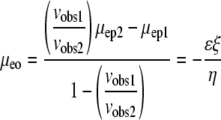(7)

MATERIALS AND METHODS

Chemicals and solutions

The following materials were purchased from Sigma (St. Louis, MO) and were used as received. The culture medium contained basal medium Eagle (50%), Earl's basal salt solution (20%), horse serum (23%), penicillin/streptomycin (25 units/ml), L-glutamine (1 mM), and D-(+)-glucose (7.5 g/L). The culture medium was stored in a refrigerator and warmed to 37°C before use. Gey's Balanced Salt solution (GBSS) was supplemented with 27.5 mM D-(+)-glucose and 2.7 mM MgSO₄. The following solutions were prepared with 18 MΩ purified water from a Millipore Synthesis A10 system (Millipore, Billerica, MA): NaOH solutions, HEPES-buffered salt solution (HBSS) containing (mM): 143.4 NaCl, 5 HEPES, 5.4 KCl, 1.2 MgSO₄, 1.2 NaH₂PO₄, 2.0 CaCl₂, and 10 D-(+)-glucose. HBSS was filtered, stored in a refrigerator, and warmed to 37°C before use. Approximately 3% agarose type-VII in HBSS filled the apparatus shown in Fig. 1.

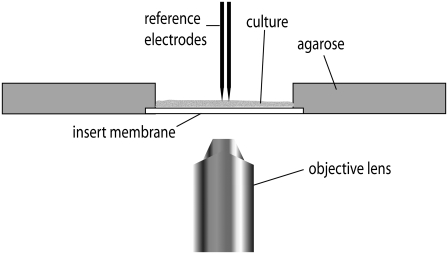
FIGURE 1.

The apparatus. The OHSC and its insert membrane are placed against the cast agarose gel. The apparatus is placed on an inverted fluorescence microscope for data acquisition. Reference electrodes measure the field strength near the fluorophore spots.

Each of the fluorescent molecules was diluted with HBSS, filtered, and frozen until use. The concentration of each probe was empirically determined to accommodate its intensity under experimental conditions. See Table S1 in Supplementary Material, Data S1 for the concentrations. Fluorescent dextran conjugates 1–6 were purchased from Invitrogen/Molecular Probes (Eugene, OR). 7 and 8 were obtained from Sigma (Table 1).

TABLE 1.

Values of μ_ep in HBSS

Fluorescent compound	μep/(10−9 m2/Vs)	Mean ± SE/(10−9 m2/Vs)
Alexa Fluor 568 dextran conjugate 10 kDa* (1)	−1.92	±0.15
BODIPY FL dextran conjugate 10 kDa* (2)	−0.89	±0.22
Fluorescein dextran conjugate 70 kDa* (3)	−9.75	±0.82
Oregon Green dextran conjugate 10 kDa* (4)	−18.0	±0.1
Rhodamine Green dextran conjugate 3 kDa* (5)	−1.72	±0.19
Texas Red dextran conjugate 70 kDa* (6)	−0.55	±0.19
Fluorescein sodium salt (7)	−26.3	±0.3
Tris(2,2′-bipyridine)ruthenium (8)	26.0	±0.0

^*Dextran conjugate.

Instrumentation

Capillary electrophoresis

Electrophoretic mobilities in HBSS were determined using an ISCO Capillary Electropherograph (Lincoln, NE) with vacuum injection (10 s, 0.5 psi) and ultraviolet-visible absorbance detection. A section of the polyimide coating was removed with a low-temperature flame to create the window. New capillaries were flushed with base overnight. Before each series of experiments, capillaries were flushed with 200 μL of distilled, deionized water, followed by the same volume of the running buffer. The high voltage was then applied to the capillary, and the system equilibrated for 5–20 min. All injections included rhodamine B as the EO flow marker and were performed at ambient temperature (23°C ± 2°C). The EO flow marker is a neutral molecule with a mobility equal to zero. Its velocity in a capillary electrophoresis (CE) experiment is the electroosmic velocity.

CE measurements of mobilities were performed using 360-μm outside diameter (OD) capillaries with inner diameters (IDs) of 40 or 50 μm. The total capillary length ranged from 50.3 to 118.4 cm, with 25.5–48.1 cm from the injection end to the detection window using −9.0 to −22.1 kV. Detection was at 495, 505, or 595 nm. See Table S2 for the parameters used for each particular molecule.

Apparatus for tissue experiments

The apparatus in Fig. 1 was manufactured from Lucite locally. A 40-V direct current power supply (Heath, Benton Harbor, MI) applies a low homogeneous field (∼22 V/cm at the tissue) across the organotypic hippocampal slice culture (OHSC). Two Goodfellow (Cambridge, England) tubular platinum electrodes (1 mm OD, 0.1 mm wall thickness, and ∼3.8 cm long) were placed into separate cylindrical reservoirs (19 mm in diameter and 12 mm deep) separated by a narrow rectangular channel 44 mm in length. These reservoirs are not shown in Fig. 1. The OHSC remained on the insert membrane during the measurements. Electrical contact between the OHSC and the electrodes was made by agarose-containing HBSS.

Ag/AgCl electrodes

A pair of in-house fabricated Ag/AgCl microelectrodes measured the potential gradient in the tissue. The electrodes were made from 0.1-mm-diameter silver wire from JMC (Hertfordshire, England). Two sets were made: one spaced 0.80–0.90 mm apart and another spaced 0.35–0.40 mm apart. Distances were determined using a scale bar and micrographic images of each individual experiment.

Injection capillary

A 250 μm (ID) fused-silica capillary was pulled to a tip (∼12 μm OD) using a P-2000 capillary puller from Sutter (Novato, CA). A Sutter MP-285 micromanipulator lowered the capillary into the OHSC. The distal end of the capillary was attached to a Harvard PHD 4400 Hpsi syringe pump (Holliston, MA) with a 50 μL Hamilton Gastight syringe (Reno, NV). The pump delivered fluid at a flow rate of 120 nL/min for ∼1 s.

Imaging

An inverted fluorescent microscope (Model IX71) with a U Plan Apo 4× objective lens (both from Olympus, Melville, NY) imaged the tissue experiment using a charge-coupled device camera (ORCA-285 Hamamatsu, Hamamatsu City, Japan). Depending on the fluorescent properties, an appropriate cube was chosen. The Olympus fluorescence cubes are a wide interference filter blue cube (exciter 460–495 nm, dichromatic mirror 505 nm, emitter 510–550 nm interference filter) and a wide interference filter green cube (exciter 530–550 nm, dichromatic mirror 570 nm, emitter 575 nm interference filter). A Semrock (Rochester, NY) DA/Fl/TA-3X-A Triple-band “Pinkel” filter set (exciter 1 387 nm, exciter 2 494 nm, exciter 3 575 nm, dichromatic mirror: 394–414 nm, 484–504 nm, 566–586 nm, emitter: 457, 530, 628 nm) was used for multiple fluorophore experiments.

Image processing and distance measurements were done with SimplePCI 6.0 software (Compix, Cranberry, PA). Images of the paired Ag/AgCl electrodes using the microscope camera were captured daily to measure the distance between the electrodes. The same was done for measuring IDs of new injection capillaries.

Procedures

Hippocampal organotypic slice cultures

The Stoppini culturing method was used with small variations (61). The procedures described here have been approved by the University of Pittsburgh IACUC. The hippocampi were dissected bilaterally from decapitated, 7-day postnatal Sprague-Dawley albino rats. The hippocampi were cut transversely into 500-μm-thick slices with a McIlwain tissue chopper from The Mickle Laboratory Engineering (Surrey, England). The cultures were placed on Millicell membrane inserts from Millipore and incubated over culture medium at 95% air/5% CO₂. Cultures may be incubated for up to 2 weeks. All data reported here are from cultures incubated for 3–7 days. The mean slice thickness in this time period was 148 μm, consistent with other reports (61,64,65). On the day of the experiment, 37°C GBSS replaced culture medium, followed by 30 min of tissue incubation. This procedure was repeated once more. Lastly, 37°C HBSS replaced GBSS before the experiment.

Using an X-Acto knife, the insert membrane was cut to liberate the tissue and the insert membrane under it from excess insert membrane. Edges of the insert were left to allow moving the OHSC into the apparatus without damage, as in Fig. 1. A portion of the agarose gel was cut away to make room for the OHSC. The OHSC was placed into the apparatus in such a way that the insert edges are under the agarose but the slice is adjacent to the gel, as show schematically in Fig. 1.

ζ-potential determination

The tip of the injection capillary, preloaded with fluorescent probe-containing solution at room temperature, was inserted approximately midway (∼75 μm) into the OHSC with the aid of a micromanipulator. The pump delivered ∼2 nL of the fluorescent material. On occasion, placing the capillary into tissue alone delivered enough fluorophore by capillary effects. The capillary was carefully pulled out of the slice, and the microelectrodes were placed in the tissue. Before the voltage supply is turned on, the exposure time is set using autoexposure and the SimplePCI 6.0 software begins recording the fluorescence. The voltage supply was switched on, applying ∼22 V/cm through the slice. Measurements of electric field and velocity are taken once the electric field stabilizes (a few seconds). Images were acquired once per second. Movement of a fluorophore toward the cathode is defined as positive.

Two-fluorophore experiments

Two sets of paired molecules were used. One set was 1 and 7, and the other set was 3 and 8. To measure the velocity of each fluorophore simultaneously, the “Pinkel” filter set was used. At first, each fluorophore is injected into an OHSC separately. The separate exposure times are set using the autoexposure command for a two-color image in the SimplePCI 6.0 software. A mixture of the paired fluorophores is then injected into a different OHSC for measurement.

RESULTS

Table 1 shows the CE-determined mobilities for each fluorophore. Fig. 2 shows images from an experiment in an OHSC. The OHSC received three injections, labeled A, B, and C. A and C are injections into the insert membrane, and B is in the OHSC. We find that fluorophore injected into the insert membrane is immobile regardless of the selected fluorophore or applied field. Each point in Fig. 2 (1–8) functions as an intensity detector. We measure the intensity at each point as a function of time (Fig. 3).

FIGURE 2.

Alexa Fluor 568 10 kDa dextran conjugate was injected into the insert membrane (injections A and C) and into the tissue culture (injection B). After applying the potential, injection B migrates toward the cathode, as shown in the sequence of images. Injections A and C remain in place despite the electric field. Intensities are measured at points 1–8 as a function of time. The smaller injections A and C are ∼135 μm in diameter. Injection B is ∼500 μm in diameter.

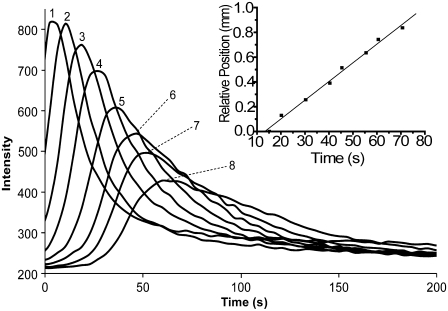
FIGURE 3.

The intensity profiles recorded at each of the eight detection points on the cathodic side of the original injection. Inset: The relative position of the detection points (1–8) in Fig. 2 are plotted as a function of the times of the peak maxima (inset). The linearity implies that the fluorophore's velocity is constant throughout the experiment.

v_obs corresponds to the slope of a plot of the relative positions of the detection points versus the peak times (Fig. 3, inset). This plot routinely yields straight lines, indicating that fluorophore velocity and electric field are constant during the experiment. Dividing the velocity by the applied electric field, measured using an Ag/AgCl reference electrode pair placed in the tissue, yields the observed mobility (μ_obs) as shown in Eq. 4.

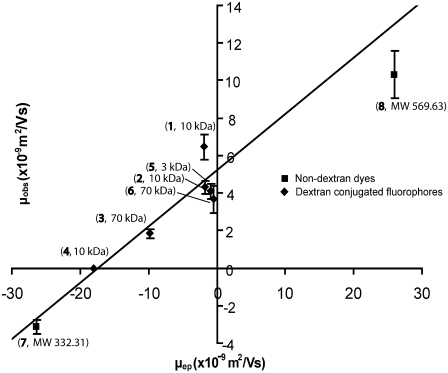
Fig. 4 is a plot of μ_obs versus μ_ep. The errors are the mean ± SE and are also given in Table 2. Analysis of the results (linear regression) according to Eq. 4 leads to Eq. 8.

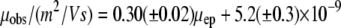(8)

The slope of 0.30 ± 0.02 is equal to the inverse square of the average tortuosity. The average (electrokinetic) tortuosity is therefore 1.83 ± 0.06. The ζ-potential in the OHSC is −22 ± 2 mV.

FIGURE 4.

The effective mobility in tissue as a function of the electrophoretic mobility. The line is the best fit to all of the data (linear regression). The labels at each point identify the identity of the fluorophore (see Table 1) and its molecular mass.

TABLE 2.

A summary of the average observed mobilities in tissue and their mean ± SE

Fluorophore	μobs/(10−9 m2/Vs)	Mean ± SE/(10−9 m2/Vs)	n
1	6.46	±0.67	58
2	4.09	±0.39	19
3	1.85	±0.24	22
4	0*	-	14
5	4.31	±0.35	13
6	3.66	±0.71	12
7	−3.15	±0.39	55
8	10.3	±1.3	10

^*No measureable movement. n is the number of experimental runs for that specific fluorophore.

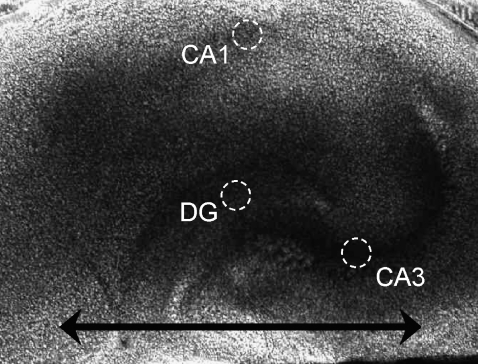
The ζ-potential described above is an average from all areas of the OHSC in the direction of the line, as indicated in Fig. 5 (approximately along the medial-lateral axis). As noted in the introduction, there are regional differences in the hippocampus. Are there different ζ-potentials in different regions? A micrograph of an OHSC (Fig. 5) shows areas interrogated with the two-fluorophore experiments; 1 was paired with 7 in 41 experimental runs. The 3 and 8 pair was run twice.

FIGURE 5.

A micrograph of an organotypic hippocampal slice culture. The circumscribed areas represent the portions of the CA1, CA3, and dentate gyrus (DG) investigated. The horizontal line represents the direction in which the tortuosity is measured in the single-fluorophore experiment.

The CA1 stratum pyramidale, CA3 stratum pyramidale, and dentate gyrus have ζ-potentials, respectively, of (mV) −25.1 ± 1.7 (n = 12), −20.3 ± 1.6 (n = 14), and −25.4 ± 1.0 (n = 34). Analysis of variance reveals that there is a significant difference among the regions (p < 0.05), which is accounted for by the difference between the value in CA3 and the other two.

DISCUSSION

Analysis of the method

CE measures the electrophoretic mobility of the fluorophores used in the tissue experiment. As a result of the high electrolyte concentration, we had to modify typical CE procedures. To minimize the effect of thermal gradients, a narrow (40 μm ID) and long (∼100 cm) capillary replaces the more common 75 μm ID, 50-cm-long capillary. With the longer, narrower capillary, peak shape is good.

Labeled dextrans (Data S1) are the most successful category of fluorophores for our experiments. Dextran fluorophores are easily visible with a fluorescence microscope; they have minimal “nonspecific” binding (1,66,67); and their CE results are unambiguous. Apparently, the fluorescent labels on each of the dextrans account for their different mobilities; 7 and 8, both nondextran conjugate fluorophores, also have similar characteristics, thus are acceptable for our study. Several other fluorophores, on the other hand, do not meet the necessary criteria (Data S1).

Although an in vivo model preserves the true environment of tissue, several advantages make the OHSC the optimal model for our purposes. We can easily track temporal changes in tissue slice cultures using an inverted microscope. Moreover, tissue slices are viable models because the cytoarchitecture and electrophysiology are preserved after explantation (1,61–63,68–70). Additionally, cultured slices are easier to manipulate than acute slices.

A tissue culture is easily placed in the apparatus as shown in Fig. 1. We use the apparatus to apply a potential gradient along the tissue by providing electrical contact through agarose gel. The design of the apparatus is such that the tissue sits in a narrow channel between two reservoirs, thus increasing the resistance in the channel. The increased resistance amplifies the electric field. The change in depth from the agarose gel to the OHSC further concentrates the field in the tissue. Thus, the field is largest within the OHSC. Applying a large field through a tissue can alter its permeability or electroporate the cells (71). Typical fields in electroporation, ∼1 kV/cm, are ∼45 times larger than the field strengths applied in the apparatus. To isolate the experiment from any electrolysis products created at the platinum electrodes, the electrodes are placed in deep reservoirs far from the tissue. Early designs of the apparatus had much smaller reservoirs. pH-responsive fluorophore experiments showed that electrolysis products moved into the channel within 6 min and altered the properties of the gel. The same pH-responsive fluorophore experiments repeated in the current apparatus design show that the electrolysis products remain in the reservoirs for well over 30 min. This provides plenty of time to run the tissue experiment.

To preserve the integrity of the tissue while injecting fluorescent material, several provisions are taken. Primarily, the injection capillary is pulled to a 12 μm OD tip to minimize tissue damage. A micromanipulator allows control over the depth of the injection. The injection capillary delivers ∼2 nL of fluorophore into the tissue to maintain the microenvironment. There is no obvious damage to the tissue as a result of injection.

The membrane insert has completely different properties than tissue. The membrane itself is made of poly(tetrafluoroethene) with a proprietary hydrophilic surface modification. When fluorescent material is injected into the membrane, it appears to stay in place (Fig. 2, injections A and C). Therefore, fluorescent compounds moving in the visual field are in fact injected into the tissue and not into the insert membrane.

Analysis of the results

The measured ζ-potential is −22 ± 2 mV. The value is in the range of isolated biological materials, such as mouse N-18 cells measured by a microelectrophoretic apparatus with a ζ-potential of −15 mV (49,72), chromaffin granules, −14.4 mV (53), and rat brain synaptosomes using particle electrophoresis, −11.8 mV (54). Theoretical calculations determined a cartilage model containing glycogen to have a ζ-potential of −27 mV (60). Ranck estimated the ζ-potential in brain to be −15 mV based on the constituents of the plasma membranes of neurons and glial cells (57).

The ζ-potential determined using two fluorophores simultaneously is independent of the average tortuosity factor and field (Eq. 7). The mean ζ-potential from the simultaneous fluorophore experiments is essentially the same as that in the single fluorophore experiments. We infer from this either of two things: the values of the field and tortuosity from the single-fluorophore experiments are correct, or there is a fortuitous cancellation of deterministic errors. We view the latter conclusion as a remote possibility. Thus, the two-fluorophore experiment further validates the experimental method.

The two-fluorophore method is capable of distinguishing small differences in ζ-potential between different structures in the brain: CA1 (−25.1 ± 1.7 mV), CA3 (−20.3 ± 1.6 mV), and dentate gyrus (−25.4 ± 1.0 mV). The CA1 and dentate gyrus regions have statistically the same ζ-potential at a 95% confidence level. However, a single-factor analysis of variance analysis reveals that there is a statistical difference among the three areas (p < 0.05). It is interesting to note that these regions have different vulnerabilities to excitotoxicity correlated with the differences in ζ-potential. The CA1 and dentate gyrus regions are more susceptible to N-methyl-D-aspartic acid excitotoxicity than the CA3 region (73). Perhaps the ζ-potential differences between the regions take part in mechanistic differences.

The experiments yield an average (electrokinetic) tortuosity. Tortuosity in the neurochemical context as determined through diffusion measurements is defined as 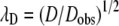where D is the molecular diffusion coefficient in an unobstructed medium, D_obs is the observed diffusion coefficient, and the subscript D denotes diffusion. It is noteworthy that tortuosity influences fluid flow (21) and electrophoresis (64) through porous media. Boyack considers two contributions to tortuosity in electrophoresis: one is purely geometrical—the ratio of the actual distance that a molecule travels in its path around obstacles to get from point A to point B to the straight line distance between A and B—whereas the other is related to the amplification of the electric field in narrow conduits. Similarly, tortuosity as measured by diffusion is related to a geometrical component and other factors, e.g., local viscosity (74). Thus measurements made by diffusion and by electrokinetic experiments may not yield the same result.

In the development of the data treatment (Eq. 4), we assumed that the tortuosity (as determined by electrokinetic experiments) is independent of brain region and fluorophore size and charge. In fact, there is a dependence of tortuosity (as measured by diffusion) on molecular mass and type of polymer (in acute cortical slices) (1,75,76). Using a small probe molecule, TMA⁺, differences in tortuosity (as measured by diffusion) in different regions of the hippocampus have been found (13,15,77). In cortical slices, Nicholson found that the range of tortuosities for fluorescein-conjugated dextrans in the same molecular mass range that we used (3–70 kDa) was from 1.77 to 2.25 (76). Thus, to the degree that the tortuosities measured electrokinetically and diffusionally are the same, our measured tortuosity has to be considered an average over the molecular masses and the brain regions studied.

If there is a correlation between the observed mobility and fluorescent species molecular mass, molecular mass effects on tortuosity may lead to a deterministic error in ζ. If there is no correlation, differences in tortuosity will add to the error in ζ but will not affect its magnitude. From Fig. 4, it can be seen that there is no significant pattern of deviation from the line due to molecular mass. The correlation coefficient of the molecular mass and electrophoretic mobility (data in Table 1) is −0.07, demonstrating the lack of correlation. Thus, the assumption of an average tortuosity adds to the error in ζ but does not influence the measured magnitude of ζ. Furthermore, recall that the two-fluorophore experiment yields a result that is independent of tortuosity (if it is again assumed that one tortuosity applies to both dyes). The average ζ-potential from these results, as mentioned above, is indistinguishable from the value determined from Eq. 4. Thus, although the assumptions about the tortuosity certainly must add to the uncertainty, they are apparently not influencing the result for ζ-potential.

Potential applications and implications

A plot of μ_obs versus μ_ep (e.g., Fig. 4) relates an easily measured quantity, μ_ep, to information about how fast a molecule moves in the brain. This is useful in the context of experimental procedures like iontophoresis. The μ_obs for a solute dictates whether it will move into or away from an iontophoresis capillary. A neutral molecule, for example, has a μ_ep of 0 m²/Vs. By applying Eq. 8, the μ_obs is expected to be ∼5.2 × 10⁻¹⁰ m²/Vs. Therefore, in the OHSC and with the proviso that the iontophoresis capillary ζ-potential matches the tissue ζ-potential, a neutral compound would move toward the cathode. To eject a neutral compound iontophoretically, it must be in the anodic chamber.

It is instructive to consider under what conditions EO flow contributes to the transport of a neutral molecule by comparing the magnitudes of EO velocity and diffusive velocity. This is done with the Peclet number, Pe. The Peclet number is the ratio of the time required to diffuse a characteristic distance a, (∼a²/D), to the time required to move with the fluid flowing at velocity v over the same distance, a (a/v).

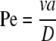(9)

For a neutral solute, the Smoluchowski equation (Eq. 3) for ζ with the Stokes-Einstein equation for D yields the following Peclet number:

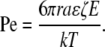(10)

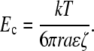
In Eq. 10, r is the radius of the presumed spherical solute, k is Boltzmann's constant, and T is temperature. If we assume that tortuosity influences diffusion and migration to the same degree, it does not appear in Pe. The field at which diffusive and electrokinetic velocities are equal, E_c, is thus

(11)

Finally, equating E_c with a critical voltage difference over the characteristic length, ΔV_c/a, the critical voltage is given as Eq. 12:

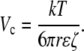(12)

Note that the characteristic distance divides out. We can use a correlation (78) to relate molecular radius and molecular mass. For a 1 kDa (r = 0.84 nm) neutral molecule, the critical voltage is 19 mV (for the ζ-potential that we measured, −22 mV). For a 10 kDa neutral (r = 2.6 nm), the critical voltage is only 6 mV. Clearly, this magnitude of potential difference is plausible, leading to the conclusion that EO flow may in fact play a role in extracellular transport.

If EO flow does play a role, how would it influence charged neurotransmitters/modulators? The direction of EO flow when ζ is negative is the same as the electrophoretic direction of a cation. Thus, an electric field would drive a cation more rapidly, and an anion less rapidly, in the presence of EO flow in comparison to the absence of EO flow. It is interesting to note that the influence of dopamine, a cation, is felt outside the synapse. Further, its local concentration and concentration dynamics are important in its actions (79,80). The presence of an electric field would cause dopamine to move relatively rapidly. In vertebrate brain, the anionic amino acid glutamate is responsible for fast neurotransmission. Unrestricted diffusion of glutamate over larger areas may cause synchronous activation of neurons and epilepsy. Thus this type of transmission has to be tightly localized to the individual synapse from which glutamate is released. The main system to regulate this process is reuptake. However, it is worth noting that any electric field that exists would have very little impact on glutamate's motion—its electrophoretic velocity and the extracellular fluid's EO velocity will counteract each other.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org.