An Error Analysis for Two-State Protein-Folding Kinetic Parameters and ϕ-Values: Progress toward Precision by Exploring pH Dependencies on Leffler Plots

Abstract

The interpretation of ϕ-values has led to an understanding of the folding transition state ensemble of a variety of proteins. Although the main guidelines and equations for calculating ϕ are well established, there remains some controversy about the quality of the numerical values obtained. By analyzing a complete set of results from kinetic experiments with the SH3 domain of αspectrin (Spc-SH3) and applying classical error methods and error-propagation formulas, we evaluated the uncertainties involved in two-state-folding kinetic experimental parameters and the corresponding calculated ϕ-values. We show that kinetic constants in water and m values can be properly estimated from a judicious weighting of fitting errors and describe some procedures to calculate the errors in Gibbs energies and ϕ-values from a traditional two-point Leffler analysis. Furthermore, on the basis of general assumptions made with the protein engineering method, we show how to generate multipoint Leffler plots via the analysis of pH dependencies of kinetic parameters. We calculated the definitive ϕ-values for a collection of single mutations previously designed to characterize the folding transition state of the αspectrin SH3 domain. The effectiveness of the pH-scanning procedure is also discussed in the context of error analysis. Judging from the magnitudes of the error bars obtained from two-point and multipoint Leffler plots, we conclude that the precision obtained for ϕ-values should be ∼25%, a reasonable limit that takes into account the propagation of experimental errors.

INTRODUCTION

Rate-equilibrium free-energy relationships (REFERs), commonly used to characterize kinetic mechanisms in chemical processes, have been shown to provide information about transition states in protein-folding reactions. This information is provided by comparing changes in the activation and equilibrium Gibbs energies obtained upon introducing a perturbation (mutation) (1–5). The most universally known REFER is the ϕ-value, calculated from individual perturbations throughout the protein that modify energetic aspects related to them. Therefore ϕ = ΔΔG_‡-U/ΔΔG_F-U, where ΔΔG_‡-U is the change in the Gibbs energy of activation and ΔΔG_F-U the overall change in the Gibbs energy of folding on mutation. The relationship between the value obtained and the distribution of mutations along the protein sequence allows us to map the energetic organization of the transition state of folding compared to the native state. This is the so-called protein engineering method (6–10).

During the past decade, the interpretation of ϕ-values has allowed us to understand the folding transition state ensemble of a variety of proteins and to formulate some important hypotheses (11–17). Although the main guidelines for calculating ϕ are well established, there is a dearth of information concerning the quality of the numerical values deriving from them. Some controversy has recently arisen about their low reproducibility and wide margins of uncertainty (18–23). Furthermore, some other REFER strategies that take advantage of experimental limitations in the determination of the value of ϕ have emerged as alternatives, although they do not seem to solve the problem since disagreement in their values merely serves to increase the confusion (24–26).

Some globular proteins are considered to be models for carrying out folding studies. This is the case with the α-spectrin SH3 domain (Spc-SH3), which has provided us with a detailed picture of its transition-state ensemble and folding pathway (12–15,27–31). Our intention here is twofold: first, to evaluate the uncertainties involved in kinetic experimental parameters and the corresponding calculated ϕ-values by applying classical error methods to the analysis of a large set of data obtained from the Spc-SH3 domain under different pH conditions; and second, to derive some general protocols concerning routine data analysis based on the evaluation of error propagation and on the general assumptions involved in the protein engineering method (6–10).

THEORY

Estimation of errors: random errors from instrumental uncertainties

Error can be defined as the difference between an observed or calculated value and the true value. To begin to evaluate error, it is important to distinguish between the terms “accuracy”, or how close the result of the experiment is to the true value, and “precision”, or how well the result has been determined, without reference to its agreement with the true value. The accuracy of an experiment generally depends upon how well we can control or compensate for systematic errors (reproducible discrepancies). Precision is a measurement of the reproducibility of the result due to random errors. Absolute precision indicates the magnitude of the uncertainty in the result (in the same units as the result), whereas relative precision indicates uncertainty in terms of a fraction of the value of the result (normally as a percentage) (32).

The mean (μ) and the standard deviation are the general choice to characterize precision (random errors) in our experimental data set, as they are sufficient to describe our experimental data distribution. The former is considered an estimation of the true value, whereas the latter reflects the uncertainty due to fluctuations in the observations in our attempt to determine the true value.

The most probable estimation of the mean (μ) of a random set of observations can be calculated as their average, assuming a Gaussian distribution of measurements. For a set of N data points with values x_i the mean can be defined as

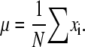(1)

In the same way, the standard deviation can be calculated using

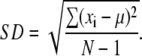(2)

Under the assumption that all data points x_i are drawn from the same parent distribution and consequently were obtained with an uncertainty characterized by the same standard deviation the uncertainty in mean determination can be expressed by the standard error (σ_μ):

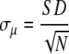(3)

from which it might be deduced that standard errors can be reduced infinitely by an increase of repetitions, whereas in practice we must make four times as many measurements to decrease uncertainty by a factor of 2.

Propagation of errors

To calculate the value of a dependent variable x, which is a function of one or more different measured variables (v, w, etc.), we must know how to propagate or carry over the uncertainties in the measured variables to determine the uncertainty in the dependent variable. The approximation for the standard error, σ_x, for x can be written as

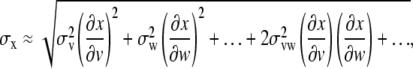(4)

where … indicates other possible measured variables. The first two terms can be considered to be an average of the squares of deviations in x, produced by uncertainties in v and w, respectively. These are the terms that usually dominate uncertainties. If the fluctuations in the measured quantities v and w… are uncorrelated, on average we should expect to find equal distributions of positive and negative values and thus the disappearance of the third term (referred to as the cross-term) at the limit of a range of random selection of observations (32).

Using the error-propagation formula (Eq. 4), we can estimate the standard error of the mean as

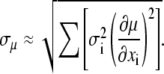(5)

This approximation neglects correlations between measurements x_i as well as second- and higher-order terms in the expansion of variance 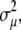but it should be a reasonable approximation as long as none of the data points contribute a major portion to the final result. Under these considerations, this equation can be assumed, as a general rule, to be equivalent to Eq. 3 (32).

Errors associated to a least-squares fitting to a straight line

Let us now assume that, instead of making a number of measurements of a single quantity x, we make a series of N measurements of a pair (x_i, y_i), where index i runs once more from 1 to N. Bearing in mind that the functional relationship between both variables can be approximated by a straight line of the form y = a + bx, the standard errors are estimates of uncertainties in the estimates of regression coefficients a and b, which is analogous to the standard error of the mean (defined by Eqs. 3 and 5):

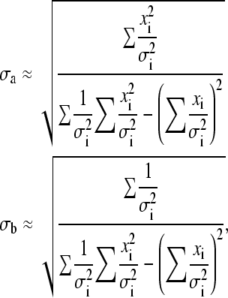(6)

where σ_i are the standard errors in y_i values, assuming errors in x_i to be negligible. The contribution of σ_x to errors in the y_i values can be evaluated as σ_x × b and should be added to the value of σ_i.

An alternative and much simpler strategy to Eq. 6, assuming that all errors make the same contribution (σ_i ≈ σ), could be (32)

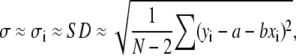(7)

where it should be noted that errors in y_i can be directly estimated from data scattering and the fitting results, no knowledge of individual error bars being required. In this case, Eq. 6 can be written as

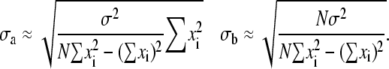(8)

Errors calculated from Eq. 8 are commonly known as “fitting errors”.

Errors associated to a least-squares fitting to an arbitrary function

In practice, the errors associated to any least-squares fitting can be easily obtained from any computer approximation capable of giving an analytical solution via a minimization procedure. The Marquardt method is the best choice among software used for the least-squares fitting of experimental kinetic traces and has therefore been included within software packages of most common stopped-flow instruments. This method has the considerable advantage of being reasonably insensitive to the starting values of the parameters and provides an estimate of standard errors based on the considerations in this section (32). The graphics program Sigma Plot 2000 (SPSS, Jandel, Chicago, IL), which was used to analyze the chevron plots and error propagation, is also based on the Marquardt method.

RESULTS AND DISCUSSION

Data set development

We considered the results of five different sets of kinetic experiments (urea unfolding and refolding) conducted with the Spc-SH3 D48G mutant in 50 mM phosphate buffer (pH 7.0, 25°C), which amounted to ∼100 independent determinations of kinetic constants, to evaluate the experimental and propagated errors for the kinetic parameters deriving from chevron plots. Our experiments were made with two different instruments (an SX.18MV-R from Applied Photophysics, Leatherhead, Surrey, UK and an SFM-3 from Bio-Logic, Claix, France) by different operators at different times over several years (Table 1), thus avoiding all possible experimental error sources, such as any possible bias deriving from wrong instrumental calibration or time-dependent tuning derivations. For comparison, we carried out a parallel analysis with chevron plots at pH 3.5 and 2.5 obtained from a single experimental set. Details about protein purification and experimental kinetic procedures done here can be obtained from previous works since some of our experiments have been published previously (12,14,30).

TABLE 1.

Details for the data set built to analyze errors in folding kinetic parameters

Conditions	Experiment	Operator	Date (location)	Instrument
50 mM phosphate pH 7.0	1*	JCM†	1997 (EMBL)	SFM-3 Bio-Logic
	2*	JCM†	1998 (EMBL)	SFM-3 Bio-Logic
	3*	ESC‡	2002 (EMBL)	SFM-3 Bio-Logic
	4	ESC‡	2007 (UGR)	SX.18MV-R Ap Phot.
	5	AMC§	2007 (UGR)	SX.18MV-R Ap Phot.
50 mM glycine pH 3.5	1*	JCM†	1997 (EMBL)	SFM-3 Bio-Logic
50 mM glycine pH 2.5	1*	JCM†	1998 (EMBL)	SFM-3 Bio-Logic

^*Previously published in Martinez et al. (12), Martinez and Serrano (14), and Cobos et al. (30).

^†Jose C. Martínez.

^‡Eva S. Cobos.

^§Adela M. Candel.

We also built a second data set to evaluate propagated errors in ϕ-values from these kinetic parameters and to develop the pH-scanning procedure. We used a mutational analysis that we had previously carried out on Spc-SH3 (12,14,30). The fitting errors included in these previous works were the starting point for this analysis.

Errors in the first-order kinetic constants

Our intention was to obtain the standard errors estimated for every kinetic constant from a nonlinear fitting of the kinetic curves (fluorescence versus time) to the equation

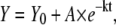(9)

where Y is the fluorescence signal, Y₀ is its value at t = 0, A is the amplitude, and k is the first-order kinetic constant. An analysis of the distribution of the residuals of this fitting constitutes a criterion in discerning whether the first-order kinetic scheme is adequate. This step is fundamental since kinetic phases can be easily masked in the analysis and lead to wrong estimations of k. To improve the signal/noise ratio, a strategy involving the averaging of the different kinetic traces under the same solvent conditions is widely accepted in experimental kinetics. Although this averaging strategy reduces errors, our experience has shown us that it might be one of the main sources of a decrease in accuracy by introducing sometimes “artificial” phases.

Based on error-theory considerations, σ_k = ±3σ_i (where σ_i is the fitting standard error to Eq. 9) should ensure that 99% of k values for such experimental conditions would be included within the interval. In Fig. 1 some representations of the kinetic constants versus the denaturant concentration at pH 7.0 are shown, including error bars. From Fig. 1 B (σ_k = ±3σ_i), it can be observed that in practice ∼90% of the error bars overlap the fitting line, which constitutes a considerable quantity of data. In fact, this interval might constitute a realistic limit since a perusal of Fig. 1 C (σ_k = ± 6σ_i) does not reveal much better overlapping, whereas in Fig. 1 A (σ_k = ± 2σ_i) it is noticeably worse.

FIGURE 1.

Kinetic constants obtained at different urea concentrations for the Spc-SH3 D48G mutant in 50 mM phosphate buffer (pH 7.0, 25°C). Experiments were done with two different instruments by different operators at different times (see text for details). The solid line represents the least-squares fitting to an exponential function. Open and filled symbols represent data obtained from refolding and unfolding experiments, respectively. Arrows indicate data whose error bars do not overlap the fitting line. Error bars were calculated from a different weighting of the fitting errors resulting from Eq. 9. (A) Twice fitting errors (2σ_i); (B) three times fitting errors (3σ_i); (C) six times fitting errors (6σ_i).

Therefore, a suitable weighting of the standard errors deriving from our least-squares fitting seems to correctly reflect the precision of k (random errors), although some other error sources appear to contribute in the most diverging cases to the decrease in accuracy (systematic errors), mainly those related to a bias in instrumental calibration (thermostat, syringes, pipettes, refractometer, etc.) and/or those coming from a mistaken averaging of the kinetic curves. The values obtained for σ_k = ±3σ_i range from 1% to 10% in relative values (4.7% on average, Fig. 2 D). These observations agree with previously reported ones obtained by the comparison of repeated experiments, which were also made at different laboratories using different instruments but not over a lengthy period of time as ours were (23). The authors assess that fitting errors (±σ_i) result in a certain degree of underestimation and that more reasonable error bars might be ∼10% (approximately equivalent to ±6σ_i in our calculations). Nevertheless, from an analysis of our experimental data set, we conclude that, as a general rule, it might be enough to consider σ_k = ±3σ_i (≈ 5%) for common k errors.

FIGURE 2.

Chevron plot of the Spc-SH3 D48G mutant obtained in 50 mM phosphate buffer (pH 7.0, 25°C). Experiments were done in two different instruments by different operators at different times (see text for details). The solid lines in A, B, and C represent the least-squares fitting to the chevron equation (see Martinez and Serrano (14) for details). Open and solid symbols represent data obtained from refolding and unfolding experiments, respectively. Error bars were calculated from a different weighting of the fitting errors resulting from Eq. 9. (A) Twice fitting errors (2σ_i/k); (B) three times fitting errors (3σ_i/k) at three pH values: pH 7.0 (50 mM phosphate), pH 3.5, and pH 2.5 (50 mM glycine); (C) six times fitting errors (6σ_i/k). (D) The relative errors in k weighted in the same way as in B as a function of their respective urea concentrations. In this case the solid line represents the average value of 4.7% (0.047).

Errors in chevron plot parameters

A chevron plot represents the logarithmic dependence of kinetic rate constants upon urea concentration at a given temperature. The plot corresponding to all the experiments made with the Spc-SH3 D48G mutant is shown in Fig. 2, A–C. Error bars for the kinetic constants were calculated as set out in Fig. 1 (σ_k = ±2σ_i (panel A), σ_k = ±3σ_i (panel B), and σ_k = ±6σ_i (panel C)), σ_i being the standard error provided by the Marquardt algorithm after each least-squares fitting to Eq. 9. Thus, for a natural logarithm, the error will coincide with the relative error of the magnitude σ_lnk = σ_k/k.

In the chevron plots shown in Fig. 2 the least-squares fitting to the equation describing the chevron (see Martinez et al. (12) and Martinez and Serrano (14) for details) is represented as a solid line. From this analysis, we obtained the values included in Table 2 for k_‡-U, k_‡-F, and m_‡-U. Focusing on the fittings at pH 7.0, the value of m_‡-F was fixed at −0.42 M⁻¹ (the average value for mutants studied in the ϕ-value analysis at pH 7.0; see below) due to the lack of information about the unfolding arm as a consequence of the high stability of the protein at this pH. Since experimental data have been collected from several independent sets of experiments, the errors obtained should account for “real” errors, which means ∼68% probability of including the true value. Relative errors obtained as 3σ_x/x (≈ 90% “real” confidence, as can be concluded from the analysis in Fig. 1) give 13% for k_‡-U, 22% for k_‡-F, and 4% for m_‡-U estimations. The differences in the relative errors obtained for both kinetic constants (almost double) may well be related to the longer extrapolation of the unfolding arm to 0 M denaturant.

TABLE 2.

Kinetic parameters with error estimations for the Spc-SH3 D48G mutant under different buffer conditions at 25°C

pH	Method	m‡-F (M−1)	m‡-U (M−1)	k‡-F (s−1)	k‡-U (s−1)
50 mM phosphate pH 7.0	Global fitting	0.42*	−0.80 ± 0.03 (4%)	0.00160 ± 0.00036 (22%)	69 ± 9 (13%)
	Individual fitting	0.42*	−0.79 ± 0.03 (4%)	0.00165 ± 0.00012 (8%)	71 ± 8 (12%)
	Average of mutant values	0.42 ± 0.02 (4%)	−0.90 ± 0.02 (4%)
50 mM glycine pH 3.5	Individual fitting	0.50 ± 0.06 (12%)	−1.20 ± 0.09 (8%)	0.08 ± 0.02 (25%)	50 ± 7 (14%)
	Average of mutant values	0.52 ± 0.06 (12%)	−1.24 ± 0.09 (8%)
50 mM glycine pH 2.5	Individual fitting	0.37 ± 0.03 (8%)	−0.92 ± 0.18 (20%)	0.94 ± 0.18 (19%)	11.6 ± 1.5 (13%)
	Average of mutant values	0.39 ± 0.06 (15%)	−0.96 ± 0.09 (9%)

Errors are calculated as 3σ_x, where σ_x is the fitting or averaging error of x. Values in parentheses represent the relative errors calculated as (3σ_x/x) × 100.

^*Value fixed in the least-squares fitting.

An alternative approach to error analysis is possible only at pH 7.0 from the individual fitting of the different data sets and further averaging of results (Table 2). No dispersion of the data values is observed compared to the global fitting. The errors were calculated as in Eq. 3 and were approximately of the same magnitude, except for the improvement found in the error estimated for k_‡-F. This improvement is a consequence of the acceptable reproducibility (low scattering) of the k_‡-F data obtained from the different fitting sessions. Nevertheless, it may be unreliable since, as mentioned above, the value of m_‡-F was fixed to −0.42 M⁻¹, which noticeably reduces scattering in the k_‡-F values.

Otherwise, errors in lnk obtained at different denaturant concentrations (Fig. 2 D) are randomly distributed around the average value (4.7% in our example) because of a lack of correlation with the denaturant concentration. This is also explicable by the low range of variability in the lnk values, which definitely masks any correlation between the magnitude of these values and their corresponding errors (which should translate into a V-shape of points in Fig. 2 D), due to a predominance of other experimental uncertainties. Therefore, according to the Theory section, error bars in the kinetic constants at different urea concentrations can be considered equal on average (σ_i ≈ σ), and their values extrapolated at 0 M denaturant can be correctly estimated from fitting errors (σ_a in Eq. 8) instead of using propagation formulas (Eq. 6), all of which simplifies our error calculations. The availability of a complete set of experimental data also contributes positively to this equivalency. Thus, kinetic constants in water can also be correctly estimated from an adequate weighting of fitting errors, as previously done by Zarrine-Afsar and Davidson (33), although the 9% given therein could still be a bit of an underestimation, probably because repetitions in that case were carried out under better “reproducibility” conditions, since the experiments were conducted with the same instrument and probably by a single operator.

Comparing the results obtained at pH 7.0 to those of the analysis of single experiments at pH 3.5 and 2.5, we can conclude that the errors in the kinetic constants are similar in magnitude, whereas those associated to m values increase dramatically (Table 2). In neither case was there any restriction on parameter values, which turns these analyses into a more realistic approach to an ordinary kinetic evaluation. There is also an expected discrepancy in the magnitudes of the relative errors in k_‡-U (12%–14%) and k_‡-F (19%–25%). The comparatively higher error found in the unfolding kinetic constants results from the longer extrapolation to the 0 M denaturant in this case. Furthermore, the value of 25% should even be considered as the lower limit of the real experimental error since in cases of extremely high stability the corresponding kinetic constants cannot be freely determined. Thus, using the pH 7.0 data as an example, the error in the unfolding kinetic constant will be significantly larger in a fitting with a free-floating unfolding slope since fluctuations in the latter will redound on the former.

Another interesting observation is the absence of any significant influence of accuracy in the errors. Thus, if the errors obtained for kinetic parameters deriving from chevron representations at pH 7.0 (including all the data of the five different experimental sets) are compared to those estimated at pH 3.5 and 2.5 (one single experimental set) (Table 2), it can be seen that at pH 7.0, errors account for the most common and relevant effects on accuracy, together with the unavoidable fluctuations that worsen precision, whereas at pH 3.5 and 2.5 they account only for the latter. It is surprising that errors are comparable in magnitude. Thus, the possible contribution of systematic errors (accuracy) seems to be counteracted by the higher number of kinetic constants collected at pH 7.0, which might reduce the magnitude of the error (see Theory section).

Errors related to m values can also be evaluated using the data obtained for different mutants designed for ϕ-analysis, which is our only possibility in the case of m_‡-F. It is to be hoped that the nondisruptive character of mutations designed for ϕ analysis (12,14,27–30) will avoid any significant effect on m values, mainly related to macroscopic exposure of hydrophobic groups (34). In fact, a comparison of the chevron plots for the different mutants does not reveal any significant differences between their slopes (see Table 1 from Martinez and Serrano (14)), which is also reflected in the low standard error of the average (Table 2). We determined the mean values of m_‡-F and m_‡-U according to Eqs. 3 and 5. As can be seen in Table 2, the errors edge the values toward coinciding with those obtained from the global and individual fittings.

Analysis of errors in Gibbs energies and ϕ-values

Once the values of k_‡-F and k_‡-U are estimated from chevron plot analysis, the values of ΔΔG and ϕ can easily be obtained using the well-known formulas

(10)

and

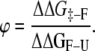(11)

ΔΔG_F-U should be calculated from an independent equilibrium denaturation curve, although it can also be obtained from the kinetic data by ΔΔG_F-U = ΔΔG_‡-U − ΔΔG_‡-F.

By means of Eqs. 4 and 10, we can obtain the following expressions for σ_ΔΔG

(12)

where the third term is the estimated cross-term accounting for the interdependence of both errors. This, together with Eq. 11, gives rise to the following definitive formula for errors in ϕ-values

(13)

where σ_ΔΔGF-U = σ_ΔΔG‡-U + σ_ΔΔG‡-F or, alternatively, the error corresponding to equilibrium unfolding experiments, which in practice should be of the same magnitude or higher. The first two terms estimate the errors both in activation and equilibrium Gibbs energies, respectively, whereas the third arises from the cross-term of Eq. 4. In all cases, we considered that σ_vw = σ_v × σ_w.

The error bars calculated from Eq. 13 for the different ϕ-values obtained previously for the Spc-SH3 domain (obtained from Table 1 of Martinez and Serrano (14)) under three different pH conditions (panels A, B, and C, respectively) are represented in Fig. 3. Different strategies to analyze errors have been considered (errors in bars from left to right): i), errors in black bars are drawn as the propagated errors in kinetic constants calculated by Eqs. 12 and 13 (obtained as three times the fitting standard errors from chevron plots); ii), errors in gray bars were calculated from a simplified way in which the cross-terms in Eqs. 12 and 13 were avoided; and iii), and iv), errors in dark-gray and light-gray bars are analogous to i), and ii), respectively, but take only the fitting errors into account.

FIGURE 3.

ϕ-values obtained for all mutants compared to their reference values. Fitting errors were estimated from a two-point Leffler analysis (Eq. 11) after propagation of least-squares fitting k_‡-F and k_‡-U standard errors (see text for details). (A) Values obtained in 50 mM phosphate buffer (pH 7.0, 25°C). (B) Values obtained in 50 mM glycine/HCl buffer (pH 3.5, 25°C). (C) Values obtained in 50 mM glycine/HCl buffer (pH 2.5, 25°C). Errors have been calculated in different ways: i), errors in black bars were drawn from propagation by Eqs. 12 and 13 of errors in kinetic constants (obtained as three times the fitting standard errors from chevron plots); ii), errors in gray bars were calculated from a simplified Eq. 13 in which the cross-term has been omitted; and iii), and iv), errors in dark-gray and light-gray bars are analogous to i), and ii), respectively, but take into account nonweighted fitting errors (σ_lnk = σ_i/k). The whole set of values was taken from Table 1 of Martinez and Serrano (14).

The general tendency of error magnitudes for the three pH conditions is black > dark-gray ≥ gray > light-gray. Calculation of the ratio σ_ϕ+cross/σ_ϕ-cross (i.e., the quotient between errors black/gray and dark-gray/light-gray) for each mutant allows us to estimate the contribution of the cross-term to σ_ϕ. Our results suggest that the cross-term increases error by a factor of 2.9 ± 0.8. Similar conclusions have been drawn from a computational study with randomly simulated chevron data (22), where the need to take into account the cross-term in ϕ-error estimations is emphasized by showing here the different error bars obtained from the analysis. Thus, avoiding covariance leads to a significant underestimation of σ_ϕ (on average, around three times according to our estimations).

Another interesting effect appears from a comparison of the black/dark-gray and gray/light-gray quotients (Fig. 3). We obtained an average value of 3.3 ± 0.7, which affords the ratio σ_ϕ(3σ_lnk)/σ_ϕ(1σ_lnk). Thus, a threefold increase in the error in the kinetic constants practically translates into a parallel triplication in the ϕ-errors, as might be expected.

For a more thorough analysis of these effects, we represented the errors in the ϕ-values calculated from Eq. 13 (black bars in Fig. 3) versus the absolute errors in every ΔΔG function (Fig. 4) and also versus the global ΔΔG functions (Fig. 5). In all representations, we included the whole data set (reference and mutant proteins) under the three pH conditions assayed. Some correlation among variables can be seen (Fig. 4), as it is clear that higher errors in ϕ-values were obtained with lower ΔΔG values (Fig. 5), as expected (18). An unambiguous correlation (r = 0.87) results when the relative errors of ΔΔG_F-U versus the error in the ϕ-values are represented (Fig. 6 A), which is not to be found with either of the individual activation ΔΔG values (Fig. 6, B and C). The relation found with a 99% confidence is

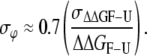(14)

FIGURE 4.

A test for correlation among errors in ϕ-values and absolute errors in the different Gibbs energy functions. (A) Absolute errors in ΔΔG_F-U. (B) Absolute errors in ΔΔG_‡-F. (C) Absolute errors in ΔΔG_‡-U. The solid lines represent linear regression through each pH data set. (Solid circles) pH 7.0; (open circles) pH 3.5; (solid triangles) pH 2.5.

FIGURE 5.

A test for correlation between errors in ϕ-values and the different Gibbs energy functions. (A) ΔΔG_F-U function. (B) ΔΔG_‡-F function. (C) ΔΔG_‡-U function. (Solid circles) pH 7.0; (open circles) pH 3.5; (solid triangles) pH 2.5.

FIGURE 6.

A test for correlation between errors in ϕ-values and relative errors in the different Gibbs energy functions. (A) Relative errors in ΔΔG_F-U. (B) Relative errors in ΔΔG_‡-F. (C) Relative errors in ΔΔG_‡-U. Solid lines represent linear regression through the whole data set.

Thus, as a general rule, errors in the ϕ-values can be taken to represent 70% of the relative errors in the equilibrium Gibbs energies, which were obtained from kinetic experiments as the sum of the relative errors in the activation Gibbs energy values. This correlation clearly reveals that the lowest ΔΔG_F-U values are affected by the highest relative errors (18).

Evaluation of pH dependencies via Leffler plots (pH-scanning)

As shown by Fersht et al. (20), the change in Gibbs energy on mutating a residue into a protein can be split into three main notional components: 1), the change in energy of the covalent bond that is mutated; 2), the change due to noncovalent interactions at the site of mutation plus that deriving from any additional changes due to protein reorganization; and 3), the change in solvation Gibbs energy. The authors propose that comparison of individual ϕ-values for different mutations at a particular site can be made correctly by using multipoint Leffler plots; this is also a way of detecting deviations arising from inadequate mutations for transition-state analysis. Thus, deviations from linearity are due mainly to different values of the solvation component for different mutants, as well as to some additional differences in the reorganization term.

Here we propose an alternative and fully complementary way to obtain multipoint Leffler plots using just the kinetic data for a single mutation (designed to be nondisruptive) under different pH conditions; as many points as desired are used in the Leffler representation. It is generally accepted that the differences observed in the pH stability of small proteins generally derives from purely entropic contributions to Gibbs energies and that it is possible to obtain a unique Gibbs energy function for the protein, ΔG_F-U(T) or ΔG_F-U(denat), using the different stability values obtained under the different pH conditions (28,35–41). From this point of view pH can be considered an almost “neutral” strategy to modify changes in the Gibbs energy of folding (both activation and equilibrium). This approach avoids any reorganization within the structure and minimizes any possible changes in solvation energies compared to the effects caused by mutational analysis, since neither the solvation nor the reorganization components of a single mutation differ significantly under the various pH conditions. The only assumption from a kinetic point of view might be the maintenance of the folding mechanism and the rate-limiting step of the folding reaction throughout the pH interval assayed, which is easily corroborated by the linearity of the Leffler plots for each mutation ((18) and references therein).

The multipoint Leffler plots for different Spc-SH3 mutants taken from Table 1 of Martinez and Serrano (14) are set out in Fig. 7. A glance at Eq. 11 reveals that the respective ϕ-values result from the slopes of every least-squares linear regression, with standard errors (Eq. 8). The regressions contained from three to four points (at three different pH conditions; Table 3) and, using the correlation coefficient to test the quality of the fittings, we always arrived at values of r ≥ 0.8, most of them higher than 0.9. Therefore, we can draw the conclusion that the folding mechanism is confined to within the pH range studied (2.5–7.0), which is confirmed by the similarity of the ϕ-values deriving from the two-point plots (Fig. 3), although the low number of data could be insufficient to definitely confirm such a linear behavior.

FIGURE 7.

Multipoint Leffler plots for all the mutations of the Spc-SH3 domain. The majority of residues have ϕ-values of between 0 and 1 and lie between the solid black lines of slopes 0 and 1. Fitting lines, calculated from linear regression to the equation y = bx, are shown in the same color code as their respective data points. The whole set of values was taken from Table 1 of Martinez and Serrano (14).

TABLE 3.

The definitive ϕ-values and error bars for the α-spectrin SH3 domain (Spc-SH3), calculated from pH-scanning analysis

Mutation	ϕ-values (multipoint Leffler analysis)* pH-scanning	σϕ (multipoint Leffler analysis) pH-scanning	σϕ (two-point Leffler analysis) pH 7.0	σϕ (two-point Leffler analysis) pH 3.5	σϕ (two-point Leffler analysis) pH 2.5	σϕ (two-point Leffler analysis) AVERAGE
L8S	0.14 (4)	0.14	0.21	0.70	0.44	0.45
A11G	0.03 (3)	0.08	0.08	0.26		0.17
D14S	0.14 (4)	0.10	0.20		1.82	1.00
V23A	0.32 (3)	0.19	0.19	1.02		0.61
T24A	0.27 (4)	0.30	0.30	0.71	0.32	0.44
D29A	0.22 (4)	0.05	0.40	0.73	0.66	0.60
L33V	−0.28 (4)	0.21
S36N	0.26 (4)	0.32	0.94	1.10	0.65	0.90
K43A	0.24 (4)	0.27	0.32	1.08	0.42	0.61
V44A	0.50 (3)	0.12	0.09	0.31		0.20
V46A	1.20 (4)	0.21		0.58	0.16	0.37
N47G	0.40 (4)	0.34	1.05	1.60	0.45	1.03
D48G	1.27 (4)	0.44		2.35		2.35
F52A	0.61 (3)	0.19	0.12	0.28		0.20
V53A	0.72 (3)	0.69		0.26	0.54	0.40
A55G	0.61 (3)	0.41	0.24	0.30		0.27
V58A	0.18 (3)	0.16	0.21	0.36		0.28

^*Values in parentheses indicate the number of data points in the Leffler representation (Fig. 7).

In Table 3 we considered that σ_ϕ = ±3σ_i (99% confidence), in which σ_i is the respective fitting standard error in the slope for each mutant, together with the definitive ϕ-values obtained from multipoint Leffler analysis. Errors corresponding to the two-point analysis at the three pH values, respectively (also with 99% confidence; black bars of Fig. 3), and their averages, are also included.

Initially it should be noted that the error bars from the multipoint Leffler analyses are not the highest ones, except for mutants V53A and A55G, which were only measured under two pH conditions and show considerable dispersion (Fig. 7). In general, the errors in the ϕ-values are either clearly improved or at least stay the same (for simplicity's sake a comparison can be made with the averaged error bars). Interestingly, after a closer examination of Fig. 7 and Table 3 for all mutations, it can be seen that the improvement in the errors is better for the ϕ-values calculated from lower ΔΔG_F-U values, whereas the errors with the mutations in which ΔΔG_F-U > 2 kcal × mol⁻¹ do not improve to the same extent, being in general similar to those deriving from the two-point analysis. This is the case with mutants V53A and A55G (ΔΔG_F-U ≈ 2 kcal × mol⁻¹) as well as mutants V44A, F52A, and V58A. It is also of interest that the closest positions to ϕ-values 0 and 1, corresponding to the A11G and D48G mutants, are the only two to show clear improvement.

These observations show that this approach is quite useful since errors resulting from lower ΔΔG_F-U values are worse when estimated from two-point Leffler plots (as shown here and in Sanchez and Kiefhaber (18) and Fersht and Sato (20)), and through pH scanning the error in the analysis can be reduced considerably, and even more so if we obtain different ΔΔG_F-U results at the different pH values assayed (as with the L8S, A11G, D14S, and V23A mutants). On the other hand, mutants with higher ΔΔG_F-U values do not improve appreciably, although a better estimation can be achieved in most cases. From a statistical point of view, this effect might be explained by the higher degree of complementation of data sets in those cases where a gradation of ΔΔG_F-U values exists, whereas the worst improvements result as a consequence of having similar values. Thus, in almost all cases a better improvement is achieved rather than considering some repetitions under the same experimental conditions, which could be correctly represented by the averaged values in Table 3. It is also important to mention that individual errors are frequently undefined from propagation estimations (absent errors in Table 3), mainly at pH 2.5, where the most unstable mutants (those with a higher ΔΔG_F-U) have been found to have significant errors due to an inadequate amount of refolding information. In the case of mutation L33V (negative ϕ-value), the error could be determined only from Leffler analysis.

Judging by the magnitudes of the error bars shown in Table 3 and bearing in mind that the ϕ-value is a relative quantity (calculated from a quotient of two Gibbs energy changes; Eq. 11), the errors are obtained directly as relative values. The obtained values are quite variable, ranging from 5% (0.05) to 70% (0.69), being 25% on average; the errors from two-point analysis are more dispersed (17%–235%; 60% on average). In our opinion, the average value obtained of 25% might be a reasonable value for σ_ϕ, which basically propagates both routine and typical experimental random errors. Lower errors can be obtained when a combination of optimum ΔΔG_F-U values and low data dispersion give rise to symmetrical and well-defined chevron plots. Higher errors will, therefore, include contributions deriving from asymmetry and/or excessive data scattering in the chevron plots.

Therefore, precision can be significantly improved by pH-scanning analysis (as much as 35% on average), since protein stability is normally affected by changes in the pH value and thus asymmetry can be corrected. It is also evident that the more data points added to the Leffler plot the more error is reduced, probably until the limit imposed by experimental error propagation. This also happens when the data points are numerically different, which ensures a better complementation among them. The fact that in this kind of representation the fitting line must cross the origin (Fig. 7) contributes significantly to a decrease in error. Thus, in a two-point plot the fitting line is scattered only by the second value corresponding to the mutation, as it is evident that additional points positively contribute to the accuracy in line position. Of course, the farther the point is from the origin (higher ΔΔG_F-U values) the lower the scattering, which translates into a lower σ_ϕ (18).

In summary, a proper error analysis such as the one presented here constitutes an easy way to evaluate the precision of each ϕ-value, whereas an analysis of pH dependencies of kinetic parameters allows a further improvement wherever necessary. Proceeding in this way, the three-class gradation of individual ϕ-determinations (weak, medium, and strong), as suggested by Fersht (42) and also derived from our two-point Leffler analysis, can be increased to four or even five classes. Moreover, it could be a useful tool to discard wrong ϕ-value estimations. Certainly, it involves an increase in experimental work, but a multiple mutational analysis additionally includes cloning and purification procedures, as well as possible uncertainties deriving from the differential nondisruptivity of the mutations. For example, in the Ala→Gly scanning, Gly can induce additional conformational freedom within the protein backbone compared to Ala (43). In any case, Ala→Gly and pH scanning emerge as fully compatible methods, and their combination will allow multipoint Leffler plots when necessary.

Strategies for experimental work and error analysis

On the basis of the arguments outlined above, a correct error analysis (≥90% confidence in practice) can be easily made starting from σ_{lnk =} ±3σ_i/k, where σ_i represents the fitting standard errors in k_‡-U and k_‡-F, which are obtained from chevron plots. Eqs. 12 and 13 can then provide the estimations of errors in the ΔΔG functions and ϕ-values, respectively. A more straightforward approach could be the use of Eq. 14 instead of Eq. 13 for ϕ-errors. In principle, no limitations for this application are envisioned from the analysis here. It is important to bear in mind that an independent determination of equilibrium Gibbs energies through equilibrium denaturation experiments not only reduces errors in ϕ but also provides an alert for systematic instrumental deviations (33). Anyhow, in cases where higher precision might be necessary, a pH-scanning analysis through Leffler representations could be done, paying special attention to their linear behavior, which verifies the maintenance of the folding mechanism (25). As we have shown here, errors in this case can be easily obtained as three times the fitting standard errors to a straight line. Proceeding in this way, ϕ-errors should not be higher than 25%.