Formation of the Open Complex by Bacterial RNA Polymerase—A Quantitative Model

Abstract

Over the last two decades, a large amount of data on initiation of transcription by bacterial RNA polymerase (RNAP) has been obtained. However, a question of how the open complex is formed still remains open, and several qualitative hypotheses for opening of DNA by RNAP have been proposed. To provide a theoretical framework needed to analyze the assembled experimental data, we here develop the first quantitative model of the open complex formation by bacterial RNAP. We first show that a simple hypothesis (which might follow from recent bioinformatic and experimental results), by which promoter DNA is melted in one step through thermal fluctuations, is inconsistent with experimental data. We next consider a more complex two-step view of the open complex formation. According to this hypothesis, the transcription bubble is formed in the −10 region, and consequently extends to the transcription start site. We derive how the open complex formation rate depends on DNA duplex melting energy and on interaction energies of RNAP with promoter DNA in the closed and open complex. This relationship provides an explicit connection between transcription initiation rate and physical properties of the promoter sequence and promoter-RNAP interactions. We compare our model with both biochemical measurements and genomics data and report a very good agreement with the experiments, with no free parameters used in model testing. This agreement therefore strongly supports both the quantitative model that we propose and the qualitative hypothesis on which the model is based. From a practical point, our results allow efficient estimation of promoter kinetic parameters, as well as engineering of promoter sequences with the desired kinetic properties.

INTRODUCTION

Bacterial RNA polymerase (RNAP) is the central enzyme of gene expression. Transcription by RNAP consists of transcription initiation, elongation, and termination. Transcription initiation is both the first step and a major point in regulation of gene expression. For promoter-directed transcription initiation, the RNAP core must make a complex with a σ-subunit to form the RNAP holoenzyme (1). Transcription initiation involves binding of the RNAP holoenzyme to double-stranded (ds) DNA, subsequent promoter melting, abortive transcription initiation, and promoter clearance (2).

Transcription initiation starts by a reversible binding of RNAP holoenzyme to dsDNA that constitutes a core promoter. This step is referred to as the closed complex formation. Core promoters are often characterized by the two conserved hexamers, which are denoted as −10 box and −35 box, based on their (typical) distance from the transcription start site (3). Binding of RNAP holoenzyme leads to promoter melting, i.e., a transcription bubble—corresponding roughly to positions −12 to +2 is formed, which is referred to as the open complex formation (4). After the open complex is formed, RNAP enters abortive initiation, which is followed by irreversible promoter escape and is subsequently preceded by processive transcription elongation and transcription termination (2). In this article, we concentrate on the first two stages of transcription initiation, i.e., RNAP binding and the open complex formation.

Despite significant experimental efforts, the mechanism by which RNAP forms the open complex is still an open research problem (5,6), and several mechanisms for the open complex formation were proposed. For example, a popular hypothesis proposes that the open complex is formed by RNAP applying a torque across the region of promoter that is melted in the open complex (3,7), thus destabilizing the region in which the transcription bubble is formed. Such a mechanism has, however, been questioned recently (6), given that it is unclear which parts of RNAP would exhibit the torque, and what would be the extent of the DNA torquing. Specifically, recent experiments (6), which addressed minimal RNAP machinery necessary for the open complex formation, determined that, even in the absence of RNAP parts that should be responsible for exhibiting the torque, the open complex can still be formed. These results indicate that torquing is not the main mechanism responsible for the formation of transcription bubble, although it cannot be excluded that this effect might contribute to the open complex formation at conditions other than those in the experiment.

On the other hand, two new hints that appear to be relevant for the open complex formation have emerged recently. First, a bioinformatic study (8) reported that 15-bp-long regions centered immediately upstream of experimentally determined Escherichia coli transcription start sites are more prone to melting, i.e., have a significantly lower DNA melting energy compared to other genomic regions. One should note that 15 bps approximately corresponds to the total length of a transcription bubble in the open complex (4). Second, a sophisticated single molecule study (9) obtained that the open complex is formed in a single step, at least on the timescales equal or larger than the experimental time resolution (∼1 s).

Taken together, the above two studies may indicate a mechanism by which the open complex is formed in a single step, through thermal fluctuations of the promoter region that is prone to melting, followed by the stabilization of the transiently formed transcription bubble through interactions of RNAP with the exposed nontemplate ssDNA. Alternatively, more complex mechanisms for the open complex formation have been considered. Specifically, experimental kinetic studies indicated that transcription bubble formation is likely exhibited as a multistep process, although proposed kinetic intermediates were not explicitly connected with different physical stages of the open complex formation (10,11). While different qualitative hypotheses of promoter melting can be formulated, the fact that only short living intermediates (if any) exist in the transition from closed to open complex makes it very hard to design an experiment which would test the validity of these hypotheses. Specifically, to experimentally test a hypothesis directly, one needs either direct mechanistic evidence or high resolution structures of transcription intermediates, and neither of these is currently available, although significant work was done on characterizing transcription intermediates through more indirect approaches (12–14). On the other hand, the rate of transition from closed to open complex can be directly experimentally measured (15,16), and, additionally, a number of experimentally confirmed transcription start sites are known in bacterial genomes (17). This creates a dataset that can be potentially used to test different hypotheses of the open complex formation, but a problem is that it is not possible to compare qualitative hypotheses against such quantitative data.

The idea behind the work presented here is to develop a quantitative model, which can be directly tested against the available biochemical and genomics data. Comparing such a model with the experimental data would enable us to 1), test whether a proposed mechanism of the open complex formation is correct; and 2), explicitly connect the relevant promoter kinetic parameters with physical properties of promoter sequence and promoter-RNAP interactions. Motivated by the above, we here develop the first quantitative model of the open complex formation by bacterial RNA polymerase, and show that our model is in a good agreement with the experimental data.

The outline of the article is as follows. We will start from a general kinetic scheme of the transcription cycle, from which we will derive the general relationship for the rate of transcription initiation. Given this relation, the main question will be how to connect the rate of transition from closed to open complex, with physical properties of promoter. We will next consider a one-step hypothesis for the open complex formation described above, and show that this hypothesis is in disagreement with experimental data. However, considerations of this model will lead us to a more complex two-step hypothesis for the open complex formation, where the first rate-limiting step corresponds to melting of the −10 box, while in the second step the transcription bubble is extended from the downstream edge of the −10 box to just upstream of the transcription start site. We will next show that a quantitative model based on this two-step hypothesis is in a good agreement with both biochemically determined rates of transition from closed to open complex and with experimentally determined transcription start sites in genome. We will finally discuss some possible bioinformatics applications of our model and its implications for recent and future experiments.

GENERAL KINETIC SCHEME

We start with a general kinetic scheme for a transcription cycle:

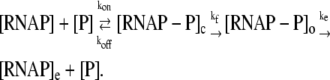(1)

In the above reaction, [RNAP] and [P] are, respectively, concentrations of free RNAP and promoter DNA, while k_on and k_off are on- and off-rates of closed promoter-RNAP complex formation. [RNAP−P]_c and [RNAP−P]_o are, respectively, concentrations of RNAP-promoter closed and open complexes, while k_f is the transition rate from closed to open complex. The formation of an open complex can be considered irreversible, due to the observed much lower backward rate of the open complex dissociation (4). The rate of irreversible promoter escape (2) is denoted by k_e, which leads to transcription elongation complex denoted by [RNAP]_e. For simplicity, individual steps of processive transcription elongation and transcription termination are not shown in Eq. 1.

RNAP that enters elongation is terminated after mRNA synthesis, which allows it to again initiate transcription. Similarly, once the promoter P is cleared, it can be occupied again by RNAP. This cycling of free RNAP and free promoter DNA allows for the transcription cycle to reinitiate, and a steady state is consequently established. Further, from the kinetic measurements follows that the measured k_off values are typically significantly larger compared to k_f (18–21). That is, there is a separation of timescales to fast binding and unbinding of RNAP to promoter DNA (∼1 s), and a much slower transition from closed to open complex (∼10–100 s). In Appendix A, we show that with this separation of timescales, together with an assumption (7,22,23) that the open complex formation is a rate-limiting step in the transition from closed complex to initiation of transcription, the rate of transcription initiation ϕ in a steady state is given by

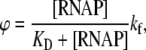(2)

where K_D is the dissociation constant for the closed complex formation, which is given by K_D = k_off/k_on. Note that the assumption that the open complex formation determines the rate of transcription initiation is widely used in literature (7,23), but yet remains to be systematically tested on a large enough sample of promoters. Therefore, the rate of the open complex formation, which is in a steady state equal to the rate of transcription initiation, effectively decouples to the product of equilibrium-like binding probability of RNAP to DNA (given by [RNAP]/(K_D + [RNAP]), and the rate of transition from closed to open complex k_f. The expression for the rate of transcription initiation will be used later in the article to compare our model with the information inferred from experimentally determined transcription start sites.

A ONE-STEP MECHANISM OF THE OPEN COMPLEX FORMATION

A recent bioinformatic study (8) showed that 15-bp windows that are centered immediately upstream of the experimentally verified Escherichia coli promoters have significantly lower melting energy compared to the windows of the same length sampled from genomic background. Additionally, note that a 15-bp window centered just upstream of a transcription start site roughly corresponds to the total length of transcription bubble formed during the open complex formation. These observations suggest that dsDNA regions that correspond to the formed open complex bubbles are under a selection pressure to be prone for melting. Furthermore, a recent single molecule measurements of transcription initiation showed that open complexes, i.e., transcription bubbles of size approximately equal to one helix length, are formed in a single step at a time resolution of ∼1 s (9).

The above observations may suggest the following simple one-step hypothesis of promoter formation: The promoter region of length ∼15 bp is melted by thermal fluctuations that cause transient breaking of Watson-Crick basepairs in dsDNA. Once a transient bubble of size ∼15 bp is formed, it can be stabilized through interactions of RNAP with exposed nontemplate ssDNA. Therefore, according to this hypothesis, an open complex is formed if both a transient bubble is formed through thermal fluctuations, and RNAP is bound to promoter. This requirement is quantitatively reflected by the fact that in Eq. 2 the rate of the open complex formation is equal to the product of probability that RNAP is bound to promoter and the rate of bubble opening. One should note that, in this simple mechanism, formation of a bubble is considered to be independent from RNAP, except that, once a final, ∼15-bp bubble is formed through thermal fluctuations, RNAP has a role to stabilize it.

Within the simple one-step mechanism introduced above, the transition rate from closed to open complex k_f (see Eqs. 1 and 2) is equal to the rate of opening k_o(S) of a transcription bubble in dsDNA with the sequence S through thermal fluctuations. In Appendix B we derive the expression for the rate of bubble formation k_o(S) (see Eq. 20), in which enters the energy needed to melt a dsDNA segment with sequence S and the timescale on which bases close when broken by thermal fluctuations. The parameters of DNA melting have been extensively experimentally measured (24), while the rates of base closing were also experimentally determined (25,26). One should note that individual bases open very fast, on the timescale of ∼10⁻⁷ s (25), while opening of transcription bubbles happens on a more-than eight orders-of-magnitude slower timescale (10–100 s). Given the large difference in the two timescales, and the reported significant melting destabilization of genomic regions corresponding to transcription bubbles, we want to determine whether the simple one-step mechanism can be fast enough to account for the experimentally determined rates of transcription bubble opening.

To determine this, we start by using the RegulonDB database (17) to extract the −10 regions for experimentally confirmed E. coli promoters. To identify the 6-bp-long −10 boxes within the DNA segments extracted from the database, we use a Gibbs-search-based algorithm (27,28), as described in Appendix D. As the result, we identified 322 −10 boxes that correspond to experimentally confirmed σ⁷⁰ transcription start sites. For the purpose of further analysis, we next define set A that consists of 322 DNA segments S, which span the region from the upstream edge of the aligned −10 box to the position +2 of the experimentally identified transcription start site. Therefore, the segments in set A correspond to the entire DNA region that is melted in the formation of the (final) open complex.

We next use our model (i.e., Eq. 20) to calculate the predicted transition rates from closed to open complex k_f for the sequences in set A. We obtain that the mean value of k_f rates for sequences in A is several orders-of-magnitude smaller compared to the experimentally measured transition rates (see Appendix B for the details of the calculation and used parameter values). We, therefore, conclude that the one-step mechanism is inconsistent with the experimental data. However, this result motivated the analysis presented in the next section, which will consequently lead us to a more complex two-step model of the open complex formation.

MELTING DESTABILIZATION OF PROMOTER REGIONS

A motivation for the one-step model, which was derived in the previous section, was the reported significant melting destabilization of the whole ∼15-bp-long region that forms the open complex transcription bubble (8). However, the poor agreement of the one-step model with the experimental data motivated us to additionally investigate melting properties of this region.

To investigate the melting energies corresponding to relevant fragments of E. coli promoters, we defined three sets of DNA segments: The set A, defined in the previous section, consists of 322 DNA segments that correspond to ∼15-bp-long fragments that are melted in the final open complex; The set B consists of 322 −10 boxes that were identified through Gibbs search; The set C consist of 322 regions that span from the downstream edge of the −10 box to position +2 relative to transcription start site. One should note that each fragment in set A is a fusion of the two corresponding fragments in sets B and C.

In addition to sets A–C, we also generate three corresponding sets of random sequences in the following way. We first use all intergenic regions of the E. coli genome (29) to sample dinucleotide base background probabilities, i.e., frequencies of different dinucleotides in the intergenic regions. We next use a first-order Markov model to generate random sequences that have the same dinucleotide distribution as E. coli intergenic regions. Three sets of DNA sequences, A^rnd, B^rnd, and C^rnd that have, respectively, the same average lengths as the sequences in A, B, and C are generated in this way. We generated 10⁴ random fragments in each set, to obtain a good statistics.

We next wanted to compare distributions of melting energies corresponding to fragments in sets A–C with the corresponding melting energies of generated random sets A^rnd, B^rnd, and C^rnd. One should note that sequences within sets A and C can have different lengths as a consequence of the fact that the −10 box has a variable distance relative to transcription start site. Due to this we take into account only the sequence-dependent part of the melting energy (see Appendix C), and we scale melting energy of each fragment with the corresponding fragment length.

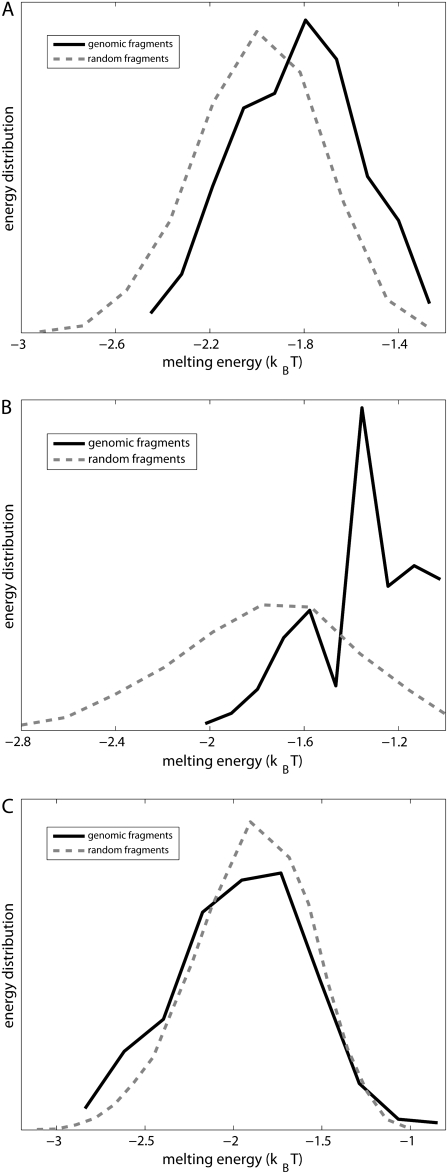
The calculated energy distributions are shown in Fig. 1. The comparison of the melting energy distributions for A and A^rnd are shown in Fig. 1 A. From the figure we see that ∼15-bp regions that are melted in the open complex have significantly smaller melting energy (i.e., are more prone to melting) compared to genomic background. This result is, therefore, consistent with the findings reported in Kanhere and Bansal (8). Further, the comparison of the melting energy for B and B^rnd is shown in Fig. 1 B. We see that the difference in the energy distributions is significantly larger compared to Fig. 1 A, and that −10 boxes have a very pronounced tendency to melt. Specifically, the difference in the means of the melting energy distributions for B and B^rnd shown in Fig. 1 B is almost three times larger compared to the corresponding difference in the means for A and A^rnd. The t-scores (Student's t-test) corresponding to these two differences are 21 and 11.5, respectively, and the corresponding P-values differ for >60 orders of magnitude (the P-values are ∼10⁻⁹⁴ and ∼10⁻³⁰, respectively). Importantly, the comparison of melting energies of C and C^rnd (Fig. 1 C) shows that the regions that span from the downstream end of the −10 box, to the transcription start site, have a melting energy distribution that is not notably different from random genomic background. Actually, the mean of the distribution of the melting energies corresponding to C is even slightly shifted toward higher melting energies corresponding to the mean of C^rnd, which may be due to the existence of promoters with higher melting energy of the region between −10 box and transcription start site, such as promoters of rRNA or tRNA genes (30). We, therefore, conclude that the apparent melting destabilization of the whole ∼15-bp region is actually an artificial consequence of the fact that 6-bp-long −10 regions have much lower melting energies compared to genomic background; actually, the majority of the ∼15-bp-long region, i.e., the whole segment between the −10 box and the transcription start site, is not predisposed for melting.

FIGURE 1.

Melting energies of promoter fragments compared to random genomic background. The values on the horizontal axis give the sequence-specific part of the melting energy scaled by the fragment length (i.e., melting energy per basepair). The dashed-lines give energy distributions for randomly generated DNA fragments. Melting energies are calculated at the physiological values of temperature and salt concentration (37°C and 0.15 M, respectively), and the parameters used in calculations are summarized in Blake et al. (24). (A) The solid line shows the energy distribution corresponding to the genomic fragments that include the entire −10 box and span up to position +2, relative to transcription start. (B) The solid line shows the energy distribution of 6-bp-long genomic fragments corresponding to just −10 promoter regions. (C) The solid line shows the energy distribution of genomic fragments spanning from the downstream edge of the −10 promoter element (position −6) to just upstream of transcription start site (position +2).

The fact that there is a selection pressure to keep only the −10 region prone for melting suggests that only the −10 box, and not the entire ∼15 bp region, is melted through thermal fluctuations. That is, the most likely reason to keep (through a selection pressure) a genomic segment with low melting energy is to be able to excite it to the open (melted) state through thermal fluctuations. The result that the entire part of the transcription bubble from the upstream edge of the −10 box to the transcription start site is not prone for melting renders our earlier result more plausible, namely that the one-step model does not agree with the experimental data. That is, contrary to the assumption of the simple one-step mechanism considered in the previous subsection, the results presented in this section make likely that the region of the transcription bubble outside of the −10 box is melted through a mechanism other than thermal fluctuations. In the next section we will further consider a more complex mechanism, in which only the −10 region is opened through thermal fluctuations in the first step of the open complex formation.

A TWO-STEP MELTING MECHANISM

As mentioned in the previous section, the fact that only −10 boxes are significantly prone for melting, may indicate that only −10 region (and not the entire ∼15 bp region) is melted through natural breathing of DNA, i.e., due to the thermal fluctuations that transiently break the double-stranded DNA bonds. Additional support for such a hypothesis comes from recent structural data (31–33), as noted in Murakami and Darst (34). That is, the structural data indicate that conserved aromatic residues in σ-subunit are ideally positioned to take advantage of transient exposure of the nontemplate strand bases of the −10 element. These RNAP-ssDNA interactions are supposed to facilitate formation of an initial short segment (∼5 bps) of melted DNA, which would form the upstream edge of the final transcription bubble.

The second step in the mechanism of the open complex formation described above should involve extension of the transcription bubble from −10 region to position +2, together with the insertion of the template strand in the active site channel of RNAP. (The template strand has to be inserted in the active site channel, so that RNA can start to be synthesized during the abortive initiation.) There is significant evidence indicating that conformation changes in RNAP would have to play an important role in the second step of the transition from closed to open complex (34). For example, domain 1.1 of RNAP has to be displaced from the active site channel, so that the template strand can be inserted. Furthermore, melting of −10 region may allow for DNA to be more easily bent or kinked to be placed in the entrance of the active site channel, as might be indicated by the experiments in which bending properties of DNA sequences with introduced bubbles are investigated (35). The mechanism through which the second step in the open complex formation would be exhibited is, therefore, likely complicated and remains qualitatively unclear.

However, a result important for modeling comes from recent single molecule experiments (9), which show that there are no intermediates in the transition form closed to open complex, with the lifetimes >1 s. Therefore, since it takes ∼10–100 s for the transition from closed to open complex (i.e., the experimentally inferred transition rates are typically ∼0.1–0.01 1/s), it follows that the first step in the open complex formation, described above, has to be rate-limiting. This conclusion is also indirectly supported by previous kinetic measurements (3,5). Since the experimentally observable quantity is the transition rate from closed to open complex, together with the related rate of the open complex formation, one can focus only on the quantitative modeling of the rate-determining step in the transition from closed to open complex. We, therefore, concentrate below at the first step of the open complex formation.

We start from the kinetic scheme of the two-step mechanism, which can be presented by the following reactions:

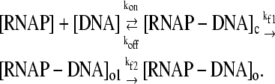(3)

Here [RNAP–DNA]_o1 is the intermediate open complex in which only −10 box is melted, while [RNAP–DNA]_o is the final open complex in which the transcription bubble is extended to just downstream of the transcription start site (2). The transition rate from closed complex to the intermediate open complex is denoted by k_f1 and the transition rate from the intermediate to the final open complex is denoted by k_f2. Rest of the notation is the same as in Eq. 1. As discussed above, the formation of the intermediate complex [RNAP–DNA]_o1 is rate-limiting in the transition from closed to open complex, so the composite transition rate k_f (see Eq. 1), which is the quantity that we are directly interested in, is approximately determined by k_f1 (i.e., k_f ≈ k_f1).

We next address how k_f1 depends on DNA sequence and RNAP-DNA interaction energies. In Appendix E we show that the rate of −10 region melting in the presence of RNAP is proportional to

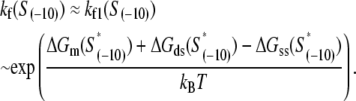(4)

In the expression above, 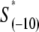denotes the sequence corresponding to positions from −11 to −7, which is the portion of the −10 box that is melted during the open complex formation. One should note that KMnO4 probing (22) indicates that the most upstream base of the −10 region (−12) remains double-stranded in the open complex (33), which is why 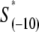does not include base −12. 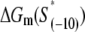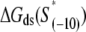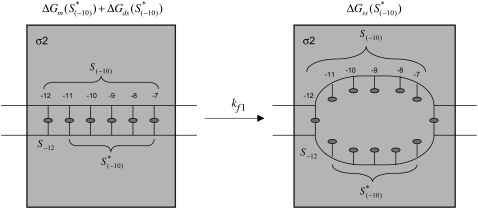The energy terms are denoted as follows: is the melting energy of −10 region of promoter DNA in the absence of RNAP, which originates from Watson-Crick basepairing and stacking interactions; is the sequence-specific interaction energy of σ-subunit with −10 region dsDNA in the closed complex; and, the interaction energy of σ-subunit with the nontemplate strand of −10 region in the open complex is denoted by 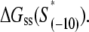Mechanistically, interactions of σ-subunit with dsDNA and ssDNA are exhibited, respectively, through its subdomains 2.4 and 2.3 (34). One should note that the signs of all energy terms in Eq. 4 are such that more negative terms correspond to stronger interactions. Therefore, stronger interaction energy of σ with −10 box dsDNA and larger energy needed to melt the −10 region in the absence of RNAP decrease the k_f values, while the stronger interaction energy of σ with −10 box ssDNA leads to increase of k_f. Fig. 2 illustrates the relationship between the intermediate open complex formation and the energy terms in Eq. 4.

FIGURE 2.

Illustration of the first step in the open complex formation. The left-hand side of the figure illustrates interaction of σ with the −10 region in the closed complex. The right-hand side of the figure indicates the melted −10 box, which corresponds to the intermediate open complex. Six bases that correspond to the −10 box are indicated by their positions (−12 to −7) relative to the transcription start site. The transition, with the rate k_f1, from closed to intermediate open complex is indicated by the arrow. The shaded square indicates σ2 domain, which interacts with the −10 region. The energies that correspond to the closed and open states, as well as the sequence notation that is used in the text are indicated in the figure.

We next want to combine the relationship for transcription initiation rate, given by Eq. 2, with the relationship for the transition rate between closed and open complex, given by Eq. 4. We start with the relation between the dissociation constant and binding energy (see, e.g., (36))

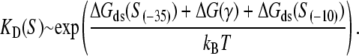(5)

In the above expression, 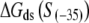is the interaction energy of −35 box dsDNA with the σ-domain 4, ΔG(γ)are energy differences associated with variable spacer length between the −35 box and the −10 box, and the rest of the quantities are as defined in Eq. 4. One should note that the spacer length varies from 21 to 15 bps, with the optimal value of 17 bps (37). Note the difference in the notation between S₍₋₁₀₎ in the equation above, and 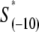introduced in Eq. 4. While the former denotes the entire −10 box (positions −12 to −7), the latter denotes only the portion of −10 box that is melted in the open complex (positions −11 to −7).

Further, it is commonly assumed (38) that K_D ≫ [RNAP], i.e., the saturation effects are neglected (39,40), so the expression for transcription activity given by Eq. 2 simplifies to 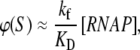which leads to a considerable computational simplification (see, e.g., (39)). One should note that the multiplicative constant (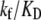) in this (approximate) expression for transcription activity is equal to the inverse slope of τ-plot measurements (15), which is commonly used as a measure of promoter strength (41). We adopt this approximation here, so Eqs. 2, 4, and 5 lead to the following expression for the rate of transcription initiation:

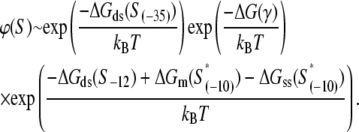(6)

Here 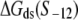is the interaction energy of σ with the −10 box base at position −12, while S₋₁₂ indicates a (single) base that is present at the position −12. In simplifying Eq. 6, we used an additivity assumption, i.e., that 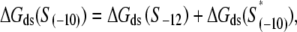which was found to hold well for protein-DNA interactions (42). The reason for the appearance of the term 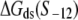in Eq. 6 is that only base −12 in the −10 region remains double-stranded in the open complex.

The expression on the right-hand side of Eq. 6 relates the transcription initiation rate with physical properties of promoter and promoter-DNA interactions. Interpretation of the terms in Eq. 6 is as follows. Both stronger binding of RNAP to −35 box dsDNA 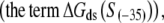and the more optimal spacer length (the term ΔG(γ)), lead to a decrease of the closed complex dissociation constant (see Eq. 5) and consequently increase the rate of transcription initiation. Further, stronger interaction of σ with the nontemplate strand in the open complex 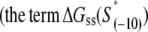and lower melting energy in the absence of RNAP 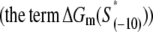increase the rate of the open complex formation, through the increase of k_f (see Eq. 4). Finally, stronger interactions of σ with the bases −12 to −7 in the duplex form increase the closed complex binding affinity (see Eq. 5), but the stronger interactions of σ with dsDNA from −11 to −7 also decrease the rate of transition from closed to open complex (see Eq. 4). Due to these opposing effects, the terms with σ-dsDNA interactions cancel out for bases from −11 to −7, and only the term corresponding to base −12 remains (the term In the next two sections we will use the relationships given by Eqs. 5 and 6 to test the model against experimental data.

TESTING THE TWO-STEP MELTING MECHANISM AGAINST BIOCHEMICAL DATA

We now want to test how well the expressions derived in the previous section agree with the available experimental data. We start by testing the expression for the transition rate from closed to open complex (k_f), given by Eq. 4. In Heyduk et al. (16), the values of k_f were measured for the total of 13 mutants, for which single-nucleotide mismatches were introduced into consensus −10 box. Such a data-set is suitable for testing our model, since all k_f values are measured in a single experiment, i.e., under the same experimental conditions. The −10 box sequences of all mutants, together with the corresponding measured values of k_f, are summarized in Table 1.

TABLE 1.

Biochemical parameters corresponding to the relevant −10 box mutants

Mutant	Sequence	kf(1/s)	†	†	†
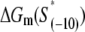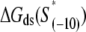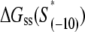Consensus	TATAAT	3.2 × 10−1	0	0	0
12 T→A	AATAAT	3.2 × 10−2	−0.5	0	0
12 T→C	CATAAT	7.5 × 10−2	−0.8	0	0
11 A→T	TTTAAT	5.0 × 10−3	−1.4	2.8	3.0
11 A→C	TCTAAT	1.5 × 10−3	−2.6	2.8	3.0
11 A→G	TGTAAT	1.5 × 10−3	−2.8	2.8	3.4
10 T→C	TACAAT	2.4 × 10−1	−2.4	1.5	0
9 A→T	TATTAT	1.3 × 10−1	0	1.0	2.5
9 A→C	TATCAT	1.4 × 10−1	−2.0	1.3	0
8 A→T	TATATT	7.7 × 10−2	0	1.5	2.5
8 A→C	TATACT	2.5 × 10−1	−1.4	1.0	0
7 T→C	TATAAC	5.0 × 10−3	−2.8	1.0	3.0
7 T→G	TATAAG	1.0 × 10−2	−1.3	1.0	3.0
7 T→A	TATAAA	1.0 × 10−2	0.3	1.0	3.0

^†Energy is given in k_BT units. Experimental conditions and sources of data for the entries in the table are given in the legend of Fig. 3.

To compare the measured k_f values with the ones predicted from our model (see Eq. 4), one needs to know for each mutant sequence: 1), the melting energy 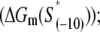2), the interaction energy with the nontemplate strand in the open complex 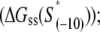and 3), the interaction energy of σ with duplex DNA in the closed complex 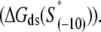As we noted above, the parameters needed to determine the melting energy 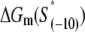have been experimentally measured. To estimate 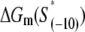we use the MFOLD program (43), which takes into account the Watson-Crick bonds and stacking energies mentioned above, as well as how the bubble initiation energy depends on the initiating nucleotides. The values of 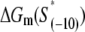for each of the mutants, obtained by MFOLD, are given in Table 1. Furthermore, measurements of RNAP binding to −10 region DNA in both duplex form and in the form that mimics the intermediate open complex were done for all 3*6 single-base mutants of the consensus −10 box (11). These measurements allow inferring interaction energies 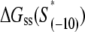and 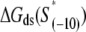for all 13 mutants for which the k_f values are measured in Heyduk et al. (16), as described in Appendix E and summarized in Table 1. Since 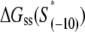should reflect only the interactions of σ with the nontemplate strand in the open complex, and since heparin ensures that only open (but not closed complex) is present, the listed values of 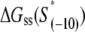correspond to the binding energies inferred from the measurements done in the presence of heparin (see Appendix E). 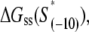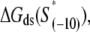Also, note that the zero value of energy for 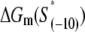listed in Table 1 corresponds to the consensus −10 box, since the interaction energy values are inferred from the binding measurements in which the appropriate consensus −10 box constructs are used as the references.

For notational simplicity, we will hereafter refer to 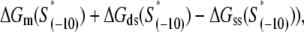which appears in the exponent on the right-hand side of Eq. 4, as effective energy. Consequently, two predictions follow directly from Eq. 4. First, the values of log(k_f) should correlate well with the effective energy. That is, if log(k_f) is plotted versus the effective energy, the points should (approximately) be on a straight line. Second, the slope of this line should be equal to one, provided that the effective energy is expressed in the units of k_BT.

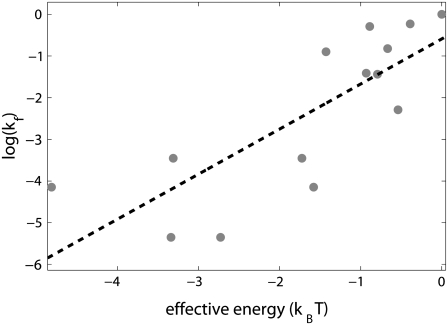
In Fig. 3, we show the test of these two predictions, i.e., the logarithm of the experimentally measured k_f values (16) is plotted against the values of the effective energy (see Table 1). One can observe that the two relevant quantities correlate well with each other, with the value of correlation constant equal to 0.79. This correlation is highly statistically significant with the P-value of ∼10⁻³. Furthermore, the value of the slope of the line fitted to the points shown in Fig. 3 equals to 1.1 ± 0.5 (with 95% confidence), which is very close to the slope of 1 predicted by our model.

FIGURE 3.

Comparison of the model with biochemical data. The values on the vertical axis give the logarithm of the experimentally measured rates of transition from closed to open complex k_f, and correspond to measurements at 25°C and 0.1 M salt concentration (16). All k_f values are scaled with the transition rate that corresponds to the consensus −10 box sequence. The values on the horizontal axis give the effective energy in units of k_BT (k_BT ∼ 0.6 kcal/mol). The zero of energy coincides with the effective energy of the consensus −10 box sequence. The values of melting energy, which enter the expression for the effective energy, were calculated for each sequence by using MFOLD (43), under the same conditions as those in k_f measurements. Interaction energies of RNAP with DNA in duplex form, and in the form that mimics the intermediate open complex, were inferred from binding measurements in Fenton and Gralla (11). The conditions for the binding measurements in Fenton and Gralla (11) were 0°C (to reduce melting of DNA upon RNAP binding to DNA in duplex form) and 0.1 M salt concentration, while RNAP was in large excess over DNA probes (the respective concentrations were 100 nM and 1 nM). The dashed line is the linear fit to the data.

While the obtained correlation constant is quite high and highly statistically significant, some of the scatter between the predicted and experimentally observed values (Fig. 3) may be a consequence of nonuniform experimental conditions. That is, while the transition rates are measured at 25°C (16), the σ-DNA interaction energies are inferred from measurements done at 0°C (11). Although σ-DNA interaction energies (scaled by k_BT) should not significantly change in that temperature range, which is roughly supported by an absence of a significant change of dissociation constant with temperature (44), we believe that eliminating the difference in the experimental conditions would further improve the correlation in Fig. 3. Furthermore, a possibly more important source of the scatter in Fig. 3 is the fact that interaction energies of σ with promoter DNA in the closed complex 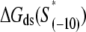may be subject to errors due to possible melting of dsDNA construct upon RNAP binding. That is, despite the lower temperature at which the measurements were performed (0°C), some of the duplex DNA constructs may be melted as a consequence of RNAP binding, thus introducing errors in the measurements of σ-dsDNA interaction energies, which we further discuss in the next section.

TESTING THE TWO-STEP MELTING MODEL AGAINST GENOMICS DATA

We next want to test whether our model is consistent with the available genomics data, where by genomics data we consider the experimentally confirmed core promoter sequences. The test is based on the following general idea. We can first infer contributions of different bases at different positions in promoter regions to the rate of transcription initiation (i.e., the weight matrix elements) from genomics data, by using statistical methods. On the other hand, provided that our model (i.e., Eq. 6) is correct, the same combination of parameters can be directly connected with the measured biochemical quantities (interaction energies and melting energy). The two independently inferred sets of weight matrix elements can then be directly compared with each other, as a test of our model.

We start with the independent nucleotide assumption, which is widely used in weight matrix searches of core promoter sequences (37,45), according to which the rate of transcription initiation is given by the product of terms that correspond to different bases in promoter regions and different spacer lengths. Under this assumption, it is straightforward to obtain that the rate of transcription initiation can be written in a general form, in terms of weight matrices:

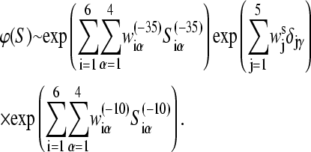(7)

Here w_iα presents weight matrices, with superscript ((−35), (−10), or s) indicating that the weight matrix corresponds, respectively, to −35 box, −10 box, or spacer. The index i denotes different positions within the −35 box and −10 box, while the index j denotes five possible spacer lengths. Specifically, in the case of the −10 box, i = 1 corresponds to the position −12, while i = 6 corresponds to the position −7, relative to the transcription start site. Further, α denotes the four different bases (A, T, C or G), while S_iα is equal to one if base α is present at position i in sequence S, and is equal to zero otherwise. Similarly, δ_jγ is the Krönecker delta symbol, which is equal to one if j is equal to the promoter spacer length γ, and is equal to zero otherwise. Superscripts (−35) and (−10) in S_iα indicate, respectively, whether the sequence corresponds to the −35 or −10 region.

In the further test, we will concentrate on 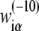in Eq. 7, since the −10 region is directly involved in the first (rate-limiting) step of promoter melting. The matrix 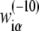can be first determined only from genomics data, i.e., from DNA sequences associated with the experimentally confirmed transcription start sites. The underlying assumption is that the probability that a given promoter sequence S is sampled (i.e., present) in the database is proportional to transcription activity ϕ(S) associated with this sequence. The weight matrix parameters can then be determined by a maximum likelihood approach, in a similar way as described previously (36,45). Briefly, the initially unknown weight matrix elements are determined such that they maximize the probability that the sequences in the database are sampled as promoters (where the sampling probability is proportional to ϕ(S)), while those sequences that are not observed in the database are not sampled. As the end result, the matrix elements 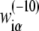are equal to the logarithm of the ratio of probability to observe base α at position i in a collection of aligned −10 regions, compared to the probability of observing the base in the genome as a whole. By using this method, we calculate the weight matrix elements 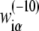from the set of 322 −10 regions, which are associated with experimentally confirmed E. coli transcription start sites. The −10 regions were obtained by using the Gibbs search algorithm, as described above (see also Appendix D). We will hereafter refer to the weight matrix determined in this way (from the genomics data) as the genomics weight matrix.

On the other hand, 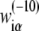can also be inferred from our model, by directly comparing Eqs. 6 and 7. The following identification is apparent:

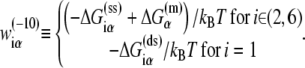(8)

Here 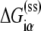denotes the energy matrix of interactions of σ with −10 box ssDNA in the open complex, while 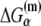denotes the energy required to melt base α in the absence of RNAP (see Appendix C). The asymmetry with respect to the index i on the right-hand side of Eq. 8 comes from the fact that the base −12 remains double-stranded in the closed complex, while bases −11 to −7 are melted. Since binding measurements were done for all 3*6 mutants of the −10 box in the configuration that mimics the open complex (see the previous section), this directly provides the experimental estimate of the energy matrix 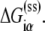Similarly, energy parameters of dsDNA melting were also experimentally measured (46), from which parameters 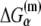can be inferred, as we describe in Appendix C. We will hereafter refer to the expression on the right-hand side of Eq. 8 as the effective energy matrix. One should note that interactions of RNAP with −35 box and the effects of different spacer lengths do not enter the effective energy matrix (i.e., Eq. 8), since, as noted above, we address how rate of transcription initiation changes with change of bases in the −10 box.

As a test of our model, we next want to compare the genomics weight matrix with the effective weight matrix. One should note that the two weight matrices are inferred independently from each other. That is, to infer the genomics weight matrix, we used the experimentally determined transcription start sites together with the maximum likelihood method. On the other hand, the effective weight matrix is obtained independently from either genomics data or any statistical inference test, i.e., it is obtained directly from our model and experimentally inferred interaction and melting energies. Consequently, similarly to the previous section, two predictions follow from our analysis. First, the matrix elements that correspond to the genomics weight matrix and the effective weight matrix have to correlate well with each other. Second, if the genomics weight matrix elements are plotted versus the effective weight matrix elements, the slope of the corresponding line should be equal to one, provided that the energies that enter the effective weight matrix are in units of k_BT.

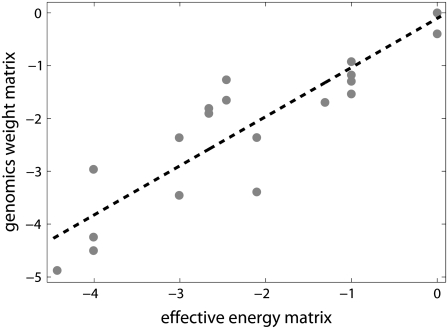
The test of these two predictions is shown in Fig. 4. The correlation between the two quantities is very high, with the correlation constant of 0.92. This value of correlation is statistically highly significant, with the P-value of ∼10⁻¹⁰. The value of the slope of the line fitted to the points in the figure is 0.93 ± 0.2 (with 95% confidence), which is in a very good agreement with our prediction. Therefore, our model shows a very good agreement with the genomics data. Similarly as with the comparison with the biochemical data (previous section), no free parameters were used in model testing.

FIGURE 4.

Comparison of the model with genomics data. The values on the vertical axis are elements of the genomics weight matrix, which correspond to −10 region. The genomics weight matrix was constructed based on experimentally determined transcription start sites assembled in RegulonDB database (17). The values on the horizontal axis are the corresponding elements of the effective energy matrix, in units of k_BT. The melting energy part of the effective energy matrix was calculated based on the parameters summarized in Blake et al. (24), at physiological conditions (37°C and 0.15 M, respectively) under which most of the experimentally determined transcription start sites are likely sampled. The source of data and the experimental conditions used to infer interaction energies of RNAP with DNA that enter the effective energy matrix are the same as those in the legend of Fig. 3. The zero at each column of the matrices is chosen to coincide with the consensus base at the given position in −10 box. (Note that an arbitrary base independent value can be added to each column of the weight matrix, which corresponds to shifting the position of zero of energy.) The dashed line is the linear fit to the data.

Finally, in the previous section we commented that possible melting of dsDNA upon RNAP binding would introduce errors in the measurements of the interaction energies of σ with −10 region in the closed complex. This is actually implicitly confirmed by the comparison of our model with the genomics data presented in this section, since this comparison is based on the derived relationship for transcription initiation rate, in which σ−dsDNA interaction energies in the closed complex cancel for most of the bases in the −10 region. This cancellation eliminates sensitivity of the comparison with the genomics data to the possible systematic errors in the measured σ-dsDNA interaction parameters, which is expected to lead to a better agreement of the model with the experiment. Indeed, the correlation constant obtained in the case of the genomics data (0.92) is higher compared to the correlation constant obtained in the case of the biochemical data (0.79), where such cancellation does not happen.

DISCUSSION

Significant experimental advances in understanding transcription initiation have recently emerged, such as the determination of the structure of bacterial RNAP holoenzyme both alone and in complex with DNA (31–33). These new advances came in addition to more than two decades of intensive experimental work, which analyzed a number of properties of the transcription initiation process. However, despite many elegantly posed experiments, the mechanism by which RNAP forms an open complex has not yet been understood (6). A part of the difficulty in understanding the open complex formation lays in the fact that the large amount of quantitative measurements were not matched by quantitative models that would allow appropriate analysis of such data. Motivated by this, we here developed the first quantitative model of the open complex formation by bacterial RNA polymerase. The model is based on a biophysics approach, while bioinformatic methods and statistical analysis were used in testing the model against available biochemical and genomics data.

As the initial approach, we started from a simple one-step mechanism of the open complex formation, and showed that this mechanism cannot be reconciled with the available experimental measurements. We furthermore showed that previously reported melting destabilization of an ∼15-bp region (that roughly corresponds to the total length of the transcription bubble), which provided an initial motivation for a simple one-step hypothesis, is an artificial consequence of the fact that only the 6 bp −10 region is highly prone to melting. Considerations of a simple mechanism lead us to a more complex two-step hypothesis of the open complex formation, where the first step corresponds to melting of the −10 box, while in the second step the transcription bubble is extended from the downstream edge of the −10 box to just upstream of the transcription start site. The fact that the transition from closed to intermediate open complex is rate-determining (9) allowed us to quantitatively model only the first step of the open complex formation, to obtain the rate of transition from closed to open complex. This proved to be useful, since it remains qualitatively unclear how exactly the extension of the transcription bubble toward the transcription start site and insertion of the template strand in the active site channel is physically exhibited. One possibility is that interaction of the melted −10 region ssDNA with σ-domain 2 induces conformation changes in RNAP, which lead to the extension of the transcription bubble from −10 region to transcription start site. Future experiments aimed at mapping conformation changes in RNAP as well as interactions of RNAP with promoter DNA that likely happen during the second step of the open complex formation could help resolving this issue.

The quantitative model resulted in an explicit relationship, which connects the rate of transition from closed to open complex, and consequently the rate of open complex formation, with the physical properties of promoter and σ-promoter interactions. The model was tested against both biochemical and genomics data, and showed a very good agreement with the experimental data, with no free parameters used in model testing. The quantitative model also appears to be qualitatively consistent with recent experimental findings, which report that the core of promoter melting activity of the polymerase is localized to contacts of σ-subunit with −10 box (47,48), and with structural studies (31–33), indicating that aromatic residues of σ-subunit are well positioned to take advantage of transiently exposed nontemplate strand bases of the −10 element. Good agreement of our model with experimental data indicates that the model is valid for majority of promoter sequences. However, we note that for some promoters the mechanism for the open complex formation may be different from the one considered here. The cases in which this may be true are rRNA and tRNA promoters, which require presence of ribonucleotides to form a stable open complex (7). Additionally, the work presented here concerns only the basal process of transcription initiation, and how this process is influenced by different regulatory mechanisms, such as changes in DNA supercoiling (49) or regulation by transcription factors, is not addressed in this article. However, we think that our model is a useful starting point for such studies, and we believe that a way to include the effects of regulators is by considering how different mechanical stresses that they induce will modify kinetic parameters considered in this article.

From a practical point, our results allow estimating the rate of transition from closed to open complex for a given promoter sequence, which would otherwise require performing quite demanding experimental measurements, individually for each promoter of interest. This in turn allows efficient engineering of promoter sequences with desired kinetic properties. From a bioinformatics perspective, our model allows analysis of kinetic properties of DNA sequences on the whole genome scale. For example, the model allows detection of so-called poised promoters (50), which are sequences where RNAP is recruited (bound) with high efficiency, but has inherently low rate of transition from closed to open complex. Such promoter sequences may be dependent on activators or negative supercoiling to increase their inherently slow rate of transition from closed to open complex, and our model can help in detecting such cases.

Related with the above, in a recent work (50) it was noted that poised promoters are quite common, i.e., that there is a significant fraction of genomic regions where RNAP is bound with high occupancy, but which are not associated with transcription activity. The authors further showed that bound genomic fragments associated with transcriptionally active genes tend to have lower values of melting energies of ∼15 bp regions (corresponding to the length of entire transcription bubbles), compared to the bound genomic fragments that appear to be poised. It was, however, also noted that the distinction between the transcriptionally active and poised group of promoters is not very clear through such analysis, i.e., that the two corresponding distributions of melting energies significantly overlap with each other. We point out that our model can allow accurately analyzing transcription poising: That is, calculating melting energies for 15-bp windows only introduces noise in the analysis, since we here explicitly showed that the regions from the downstream edge of −10 box to transcription start sites, associated with transcriptionally active promoters, are not prone for melting. Furthermore, in addition to the energy needed to melt DNA in the absence of RNAP, transition from closed to open complex also significantly depends on interactions of RNAP with DNA. All these effects are straightforwardly taken into account through a relatively simple relation given by Eq. 4, which can be used to analyze RNAP poising on a genomewide scale.

Another bioinformatics issue is connected with our analysis, and is related with the fact that weight matrix searches result in an apparently too-high number of predicted promoters. The good correlation between the weight matrix that is inferred from experimentally determined transcription start sites (genomics weight matrix) and the weight matrix that originates from our model of transcription initiation (effective weight matrix) was used as a test of our model. However, if this argument is turned the other way, this good agreement also indicates that searches for transcription start sites based on maximum-likelihood method (i.e., using genomics weight matrix) are indeed capable of adequately predicting basal rates of transcription initiation. Therefore, a relatively high number of false positives is likely a consequence of the fact that there are factors that are not taken into account by weight matrices, such as regulation of transcription initiation by transcription factors. More technical bioinformatics issues may also contribute to (too) large number of predicted promoters, such as a difficulty to accurately align −35 boxes, given that the −35 box is considerably less conserved and at a variable distance from −10 region, as well as how to optimally set a threshold value that classifies a given DNA sequence as a predicted promoter.

We finally note that a mechanism different from the one on which our model is based has been considered in literature (see, e.g., (5)), According to this proposition, RNAP actively flips the base at the position −11 as the first step of transcription bubble formation. This mechanism is different from a passive mechanism that we consider here, according to which the entire −10 box is melted through thermal fluctuations facilitated by interactions of σ-subunit with −10 box ssDNA. The main motivation behind this active hypothesis comes from several experiments that demonstrated the importance of A at position −11 for the open complex formation (see, e.g., (16) and references therein), but there has been no proof for this hypothesis. We, however, note that experiments which demonstrate the importance of −11A for the open complex formation are in a very good agreement with our model since base −11A (preceded by −10T) has the lowest melting energy and since the base at this position has a significantly larger energy of interaction with ssDNA compared to other bases in −10 region. Due to this, it directly follows from our model (see Eq. 6) that mutation of base −11A leads to a significantly larger effect compared to mutating other bases in the −10 region. We furthermore note that a mechanism, by which flipping of (only) −11A presents the first step in the transcription bubble formation, appears to be unlikely since the first step in the bubble formation has to be rate-determining and since bases in −10 region downstream of −11 show significant contribution to the rate of transition from closed to open complex. At the same time, the model considered here shows a very good quantitative agreement of contributions of different bases in the −10 region to the rates of open complex formation, as reflected through comparison with both biochemical and genomics data. Therefore, while we are currently not able to model active flipping of −11A by RNAP, and consequently cannot outright eliminate possibility that RNAP is opened through such process, we think that this possibility is unlikely given the above arguments.

In summary, we here developed the first quantitative model of the open complex formation by bacterial RNA polymerase, and showed that the model is in a good agreement with experimental data. Such good agreement justifies the quantitative model that we developed, and it furthermore strongly supports the qualitative hypothesis by which the open complex is formed through the two-step mechanism described above. This result is biologically highly significant, since it is very hard to experimentally observe the short-living intermediates in the open complex formation. That is, the way to currently test different hypothesis of the open complex formation is to map a qualitative hypothesis to a corresponding quantitative model, which can be compared against measurable experimental quantities. From a more practical point, our results allow both efficient design of promoters with desired kinetic properties, and bioinformatic analysis of kinetic properties of promoter sequences on the whole genome scale. We therefore expect that our model together with further experimental studies will provide a basis to significantly improve conceptual and practical understanding of the transcription initiation process.

APPENDIX A: GENERAL KINETIC SCHEME

We start with a simplified kinetic scheme for a transcription cycle, which is given by the following reactions:

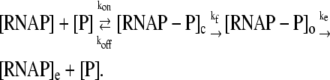(9)

In the above reaction, [RNAP], [P], and [RNAP−P]_e are, respectively, concentration of free RNAP, concentration of free promoter DNA, and concentration of RNAP in elongation state; [RNAP−P]_c is concentration of the closed RNAP-promoter complex and [RNAP−P]_o is concentration of the open RNAP-promoter complex. On- and off-rates of the closed complex formation are denoted by k_on and k_off. The forward rate of transition from closed to open complex is denoted by k_f, while the rate of promoter escape is denoted by k_e. For simplicity, individual steps of processive elongation and transcription termination are not included in the scheme given by Eq. 9.

We further assume that a steady state is established in the above reactions, which leads to the following balance equation for [RNAP−P]_c,

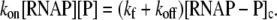(10)

Similarly, the steady-state assumption leads to the balance equation for [RNAP−P]_o,

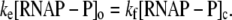(11)

We further use that the total concentration of promoter [P_t] has to be equal to the sum of free promoter concentration and the concentration of promoter in closed and open complexes:

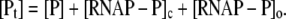(12)

A common assumption (7,22), which we will further adopt, is that the open complex formation is rate-limiting in the transition from the closed complex to the elongation complex (k_f ≪ k_e). With this assumption, Eq. 11 leads to [RNAP−P]_o ≪ [RNAP−P]_c, so the last term on the right-hand side of Eq. 12 can be neglected.

If we introduce the closed complex promoter occupancy as 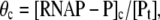the rate ϕ of the open complex formation is given by the flux density ϕ = θ_ck_f. By using Eqs. 10 and 12, we obtain that

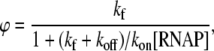(13)

where all the notation is defined in Eq. 9. One should note that the rate of the open complex formation given by Eq. 13 is equal to the rate of transcription (i.e., elongation) initiation, since in steady state the balance Eq. 11 has to be satisfied, i.e., the flux has to be conserved.

From Eq. 13, it can be seen that the sum of rates k_off and k_f enters the expression for ϕ. Therefore, binding of RNAP to DNA and the transition from closed to open complex are, in principle, coupled in the expression for transcription activity. However, kinetic experiments indicate that the measured k_off values are significantly larger compared to k_f (18–21), and by using k_off ≫ k_f, Eq. 13 can be simplified to

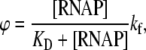(14)

where K_D is the dissociation constant for the closed complex formation, which is equal to k_off/k_on. As a final note, Eq. 14 justifies an assumption used in thermodynamic modeling that the rate of transcription initiation is proportional to the equilibrium binding probability of RNAP to promoter, which is given by the term [RNAP]/(K_D + [RNAP]) (51,52).

APPENDIX B: KINETICS OF BUBBLE FORMATION IN dsDNA

We here address the kinetics of a bubble formation in a segment of dsDNA. The (free) energy cost to initiate a bubble in dsDNA is ∼11 k_BT (k_B is Boltzmann constant and T is temperature), which is significantly higher compared to the cost to extend the bubble for one bp (which is 1–4 k_BT). Due to this, the bubble is formed as a zipper (26), so the bubble dynamics corresponds to a biased random walk, which is described by the following master equation:

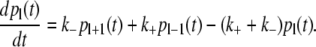(15)

Here p_l(t) is a probability to observe a bubble of size l, while k₊ and k₋ are, respectively, the rates with which the bubble grows or shrinks for one bp. For a simpler notation, we here assume that the bubble is formed in a homopolymer DNA, but the same arguments apply for heteropolymer DNA (53). In the continuous limit, the master equation (Eq. 15) leads to the following drift-diffusion equation:

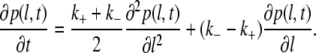(16)

If one starts from a bubble of size l₀ and assumes that the dynamics is determined by Eq. 16, the mean bubble closing time τ_c is given by the mean first passage time to reach l = 0. From Eq. 16 follows (see also (53)) that the mean time of bubble closing (τ_c) is approximately given by

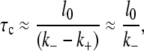(17)

where the last approximate equality uses k₋ ≫ k₊, due to the energy barrier needed to open a base.

To obtain the rate (time) of opening of a bubble of size l₀, one should observe the reversible reaction of bubble formation:

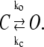(18)

Here C is a closed bubble, O is an open bubble, while k_o and k_c are, respectively, the rates of bubble opening and closing. The two rates are connected via

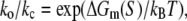(19)

where ΔG_m(S) is the energy needed to melt a DNA segment of sequence S and length l₀. Finally, by using Eqs. 17 and 19, we obtain

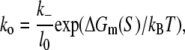(20)

where l₀ is the length of DNA sequence S. The parameters needed to determine ΔG_m(S) depend on temperature and salt concentration and have been extensively experimentally measured, and melting of DNA has been theoretically modeled (24,54). Calculation of the melting energy ΔG_m(S) will be the subject of the next subsection. The base closing rate k₋ was measured to be 10⁵ s⁻¹ by spectroscopic studies (26) and 10⁸ s⁻¹ by NMR experiments (25), and we use both of these values in parallel in the estimates given below.

We next calculate k_f for the sequences in set A, which is in this model determined by the rate of bubble opening k₀ given by Eq. 20. To calculate k_f for the sequences in set A we use the values of the melting energy calculated at a temperature of 37°C and salt concentration of 0.1 M, which are the conditions that correspond to most in vitro measurements of k_f. One should note that we do not take into account DNA supercoiling, since the experimental measurements of k_f that we used to test the model were performed on linear (i.e., not supercoiled) DNA templates. We obtain that the mean value of k_f rates for sequences in A is between 10⁻⁷ and 10⁻¹⁰, depending on whether k₋ rate from NMR or spectroscopic studies is used. These values are approximately five-to-eight orders of magnitude smaller compared to the experimentally measured k_f values, which are typically in the range from 0.1 to 0.01 s⁻¹ (18–21).

APPENDIX C: DNA MELTING ENERGY

The free energy ΔG_m(S) needed to form a bubble with length l and sequence S is given by the following expression:

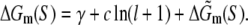(21)

Here γ is the energy cost to initiate the bubble (γ = 11.3 k_BT), the second term on the right-hand side is the entropy cost to form a loop of length l (c = 1.7 k_BT), while 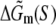corresponds to the sequence-dependent part of energy needed to melt DNA (46). 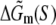results from the energy needed to break Watson-Crick hydrogen bonds on the opposing strands of DNA, as well as stacking interaction between nearest-neighbor nucleotides. We use the model given by Eq. 21 in the order-of-magnitude estimates, which are done in testing the one-step model of open complex formation. A more accurate parameterization, exhibited by MFOLD (43), which also takes into account the sequence dependence of the bubble initiation energy, and a more accurate estimate of the loop entropy cost for the small bubble lengths, is used in comparing the model with the measured transition rates.

The parameters needed to calculate 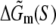have been experimentally measured and summarized in Blake et al. (24). 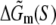has been parameterized in terms of the energies 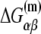needed to denature base β given its nearest-neighbor base α. There are total of 16 parameters 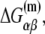but only10 are independent due to symmetry (e.g., 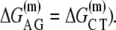The free energy 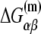can be separated in enthalpy 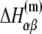and entropy 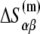contribution in the following way:

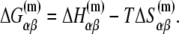(22)

The above equation gives dependence of the parameters 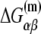on temperature. While the physiological temperature is 37°C, relevant in vitro experiments are sometimes performed on different temperatures. The experimentally measured parameters (24) 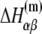and 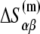are summarized in Table 2.

TABLE 2.

The enthalpy and entropy contributions to dinucleotide melting free energy

	A	T	C	G
*
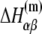A	7.9	7.2	8.4	7.8
T	7.2	7.9	8.2	8.5
C	8.5	7.8	8.0	10.6
G	8.2	8.4	9.8	8.0
*
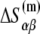A	22.2	20.4	22.4	21.0
T	21.3	22.2	22.2	22.7
C	22.7	21.0	19.9	27.2
G	22.2	22.2	24.4	19.9

^*The enthalpy and entropy values are in kcal/mol and cal/(mol K), respectively, and correspond to the salt concentration of 1 M (24).

The experimentally measured values listed in Table 2 correspond to 1 M salt concentration (46), however physiological salt concentration is between 0.1 M and 0.2 M, and most in vitro measurements related with transcription initiation are done in that range. The correction for the salt concentration is given by (46)

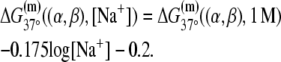(23)

In the equation above (α,β) denotes dinucleotide pair, 0.175 and 0.2 are in kcal/mol, [Na⁺] is salt concentration, and the first term on the right-hand side is the denaturation energy corresponding to 1 M salt concentration. One should note that the small nonzero intercept term (0.2 kcal/mol), i.e., the fact that the expression on the right-hand side does not exactly go to 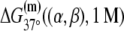when [Na⁺] goes to 1 M, is the consequence of the fact that Eq. 23 is obtained as the best linear fit to the experimental data.

Finally, given the DNA sequence S, the sequence-dependent part of the melting energy is given by

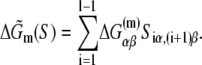(24)

Here 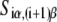is equal to 1 if bases α and β are present, respectively, at the positions i and i+1 in sequence S, and is equal to zero otherwise. The values of 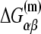in Eq. 24 should be calculated at the appropriate temperature and salt concentrations, by using Eqs. 22 and 23. Here 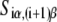is equal to 1 if bases α and β are present, respectively, at the positions i and i+1 in sequence S, and is equal to zero otherwise.

Finally, while the parameters 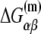reflect the dependence of melting energy on nearest-neighbor nucleotides, we also use the values of the melting energy 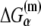in the single nucleotide approximation. That is, 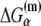reflect the energy needed to melt base α, where one averages the dinucleotide parameters 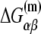over the nearest-neighbor correlations. A natural choice for the averaging is

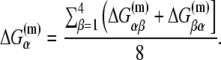(25)

One should note that the expression in Eq. 25 preserves the symmetry of the two DNA strands, i.e., 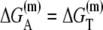and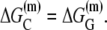

APPENDIX D: RegulonDB SEQUENCE EXTRACTION AND −10 BOX ALIGNMENT

We here describe the identification of −10 boxes from the assembly of transcription start sites in the RegulonDB database (17). The list of transcription start sites in RegulonDB consists of promoters that correspond to both σ⁷⁰ and alternative σ-factors (55), and computational predictions are assembled together with the experimentally verified promoters. Since σ⁷⁰ is responsible for majority of transcription activity in cells, we here focus at σ⁷⁰ promoters, and we select only those sequences that correspond to experimentally verified σ⁷⁰ transcription start sites. This selection results in the total of 342 transcription start sites, and we use the obtained start sites to extract DNA segments corresponding to positions −17 to −2, relative to the transcription start sites. Positions −17 to −2 were chosen by having in mind that the distance of the −10 box from the transcription start site varies from 4 bp to 12 bp (56), to which we added an additional 2-bp flexibility to insure that −10 boxes are located within the selected DNA segments.

To identify the 6-bp-long −10 boxes within the selected DNA segments, we used the Gibbs sampler (27). The Gibbs sampler implements a version of the Gibbs search algorithm (28), which is used to find mutually similar motifs in a given set of DNA sequences. Only the DNA strand defined by the direction of transcription was searched, since −10 box motifs (with the consensus TATAAT) are not palindrome-symmetric. The search was done with the initial assumption that one motif element is present in each DNA segment, since −10 box motifs are ubiquitous elements of bacterial promoters (37). However, in the end of the Gibbs sampler search, individual motif elements are added in or taken out, in a single pass of the algorithm, depending upon whether or not their inclusion improves the value of the alignment score. The last step allows excluding from the alignment those sequences that do not have −10 box motifs, e.g., due to database misassignments. The search resulted in the identification of 322 aligned −10 boxes, which were used in the further analysis.

APPENDIX E: MELTING OF THE −10 REGION IN THE PRESENCE OF RNAP

We here look at the formation of the intermediate open complex, which corresponds to −10 region melting. During opening of −10 region, RNAP interacts with −10 region in both ssDNA form and dsDNA form, and the following interactions are relevant: The closed (nonmelted) state of −10 box is stabilized by: 1), the energy of Watson-Crick basepairing and stacking interactions; and 2), the energy of interactions of σ-domain 2.4 with dsDNA in the closed complex. On the other hand, in the open complex, the nontemplate strand of −10 region interacts with σ-domain 2.3.

The ratio of the rates of opening k_f1 and closing k_c1 of the −10 region is determined by the difference of the energies in the two states given above:

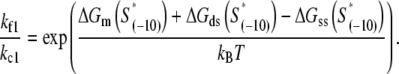(26)

Here 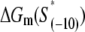is the melting energy of the −10 region with sequence S*₍₋₁₀₎ in the absence of RNAP, 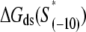is the total interaction energy of σ-subunit with −10 region in the closed complex, and 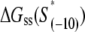is the total interaction energy of σ with −10 region in the open complex. Since experimental measurements (16) indicate that the rate of open complex dissociation k_c1 does not significantly depend on DNA sequence, Eq. 26 leads to the dependence of the transition rate k_f1 from DNA sequence S*₍₋₁₀₎,

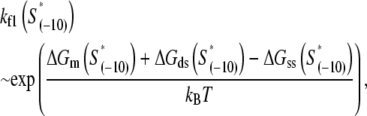(27)

which is used in the further analysis.

Values for melting energy 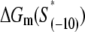in the above expression can be calculated as described in Appendix C. Furthermore, measurements of RNAP binding to −10 region in both duplex form and in the form that mimics the intermediate open complex were done for all 3*6 single-base mutants of the consensus −10 box (11). From these binding measurements, one can infer interaction energies 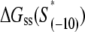and 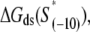as described below.

In the equilibrium, the following relations hold for RNAP binding to the consensus −10 box and a mutant sequence:

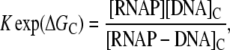(28)

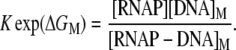(29)

In the above equations [DNA], [RNAP], and [RNAP–DNA] denote, respectively, free DNA, free RNAP, and DNA in complex with RNAP, while the indices C and M denote consensus −10 box and a mutated sequence, respectively. ΔG_C denotes binding free energy, while K is a constant with the units of concentration (see, e.g., (39)). The above equations use that the amount of free RNAP ([RNAP]) is essentially the same in binding to both the consensus and mutant DNA sequence (and approximately equal to the total RNAP concentration), since in the binding experiments (11) σ is in a large access compared to DNA (the respective concentrations are 100 nM and 1 nM). Also, if we denote total DNA (bound plus free) used in the experiment as [DNA]_t, it holds that [DNA]_t = [DNA]_C + [RNAP−DNA]_C and [DNA]_t = [DNA]_M + [RNAP−DNA]_M (11).

If these relations are used together with Eqs. 28 and 29, the relation can be obtained of

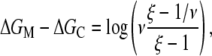(30)

where we introduced ν = [RNAP − DNA]_C/[RNAP − DNA]_M and ξ = [DNA]_t/[RNAP − DNA]_C. One should note that ΔG_M − ΔG_C gives interaction energies 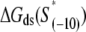and 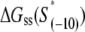for mutant −10 box with sequence S*₍₋₁₀₎, where an appropriate double-stranded or single-stranded construct is used, and zero of energy corresponds to the consensus −10 box sequence. Furthermore, the values of ν were reported in Fenton and Gralla (11), while we determined the values of ξ by analyzing gels in Fenton and Gralla (11) with the program Scion Image (Scion, Frederick, MD) (the values of ξ were estimated as Eqs. 3 and 9 in the case of binding to dsDNA and ssDNA constructs, respectively).