Hierarchical Modeling of the Elastic Properties of Bone at Submicron Scales: The Role of Extrafibrillar Mineralization

Abstract

We model the elastic properties of bone at the level of mineralized collagen fibrils via step-by-step homogenization from the staggered arrangement of collagen molecules up to an array of parallel mineralized fibrils. A new model for extrafibrillar mineralization is proposed, assuming that the extrafibrillar minerals are mechanically equivalent to reinforcing rings coating each individual fibril. Our modeling suggests that no more than 30% of the total mineral content is extrafibrillar and the fraction of extrafibrillar minerals grows linearly with the overall degree of mineralization. It is shown that the extrafibrillar mineralization considerably reinforces the fibrils' mechanical properties in the transverse directions and the fibrils' shear moduli. The model predictions for the elastic moduli and constants are found to be in a good agreement with the experimental data reported in the literature.

INTRODUCTION

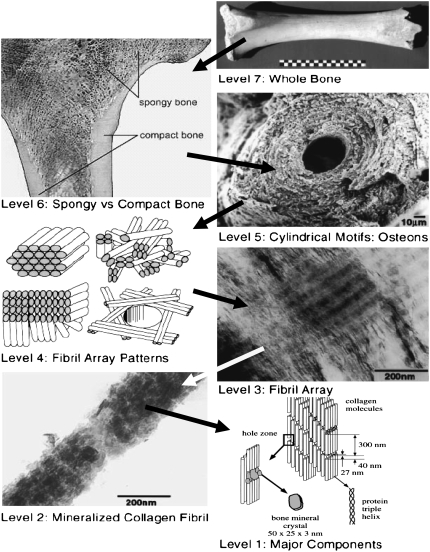
The remarkable mechanical properties of bone related to its low density are essentially due to the bone's complex, hierarchical microstructure from the macro- down to the nanoscale (1–3), Fig. 1. At length scales below several microns, the diversity of bone tissues is reduced to different arrangements of mineralized collagen fibrils (Fig. 1, Level 4) formed through self-assembly of soft collagen molecules and hard mineral nanoparticles. At this level of organization, the effective mechanical properties of bone depend on the properties of the fibrils' constituents, the fibrils' microstructure, and orientation distribution, as well as on the mineral content and the shape of the mineral particles. Clearly, the development of reliable structure-properties relations for mineralized collagen fibrils and for fibril arrays incorporating these dependencies is of crucial importance, not only for the evaluation of the mechanical properties of bone, but also for better understanding of how the governing material-design principles, growth processes, or diseased states influence the mechanical properties at submicron length scales. Such relations can also help answer some still unclear questions about the bone structure and serve as a tool for designing of new bone implants and bioinspired nanocomposites.

FIGURE 1.

Hierarchical structure of bone. Images for Levels 2–5 and 7 after Weiner and Wagner (1); for Level 1 after Rho et al. (2); for Level 6 from Functional Anatomy & Biomechanics (University of Glasgow, http://www.gla.ac.uk/ibls/US/fab/tutorial/generic/bone2.html). The arrows point from a higher to a lower hierarchy level. Levels 6 and 7, macroscopic length scale; Level 5, mesoscale; Levels 3 and 4, micron scale; Levels 1 and 2, nanoscale.

At the nanoscale (Fig. 1, Levels 1 and 2), bone consists of:

• Collagen type I molecules (triple helices ∼300 nm long and ∼1.5 nm in diameter), self-assembled in a staggered fashion to form collagen fibrils with diameter of ∼100 nm (1).

• Biological hydroxyapatite (HA) minerals with hexagonal unit cells (1).

• Water (1), part of which provides hydrogen (H) bonds for both the collagen molecules and the collagen-mineral composite (4).

• A relatively limited amount of noncollagenous proteins (NCPs) like the extrafibrillar proteins that glue together adjacent collagen fibrils (5).

It is now well established that the HA crystals inside the collagen fibrils grow primarily in the gaps between subsequent collagen molecules (2,6) and are shaped as platelets with typical average dimensions of ∼50 × 25 × 3 nm (1,2), although their length can vary from 15 to 150 nm, their width from 10 to 80 nm, and their thickness from 2 to 5 nm (7). The longest dimension of the HA platelets coincides with the c axis of the HA crystal unit cell and is oriented along the fibril axis (2). The structure and the relative fraction of the extrafibrillar minerals are less well understood and are still a matter of debate. Recent study by atomic force microscopy (AFM) (8) confirmed the existence of mineral-containing blobs on the fibrils surface. Hassenkam et al. (9) and Kindt et al. (10) obtained a more detailed picture of the extrafibrillar minerals via high-resolution AFM imaging. They observed that each collagen fibril is individually coated with extrafibrillar HA minerals with various shapes and sizes and part of these mineral formations are arranged with a period of 67 nm, the same as that of the underlying microstructure of the naked collagen fibrils.

In the past decade, mechanical models for mineralized collagen fibrils have been developed by Akiva et al. (11), Jäger and Fratzl (3), Akkus (12), and Fritsch and Hellmich (13). The cooperative collagen-mineral deformation within a single fibril has been studied by Jäger and Fratzl (3) in the framework of their shear-lag model with staggered mineral platelets. Akiva et al. (11) modeled the three-dimensional orthotropic elastic properties of a single collagen fibril as well as of lamellar and fibrolamellar bone tissues, taking into account the mineral content and the shape of the HA platelets in the fibrils. Akkus (12) and Fritsch and Hellmich (13) used continuum micromechanics homogenization to estimate the mechanical properties of mineralized collagen fibrils and bone tissues. Very recently, molecular dynamics (MD) simulations have emerged as a promising tool for investigation of the mechanical properties and the deformation of bone and its constituents at the nanoscale. For example, the properties of single collagen molecules have been assessed by Vesentini et al. (4) while Bhowmik et al. (14) investigated how the presence of HA crystals influences the mechanical behavior of the collagen molecules. Broedling et al. (15) showed that the strength and the toughness of platelet-reinforced nanocomposites with bonelike microstructure depend on the size and the arrangement pattern of the platelets. Unfortunately, realistic large-scale MD simulations of mineralized collagen fibrils including the molecular structure of collagen, water, and HA crystals require enormous computational power and are still not affordable at present. For this reason, the modeling method used here is based on continuum micromechanics.

In this work, we model the three-dimensional elastic constants of a single mineralized collagen fibril and of a bundle of fibrils with particular attention to the extrafibrillar mineralization and its influence on the mechanical properties of bone. Different homogenization methods are employed to first find the effective properties at a lower level of hierarchy, starting with the effective properties of the collagen-water composite inside the mineralized collagen fibrils, and then incorporate the obtained results in the modeling of the next higher hierarchy level.

Here we propose a new model for extrafibrillar mineralization considering that each individual collagen fibril is reinforced with HA coating rings strongly adhering to the fibrils' surface. Different mineralization scenarios are tested to establish how the fraction of extrafibrillar minerals evolves with the overall mineralization.

Another improvement in our modeling with respect to earlier models is the incorporation of the experimentally observed shape of the HA platelets in a genuine three-dimensional formulation. In some earlier works (11), the three-dimensional elastic properties of mineralized collagen fibrils were constructed using different one-dimensional models for the Young- and the shear moduli in different directions. Other authors proposed more advanced three-dimensional formulations based on continuum micromechanics but used less realistic shape assumptions for the HA minerals, needlelike (12) or spherical (13). In this approach we compute the so-called Eshelby's tensor (16), accounting for the shape of the inclusions in a particulate composite, through numerical integration using the viscoplastic self-consistent code (VPSC6) developed by Lebensohn and Tomé (17). This allows us to solve a three-dimensional equivalent inclusion problem for particles shaped as general ellipsoids and embedded in a stiffness matrix with arbitrary anisotropy, and thus to provide better estimates for the orthotropic elastic properties of mineralized collagen fibrils and fibril arrays.

HIERARCHICAL STEP-BY-STEP HOMOGENIZATION

In this section, we consider in detail a hierarchical modeling approach consisting of consecutive homogenization steps. In terms of Fig. 1, we find the effective elastic properties of bone at each of the hierarchy levels, from Level 1 up to Level 4, in a bottom-up order. For different hierarchy levels, we employ different continuum micromechanics methods to model the specific microstructure in a realistic but still reasonably simple way.

Effective properties of the collagen-water composite

Within the mineralized collagen fibrils, the collagen molecules are arranged in a staggered fashion (Fig. 1, Level 1) with axial period of 67 nm consisting of overlaps (∼27 nm) for neighboring molecules and axial gaps (∼40 nm) between two successive molecules (18). The molecular packing is quasihexagonal (19), and the intermolecular spaces are filled with water and contain a small amount of noncollagenous proteins such as proteoglycans (19).

Because the transverse properties of isolated collagen molecules are not known, we model the collagen triple helices as a hexagonal array of perfectly aligned long isotropic cylindrical fibers in an isotropic water-protein matrix, the elasticity of which is due to the hydrogen bonds linking the collagen molecules as well as to the crosslinks provided by the noncollagenous proteins. Accurate estimates for the effective properties of long-fiber composites with arbitrary volume fraction of the fibers and arbitrary contrast between the mechanical properties of the phases have been developed by Torquato (20).

Let the indices 1 and 2 denote the matrix (water) and the dispersed phase (collagen fibers), respectively. Then, the effective two-dimensional shear- and bulk moduli, G_e and k_e, in a plane perpendicular to the orientation of the collagen molecules are given by (20)

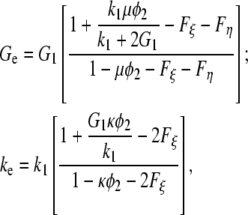(1)

where

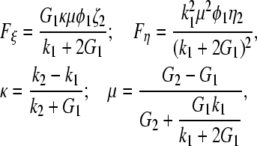(2)

with G₁ and G₂ being the shear moduli and k₁ and k₂, the plane-strain bulk moduli of water and collagen in the cross-section plane, respectively; and φ₁ and φ₂ = 1 − φ₁ represent the volume fractions of water and collagen molecules, respectively. The scalar parameters ξ₂ and η₂ are defined by threefold integrals depending on the cross section's microstructure—in our case, a hexagonal array of identical circles—and on the volume fractions of the phases. For hexagonal arrays of cylinders, their values have been numerically computed and tabulated for different volume fractions in McPhedran and Milton (21) for ξ₂ and in Eischen and Torquato (22) for η₂.

To construct the transversely isotropic stiffness tensor of the collagen-water composite, we need to find three additional constants for the properties along the collagen molecules, namely the longitudinal Young modulus, E_L, the longitudinal three-dimensional Poisson's ratio, ν_L, and the shear modulus, G_L. To estimate E_L and ν_L, we use the Hill's lower bounds for long-fiber composites (23), which for G₂ > G₁ read

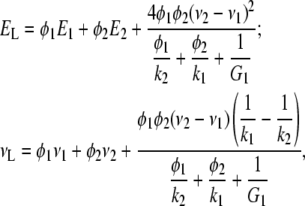(3)

where E₁ and E₂ are the conventional Young moduli, and ν₁ andν₂ stand for the three-dimensional Poisson's ratios of the water and the collagen molecules, respectively. The shear modulus along the collagen molecules, G_L, is independent of the other elastic constants but can be evaluated via numerical simulations, which for a water-collagen composite give G_L ≈ 1.04 G_e. With the obtained values for the elastic constants, one can construct the elastic stiffness tensor of the homogenized collagen-water composite .

Collagen fibril reinforced with intrafibrillar HA platelets

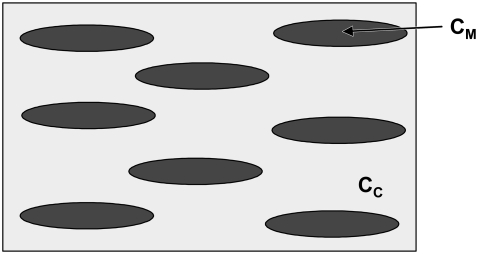
Because the Young modulus of HA significantly exceeds that of the collagen-water composite discussed above, the homogenized elastic properties of a single collagen fibril reinforced with aligned HA mineral platelets should strongly depend on the shape and the volume fraction of the platelets. Jäger and Fratzl (3) argued that the upper-bound for the mineral volume fraction within the fibrils, φ_M, must be φ_M ≤ 0.56, with a most likely value in fully mineralized bone of φ_M ≈ 0.43. On the other hand, in small deformations, the very soft collagen matrix would drastically reduce the interactions between neighboring mineral platelets. Therefore, to find the effective properties of a mineralized collagen fibril, one can employ the Mori-Tanaka homogenization scheme (24) for two-phase composites reinforced with noninteracting, aligned ellipsoidal inclusions. The representative volume element (RVE) of a mineralized collagen fibril in our model is shown in Fig. 2.

FIGURE 2.

Modeling of a mineralized collagen fibril: collagen-water matrix (light shading) with elastic constants reinforced with aligned ellipsoidal HA inclusions (solid) having stiffness tensor .

The Mori-Tanaka model for the overall properties of the fibril can be written as (25)

(4)

where

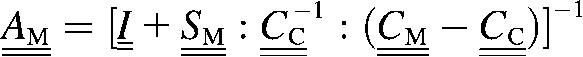(5)

is the so-called strain concentration factor for an isolated single ellipsoidal inclusion in an infinite elastic matrix; ,, and denote the stiffness tensors of the homogenized fibril, the collagen-water composite, and the HA mineral, respectively; 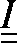is the fourth-order identity tensor; is the fourth-order Eshelby's tensor depending only on the shape of the inclusions and on the elastic constants of the matrix; and φ_C and φ_M = 1 − φ_C are the volume fractions of the collagen-water matrix and the HA crystallites, respectively. The tensor product contracted over two indices is denoted by (:) while the inverse of a matrix (fourth-order tensors are represented in matrix notation because of symmetries) is indicated by .

Mineralized collagen fibril reinforced with extrafibrillar minerals

As already mentioned in the Introduction, the most recent experimental studies on the extrafibrillar mineralization in bone (8–10) found that 1), each collagen fibril is individually coated with HA mineral particles of different sizes and shapes; 2), the HA minerals strongly adhere to the fibrils surface; and 3), the periodicity in the arrangement of part of the extrafibrillar HA shells along the fibrils is approximately the same as the 67-nm period of the underlying naked collagen fibrils resulting from the staggered arrangement of the gaps and the overlaps between the collagen molecules along the fibril axis. On the other hand, to explain the observed decrease in the lateral spacing of the collagen molecules with the increase in the mineral content, Lees (26) suggested that the HA mineral is initially deposited in the extrafibrillar space and prevents the collagen fibrils from merging. These findings are also supported by the work of Zhang et al. (27), who could experimentally mimic the formation of bundles of parallel mineralized collagen fibrils through self-assembly and obtained cylindrical fibrils consisting of pure collagen and water, individually coated with crystalline HA shells, with their c axes oriented along the fibril axes.

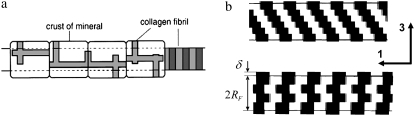
The observation that part of the extrafibrillar HA shells have the same periodicity as the 67-nm period of the collagen fibril can be explained by considering that the 40-nm gaps between consequent collagen molecules must also be present at the fibrils' surface and therefore follow the staggered patterns shown in Fig. 3 b. According to Piez and Miller (28), a single collagen fibril is composed itself by subfibrils arranged in a subsequent (Fig. 3 b, top) or alternate (Fig. 3 b, bottom) staggered pattern. It is reasonable to assume that during the mineralization process, the gaps between the collagen molecules at the fibril surface, arranged in a periodic staggered fashion as shown in Fig. 3 b, are initially filled with HA. With increase in the overall mineralization, the extrafibrillar minerals located in the gaps would first thicken above the level of the fibril surface and then start growing along the fibrils axis, thus forming a kind of reinforcing ring of HA around the fibril. As a result of this process and also the deposition of additional extrafibrillar mineral on the surface, the fibril would become considerably stiffer in directions perpendicular to the fibril axis while the increase in its bending rigidity would be less pronounced, thus preserving the fibril's flexibility.

FIGURE 3.

(a) Extrafibrillar minerals according to Sasaki et al. (8); (b) Present model based on the collagen fibril structure proposed by Piez and Miller (28). (Solid regions, HA extrafibrillar reinforcements; open regions, underlying collagen fibril.)

With the above considerations in mind, we can find the mechanical properties of a collagen fibril partially coated with extrafibrillar minerals in two steps. Firstly, let us consider the overall properties of a fibril that is fully coated with a HA layer having a uniform thickness. As the HA coating is much stiffer and harder than the core collagen fibril, the effective mechanical properties of the coated fibril will be dominated by the HA properties as long as the coating is sufficiently thick. For simplicity, we can apply the Mori-Tanaka method (25) for a composite consisting of a single inclusion (the collagen fibril) embedded in a HA matrix,

(6)

with strain concentration factor

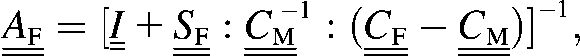(7)

where is the stiffness tensor of the coated fibril; 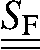is the Eshelby's tensor for the needlelike fibril; and φ_F and φ_coat = 1 − φ_F are the volume fractions of the fibril and the coating, respectively. The remaining quantities were defined in Collagen Fibril Reinforced with Intrafibrillar HA Platelets.

The actual effective properties of fibrils with extrafibrillar minerals must be within the upper bound for a fully coated fibril, , and the lower bound for a naked fibril, . In terms of our modeling, it is clear that the effective properties of a partially coated fibril will be closer to the upper bound in certain directions, like tension/compression in directions normal to the fibril's surface, and closer to the lower bound in others. In fact, for the extrafibrillar reinforcements shown in Fig. 3 b, only two deformation modes would be not stiffened by the extrafibrillar mineralization, namely, tension/compression along the fibril axis and shear in the 1-2 plane (see Fig. 4). Shear in the 1-3 plane must be a stiff deformation mode because of the additional resistance to shear due to the specific staggered geometry of the extrafibrillar and intrafibrillar minerals (Fig. 3 b).

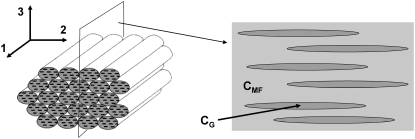
FIGURE 4.

(Left) Bundle of aligned mineralized fibrils (extrafibrillar minerals are not shown). (Right) Modeling equivalent: two-dimensional cut of the RVE of the bundle along the indicated plane. The needlelike inclusions (dark-shaded) represent the extrafibrillar noncollagenous proteins.

Let α_EM be the fraction of the fibril surface coated with extrafibrillar minerals. If all deformation modes of the fibril were equally strengthened by the extrafibrillar mineralization, then a simple Voigt-like estimate for the effective elastic constants of the mineralized fibril, , would give

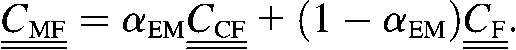(8)

To account for the non-reinforced modes, from the stiffness tensors and we first compute the Young moduli along the fibril axis, 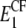and 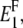as well as the shear moduli, 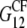and 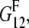in the 1-2 plane corresponding to coated and naked fibrils, respectively. Then we obtain the effective Young modulus 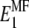and shear modulus 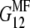in the soft deformation modes using asymptotic homogenization method (29), which in our case gives the lower Hashin-Strikman bound for the mechanical properties, known to be more realistic than the simple Reuss estimate. The effective moduli 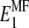and 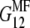are estimated as

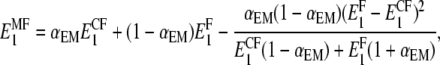(9)

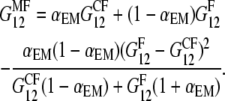(10)

Then one can immediately substitute in the stiffness matrix . To replace with the updated value found via Eq. 9, it is necessary to first find the compliance matrix, 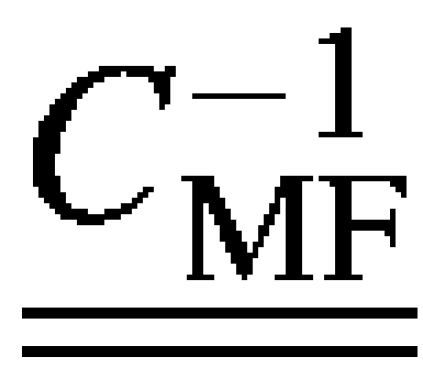, replace the old value for 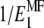with the new estimate there, and then invert the updated compliance matrix again to obtain the corrected stiffness . This approach is simple and gives a satisfactory estimate of the properties of the mineralized collagen fibrils decorated with extrafibrillar minerals, introducing only insignificant error for some of the Poisson's ratios.

To be able to use the above-described model, we need an additional formula for the extrafibrillar mineral content. By definition, the total mineral volume fraction is φ_TM = V_M/V_T with V_M and V_T being the total volume of the mineral and the tissue volume, respectively. On the other hand, V_T can be expressed as V_T = V_MF/φ_MF with the volume, V_MF, and the volume fraction, φ_MF, of the mineralized fibrils. Then, the total mineral volume can be expressed as V_M = (φ_TM/φ_MF)V_MF. Introducing an equivalent thickness δ for the HA coating rings (Fig. 3 b), we can write the volume of the extrafibrillar minerals as

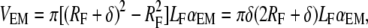(11)

where R_F and L_F are the radius and the length of the fibril and α_EM is the fraction of the coated fibril surface.

Taking the volume of the fibril as 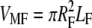and using V_M = (φ_TM/φ_MF)V_MF, we can write the volume fraction of the extrafibrillar minerals to the total mineral volume as

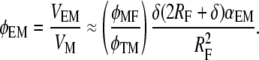(12)

The volume fraction of the minerals within the fibrils, φ_IF, referred to as the fibril volume, V_MF, can be found starting with the basic expression

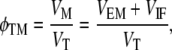(13)

where V_IF is the volume of the intrafibrillar minerals. Using V_T = V_MF/φ_MF together with Eqs 12 and 13, after some manipulation we obtain

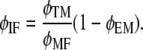(14)

Equation 14 establishes a relationship between the extrafibrillar and the intrafibrillar mineralization.

Effective properties of a bundle of aligned mineralized collagen fibrils

We now consider the overall properties of a bundle of parallel, closely packed mineralized collagen fibrils (Fig. 4, left). The HA platelets within all the fibrils are assumed to have the same orientation and shape and the adjacent fibrils are held together by gluelike noncollagenous proteins (5). This type of microstructure is observed in several important bone tissues like the parallel-fibered bone, for example. More importantly, such a bundle can be viewed as a basic unit for the structure of any bone tissue at micron scale (Fig. 1, Level 4) where different types of fibril arrays can be modeled as consisting of bundles of parallel fibrils with different orientation and volume fractions.

In this case, we cannot apply directly the modeling used in Effective Properties of the Collagen-Water Composite, and Collagen Fibril Reinforced with Intrafibrillar HA Platelets. The method of Torquato is valid only for isotropic phases while the individual collagen fibers possess markedly orthotropic properties (1). On the other hand, the volume fraction of the fibrils in the RVE of the bundle is ≫50%, given that their diameter is ∼100 nm while the separation distance between two adjacent fibrils is only 1–2 nm (30). In addition, the interactions between neighboring fibrils cannot be neglected, which prevents us from using the Mori-Tanaka method if we model the fibrils as inclusions embedded in a NCP matrix. Instead, we use an “inverse Mori-Tanaka” homogenization by simply inverting the matrix and the inclusions. Thus, we consider a bundle of aligned fibrils as a two-phase composite where the matrix properties are those of a single mineralized fibril and the needlelike inclusions represent the interfibrillar spaces filled with NCPs (Fig. 4, right). In fact, this approximation is more realistic than it may seem at a first glance because adjacent collagen fibrils have the tendency to merge together (1), and at certain places are bonded with bridges containing HA minerals (9).

With the above considerations in mind, we can express the effective stiffness tensor of a bundle of aligned fibrils, , as (25)

(15)

with concentration factor

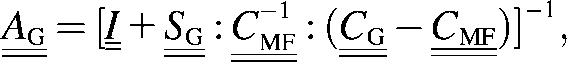(16)

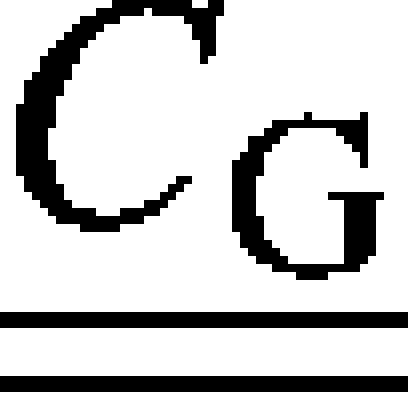where and denote the stiffness tensors of the mineralized collagen fibrils and the extrafibrillar NCPs, respectively; 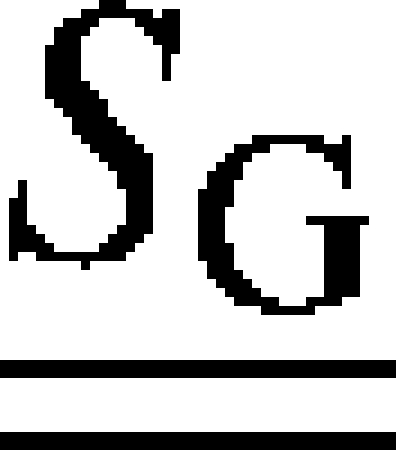is the Eshelby's tensor for the needlelike NCPs inclusions; and φ_MF and φ_G = 1 − φ_MF are the volume fractions of the fibrils and the interfibrillar spaces, respectively.

Effective properties of fibril arrays with narrow orientation distribution of the fibrils

Once the stiffness tensor 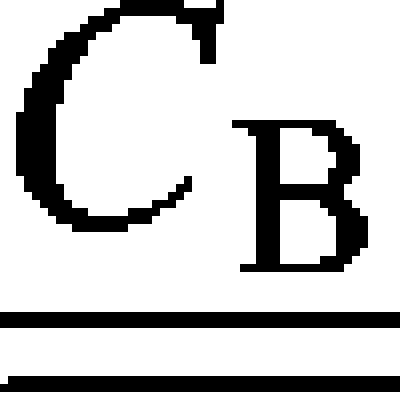for the effective properties of aligned fibrils is known, one can model other types of fibril arrays (Fig. 1, Level 4), provided that the orientation distribution of the fibril packets and the volume fractions corresponding to different orientations are known.

Consider a fibril array where the fibrils are oriented along i different directions, with ()_i being the stiffness tensor for a fibril bundle along the i^th orientation and φ_i the volume fraction of the bundle. Here we consider only the case where the fibrils have narrow orientation distribution, like in the rotated plywood structure of lamellar bone (1), for example. Then, we can safely assume that the deformation within the fibril array due to external loading would be more or less uniform and therefore, the effective properties of a fibril array without pores, , defined in a fixed coordinate frame, can be written as the volume average,

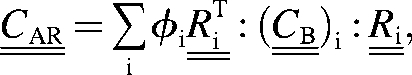(17)

where 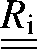is a 6×6 rotation matrix constructed from the conventional 3×3 rotation matrix (31) and the symbol denotes the transpose of a matrix. The introduction of 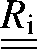comes from the fact that the effective elastic properties in a given direction are found with respect to a local frame (as shown in Fig. 4, left) coinciding with the axes of symmetry of the bundle, and that frame in general does not coincide with the fixed coordinate system where is defined.

The Mori-Tanaka method can be further applied for modeling of porosity at micron scale by considering the pores as ellipsoidal inclusions with zero stiffness, but we do not consider this topic here. As for fibril arrays with broad orientation distribution in wovenlike patterns, the Mori-Tanaka method can be used once again for finding the overall properties, as done for textile tissues in Gommers et al. (32), for example.

MODEL PARAMETERS

Collagen-water composite

Because of the extreme smallness of the collagen molecules, only their longitudinal Young modulus has been evaluated by various experimental and theoretical approaches. The Young modulus of collagen molecules obtained via electron microscopy (33) ranges from 3 to 5.1 GPa, x-ray diffraction yields 2.8–3 GPa (34) while MD simulations (4) predict 1.3–2.4 GPa. Here we choose E₂ = 2.4, which seems to be a good compromise between simulations and experiment. The Poisson's ratio of the collagen molecule is not known exactly. We set ν₂ = 0.28 to have an overall Poisson's ratio for the collagen-water composite ∼0.35, as estimated by Katz (35). For the water-protein matrix, as a first guess we choose Poisson's ratio of ν₁ = 0.47 corresponding to a nearly incompressible material. The associated Young modulus is taken as E₁ = 0.4 GPa to match the measured bulk modulus for water, K₁ = 2.3 GPa. With these values we determine the shear moduli, G_i = E_i/(1 + ν_i), the three-dimensional bulk moduli K_i = E_i/3(1 – 2ν_i), and the two-dimensional bulk moduli k_i = K_i + G_i/3, where i = 1, 2 stand for water and collagen, respectively. From geometry, the volume fraction, φ₂, of the collagen molecules modeled as cylindrical fibers with hexagonal packing is

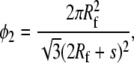(18)

where R_f and s denote the fiber radius and the lateral separation between the fibers, respectively.

With Eq. 18, for φ₂ = 0.65 and diameter of the collagen molecule of 1.5 nm, the separation between two collagen molecules is obtained as 2.5 Å, or approximately the length of one H-bond (4). The corresponding three-point statistics parameters are ξ₂ = 0.016 (21) and η₂ = 0.42 (22). Substituting the above values in Eqs. 1–3 and assuming that the collagen molecules are aligned along axis 1 of a Cartesian coordinate system, the elastic constants of the collagen-water system expressed in Voigt notation are obtained as

(19)

Because the properties of the water-protein matrix are subject to uncertainty, we also test a higher Young modulus for the matrix, E₁ = 0.7 GPa with corresponding Poisson's ratio of ν₁ = 0.45, keeping the collagen properties and volume fraction unchanged. This results in a somewhat stiffer collagen-water composite,

(20)

Properties of HA crystallites and extrafibrillar proteins

As in the case of collagen, there are no reliable experimental measurements for the properties of HA nanocrystals in bone. The measured properties of synthetic HA obtained through various processes vary wildly with Young modulus ranging from 6 (36) to 147 GPa (37). For the Young modulus of biological HA, we first take a typical value of E_M = 100 GPa (30), and Poisson's ratio ν_M = 0.23, as measured by Gilmore and Katz (38) and computed with ab initio calculations (37). We also use the Young modulus for single HA crystals, E_M = 114 GPa (38). For the sake of simplicity, we assume that the properties of the HA crystals are isotropic.

The mechanical properties of the extrafibrillar proteins are not known at present. Given that they consist of flexible, coiling macromolecules, their Young modulus must be lower than that of the collagen with its relatively stiff triple-helix molecules. We assume that the extrafibrillar NCPs have isotropic properties with Young modulus E_G = 1 GPa (30) and Poisson's ratio ν_G = 0.45, a typical value for soft polymers with flexible molecules. The volume fractions of the mineralized fibrils, φ_MF, and the interfibrillar proteins, φ_G, are determined with the help of Eq. 18 assuming that the fibrils have a diameter of 100 nm and are packed in a hexagonal array with separation between the fibrils of 1.5 nm (30). This gives φ_MF = 0.88 for the fibrils and φ_G = 0.12 for the extrafibrillar glue.

Mineralization parameters

The volume fraction of the overall mineral content is assumed to vary from 32 to 52 vol %, which comprises a large amount of literature data for wet bone (13,39). The most important issues concerning the mineralization in fibril arrays are the ratio between the extrafibrillar and the intrafibrillar mineral content, the evolution laws for mineralization outside and inside the fibrils as functions of the total mineral content, and the relation between the shape of the intrafibrillar HA crystals and the mineral content in the fibrils. To our knowledge, these dependencies are not known beyond some contradictory data about the extrafibrillar mineral content. X-ray diffraction methods (40,41) determined that between 70 and 80% of the total mineral content must be within the fibrils. On the other hand, AFM and transmission electron micrographs of turkey leg tendon (42) and AFM measurements of bone (8) have been interpreted in a way indicating that as much as 70–77% of the mineral is extrafibrillar.

Using Eq. 14, one can deduce that the results of Katz and Lee (40) and Sasaki and Sudoh (41), namely that in a mature bone between 20 and 30% of the minerals are extrafibrillar, are consistent with the model of Jäger and Fratzl (3), for the mineral content within the fibrils. For overall mineral volume fraction φ_TM = 0.52, fibril volume fraction φ_MF = 0.88, and extrafibrillar mineral fraction φ_EM = 0.27, Eq. 14 gives the volume fraction of HA within the fibrils as φ_IF = 0.43, the most probable value in a fully mineralized cortical bone estimated in Jäger and Fratzl (3).

RESULTS

Elastic moduli of a bundle of aligned fibrils

Elastic moduli of aligned fibrils without extrafibrillar mineralization

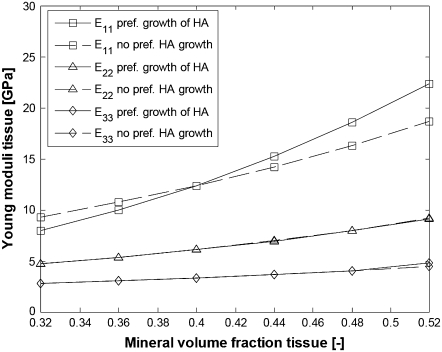
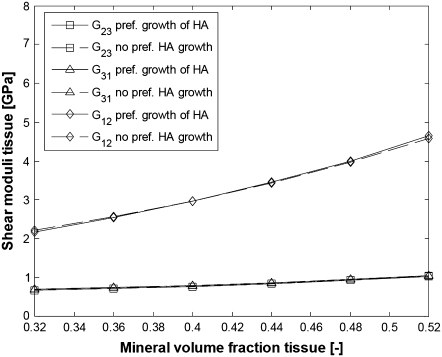
Initially, we consider the elastic moduli for a hypothetical bundle of naked aligned fibrils without extrafibrillar minerals. We first assume that the shape of the HA platelets remains unchanged for the studied volume fractions and the minerals are ellipsoids, with shape determined by the typical dimensions of the HA platelets of 50 × 25 × 3 nm. Alternatively, we consider that the longest dimension of the platelets (along the fibril axis) grows proportionally with increasing the mineral volume fraction. Thus, for mineral content 32 vol % we assume that the platelets have average dimensions of 40 × 25 × 3 nm, i.e., they completely fill the gaps within the collagen fibrils but do not penetrate in the overlap zones. For mineral content of 52 vol %, their longest dimension must evolve linearly to 65 × 25 × 3 nm while their width and thickness would remain unchanged. The resulting elastic moduli of bundles of aligned fibrils without extrafibrillar minerals are shown in Figs. 5 and 6. Hereafter, the subscripts 1, 2, and 3 are with respect to the coordinate system shown in Fig. 4. The collagen-water properties are given by Eq. 19 and the Young modulus of HA is taken as E_M = 100 GPa.

FIGURE 5.

Young moduli of a bundle of aligned fibrils without EF minerals. (Solid lines, HA platelets growing preferentially along the fibril axis with increase in φ_TM; dashed lines, HA platelets with constant shape; squares, E₁₁; triangles, E₂₂; diamonds, E₃₃.)

FIGURE 6.

Shear moduli of a bundle of aligned fibrils without EF minerals. (Solid lines, HA platelets growing preferentially along the fibril axis with increase in φ_TM; dashed lines, HA platelets with constant shape; squares, G₂₃; triangles, G₃₁; diamonds, G₁₂.)

It is seen that the preferential growth of the HA platelets along the fibril axis changes only the longitudinal Young modulus of the fibrils and the obtained values in this case are more realistic than the values obtained assuming constant platelet shape. The preferential growth of the HA crystals along the fibril axis seems to explain the experimental fact that the longitudinal Young modulus in parallel-fibered and fibrolamellar bone increases considerably for relatively small increase in the total mineral content (39).

The bundles of aligned naked fibrils possess excessive orthotropy and only two deformation modes are stiff enough to match the experimentally observed stiffness in bone—these are tension/compression along the fibril axis and shear in the 1-2 plane. The other deformation modes are too soft to insure sufficient load-bearing capacity of the bone tissue, which indirectly proves the importance of the extrafibrillar mineralization for the mechanical properties.

Elastic moduli of aligned fibrils with extrafibrillar mineralization

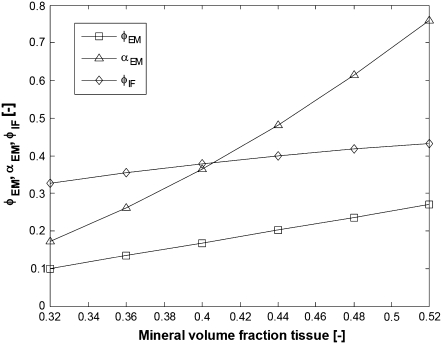
Next, we consider the elastic moduli of a bundle of aligned fibrils with extrafibrillar mineralization. We test two different mineralization scenarios. Firstly, it is assumed that the extrafibrillar and the intrafibrillar mineralization develop simultaneously in a way that keeps the extrafibrillar mineral fraction fixed at φ_EM = 0.27 for all φ_TM. Alternatively, we suppose that the volume fraction of the extrafibrillar minerals grows linearly with the overall mineral content starting from φ_EM = 0.10 (for φ_TM = 0.32) to φ_EM = 0.27 for φ_TM = 0.52. The equivalent thickness of the HA rings is assumed to be δ = 5 nm (Fig. 3 b) so that at total mineral volume fraction of φ_TM = 0.52, 76% of the fibrils' surface is coated with HA, which is a reasonable value. The minimum fibril surface fraction corresponds to HA reinforcing rings 5-nm thick and 59-nm long. The values for the extrafibrillar fraction, φ_EM, the surface fraction occupied by the HA coating, α_EM and the mineral volume fraction within the fibrils, φ_IF, for the two scenarios (constant φ_EM and evolving φ_EM) and for different total volume fractions φ_TM are calculated with Eqs 12 and 14 and are listed in Table 1.

TABLE 1.

Parameters for extrafibrillar mineralization with equivalent thickness of the coating rings δ = 5 nm; l_p denotes the longest average dimension of the HA platelets

	φTM [−]	0.32	0.36	0.40	0.44	0.48	0.52
Constant φEM	φEM [−]	0.27	0.27	0.27	0.27	0.27	0.27
	αEM [−]	0.468	0.526	0.584	0.643	0.701	0.76
	φIF [−]	0.265	0.299	0.332	0.365	0.398	0.431
	lp nm	40	45	50	55	60	65
Evolving φEM	φEM [−]	0.10	0.134	0.168	0.202	0.236	0.27
	αEM [−]	0.173	0.261	0.363	0.481	0.613	0.76
	φIF [−]	0.327	0.354	0.378	0.399	0.417	0.431
	lp nm	43	46.6	49.8	52.6	55	56.8

The mineralization parameters for linear evolution of φ_EM with the total mineral content φ_TM are visualized in Fig. 7 and one can notice that in this case, the mineral content within the fibrils grows only slightly with the total mineralization while the increase in the fibril surface fraction covered with HA is more significant.

FIGURE 7.

Evolution of the mineralization parameters (see bottom half of Table 1) for linear increase in φ_EM with the total mineral content. (Squares, φ_EM; triangles, α_EM; diamonds, φ_IF.)

The mineralization scenario shown in Fig. 7 also suggests that for mineral grades <30% volume fraction, the intrafibrillar mineralization would develop much faster than the extrafibrillar one, while for mineral levels >30 vol %, the rate of intrafibrillar mineralization saturates and is compensated by a higher growth rate of the extrafibrillar HA.

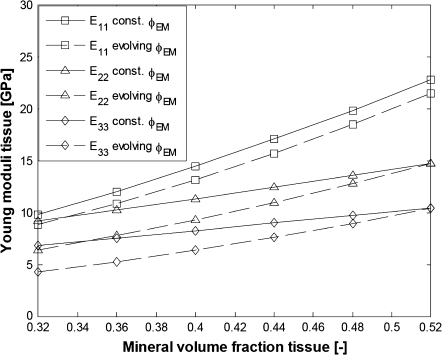
In these simulations, the collagen-water properties are given by Eq. 19 and the Young modulus of HA is E_M = 100 GPa. The results for the elastic moduli are shown in Figs. 8 and 9.

FIGURE 8.

Young moduli of bundles of aligned fibrils with EF mineralization (parameters from Table 1). (Solid lines, constant φ_EM; dashed lines, evolving φ_EM; squares, E₁₁; triangles, E₂₂; diamonds, E₃₃.)

FIGURE 9.

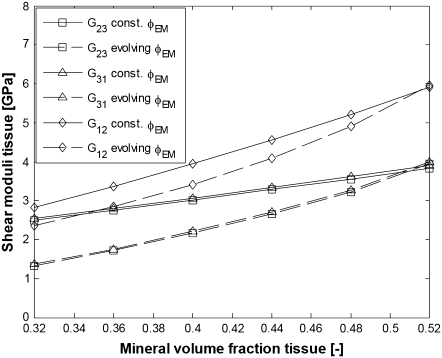
Shear moduli of bundles of aligned fibrils with EF mineralization (parameters from Table 1). (Solid lines, constant φ_EM; dashed lines, evolving φ_EM; squares, G₂₃; triangles, G₃₁; diamonds, G₁₂.)

It is seen that the assumption of constant proportion φ_EM of the extrafibrillar minerals for all mineral volume fractions results in a degree of orthotropy that changes with the overall mineral content, while linear evolution of φ_EM yields a self-similar pattern for the evolution of the elastic moduli where the degree of orthotropy is little changed with increasing the mineral content. The literature data for the three-dimensional elastic constants of bone summarized by Espinoza Orías (43) suggest that the degree of orthotropy does not change much for considerable changes in the values for the elastic constants. Therefore, we conclude that the fraction of extrafibrillar minerals and the longest dimension of the HA platelets within the fibrils develop with increasing the total mineral content in a way similar to the evolution laws visualized in Fig. 7. From Figs. 8 and 9 one can see that the elastic moduli for high degree of mineralization are slightly underestimated, most probably because the properties of the collagen-water composite and HA are somewhat stiffer than the so-far assumed values.

We therefore perform simulations where the collagen-water properties are given by Eq. 20, the Young modulus for HA is taken as E_M = 114 GPa, and the extrafibrillar mineralization parameters are the same as in the bottom half of Table 1. The results for the elastic moduli are shown in Figs. 10 and 11. For comparison, we superpose the moduli of a fibril bundle without extrafibrillar minerals where the longest dimension of the HA platelets evolves linearly with the mineralization from 40 to 65 nm.

FIGURE 10.

Young moduli of bundles of aligned fibrils with and without EF mineralization; from Eq. 20, E_M = 114 GPa. Parameters for EF mineralization: see bottom half of Table 1. (Dashed lines, bundle without EF minerals; squares, E₁₁; triangles, E₂₂; diamonds, E₃₃.)

FIGURE 11.

Shear moduli of bundles of aligned fibrils with and without EF mineralization; from Eq. 20, E_M = 114 GPa. Parameters for EF mineralization: see bottom half of Table 1. (Dashed lines, bundle without EF minerals; squares, G₂₃; triangles, G₃₁; diamonds, G₁₂.)

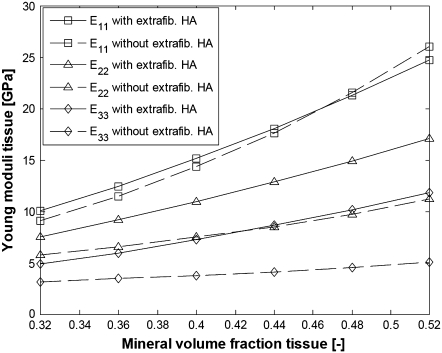
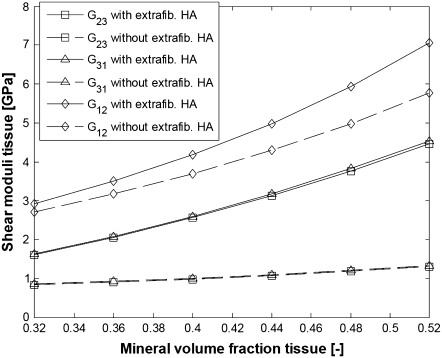
From Figs. 10 and 11, it is seen that collagen fibrils with extrafibrillar (EF) mineralization have superior mechanical properties compared to fibrils where all minerals are inside the fibrils. The only moduli that are not considerably enhanced by the EF minerals are longitudinal Young modulus E₁₁ and shear modulus G₁₂, which are already strengthened by the HA platelets inside the fibrils. However, in a bundle with EF minerals, the same Young modulus as that for naked fibrils is achieved with only slight increase in the intrafibrillar mineral content and in the dimensions of HA platelets along the fibril axis. The latter range from 43 to 56.8 nm compared to an increase from 40 to 65 nm for the naked fibrils. Also, one can notice that the softest deformation modes, shear in the 2-3 and 3-1 planes, have practically the same moduli and are the most strengthened by the EF mineralization.

The values obtained for the longitudinal Young modulus are in a good agreement with those obtained for hydrated fibrolamellar bone via microtensile testing (30), and also correspond to the longitudinal Young modulus obtained through nanoindentation on individual trabecula (44) and osteons (45). In our simulations, E₁₁ increases from 10 to 25 GPa compared to the experimentally measured range from 5 to 23 GPa (30). The values <10 GPa can be explained not only with total mineral content <32% but also with imperfect packing (square array of aligned fibrils with total mineralization of 32% has longitudinal Young modulus of 8.9 GPa), misalignment of the fibrils in the sample with respect to the tensile axis, and <10% EF mineral content. As for the cases where the experimentally measured longitudinal Young modulus of hydrated bone tissues is >25 GPa, one can explain such values by longer than 59-nm dimensions of the HA platelets.

Three-dimensional elastic constants of bone

In Voigt notation, the elastic constants of a bundle of aligned parallel fibrils (in a coordinate frame oriented as in Fig. 4 with the fibril axis along axis 1) with total mineral content of 52%, extrafibrillar mineral fraction of 27% and average dimensions of the HA platelets within the fibrils of 56.8 × 25 × 3 nm read

(21)

The local properties are relevant for a length scale ofseveral microns while the ultrasonic measurements of cortical bone found in the literature are for samples with characteristic length of several mm, where the mineralized collagen fibrils are organized in a much more complex manner to form rotated plywood structures, osteons, Haversian canals. etc. (Fig. 1, Level 5). The explicit modeling of the microstructure at higher levels of hierarchy within the frame of our approach is possible but is beyond the scope of this work. Here we use a simple phenomenological model to reproduce the properties of compact bone observed at macroscopic scales. Let us assume that in a first approximation, cortical bone can be represented as a composite of aligned fibrils where 67% of the fibrils are oriented like the bundle in Fig. 4 and 33% of the fibrils are rotated about their axes (parallel to coordinate axis 1) at an angle π/2. The volume fraction of 33% for the rotated fibrils was chosen so that the simulated elastic constant C₆₆ matches the value obtained via ultrasonic measurements reported in Espinoza Orías (43). The elastic constants of this composite can be found using Eq. 17 and are listed in Table 2 along with experimental measurements for hydrated compact bone from different sources.

TABLE 2.

Elastic constants of cortical bone

Coefficient	This work	Espinoza Orías (43)	Van Buskirk et al. (47)	Ashman et al. (48)
C11	27.68	27.33 ± 1.64	25.00 ± 4.30	27.60 ± 1.74
C22	18.23	19.66 ± 2.09	18.40 ± 2.70	20.20 ± 1.79
C33	16.06	16.75 ± 2.27	14.10 ± 2.40	18.00 ± 1.60
C44	4.45	4.64 ± 0.43	5.38 ± 0.46	4.52 ± 0.37
C55	5.36	5.65 ± 0.53	6.30 ± 0.67	5.61 ± 0.40
C66	6.22	6.22 ± 0.31	7.00 ± 0.67	6.23 ± 0.48
Source	—	Wet femur	Wet femur	Wet femur
Species	—	Human	Bovine	Human

From Table 2 is seen that our simple phenomenological estimate yields surprisingly good predictions for the macroscopic three-dimensional elastic constants despite the fact that the bone microstructure and porosity at higher hierarchy levels has been discarded. While we do not pretend to have explained in detail the macroscopic three-dimensional elastic constants of bone, the obtained values indicate that our modeling is able to quantitatively describe the essential features of bone elasticity at micron and submicron length scales and is rich enough to serve as a basis for a physically relevant modeling of the bone properties at all length scales.

CONCLUSIONS

We have shown that extrafibrillar mineralization considerably enhances the overall mechanical properties of the mineralized collagen fibrils in bone when the extrafibrillar crystals strongly adhere to the fibrils surfaces and individually coat each collagen fibril, as suggested by the most recent experimental data. Part of the extrafibrillar minerals most probably form effective coating rings with the same period and staggered geometry as the underlying naked fibrils and start growing in the 40-nm gaps between the successive collagen molecules situated at the fibrils surface. Mineralization enhances the stiffness of the fibrils by two mechanisms: firstly, the intrafibrillar HA platelets strengthen the collagen fibrils in tension/compression along the fibril axis and in shear in the platelets' plane. The extrafibrillar mineralization further strengthens the fibrils in all remaining deformation modes except those already stiffened by the intrafibrillar minerals.

We have established that typically, if the mineral content within the fibrils does not exceed 43 vol % in fully mineralized cortical bone (3), no more than 30% of the total mineral content is extrafibrillar, in accord with the experimental findings in the literature (40,41). More importantly, it is shown that the percentage of the extrafibrillar minerals must evolve proportionally to the overall mineral content to have a relatively small change in the degree of orthotropy of the elastic constants for different degrees of mineralization. In this case, for a typical mineral content of 44 vol %, the gain in stiffness from extrafibrillar mineralization compared to fibrils where all minerals are intrafibrillar is ∼2 times for the weakest Young modulus (in direction perpendicular to the HA platelets) and ∼3 times for the weakest shear moduli. The obtained three-dimensional elastic constants for bundles of parallel fibril arrays are close to the elastic constants for macroscopic samples obtained via ultrasonic measurements.

The model predictions for the longitudinal Young modulus of arrays of parallel mineralized collagen fibers are in a good agreement with the experimental data from microtensile testing of fibrolamellar bone with the assumption that for mineral content of >30 vol %, the HA platelets within the fibrils grow preferentially in the fibrils direction and the growth of the longest dimension of the HA platelets is proportional to the increase in the overall mineral content.