Abstract
We suggest that bubbles are the bistable hydrophobic gates responsible for the on-off transitions of single channel currents. In this view, many types of channels gate by the same physical mechanism—dewetting by capillary evaporation—but different types of channels use different sensors to modulate hydrophobic properties of the channel wall and thereby trigger and control bubbles and gating. Spontaneous emptying of channels has been seen in many simulations. Because of the physics involved, such phase transitions are inherently sensitive, unstable threshold phenomena that are difficult to simulate reproducibly and thus convincingly. We present a thermodynamic analysis of a bubble gate using morphometric density functional theory of classical (not quantum) mechanics. Thermodynamic analysis of phase transitions is generally more reproducible and less sensitive to details than simulations. Anesthetic actions of inert gases—and their interactions with hydrostatic pressure (e.g., nitrogen narcosis)—can be easily understood by actions on bubbles. A general theory of gas anesthesia may involve bubbles in channels. Only experiments can show whether, or when, or which channels actually use bubbles as hydrophobic gates: direct observation of bubbles in channels is needed. Existing experiments show thin gas layers on hydrophobic surfaces in water and suggest that bubbles nearly exist in bulk water.
INTRODUCTION
We suggest that many channels open and close by filling or forming bubbles. Bubbles in channels are unlikely to permit the flow of ions. Indeed, bubbles are likely to completely block the flow of matter—including ions—because a bubble is the ultimate form of the hydrophobic gate proposed by the literature (1–3), seen in the calculations of many others (4–20).
Single channel currents of a wide variety of types of channels (21) follow a single pattern of opening and closing (22–25). We propose that a single mechanism produces this pattern. In this view, channels open and close using the same physical mechanism, but different channels use different structures and mechanisms to trigger and modulate the opening and closing. In this view, single channel currents are “random telegraph” signals that switch between a nonconducting and conducting value as bubbles form and fill with water and ions.
The phenomenon of bubble formation is more properly called capillary evaporation. Capillary evaporation and condensation are well known on the macroscopic scale as a special case of dewetting and wetting at interfaces. Capillary effects have fascinated scientists for centuries—e.g., Newton, Young, Laplace, Maxwell, Raleigh, and von Neumann (26,27)—perhaps because simple systems show curious effects, movements without obvious sources of force or energy—for example, water lifted against gravity in a vertical capillary without an obvious source of an uplifting force. These effects arise (we now know) from the often unstable balance between strong cohesive volume forces and nearly as strong surface effects (28,29).
We suppose that hydrophobic regions of the channel wall help control bubble formation much as hydrophobic surfaces control wetting and dewetting: a hydrophobic surface allows the cohesive forces of water to pull the fluid away from the wall. Bubbles are localized and controlled by the rings of nonpolar amino acids of the Ach channel (30,31); the hydrophobic intracellular pore of the KcsA channel (32), among others (33–37); and gating structures in general (1,3–5,7–9,11,13,14,16–19,38). Perhaps, the spherical regions of channel structures (32,39) have important roles in bubble formation and breaking.
The wetting behavior that fills channels reflects the competition between the cohesive (volume) forces in a fluid and the adhesive forces between the fluid and a surface and can have dramatic effects—unexpected by scientists who think of only bulk properties of liquids. Bubbles in capillaries are a serious nuisance in the laboratory, whether chemical or biological. Everyone who works in a lab knows how hard it is to break bubbles and fill capillaries. Hydrophobic surfaces are often covered with a vacuum layer a few Ångstroms thick (40–44).
The ideas of wetting and dewetting used in this article are not new or novel, nor is their context: much work has been done on wetting transitions in general and in nanostructures and the possibility of a hydrophobic gate has been suggested before (1–3), and seen in the calculations of others (4–20). Experiments have suggested the existence of gating phenomena without conformation changes of proteins (7,13,33,45) involving substantial volume changes (46,47). What is new is the suggestion that dewetting transitions create the characteristic current signal that defines a healthy channel (22–25). We suggest that a pore in a channel becomes a conducting column when its bubbles break and ions and water suddenly fill the channel, along with the side chains of the channel protein (48). What is also new is the suggestion that noble gas anesthetics act by modifying the energetics of bubble formation and filling (see Discussion) and that the well-known effects of hydrostatic pressure on anesthesia involve anesthetic effects on bubbles in channels.
In our view, ion channel proteins contain a variety of sensors connected to special structures that modulate the energetics of bubbles in the channel and thus produce or relieve “channel block” (25) by bubbles. Wetting is very sensitive to the local chemical and electrical environment (de Gennes et al. (28)) and could be easily modulated by the surrounding channel protein because the pores of channels (and bubbles within them) have tiny volumes and large surface/volume ratios.
Several examples come to mind. An ion-gated channel—e.g., Ca2+-activated K channel (49,50)—would use ion binding to a specific site to modulate the unstable balance of cohesive and disruptive energies in the pore of the channel, perhaps by slightly changing the electric field, or diameter of the pore. An agonist-gated channel (e.g., the nicotinic acetylcholine channel (3,17,39,51)) would use agonist binding to upset the balance. Voltage-gated channels (like the Na and K channels that control the action potential of nerve cells (25,52–55)) might use a special charged group as a voltage sensor that detects changes in the electric field and moves slightly to change the diameter of the channel, sterically upsetting the unstable balance between cohesive and disruptive forces to make and fill bubbles. Or the forces exerted by the electric field might themselves break the balance of cohesive and disruptive forces, filling or forming a bubble that would interrupt current flow (1,2,28). In this view, gating depends on the balance of steric and electrostatic forces, just as selectivity (56–64) and wetting/dewetting phenomena depend on that balance.
Bubbles in channels can be modified because adhesive (surface) forces between the wall of the channel and water in the channel (often misleadingly called hydrophobic forces) are in balance with the cohesive (volume) forces that keep bulk water in a liquid state. Water in a bulk condensed phase usually is without bubbles because cohesive forces dominate when surfaces are not present. However, bubbles easily form in water: “…under standard conditions, liquid water and vapor nearly coexist…” (65) because their “free energy difference is small compared to thermal energy” (66). If a capillary or channel is introduced into water, and the surface forces holding the water to the wall of the channel are not as strong as the volume forces holding water together, bubbles can form.
Bubbles can form when water touches a hydrophobic surface, for example, the hydrophobic parts of the channel protein. The interaction of the hydrophobic surface and water is weaker than the interaction of water with itself. Atomic size channels are particularly likely to contain bubbles because their surface is so large compared to their tiny volume (15,67–69). If the hydrophobic surface attracts water sufficiently weakly, part of the water column in the channel changes phase and becomes a gas bubble, nearly a vacuum. The water phase inside the channel is no longer condensed. Bubble formation is a pseudo-phase change produced by an imbalance between surface and volume forces, between wetting and dewetting (26–28,66).
We show how gating transitions can be explained by a general thermodynamic analysis of confined fluids. We use thermodynamic scaling laws of confined fluids that show how the macroscopic phenomena of capillary evaporation would behave on the atomic length scale of channels (4,58). We use a morphometric form of density functional theory of fluids (not quantum mechanics) to reach from macroscopic to atomic scales and show that bubbles are likely to occur in the pores of channel proteins. The morphometric form of density functional theory separates thermodynamic and morphological effects, as explained in the literature (70–74) and so is particularly well suited to our purposes. Density functional theory is reviewed in Evans (75) in the context of the properties of inhomogeneous fluids (76).
Bubble filling and formation are also likely to have an important role in the action of anesthetic gases as shown by our calculations of the effects of xenon (under atmospheric or hydrostatic pressure) on bubbles in channels. The actions of anesthetic gases have resisted analysis for many years because they do not seem to conform to the paradigm of receptor-mediated action that underlies most of pharmacology. The possibility of a physical explanation of anesthetic action has always been considered and receptor-mediated explanations have seemed more and more remote as knowledge of the ionic and then molecular basis of nerve activity increased (77–86). These articles are a few examples from a very large literature. The discussion of Heimburg and Jackson (87) seems convincing to outsiders like us. They show that simple thermodynamic scaling called the Meyer-Overton law relates the partition coefficient (i.e., lipid solubility) and anesthetic action of a range of agents with different chemical properties (87). It seems clear that lipid solubility is likely to scale monotonically, nearly linearly, with the parameters of our bubble model, suggesting a simple explanation of anesthetic action on both the atomic and protein length scales. It is easy to understand the marked effect of small excess hydrostatic pressures (∼1 atm) in the presence of gas anesthetics compared to the negligible effect of such pressures in the absence of gas anesthetics (79,88).
THEORY AND METHODS
Confined fluids in general
Any fluid, like water, or an ionic solution, can exist in two states below a certain temperature if its solvent particles repel each other at short distances but attract each other sufficiently at long and intermediate distances. For example, water can exist as both a high density liquid and low density gas below its critical temperature Tc of 647 K. Particles in a high density liquid phase gain much potential energy because they are close together and are located in the attractive parts of the interparticle potential (89). The entropy of the high density liquid is low because particles do not have much space to move in. High density liquids are a condensed phase with little space between molecules. The situation is reversed in the low density gas phase, where particles are far apart and so interact weakly. Particles in low density gas phases have more entropy because they have a great deal of free space to move in.
At the liquid-gas phase transition—where both a high density liquid and a low density gas can coexist—the loss of energy (in the liquid compared to gas) is precisely compensated by the gain of entropy (in the gas compared to liquid). Liquid and gas coexist at mechanical and chemical equilibrium when the pressure and the chemical potentials are equal in both the liquid and gas phase. As the density of the liquid is increased above its value at coexistence, the liquid phase becomes the only phase that is stable in an unconfined bulk system. Confinement changes the situation, as we shall soon see.
Fluid systems that can undergo a phase transition are best described as a grand canonical ensemble in which the system volume V, the temperature T, and the chemical potential μ are fixed (90). The corresponding grand canonical free energy is called the grand potential Ω. In an unconfined bulk system, the grand potential equals the volume term, which is the negative of the pressure p times the volume V, i.e., Ωbulk = −pV. Confinement adds extra terms to the grand potential that produce phenomena not seen in bulk, e.g., capillary evaporation. The grand potential is discussed in Evans (75) in the context of the properties of inhomogeneous fluids in general (76). Detailed discussion of our theory of the grand potential, the model and role of water, and the effect of surfaces and capillaries can be found in Roth and Kroll (4).
For a long time (26,27), it has been known that a hydrophobic confining environment, such as a capillary, can change a stable liquid into a gas even though that gas could not exist in the bulk (at that temperature and pressure). The change from liquid to gas is called capillary evaporation and is closely related to the reverse phenomenon, capillary condensation. Capillary condensation occurs when a stable gas phase confined by a hydrophilic surface—for example, a capillary—condenses into a liquid. The capillary introduces a surface term at the confining wall that modifies the grand potential Ω and thus produces the phenomena of capillary condensation and evaporation.
When a fluid is brought into contact with a single wall, the molecules of the fluid are usually found in different concentration (i.e., number density) close to the wall. The inhomogeneous distribution is produced because the neighbors of particles in the bulk are other fluid particles but the neighbors of particles at the wall are the molecules of the wall. Interactions are different at the wall compared to the bulk because 1), the wall is chemically different from the bulk; and 2), the wall does not move (on the average) even when a fluid particle collides into it. The wall can be described as an external potential acting on the fluid that depends on the chemical nature of the wall and fluid, and on the geometry. If the (integrated) wall-fluid interaction is more attractive than the (integrated) fluid-fluid interaction, the wall is called hydrophilic and the contact angle is <90°. If the (integrated) wall-fluid interaction is less attractive than the (integrated) fluid-fluid interaction, the wall is called hydrophobic and the contact angle is >90° (28,29).
The energy gain or loss of bringing a liquid or a gas into contact with a wall is measured by the wall surface tension. The grand potential of a fluid in contact with a wall is given by Ωwall = −pV + σA, where A is the area of the wall. The (second) surface term defines the wall surface tension σ. If the wall is hydrophilic, then the value of the wall surface tension for the liquid phase is lower than for the gas phase, σliquid < σgas. In the case of a hydrophobic wall, the relation is reversed, σliquid > σgas.
While a single hydrophilic or hydrophobic wall can change the local concentration close to the wall, the overall effect on the fluid is often small, even if a monatomic layer of gas is formed (42,43). The stable bulk phase remains stable at macroscopic distances from a single wall.
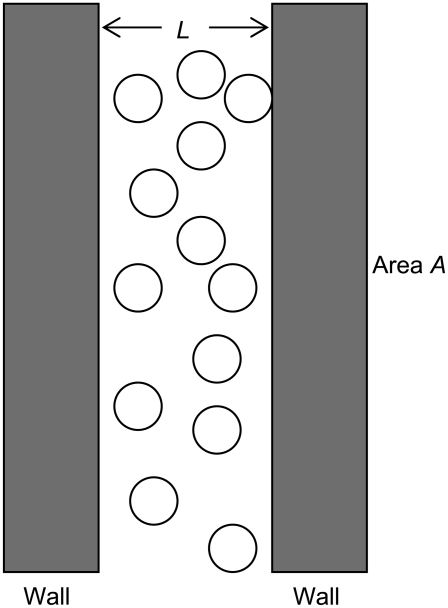
If the fluid is confined in a narrow slit of two parallel walls, surface effects are much larger and gas phases can form more easily because the fluid inside a slit is in contact with two walls (our Fig. 1; see also Figs. 2 and 3 of (4)). Each wall contributes a surface term of the form σA to the grand potential so that the resulting grand potential for a fluid inside a slit is given by
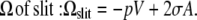 |
(1) |
Since the volume inside the slit is V = AL, where L is the slit width, the grand potential can be divided by the surface area and takes the form Ωslit/A = −pL + 2σ. The grand potential depends linearly on the slit width L. The slope of the grand potential (per area) is the negative of the pressure and the offset is given by twice the wall surface tension.
FIGURE 1.
Schematic drawing of a fluid inside a slit of two parallel walls. The slit width is L and the area of the wall is A. The volume in the slit is V = A · L . In the thermodynamic limit, A → ∞, so the total volume is infinite.
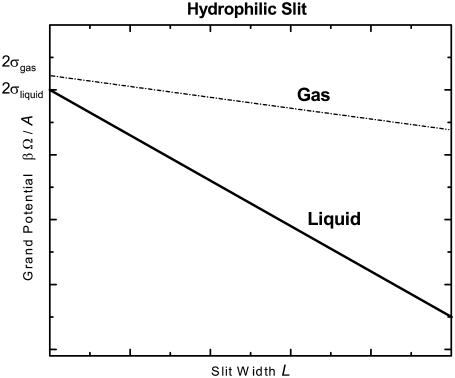
FIGURE 2.
Schematic plot of the grand potential per area βΩ/A of a liquid and a gas in a hydrophilic slit as a function of the slit width L. The properties of the liquid define the solid line; the pressure in the liquid sets the slope of the solid line. The properties of the gas define the dashed line; the pressure in the gas sets the slope of the dashed line. The pressure in the liquid phase is larger than the pressure in the gas phase. The wall surface tension for the liquid defines the vertical offset of the lines and is more negative than for the gas. Thus, the grand potential for the liquid is always more negative than for the gas. As a result, the liquid in a hydrophilic slit remains stable (independent of the slit width) and no gas bubble forms.
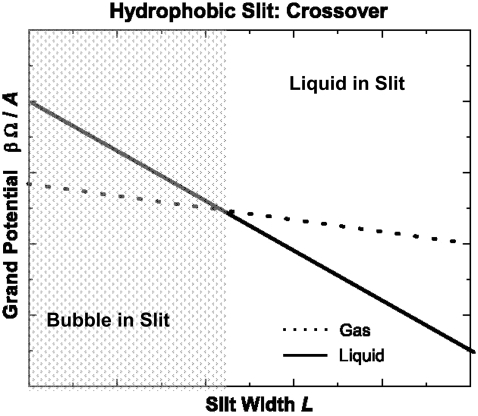
FIGURE 3.
Schematic plot of the grand potential Ω of a liquid and a gas in a hydrophobic slit as a function of the slit width L. In this hydrophobic case, the grand potential (per area) of the liquid (solid line) and the gas (dashed line) phase can intersect. The intersection point marks the capillary evaporation phase transition. To the right, liquid fills the slit; to the left, a bubble of gas will form and fill the slit. Note the comparison to the hydrophilic case of Fig. 2, where bubbles cannot form because the offsets are interchanged compared to the hydrophobic case shown here. The offsets are given by twice the wall surface tensions.
The hydrophilic slit has a wall surface tension for liquid more negative than for a gas: σliquid(hydrophilic) < σgas(hydrophilic). Furthermore, it follows from the form of the grand potential in the bulk, Ω = −pV, that the pressure in a stable bulk liquid is larger than in the gas phase at the same chemical potential, i.e., pliquid > pgas, because the stable bulk phase corresponds to the lowest grand potential at a given chemical potential. The grand potential (per area) for a hydrophilic slit is schematically plotted as a function of the slit width L in Fig. 2. The full line shows the grand potential (per area) for the liquid phase. The dashed line shows the grand potential (per area) for the gas phase. One finds that, independent of the slit width L, the grand potential (per area) for the liquid phase is more negative than that of the grand potential (per area) for the gas phase because the pressure in the liquid is larger than in the gas and the surface tension of the liquid is smaller than for the gas. The liquid phase in the hydrophilic slit is thermodynamically stable for all values of L: its grand potential is more negative than the grand potential of the gas phase. A bubble of gas will not form in a hydrophilic slit. The presence of two hydrophilic walls cannot destabilize the liquid phase, under these conditions.
In Fig. 3, we plot schematically the grand potential (per area) of a fluid inside a hydrophobic slit. The offset of the two lines for liquid and gas phases in a hydrophobic slit are reversed compared to Fig. 1 because now σliquid(hydrophobic) > σgas(hydrophobic). In the hydrophobic case, the curve describing the grand potential (per area) in the liquid and the curve describing the grand potential in the gas phase can intersect and cross each other. The intersection point, at which the grand potential for the liquid phase equals precisely that for the gas phase, is called the phase transition point for capillary evaporation.
In the hydrophobic case of Fig. 3, the transition depends on slit width L. For sufficiently large slit width L, the grand potential (per area) for the liquid phase is more negative than that for the gas phase and the liquid phase is the stable phase. For small values of L, however, the grand potential (per area) of the gas phase (in the hydrophobic case) is more negative than that for the liquid phase. Then the gas phase becomes the stable phase. If L changes for some reason or other—because of an external intervention, for example—the system contents can switch phase, from gas to liquid or vice versa.
We propose that channel proteins are built to change L (or something equivalent), thereby creating a pseudo-phase change in the channel, which is blocked by a bubble when the channel is filled with a bubble of gas, and open when the channel is filled with a liquid. In this view, the bubble is the gate that controls the conductance of the channel, switching it stochastically from nearly zero to a single open value (see Eq. 6).
Morphometric approach
Biological and engineering systems use complex geometries to make devices and machines utilizing thermodynamic driving forces and so it is useful to cast theory and simulations in a form that displays the separate effects of structure and physics. To study bubbles in a complex geometry like that shown in Fig. 4 we use the morphometric approach (70–74) to separate the role of geometrical confinement and thermodynamics in capillary evaporation for capillaries of different size, ranging from atomic to mesoscopic. Density functional theory (4,58,91,92) is explained in Evans (75) in the context of the properties of inhomogeneous fluids (76) and the morphometric approach is developed in detail with extensive discussion in the literature (70–74).
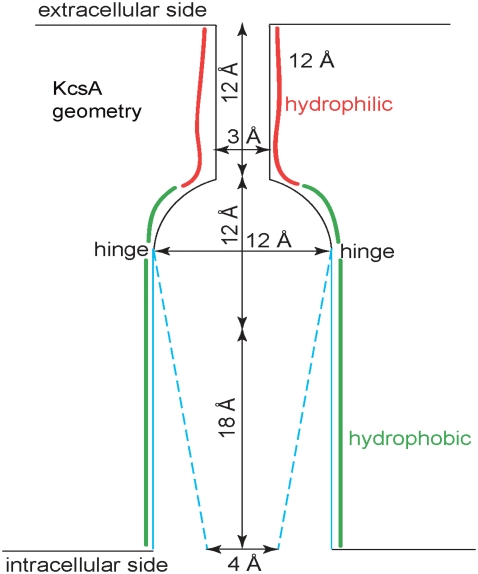
FIGURE 4.
A simplified model of the KcsA channel. In our model, bubbles form on the hydrophobic side of the channel below the semispherical cavity. The hydrophilic selectivity filter is on the extracellular side. The hydrophobic gate is shown in two possible conformations, starting from a diameter of d2 = 12 Å and closing to diameter d2 = 4 Å. We consider bubble formation as d2 changes. Confinement by a hydrophobic region is required to make bubbles persist long enough to observe them or their biological effects, i.e., to make bubbles stable.
The morphometric form of the grand potential of a fluid confined by a complexly shaped wall is given by
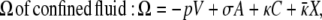 |
(2) |
where the first two terms are the volume and surface terms, described earlier. The new terms describe the effect of curvature on the grand potential (see (93) for further curvature effects). The geometrical measures C and X are the integrated (over the surface area) mean and Gaussian curvatures of the wall (70–74) and the corresponding thermodynamic coefficients κ and 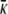 are bending rigidities. Morphometric theory (70–74) is an accurate theory that separates geometry and thermodynamics and so thermodynamic coefficients are independent of geometry and scale (e.g., the size of the capillary) and can be applied universally in many geometries; changing the geometry will only change the geometric coefficients, not the thermodynamic coefficients, as illustrated, for example, in Roth's physical analysis of capillary evaporation (4). As the pore becomes more narrow, the terms proportional to C and X in Eq. 2 become more important, and describe accurately this highly confined fluid.
are bending rigidities. Morphometric theory (70–74) is an accurate theory that separates geometry and thermodynamics and so thermodynamic coefficients are independent of geometry and scale (e.g., the size of the capillary) and can be applied universally in many geometries; changing the geometry will only change the geometric coefficients, not the thermodynamic coefficients, as illustrated, for example, in Roth's physical analysis of capillary evaporation (4). As the pore becomes more narrow, the terms proportional to C and X in Eq. 2 become more important, and describe accurately this highly confined fluid.
Channel gate: grand potential
In the following, we employ the morphometric approach to describe the thermodynamic state of the fluid inside a hydrophobic gate. We focus only on the gate, assuming (for simplicity) that other parts of the channel are not affected by the presence or absence of a bubble. When we explicitly describe the gating of a channel, the geometry of the channel is represented as an idealized K channel (Fig. 4). In other cases, we use a simple regular cylinder to illustrate our ideas. The previous discussion motivates a model in which a gate can either be filled with fluid that allows ion flux through the channel, or be blocked by a bubble and thereby stop ion flux.
Our model—specified in detail in Roth and Kroll (4)—represents gating as the transition between a pair of equilibrium states with grand potential either Ωopen or Ωclosed, the more negative grand potential being the more probable, ignoring nonequilibrium effects,
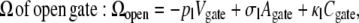 |
(3) |
where the thermodynamic coefficients pl, σl, and κl describe the pressure, the wall surface tension, and the bending rigidity of the liquid in the gate. The corresponding geometrical measures, Vgate (the volume inside the gate), Agate (the surface area accessible to the liquid), and Cgate (the integrated mean curvature of the accessible surface area) describe the structure, the geometrical configuration of the gate. Note that in all the geometries used here, the integrated Gaussian curvature X vanishes and so Eq. 3 has only three terms.
The grand potential of the gate in the closed state is more complicated because the gate is partially filled by the liquid and partially filled by the gas with two liquid-gas interfaces bounding the bubble. From Eqs. 2 and 3, and following Roth and Kroll (4), the grand potential for the closed state is given by
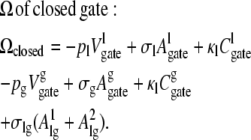 |
(4) |
In Eq. 4, the thermodynamic coefficients marked with subscript l (pl, σl, and κl) describe the liquid part filling the gate, while pg, σg, and κg describe the gas bubble in the gate. The term 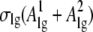 accounts for the two liquid-gas interfaces forming at the top and at the bottom of the bubble with surface area
accounts for the two liquid-gas interfaces forming at the top and at the bottom of the bubble with surface area 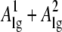 and the liquid-gas surface tension σlg. The geometrical measures in Eqs. 3 and 4 are related. The total volume Vgate of the gate is the volume filled by liquid plus the volume filled by gas
and the liquid-gas surface tension σlg. The geometrical measures in Eqs. 3 and 4 are related. The total volume Vgate of the gate is the volume filled by liquid plus the volume filled by gas 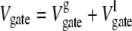 with corresponding area
with corresponding area 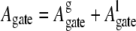 with total (i.e., integrated) mean curvature
with total (i.e., integrated) mean curvature 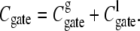
The difference in grand potential ΔΩ between open and closed states determines the probability of opening, and so this is the quantity of interest in our model. The difference ΔΩ is the driving force for gating:
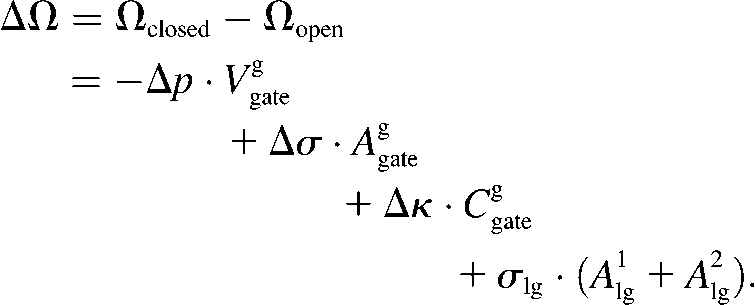 |
(5) |
If ΔΩ is positive, then the gate is most probably in the open state, because the open state is thermodynamically favorable over the closed state. If ΔΩ is negative, the closed state is most probable. Here, Δp = pg − pl, Δσ = σg − σl, and Δκ = κg − κl. ΔΩ is a macroscopic measure of atomic-scaled quantities. The morphometric version (70–74) of density functional theory shows that atomically narrow pores—in which the size of water molecules and natural grain of protruding side chains are significant—are accurately described by variables of this type, as illustrated by Roth's theory of capillary evaporation (4).
The physical interpretation of Eq. 5 is important. The first term in Eq. 5, the volume term 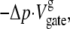 always favors the stable bulk phase in the gate, which is the liquid phase, although it is often small in tiny channels. Therefore, the volume term helps to stabilize the open state of the gate.
always favors the stable bulk phase in the gate, which is the liquid phase, although it is often small in tiny channels. Therefore, the volume term helps to stabilize the open state of the gate.
Making the liquid-gas interface of a bubble costs the energy of two liquid-gas interfaces 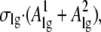 and so this term also works in favor of the open state of the gate. The curvature term
and so this term also works in favor of the open state of the gate. The curvature term 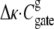 is also positive in a cylinder, favoring an open state and so the only term that can make the gating driving force ΔΩ favorable for bubble formation (i.e., make ΔΩ < 0) is the surface term
is also positive in a cylinder, favoring an open state and so the only term that can make the gating driving force ΔΩ favorable for bubble formation (i.e., make ΔΩ < 0) is the surface term 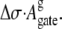 (The gate is hydrophobic in our model, with Δσ < 0. Note that more realistic models of channel structure would have regions where
(The gate is hydrophobic in our model, with Δσ < 0. Note that more realistic models of channel structure would have regions where 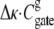 might have different values (93), and even be negative. Those regions might have specific roles in channel gating.) Only the interaction between the fluid in the gate and the hydrophobic wall can overcome the attractive interparticle interaction between fluid particles, destabilize the liquid phase, and create a gas bubble. Bubbles can form only if the wall-fluid interaction is sufficiently hydrophobic and the gate is sufficiently narrow. Only then can the surface term
might have different values (93), and even be negative. Those regions might have specific roles in channel gating.) Only the interaction between the fluid in the gate and the hydrophobic wall can overcome the attractive interparticle interaction between fluid particles, destabilize the liquid phase, and create a gas bubble. Bubbles can form only if the wall-fluid interaction is sufficiently hydrophobic and the gate is sufficiently narrow. Only then can the surface term 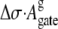 overcome the sum of the other terms.
overcome the sum of the other terms.
Influence of hydrophobic gases
Dissolved gases are known to have striking effects on channel gating (even at small excess pressures—∼1–2 atm—that themselves have no effect on gating (79,88)) and so it is interesting to study the effects of a small concentration of hydrophobic gas dissolved in the liquid on bubble formation in the gate of our model. We compute a small concentration of dissolved gas modeled as spheres with a square-well water-gas interaction with the diameter of xenon. If the interaction of the gas with water is weaker than the interaction of water with water, the gas is hydrophobic. Here we fix the water-gas interaction so the solubility of the gas is similar to that of xenon in water.
The behavior of the liquid with dissolved gas is nearly the same as that of the pure liquid because the small concentration of gas changes the pressure pl, the wall surface tension σl, or the bending rigidity κl only slightly. The effects of the dissolved gases can still be dramatic because the bistable process of bubble formation depends sensitively on the differences Δp, Δσ, and Δκ that appear in Eq. 5.
If the bubble is mainly filled by particles of the hydrophobic gas then it is clear that the difference of the thermodynamic coefficients Δp, Δσ, and Δκ that appear in Eq. 5 change significantly from their corresponding values without dissolved gas. Hence the gating mechanism we propose here will depend sensitively on concentration of a dissolved hydrophobic gas and on the hydrostatic pressure, (only) when dissolved gases are present.
Open and closed probability
The ratio of the probability of finding the gate in the open state to the probability of finding it closed is written in traditional form (94) as the ratio of the corresponding Boltzmann factors,
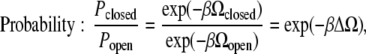 |
(6) |
where β = 1/(kBT) and, as usual, Pclosed + Popen = 1, so the open and closed probabilities are
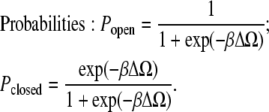 |
(7) |
Note that the grand potential of the closed state used for the computation of probabilities corresponds to the minimum of the grand potential with respect to (a measure of the) size of the bubble. (The grand potential of the closed state Ωclosed in Eq. 6 should really be called min{Ωclosed}.) This minimum was found analytically from Eq. 4 with the geometric measures expressed as functions of bubble axial length. The minimum of grand potential corresponds to a bubble length substantially greater than zero because states with shorter bubble lengths have a larger grand potential and thus are not stable.
Computational details
Phenomena such as capillary condensation, capillary evaporation, or bubble formation, are generic for fluids below their critical temperature but whether they are actually used by biological channels remains to be seen, and is fundamentally an experimental question. Until that is settled, i.e., until measurements are made of fluid, gas, ions and side chains inside a protein channel, we feel it appropriate (and judicious) to use the simple models described in detail in Roth and Kroll (4).
We use, for example, a simple square-well model of fluids to describe our solvent following Roth and Kroll (4) and other users of density functional theory reviewed in Evans (75) (see also (74,92,95–97)),
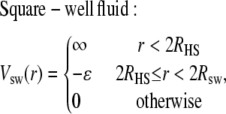 |
(8) |
with the hard core radius RHS, depth of the attractive potential −ɛ, and the range (i.e., width) of the square-well given by Rsw.
As described by Eqs. 1–3 in Roth and Kroll (4), the full interaction potential is split into a hard-core reference part and a square-well attraction part. The resulting functional is minimized in an infinitely long cylindrical pore with diameter dcyl. As output we obtain the density profile ρ(r) of the fluid in the cylindrical pore (see Fig. 2 of (4)) and the grand potential Ω[ρ(r)] of the system—shown by the symbols in Fig. 3 of Roth and Kroll (4)—as a function of dcyl. Having calculated both the density profile and the corresponding grand potential for various values of dcyl we can separate the results into a liquid branch, with liquidlike density distributions in the pore, and a gas branch, with gaslike density distributions in the pore. We determine the value of the morphometric coefficients p1, σl, and κl by least-squares fitting the morphometric form of the grand potential in cylindrical geometry to our numerical results for the liquid branch of the grand potential (see solid line in Fig. 3 of (4)). Similarly we determine the value of pg, σg, and κg by a fit to our results for the gas branch of the grand potential (see dashed line in Fig. 3 of (4)). To calculate the grand potential in our model gate geometry we make use of the separation of the morphometric form into geometrical measures and thermodynamic coefficients (70–74). This separation means that the thermodynamic coefficients, which we determined in a cylindrical geometry, are independent of the geometry and can be applied universally in all geometries, including our model of the geometry of the channel gate.
When we consider a mixture of water and xenon inside the pore, we obtain—as a result of the minimization of the functional—the inhomogeneous density distributions of both water and xenon, and the corresponding grand potential. From these data we determine the thermodynamic coefficients for the mixture. Since xenon is a hydrophobic gas, it tends to accumulate at the protein wall and thereby influences the interaction of the water and xenon mixture with the protein, which is measured in the surface tension and the bending rigidity. The concentration of xenon in the liquid phase is too small to have a noticeable effect on the coefficients p1, σl, and κl. However, in the gas phase the xenon concentration is sufficient to significantly influence the values of pg, σg, and κg, thereby changing the balance between the open and the closed state of the gate.
Note that the precise numerical values of the thermodynamic coefficients are determined by the fluid interaction potential, with the calculations outlined in this section and shown in detail in Roth and Kroll (4). Clearly, a more realistic model of water including directional water-water bonds would change these values. But values of parameters of the models would have to be measured in the atomic-scaled confines of a protein channel. Parameters of water in the bulk cannot be assumed to describe water confined on the atomic scale inside a specialized protein, an ion channel.
The phenomenon of bubble formation and breaking, described here, depends on a balance between volume and surface terms rather than on the absolute value of certain quantities. With our choice of parameters we try to create a reasonably general model of this balance in water near a hydrophobic surface.
Equilibrium assumptions
Our model represents gating as the transition between a pair of equilibrium states, ignoring nonequilibrium effects in the open channel or in the transition between states. This approach has ample precedent in channel biology (25), ranging back to Hodgkin and Huxley (94,98,99). In essence, we assume that all additional contributions to the grand potential of the whole system (including nonequilibrium effects of flow) remain the same as the state of the gate changes. Dissipation of energy (e.g., generation of heat) as the bubble forms or breaks is ignored.
Phenomena such as capillary condensation, capillary evaporation, or bubble formation, described above, are generic for fluids below their critical temperature. Since water-water interactions are very complicated and water-protein interactions are not well established, we perform here model calculations with a simple fluid and with idealized protein-fluid interactions. However, it is important to keep in mind that the phenomena described here are commonly observed in the most realistic atomic simulations available, for example, in the literature (5–10,12–14,16–20), as well as in coarse-grained lattice models of confined water (6,8,10) and density functional models (see (4)). By using a simple fluid and idealized protein-fluid interaction, it is possible to study the phenomena related to bubble formation in a hydrophobic gate systematically and also to add a hydrophobic gas to study the influence of a small concentration of a general anesthesia. More realistic models of bulk fluids are not likely to be helpful because they cannot be safely assumed to be realistic models of fluids in atomic-sized channels. Direct measurements of fluids in tiny channels are needed to establish realistic models of fluids in that environment, in our opinion.
Parameters of the model
The parameters for water used in our model calculations are ɛ = 1.2 kBT, RHS = 1.4 Å, and Rsw = 2.1 Å. These parameters ensure that the square-well fluid at room temperature is significantly below the critical temperature while the liquid is relatively close to phase separation at 55 M, both important characteristics of water at room temperature.
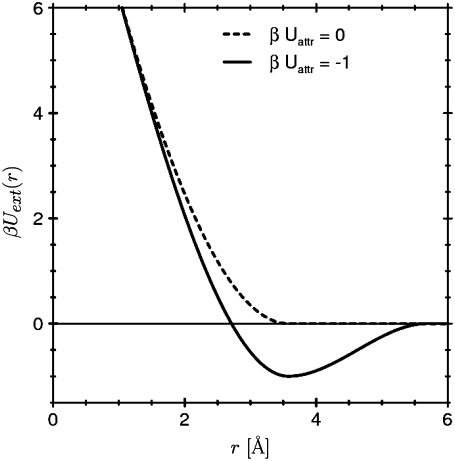
The channel protein is represented in our calculations as an external potential acting on the fluid inside the channel. Following the approach explained in Roth and Gillespie (58), we represent the channel as a fluid of hard spheres confined with a hard wall potential that defines the channel radius. The hydrophobicity of the wall is controlled by adding an additional short-ranged attractive potential-well close to the protein wall, with well-depth Uattr. Two examples of the resulting protein-fluid interaction are shown later in Fig. 6.
FIGURE 6.
The protein-fluid interaction potential Uext(r) of our model as function of the normal distance r from the protein. The case βUattr = 0 (dashed curve) labels the most hydrophobic case in which the protein-fluid interaction is purely repulsive. The potential well (of depth Uattr) is short-ranged and makes the protein-fluid interaction less hydrophobic. The specific case illustrated by the solid curve has βUattr = −1 and is significantly less hydrophobic than the case illustrated by the dashed curve where βUattr = 0.
We take advantage of the separation between geometrical measures and thermodynamic coefficients to compute the thermodynamic coefficients. Density functional calculations are performed inside an infinitely long cylindrical channel of various diameters d as described in detail in Roth and Kroll (4). From the values of the grand potential Ω(d), as a function of the pore diameter d, we can extract the numerical values of the thermodynamic coefficients pl, σl, and κl for the liquid phase. Calculations of the gas phase give us the values of the thermodynamic coefficients pg, σg, and κg for the gas phase as described in detail in Roth and Kroll (4). Because morphometric analysis separates geometry and thermodynamics (70–74), the thermodynamic coefficients computed this way are directly transferable to a more complex channel geometry.
Parameters of hydrophobic gases
Hydrophobic gases are modeled by adding a second component to our fluid. The gases are hydrophobic because the (integrated) interaction of the gas with the water particles (described by a square well potential with RHS = 2.1 Å, Rsw = 5.6 Å, and ɛ = 0.63) is weaker than the interaction of one water particle with another. We repeat our density function theory calculations for a liquid and a gas inside an infinitely long cylindrical channel and extract the corresponding thermodynamic coefficients.
The influence of hydrostatic pressure at a fixed temperature, which produces a change in the fluid density, can be described by the isothermal compressibility cT that is defined as
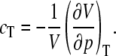 |
(9) |
The bulk density of the fluid defined by ρ0 = N/V changes when the hydrostatic pressure changes according to
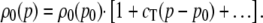 |
(10) |
At room temperature, cT = 0.44 (GPa)−1, implying that the number density of water changes 0.44% when a pressure of 10 MPa is applied. This seemingly small change is enough to modify both the solubility of xenon and also the balance of volume and surface forces that governs bubble formation and filling. Bubble formation is a threshold phenomena sensitive enough that we must include effects on the density of bulk water.
Comparison with simple point charge (SPC) water
Understanding the physics of bubble formation and breaking requires a model of water that accounts for the balance between the cohesive volume forces (that come from water-water interactions) and surface forces (that come from protein-water interactions). In this section, we compare bubble formation computed with our morphometric treatment of a simple model of water (Eq. 8) with the computations of bubble formation of Huang et al. (100), who used the simple point charge (SPC) model of water (101) and both molecular dynamics simulations and a reduced model. We adopt the geometry of Huang et al. (100) and their value of the hydrophobic interaction between water and wall (i.e., contact angle of 140°) and use our morphometric approach and our model of water to compute curves comparable (and in fact quite similar) to their Fig. 2 A.
Following Huang et al. (100), we consider the geometry depicted in their Fig. 1, which is given by two parallel biaxial oblate ellipsoids with half-axes σ⊥ > σ‖ and a center-to-center separation D. Assuming, like (100), that any bubble present fills the whole space between the two hydrophobic ellipsoids, we can specify the geometrical measures of the bubble as follows. The volume of the bubble is
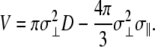 |
(11) |
The area of one hydrophobic surface is (100,102)
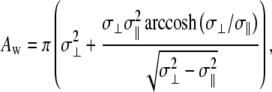 |
(12) |
with a mean curvature (integrated over the surface area) of (102)
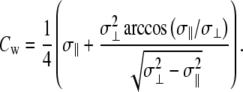 |
(13) |
The surface area of the liquid/gas interface is (100)
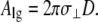 |
(14) |
The driving force for bubble formation is the difference in the grand potential Eq. 5 between the two ellipsoids, one with a gas bubble and the other with liquid in between, Huang et al. (100)
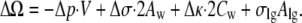 |
(15) |
For two ellipsoids, ΔΩ is a function of the center-to-center separation D and one can calculate the critical distance Dc for which ΔΩ = 0. This separation is
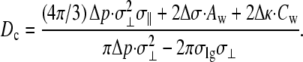 |
(16) |
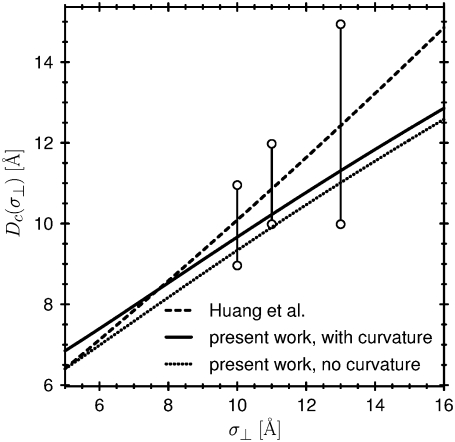
We compare our estimates of Dc with those of Huang et al. (100) in Fig. 5. The critical distance Dc was calculated in Huang et al. (100) with an equation similar to Eq. 16 and compared to molecular dynamics simulations. In their computer simulations, σ‖ was fixed at 3.1 Å, while the value of σ⊥ was varied between 5 and 16 Å. Huang et al. (100) set the interaction between the hydrophobic ellipsoids and the SPC water so the contact angle was 140°. Fig. 5 shows the results of Huang et al. (100) for Dc as a dashed line, together with the error bars of their molecular dynamics simulations, that estimate upper and lower bounds of simulations, as described in their article.
FIGURE 5.
Comparison with other calculations that used SPC water. The critical separation Dc at which bubbles form between two hydrophobic ellipsoids. The dashed line and the error bars are taken from Huang et al. (100) and represent results from their molecular dynamics simulations with SPC water. The dotted line is the result of our morphometric approach when the curvature of the wall is neglected, as in the thermodynamic treatment of Huang et al. (100). The solid line is the result of our morphometric approach, but taking the curvature of the ellipsoids into account. The agreement between our approach using a simple water model equation (8) and the computer simulations of SPC water is very good. Indeed, it is nearly quantitative at small values of σ⊥ of interest in ion channels.
To compare against these results using the present morphometric approach, we use our model of water to calculate the differences in the thermodynamic coefficients Δp, Δσ, and Δκ as well as the surface tension of the liquid-gas interface σlg. Of these coefficients, Δp and σlg are independent of the interaction of the hydrophobic ellipsoids with the water, while Δσ and Δκ depend on this interaction. To compute the results in Fig. 5, we chose the wall–water interaction in our model so that the contact angle was 140°, the same contact angle used in Huang et al. (100). Only the wall–water interaction (i.e., the hydrophobicity of the wall) was adjusted in our model to reproduce the system of Huang et al. (100); the water–water interaction was not changed in any way and is the same as used in the rest of our article.
If the curvature of the wall is neglected (following (100)), the morphometric approach applied to our simple model of water gives the dotted line in Fig. 5. The agreement between their results and our morphometric approach is quite good. The agreement of our approach and the results of Huang et al. (100) improves even further if we take the curvature term (the term proportional to Cw) into account—see the solid line in Fig. 5. Both the different models of water and the different computational methods give mutually consistent results, particularly when bubbles are small as in ionic channels.
RESULTS
We first study the behavior of our model water equation (Eq. 8) in a reduced model, a simple cylindrical pore 12 Å in diameter and 24 Å long. This simple geometry surrounds a column of liquid water or a bubble of water vapor, depending on conditions and parameters that can change and modulate the physiological operation of an ion channel.
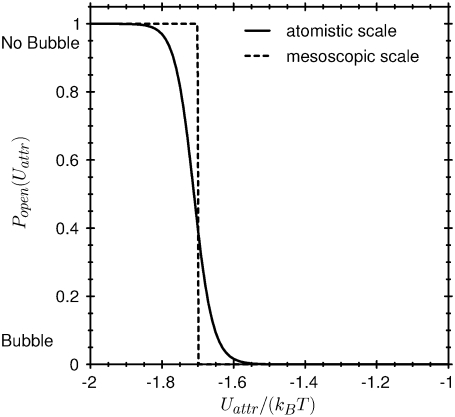
The hydrophobicity of the pore wall changes the state of the water in the pore (see Methods; see also Figs. 2 and 3). The interaction between the pore wall and water is described in our model by the potential profile shown in Fig. 6. When the strength of the attractive part of this potential Uattr is varied over a small range, the cylinder empties, i.e., the probability of finding liquid water in the pore is changed from a value close to one to a value close to zero (Fig. 7, solid line). A small change in Uattr—just a fraction of kBT—changes the grand potential (Eq. 5) enough to dramatically change the probability of the open (i.e., liquid-filled) state of the pore (Eq. 7). An ion channel can gate (i.e., open or close, by filling or making a bubble) by changing the hydrophobicity of the wall just a small amount, for example by moving or exposing a hydrophobic side chain of the channel protein (13,103). The hydrophobicity of the wall would be a sensitive control parameter of gating in this case. Allosteric binding sites remote from the channel itself could produce small conformational changes in the protein wall, changing its hydrophobicity thereby modulating or controlling gating.
FIGURE 7.
Probability Popen of a conducting channel, in tiny atomistic scale and mesoscopic scale channels. Popen on the atomistic scale (solid curve) is the probability of finding liquid in a cylindrical pore of diameter dcyl = 12 Å and height H = 2dcyl = 24 Å. Popen on the mesoscopic scale (dashed curve) is the probability of finding liquid in a cylindrical pore of diameter dcyl = 14 nm and height H = 2dcyl = 28 nm. The abscissa is the hydrophobicity defined here by Uattr. Hydrophobicity of Uattr = −1 kBT means the wall is very hydrophobic and Popen ≃ 0. Hydrophobicity of Uattr = −2 kBT means the wall is very hydrophilic and Popen ≃ 1.
The transition between liquid and a vapor bubble in the channel pore has many of the properties of a phase transition, but strictly speaking the transition is a pseudo-phase transition because only a small number of molecules are involved. The effect of the number of cooperating molecules is shown by increasing the size of the cylinder tenfold (Fig. 7, dashed line). The larger cylinder shows a much sharper transition than the channel-sized system. Systems smaller than the channel pore shown here will produce less crisp transitions than shown in Fig. 7, other things being equal.
In many ion channels, mechanical changes that narrow or widen a pore section have been observed and are thought to be important in gating (39,104–110). Our model shows how a small geometrical change might produce a very steep nearly all-or-none behavior of the current through a single channel protein. The pseudo phase transition of bubble produces a sudden change of current, the opening and closing of a single channel. The pseudo phase transition makes the small change in pore size a highly effective controller of channel conductance, both in a single channel and in the ensemble of channels that makes its ionic conductance. The sensitivity of gating to diameter depends on the hydrophobicity of the wall.
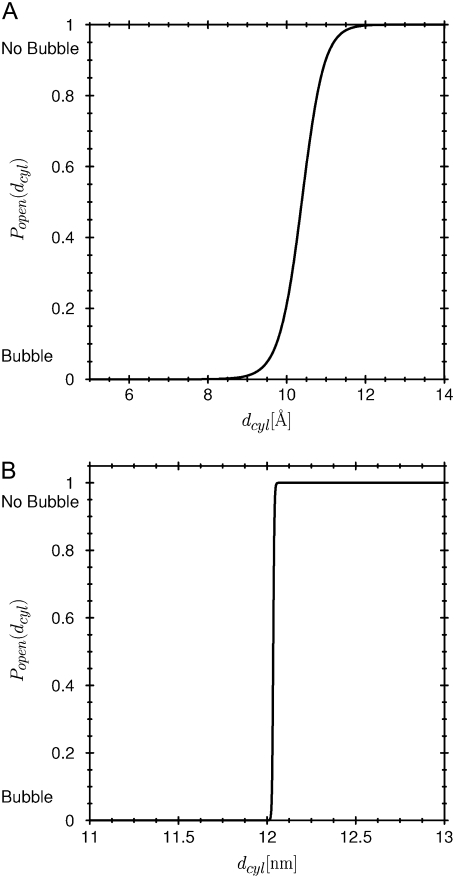
Fig. 8 shows the dependence on diameter explicitly. A reduction of pore diameter by only 2 Å in the geometry of the small cylinder can produce much of the change in open probability (Fig. 8 A). The vapor bubble of the pore switches off (i.e., blocks) conduction in a pore much wider than a water molecule. The bubble stops ionic conduction and the pore does not have to be pinched off to a diameter less than that of the conducted particles to block conduction. Fig. 8 B shows the open probability in a mesoscopic pore 10× larger than the channel pore. The transition between liquid and vapor bubble is much sharper in this larger (now mesoscopic) pore because of the larger number of water molecules. The transitions between open and closed occur at similar ratios of pore diameter to pore length (i.e., aspect ratios) in the small (nearly atomic, Fig. 8 A) and the large (mesoscopic) pore (Fig. 8 B).
FIGURE 8.
Probability Popen of a channel with atomistic or with mesoscopic dimensions. (A) The probability Popen of finding liquid in a cylindrical pore of diameter dcyl = 12 Å and height H = 2dcyl = 24 Å as a function of the pore diameter dcyl. A wide channel with dcyl = 14 Å is conducting, i.e., filled with liquid and Popen ≃ 1. A narrow channel with dcyl = 8 Å is nonconducting, blocked by a bubble with Popen ≃ 0. (B) Mesoscopic channel dcyl = 12 nm. The transition between a conducting (open) and a nonconducting (closed) cylinder is much steeper in the larger mesoscopic scale pore, because more particles are involved in the transition. In the case of a macroscopic pore, the transition would be even steeper.
These computations with a simple pore geometry are consistent with the idea that bubble filling and forming are the long-sought gating mechanism of ion channels (94,111–113)—sometimes seen in the absence of channels (33,45)—as illustrated in the hydrophobic gates postulated from molecular dynamics simulations (1–3,5–11,13,14,16–20,114–122). Or in more formal language, our calculations show that a liquid/vapor bubble transition in a hydrophobic pore could produce the sudden change of conductance that is the defining characteristic of single ionic channels (22,23). This transition is a pseudo-phase transition that retains steep dependencies on pore parameters even in tiny channels containing water columns only a few molecules in diameter.
Gating in a KcsA-like channel geometry
The morphometric approach used to compute the thermodynamics of the confined water (70–74) allows easy calculation of the effects of geometry on gating, i.e., bubble formation. For example, channels that share the KcsA pore structure have been proposed to gate in response to a small conformation change. Specifically, the swinging helical protein segments about a hinge (formed by glycine residues located near the central cavity (123,124)), are thought to narrow a pore section near the central cavity, on the intracellular side. Fig. 4 shows a model in which the protein controls the diameter (on the intracellular side) of a conical pore section while the other diameter of the cone (on the extracellular side) is fixed equal to the diameter of the central cavity. Our computations show the effects of a specific movement in a specific model. We find that variation of the intracellular pore diameter sketched in Fig. 4 is enough to control the formation of a vapor bubble in this KcsA-like pore.
Fig. 9 shows a graph of the open probability versus the controlling diameter. In our view, a small conformational change in any hydrophobic channellike geometry is likely to dramatically change bubble formation and filling (Fig. 7 and Eqs. 5–7). Here, bubble formation (i.e., gating) is controlled only by the diameter of the conical pore on the intracellular side (see Fig. 4). The relation between open probability and this diameter is less steep than that between open probability and the diameter of a cylinder, shown in Fig. 8 A. The difference is solely due to geometry. All other parameters of the model are fixed. Specifically, the thermodynamic coefficients in the (change in) grand potential (Eq. 5) are the same in both computations, so that only the geometrical variables—volume, surface area, and integrated curvature—determine the (change in) grand potential. The calculations used here involve only a small amount of algebra but they allow predictions of gating of pores of different shape or type. Simulations on the atomic scale involve huge computational cost and must be redone for each geometry. The small computational burden of our model allows bubble gating to be incorporated into complex schemes of gating used to describe activation, deactivation, inactivation, and slow inactivation (53,125). The power of the morphometric approach (70–74) is that it separates geometry from thermodynamics and so allows easy understanding of changes in shape and size. A simple geometrical scaling rule depending on the aspect ratio seems to govern the transition (see (4)). The aspect ratio of the pore cylinder determines the surface/volume ratio regardless of absolute pore dimensions.
FIGURE 9.
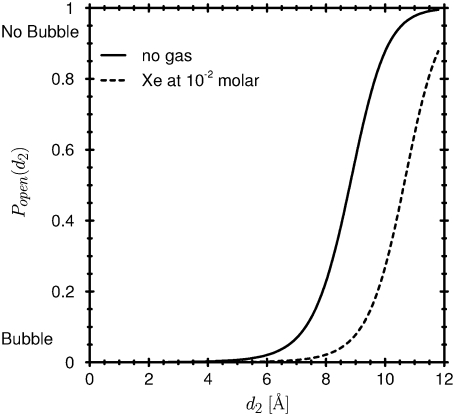
Open probability. Probability Popen of a conducting channel, i.e., probability of finding liquid in the pore shown in Fig. 4 as a function of the diameter of the intracellular gate d2. The solid line is without anesthetic. The dashed curve is computed for xenon (as defined in the text) and shows a large anesthetic effect, i.e., the probability of opening is dramatically decreased at an diameter d2. Xenon is computed at concentration 10−2 M.
Bubble gating and general anesthesia
The mechanism of action of anesthetic gases and vapors is presently unknown (see Discussion). Various kinds of ion channels, of the transmitter-gated and potassium channel families, have been discussed as potential targets of general anesthetics (83,85,126) and references cited in discussion. These anesthetics are chemically diverse, but their efficiency is correlated with their solubility in oil (127,128). Specific receptor sites of such anesthetics have not been found. The anesthetics are thought to act through an essentially nonspecific physical mechanism (87). We consider how a gaseous molecular species might modulate the energy of the formation of a gas bubble in an atomic pore and in this way might control the open probability of a bubble-gated ion channel.
We model the simplest variety of general anesthetic, a noble gas species that has the hard-core diameter of xenon (83,85,126) and is attracted to water by a weak potential. We choose xenon because it is hard to imagine chemically specific reactions between this inert element and protein receptors. Our model noble gas dissolves in bulk water much as xenon does (some millimoles at atmospheric pressure). Our xenon is dissolved in a bulk water phase (at the equilibrium concentration of 10 mM), and the water/gas solution is equilibrated with a pore. Bubble formation in a (KcsA like) pore is changed substantially (Fig. 9). A gas bubble that closes the channel can more easily arise in wider pores when xenon is present than when xenon is absent. The curve relating open probability to pore diameter d2 (solid line in Fig. 9) is shifted toward larger d2, indicating that the presence of xenon shifts the equilibrium between open and closed states toward the closed state. Most of the effect of the general anesthetic is in the gas phase, i.e., in the bubble, not in the liquid phase. Indeed, some of the xenon will actually become a vapor in the bubble.
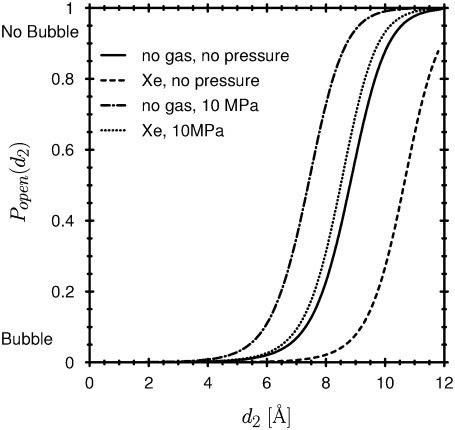
The general anesthetic effect is known to be reversed by elevated pressure (a few atmospheres, see (79,88) and other references in Discussion). Indeed, when hydrostatic pressure is increased in our model, the probability of the open channel is shifted back approximately to the curve observed at atmospheric pressure without xenon (compare the dashed and dotted curves in Fig. 10). The effect of pressure on open probability is larger when xenon is present than when xenon is absent (compare the offsets between the high- and low-pressure curves computed with or without presence of xenon in Fig. 10). Thus, the open probability of the channel without anesthetic is much less sensitive to pressure than that of the anesthetized channel, as shown in measurements of biological channels (see (79,88) and other references in Discussion).
FIGURE 10.
Anesthetic and hydrostatic pressure effects on open probability. The figure is similar to Fig. 9 but here xenon is applied with and without hydrostatic pressure. We apply enough xenon so that a given amount is dissolved in the bulk water. The hydrostatic pressure is then varied while keeping the concentration of xenon in the bulk water fixed. (We do not apply a higher pressure of Xe.) The solid line is that of Fig. 9, namely, no hydrostatic pressure and no anesthetic. The dashed line is also that of Fig. 9, namely, xenon without hydrostatic pressure. The dotted line is xenon plus hydrostatic pressure, showing that pressure reverses the effect of the anesthetic gas. The dashed-dot line shows the effect of hydrostatic pressure without gas and when 10 MPa of hydrostatic pressure is applied.
These computations involving xenon suggest a specific physical mechanism of general anesthetic gases, namely its action on bubble formation and filling. The atomic resolution details of the action of anesthetic gases and pressure are beyond the resolution of our methods and models. It is not clear that such details are needed to explain the action of general anesthetic gases and such details will be very hard to determine. Reliable simulations must be calibrated in an environment like that inside an (atomic-scale) channel and performed on a biological timescale. Both calibration and timescale are challenging goals. Measurements of the atomic-scale interactions of gas, water, ions, and side chains of the channel protein inside a channel are also likely to be difficult.
DISCUSSION
Bistable currents have been recorded by electrophysiologists from single channel proteins for nearly 30 years (22,23,129,130) and clearly (53) produce cellular phenomena of extraordinary importance. The physical basis for the binary nature of single channel currents is not clear, however, despite the best efforts of a large community of electrophysiologists. Here we propose that current flow through an open channel is blocked when a bubble forms spontaneously in a hydrophobic region of the channel. Many experiments in electrophysiology are terminated by air bubbles forming in the wet tubes of an electrophysiology rig; the bubbles interrupt the flow of current, making recording impossible. We suggest here that the very ion channels studied by these rigs could use an air bubble in their pore to control single-channel current in a switchlike manner.
The thermodynamic analysis presented in this article shows how microcapillaries like the pores of ion channels—that are nano, nearly pico-capillaries—can reversibly switch between a water-filled (and potentially conductive) state and a vapor-locked (nonconductive) state. This kind of gate is not among the mechanisms that appear in classical discussions of voltage- or ligand-gated ion channels (25). The idea of a gas bubble forming inside a gated ion channel itself was not found in the channel literature before computational studies suggested the possibility (1–5,7,11,13), although it probably had occurred to workers who had seen gating in systems without channels (33,45).
Simulations of dewetting
Spontaneous emptying (and refilling) of channels has been seen in many simulations and calculations of channels and narrow spaces (1–3,5,7,11,13,15,45,114,116,118,121,131–148) as well other references cited previously in this article. Indeed, it has been seen so widely that we certainly have left important works uncited inadvertently.
Simulations and calculations show that spontaneous emptying and refilling is sensitive to many parameters and assumptions. By their very nature, wetting phenomena are sensitive to perturbations. The balance of cohesive and disruptive forces that produce a phase change is easy to disturb. Any perturbation—in nature or in calculation—is likely to cross a threshold and have a large effect on wetting or dewetting.
Unstable threshold phenomena and phase changes are inherently (and necessarily) difficult to simulate reproducibly and convincingly because they depend on the difference of large forces. The sensitivity comes from the inherent physical properties of the system, and the concomitant properties of the mathematics describing the system, and not from any particular sensitivity or proclivity to error in one calculation, laboratory, or model. Small changes (or errors) in the simulation of forces will have large effects on their difference and this has been clearly described by many authors, much to their credit, in our view (see for example the extensive discussions of sensitivity (and thus reliability of results) in the literature (3,7,8,13,145,149)). Thus, simulations of bubble forming and filling are sensitive to details of methods, to assumptions and artifacts of calculation, and are hard to reproduce because of the physics involved in a threshold process.
It is difficult to persuade other scientists of the general significance of a simulation that depends on the special details of calculations and assumptions. Simulations of molecular dynamics cannot provide convincing evidence for a general mechanism for gating if they involve large extrapolations in time (from nanoseconds of the longest duration simulations to biological timescales of microseconds) and depend sensitively on interatomic forces hard to parameterize or use in more than one set of conditions, i.e., hard to transfer from one computation to another.
Here, we use a unifying thermodynamic approach to show how gating transitions from closed to open can be explained by a general thermodynamic analysis of confined fluids. The analysis also explains why the simulation results are so sensitive to force-field parameters (Fig. 7). We try to show that bubble forming and breaking are part of a general widely known phenomena of wetting and dewetting by liquids, including the spontaneous evaporation of fluid in confined fluids, i.e., capillary evaporation. We use thermodynamic scaling laws of confined fluids and the morphometric approach of density functional theory (70–74) that show how the macroscopic phenomena of capillary evaporation would behave on the atomic length scale of channels (4,58,92). We show how the effects of anesthetic gases and the effect of small hydrostatic pressures on anesthesia (79,88) can be understood naturally by their effects on bubbles in channels.
Weaknesses in our analysis
Our model is limited by its lack of structural detail. The channel structure is flexible and this flexibility may enter into phenomena like subconductance states and flickers in channel current. Obviously, some of the atomic detail of channel structure, its flexibility, and its response to anesthetics must be involved in gating and our model will not resolve that. This flaw, however, is also a strength.
The calculations of this article show how bubbles can form, independent of detail, hopefully motivating the experimental measurements needed to determine if channels actually use bubbles as their bistable hydrophobic gates. Simulations have been, in a way, too sensitive to motivate such experiments. Our more general thermodynamic analysis complements the simulations, as do the literature (6,8,10). Our analysis of anesthesia supplements the simulations. We hope both will help motivate the needed difficult experiments. Only experiments can show whether bubble formation and breaking contribute the instability needed to explain single channel records and are modulated by the channel protein to form the gating process so important in channel function.
Proposed experiments
Our idea of bubble gating suggests specific experiments. Experiments can look directly for bubbles in channels, using the most modern methods of molecular biology (150). Indeed, bubbles may already have been observed as volume changes associated with gating (46,47) although this view was not universally accepted when published (151,152).
Biophysical experiments can check for the “…very remarkable…interactions of high pressure with anesthetic gases” (153) known from studies of high pressure and anesthetic gases on animals and man (87). Biophysical experiments can compare the effects of hydrostatic pressure and anesthetics (with and without pressure): 1), on channel gating; and 2), on bubbles and their filling. For example, inert gases might anesthetize or create “rapture of the deep” (i.e., nitrogen narcosis (77,79,154)) by filling natural bubbles normally found in closed channels, thereby changing gating (83–85,126,155): when anesthetics are present, hydrostatic pressure would be expected to have substantial effects on bubbles in channels (78,79,83–85,155–158), as we find (Figs. 9 and 10). Pressure would modify the number of (previously dissolved) gas or anesthetic molecules in the bubble (and on its surface). Pressure in this case would alter the unstable balance between cohesive and disruptive forces and make the system cross a threshold between closed and open.
On the other hand, pressure would have a relatively small effect on bubble gating in the absence of dissolved (e.g., anesthetic) gases (46,47,88,159–167) even if a substantial volume change occurs during gating because of a bubble formation or filling (46,47). Pressure might have a small effect on open channels or crevices in the protein because pressure might hardly change the diameter of an incompressible column of water. Pressure also would have a small effect on closed channels because changes in diameter would have little effect on a channel containing a bubble, until the bubble fills. Pressure would have a large effect on a channel containing a bubble only if anesthetic gases or molecules are dissolved in the bulk solution and so can fill and modify empty bubbles in channels or crevices. Indeed, we find that the open probability of the channel without anesthetic is less sensitive to pressure than that of the anesthetized channel (compare the offsets between the high- and low-pressure curves computed with or without presence of xenon in Fig. 10).
Our model of anesthesia fits with the “completely unspecific” (87) property of anesthetics, which do not follow the general receptor model of drug action. Anesthesia instead follows a general thermodynamic law (more or less) independent of the particular chemical nature of the anesthetic, the Meyer-Overton law relating partition coefficient and anesthetic action ((87) and references cited there).
More direct tests of bubble gating should be possible as biophysicists think through the mechanism suggested here. A bubble is a vacuum phase very different from a condensed phase: the phase difference should have physical signatures. For example, the location and optical properties of chemical groups in the wall of the channel will change when a bubble forms or fills. The diameter of the channel is likely to change as well.
Implications
The idea of capillary evaporation/condensation in channels being responsible for gating may also be a starting point for understanding other important phenomena. The large spherical structures seen in the structure of some channel proteins (32,39) may prevent bubbles from forming in those locations, or rather may make bubble formation much harder in the spheres, because of their small surface/volume ratio. If somehow bubbles did form in such spherical structures, they would be very stable, hard to fill, and thus would inactivate or desensitize channels and prevent current flow for long times. The amino acids that form the surface of these spherical cavities need not be particularly hydrophobic to prevent bubble formation. The geometry will do that (mostly) and thus the amino acids in the wall might have permanently charged (i.e., acid or basic) or polar side chains in (for example) an α-helix. A spherical structure connected in series between two pores might be constructed to isolate bubbles in one pore from the other, leading to (more or less) independent gating processes, described by two probabilities multiplied together, as probabilities are multiplied in the Hodgkin Huxley model of voltage activation and inactivation in Na channels (94,168).
Transporters seem to be permanently closed ion channels that open reciprocally, only one end at a time. Many properties of transporters can be easily explained by the gating phenomena of channels called activation, inactivation, and slow inactivation (25,52,54) if the activation and inactivation processes (i.e., gates) are in series and if the opening and closing of these processes are correlated so that one gate or the other is always closed (169–171). The closed gate can block the passive flux of gases, protons, or ions, with remarkably little leakage (12,120,172–174). Many properties of transporters could arise from correlated bubble filling (and formation) in straight or branched channels (175). Correlations of this sort are known to extend long distances (10 nm) in physical systems involving wetting and dewetting (28). A single bubble could also produce sensitive correlated behavior in a Y-shaped structure of a channel (175) or transporter (120,176), working much as the extraordinarily voltage-sensitive Y-branch switches work in semiconductors (177–180).
Bubble formation in our model pores is found to be very sensitive to pore geometry and wall hydrophobicity. This sensitivity of bubbles involves the interplay of many contributions to the grand potential of the system and thus is difficult to predict in even simple scenarios without numerical analysis. We have found interesting behaviors of bubbles even in the few simple cases that we have studied and so a wealth of surprising bubble phenomena might be expected to occur and be used in real channel and transporter proteins, beyond those we have imagined.
HISTORICAL APPENDIX: INSTABILITY IN NEURONS, MEMBRANES, AND CHANNELS
A central phenomena studied by neurobiologists for a century (181) is the action potential, the electrical signal, the traveling wave, that carries digital information (“all or nothing”) along the wires of the nervous system, the axons of nerve cells. The action potential is a propagating wave, one of the original solitons. Action potentials are binary signals, bistable phenomena with thresholds: nerves respond qualitatively differently for small changes in input signals. An input slightly below threshold produces no output (far away). An input slightly above threshold produces a full output, namely an action potential that propagates indefinitely far away.
The sensitive response to input led early workers to propose instability “in the membrane” as a mechanism of the action potential. The two-factor theory of conduction computed the action potential from Rashevsky's and Hill's theory of excitation (182,183). However, direct measurement of ionic conductances (the summed properties of many ion channels) showed that the macroscopic system was stable when voltage was controlled (184,185). The action potential arose from electrical coupling (“positive electrical feedback”) between the current carried by channels and the number of channels that were open, mediated by the voltage change accompanying the channel current. Inward channel current produced a positive voltage change that opened more channels. If the voltage is clamped and so does not change (because the inward current is balanced by an outward current supplied by an amplifier), the system is unconditionally stable: instability in macroscopic conductances does not cause the action potential (54,94,186–188).
Measurement of properties of a single channel protein shows instability, however, even when the voltage is controlled (22,129). A single channel opens and closes stochastically in a random telegraph signal. The probability of opening is a steep function of potential, but a single channel itself is unpredictable. The opening process has been (almost always) explained as a conformational change (25), but this idea has been too vague to be tested clearly, and has led to more complex models, some involving hundreds of rate constants, rather than more specific or physical explanations. The idea that the conformation change is (mostly) a change in the shape of the electric field—and not mostly a change in the location of atoms of the protein—is more promising (175,189) but also has not led to specific or testable models or predictions for gating. So far, the instability of single channels has been described much more than explained.
Here we propose that bubble formation and breaking are the physical mechanisms of single channel instability. We replace and downsize “instability in the membrane”. Instability is now in bubbles in the channel. We suggest that the sensitivity of channels on the atomic scale arises (in large measure) from the instability of bubble formation and filling. The sensitivity of macroscopic systems of channels thus arises from instability as originally postulated by (then) Mr. Hodgkin (190), but in our model the instability is produced by a bubble within a channel protein, not by a nerve membrane. Thermal noise is too small to create instability in a nerve cells or endings, as was shown some time ago (191) because those are macroscopic systems. Even the open channel is too large to show biologically significant noise (192–194). Thermal noise acting on the unstable balance of cohesive and surface forces in an atomic size channel may be enough to cause biologically significant effects—by modulating bubbles and thus gating—thereby producing the fluctuations that the young Hodgkin sought so long ago, and are now seen in single channels (22,129) of hundreds of types of proteins (21). The mathematics of the time dependence of bubble formation might turn out to resemble the mathematics of excitation proposed by Rashevsky and Hill (182,183).
Acknowledgments
Note added in proof: Hilf and Dutzler have shown that xenon is found at particular locations in a ligand-gated ion channel (see Fig. 3 in Hilf et al. (195)).
We thank Greg Voth, the editor of this article, and an anonymous member of the Editorial Board for telling us of Huang et al. (100) and suggesting the calculation shown in Fig. 5. We are grateful for the encouragement and support of Dr. James Mulshine.
We thank the G. Harold & Leila Y. Mathers Foundation without which this article would not have been written. R.S.E. is continually grateful to Rush Medical College for providing generous time for science, and to National Institute of General Medical Sciences for irreplaceable continuing support (grant No. GM 076013.)
Editor: Gregory A. Voth.
References
- 1.Dzubiella, J., R. J. Allen, and J. P. Hansen. 2004. Electric field-controlled water permeation coupled to ion transport through a nanopore. J. Chem. Phys. 120:5001–5004. [DOI] [PubMed] [Google Scholar]
- 2.Dzubiella, J., and J.-P. Hansen. 2005. Electric-field-controlled water and ion permeation of a hydrophobic nanopore. J. Chem. Phys. 122:234706. [DOI] [PubMed] [Google Scholar]
- 3.Beckstein, O., and M. S. Sansom. 2006. A hydrophobic gate in an ion channel: the closed state of the nicotinic acetylcholine receptor. Phys. Biol. 3:147–159. [DOI] [PubMed] [Google Scholar]
- 4.Roth, R., and K. M. Kroll. 2006. Capillary evaporation in pores. J. Phys. Condens. Matter. 18:6517–6530. [DOI] [PubMed] [Google Scholar]
- 5.Sansom, M. S., P. Bond, O. Beckstein, P. C. Biggin, J. Faraldo-Gomez, R. J. Law, G. Patargias, and D. P. Tieleman. 2002. Water in ion channels and pores—simulation studies. Novartis Found. Symp. 245:66–83,165–168. [PubMed] [Google Scholar]
- 6.Trasca, R. A., M. M. Calbi, and M. W. Cole. 2002. Lattice model of gas condensation within nanopores. Phys. Rev. E Stat. Nonlin. Soft Matter Phys. 65:061607. [DOI] [PubMed] [Google Scholar]
- 7.Hummer, G., J. C. Rasaiah, and J. P. Noworyta. 2001. Water conduction through the hydrophobic channel of a carbon nanotube. Nature. 414:188–190. [DOI] [PubMed] [Google Scholar]
- 8.Waghe, A., J. C. Rasaiah, and G. Hummer. 2002. Filling and emptying kinetics of carbon nanotubes in water. J. Chem. Phys. 117:10789–10795. [Google Scholar]
- 9.Grubmuller, H. 2003. What happens if the room at the bottom runs out? A close look at small water pores. Proc. Natl. Acad. Sci. USA. 100:7421–7422. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Maibaum, L., and D. Chandler. 2003. A coarse-grained model of water confined in a hydrophobic tube. J. Phys. Chem. B. 107:1189–1193. [Google Scholar]
- 11.Allen, R., J.-P. Hansen, and S. Melchionna. 2003. Molecular dynamics investigation of water permeation through nanopores. J. Chem. Phys. 119:3905–3919. [Google Scholar]
- 12.Khademi, S., J. O'Connell 3rd, J. Remis, Y. Robles-Colmenares, L. J. Miercke, and R. M. Stroud. 2004. Mechanism of ammonia transport by Amt/MEP/Rh: structure of AmtB at 1.35 Å. Science. 305:1587–1594. [DOI] [PubMed] [Google Scholar]
- 13.Anishkin, A., and S. Sukharev. 2004. Water dynamics and dewetting transitions in the small mechanosensitive channel MscS. Biophys. J. 86:2883–2895. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Saparov, S. M., and P. Pohl. 2004. Beyond the diffusion limit: water flow through the empty bacterial potassium channel. Proc. Natl. Acad. Sci. USA. 101:4805–4809. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Urbic, T., V. Vlachy, and K. A. Dill. 2006. Confined water: a Mercedes-Benz model study. J. Phys. Chem. 110:4963–4970. [DOI] [PubMed] [Google Scholar]
- 16.Treptow, W., and M. Tarek. 2006. Molecular restraints in the permeation pathway of ion channels. Biophys. J. 91:L26–L28. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Bali, M., and M. H. Akabas. 2007. The location of a closed channel gate in the GABAA receptor channel. J. Gen. Physiol. 129:145–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Li, J., X. Gong, H. Lu, D. Li, H. Fang, and R. Zhou. 2007. Electrostatic gating of a nanometer water channel. Proc. Natl. Acad. Sci. USA. 104:3687–3692. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Wang, Y., and E. Tajkhorshid. 2007. Molecular mechanisms of conduction and selectivity in aquaporin water channels. J. Nutr. 137:S1509–S1515. [DOI] [PubMed] [Google Scholar]
- 20.Bostick, D. L., and C. L. Brooks 3rd. 2007. Deprotonation by dehydration: the origin of ammonium sensing in the AmtB channel. PLoS Comp. Biol. 3:e22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Conley, E. C., and W. J. Brammar. 1999. The Ion Channel Facts Book IV: Voltage-Gated Channels. Academic Press, New York.
- 22.Hladky, S. B., and D. A. Haydon. 1970. Discreteness of conductance change in bimolecular lipid membranes in the presence of certain antibiotics. Nature. 5231:451–453. [DOI] [PubMed] [Google Scholar]
- 23.Neher, E., and B. Sakmann. 1976. Single channel currents recorded from the membrane of denervated muscle fibers. Nature. 260:799–802. [DOI] [PubMed] [Google Scholar]
- 24.Hamill, O. P., A. Marty, E. Neher, B. Sakmann, and F. J. Sigworth. 1981. Improved patch-clamp techniques for high-resolution current recording from cells and cell-free membrane patches. Pflugers Arch. 391:85–100. [DOI] [PubMed] [Google Scholar]
- 25.Hille, B. 2001. Ionic Channels of Excitable Membranes. Sinauer Associates, Sunderland, MA.
- 26.Rowlinson, J. S. 1992. Development of theories of inhomogeneous fluids. In Fundamentals of Inhomogeneous Fluids. D. Henderson, editor. Marcel Dekker, New York.
- 27.Pomeau, Y., and E. Villermaux. 2006. Two hundred years of capillarity research. Phys. Today. 59:39–44. [Google Scholar]
- 28.Gennes, P.-G. d., F. Brocard-Wyatt, and D. Quere. 2004. Capillarity and Wetting Phenomena: Drops, Bubbles, Pearls, and Waves. A. Reisinger, translator. Springer, New York.
- 29.Gennes, P.-G. d. 1997. Soft matter. In Nobel Lectures in Physics 1991–1995. G. Ekspong, editor. World Scientific, Singapore.
- 30.Stuhmer, W., C. Methfessel, B. Sakmann, M. Noda, and S. Numa. 1987. Patch clamp characterization of sodium channels expressed from rat brain cDNA. Eur. Biophys. J. 14:131–138. [DOI] [PubMed] [Google Scholar]
- 31.Numa, S., and M. Noda. 1986. Molecular structure of sodium channels. Ann. N. Y. Acad. Sci. 479:338–355. [DOI] [PubMed] [Google Scholar]
- 32.Doyle, D. A., J. Morais Cabral, R. A. Pfuetzner, A. Kuo, J. M. Gulbis, S. L. Cohen, B. T. Chait, and R. MacKinnon. 1998. The structure of the potassium channel: molecular basis of K+ conduction and selectivity. Science. 280:69–77. [DOI] [PubMed] [Google Scholar]
- 33.Sachs, F., and F. Qin. 1993. Gated, ion-selective channels observed with patch pipettes in the absence of membranes: novel properties of a gigaseal. Biophys. J. 65:1101–1107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Jiang, Q. X., D. N. Wang, and R. MacKinnon. 2004. Electron microscopic analysis of KvAP voltage-dependent K+ channels in an open conformation. Nature. 430:806–810. [DOI] [PubMed] [Google Scholar]
- 35.Kuo, A., J. M. Gulbis, J. F. Antcliff, T. Rahman, E. D. Lowe, J. Zimmer, J. Cuthbertson, F. M. Ashcroft, T. Ezaki, and D. A. Doyle. 2003. Crystal structure of the potassium channel KirBac1.1 in the closed state. Science. 300:1922–1926. [DOI] [PubMed] [Google Scholar]
- 36.Bass, R. B., P. Strop, M. Barclay, and D. C. Rees. 2002. Crystal structure of Escherichia coli MscS, a voltage-modulated and mechanosensitive channel. Science. 298:1582–1587. [DOI] [PubMed] [Google Scholar]
- 37.Zhou, Y., J. H. Morais-Cabral, A. Kaufman, and R. MacKinnon. 2001. Chemistry of ion coordination and hydration revealed by a K+ channel-Fab complex at 2.0 Å resolution. Nature. 414:43–48. [DOI] [PubMed] [Google Scholar]
- 38.Freites, J. A., D. J. Tobias, and S. H. White. 2006. A voltage-sensor water pore. Biophys. J. 91:L90–L92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Unwin, N. 2005. Refined structure of the nicotinic acetylcholine receptor at 4Å resolution. J. Mol. Biol. 346:967–989. [DOI] [PubMed] [Google Scholar]
- 40.Poynor, A., L. Hong, I. K. Robinson, S. Granick, Z. Zhang, and P. A. Fenter. 2006. How water meets a hydrophobic surface. Phys. Rev. Lett. 97:266101. [DOI] [PubMed] [Google Scholar]
- 41.Park, C., P. A. Fenter, K. L. Nagy, and N. C. Sturchio. 2006. Hydration and distribution of ions at the mica-water interface. Phys. Rev. Lett. 97:016101. [DOI] [PubMed] [Google Scholar]
- 42.Mezger, M., H. Reichert, S. Schoder, J. Okasinski, H. Schroder, H. Dosch, D. Palms, J. Ralston, and V. Honkimaki. 2006. High-resolution in situ x-ray study of the hydrophobic gap at the water-octadecyl-trichlorosilane interface. Proc. Natl. Acad. Sci. USA. 103:18401–18404. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Netz, R. R. 2004. Water and ions at interfaces. Curr. Opin. Colloid Interface Sci. 9:192–197. [Google Scholar]
- 44.Fenter, P. A., and N. C. Sturchio. 2004. Mineral-water interfacial structures revealed by synchrotron x-ray scattering. Prog. Surf. Sci. 77:171–258. [Google Scholar]
- 45.Lev, A. A., Y. E. Korchev, T. K. Rostovtseva, C. L. Bashford, D. T. Edmonds, and C. A. Pasternak. 1993. Rapid switching of ion current in narrow pores: implications for biological ion channels. Proc. R. Soc. Lond. B. Biol. Sci. 252:187–192. [DOI] [PubMed] [Google Scholar]
- 46.Zimmerberg, J., and V. A. Parsegian. 1986. Polymer inaccessible volume changes during opening and closing of a voltage-dependent ionic channel. Nature. 323:36–39. [DOI] [PubMed] [Google Scholar]
- 47.Zimmerberg, J., F. Bezanilla, and V. A. Parsegian. 1990. Solute inaccessible aqueous volume changes during opening of the potassium channel of the squid giant axon. Biophys. J. 57:1049–1064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Boda, D., W. Nonner, M. Valisko, D. Henderson, B. Eisenberg, and D. Gillespie. 2007. Steric selectivity in Na channels arising from protein polarization and mobile side chains. Biophys. J. 93:1960–1980. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Barrett, J. N., K. L. Magleby, and B. S. Pallotta. 1982. Properties of single calcium-activated potassium channels in cultured rat muscle. J. Physiol. 331:211–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Zhang, Y., X. Niu, T. I. Brelidze, and K. L. Magleby. 2006. Ring of negative charge in BK channels facilitates block by intracellular Mg2+ and polyamines through electrostatics. J. Gen. Physiol. 128:185–202. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Unwin, N. 2000. The Croonian Lecture 2000. Nicotinic acetylcholine receptor and the structural basis of fast synaptic transmission. Philos. Trans. R. Soc. Lond. B Biol. Sci. 355:1813–1829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Bezanilla, F., and E. Stefani. 1994. Voltage-dependent gating of ionic channels. Annu. Rev. Biophys. Biomol. Struct. 23:819–846. [DOI] [PubMed] [Google Scholar]
- 53.Vandenberg, C. A., and F. Bezanilla. 1991. A sodium channel gating model based on single channel, macroscopic ionic, and gating currents in the squid giant axon. Biophys. J. 60:1511–1533. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 54.Hodgkin, A. L. 1971. The Conduction of the Nervous Impulse. Liverpool University Press, Liverpool, UK.
- 55.Hodgkin, A. L., and B. Katz. 1949. The effect of sodium ions on the electrical activity of the giant axon of the squid. J. Physiol. 108:37–77. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Nonner, W., L. Catacuzzeno, and B. Eisenberg. 2000. Binding and selectivity in L-type Ca channels: a mean spherical approximation. Biophys. J. 79:1976–1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Eisenberg, B. 2003. Proteins, channels, and crowded ions. Biophys. Chem. 100:507–517. [DOI] [PubMed] [Google Scholar]
- 58.Roth, R., and D. Gillespie. 2005. Physics of size selectivity. Phys. Rev. Lett. 95:247801. [DOI] [PubMed] [Google Scholar]
- 59.Wang, Y., L. Xu, D. Pasek, D. Gillespie, and G. Meissner. 2005. Probing the role of negatively charged amino acid residues in ion permeation of skeletal muscle ryanodine receptor. Biophys. J. 89:256–265. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Boda, D., M. Valisko, B. Eisenberg, W. Nonner, D. Henderson, and D. Gillespie. 2006. Effect of protein dielectric coefficient on the ionic selectivity of a calcium channel. J. Chem. Phys. 125:034901. [DOI] [PubMed] [Google Scholar]
- 61.Miedema, H., M. Vrouenraets, J. Wierenga, B. Eisenberg, D. Gillespie, W. Meijberg, and W. Nonner. 2006. Ca2+ selectivity of a chemically modified OmpF with reduced pore volume. Biophys. J. 91:4392–4440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Varma, S., and S. B. Rempe. 2007. Tuning ion coordination architectures to enable selective partitioning. Biophys. J. 93:1093–1099. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Noskov, S. Y., and B. Roux. 2007. Importance of hydration and dynamics on the selectivity of the KcsA and NaK channels. J. Gen. Physiol. 129:135–143. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Roux, B. 2005. Ion conduction and selectivity in K+ channels. Annu. Rev. Biophys. Biomol. Struct. 34:153–171. [DOI] [PubMed] [Google Scholar]
- 65.Chandler, D. 2007. Oil on troubled waters. Nature. 445:831–832. [DOI] [PubMed] [Google Scholar]
- 66.Chandler, D. 2005. Interfaces and the driving force of hydrophobic assembly. Nature. 437:640–647. [DOI] [PubMed] [Google Scholar]
- 67.Lum, K., D. Chandler, and J. D. Weeks. 1999. Hydrophobicity at small and large length scales. J. Phys. Chem. B. 103:4570–4577. [Google Scholar]
- 68.Weeks, J. D. 2002. Connecting local structure to interface formations: a molecular scale van der Waals theory of nonuniform liquids. Annu. Rev. Phys. Chem. 53:533–562. [DOI] [PubMed] [Google Scholar]
- 69.Urbic, T., V. Vlachy, Y. V. Kalyuzhnyi, and K. A. Dill. 2007. Theory for the solvation of nonpolar solutes in water. J. Chem. Phys. 127:174505. [DOI] [PubMed] [Google Scholar]
- 70.Mecke, K. R. 1998. Morphological thermodynamics of composite media. Fluid Phase Equil. 150,151:591–598. [Google Scholar]
- 71.Mecke, K. R. 1998. Integral geometry in statistical physics. Int. J. Mod. Phys. B. 12:861–899. [Google Scholar]
- 72.König, P.-M., R. Roth, and K. R. Mecke. 2004. Morphological thermodynamic of fluids: shape dependence of free energies. Phys. Rev. Lett. 93:160601. [DOI] [PubMed] [Google Scholar]
- 73.Roth, R. 2005. Fluid mixtures at curved walls. J. Phys. Condens. Matter. 17:S3463–S3468. [Google Scholar]
- 74.Hansen-Goos, H., and R. Roth. 2006. Density functional theory for hard-sphere mixtures: the White Bear version mark II. J. Phys. Condens. Matter. 18:8413–8425. [DOI] [PubMed] [Google Scholar]
- 75.Evans, R. 1992. Density functionals in the theory of nonuniform fluids. In Fundamentals of Inhomogeneous Fluids. D. Henderson, editor. Marcel Dekker. New York.
- 76.Henderson, D., editor. 1992. Fundamentals of Inhomogeneous Fluids. Marcel Dekker, New York.
- 77.Burnett, W. A. 1955. The problem of nitrogen narcosis. J. R. Nav. Med. Serv. 41:188–192. [PubMed] [Google Scholar]
- 78.Macdonald, A. G. 1972. The role of high hydrostatic pressure in the physiology of marine animals. Symp. Soc. Exp. Biol. 26:209–231. [PubMed] [Google Scholar]
- 79.Kendig, J. J. 1984. Nitrogen narcosis and pressure reversal of anesthetic effects in node of Ranvier. Am. J. Physiol. 246:C91–C95. [DOI] [PubMed] [Google Scholar]
- 80.Meyer, R., and S. H. Heinemann. 1997. Temperature and pressure dependence of Shaker K+ channel N- and C-type inactivation. Eur. Biophys. J. 26:433–445. [DOI] [PubMed] [Google Scholar]
- 81.Schmalwasser, H., A. Neef, A. A. Elliott, and S. H. Heinemann. 1998. Two-electrode voltage clamp of Xenopus oocytes under high hydrostatic pressure. J. Neurosci. Methods. 81:1–7. [DOI] [PubMed] [Google Scholar]
- 82.Macdonald, A. G., and B. Martinac. 1999. Effect of high hydrostatic pressure on the porin OmpC from Escherichia coli. FEMS Microbiol. Lett. 173:327–334. [DOI] [PubMed] [Google Scholar]
- 83.Sanders, R. D., and M. Maze. 2005. Xenon: from stranger to guardian. Curr. Opin. Anaesthesiol. 18:405–411. [DOI] [PubMed] [Google Scholar]
- 84.Stimson, L. M., I. Vattulainen, T. Rog, and M. Karttunen. 2005. Exploring the effect of xenon on biomembranes. Cell. Mol. Biol. Lett. 10:563–569. [PubMed] [Google Scholar]
- 85.Preckel, B., N. C. Weber, R. D. Sanders, M. Maze, and W. Schlack. 2006. Molecular mechanisms transducing the anesthetic, analgesic, and organ-protective actions of xenon. Anesthesiology. 105:187–197. [DOI] [PubMed] [Google Scholar]
- 86.Tonner, P. H. 2006. Xenon: one small step for anesthesia…? Curr. Opin. Anaesthesiol. 19:382–384. [DOI] [PubMed] [Google Scholar]
- 87.Heimburg, T., and A. D. Jackson. 2007. The thermodynamics of general anesthesia. Biophys. J. 92:3159–3165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 88.Kendig, J. J. 1984. Ionic currents in vertebrate myelinated nerve at hyperbaric pressure. Am. J. Physiol. 246:C84–C90. [DOI] [PubMed] [Google Scholar]
- 89.Hansen, J.-P., and I. R. McDonald. 1986. Theory of Simple Liquids. Academic Press, New York.
- 90.Landau, L. D., and E. M. Lifshitz. 1996. Course of Theoretical Physics. Vol. 5: Statistical Physics. Butterworth Heinemann, London, UK.
- 91.Evans, R. 1990. Fluids adsorbed in narrow pores—phase-equilibria and structure. J. Phys. Condens. Matter. 2:8989–9007. [Google Scholar]
- 92.Roth, R., R. Evans, A. Lang, and G. Kahl. 2002. Fundamental measure theory for hard-sphere mixtures revisited: the White Bear version. J. Phys. Condens. Matter. 14:12063–12078. [Google Scholar]
- 93.Southall, N. T., and K. A. Dill. 2000. The mechanism of hydrophobic solvation depends on solute radius. J. Phys. Chem. B. 104:1326–1331. [Google Scholar]
- 94.Hodgkin, A. L., and A. F. Huxley. 1952. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 117:500–544. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Evans, R. 1979. Nature of the liquid-vapor interface and other topics in the statistical-mechanics of nonuniform, classical fluids. Adv. Phys. 28:143. [Google Scholar]
- 96.Rosenfeld, Y. 1989. Free-energy model for the inhomogeneous hard-sphere fluid mixture and density-functional theory of freezing. Phys. Rev. Lett. 63:980–983. [DOI] [PubMed] [Google Scholar]
- 97.Wu, Y. X., and J. Wu. 2002. Structures of hard-sphere fluids from a modified fundamental-measure theory. J. Chem. Phys. 117:10156–10164. [Google Scholar]
- 98.Hodgkin, A., A. Huxley, and B. Katz. 1949. Ionic currents underlying activity in the giant axon of the squid. Arch. Sci. Physiol. (Paris). 3:129–150. [Google Scholar]
- 99.Magleby, K. L. 1992. Ion channels. Preventing artifacts and reducing errors in single-channel analysis. Methods Enzymol. 207:763–791. [DOI] [PubMed] [Google Scholar]
- 100.Huang, X., C. J. Margulis, and B. J. Beme. 2003. Dewetting-induced collapse of hydrophobic particles. Proc. Natl. Acad. Sci. USA. 14:11953–11958. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 101.Berendsen, H. J. C., J. P. M. Postma, W. F. van Gunsteren, and J. Hermans. 1981. Interaction Models for Water in Relation to Protein Hydration In Intermolecular Forces. B. Pullman, editor. Reidel, Dordrecht, The Netherlands.
- 102.Oversteegen, S. M., and R. Roth. 2005. General methods for free-volume theory. J. Chem. Phys. 122:214502. [DOI] [PubMed] [Google Scholar]
- 103.Sukharev, S., and A. Anishkin. 2004. Mechanosensitive channels: what can we learn from “simple” model systems? Trends Neurosci. 27:345–351. [DOI] [PubMed] [Google Scholar]
- 104.Perozo, E. 2006. Gating prokaryotic mechanosensitive channels. Nat. Rev. Mol. Cell Biol. 7:109–119. [DOI] [PubMed] [Google Scholar]
- 105.Blunck, R., J. F. Cordero-Morales, L. G. Cuello, E. Perozo, and F. Bezanilla. 2006. Detection of the opening of the bundle crossing in KcsA with fluorescence lifetime spectroscopy reveals the existence of two gates for ion conduction. J. Gen. Physiol. 128:569–581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Bezanilla, F., and E. Perozo. 2003. The voltage sensor and the gate in ion channels. Adv. Protein Chem. 63:211–241. [DOI] [PubMed] [Google Scholar]
- 107.Unwin, N., A. Miyazawa, J. Li, and Y. Fujiyoshi. 2002. Activation of the nicotinic acetylcholine receptor involves a switch in conformation of the α-subunits. J. Mol. Biol. 319:1165–1176. [DOI] [PubMed] [Google Scholar]
- 108.Smith, P. L., and G. Yellen. 2002. Fast and slow voltage sensor movements in HERG potassium channels. J. Gen. Physiol. 119:275–293. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Perozo, E., L. G. Cuello, D. M. Cortes, Y. S. Liu, and P. Sompornpisut. 2002. EPR approaches to ion channel structure and function. Novartis Found. Symp. 245:146–168. [DOI] [PubMed] [Google Scholar]
- 110.Yang, N., and R. Horn. 1995. Evidence for voltage-dependent S4 movement in sodium channels. Neuron. 15:213–218. [DOI] [PubMed] [Google Scholar]
- 111.Mullins, L. 1959. The penetration of some cations into muscle. J. Gen. Physiol. 42:817–829. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Mullins, L. J. 1959. An analysis of conductance changes in squid axon. J. Gen. Physiol. 42:1013–1035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Mullins, L. J. 1968. Single or dual channel mechanisms. J. Gen. Physiol. 52:555–556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Sriraman, S., I. G. Kevrekidis, and G. Hummer. 2005. Coarse nonlinear dynamics and metastability of filling-emptying transitions: water in carbon nanotubes. Phys. Rev. Lett. 95:130603. [DOI] [PubMed] [Google Scholar]
- 115.Peter, C., and G. Hummer. 2005. Ion transport through membrane-spanning nanopores studied by molecular dynamics simulations and continuum electrostatics calculations. Biophys. J. 89:2222–2234. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Collins, M. D., G. Hummer, M. L. Quillin, B. W. Matthews, and S. M. Gruner. 2005. Cooperative water filling of a nonpolar protein cavity observed by high-pressure crystallography and simulation. Proc. Natl. Acad. Sci. USA. 102:16668–16671. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Anishkin, A., C. S. Chiang, and S. Sukharev. 2005. Gain-of-function mutations reveal expanded intermediate states and a sequential action of two gates in MscL. J. Gen. Physiol. 125:155–170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Sukharev, S., and D. P. Corey. 2004. Mechanosensitive channels: multiplicity of families and gating paradigms. Sci. STKE. 2004:re4. [DOI] [PubMed]
- 119.Beckstein, O., K. Tai, and M. S. Sansom. 2004. Not ions alone: barriers to ion permeation in nanopores and channels. J. Am. Chem. Soc. 126:14694–14695. [DOI] [PubMed] [Google Scholar]
- 120.Wikstrom, M., M. I. Verkhovsky, and G. Hummer. 2003. Water-gated mechanism of proton translocation by cytochrome c oxidase. Biochim. Biophys. Acta. 1604:61–65. [DOI] [PubMed] [Google Scholar]
- 121.Beckstein, O., and M. S. Sansom. 2003. Liquid-vapor oscillations of water in hydrophobic nanopores. Proc. Natl. Acad. Sci. USA. 100:7063–7068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Beckstein, O., P. C. Biggin, and M. S. P. Sansom. 2001. A hydrophobic gating mechanism for nanopores. J. Phys. Chem. B. 105:12902–12905. [Google Scholar]
- 123.Valiyaveetil, F. I., M. Sekedat, R. MacKinnon, and T. W. Muir. 2006. Structural and functional consequences of an amide-to-ester substitution in the selectivity filter of a potassium channel. J. Am. Chem. Soc. 128:11591–11599. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 124.MacKinnon, R. 2004. Potassium channels and the atomic basis of selective ion conduction (Nobel Lecture). Angew. Chem. Int. Ed. Engl. 43:4265–4277. [DOI] [PubMed] [Google Scholar]
- 125.Zagotta, W. N., T. Hoshi, and R. W. Aldrich. 1994. Shaker potassium channel gating. III. Evaluation of kinetic models for activation. J. Gen. Physiol. 103:321–362. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Sanders, R. D., D. Ma, and M. Maze. 2004. Xenon: elemental anesthesia in clinical practice. Br. Med. Bull. 71:115–135. [DOI] [PubMed] [Google Scholar]
- 127.Meyer, H. 1899. On the theory of alcohol narcosis: first communication. Which property of anesthetics determines its narcotic effect? any. Arch. Exp. Pathol. Pharmacol. 425:109–118. [Google Scholar]
- 128.Overton, C. E. 1899, reprinted 1991. Studies of narcosis. In Studies of Narcosis. R. L. Lipnick, editor. Springer, New York.
- 129.Sakmann, B., and E. Neher. 1995. Single Channel Recording. Plenum Press, New York.
- 130.Hladky, S. B., and D. A. Haydon. 1972. Ion transfer across lipid membranes in the presence of gramicidin A. I. Studies of the unit conductance channel. Biochim. Biophys. Acta. 274:294–312. [DOI] [PubMed] [Google Scholar]
- 131.Henderson, J. R. 1986. Complete-wetting exponents from capillary-wave theory. Phys. Rev. B Condens. Matter. 33:614–616. [DOI] [PubMed] [Google Scholar]
- 132.Evans, R., U. M. B. Marconi, and P. Tarzaona. 1986. Fluids in narrow pores: adsorption, capillary condensation, and critical points. J. Chem. Phys. 84:2376–2399. [Google Scholar]
- 133.Henderson, D., and S. Sokolowski. 1995. Adsorption in a spherical cavity. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 52:758–762. [DOI] [PubMed] [Google Scholar]
- 134.Sansom, M. S., I. D. Kerr, J. Breed, and R. Sankararamakrishnan. 1996. Water in channel-like cavities: structure and dynamics. Biophys. J. 70:693–702. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 135.Sansom, M. S., G. R. Smith, C. Adcock, and P. C. Biggin. 1997. The dielectric properties of water within model transbilayer pores. Biophys. J. 73:2404–2415. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 136.Henderson, D., P. Bryk, S. Sokolowski, and D. T. Wasan. 2000. Density-functional theory for an electrolyte confined by thin charged walls. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 61:3896–3903. [DOI] [PubMed] [Google Scholar]
- 137.Neimark, A. V., P. I. Ravikovitch, and A. Vishnyakov. 2000. Adsorption hysteresis in nanopores. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 62:R1493–R1496. [DOI] [PubMed] [Google Scholar]
- 138.Tata, B. V., D. Boda, D. Henderson, A. Nikolov, and D. T. Wasan. 2000. Structure of charged colloids under a wedge confinement. Phys. Rev. E Stat. Phys. Plasmas Fluids Relat. Interdiscip. Topics. 62:3875–3881. [DOI] [PubMed] [Google Scholar]
- 139.Varga, S., D. Boda, D. Henderson, and S. Sokolowski. 2000. Density functional theory and the capillary evaporation of a liquid in a slit. J. Colloid Interface Sci. 227:223–226. [DOI] [PubMed] [Google Scholar]
- 140.Miyahara, M., H. Kanda, T. Yoshioka, and M. Okazaki. 2000. Modeling capillary condensation in cylindrical nanopores: a molecular dynamics study. Langmuir. 16:4293–4299. [Google Scholar]
- 141.Sansom, M. S., and R. J. Law. 2001. Membrane proteins: aquaporins—channels without ions. Curr. Biol. 11:R71–R73. [DOI] [PubMed] [Google Scholar]
- 142.Allen, R., S. Melchionna, and J. P. Hansen. 2002. Intermittent permeation of cylindrical nanopores by water. Phys. Rev. Lett. 89:175502. [DOI] [PubMed] [Google Scholar]
- 143.Domene, C., and M. S. Sansom. 2003. Potassium channel, ions, and water: simulation studies based on the high resolution x-ray structure of KcsA. Biophys. J. 85:2787–2800. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 144.Hummer, G., F. Schotte, and P. A. Anfinrud. 2004. Unveiling functional protein motions with picosecond x-ray crystallography and molecular dynamics simulations. Proc. Natl. Acad. Sci. USA. 101:15330–15334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 145.Vaitheeswaran, S., J. C. Rasaiah, and G. Hummer. 2004. Electric field and temperature effects on water in the narrow nonpolar pores of carbon nanotubes. J. Chem. Phys. 121:7955–7965. [DOI] [PubMed] [Google Scholar]
- 146.Marti, J., G. Nagy, E. Guardia, and M. C. Gordillo. 2006. Molecular dynamics simulation of liquid water confined inside graphite channels: dielectric and dynamical properties. J. Phys. Chem. B Cond. Matter Mater. Surf. Interfaces Biophys. 110:23987–23994. [DOI] [PubMed] [Google Scholar]
- 147.Setny, P., and M. Geller. 2006. Water properties inside nanoscopic hydrophobic pocket studied by computer simulations. J. Chem. Phys. 125:144717. [DOI] [PubMed] [Google Scholar]
- 148.Yin, H., G. Hummer, and J. C. Rasaiah. 2007. Metastable water clusters in the nonpolar cavities of the thermostable protein tetrabrachion. J. Am. Chem. Soc. 129:7369–7377. [DOI] [PubMed] [Google Scholar]
- 149.Chen, Y. G., and G. Hummer. 2007. Slow conformational dynamics and unfolding of the calmodulin C-terminal domain. J. Am. Chem. Soc. 129:2414–2415. [DOI] [PubMed] [Google Scholar]
- 150.Sandtner, W., F. Bezanilla, and A. M. Correa. 2007. In vivo measurement of intramolecular distances using genetically encoded reporters. Biophys. J. 93:L45–L47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 151.Eisenberg, R. S. 1987. Volumes apart. (Scientific correspondence on an article of Zimmerberg and Parsegian.) Nature. 325:114.3808069 [Google Scholar]
- 152.Zimmerberg, J., and V. A. Parsegian. 1987. Volumes apart. Nature. 325:114.3808069 [Google Scholar]
- 153.Wann, K. T., and A. G. Macdonald. 1988. Actions and interactions of high pressure and general anesthetics. Prog. Neurobiol. 30:271–307. [DOI] [PubMed] [Google Scholar]
- 154.Baddeley, A. D., J. W. De Figueredo, J. W. Curtis, and A. N. Williams. 1968. Nitrogen narcosis and performance under water. Ergonomics. 11:157–164. [DOI] [PubMed] [Google Scholar]
- 155.Grocott, H. P., Y. Sato, H. M. Homi, and B. E. Smith. 2005. The influence of xenon, nitrous oxide and nitrogen on gas bubble expansion during cardiopulmonary bypass. Eur. J. Anaesthesiol. 22:353–358. [DOI] [PubMed] [Google Scholar]
- 156.Macdonald, A. G., and B. Martinac. 2005. Effect of high hydrostatic pressure on the bacterial mechanosensitive channel MscS. Eur. Biophys. J. 34:434–441. [DOI] [PubMed] [Google Scholar]
- 157.Ashford, M. L., A. G. Macdonald, and K. T. Wann. 1984. Hydrostatic pressure modifies the action of octanol and atropine on frog endplate conductance. Br. J. Pharmacol. 83:477–484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 158.Youngson, A. F., and A. G. Macdonald. 1970. Interaction between halothane and hydrostatic pressure. Br. J. Anaesth. 42:801–802. [PubMed] [Google Scholar]
- 159.Conti, F., I. Inoue, F. Kukita, and W. Stuhmer. 1984. Pressure dependence of sodium gating currents in the squid giant axon. Eur. Biophys. J. 11:137–147. [DOI] [PubMed] [Google Scholar]
- 160.Conti, F., B. Hille, and W. Nonner. 1984. Non-stationary fluctuations of the potassium conductance at the node of Ranvier of the frog. J. Physiol. 353:199–230. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 161.Benz, R., F. Conti, and R. Fioravanti. 1984. Extrinsic charge movement in the squid axon membrane. Effect of pressure and temperature. Eur. Biophys. J. 11:51–59. [DOI] [PubMed] [Google Scholar]
- 162.Benz, R., and F. Conti. 1986. Effects of hydrostatic pressure on lipid bilayer membranes. II. Activation and reaction volumes of carrier mediated ion transport. Biophys. J. 50:99–107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 163.Benz, R., and F. Conti. 1986. Effects of hydrostatic pressure on lipid bilayer membranes. I. Influence on membrane thickness and activation volumes of lipophilic ion transport. Biophys. J. 50:91–98. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 164.Heinemann, S. H., F. Conti, W. Stuhmer, and E. Neher. 1987. Effects of hydrostatic pressure on membrane processes. Sodium channels, calcium channels, and exocytosis. J. Gen. Physiol. 90:765–778. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 165.Heinemann, S. H., W. Stuhmer, and F. Conti. 1987. Single acetylcholine receptor channel currents recorded at high hydrostatic pressures. Proc. Natl. Acad. Sci. USA. 84:3229–3233. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 166.Stuhmer, W., F. Conti, H. Suzuki, X. D. Wang, M. Noda, N. Yahagi, H. Kubo, and S. Numa. 1989. Structural parts involved in activation and inactivation of the sodium channel. Nature. 339:597–603. [DOI] [PubMed] [Google Scholar]
- 167.Heinemann, S. H., and F. J. Sigworth. 1990. Open channel noise. V. Fluctuating barriers to ion entry in gramicidin A channels. Biophys. J. 57:499–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 168.Hodgkin, A. L., and A. F. Huxley. 1952. The dual effect of membrane potential on sodium conductance in the giant axon of Loligo. J. Physiol. 116:497–506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 169.Frohlich, O., C. Leibson, and R. B. Gunn. 1983. Chloride net efflux from intact erythrocytes under slippage conditions. Evidence for a positive charge on the anion binding/transport site. J. Gen. Physiol. 81:127–152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 170.Wang, J., J. M. Tang, and R. S. Eisenberg. 1992. A calcium conducting channel akin to a calcium pump. J. Membr. Biol. 130:163–181. [DOI] [PubMed] [Google Scholar]
- 171.Matsuoka, S., and D. W. Hilgemann. 1992. Steady-state and dynamic properties of cardiac sodium-calcium exchange. Ion and voltage dependencies of the transport cycle. J. Gen. Physiol. 100:963–1001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 172.Decoursey, T. E. 2003. Voltage-gated proton channels and other proton transfer pathways. Physiol. Rev. 83:475–579. [DOI] [PubMed] [Google Scholar]
- 173.Schulten, Z., and K. Schulten. 1985. A model for the resistance of the proton channel formed by the proteolipid of ATPase. Eur. Biophys. J. 11:149–155. [DOI] [PubMed] [Google Scholar]
- 174.Chen, H., B. Ilan, Y. Wu, F. Zhu, K. Schulten, and G. A. Voth. 2007. Charge delocalization in proton channels, I: the aquaporin channels and proton blockage. Biophys. J. 92:46–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 175.Eisenberg, R. S. 1996. Atomic biology, electrostatics and ionic channels. In New Developments and Theoretical Studies of Proteins. R. Elber, editor. World Scientific, Philadelphia.
- 176.Kim, Y. C., M. Wikstrom, and G. Hummer. 2007. Kinetic models of redox-coupled proton pumping. Proc. Natl. Acad. Sci. USA. 104:2169–2174. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 177.Forsberg, E. 2004. Reversible logic based on electron waveguide Y-branch switches. Nanotechnology. 15:S298–S302. [Google Scholar]
- 178.Worschech, L., H. Q. Xu, A. Forcel, and L. Samuelson. 2001. Bias-voltage-induced asymmetry in nanoelectronic Y-branches. applied. Phys. Lett. 79:3287–3289. [Google Scholar]
- 179.Reitzenstein, S., L. Worschech, P. Hartmann, M. Kamp, and A. Forchel. 2002. Capacitive-coupling-enhanced switching gain in an electron Y-branch switch. Phys. Rev. Lett. 89:226804. [DOI] [PubMed] [Google Scholar]
- 180.Wesström, J.-O. J. 1999. Self-gating effect in the electron Y-branch switch. Phys. Rev. Lett. 82:2564–2567. [Google Scholar]
- 181.Adrian, E. 1932. The Activity of the Nerve Fibers: Nobel Lecture in Physiology or Medicine. Nobel Lecture in Physiology or Medicine. Elsevier, Amsterdam, The Netherlands.
- 182.Rashevsky, N. 1938. Mathematical Biophysics. The University of Chicago, Chicago, IL.
- 183.Hill, A. V. 1936. Excitation and accommodation in nerve. Proc. R. Soc. Lond. B. Biol. Sci. 119:305–355. [Google Scholar]
- 184.Hodgkin, A. L., and A. F. Huxley. 1952. Currents carried by sodium and potassium ions through the membrane of the giant axon of Loligo. J. Physiol. 116:449–472. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 185.Hodgkin, A. L., and A. F. Huxley. 1952. The components of membrane conductance in the giant axon of Loligo. J. Physiol. 116:473–496. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 186.Hodgkin, A. L. 1992. Chance and Design. Cambridge University Press, New York.
- 187.Hodgkin, A. L., A. F. Huxley, and B. Katz. 1952. Measurement of current-voltage relations in the membrane of the giant axon of Loligo. J. Physiol. 116:424–448. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 188.Hodgkin, A. L., and A. F. Huxley. 1952. Propagation of electrical signals along giant nerve fibers. Proc. Roy. Soc. London. B Biol. Sci. 140:177–183. [DOI] [PubMed] [Google Scholar]
- 189.Eisenberg, R. S. 1996. Computing the field in proteins and channels. J. Membr. Biol. 150:1–25. [DOI] [PubMed] [Google Scholar]
- 190.Fatt, P., and B. Katz. 1950. Some observations on biological noise. Nature. 166:597–598. [DOI] [PubMed] [Google Scholar]
- 191.Fatt, P., and B. Katz. 1952. Spontaneous subthreshold activity at motor nerve endings. J. Physiol. 117:109–128. [PMC free article] [PubMed] [Google Scholar]
- 192.Sigworth, F. J. 1985. Open channel noise. I. Noise in acetylcholine receptor currents suggests conformational fluctuations. Biophys. J. 47:709–720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 193.Heinemann, S. H., and F. J. Sigworth. 1991. Open channel noise. VI. Analysis of amplitude histograms to determine rapid kinetic parameters. Biophys. J. 60:577–587. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 194.Hainsworth, A. H., R. A. Levis, and R. S. Eisenberg. 1994. Origins of open-channel noise in the large potassium channel of sarcoplasmic reticulum. J. Gen. Physiol. 104:857–883. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 195.Hilf, R. J. C., and R. Dutzler. 2008. X-ray structure of a prokaryotic pentameric ligand-gated ion channel. Nature. 452:375–379. [DOI] [PubMed] [Google Scholar]