An Entropic Perspective of Protein Stability on Surfaces

Abstract

The interaction of proteins with surfaces regulates numerous processes in nature, science, and technology. In many applications, it is desirable to place proteins on surfaces in an active state, and tethering represents one manner in which to accomplish this. However, a clear understanding of how tether placement and design affects protein activity is lacking. Available theoretical models predict that proteins will be stabilized when tethered to substrates. Such models suggest that the surface reduces the number of states accessible to the unfolded state of the protein, thereby reducing the entropic cost of folding on the surface compared to the bulk case. Recent studies, however, have shown that this stabilization is not always seen. The purpose of this article is to determine the validity of the theory with a thorough thermodynamic analysis of the folding of peptides attached to surfaces. Configuration-temperature-density-of-states Monte Carlo simulations are used to examine the behavior of four different peptides of different secondary and tertiary structure. It is found that the surface does reduce the entropic cost of folding for tethered peptides, as the theory suggests. This effect, however, does not always translate into improved stability because the surface may also have a destabilizing enthalpic effect. The theory neglects this effect and assumes that the enthalpy of folding is the same on and off the surface. Both the enthalpic and entropic contributions to the stability are found to be topology- and tether-placement-specific; we show that stability cannot be predicted a priori. A detailed analysis of the folding of protein A shows how the same protein can be both stabilized and destabilized on a surface depending upon how the tethering enhances or hinders the ability of the peptide to form correct tertiary structures.

INTRODUCTION

The interaction of proteins with surfaces is ubiquitous in science and technology. These interactions have garnered significant attention in recent years because of their importance in numerous applications, including medical implants, biosensors, protein arrays, and microfluidic devices (1). For certain technologies, such as medical implants, the main purpose is to control nonspecific protein adsorption. Blood proteins, such as albumin, fibrinogen, and immunoglobulin G, quickly adsorb to foreign surfaces placed in the body (2,3) leading to possible infection, heart attack, stroke, or even death (4), and such failures cost billions of dollars annually to treat (5–10). In other applications, such as antibody arrays and biosensors, the aim is to place proteins on the surface in a manner that preserves biological activity to perform high-throughput, parallel assaying of serums under investigation. The task is complicated as proteins generally change conformation when bound or adsorbed to a surface. This phenomenon was discovered decades ago (11–13) and more recent studies have confirmed its existence (1,14). Since protein structure is directly related to protein function, such transformations prevent proteins present on the surface from complexing with complimentary molecules in solution, rendering the diagnostic ineffective.

Due to the value of controlling and manipulating proteins in inhomogeneous systems, an increasing amount of research is aimed at providing new techniques and insights for development of tailor-made surfaces of controlled energy (1,15–20). Self-assembled monolayers (SAMs) of alkanethiolates on Au(111) have proved particularly useful in this endeavor (21–26). This platform can prevent nonspecific protein adsorption and allow controlled placement of protein on the surface. However, use of SAMs in biotechnology applications has been limited for several reasons including difficulty in synthesis on nongold substrates (27–33), instability leading to short shelf life (34), and oxidation (35,36). Polymer-coated surfaces have also shown promise in mediating protein-surface interactions (33,37,38). Polyethylene glycol, which possesses significant nonfouling properties and is more stable than SAMs (37), is used in a variety of devices (33,39–41). However, despite recent advances, it is still difficult to control protein structure, stability, or orientation on surfaces (1,42,43).

Conformational changes induced by the surface on adsorbed proteins can sometimes be overcome by covalently tethering the molecules to a weakly-interacting surface (37,44,45). The theory behind such an approach has been described by Dill and Alonzo (46) and Zhou and Dill (47). As shown schematically in Fig. 1, the basic idea is that the folded state of a peptide tethered to a noninteracting surface is entropically stabilized over that of the peptide in a bulk solution. The enhancement arises from the fact that fewer unfolded conformations are available to the bound protein, thereby reducing the entropy (and hence increasing the free energy) of the unfolded state (relative to that of the folded state) and forcing the peptide into more folded conformations. The folded state, being more compact, is affected little by the surface. The enthalpic contribution to the free energy of folding is assumed to be the same for both tethered and free peptide. An alternate, but equivalent, view of the phenomena can be understood by noting that an entropic penalty for folding exists. This entropic cost is greater in the bulk case than near a surface because the unfolded state of the bulk protein has more entropy to lose.

FIGURE 1.

The theory behind the stabilizing influence of surfaces on tethered proteins. (a) In the absence of a surface, the unfolded state of the protein experiences full access to all conformation space. (b) In the presence of a surface, the conformational states accessible to the unfolded protein are reduced.

Recent work by us and others has shown that such stabilization is not always observed (48–50). In these studies, two different proteins, one all-α and one all-β, were attached to weakly-interacting, purely repulsive surfaces. The studies of Friedel et al. (49,50) used a four-stranded, β-barrel protein in the bulk and attached to the surface at different sites. It was found that while tethering the peptide at certain residues on the surface did increase the melting temperature of the protein compared to the bulk case, other tethering sites caused the melting temperature to decrease. Similar behavior had been observed previously with the all-α, three-helix-bundle surface protein from Staphylococcus aureus. In that study, the mechanical and thermal stability of the peptide was reduced when tethered to the surface (48). The melting temperature of the surface-bound peptide diminished by as much as 9 K compared to the bulk case, with the degree of destabilization depending upon the tethering site on the molecule. The thermodynamic analysis showed that a stabilizing entropic effect did exist, but that it was offset by a greater destabilizing enthalpic contribution to the free energy.

One difference between both simulated systems and that considered in the theory of Dill and co-workers (46,47) was in the formers' use of a short-ranged, repulsive surface rather than the hard surface of the theory. The distinction is important due to the dramatic effect of the free energy of folding on melting temperatures. A change of <1 kcal/mol in the free energy of folding can shift the melting temperature of a protein several Kelvins (48). Consequently, it is foreseeable that the enthalpy of folding on a repulsive surface, even if the surface interaction is short-ranged (compared to the other forces in the system), will differ from that of a hard wall enough to significantly affect stability.

To determine whether the repulsive-versus-hard-surface issue is responsible for the discrepancy between theory and simulation, in this work we conduct simulations of several proteins in the vicinity of a hard wall. Stated explicitly, the hypothesis we wish to address is: a protein will be stabilized when tethered to a hard surface. Thus, the first aim of this study is to prove or disprove this statement. A second aim is to address the influence of protein structure and tethering configuration on these phenomena. We do so by using configurational-temperature-density-of-states Monte Carlo methods to determine the effect of a hard surface on the stability of attached proteins of different secondary and tertiary structure. The article is organized as follows. First, the proteins and models are presented. This is followed by a description of the simulation formalisms and our experimental design. In the following section, our results are presented and discussed. We end with an analysis of the hypothesis, a summary of the findings, and concluding remarks.

METHODS

Proteins

To understand the stability that different secondary and tertiary structures exhibit on a surface, several peptides of different topologies were investigated. The specific peptides were identified with the CATH (51) classification system using the class and architecture levels of hierarchy. The proteins were:

1. A fragment of protein A that is mostly α and forms an up-down bundle.

2. A repressor protein from bacteriophage 434 that is mostly α and forms an orthogonal bundle.

3. The mostly β, SH3 domain of the SRC protein kinase.

4. The α/β, immunoglobulin G-binding domain of protein G.

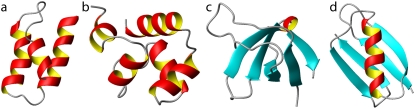
Fig. 2 shows a schematic representation of each peptide. Table 1 summarizes the CATH class and architecture, and the PDB ID of each protein.

FIGURE 2.

Schematic representation of the four proteins investigated in this study: (a) protein A, (b) 434 repressor, (c) SH3, and (d) protein G.

TABLE 1.

CATH description of proteins

Protein name	Class	Architecture
Protein A (1BDD)	Mainly α	Up-down bundle
434 Repressor (1R69)	Mainly α	Orthogonal bundle
SH3 (1SRL)	Mainly β	Roll
Protein G (2GB1)	α/β	Roll

Models

Protein model

The proteins used in this study were modeled using a coarse-grain Gō-like approach. Many studies have used variations of the Gō model (52) to investigate various aspects of protein folding of several peptides, analyzing both the kinetic and thermodynamic properties of the system (53–56). Though minimalistic in nature, these models have been shown to be in qualitative, and sometimes quantitative, agreement with experimental results (53,57,58). Gō-like models do have their limitations and cannot always capture two-state cooperativity. However, despite this fact, they do provide useful insights into real protein energetics (59). Several studies have shown that they are sufficient to determine the effects of external forces, such as those present in inhomogeneous systems, on protein stability (48,49,60).

The model used in this study is that of Hoang and Cieplak (61). The peptide is modeled with a bead and spring representation, with the beads placed at the C_α positions obtained from the PDB. The interaction between the peptide atoms, V_pp, is governed by the potential energy function

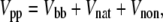(1)

where V_bb is the backbone potential, V_nat is the energy between native contacts, and V_non is the energy between nonnative contacts. The backbone potential takes the form

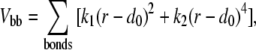(2)

where r is the distance between adjacent beads, d₀ is the equilibrium bond distance, k₁ = ε, and k₂ = 100ε, where ε is the Lennard-Jones parameter defined in V_nat below. We set d₀ = 3.8 Å following the convention of Hoang and Cieplak (61).

Nonadjacent (nonbonded) beads are subject to one of two interactions—native and nonnative. Two nonadjacent residues are considered to form a native contact if their separation distance, d_ij, as taken from the PDB coordinates, is <7.5 Å. Pairs of sites that form native contacts are then subject to the potential energy function,

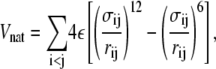(3)

where ε is the Lennard-Jones parameter, r_ij = |r_i – r_j| is the distance between sites i and j, and σ_ij = 2^−1/6d_ij, where d_ij is the native contact distance described above. These interactions are cut and shifted to zero at 18 Å.

The final term of Eq. 1 describes the contribution to the energy from two nonadjacent residues that are not native contacts. The interaction between such sites is purely repulsive and is described by

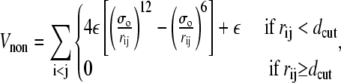(4)

where σ_o = 2^−1/6d_cut. For the mainly α-peptides in this study, protein A and 434 repressor, 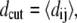and for the other peptides, protein G and SH3, d_cut = 7.5 Å.

Surface model

The purpose of this study is to determine the effect of an inert surface on the stability of tethered proteins. The surface is defined as the z = 0 plane. The interaction of the surface with the peptide is described by

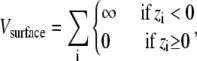(5)

where the summation is over all sites.

The peptide is bound to the surface by a harmonic restraint at either its N- or C-terminus (the first or last site) with an interaction potential of the form

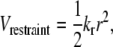(6)

where k_r is the parameter describing the strength of the restraint and r is the distance of the restrained site from its original position of (0, 0, 5.8) Å. For each type of surface, k_r = 100ε. In the presence of a surface, the total potential energy of the system, U, is therefore the sum of the protein-protein, surface-protein, and restraint interactions and is

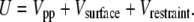(7)

For the case where no surface is present, the bulk, the total interaction energy is simply

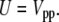(8)

EXPERIMENTAL DESIGN

Simulation protocols

The thermal stability of the proteins was probed using configurational-temperature-density-of-states (CTDOS) simulations (62). Density-of-states (DOS) methods, based upon the Wang-Landau algorithm (63,64), have been used with considerable success to study several protein-folding/unfolding scenarios. These include a coarse-grained approach on a lattice (65), an atomistic representation in a continuum (62,66), and the reversible, mechanical unfolding of atomistic proteins (67). More recently, these methods have been used to understand the stability of proteins in inhomogeneous environments, such as surfaces and confined situations, using a Gō-like model (48,60).

The CTDOS method has been described previously (62). Here we only note that the key quantity obtained from these simulations is the density of states, Ω(U), which is the degeneracy of energy state U. The advantage of CTDOS over traditional DOS lies in the method employed to determine Ω(U). The former calculates Ω(U) directly using thermodynamic information about the system, whereas the latter obtains Ω(U) from accumulating histograms of stochastic visits to each energy state U. For this reason, the errors and the noise in the estimate of Ω(U) obtained from CTDOS are reduced compared to those from DOS as the simulation progresses. In this particular study, the CTDOS simulations were performed until the convergence factor, f, reached a final value of 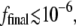which gives accuracies as good or better than traditional DOS method (62).

Different Monte Carlo moves—pivot moves, random atom displacements, and hybrid Monte Carlo/molecular dynamics moves—were utilized to efficiently sample phase space. For each peptide, three different situations were investigated: the bulk case; tethering to the surface at the N-termini; and tethering to the surface at the C-termini. For each system, N = 3 independent simulations were performed with different random number seeds. Results reported for an arbitrary property, P, are presented as the average, 〈P〉, of the N values. Uncertainties were calculated from these N quantities as 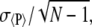where σ〈_P〉 is the standard deviation of the N averaged property values. The uncertainties associated with derived quantities, such as TΔS, were determined through standard error propagation techniques.

Stability assessment

One of the advantages of the CTDOS method is that once the density of states is known, any thermodynamic quantities of interest can be determined as a continuous function of temperature. In general, the value of an arbitrary property, X, evaluated at temperature T is related to Ω(U) by

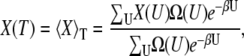(9)

where 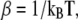k_B is Boltzmann's constants, and X can be a thermodynamic property, such as internal energy, or an order parameter. Order parameters important in this study are the radius of gyration, R_g, and the fraction nativeness (fraction of native contacts present), q, which are used to analyze the structure of the peptide.

The capacity to obtain information about the system as a continuous function of temperature is particularly helpful in determining stability. One measure of the stability of a protein is its melting temperature. A protein is considered more stable than another if its melting temperature is higher. The melting temperature (or transition temperature), T_f, can be determined from the location of the peak in the heat capacity curve if the resolution of the temperature scale is sufficiently high—CTDOS results are so compliant. The heat capacity, C(T), as a function of temperature is related to the fluctuations of the internal energy, U, according to

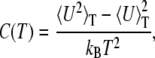(10)

where 〈U²〉 and 〈U〉² are calculated according to Eq. 9.

A more thermodynamically rigorous means of assessing stability is to compare the free energy of folding of the peptide in each environment. The free energy, enthalpy, and entropy of folding of each peptide can be calculated if the proteins are assumed to be two-state folders. This allows the configurations sampled during the simulation to be classified into “folded” and “unfolded” ensembles based upon the instantaneous fractional nativeness. The free energy of folding at any temperature can then be calculated from

(11)

where P_f is the probability of the folded state at temperature T. The enthalpy change, ΔH, associated with the folding can be computed from the difference between the average potential energy of the folded and unfolded states. (Strictly, H = U + PV, but the changes in the PV term are assumed to be negligible as has been done previously (68).) The change in entropy is then obtained from TΔS = ΔH – ΔG. To be consistent, and to facilitate comparison between results of different systems, a protein is considered folded if q > q(T_f). The value of q(T_f) may vary from protein to protein, but such a treatment will yield ΔG = 0 for all proteins at its melting temperature—a relationship which must be true by definition. The results of this thermodynamic treatment of stability are presented in tabular form at the melting temperature of the peptides in the bulk.

Mechanisms of folding for protein A

When the aforementioned analysis was performed on various proteins, it was found that protein A exhibits a behavior that is different than that of the other peptides. To determine the origins of these changes, it was useful to project the free energy, or potential-of-mean force Φ_β at temperature T, onto different order parameters or structural properties. One combination of parameters is the radius of gyration and the fractional nativeness. The potential-of-mean force is related to the probability density P_β according to

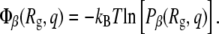(12)

The probability distribution is related to the density of states by

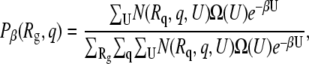(13)

where N(R_q, q, U) is the number of configurations in the sampled trajectory with radius of gyration, fractional nativeness, and potential energy R_g, q, and U, respectively. As Eq. 12 suggests, the same information can be obtained by plotting either Φ_β or P_β as a function of the order parameters of interest. In this work, we choose to use both formalisms. Also, the temperature at which the probabilities are evaluated is the melting temperature of the protein in the bulk.

Any combination of structure parameters may be used in Eq. 12. To gain additional insights into the origins of the folding behavior of protein A in each environment, it is useful to project the free energy (or probability of a particular state) onto other parameters that highlight specific structural elements. Suitably chosen progress variables can identify the extent to which a particular secondary or tertiary element contributes to the overall nativeness of the protein. Protein A is an up-down bundle of three helices where Helix 1 is positioned at an angle of ≈30° with respect to the plane formed by Helices 2 and 3 (69). Thus, appropriate order parameter variables include the total fractional nativeness, q, and the fractional nativeness of the individual secondary elements, namely Helices 1, 2, and 3 (denoted q_H1, q_H2, and q_H3, respectively). Also of interest are the fractional nativeness of the tertiary contacts between Helices 1 and 3, q_H1–H3, and Helices 2 and 3, q_H2–H3.

RESULTS AND DISCUSSION

Melting temperatures

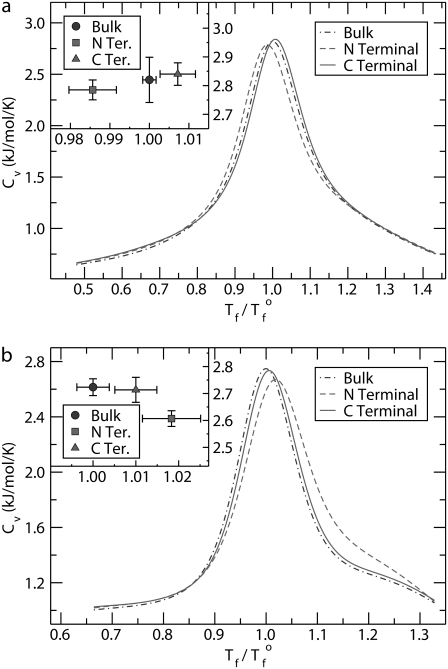
The relative stabilities of the proteins in each environment, bulk and tethered to a hard surface at the N- and C-termini, can be ascertained by comparing the melting temperatures of each case. As described above, the melting temperatures were determined from the location of the peak in the heat capacity curves. Fig. 3 shows representative results for the head capacity of two peptides; protein A is depicted in Fig. 3 a and SH3 in Fig. 3 b. The temperature is normalized with respect to the transition temperature of each peptide in the bulk, T_f°. Thus, the peak for the bulk cases are located at T_f/T_f° = 1.0.

FIGURE 3.

Heat capacity as a function of temperature for (a) protein A and (b) SH3 in three different environments: bulk and tethered to a hard surface at the N- and C-termini. The inset shows the values of the peaks for each case and the associated errors. The temperature is normalized with respect to the transition temperature of the peptide in bulk, T_f°.

One important feature seen in these curves is the temperature resolution at which the heat capacity is obtained. Using traditional molecular dynamics or Monte Carlo methods, each simulation would yield one temperature point on such a plot. Consequently, many simulations would be required for us to reliably locate the peak in the curve. With density-of-states methods, one simulation gives the heat capacity curve as a continuous function from which the transition temperature can be easily determined.

For protein A, the surface effects are different between the two tethering configurations. If the protein is bound to the surface at the N-terminus, the melting temperature is reduced over that of the peptide in the bulk. Fig. 3 a, inset, which highlights the errors, demonstrates that the reduction is statistically significant. For binding at the other end of the molecule, the C-terminus, the melting temperature is increased over that in the bulk. Fig. 3 b demonstrates that not all proteins exhibit this multiple-personality with respect to stability and tethering orientation at the N- and C-termini. For SH3, the melting curves for both surface configurations are shifted to the right compared to the bulk case.

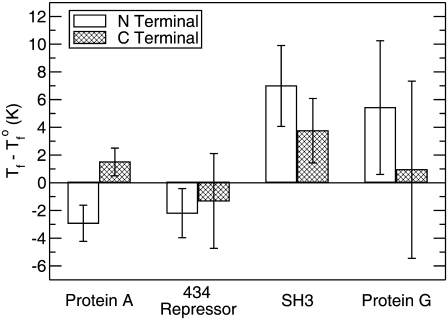
To summarize and quantify the results for each peptide in the study, Fig. 4 shows the change in the transition temperature for each surface case from that of the bulk, T_f – T_f°. For protein A and SH3 we see that the results correspond to Fig. 3, a and b, respectively. If T_f – T_f° > 0, the surface case has a higher melting temperature than that of the bulk protein, and for T_f – T_f° < 0 the surface case has a lower melting temperature.

FIGURE 4.

Change in the transition temperature, T_f – T_f°, of the proteins upon tethering to a hard surface.

The results in Fig. 4 also show that for 434 repressor and protein G attached at their C-termini the errors are too large to determine unambiguously whether the protein is stabilized or destabilized. One interpretation of this is that the surface affects these configurations to little or no degree. The other cases, however, show statistically significant results. The N-terminal case of protein G is stabilized over the bulk. The outcomes of both surface orientations of protein A are also significant and show that the same peptide can be either stabilized or destabilized depending upon tether placement. The large degree of stabilization of SH3 seen in both surface cases is similarly significant, as well as the destabilization of the N-terminal case of 434 repressor.

Thermodynamics of folding

In the theory of Dill and co-workers (46,47), the surface reduces the number of conformations available to the unfolding protein, and hence decreases its entropy, but affects the folded state little. The theory also assumes that the enthalpy of folding is the same in the bulk and on a surface. Thus, compared to the bulk, the free energy of the unfolded state increases on a surface while that of the folded state experiences no change. The overall result is a reduction in the free energy of folding. To examine these assumptions, we calculated the thermodynamic changes of folding for each peptide. Table 2 gives the free energy, enthalpy, and entropy of folding for each peptide at the melting temperature of the protein in the bulk, T = T_f°. The free energy values, along with the transition temperatures of Fig. 4, provide a useful consistency check of the results. If the melting temperature of the protein on the surface is greater than in the bulk, the thermodynamic analysis should show that ΔG_f < 0. If the surface melting temperature decreased compared to the bulk case, ΔG_f should be >0. Comparison of the free energies values contained in Table 2 with the changes in the melting temperatures depicted in Fig. 4 show this to be the case. It is also expected that, at this temperature, ΔG_f = 0 for the bulk case; the data exhibit this behavior.

TABLE 2.

Thermodynamics of folding for protein A, 434 repressor, SH3, and protein G at their respective folding temperatures in the bulk

Protein	Environment	ΔGf (kJ/mol)	ΔHf (kJ/mol)	TΔSf (kJ/mol)
	Bulk	0.0	−49.3 ± 1.0	−49.3 ± 1.0
Protein A	N-Terminus	0.77 ± 0.13	−49.0 ± 0.3	−49.7 ± 0.4
	C-Terminus	−0.28 ± 0.17	−49.6 ± 0.5	−49.3 ± 0.4
	Bulk	0.0	−83.6 ± 2.0	−83.6 ± 1.5
434 Repressor	N-Terminus	0.87 ± 0.60	−82.9 ± 4.5	−83.8 ± 3.9
	C-Terminus	0.43 ± 0.82	−81.7 ± 3.7	−82.1 ± 2.9
	Bulk	0.0	−88.6 ± 0.7	−88.6 ± 0.9
SH3	N-Terminus	−1.28 ± 0.34	−85.3 ± 0.9	−84.0 ± 1.0
	C-Terminus	−0.70 ± 0.32	−88.3 ± 1.1	−87.6 ± 1.2
	Bulk	0.0	−62.6 ± 0.3	−62.6 ± 0.4
Protein G	N-Terminus	−0.74 ± 0.43	−59.9 ± 0.5	−59.2 ± 0.5
	C-Terminus	−0.20 ± 0.62	−61.0 ± 0.5	−60.8 ± 0.8

Several observations can be made from the results in Table 2. First, in some cases, the errors are too large to enable us to determine, with certainty, that any trends exist. However, several statistically significant comparisons can be made. These will now be addressed.

Two proteins show statistically significant destabilization, ΔG_f > 0, on the surface: protein A and 434 repressor in the N-terminal position. This is consistent with the melting temperature results obtained from the heat capacity curves. Unfortunately, we cannot determine whether the destabilization is enthalpic or entropic in origin due to the large errors in those values.

Three proteins show stabilization, ΔG_f < 0, on the surface: protein A attached at the C-terminus, SH3 attached at both the N- and C-termini, and protein G at the N-terminus. This observation is consistent with the heat capacity results. For the case of protein A, 434 repressor, and SH3 in the C-terminus orientation, the errors in ΔH_f and TΔS_f are too large for us to determine the origin of the stabilization. However, for SH3 attached at the N-terminus, and for both protein G surface cases, it is seen that the entropic cost of folding on the surface is reduced compared to the bulk case. We also note that, for each of these cases, the enthalpy of folding is less favorable on the surface compared to the bulk. Because these results are critical to evaluating the validity of the hypothesis considered in this article, they are now summarized:

• There are three, statistically significant instances where the entropic cost of folding on the surface is less than that in the bulk.

• No instances show a statistically significant increase in the entropic cost of folding on the surface.

• The surface shows a destabilizing effect enthalpically for the same three instances where the entropic cost is reduced.

• The surface never causes a statistically significant, enthalpically stabilizing effect.

Protein A

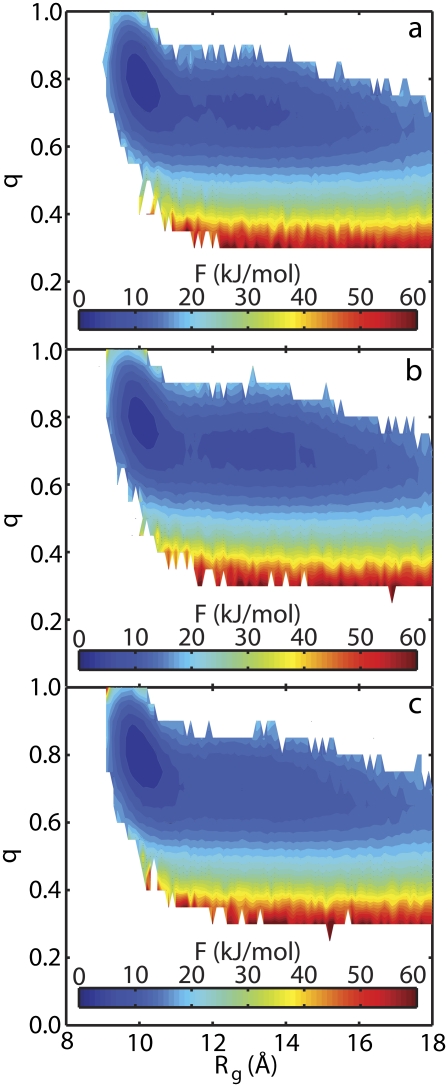
Protein A showed interesting behavior in that the same protein was both stabilized and destabilized by the same surface depending upon the point of attachment. These results allow for further investigation into the origins of each phenomena. Fig. 5 shows the free energy of protein A as a function of the radius of gyration, R_g, and the fractional nativeness, q, for each of the three environments considered in this study at the melting temperature of the peptide in the bulk. Fig. 5 a shows the values in the bulk, Fig. 5 b shows the values for tethering at the N-terminus, and Fig. 5 c shows the values for tethering at the C-terminus. For the highest melting, C-terminal case, one energy basin exists at low values of R_g and high values of q. This corresponds to the folded peptide. The other two environments show a different landscape. In both of these, a low energy state is present for not only the folded state but also for more unfolded configurations. This second basin is centered at R_g ≈ 13 Å and q ≈ 0.7. For the vacuum case, both basins are connected by a low energy pathway which the protein can easily traverse. For the lowest-melting, N-terminus case, these basins are separated by an energy barrier. Thus, configurations in the unfolded state have difficulty refolding into the native form. These results demonstrate that the surface restricts the conformations of protein A to folded configurations when tethered at the C-terminus but stabilizes unfolded configurations in the N-terminal orientation.

FIGURE 5.

The free energy, F, of protein A as a function of the radius of gyration, R_g, and the fractional nativeness, q, in three separate environments: (a) bulk, (b) tethered at the N-terminus, and (c) tethered at the C-terminus. The temperature in each case is equal to the melting temperature of the peptide in the bulk.

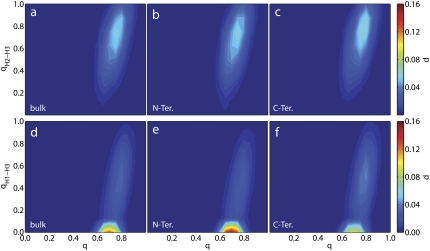
To further uncover the origins of these phenomena, it is useful to project the free energy (or probability of a particular state) onto reaction coordinates that can shed light onto the relative importance of different structural elements on the folding behavior of the protein. Fig. 6 shows the probability as a function of q, q_H2–H3, and q_H1–H3 for protein A in each environment. The latter two quantities are the fraction of tertiary contacts formed between Helices 2 and 3 and Helices 1 and 3, respectively. The columns of Fig. 6 (read from left to right) correspond to the bulk, tethering at the N-terminus, and tethering at the C-terminus. For the top row of panels, little difference is seen between each environment, suggesting that the surface does not affect the tertiary contacts between Helices 2 and 3. This same behavior is seen in the results for q versus q_H1, q_H2, and q_H3 (results not shown). However, a difference is found when examining the tertiary contacts between Helices 1 and 3. The bottom row of panels of Fig. 6 depicts the probability distribution as a function of q and q_H1–H3 for each environment. In each case, a vast majority of the population resides at q ≈ 0.7 and q_H1–H3 ≈ 0. When these features are analyzed, it is found that the maximum probability in each case is 0.13, 0.15, and 0.096 for the bulk, N-terminus, and C-terminus, respectively. The heat capacity data (see Fig. 4) showed that tethering at the N-terminus yields the lowest-melting configuration and the C-terminus yields the highest-melting. The bottom row of Fig. 6 demonstrates that the origin of this phenomenon lies in the contacts that Helix 1 makes with Helix 3. The lowest-melting case (Fig. 6 e) has the highest population of unfolded q_H1–H3; the highest-melting case (Fig. 6 f) has the lowest. The C-terminal case (Fig. 6 f) also shows a large population, at q ≈ 0.8 and q_H1–H3 ≈ 0.5, which is not present in the other populations.

FIGURE 6.

The probability, p, of protein A as a function of the total fractional nativeness, q, and the fractional nativeness of different tertiary contacts. The top row of panels corresponds to tertiary contacts between Helices 2 and 3, q_H2-H3, in three separate environments: bulk; tethered at the N-terminus; and tethered at the C-terminus. The bottom row corresponds to tertiary contacts between Helices 1 and 3, q_H1-H3, in the same environments. The temperature in each case is equal to the melting temperature of the peptide in the bulk.

The fact that the population maps of all the other secondary and tertiary contacts (top row of Fig. 6 and not shown) do not exhibit any significant changes from one system to another, while the results for q_H1–H3 and q do, demonstrates that the positioning of Helix 1 in the bundle is the origin of stabilization or destabilization of protein A on a surface. Helix 1 has the smallest number of residues (10) compared with Helices 2 and 3 (13 and 14, respectively) and also makes fewer tertiary contacts. In the N-terminal case, Helix 1 is tethered to the surface. Being the smallest, and possessing the fewest number of tertiary contacts, it is not able to hold up the rest of the protein. In its native state, this helix is positioned at an angle of ≈30° with respect to the other helices. It is difficult to maintain this configuration when tethered to the surface, and the result is a more coplanar configuration where each helix lies on the same plane. When tethered at the C-terminus, Helix 3 is tied to the surface. This allows the less-stable Helix 1 to find its place on the bundle with ease compared to the bulk case. These results are also in agreement with those obtained for protein A on attractive and purely-repulsive surfaces (48).

Secondary structure, tethering configuration, and stability on surfaces

One of the purposes of this work was to determine if general statements can be made about secondary structure and its influence on the stability of proteins on surfaces. The results of the preceding sections demonstrate that the stability of proteins on surfaces does not seem to follow secondary structure. Protein A and 434 repressor are both all-α peptides, but they display different behavior. Moreover, as the results from protein A suggest, the same protein can be stabilized or destabilized depending upon the placement of the tether. Thus, it is our view that no general statements can yet be made about secondary structure and its role in protein/surface interactions. Further investigation is needed on this subject.

One observation that can be made is that only all-α proteins, protein A and 434 repressor, showed statistically significant destabilization. This does not prove that only all-α proteins can be destabilized (especially in light of the analysis of protein A given above), but serves to show that additional studies on more proteins are required. Also note that Friedel et al. (49,50) demonstrate that an all-β protein can be destabilized. Our own view is that protein stability on surfaces is protein-specific, and it is difficult to make generalized statements because protein structure is so diverse.

Weak versus strong confinement

Proteins in strongly confined environments have recently been an area of active research (58,60,70–76). Such situations arise in technologies that include micro- and nanofluidic devices and size exclusion chromatography, as well as in the protein's natural environment in cells where molecular crowding caused by cosolutes cages the protein. It has been demonstrated that proteins are stabilized when placed in such environments with the degree of enhancement dependent upon the size of the confining potential (58,60). Generally, proteins are more stable in tighter places.

In contrast to these situations, surfaces can be viewed as weakly confined environments which result in different behavior compared to strong confinement. Only stabilization (compared to the bulk case) has been observed when proteins are placed in strongly confined environments; destabilization is never observed (58,60). As this study demonstrates, such is not always the case for weak confinement. On surfaces, stabilization seems to be protein- and orientation-specific. SH3 was stabilized on the surface when tethered at both its N- and C-termini. For protein A, the N-terminal case was destabilized while the C-terminal stabilized. Protein G showed stabilization in one orientation but no discernable change in the other, and 434 repressor was destabilized in one case. The results of previous studies also demonstrate that weak confinement does not guarantee stabilization (48,49).

There is another important difference between strong and weak confinement. With the former, it has been seen that entropy plays the dominant role (over the enthalpy) in changing the stability of the protein with respect to the bulk case (60). Strong confinement severely reduces the ability of the protein to experience unfolded states and hence maintains the protein in a folded state. This is not the case under weak confinement such as surfaces. Here, the contributions to the free energy from the enthalpy and entropy are more similar. The surface reduces the configurations available to the unfolded peptide, but not to the same extent that is seen for strong confinement. In short, for strong confinement, entropy dominates and for weak confinement it is a balance between entropy and enthalpy that governs stability compared to the bulk case.

One final comment is noteworthy. Compared to strong confinement, the stabilizing effects of surfaces are small. For example, Fig. 4 shows that for protein G tethered at the N-terminus, the melting temperature increase is ∼6 K. For strong confinement, we previously found that the same protein was stabilized by ∼15 K in the smallest case and by 103 K for the most extreme case (60). Similarly, Table 2 shows that the free energy of folding for the surface case at the melting temperature of the bulk case was −0.74 kJ/mol while for strong confinement we previously reported a value of −1.42 to −7.14 kJ/mol. Similar trends are seen for other proteins. Thus, higher degrees of confinement lead to a greater shift in the stability of proteins.

CONCLUSION

Analysis of hypothesis

In previous work, we and others have shown that the melting temperatures of peptides tethered to purely repulsive surfaces can decrease compared to the bulk (48,49). The results of this work, which correspond to a hard surface, are in agreement with previous results (49), and serve to demonstrate that the question of stability of a peptide tethered to a surface is protein- and orientation-specific. It is not correlated to secondary structure. Even within a specific protein, the stability is dependent upon the site at which the protein is tethered. We cannot yet say, a priori, whether a protein will be stabilized or destabilized.

We can, however, say that the argument behind the reasoning of Dill and co-workers (46, 47) is valid. Specifically, the theory that the entropic cost of folding on the surface is less than that of the bulk is supported by the data seen in Table 2. No instances show an increase in the entropic cost of folding, but three show a decrease. What the theory neglects to take into account is that the enthalpic contribution to the free energy can differ on the surface compared to the bulk case. The stability of a protein on a surface, as in the bulk, is governed by a balance of enthalpy and entropy, and cannot be analyzed by focusing on entropy alone.

SUMMARY

Configurational-temperature-density-of-states (CTDOS) simulations have been performed in an effort to prove the hypothesis that proteins will be stabilized when tethered to a hard surface. The differences in stability between proteins in the bulk phase and tethered at their N- and C-termini on hard surfaces were ascertained from melting temperature data and thermodynamic quantities of folding. The results disprove the hypothesis and indicate that proteins will not always be stabilized when tethered to a hard surface. One example is protein A. This peptide was destabilized in the N-terminal configuration, while stabilized in the C-terminal compared to the bulk case. Upon further analysis of protein A, it was found that this behavior arises from the hindered or enhanced ability of one of the helices of the peptide to make appropriate tertiary contacts with the rest of the molecule.

The results also demonstrate that protein stability cannot be correlated to secondary structure or tethering configuration but is protein- and orientation-specific. It was also found that surfaces, viewed as weakly confining environments, show the same ability to reduce the entropic cost of folding as do systems with higher degrees of confinement, but do so to a lesser extent. Theory has previously predicted this effect, but neglected to account for the change in enthalpy that a protein would experience upon the surface.