Abstract
The membrane potential measured by intracellular electrodes, Em, is the sum of the transmembrane potential difference (E1) between inner and outer cell membrane surfaces and a smaller potential difference (E2) between a volume containing fixed charges on or near the outer membrane surface and the bulk extracellular space. This study investigates the influence of E2 upon transmembrane ion fluxes, and hence cellular electrochemical homeostasis, using an integrative approach that combines computational and experimental methods. First, analytic equations were developed to calculate the influence of charges constrained within a three-dimensional glycocalyceal matrix enveloping the cell membrane outer surface upon local electrical potentials and ion concentrations. Electron microscopy confirmed predictions of these equations that extracellular charge adsorption influences glycocalyceal volume. Second, the novel analytic glycocalyx formulation was incorporated into the charge-difference cellular model of Fraser and Huang to simulate the influence of extracellular fixed charges upon intracellular ionic homeostasis. Experimental measurements of Em supported the resulting predictions that an increased magnitude of extracellular fixed charge increases net transmembrane ionic leak currents, resulting in either a compensatory increase in Na+/K+-ATPase activity, or, in cells with reduced Na+/K+-ATPase activity, a partial dissipation of transmembrane ionic gradients and depolarization of Em.
INTRODUCTION
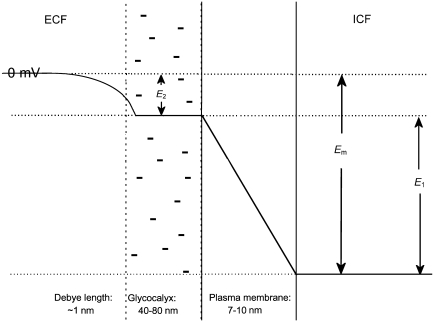
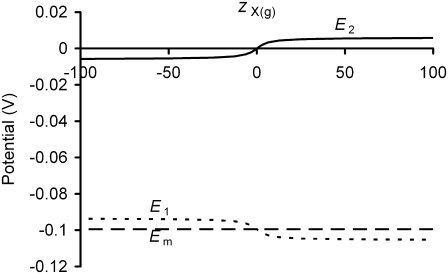
The electrical potential difference between the intracellular and bulk extracellular spaces (Em), as classically measured by intracellular microelectrodes, is thought to consist of at least two distinct components, as shown in Fig. 1, such that Em = E1 + E2. The larger E1 term reflects the potential difference between the inner and outer membrane surfaces. The smaller E2 term is the potential difference between regions containing fixed negative charges on or near the outer membrane surface, and the bulk extracellular space. A further potential difference between the inner membrane surface and the bulk intracellular space is also likely, but would be constant in the absence of large alterations in intracellular fluid composition (1). Previous investigations of the physiological effects of alterations in E2 by Ca2+ adsorption onto these fixed negative charges (2,3) demonstrated alterations in ion channel function at a constant Em that suggested they were gated by E1 rather than by Em itself (1,3,4). However, these previous studies did not explore the possible consequences of alterations in E2 upon electrophysiological homeostasis in intact whole cells, instead investigating isolated ionic currents studied under voltage clamp.
FIGURE 1.
Diagrammatic representation of electrical potential differences between the intracellular and bulk extracellular spaces (not to scale). Electrical potential differences exist between the bulk extracellular fluid (ECF) and the region near the cell surface containing fixed charges (this potential difference is denoted as E2), as well as across the cell membrane itself (E1) between the glycocalyx and intracellular fluid (ICF). The potential recorded with an intracellular microelectrode, Em, is the sum of these two potential differences. Existing studies have assumed that E1, but not Em, is influenced by E2. This study explores the influence of E2 upon both E1 and Em.
This study thus extends and complements the earlier works through an investigation of the influence of E2 upon transmembrane ionic currents and intracellular ionic homeostasis. Computational methods were used to develop testable theoretical predictions derived from the charge-difference (CD) approach (5) previously used to investigate the determinants of intracellular ion concentrations, membrane potential, and cell volume in complex multicompartment systems involving both passive and active ion fluxes (5–8). The theoretical predictions were tested against focused experimentation in frog skeletal muscle.
First, the existence of a discrete, negatively charged, glycoproteinaceous glycocalyx known to possess Ca2+-adsorptive properties surrounding skeletal muscle prompted the development of a mathematical description of the influence of fixed charges distributed within a three-dimensional volume. Electron microscopy showed the glycocalyx to be 35–70 nm thick in this study, one to two orders of magnitude greater than the Debye length calculated for the Ringer solutions employed. This theoretical analytic approach was developed from Gibbs-Donnan (GD)-type equilibrium constraints that simulated the effects of alterations in the magnitude of fixed glycocalyceal charges within a three-dimensional volume. This required consideration of whether osmotic alterations in glycocalyceal volume would influence the relationship between glycocalyceal charge adsorption, E2, and local ion concentrations. Electron micrographic measurements demonstrated that the thickness of the glycocalyx was influenced by extracellular [Ca2+], in agreement with predictions from a GD analysis that assumed constant osmolyte concentration within the glycocalyx. This suggested a nonlinear relationship between glycocalyceal [Ca2+] adsorption and steady-state glycocalyceal charge density, in contrast to the linear relationship predicted by the classical Gouy-Chapman (GC) equation (9). The GC equation requires the assumption of a two-dimensional distribution of surface charge and was therefore not suitable for simulation of the glycocalyx. Nevertheless, the GD equations were shown to reduce to the GC equations when identical assumptions of a two-dimensional charge distribution were invoked, thereby allowing comparison of this approach with that from the classical literature.
Second, computational modeling of the influence of glycocalyceal charge upon intracellular ionic homeostasis was performed using the CD cellular model of Fraser and Huang (5). This model has been used previously to investigate the determinants of intracellular ion concentrations and Em in complex multicompartment systems containing both passive and active ion fluxes (5–8). E2 and near-membrane ion concentrations were calculated from glycocalyceal charge using the GD analysis, allowing their influence upon Em and intracellular ion concentrations to be simulated using the CD model. These modeling studies predicted that more negative glycocalyceal charge would provoke an increase in net transmembrane ionic leak currents. However, the functional properties of the Na+/K+-ATPase (10) in normal resting muscle (11) were sufficient to conserve normal intracellular ion concentrations, and hence Em, despite such increases in ionic leakage. These predictions were confirmed by experimental microelectrode measurements of stable Em over prolonged (>5-h) periods, despite alterations in glycocalyceal charge produced by varying extracellular [Ca2+]. In contrast, both the model and experiments demonstrated that under conditions where Na+/K+-ATPase activity reserve was reduced by reduction in extracellular [K+], similar manipulations of glycocalyceal charge resulted in partial dissipation of transmembrane ion gradients and Em.
This study thus demonstrates an influence of glycocalyceal charge upon transmembrane ionic leak currents. Consistent with assumptions made in earlier studies, this had little influence upon Em under normal physiological conditions due to a compensatory increase in Na+/K+-ATPase activity. However, under conditions of compromised Na+/K+-ATPase activity produced by reduced extracellular [K+], glycocalyceal charge was shown to influence intracellular electrolyte homeostasis and Em. These findings lead to a prediction that clinical conditions associated with reduced Na+/K+-ATPase activity, such as ischemia, hypokalemia, and cardiac failure (12), might also be exacerbated by reduced extracellular [Ca2+].
MATERIALS AND METHODS
Analytic equations based on GD theory were derived to assess the influence of extracellular fixed charges upon E2. This approach was compared to the classical GC equations. Simulation of the physiological effects of E2 upon intracellular ionic homeostasis employed the CD approach, introduced and fully described on earlier occasions (5,7,8), and modified to include the GD equations. Finally, the related experimental studies involved conventional microelectrode measurements of membrane potential, and electron-microscope studies of glycocalyceal thicknesses. The symbols used in the text are summarized in Table 1.
TABLE 1.
Symbol definitions
| Symbol | Meaning |
|---|---|
| η | A dimensionless correction factor permitting steady-state osmotic activity within the glycocalyx to be greater than in the bulk extracellular space. It may represent a relative gel pressure. |
| φ | Osmotic coefficient |
| Π | Osmolarity |
| σ | Surface charge/unit area |
| Σg | Glycocalyceal fixed charge/unit volume |
| Ψx | Electrical potential at a distance, x, from a charged surface |
| a | Ionic activity |
| [C] | Mobile salt concentration |
| e (subscript) | A position within the bulk extracellular space |
| E1 | The potential difference between inner and outer membrane surfaces |
| E2 | The potential difference between the outer membrane surface and the bulk extracellular space |
| Em | The membrane potential as conventionally measured with microelectrodes |
| g (subscript) | A position within the glycocalyx |
| i (subscript) | A position within the intracellular space |
| N | Membrane Na+/K+-ATPase density |
| V | Volume |
| X | Nonmobile ions |
| zX | The mean charge valency of X |
Experimental methods
Membrane potential recordings
Resting membrane potentials, Em, were recorded in sartorius muscles dissected from cold-adapted winter frogs, Rana temporaria, killed by concussion followed by pithing (Schedule 1, Animal Procedures Act, Home Office, United Kingdom). The frogs had been maintained together to minimize any variations that might reflect differing environmental influences. The muscles were stretched to ∼1.5 times their in situ length as previously described by Koutsis et al. (13) and placed in a bath initially filled with standard isotonic Cl−-Ringer solution titrated to pH 7.2 (in mM, 115 NaCl, 2.5 KCl, 1.8 CaCl2, and 3.0 HEPES).
Experiments were conducted at 5–10°C. Bath temperature was controlled by circulating cooled water through a glass coil placed in the chamber using a Minipuls 3 peristaltic pump (Gilson, France) and monitored using a digital thermometer incorporating a remote thermistor close to the muscle, previously linearized and calibrated against a platinum film resistor. Em values from surface fibers were measured against bath voltage using standard glass capillary microelectrodes (3 M KCl; resistance 5–20 MΩ; tip potential <5 mV (14)) mounted through an Ag/AgCl reference junction to a high impedance voltage follower and controlled using a micromanipulator. Microelectrode resistances were further tested after impaling each muscle fiber, and microelectrodes were rejected if they were not within the above range. Em values were recorded from at least 30 fibers over a period of at least 30 min in normal Cl−-containing Ringer solution to confirm stable baseline values that could be subsequently compared against Em values after each solution change. The bathing solution was then changed for an experimental solution containing an adjusted [K+] (from 0.75 to 2.5 mM) and/or [Ca2+] (from zero-added to 10 mM) using two washouts. The NaCl concentrations of the experimental solutions were adjusted to ensure isosmolality with the control Ringer solutions, as measured using a standard calibrated vapor pressure osmometer.
Experimental recordings of the influence of the experimental solutions upon Em were pooled from a time period (150–300 min) that under each experimental condition permitted detection of small changes in Em without visible deterioration or twitching of the muscle fibers under light microscopy.
Electron microscopy
Cutaneous pectoris muscles were obtained for electron microscopy from the same frogs used in the microelectrode experiments and exposed to the experimental solutions for 30 min. They were then fixed in isotonic fixative containing 3% glutaraldehyde, 0.3% hydrogen peroxide and 2 mM CaCl2 in PIPES buffer. After fixation, they were rinsed in deionized water and treated with osmium ferricyanide to increase the contrast of the glycocalyx. Thin sections were cut at 60 nm transversely through the muscle and viewed in an FEI Philips CM100 electron microscope operated at 80 kv. Images were projected onto a monitor at a magnification of 200,000× and overlain with a parallel lattice with a spacing of 1 cm. Where the line intersected the plasma membrane an orthogonal intercept of the thickness of the glycocalyx was measured using a Quantimet 500 (Leica Cambridge, Cambridge, United Kingdom). Ten measurements were taken from each of 10 fibers under each experimental condition.
Theoretical methods
Mathematical treatment of the influence of glycocalyceal fixed charges upon local potentials and ion concentrations
This study develops an approach that permits calculation of the influence upon E1 (Fig. 1) and local ion concentrations of glycocalyceal fixed charges that are distributed over a volume with a thickness (40–80 nm) that significantly exceeds the Debye length (∼1 nm in normal Ringer solution).
Mathematical analysis of the relationship between glycocalyceal fixed charge and E2
An analytic relationship between glycocalyceal fixed charge density, Σg, glycocalyceal potential, E2, and local ion concentrations may be derived from two basic steady-state constraints: 1), electroneutrality, and 2), absence of net ion currents. First considering the situation in which Σg is known, the electroneutrality constraint may be stated as
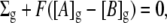 |
(1) |
where Σg is the fixed charge/unit volume (C l−1); F is Faraday's constant; A represents a monovalent cation; B represents a monovalent anion; and the subscript g denotes the glycocalyx. At equilibrium, ionic currents are zero and thus ions are passively distributed between the bulk extracellular solution and the glycocalyx according to their Nernst potentials:
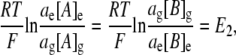 |
(2) |
where a denotes mean ionic activity in the extracellular fluid (ECF) and glycocalyx compartments, denoted by the subscripts e and g, respectively. This allows for the possibility that the glycocalyx may alter local ionic activities. This relationship may be simplified by defining [C] as the total salt concentration such that [C]e = [A]e = [B]e. Thus,
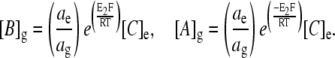 |
(3) |
Combining these two constraints (Eqs. 1 and 3) demonstrates the relationship between fixed charge density and glycocalyceal potential.
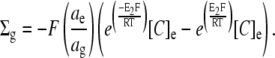 |
(4) |
Rearranging in terms of E2,
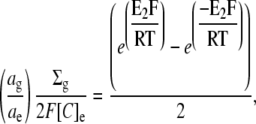 |
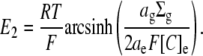 |
(5) |
This equation allows calculation of E2 if the glycocalyceal fixed charge density is known. However, if the glycocalyceal volume is not fixed, but rather determined by osmotic water movements, then there must also be an osmotic equilibrium at steady state. Under such conditions, the relationship between total glycocalyceal charge and the glycocalyceal charge density may be nonlinear, as greater charge magnitudes result in an increase in the volume over which they distribute. This would have implications for the relationship between Ca2+ adsorption and glycocalyceal charge density, and thereby for E2.
This analysis, therefore, will next develop an analytic relationship between glycocalyceal charge and E2 under conditions where glycocalyceal volume is osmotically determined. The predictions of this theory will be compared with those of the nonosmotic relationship (Eq. 5) by electron-micrographic measurement of glycocalyceal volumes under conditions of varying [Ca2+]e in Results.
Rearranging Eq. 2 gives
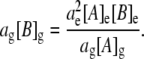 |
(6) |
The glycocalyx will be assumed to influence the equilibrium state through its charge and through its osmotic activity. Such influence is captured by defining Σg as:
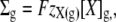 |
(7) |
where [X]g denotes the osmolar concentration of fixed ions within the glycocalyx and zX(g) its mean charge valency per osmole. Note that this permits zX(g) to be very large if the glycocalyx is significantly charged but has little osmotic activity. Thus, the electroneutrality constraint (Eq. 1) will be restated as
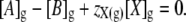 |
(8) |
Finally, the osmotic constraint is given by
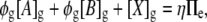 |
(9) |
where φg is the osmotic coefficient of the salt solution within the glycocalyx, Πe is the total osmolarity of the extracellular solution, and [X]g is expressed in osmoles l−1. Osmotic and chemical potentials alone may be shown to produce intrinsic instability in polyelectrolyte gels such as the glycocalyx, unless stabilized by a third force that may be considered to be a gel pressure (15). Thus, a dimensionless correction factor, η, is included in this osmotic constraint to reflect the possibility that total osmotic activity may be greater within the glycocalyx than in the ECF due to a small pressure within the glycocalyx. It will be assumed that η is constant with changing glycocalyceal volume within the range of values considered in this work.
Substituting the electroneutrality expression for [A]g (Eq. 8) into the Donnan constraint (Eq. 6) gives
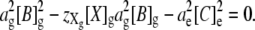 |
(10) |
Substituting Eq. 8 into the osmotic constraint (Eq. 9) gives
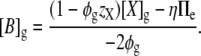 |
(11) |
Combining these equations, grouping terms into quadratic form, and solving for [X]g gives
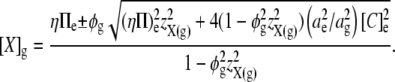 |
(12) |
This permits the expression of E2 in terms of the mean charge valency per osmole of molecules constrained within the glycocalyx (zX(g)), rather than in terms of the steady-state charge density within the glycocalyx (Σg). Thus, by combining Eqs 5, 7, and 12, E2 is shown to vary nonlinearly with zX(g):
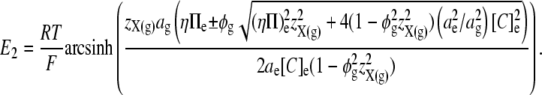 |
(13) |
Alternatively, if fixed charges in the glycocalyx itself exert no osmotic activity, then combining Eqs. 1, 6, and 9 with [X]g = 0 gives
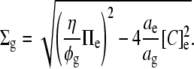 |
(14) |
Thus, in the particular case that the glycocalyx itself exerts no osmotic influence but its volume is nevertheless osmotically determined,
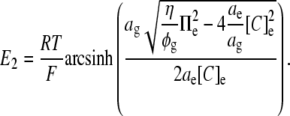 |
(15) |
The relative volume of the glycocalyx at steady state is given by
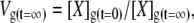 |
(16) |
or, equivalently, by
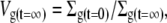 |
(17) |
where Vg is the relative volume of the glycocalyx and times t = 0 and t = ∞ denote initial conditions and eventual steady-state conditions, respectively.
By inspection, it is clear that both Eqs. 12 and 14 have values of zero when Πe = 2φg[C]e, η = 1, and ag = ae. The condition Πe = 2φg[C]e is likely to be true when the extracellular solution is a 1:1 electrolyte. Yet, as can be seen from Eq. 16 or Eq. 17, if steady-state values of [X]g or Σg are zero, the steady-state glycocalyceal volume tends toward “infinity” as the glycocalyx is then essentially indistinguishable from the bulk ECF. However, these equations additionally demonstrate that a stable, osmotically determined glycocalyceal volume would be possible 1), if total osmolarity in the glycocalyx is permitted to be higher than in the ECF, thus η > 1; 2), if the activities of mobile ions are greater in the glycocalyx than in the ECF, thus ae/ag < 1; 3), if osmotic coefficients of mobile ions are lower in the glycocalyx than in the ECF, thus φg < 1 for ions within the glycocalyx such that Πe > 2φg[C]e; or 4), if the ECF contains ions that cannot pass into the glycocalyx such that Πe > 2φg[C]e. One or more of these conditions must be true for there to exist a stable, nonzero value of [X]g or Σg if glycocalyceal volume is osmotically determined. Certain other biological gels, including the sclera, have been shown to behave as if they exert a mechanical pressure that opposes swelling (15), and this (condition 1 above) seems the most likely explanation of the above four possibilities. Thus, unless otherwise stated, it is assumed that ae/ag = 1 and φg = 1. The influence of the value of η was investigated, as shown in Results. Nevertheless, it is clear that any combination of the four possible conditions for stability presented here lead to the conclusion that if the glycocalyx volume is osmotically determined, then increasing the magnitude of zX(g) would tend to swell the glycocalyx. This hypothesis was tested experimentally.
Note that it is not necessary to consider the shape of the potential decay between the glycocalyx and the bulk ECF (Fig. 1). It can be shown that the electrochemical steady state of the glycocalyx is uniquely defined by the state of the ECF irrespective of whether intervening compartments are present. Thus, assuming activity and osmotic coefficients of 1, the steady-state value of [X]g (Eq. 12) is influenced by [C]e and Πe, but not by any other property of the ECF. Yet by the osmotic and zero-net-flux constraints, Πe and [C]e must be the same in every linked compartment between which ions are passively distributed. Thus, the presence of intervening compartments does not alter the steady state of the glycocalyx with respect to the ECF, as Πe and [C]e must, by the same argument, be the same in each such compartment. Similarly, because activity ratios and osmotic coefficients can be expressed as ratios for ions in the glycocalyx relative to those in the ECF, this analysis holds true for situations where activity coefficients and osmotic coefficients vary between the glycocalyx edge and the ECF.
Charge-difference modeling of the influence of E2 upon intracellular ionic homeostasis
The influence of glycocalyceal ion concentrations and E2 upon transmembrane ion fluxes and intracellular ionic homeostasis were explored using the CD model of Fraser and Huang (5,7,8). This employed an assumption that transmembrane ion movements were orders of magnitude slower than the passive redistribution of ions between the bulk extracellular space and the charged glycocalyx. This permitted analytic calculation of glycocalyceal ion concentrations and E2 from Σg and extracellular conditions using the GD method derived above.
CD modeling of the cell then introduced the assumption that transmembrane fluxes were determined by the electrical and respective concentration gradients between the bulk intracellular space and the glycocalyx. This contrasts with previous studies using this model in which transmembrane fluxes were determined by the concentration gradient between the bulk intracellular and bulk extracellular spaces. Extracellular ion concentrations were identical to those in the experimental solutions used. In other respects, the model was as described in Fraser and Huang (5), with the osmotic water movement terms later introduced by those authors (8), and therefore the membrane permeabilities and Na+/K+-ATPase density were calibrated to frog skeletal muscle.
RESULTS
Previous studies have employed theoretical and experimental approaches to investigate the influence of surface charges upon transmembrane potentials (1,4). However, whether implicitly or explicitly, such studies have assumed that intracellular ion concentrations are unaffected by extracellular fixed charge. However, transmembrane potentials influence transmembrane ion fluxes, and it is therefore necessary to consider whether there are circumstances under which fixed charges may influence intracellular ionic homeostasis.
It is conceivable that the influence of surface charges upon intracellular ionic homeostasis has not previously been investigated because, as shown in Methods, the expectation for a passive ionic distribution between any number of connected compartments is that the equilibrium ion concentrations within any single compartment are uniquely defined with reference to any other single compartment. In other words, each compartment must be at electrochemical equilibrium with each other compartment, irrespective of the number of intervening compartments and the equilibrium ion concentrations within them, as expected from the principle of microscopic reversibility. Thus, if ion concentrations in the extracellular space are fixed, the volume and intracellular ion concentrations of a passive GD cell are uniquely defined by the extracellular environment, irrespective of the ion concentrations within an intervening volume containing fixed charges.
However, ions are not distributed in a purely passive manner in a real cell, and it is therefore necessary to consider the consequences of a charged glycocalyx upon intracellular ionic homeostasis in a more physiologically accurate model cell. This required a method for the calculation of ion concentrations at the outer membrane surface. An immediate theoretical difficulty is that classical GC theory predicts total ion concentrations at the membrane surface that are significantly greater than those in the bulk extracellular space. However, the distribution of charges within a three-dimensional glycocalyceal volume raises the possibility that any such changes in local total ion concentration might influence osmotic water movements and therefore glycocalyceal volume.
The relationships between glycocalyceal fixed charge, volume, and electrical potential
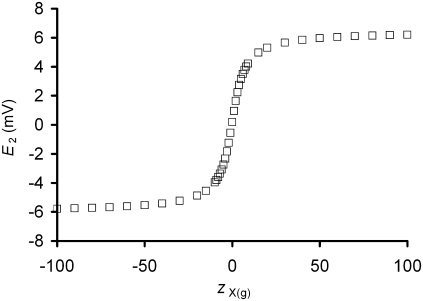
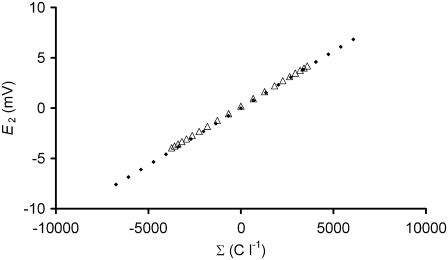
The theoretical approach presented here was developed because the glycocalyx is thick enough in skeletal muscle (some 40–80 nm) to require consideration as a three-dimensional volume rather than as a two-dimensional layer. The GD approach derived in Methods thus incorporates the concept of an osmotically determined glycocalyx volume. With this approach, the glycocalyx charge density (Σg) and potential (E2) are dependent variables influenced by the charge valency/osmole of the glycocalyx (zX(g)). Fig. 2 demonstrates this predicted relationship between E2 and zX(g) for a compartment with a stable osmotic content of molecules (Xg) of mean charge valency/osmole zX(g), but which has a volume determined by osmotically driven water movements and thus a variable concentration of Xg at steady state. The influence of osmotic water movements may be seen by comparison of the predictions of this GD-based approach with those of classical GC theory. To permit comparison of the relationship between the three-dimensional GD approach derived here and two-dimensional GC theory, Appendix 1 shows a derivation of the GC equation using conservation principles similar to those used to derive the GD-based equations. It shows that the novel GD equations reduce to a classical GC function in the limit of an adsorptive layer of zero thickness. Thus, Fig. 3 plots E2 against Σg from both the GC equation and the GD approach derived here, demonstrating an identical predicted relationship between Σg and E2 by each approach. However, because Σg = FzX(g)[X]g and [X]g decreases as the magnitude of zX(g) increases (Eq. 12), Σg is constrained to a limited range of values at steady state in GD theory. Thus, although both approaches demonstrate a similar relationship between Σg and E2, GD theory additionally suggests a limitation on the physically possible values of Σg. This limitation derives from the alterations in glycocalyceal volume predicted by the GD approach after changes in the value of zX(g).
FIGURE 2.
The influence of zX(g) upon E2 in a system at osmotic equilibrium. The GD equation was used to predict E2 from zX(g) in a system where the permitted ratio (η) between total ion concentrations within the glycocalyx relative to that in the bulk extracellular space was 1.03. This demonstrates a steep relationship between zX(g) and E2 when the magnitude of zX(g) is small. In contrast, changes in zX(g) when its magnitude is large have little influence on E2, instead influencing the volume of the glycocalyx such that there is an insignificant increase in the product F(zX(g)[X]g) due to increasing dilution of [X]g.
FIGURE 3.
Comparison of GD and GC predictions of the relationship between Σg and E2. The predicted relationship between Σg and E2 is similar whether using GC theory (solid diamonds) or a GD approach (open triangles). However, GD theory suggests that only certain values of Σg are possible at steady state, as greater initial magnitudes of Σg would result in osmotic swelling of the charged matrix, and hence, reduction in steady-state Σg. This is reflected by the “bunching” of the GD points at higher magnitudes of Σg. This occurs because although each model was initiated with the same 20 evenly spaced values of Σg (GC model) by choosing values of zX(g) that gave equal starting values of FzX(g)[X]g (GD model), the steady-state values of FzX(g)[X]g are osmotically determined in the GD model, whereas Σg is fixed in the GC model.
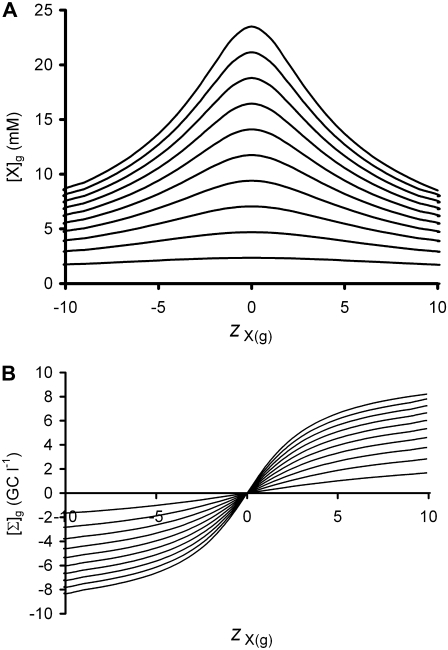
From a theoretical standpoint (Eq. 12), the two variables that would be expected to influence [X]g, and consequently glycocalyceal volume at constant extracellular osmolarity, are zX(g) and η (the mean charge valency of Xg per osmole and the permitted ratio between total ion concentrations in the glycocalyx relative to the bulk extracellular solutions, respectively). Thus, Fig. 4 demonstrates the influences of zX(g) and η upon [X]g (Fig. 4 A) and the resultant value of [Σ]g (Fig. 4 B), the latter being the product FzX(g)[X]g. This demonstrates that higher magnitudes of zX(g) result in reduced steady-state [X]g (Fig. 4 A), hence constraining [Σ]g within limits primarily determined by η (Fig. 4 B). Since, by definition, the glycocalyx contains a fixed quantity of Xg, such reductions in steady-state [X]g predict that increases in the magnitude of zX(g) would increase glycocalyceal volume from a minimum volume when zX(g) = 0.
FIGURE 4.
The influence of zX(g) upon [X]g and Σg at varying η according to Gibbs-Donnan theory. Equation 12 was used to predict the relationship between [X]g (A) or Σg (B) and zX(g) at different values of η. In both panels, the isobars show values of η from 1.01 (lines closest to the x axis) to 1.1 (lines furthest from the x axis) at intervals of 0.01. Note that η = 1 gives [X]g = 0 at any value of zX(g). As demonstrated in A, increases in the magnitude of zX(g) reduce the steady-state value of [X]g for any value of η other than 1. As total glycocalyx Xg content is fixed by definition, this implies that increases in the magnitude of zX(g) produce swelling of the glycocalyx. Furthermore, as the steady-state fixed charge density of the glycocalyx ([Σ]g, in giga-Coulombs/l, or, equivalently, C nl−1) is given by the product FzX(g)[X]g (Eq. 9), such volume changes dampen the influence of zX(g) upon [Σ]g (B), thereby limiting the range of values that [Σ]g may take according to the value of η.
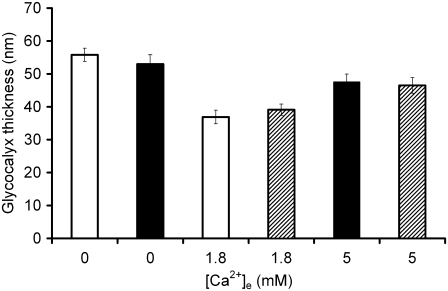
Electron micrographic analyses of glycocalyceal thicknesses after alterations in extracellular Ca2+ were employed to test this hypothesis that glycocalyceal charge and volume are related. Fig. 5 demonstrates the influence of extracellular [Ca2+] upon glycocalyceal volume. Pairs of cutaneous pectoris muscles obtained from different frogs were exposed to each condition of [Ca2+]e. This demonstrated that there was no significant variation in glycocalyceal thickness, or in the relationship of this thickness to [Ca2+]e, between muscle fibers from different frogs (p > 0.05 in each case). In contrast, pairs of cutaneous pectoris muscles obtained from the same frogs were exposed to different conditions of [Ca2+]e and demonstrated increased glycocalyceal thicknesses after both increases (to 5 mM) and decreases (to nominally zero) in [Ca2+]e.
FIGURE 5.
The influence of extracellular [Ca2+] upon glycocalyceal thickness. Glycocalyceal thicknesses were measured from electron micrographs of fixed cutaneous pectoris muscles as described in Methods. Pairs of muscles obtained from the same frog then exposed to different experimental conditions are depicted with similar shading. Two muscles from different frogs were exposed to each extracellular Ca2+ concentration. There was no significant difference between glycocalyceal thicknesses within each condition (p > 0.05 in each case). In contrast, both increases (to 5 mM) and decreases (to nominally zero) from normal (1.8 mM) [Ca2+]e produced significant (p < 0.01) increases in glycocalyceal thickness. Thus, variation between conditions was significant even with muscles from the same animal, but there was no significant variation within conditions even with muscles obtained from different animals.
The biphasic relationship between [Ca2+]e and glycocalyceal thickness observed experimentally parallels the relationship between zX(g) and [X]g shown in Fig. 4. Thus, a possible hypothesis for the observed increases in glycocalyceal diameter in response to both increases and decreases in [Ca2+]e from its normal value may be that both maneuvers increase the magnitude of zX(g). In other words, the results suggest that zX(g) may become more negative in low [Ca2+] and more positive in high [Ca2+] from an initially intermediate value, and that this is reflected in the observed volume changes. The correspondence between the experimentally observed influence of [Ca2+]e on glycocalyceal volume and the theoretical predictions permits the use of the GD analysis in the further computational studies.
The influence of glycocalyceal potential upon intracellular ion concentrations and Em
The CD model of Fraser and Huang (5) was modified as described in Methods to include the glycocalyx GD formulation, thereby allowing simulation of the influence of glycocalyceal charge upon intracellular ion concentrations. Thus, transmembrane ion fluxes were calculated in the CD model from the electrochemical gradients between the bulk intracellular space and the glycocalyx, while the potential and ion concentrations within the glycocalyx were calculated using the GD analysis. Thus, Fig. 6 demonstrates CD modeling of the influence of glycocalyceal charge upon a model resting cell with ion channel and pump density parameters within the physiological range for skeletal muscle. It shows that under physiological conditions, the model predicts that zX(g) influences E1 and E2, but not Em (Fig. 1).
FIGURE 6.
Charge-difference modeling of the influence of glycocalyceal charge upon steady-state transmembrane potentials. CD modeling was used to assess the influence of glycocalyceal fixed charge valency (zX(g)) upon transmembrane potentials. Negative fixed charges cause negative glycocalyceal potentials (E2) and relative depolarization of E1 such that Em is unchanged, whereas positive fixed charges produce positive surface potentials and hyperpolarization of E1, again leaving Em unchanged. Note that large magnitudes of E2 are prevented because osmotic swelling of the glycocalyx reduces fixed charge density as zX(g) increases. As shown in Fig. 4, higher magnitudes of η permit higher magnitudes of fixed charge density and hence increase the influence of zX(g) upon E2.
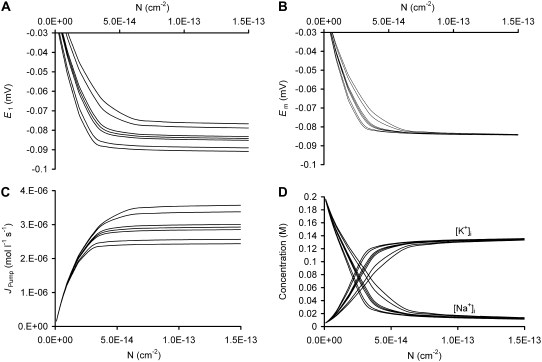
Fig. 7, A–D, shows an extension of the theoretical analysis to explore the influence of zX(g) upon critical cellular parameters E1, Em, Na+/K+-ATPase activity (JPump), and intracellular [Na+] and [K+], respectively, for model cells with a range of values for the Na+/K+-ATPase density (N). It shows that in all cases, values of N above a certain threshold have very little influence on any modeled parameter. This is because the magnitudes of Em and the transmembrane ion gradients are then close to their respective maxima and are therefore determined by the thermodynamic constraints upon Na+/K+-ATPase activity (10) rather than by N. When N is high, more negative values of zX(g) both increase the steady-state Na+/K+-ATPase activity and depolarize E1, whereas more positive values have the opposite influence. However, despite this significant influence upon E1, zX(g) at higher values of N has very little influence on Em. Very low values of N are not compatible with cell stability. It is only when N is at an intermediate value—adequate for cellular stability while permitting little increase in pump activity—that zX(g) may significantly influence Em.
FIGURE 7.
The predicted influence of glycocalyceal charge upon steady-state transmembrane potentials and Na+/K+-ATPase activity. Charge-difference modeling was used to assess the influence of membrane effective Na+/K+-ATPase density (N) upon steady-state E1 (A), Em (B); Na+/K+-ATPase activity (JPump) (C), and [K+]i and [Na+]i (D) in model muscle fibers with differing glycocalyceal charges from zX(g) = −100 (A–C, upper lines, and D, outer lines) to zX(g) = +100 (A–C, lower lines, and D, inner lines) in logarithmic intervals (thus, from top to bottom, or outside to inside, zX(g) = −100, −10, −1, 0, 1, 10, and 100). η = 1.03 in each case. Note that greater values of η increase the influence of changes in zX(g) in each case (data not shown), similar to the influence shown in Fig. 4. More negative values of zX(g) produce depolarization of E1 (A) and higher steady-state Na+/K+-ATPase activity (C). However, only at lower values of N does this influence Em (B). Note that very low values of N are insufficient to maintain a stable cell in all cases, as shown (D) by the increase in the sum of [K+]i and [Na+]i, reflecting reduced [X]i, secondary to cell swelling.
Within this intermediate range of values of N, the influence of zX(g) upon Em is increased significantly. This is reflected by a relative depolarization of both E1 and Em at more negative values of zX(g). The suggestion from Fig. 7 that zX(g) has its greatest influence upon Em under conditions where Na+/K+-ATPase activity is adequate for cellular stability despite lacking excess capacity invites the question of whether the value of N is within this intermediate range physiologically. This is unlikely to be the case under normal conditions in skeletal muscle, which is known to have a significant excess Na+/K+-ATPase capacity (16). However, conditions that reduce Na+/K+-ATPase activity or increase demand for Na+/K+-ATPase activity might nevertheless push the effective value of N into the range within which zX(g) has a significant influence upon Em.
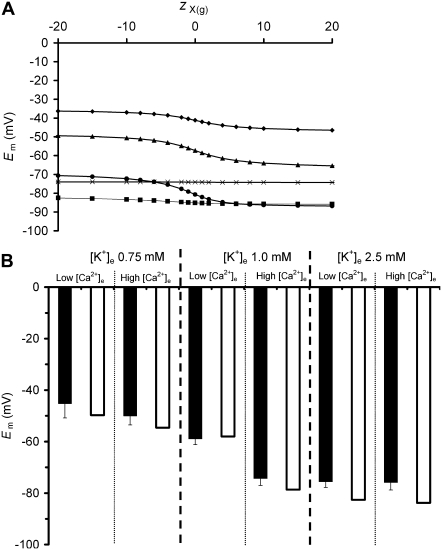
Fig. 8 demonstrates one such manipulation of extracellular conditions. It shows the influence of changes in extracellular [K+] upon Em. This is a maneuver expected to decrease the energetic favorability of Na+/K+-ATPase activity, while also increasing passive transmembrane leak currents. Fig. 8 A demonstrates the results of charge-difference modeling of the influence of zX(g) upon Em at different values of [K+]e from 5 mM to 0.75 mM for a model cell with a constant value of N within the physiological range for skeletal muscle. At higher values of [K+]e of 5 mM and 2.5 mM (Fig. 8 A, crosses and squares, respectively), zX(g) has little influence upon Em, although, as expected, the lower value of [K+]e produces a more polarized model cell. This lack of influence of zX(g) upon Em reflects the fact that Na+/K+-ATPase activity is able to increase at more negative values of zX(g), thus largely offsetting the resultant increase in leak currents. However, further reduction in [K+]e to 1.5 mM or 1 mM permitted two further observations. First, relative depolarization of Em was seen with reductions in [K+]e at certain (with 1.5 mM [K+]e) or all (with 1 mM [K+]e) values of zX(g). This results primarily from a reduction in Na+/K+-ATPase activity at low values of [K+]e. Second, this reduction in Na+/K+-ATPase activity had the effect of pushing N into the window of values within which zX(g) was able to have a significant influence on Em, such that more negative values of zX(g) produced depolarization. In contrast, this effect was not seen in solutions of higher [K+]e. Finally, when [K+]e was reduced further, the influence of zX(g) upon Em was also reduced, reflecting severe limitation of Na+/K+-ATPase activity at all values of zX(g).
FIGURE 8.
The influence of zX(g) on the relationship between extracellular [K+] and Em compared with the effects of corresponding alterations in [Ca2+]e. (A) Charge-difference modeling of the influence of five different concentrations of [K+]e (diamonds, 0.75 mM; triangles, 1 mM; circles, 1.5 mM; squares, 2.5 mM; and crosses, 5.0 mM) upon steady-state Em. Note that zX(g) has little influence on Em at 5.0 or 2.5 mM [K+]e, provokes a maximum of ∼10 mV difference at 0.75 mM [K+]e, and can produce 20 mV shifts in Em at intermediate [K+]e values of 1 to 1.5 mM. (B) Comparison of model predictions (open bars) to experimental data (solid bars) for normal (1.8 mM) versus low (nominally zero) [Ca2+]e solutions over a range of [K+]e. The experimental data demonstrate a significant (p < 0.01) depolarization of Em in low compared with normal [Ca2+]e solutions at 1 mM [K+]e, but no significant difference in Em (p > 0.01) in the different [Ca2+]e conditions at normal or very low values of [K+]e, confirming model predictions.
Fig. 8 B compares predictions from CD modeling with the influence of experimental manipulations of extracellular [K+] and [Ca2+]. The influence of [K+]e upon mean values of Em measured between 150 and 300 min after transfer from control to experimental solutions was explored in solutions of normal (1.8 mM) or low (nominally zero) [Ca2+]e. These values were compared to CD modeling of similar manipulations of [K+]e in model cells with zX(g) = −10 to mimic the low [Ca2+]e case, and zX(g) = +10 to mimic the 1.8 mM [Ca2+]e case. These values are necessarily semiarbitrary because the values of several other key parameters are not known precisely (particularly η and N). Nevertheless, the use of relatively arbitrary parameters is justified for two reasons. First, the findings are of qualitative value, suggesting that reductions in [Ca2+]e and more negative values of zX(g) have similar effects on Em, as expected. Second, as shown by Figs. 4, 6, and 7 in particular, although the magnitude of the influence of zX(g) upon Em is influenced by the values of η and N, the direction of this influence is not. Therefore, it is possible to conclude that, for example, were η higher than the value of 1.03 used in Fig. 8, smaller changes in zX(g) would be necessary to achieve the same influence upon Em. In contrast, there is no way in which, for example, a more negative value of zX(g) could cause hyperpolarization. Thus, although Fig. 8 cannot demonstrate precise quantitative agreement between theory and experiment, it does provide qualitative support for the theoretical predictions. In so doing, it demonstrates that low extracellular [Ca2+] might be expected to aggravate the depolarizing influence of very low extracellular [K+]. This provides some experimental support for the prediction that the influence of reduced Na+/K+-ATPase activity, in ischemia for example, might be exacerbated by low extracellular [Ca2+].
DISCUSSION
Em, the electrical potential recorded using intracellular microelectrodes with reference to the bulk extracellular potential, comprises two distinct components: a potential difference across the membrane itself (E1) and a potential difference between a region containing fixed charges on or near the outer membrane surface and the bulk extracellular space (E2). In such a scheme, it is the E1 component that constitutes the transmembrane potential actually sensed by integral membrane proteins such as voltage-gated ion channels (3). Previous studies have shown that alterations in extracellular Ca2+ reciprocally influence both the voltages, E1 and E2, without altering Em, at least in the short term (1,3,4). However, over longer periods of time, such changes might be expected to influence transmembrane ion fluxes, intracellular ion concentrations, and, hence, Em. This study therefore investigated the influence of extracellular fixed charges upon intracellular ionic homeostasis. It used a novel computational model to explore the effect of alterations in extracellular fixed charge upon intracellular ion concentrations and, hence, Em. The predictions of the model were corroborated by electrophysiological and morphological cellular methods.
A mathematical approach was developed that permitted analytic calculation of the influence of near-surface charges fixed in a layer of nonzero thickness, such as the glycocalyx, upon E2 and local ion concentrations. This theoretical analysis predicted a dependence of glycocalyceal volume upon extracellular [Ca2+], secondary to the influence of fixed charge magnitude upon the concentration of mobile ions within the glycocalyx. Electron micrograph studies showed that glycocalyceal volume was influenced by alterations in extracellular [Ca2+], supporting this theoretical prediction.
The influence of glycocalyceal charge adsorption upon intracellular ionic homeostasis was then explored. The mathematical treatment of the glycocalyx was combined with the CD cellular model of Fraser and Huang (5,7,8), yielding a model that was used to predict the influence of alterations in glycocalyceal charge upon steady-state electrophysiological variables under a variety of conditions. The detailed analysis predicted that although glycocalyceal charge does not influence intracellular ionic homeostasis under normal physiological conditions, thereby leaving Em unchanged, similar charge effects do significantly influence Em under conditions where the Na+/K+-ATPase is moderately challenged.
Experimental measurements of Em in frog skeletal muscle followed these theoretical predictions closely. Thus, Em values were stable over extended periods of time (up to 5 h) despite reductions in extracellular [Ca2+] sufficient to produce a more negative glycocalyceal charge. However, the CD modeling suggested that such stability of Em would have required an increase in Na+/K+-ATPase activity. This is because more negative glycocalyceal charge causes an increase in near-membrane [Na+] and [K+] that produces a small but significant increase in the transmembrane leak currents of each of these ions according to the Goldman current equation (17,18). CD modeling demonstrated that an increase in Na+/K+-ATPase activity, almost sufficient to compensate for the increased leak currents, would be expected to occur due to the influence of the depolarization of E1 and the fundamental properties of the Na+/K+-ATPase in model cells with physiological membrane Na+/K+-ATPase density (10). However, in model cells with reduced Na+/K+-ATPase density, Na+/K+-ATPase activity was not able to increase sufficiently to counteract the increased leak fluxes. Consequently, these cells showed a net loss of [K+]i, a net increase in [Na+]i, and depolarization of Em.
Similarly, CD modeling showed that a reduction in extracellular [K+] could reduce Na+/K+-ATPase activity sufficiently to prevent an adequate compensatory increase in Na+/K+-ATPase activity from occurring in model cells with more negative glycocalyceal charge. Thus, model cells exposed to both a decrease in [K+]e and a more negative glycocalyceal charge demonstrated a diminution of [Na+] and [K+] gradients and a depolarization of Em with respect to control cells, whereas neither of these maneuvers individually caused depolarization of Em. This effect was observed at [K+]e levels of around 1 mM: lower levels caused depolarization irrespective of glycocalyceal charge due to near-complete Na+/K+-ATPase suppression; higher levels allowed Na+/K+-ATPase activity to increase in response to depolarization of E1.
Such theoretical predictions were fulfilled during experimental exposures of frog skeletal muscle fibers to a range of [K+]e in the presence of normal and reduced [Ca2+]e. Thus, reduction in extracellular [Ca2+] produced depolarization of Em over time only in muscle fibers also exposed to intermediate concentrations of 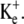 The experimental results thus supported the finding of the model that limitation of Na+/K+-ATPase activity by exposure to low [K+]e leaves insufficient reserve Na+/K+-ATPase activity to compensate for the increased transmembrane leak currents provoked by a more negative glycocalyceal charge in solutions of reduced [Ca2+]e. This finding that glycocalyceal charge can influence intracellular ion concentrations contrasts with assumptions made in the existing literature (4). It suggests, for the first time, that more negative extracellular fixed charge increases Na+/K+-ATPase activity and thereby ATP usage.
The experimental results thus supported the finding of the model that limitation of Na+/K+-ATPase activity by exposure to low [K+]e leaves insufficient reserve Na+/K+-ATPase activity to compensate for the increased transmembrane leak currents provoked by a more negative glycocalyceal charge in solutions of reduced [Ca2+]e. This finding that glycocalyceal charge can influence intracellular ion concentrations contrasts with assumptions made in the existing literature (4). It suggests, for the first time, that more negative extracellular fixed charge increases Na+/K+-ATPase activity and thereby ATP usage.
This study thus demonstrates that under normal physiological conditions, extracellular fixed charges do not significantly influence intracellular ion concentrations or Em, despite their known influence upon the true transmembrane electrical potential (E1) (4). However, it also shows that more negative extracellular fixed charges tend to increase passive ion leak currents and Na+/K+-ATPase activity. This would be expected to increase the metabolic demand upon the cell, or result in cellular K+ loss and hence depolarization of Em if Na+/K+-ATPase activity was initially near-maximal. These novel findings have possible implications for the influence of [Ca2+]e upon cells with reduced sodium pump reserve, such as in ischemic tissues, in cardiac failure (12), and under conditions of reduced extracellular [K+].
Acknowledgments
A.R.M. thanks the Caius Medical Association, Gonville and Caius College, Cambridge, United Kingdom, for support. C.L.-H.H. thanks the Medical Research Council for project and Co-operative Group Grants, and the British Heart Foundation and the Wellcome Trust for project grant support; J.A.F. acknowledges the support of a Research Fellowship from Gonville and Caius College, Cambridge.
APPENDIX 1: DERIVATION OF THE RELATIONSHIP BETWEEN THE GOUY-CHAPMAN EQUATION AND THE GIBBS-DONNAN ANALYSIS
The GD analysis considers fixed charges distributed within a three-dimensional volume of space. In contrast, the classical GC equation treats surface charges as being distributed within a two-dimensional layer. It is instructive to compare the predictions of the two approaches, not least because a large body of experimental evidence is in agreement with the GC equation under appropriate conditions (9).
To compare such a two-dimensional approach with the three-dimensional approaches considered above, it is helpful to rederive the GC equation using the same assumptions that were employed above to calculate E2 by the GD analysis. Thus, the electroneutrality constraint is given by
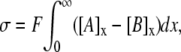 |
where σ represents surface charge density over a two-dimensional surface (C m−2) and x denotes distance from the membrane such that the membrane surface is at x = 0. Ψx is thus the potential at a distance x from the charged surface, such that Ψ0 is equivalent to E2. At equilibrium, combining this electroneutrality condition with the requirement of zero net fluxes gives
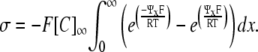 |
Ψx may then be obtained from the Boltzmann distribution and the Poisson-Boltzmann equation (2):
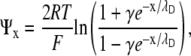 |
where 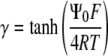 and the Debye length,
and the Debye length, 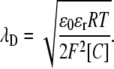
Note that the Debye length is often taken to be the thickness of the diffuse double layer (2). As shown in full in the purely mathematical argument in Appendix 2, evaluation of the integral gives the GC equation (9):
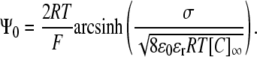 |
Comparison of the GC equation and Eq. 13 reveals several features of the relationship between potentials generated by two- and three-dimensional charge distributions, respectively. Such a comparison is facilitated if the GC equation is restated in terms of λD:
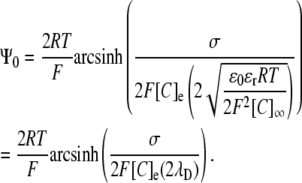 |
In this form, the similarities with Eq. 5 become clear:
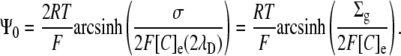 |
Thus, a charge density expressed in two dimensions (C/m2) may be divided by double the Debye length to give an equivalent charge in three dimensions. The latter then produces double the surface potential as would the same concentration of charge in a thick layer. The division of the charge density by double the Debye length is essentially equivalent to integrating the local potential, Ψ, resulting from the charge density over distance, x, from the membrane. The resultant potential is twice that produced by an equivalent density in a layer of thickness significantly greater than the Debye length, reflecting the influence of the low-permittivity membrane in Gouy-Chapman theory. Thus, according to Debye-Hückel theory (2), the potential produced by a given membrane charge at a distance, r, from the membrane, is approximately twice that produced at a similar distance from a similar charge in the bulk extracellular space. This is because ɛm/ɛe (the permittivity of the membrane relative to that of the extracellular solution) is small.
The above equation may be solved for either σ or Σg to compare the three-dimensional GD approach with the two-dimensional GC approach:
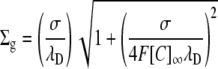 |
or
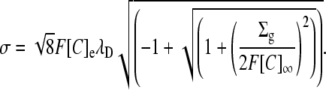 |
These equivalencies were used in Fig. 3 to express σ in terms of the equivalent three-dimensional charge concentration to demonstrate the relationship between E2 and Σg using the GD and the GC approaches.
APPENDIX 2: EVALUATION OF THE SURFACE CHARGE INTEGRAL
For simplicity, the inverse Debye length, κ = 1/λD, is used in the derivation
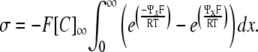 |
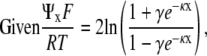 |
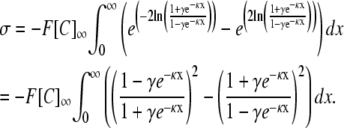 |
Using integration by substitution:
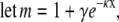 |
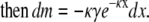 |
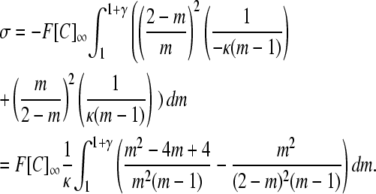 |
Expressing as partial fractions:
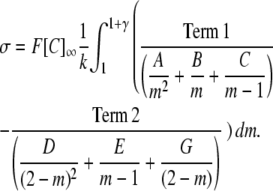 |
Evaluating the partial fraction coefficients:Term 1:
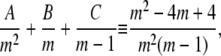 |
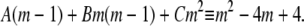 |
Comparing coefficients in:
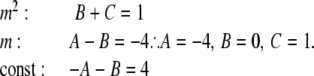 |
Evaluating the partial fraction coefficients:Term 2:
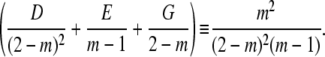 |
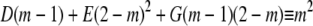 |
Comparing coefficients in:
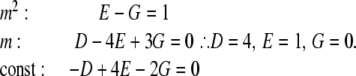 |
Substituting back:
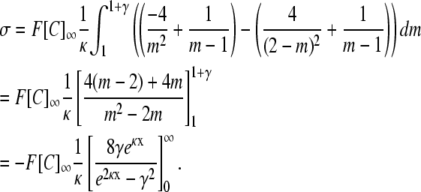 |
Since 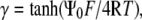 and letting
and letting 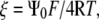 evaluation of the integral gives:
evaluation of the integral gives:
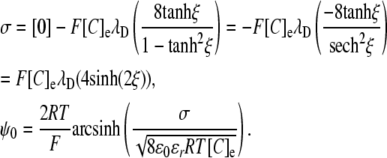 |
Editor: Dorothy A. Hanck.
References
- 1.Chandler, W. K., A. L. Hodgkin, and H. Meves. 1965. The effect of changing the internal solution on sodium inactivation and related phenomena in giant axons. J. Physiol. 180:821–836. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Israelachvili, J. 1991. Electrostatic forces between surfaces in liquids. In Intermolecular and Surface Forces. Academic Press, New York. 213–259.
- 3.Hille, B. 1973. Potassium channels in myelinated nerve. Selective permeability to small cations. J. Gen. Physiol. 61:669–686. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Frankenhaeuser, B., and A. L. Hodgkin. 1955. The effect of calcium on the sodium permeability of a giant nerve fibre. J. Physiol. 128:40–1P. [PubMed] [Google Scholar]
- 5.Fraser, J. A., and C. L. Huang. 2004. A quantitative analysis of cell volume and resting potential determination and regulation in excitable cells. J. Physiol. 559:459–478. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Fraser, J. A., and C. L. Huang. 2007. Quantitative techniques for steady-state calculation and dynamic integrated modelling of membrane potential and intracellular ion concentrations. Prog. Biophys. Mol. Biol. 94:336–372. [DOI] [PubMed] [Google Scholar]
- 7.Fraser, J. A., C. E. Middlebrook, J. A. Usher-Smith, C. J. Schwiening, and C. L. Huang. 2005. The effect of intracellular acidification on the relationship between cell volume and membrane potential in amphibian skeletal muscle. J. Physiol. 563:745–764. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Fraser, J. A., C. E. Rang, J. A. Usher-Smith, and C. L. Huang. 2005. Slow volume transients in amphibian skeletal muscle fibres studied in hypotonic solutions. J. Physiol. 564:51–63. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.McLaughlin, S. 1989. The electrostatic properties of membranes. Annu. Rev. Biophys. Biophys. Chem. 18:113–136. [DOI] [PubMed] [Google Scholar]
- 10.Hernandez, J., J. Fischbarg, and L. S. Liebovitch. 1989. Kinetic model of the effects of electrogenic enzymes on the membrane potential. J. Theor. Biol. 137:113–125. [DOI] [PubMed] [Google Scholar]
- 11.Lindinger, M. I., R. G. Willmets, and T. J. Hawke. 1996. Stimulation of Na+, K+-pump activity in skeletal muscle by methylxanthines: evidence and proposed mechanisms. Acta Physiol. Scand. 156:347–353. [DOI] [PubMed] [Google Scholar]
- 12.Schwinger, R. H., J. Wang, K. Frank, J. Muller-Ehmsen, K. Brixius, A. A. McDonough, and E. Erdmann. 1999. Reduced sodium pump alpha1, α3, and β1-isoform protein levels and Na+, K+-ATPase activity but unchanged Na+-Ca2+ exchanger protein levels in human heart failure. Circulation. 99:2105–2112. [DOI] [PubMed] [Google Scholar]
- 13.Koutsis, G., A. Philippides, and C. L. Huang. 1995. The afterdepolarization in Rana temporaria muscle fibres following osmotic shock. J. Muscle Res. Cell Motil. 16:519–528. [DOI] [PubMed] [Google Scholar]
- 14.Adrian, R. H. 1956. The effect of internal and external potassium concentration on the membrane potential of frog muscle. J. Physiol. 133:631–658. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Elliott, G. F., and S. A. Hodson. 1998. Cornea, and the swelling of polyelectrolyte gels of biological interest. Rep. Prog. Phys. 61:1325–1365. [Google Scholar]
- 16.Clausen, T. 1986. Regulation of active Na+-K+ transport in skeletal muscle. Physiol. Rev. 66:542–580. [DOI] [PubMed] [Google Scholar]
- 17.Goldman, D. E. 1943. Potential, impedance and rectification in membranes. J. Gen. Physiol. 27:37–60. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Hodgkin, A. L., and B. Katz. 1949. The effect of sodium ions on the electrical activity of the giant axon of the squid. J. Physiol. 108:37–77. [DOI] [PMC free article] [PubMed] [Google Scholar]