Modulating Temporal Control of NF-κB Activation: Implications for Therapeutic and Assay Selection

Abstract

The activation of transcription factor NF-κB (nuclear factor-κB) plays a central role in the induction of many inflammatory response genes. This process is characterized by either oscillations or stable induction of NF-κB nuclear binding. Changes in dynamics of binding result in the expression of distinct subsets of genes leading to different physiological outcomes. We examined NF-κB DNA binding activity in lipopolysaccharide (LPS)-stimulated IC-21 cells by electromobility shift assay and nonradioactive transcription factor assay and interpreted the results using a kinetic model of NF-κB activation. Both assays detected damped oscillatory behavior of NF-κB with differences in sensitivity and reproducibility. 3,4-Dichloropropionaniline (DCPA) was used to modulate the oscillatory behavior of NF-κB after LPS stimulation. DCPA is known to inhibit the production of two NF-κB-inducible cytokines, IL-6 and tumor necrosis factor α, by reducing but not completely abrogating NF-κB-induced transcription. DCPA treatment resulted in a potentiation of early LPS-induced NF-κB activation. The nonradioactive transcription factor assay, which has a higher signal/noise ratio than the electromobility shift assay, combined with in silico modeling, produced results that revealed changes in NF-κB dynamics which, to the best of our knowledge, have never been previously reported. These results highlight the importance of cell type and stimulus specificity in transcription factor activity assessment. In addition, assay selection has important implications for network inference and drug discovery.

INTRODUCTION

Nuclear factor-κB (NF-κB) is a family of structurally related and evolutionarily conserved proteins related to the proto-oncogene c-rel. In mammals, the family of NF-κB proteins includes Rel (cRel), RelA (p65), RelB, NF-κB1 (p50), and NF-κB2 (p52) (1). Homo- and heterodimers of these NF-κB proteins combine to form active and repressive complexes of gene transcription. The p50/p65 heterodimer of NF-κB is the most frequently studied and most abundant complex in cells (2). In resting cells, NF-κB is maintained inactive in the cytoplasm complexed with its inhibitors (IκBs), which exist in three isoforms, IκBα, β, and ɛ (2). Upon activation through a variety of receptor signaling pathways, including the toll-like receptor (TLR) 4 and tumor necrosis factor (TNF) receptor family members, IκBs undergo phosphorylation, ubiquitination and proteolytic degradation (1,3). Phosphorylation of the IκBs is regulated by a multisubunit kinase, termed IκB kinase (IKK), which contains two catalytic subunits, IKKα and IKKβ, and a regulatory subunit IKKγ (4). Proteolytic degradation of IκBs allows for rapid translocation of free NF-κB from the cytoplasm to the nucleus. While in the nucleus, active NF-κB binds to DNA and promotes the transcription of multiple genes, including the autoinhibitor IκBα. Newly synthesized IκBα enters the nucleus, where it binds to NF-κB, thereby enhancing NF-κB's dissociation from the DNA and causing its reexportation to the cytoplasm, where it joins the pool of inactive NF-κB complexes (1). Continuous cycling of IκBα degradation and resynthesis results in oscillations in NF-κB activity (5). Moreover, due to the importance of aberrant activation of NF-κB in a variety of diseases, more than 780 compounds have been identified that modulate NF-κB activation (6). As illustrated by efforts to recapitulate temporal regulation of the NF-κB pathway using mathematical models, e.g., by Hoffmann et al. (5), the dynamics of this process has been the subject of intense scientific scrutiny (7). However, how therapeutics modulate the dynamics of the activation of NF-κB is still unknown.

Present in all body compartments, macrophages initiate an innate immune response to bacterial pathogens through phagocytosis, thereby eliminating them by the generation of reactive oxygen and reactive nitrogen species (8,9). Macrophages also activate T lymphocytes by acting as a professional antigen-presenting cell and secreting cytokines, such as IL-6 and TNF-α (10). These cytokines are important early mediators of acute inflammatory responses contributing to downstream lymphocyte activation (11,12). Due to their importance in immune surveillance, macrophages provide a highly relevant context for the study of NF-κB.

The effects of 3,4-dichloropropionaniline (DCPA) on the immune response have been studied extensively, and its ability to suppress various macrophage functions has been characterized. It has been demonstrated that DCPA decreases both the phagocytic activity of macrophages and their ability to generate both reactive oxygen and reactive nitrogen species (13). The production of inflammatory cytokines such as TNF-α, IL-1β, and IL-6 was also decreased (14,15). A study of the effects of DCPA on the steady-state levels of NF-κB activation demonstrated a decreased nuclear localization of NF-κB accompanied by a reduced, but not entirely abrogated, binding to DNA (16).

DNA binding of activity transcription factor can be determined by different methods. The electromobility shift assay (EMSA) detects complexes of protein (e.g., NF-κB) and ³²P-labeled DNA containing transcription factor consensus sequences migrating through a nondenaturing polyacrylamide gel (17,18). DNA-protein complexes will migrate more slowly than unbound radioactive probe and are thus visualized as discrete bands of radioactivity in the upper part of an acrylamide gel image (19,20). This technique is labor-intensive and requires radioactivity.

The nonradioactive transcription factor assay (NTFA) technique employs the principle of EMSA, where protein/DNA interaction is observed in an enzyme-linked immunosorbent assay format (21–23). Active NF-κB is captured as it binds to its nonradioactive DNA consensus sequence, which has been immobilized on a streptavidin-coated plate. The transcription factor that formed complexes with DNA is then probed with specific primary antibody (anti-p65) followed by HRP-conjugated secondary antibody and substrate detection. This method makes possible the sampling of a larger number of tests in a shorter period of time and does not require radioactive labeling.

This study explores the initial phase of NF-κB oscillatory behavior induced in lipopolysaccharide (LPS)-stimulated macrophages by means of two independent methods commonly used for quantifying the binding activity of transcription factors. Immunosuppressant DCPA is used to modulate NF-κB activity and is incorporated in the dynamic model to demonstrate the changes in transcription factor activation.

METHODS

Cell culture, stimulation, and DCPA treatment

The murine peritoneal macrophage cell line, IC-21, was cultured in 5% CO₂ at 37°C to 80% confluency in complete RPMI (cRPMI) (BioWhittaker, Walkerville, MD). cRPMI consists of RPMI 1640 supplemented with 10% fetal bovine serum (Hyclone, Logan, UT), L-glutamine (2 mM), penicillin (100 U/ml), streptomycin (100 μg/ml), 2-mercaptoethanol (5 × 10⁻⁵ M), and Hepes buffer (10 mM) (all obtained from Sigma-Aldrich, St. Louis, MO). IC-21 cells were treated with 99% pure DCPA (ChemService, West Chester, PA) and simultaneously stimulated with 1 μg/ml LPS phenol (Sigma-Aldrich) extracted for various times.

The human T cell line, Jurkat clone E6-1, was cultured in 5% CO₂ at 37°C in cRPMI. Jurkat cells were treated with 99% pure DCPA and simultaneously stimulated with plate-bound anti-CD3 and anti-CD28. Anti-CD3-coated plates were prepared by adding 10 mg/ml mouse antihuman CD3 (Ancell, Bayport, MN) to the wells and incubating for 90 min at 37°C, then storing overnight at 4°C. Before the addition of the cells, the unbound anti-CD3 was aspirated out of the wells and the wells were washed three times with sterile phosphate-buffered saline. Jurkat cells were diluted to 1 × 10⁶ cells/ml in cRPMI, and DCPA was added to the cells. Next, the Jurkat cells were added to the anti-CD3-coated wells and 2 mg/ml of anti-CD28 (Ancell) was added to each well. Nuclear extracts were isolated after cells were incubated for the appropriate times.

Appropriate concentrations of DCPA were dissolved in 100% ethanol (Mallinckrodt Baker, Paris, KY) and added to cells at concentrations ranging from 0 to 150 μM. The final ethanol concentration added to all cultures was 0.1%; control cultures received equal concentrations of ethanol.

Nuclear extracts

IC-21 cells were plated at a concentration of 8 × 10⁵ cells in 5 ml of cRPMI in 60-mm dishes and incubated overnight at 37°C 5% CO₂. IC-21 cells were then treated with either 0.1% ethanol or DCPA at concentrations of 25 μM, 100 μM, and 150 μM, and stimulated with 1 μg/ml LPS. IC-21 cells were washed with 2.5 ml ice-cold Dulbecco's phosphate-buffered saline (BioWhittaker) and lysed by adding 200 μl of a buffer (lysis buffer) consisting of 10 mM Hepes, pH 7.9, 10 mM KCl, 0.1 mM EDTA, 0.1 mM EGTA, 1 mM phenylmethylsulfonyl fluoride, 1 mM dithiothreitol (DTT), and 1 μg/ml of the protease inhibitors leupeptin, antipain, chymostatin, and pepstatin A (Sigma-Aldrich). IC-21 cells were scraped off the dishes and lysates were transferred to microcentrifuge tubes. For the Jurkat cells, after anti-CD3/anti-CD28 stimulation, the cells were harvested from the wells by vigorous pipetting followed by centrifugation to pellet the cells. The cells were washed with 2.5 ml ice-cold Dulbecco's phosphate-buffered saline and lysed by adding 200 μl of the lysis buffer. Once in the lysis buffer, all cells were incubated on ice for 15 min. Then, 50 μl of 10% NP-40 was added, samples were vortexed for 30 s, and the lysates were pelleted by centrifugation for 30 s at 14,000 rpm at 4°C. The supernatants (cytoplasmic extracts) were collected and saved at −20°C. Pellets were resuspended in 30 μl of 20 mM Hepes buffer (400 mM NaCl, 1 mM EDTA, 1 mM EGTA, 1 mM phenylmethylsulfonyl fluoride, 1 mM DTT, and 1 μg/ml of the protease inhibitors (see above)), vortexed, and incubated for 15 min on ice. The lysates were pelleted by centrifugation at 14,000 rpm for 5 min under the same conditions and the supernatants containing the nuclear fraction were stored at −70°C. A total protein concentration for nuclear extracts was determined with Coomassie Plus Protein Assay Reagent, as described by the manufacturer (Pierce, Rockford, IL).

Electrophoretic mobility shift assay

NF-κB consensus oligonucleotides (sc-2505, Santa Cruz Biotechnology, Santa Cruz, CA) were labeled with γ-³²P-ATP (PerkinElmer, Boston, MA) using a Ready-To-Go T4 polynucleotide kinase kit (Amersham Pharmacia Biotech, Piscataway, NJ). Nuclear extracts, 5 μg/sample, were incubated with 50,000 cpm of labeled probe and 1 μg/ml dI/dC for 30 min at room temperature in 1 × binding buffer (5 × stock: 250 mM NaCl, 50 mM Tris-Cl, 50% (v/v) glycerol, 5 mM DTT, 2.5 mM EDTA, adjusted to pH 7.6, stored at −20°C) to allow formation of band-shift complexes. Next, complexes were resolved from free probe in 5% polyacrylamide gels (1 × TGE, 5% glycerol, 0.075% ammonium persulfate, 0.1% TEMED). Samples were electrophoresed at 125 V for 4 h, dried on Whatman 3MM paper, and placed on PhosphoImage Screens for analysis with ImageQuant TL Software (Amersham Pharmacia Biotech). The EMSA experimental results are reported as the ratio of the intensity measured for a particular condition (i.e., time > 0) relative to the intensity of NF-κB before treatment (i.e., time = 0).

Transcription factor assay

Nuclear extracts, 5 μg/sample, were analyzed by a Chemicon Non-Radioactive Transcription Factor Assay to determine NF-κB p65 DNA binding activity, as described by the manufacturer (Chemicon International, Temecula, CA). Briefly, nuclear extracts were incubated for 2 h with biotinylated NF-κB consensus DNA sequences in a transcription assay buffer containing sonicated salmon sperm DNA to allow the formation of protein/DNA complexes. Next, NF-κB protein in the nuclear extracts bound to biotinylated consensus sequences was immobilized to the streptavidin-coated plate, and any unbound material was washed away. NF-κB protein was detected with a specific rabbit anti-p65 antibody, followed by incubation with antirabbit HRP-conjugated antibody detected by TMB/E substrate. Absorbance of the samples was measured with a μQuant Universal Microplate Spectrophotometer (Bio-Tek Instruments, Winooski, VT). The NTFA experimental results are reported as the ratio of the absorbance measured for a particular condition (i.e., time > 0) relative to the absorbance before treatment (i.e., time = 0).

NF-κB model development

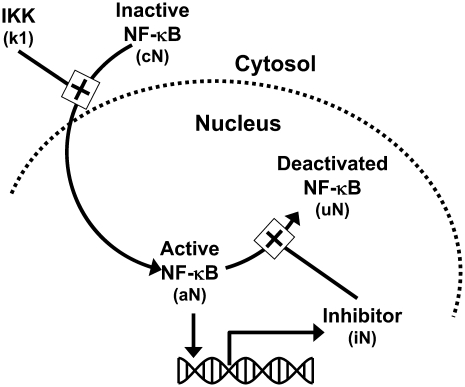
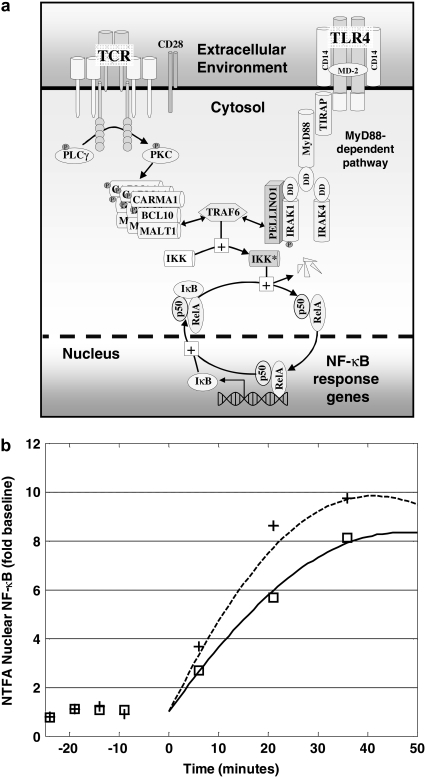
The development of a mathematical model for NF-κB activation was shaped by two primary considerations: 1), the design of experiments that minimize potential sources of biological variability; and 2), the ability to uniquely determine parameter values from replicate measurements. To quantify the effect of DCPA on LPS-stimulated NF-κB activation, we focused on the first 45 min after LPS stimulation (see Discussion). Although more detailed mathematical models for NF-κB have been proposed in the literature (e.g., Hoffman et al. (5)), the experimental objectives of this study required the development of a new mathematical model that has identifiable parameters (see Appendix). This new model implicitly represents a series of biological events that occur within the timeframe of experimental interest. The stimulation of macrophages by LPS results in the activation of the TLR4 pathway (24). The transduction of signals via TLR4 results in the activation of a series of intermediate signaling proteins and ultimately in the activation of IKK. The activation of IKK leads to the liberation of NF-κB from protein complexes with IκB inhibitor proteins. Active NF-κB translocates to the nucleus, where it initiates the transcription of various genes, including the IκB proteins. Newly transcribed and translated IκB proteins reenter the nucleus and deactivate NF-κB. Shown schematically in Fig. 1, the initial dynamics of NF-κB activation after LPS stimulation is represented by the three chemical kinetic equations

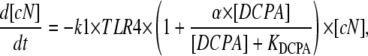(1)

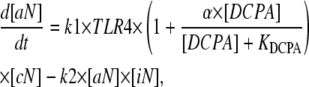(2)

and

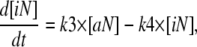(3)

where cN, aN, iN, and DCPA represent the concentrations of inactive NF-κB in the cytosol, active NF-κB in the nucleus, IκBα, and DCPA, respectively. TLR4 is a Boolean variable that is equal to 1 when the cells are stimulated by LPS. As the IC-21 macrophages were continually exposed to LPS, TLR4 is equal to 1 for all of the experiments studied. The dynamic change in NF-κB in the cytosol is represented by Eq. 1, where the impact of IKK on liberating NF-κB and transport to the nucleus is represented by a single parameter k1. We postulate that DCPA modulates the activation of NF-κB with the strength parameter α. A negative value for α signifies that DCPA inhibits the activation of NF-κB, whereas a positive value indicates potentiation. The change in active NF-κB in the nucleus is represented by Eq. 2, where the second term represents the inactivation of nuclear NF-κB by IκBα. The dynamic transcription, translation, reimport to the nucleus of the NF-κB inhibitor protein, IκBα, in response to active NF-κB, and degradation is represented by Eq. 3. Additional terms could be added to these three equations to account for recycling of the NF-κB-IκBα complex to the cytosol. However, inclusion of these additional terms did not improve the fitness of the model within the timeframe of experimental interest (data not shown). The initial normalized concentrations of aN and iN were set equal to 1 and 0, respectively. The estimates for the initial concentration of cN and parameters k1, α, k3, and k4 were determined using these three ordinary differential equations and experimental measurement of active NF-κB in the nucleus. The half-maximal inhibition constant, K_DCPA, was assumed to be 5 μM based on the study by Xie et al. (14). The rate constant for the deactivation of active NF-κB in the nucleus, k2, was assumed to be equal to 0.015 conc⁻¹ min⁻¹. These three ordinary differential equations were evaluated within MatLab V7.1 (MathWorks, Natick, MA). Summed squared error between experimentally measured and simulated values for active NF-κB in the nucleus was used to determine goodness of fit. Optimal values for the parameters were selected using a genetic algorithm and are detailed in Table 1. Parameter values were determined from the combined analysis of all DCPA conditions using a single assay platform (i.e., there are two sets of parameters: θ_EMSA and θ_NTFA). Confidence intervals for the parameters were determined using bootstrap resampling.

FIGURE 1.

Schematic diagram of the mathematical model developed to represent the initial activation of NF-κB.

TABLE 1.

List of variables and parameters for NF-κB activation model

Name	Definition	Assay	Value	95% CI	Units
k1	NF-κB activation rate constant	NTFA	0.0676	(0.0090–0.160)	min−1
		EMSA	0.0686	(0.0104–0.265)	min−1
k2	NF-κB inactivation rate constant	NTFA	0.0150	Assumed	conc−1 min−1
		EMSA	0.0150	Assumed	conc−1 min−1
k3	Synthesis of NF-κB inhibitor rate constant	NTFA	0.0041	(0.0020–0.0139)	min−1
		EMSA	0.0089	(0.0009–0.0407)	min−1
k4	Degradation of NF-κB inhibitor rate constant	NTFA	0.0005	(0.0005–0.0410)	min−1
		EMSA	0.0017	(0.0003–0.282)	min−1
α	Effect of DCPA on NF-κB activation	NTFA	0.480	(0.021–1.53)	Unitless
		EMSA	0.119	(−0.296–0.913)	Unitless
KDCPA	Half-maximum DCPA concentration	NTFA	5	See (14)	μM
		EMSA	5	See (14)	μM
cN	Initial concentration of NF-κB in cytosol	NTFA	53.0	(32.4–292)	conc
		EMSA	17.2	(8.99–88.2)	conc
aN	Initial concentration of active nuclear NF-κB	NTFA	1	Assumed	conc
		EMSA	1	Assumed	conc
iN	Initial concentration of IκBα	NFTA	0	Assumed	conc
		EMSA	0	Assumed	conc
DCPA	Concentration of DCPA	NTFA	0–150	Experimental conditions	μM
		EMSA	0–150	Experimental conditions	μM
TLR4	Stimulation via TLR4 (Boolean variable)	NTFA	1	Experimental conditions	Unitless
		EMSA	1	Experimental conditions	Unitless

Optimal values for initial conditions and parameters were determined using a genetic algorithm. Separate values were determined from dose-escalation measurements obtained using EMSA or NTFA assays. Nonparametric bootstrapping using residual errors provided estimates of confidence intervals. CI, confidence interval; conc, concentration.

Bootstrap resampling: confidence interval estimation

Bootstrap resampling is an effective method for the estimation of confidence intervals of model parameters (25). Let us assume that the experimental measurement of a dynamic system can be described by the equation

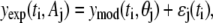(4)

where y_exp(t_i, A_j) is the measured value at time t_i using assay A_j, and θ_j is the vector of model parameters for assay j that are constant with respect to time. A mechanistic model of the dynamic system provides an estimate of the expected biological response, y_mod(t_i, θ_j), at time t_i, given the parameter vector θ_j. The measurement error for a particular assay, or residual, is represented by ɛ_j(t_i) and can be obtained at each time point, t_i. The population of ɛ_j(t_i) determined from the data set is a representative sample of the variability in observing this phenomena experimentally using a particular assay. Analysis of the variance ensures that there are no systematic errors in the residual population.

Experimentally, replication is used to establish significance of an observation. Bootstrap resampling is a computational approach that creates synthetic replicates drawn from the population of residuals. The residuals are first normalized based on the appropriate error model of the experimental assay. Normalization is performed to ensure that the residuals are independent of the dependent variables. Error models for each of the assays (NTFA and EMSA) were based upon an analysis of the residuals. The statistical significance for the difference in the variance of residuals was estimated using the ratio of variances as a test statistic. The test statistic was compared against the F-distribution, where the degrees of freedom were determined from the size of the two groups. A p value of <0.05 was considered statistically significant. Synthetic sets of experimental replicates were created using the following steps. First, optimal values for k1, k3, α, and the initial value for cN were determined based upon the DCPA dose-escalation experiments using either NTFA or EMSA. Second, expected values (y_mod(t_i, θ_j)) were calculated using Eqs. 1–3 (the NF-κB model) and the set of optimal parameters, using either θ_EMSA or θ_NTFA, for every measured experimental condition (y_exp(t_i, A_j)) to yield the residuals, ɛ_j(t_i). The residuals were normalized based upon the error model that corresponds to the particular assay. Finally, a large number (N_boot = 3000) of synthetic data sets (i.e., bootstrapped data sets) that replicate the original experimental protocol were created by sampling, with replacement, from the population of residuals. These resampled residuals are then combined with the expected values (y_mod(t_i, θ_j)) to give new synthetic data sets. A new optimal set of parameter values were determined for the NF-κB model that capture the synthetic DCPA dose-escalation experiments. Each one of the bootstrap data sets yields a novel set of values for k1, k3, α, and the initial value of cN. This collection of optimal values provides an estimate of the 95% confidence intervals for k1, k3, α, and cN(t = 0), shown in Table 1. The reported significance corresponds to the probability that the strength parameter α is positive. The bootstrap approach provides a good estimate of the confidence intervals, comparable to those found with classical statistical techniques, given a sufficiently large bootstrap sample (i.e., N_boot ≥ 1000) and data sample (i.e., N_data ≥ 30) (26). An alternative bootstrapping approach is to resample directly from the population of biological replicates, instead of from the population of residuals. Bootstrap resampling of the biological replicates would require >30 replicates performed at each experimental condition. In this study, each residual value was considered an independent observation. Bootstrap resampling of the residuals was justified as the residuals appeared to be randomly distributed around the expected values within the biological replicates for each DCPA treatment conditions (data not shown).

RESULTS

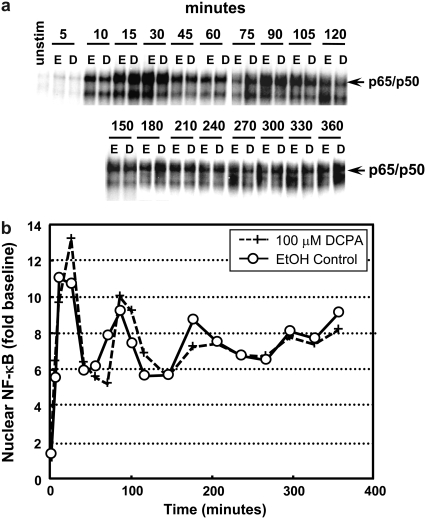
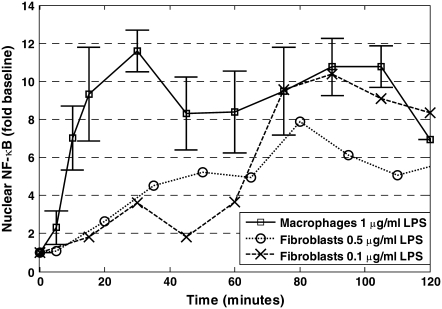
We first wanted to characterize the dynamics of NF-κB activation in macrophage cell line. As shown in Fig. 2, sustained LPS stimulation of a mouse peritoneal macrophage cell line, IC-21, resulted in damped oscillations in NF-κB DNA binding activity. Over a period of 6 h, the dynamic activation of NF-κB was quantified using an EMSA at the indicated time points (Fig. 2 a). IC-21 macrophages were treated with either ethanol (control) or 100 μM DCPA and stimulated with LPS to induce active NF-κB DNA binding. Both treatments demonstrated similar damped oscillations graphically represented in Fig. 2 b (EtOH, solid line, open circles; 100 μM DCPA, dashed line, plus signs). These damped oscillations observed in macrophages are in variance with the findings of Covert et al. (27), which demonstrate sustained NF-κB activation after LPS stimulation in mouse embryonic fibroblasts. Although the EMSA measurements shown in Fig. 2 are representative of the dynamic response in IC-21 macrophages to LPS, significant variability was observed between replicates after the initial peak in NF-κB activation (data not shown). Moreover, observed variability in amplitude of response and frequency of response inhibited the ability to quantify the pharmacological effect of a particular mediator on the dynamics of NF-κB. Based on these findings, we focused subsequent efforts on quantifying the dynamics of NF-κB activation within the first 45 min after LPS stimulation.

FIGURE 2.

Biochemical measurement of oscillations in LPS-stimulated IC-21 macrophages persists after DCPA treatment. (a) Nuclear NF-κB DNA binding activity was assessed by EMSA at the indicated times after sustained stimulation with LPS (1 μg/ml). Macrophages were treated with either ethanol (E) or 100 μM DCPA (D). (b) The specific NF-κB mobility shift phosphoimage was quantified using ImageQuant and normalized to basal levels. Control (○) and DCPA-pretreated (+) macrophages exhibit similar damped oscillatory behavior. Each experiment was performed twice.

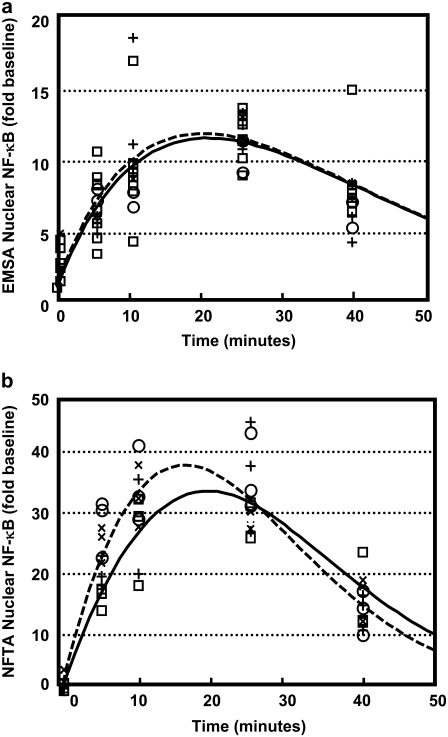
Next, both EMSA and NTFA were used to replicate measurements of active NF-κB in the nucleus at multiple time points during the initial peak of DNA binding activity (0–45 min) in response to LPS stimulation. Fig. 3 a demonstrates multiple replicates of this process using EMSA; for comparison, Fig. 3 b represents the data obtained using NTFA. Both methods demonstrated the initial peak of NF-κB activation, which reached a maximum at 20 min, caused by rapid degradation of IκBα inhibitor, and resulted in maximum DNA binding. Subsequent diminishing of NF-κB binding activity, triggered by a resynthesis of IκBα, is graphically displayed as a decline of the curve. A mathematical model, shown schematically in Fig. 1, incorporating these biochemical steps was created to capture this dynamic behavior. Parameter values that correspond to each of the assays are shown in Table 1. The EMSA measurements obtained from the LPS-induced macrophage cell line are compared with the mathematically simulated EMSA response in Fig. 3 a (ethanol, solid lines; 150 μM DCPA, dashed lines). For comparison, data from NTFA is compared with mathematically simulated NF-κB activation dynamics in Fig. 3 b. The overall kinetics of the underlying biological mechanism observed using the NTFA and EMSA assays are in agreement. The results of the comparison between the two assays revealed that the NTFA exhibits greater sensitivity and reproducibility in measuring active NF-κB relative to the EMSA, as shown by the differences in dynamic ranges observed during the control experiments.

FIGURE 3.

Modeling the potentiation by DCPA of the early activation of NF-κB in IC-21 macrophages after LPS stimulation. The dynamic response in nuclear NF-κB was measured using (a) EMSA and (b) NTFA. The active NF-κB in the nucleus was measured after LPS stimulation and treatment with 0μM (□ ; n = 8 for EMSA; n = 3 for NTFA), 25 μM (○; n = 2 for EMSA; n = 3 for NTFA), 100 μM (+; n = 4 for EMSA, n = 3 for NTFA), and 150 μM (×, n = 1 for EMSA, n = 3 for NTFA) DCPA. The simulated time courses of active NF-κB without and pretreated with 150 μM DCPA are shown as solid and dashed curves, respectively.

To manipulate the dynamics of NF-κB oscillatory behavior, a known immunosuppressant, DCPA, was introduced into the experimental system. IC-21 macrophages were treated with three different doses of DCPA—25, 100, and 150 μM DCPA—and simultaneously stimulated with LPS. To quantify the effect of DCPA on the dynamics of binding activity, we focused on the initial peak of NF-κB activation after LPS stimulation. Both assays were used to characterize alterations in NF-κB binding activity by DCPA in response to LPS stimulation, and experimental results from EMSA and NTFA are shown in Fig. 3, a and b, respectively. Each dosage of DCPA is graphically represented by a different symbol (○, 25 μM; +, 100 μM; ×, 150 μM). The effect of DCPA on the dynamic activation of NF-κB was represented in the mathematical model by modulating the activation rate of NF-κB in the cytosol, k1. The pharmacologic effect of DCPA on the initial activation of NF-κB was quantified by the strength parameter α. Using the EMSA parameter values shown in Table 1, the simulated NF-κB response to LPS after treatment with 150 μM DCPA was compared with the EMSA results in Fig. 3 a. In a similar way, the simulated NTFA measurements after DCPA treatment were compared with the NTFA results in Fig. 3 b. Overall, the simulated responses for both NTFA and EMSA showed agreement with the experimentally measured values. In comparison, the simulated results showed that, compared to EMSA, NTFA is more able to discriminate between macrophages treated with DCPA and controls. These differences were a reflection of the values of α estimated using NTFA versus those estimated using EMSA. The results from both assays suggest that DCPA potentiates the activation of NF-κB at the early time points (0–45 min). Quantitatively, the NTFA results suggest that DCPA increases the activation rate of NF-κB by 48.0% (α = 0.480). In contrast, the EMSA results suggest that DCPA increases the activation rate by 11.9% (α = 0.119).

One of the most important aspects of data analysis is the determination of confidence intervals for model parameters that represent the data. A bootstrap resampling approach applied to the residuals (ɛ_j(t_i)) between the predicted (y_mod(t_i, θ_j)) and measured (y_exp(t_i)) values was used to estimate the confidence intervals of the model parameters. Before applying the bootstrap algorithm, we analyzed the population of residuals in terms of underlying structure. The residuals are assumed to have a Gaussian distribution with a zero mean (i.e., ɛ_j(t_i) ∈ N(0, σ²(t_i, θ_j, λ)). Generally, the variance of residuals, σ²(t_i, θ_j, λ), is a function of time, the model parameters, and a parameter vector that is unique to the variance of assay j, λ_j. The underlying structure in the variance of the residuals is sometimes referred to as the error model. Separate error models were created for the EMSA and NTFA measurements. In this study, we assume that the error model is a linear function of the predicted value:

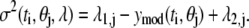(5)

The parameter λ_1,j quantifies the variance that is proportional to the underlying signal being measured for assay j. The λ_2,j parameter quantifies the contribution of a random noise distribution to the error model for assay j. Values for λ_1,j and λ_2,j can be estimated by combining the error model with the equation for the residuals (ɛ_j(t_i) = y_exp(t_i, A_j) − y_mod(t_i, θ_j)) and rearranging terms to yield

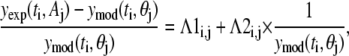(6)

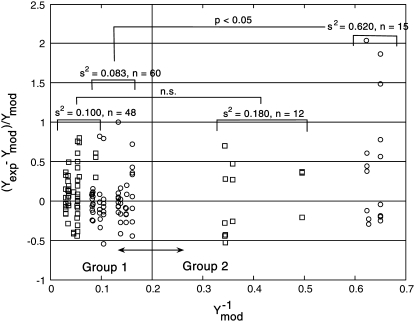
where Λ1_i,j and Λ2_i,j provide estimates of variance parameters λ_1,j and λ_2,j for assay j. The lefthand side of Eq. 6 represents the normalized error values and is plotted against 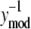in Fig. 4. As identified in Fig. 4, the normalized error values were empirically clustered into two groups based on their respective values of 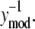The variances of the two groups for each assay are labeled in Fig. 4. The variance compared between the high and low NTFA groups was not statistically significant, whereas the difference between the EMSA groups was significant (p < 0.05). These results suggest that λ₂ = 0 for the NTFA error model and that the residuals are proportional only to the underlying signal (y_mod). In contrast, the variance in the EMSA measurements is proportional to the underlying signal and contains contributions from random noise.

FIGURE 4.

Analysis of the NTFA and EMSA residuals to construct appropriate error models. The difference between experimental measurement (y_exp) and simulated response (y_mod) of active nuclear NF-κB (residual error) after LPS stimulation in IC-21 macrophages is shown as a function of 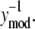EMSA measurements are shown as circles and NTFA measurements as squares. The residual errors are normalized by the simulated response. EMSA residuals with 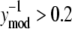were assigned to EMSA Group 2, and remaining residuals were assigned to EMSA Group 1. Similar grouping was applied to the NTFA residuals. Variances for each group are shown in the figure. The difference in variance between NTFA groups was not significant, whereas the EMSA groups exhibited significant differences in variance (p < 0.05).

Given this analysis of the residuals for the NTFA and EMSA measurements, we constructed a bootstrap sample population using the following error models:

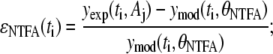(7)

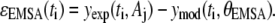(8)

The bootstrapped sample populations were used to provide estimates of the confidence intervals associated with the model parameters. The 95% confidence intervals for the model parameters are shown in Table 1. We are particularly interested in the confidence intervals associated with the strength parameter, α. Based upon bootstrapping of the EMSA residuals, the 95% confidence interval for the strength parameter α spans the range −0.296–0.913 (p < 0.2). In contrast, the 95% confidence interval for the strength parameter α based on the NTFA residuals spans 0.021–1.53 (p < 0.02). The other estimated parameters (k1, k3, and cN) exhibited wider confidence intervals from the EMSA results compared to the NFTA results (e.g., O(10^1.6) for EMSA k3 versus O(10^0.8) for NTFA k3). Differences in the size of the confidence intervals indicate the differences in signal/noise ratios for these two assays.

To test the predictive power of the mathematical model, we also studied the influence of DCPA on NF-κB activation in a human T cell line, Jurkat clone E6-1 (Fig. 5). Jurkat cells were treated with either ethanol (squares) or 100 μM DCPA (+) and cocultured with plate-bound anti-CD3 and anti-CD28 to activate NF-κB. The extent of active NF-κB DNA binding was measured using the NTFA. Activation of NF-κB in Jurkat cells was delayed compared to LPS-stimulated IC-21 macrophages. Due to the time delay associated with the activation of NF-κB, the start of the simulation occurred 24 min after the Jurkat cells were exposed to anti-CD3/CD28. As the pathways leading to NF-κB activation after anti-CD3/CD28 stimulation (29) are different from LPS-induced activation (30), the ethanol control experiment (squares) was used to adjust the parameters associated with the initial concentration of inactive NF-κB in the cytosol (cN = 19) and the NF-kB activation rate constant (k1 = 0.015 min⁻¹). All other parameters remained as specified in Table 1. The predicted response in NF-κB activation after exposure to 100 μM DCPA (dotted line) is compared with the ethanol control (solid line).

FIGURE 5.

Prediction of the DCPA potentiation of early activation of NF-κB in Jurkat cells after stimulation with plate-bound anti-CD3 and anti-CD28. (a) NF-κB activation through the T cell receptor involves different membrane proximal signaling events compared to activation through the toll-like receptor 4 (TLR4) signaling pathway. These two signaling pathways act through TRAF6 to activate the IκB-NF-κB signaling module. (b) Nuclear NF-κB was assayed by NTFA at the indicated times after stimulation with plate-bound anti-CD3 and anti-CD28 and treatment with 0 μM (□) and 100 μM (+) DCPA. Two parameters (k1 and cN) of the mathematical model were calibrated to the ethanol control results, providing a prediction of the 100 μM DCPA results. The simulated time courses of active NF-κB without and pretreated with 100 μM DCPA are shown as solid and dashed curves, respectively. Each experiment was performed six times.

DISCUSSION

The combined experimental and simulation results using IC-21 cells, a mouse macrophage cell line, suggest that DCPA potentiates the early activation of NF-κB by 48.0%. In contrast, the EMSA results suggest that DCPA increases the activation rate by 11.9% (α = 0.119). The potentiation of NF-κB activation by DCPA was also confirmed using the NTFA in a human T cell line, Jurkat clone E6-1. These results seem counterintuitive, as we have previously reported that 66 μM DCPA resulted in an 80% reduction in IL-6 mRNA and a 50% reduction in TNF-α mRNA after stimulation with 10 μg/ml LPS (14). This suppression in mRNA resulted in an inhibition of IL-6 production by 60% and TNF-α production by 50%. However, the stabilities of IL-6 and TNF-α mRNA were not affected by DCPA, which suggests that DCPA modulates cytokine production specifically at the pretranscriptional level, as inhibition of the IκB proteins would change the dynamics of NF-κB.

In particular, the dynamic resynthesis of the IκB inhibitor proteins after the initial activation induces oscillations in NF-κB (5). Conceptually, potentiating the activation of NF-κB by DCPA would cause an increase in the resynthesis of IκB proteins. This proportional increase in IκB proteins would cause a more rapid reduction in active NF-κB, thus undershooting the concentration of active NF-κB in the nucleus compared to the control experiment. In Fig. 3, this undershoot was apparent at 40 min, where the nuclear NF-κB in DCPA-exposed cells was lower than the ethanol control. If, on the other hand, DCPA inhibited the resynthesis of IκB proteins, the level of inducible NF-κB would increase after the initial rise (31), and gene expression would also increase. Such a concomitant increase in gene expression is inconsistent with prior studies (14). Further evidence supports our hypothesis that DCPA modulates the activation of NF-κB at the pretranslational level, as similar effects on NF-κB activation were observed in LPS-stimulated mouse IC-21 macrophages and in human Jurkat T cells stimulated through the T cell receptor (compare Fig. 3 b with Fig. 5). LPS activates NF-κB in IC-21 macrophages via the MyD88 pathway associated with TLR4 (30). In contrast, activation of NF-κB by stimulating the T cell receptor in Jurkat cells requires the recruitment of multiple signaling proteins to the central zone of the supramolecular activation cluster, leading to protein-kinase-C-controlled activation of NF-κB (29). These two different signaling pathways converge at the polyubiquitin ligase tumor necrosis factor receptor-associated factor 6 (TRAF6) (32,33). TRAF6 in turn activates IKK, which facilitates the degradation of the IκB inhibitory proteins. Collectively, these observations suggest that DCPA differentially regulates NF-κB-response genes via the IκB-NF-κB signaling module through a yet undefined pretranslational mechanism.

NF-κB regulates the inducible expression of a wide range of immune and inflammatory response genes (34). As a result, NF-κB is one of the most studied molecules in the area of signal transduction. Because of the complex nature of biological systems, the study of NF-κB is important for two reasons. First, the objective of biomedical research is to identify biochemical mechanisms that underpin the biological response to stimuli. Second, biomedical research aims to develop strategies that modulate aberrant biochemical mechanisms to revert to a pathogenic state. In both cases, biological assays provide avenues for observing cellular response after biochemical interrogation.

One of the most important aspects in the design of a biological assay is selecting a physiologically relevant context. We first observed damped oscillations in active NF-κB in macrophages after LPS stimulation. This observation is in contrast to other published studies examining the dynamic activation of NF-κB after LPS stimulation. In particular, Werner et al. observed that in fibroblasts the initial activation of NF-κB by 0.1 μg/ml LPS was not rapid but depended on autocrine feedback via the TNF-α pathway (35). Covert et al. observed that 0.5 μg/ml LPS induced stable NF-κB activation through a combination of MyD88-dependent and MyD88-independent pathways (27). In Fig. 6, we compare our results to the results of Werner et al. (35) and Covert et al. (27). The initial rates of NF-κB activation are similar in those studies, which used mouse embryonic fibroblasts. We observed a much higher initial rate of activation using 1.0 μg/ml LPS. This higher activation rate may be attributed to the increased expression of CD14 in macrophages compared to fibroblasts and/or increased stimulant. Cellular response to LPS is mediated by the TLR4 pathway (24). CD14, an accessory cell surface protein, interacts with TLR4 to increase the sensitivity to LPS 1000-fold (36) and facilitates the robust response to LPS. Moreover, as highlighted in Fig. 5 b, NF-κB activation exhibits different dynamics after T cell receptor stimulation in Jurkat cells than through the TLR4 pathway in IC-21 macrophages. Variations in the initial rate of activation of NF-κB reflect inherent differences in the efficacy of similar signaling pathways in different cell types that exist before stimulation. Thus, the cellular context plays an important role in determining the contribution of a particular signaling pathway on the dynamic behavior of NF-κB activation.

FIGURE 6.

The dynamic activation of NF-κB in macrophages compared with results of prior studies using fibroblasts. Nuclear NF-κB was assayed by EMSA at the indicated times after persistent stimulation with 1 μg/ml LPS in macrophages in this study (□, n = 8, values reported as average ± 95% confidence interval), 0.5 μg/ml LPS in fibroblasts, demonstrated by Covert et al. (27) (○); and 0.1 μg/ml LPS in fibroblasts, demonstrated by Werner et al. (35) (×).

Chemical manipulation of NF-κB binding activity with immunosuppressant DCPA resulted in earlier activation of the initial peak observed during the first 45 min after LPS stimulation. This earlier activation might result in altered frequency of the oscillations, which in turn will change the transcriptional regulation of some genes. Changes in number, period, and amplitude of oscillations were observed by Nelson at al. (37) in HeLa cells continuously stimulated with TNF-α. Furthermore, the transcription of NF-κB target genes was dependent on persistence of oscillations. Nelson et al. (37) also suggest that changes in oscillation could have functional consequences for NF-κB signaling in response to different stimuli. Therefore, inhibition of NF-κB-inducible cytokines TNF-α and IL-6 observed in DCPA-treated cells at the later time points (12 and 24 h after sustained LPS stimulation) may be a result of the early potentiation of NF-κB activation caused by a shift in oscillatory behavior.

An additional consideration in the design of a biological assay is how to observe a cellular response. Observed variability in measured data is due to technical variation (e.g., error in measurement) or biological variation (e.g., cellular heterogeneity, asynchrony, or stochasticity). Implicitly, design of the experimental protocol is intended to limit the contributions of biological variation by selecting cellular systems that exhibit favorable characteristics. A survey of the literature suggests experimental conditions that can reduce natural sources of biological variation. In the study by Lipniacki et al. (38), stochastic simulations revealed that the dynamics of the initial peak is independent of the number of NF-κB molecules. Similarly, Nelson et al. demonstrated that the dynamics of the initial peak were similar among cells expressing fluorescently labeled RelA (37). Collectively, these studies and our own data suggest that by focusing on the first 45 min after LPS stimulation, natural sources of biological variability can be minimized.

In contrast, the contribution of technical variation has received little attention. Moreover, the experimental tools of molecular biology have been criticized with regard to quality (39,40). Over the years, biochemical assays with improved sensitivity have been developed (23). Yet, as we have shown herein, technical variation can be attributed to multiple sources. Improved sensitivity alone is an insufficient criterion to confirm improvement of the information context of an assay. If the technical variation is associated solely with the magnitude of the signal, there will be no meaningful difference in the information extracted regarding cellular response using either assay. However, when an assay, such as the EMSA discussed here, exhibits a higher contribution of random noise, pharmacologically significant modulation of cellular response and insight into underlying biological mechanisms can be masked. Thus, an assay such as the NTFA, which has a greater signal/noise ratio, affords a clearer window into fundamental cellular behavior. The importance of developing biological assays that exhibit improved signal/noise ratios is highlighted by our study of the potentiation of NF-κB activation by DCPA.

Although much effort has focused on identifying the dynamic phenomena associated with the activation of NF-κB, we focused our efforts on understanding how these dynamic phenomena can be modulated for therapeutic aims. After our investigations into the impact of DCPA on the dynamic modulation of NF-κB activation within a mouse peritoneal macrophage cell line and a human T cell line, we have come to the following three conclusions. First, the dynamic behavior of NF-κB in response to stimuli is dependent on cell type and developmental stage. Second, DCPA potentiates early activation of NF-κB, yet suppresses inflammatory gene expression. Extraction of this counterintuitive behavior could only be achieved through the use of a mechanistic model that encoded the relevant biochemical events. Furthermore, ascribing significance to parameter values derived from a mechanistic model must include parameter identifiability considerations and the analysis of multiple biological replicates. Finally, nonradioactive transcription factor assays have a signal/noise ratio superior to that of electromobility shift assays for observing cellular NF-κB response.

APPENDIX: PARAMETER IDENTIFICATION

An important aspect of sensitivity analysis is identification of model parameters that can be uniquely determined from the available data. A priori identifiability is one approach to selecting identifiable parameters given unlimited information about the modeled system (41,42). This assessment of parameter identifiability is intimately linked to the sensitivity of the model results to changes in parameter values. Local sensitivity analysis is defined as the relative change in model variables (y_j) in response to a perturbation of the model parameters (k_i) around a local optimum (43). The resulting sensitivity function is defined as

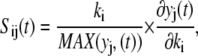(A1)

where the partial derivative values are scaled by the parameter value and the maximum value of the model variable during the simulation. In practice, the sensitivity function is approximated by obtaining the sensitivity measure, S_ij, at a set of discrete time points, t_k, and experimental conditions, [Cn]_n. In addition, measurements of only a subset of the model variables may be obtained experimentally. A reduced sensitivity matrix (M) is then constructed using a subset of the sensitivity measures 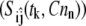such that

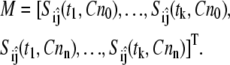(A2)

A set of correlation coefficients between model parameters is calculated from M. Parameters that are locally identifiable have correlations with all other parameters between −1 and +1. Parameters that are not locally identifiable, termed a priori unidentifiable, have correlations of exactly +1 or −1 with at least one other parameter.

The identifiability of the model parameters and initial concentration of NF-κB in cytosol (cN (t = 0)) were calculated using the NF-κB model described in Eqs. 1–3. A combined sensitivity matrix was constructed from sensitivity values obtained from simulations with 0 and 100 μM DCPA over a period of 50 min after LPS stimulation. This combined sensitivity matrix was reduced by assuming that the concentration of active NF-κB in the nucleus ([aN]) was the only experimentally observable variable in the model. We are particularly interested in the confidence intervals associated with the strength parameter α. The correlation coefficients listed in Table 2 demonstrate that estimates of the strength parameter α are unique if K_DCPA is specified as 5 μM, as determined previously (14).

TABLE 2.

Correlation coefficients of model parameters and initial concentration of NF-κB in cytosol

Correlation coefficient	k1	k2	k3	k4	α	KDCPA	cN (t = 0)
k1	1	0.391	0.391	−0.488	0.690	−0.687	0.677
k2	0.391	1	1	−0.950	0.302	−0.289	−0.348
k3	0.391	1	1	−0.950	0.302	−0.289	−0.348
k4	−0.488	−0.950	−0.950	1	−0.374	0.368	0.143
α	0.690	0.302	0.302	−0.374	1	−0.999	0.506
KDCPA	−0.687	−0.289	−0.289	0.368	−0.999	1	−0.520
cN (t = 0)	0.677	−0.348	−0.348	0.143	0.506	−0.520	1

Significantly correlated parameters (p < 0.05) are highlighted in bold.