Sustained Oscillations in Extended Genetic Oscillatory Systems

Abstract

Various dynamic cellular behaviors have been successfully modeled in terms of elementary circuitries showing particular characteristics such as negative feedback loops for sustained oscillations. Given, however, the increasing evidences indicating that cellular components do not function in isolation but form a complex interwoven network, it is still unclear to what extent the conclusions drawn from the elementary circuit analogy hold for systems that are highly interacting with surrounding environments. In this article, we consider a specific example of genetic oscillator systems, the so-called repressilator, as a starting point toward a systematic investigation into the dynamic consequences of the extension through interlocking of elementary biological circuits. From in silico analyses with both continuous and Boolean dynamics approaches to the four-node extension of the repressilator, we found that 1), the capability of sustained oscillation depends on the topology of extended systems; and 2), the stability of oscillation under the extension also depends on the coupling topology. We then deduce two empirical rules favoring the sustained oscillations, termed the coherent coupling and the homogeneous regulation. These simple rules will help us prioritize candidate patterns of network wiring, guiding both the experimental investigations for further physiological verification and the synthetic designs for bioengineering.

INTRODUCTION

Cellular functions are realized by various dynamic processes resulting from concerted actions of numerous molecular components through diverse interactions and regulations, the understanding of which is the major goal of systems biology (1–4). Many dynamic features of the cellular processes have been modeled with elementary circuits that can produce given desired functions (5,6). For instance, feedback loops have successfully accounted for diverse phenomena such as the molecular switching (7) and biological clock (8). In particular, it has been known that a negative feedback loop architecture can render the oscillatory intracellular signals, which constitutes the core of the homeostatic response and the biological clock (9,10). Therefore, the identification of feedback loop structure can be the first step to understand and/or design systems having such an oscillatory behavior. Elementary circuits with well-understood characteristics such as the negative feedback loops, however, do not always function in isolation within a cell, but rather are parts of a complex network of biological components (11,12), leading to coupling and/or interlocking with one another. From a theoretical perspective, dynamic consequences of the couplings, such as the capability of sustained oscillation for a particular set of coupled feedback loops, are not clear a priori. Furthermore, the high complexity arising from the multiplicity and biochemical details of molecular components makes it a formidable task to study them through quantitative mathematical modeling in full details. Yet, the study of specific systems (13–19) has been proved to be useful to understand the molecular origin of various dynamic behaviors. Synthetic model systems provide additional merits of controllability of the components and their mode of couplings (20). In this article, we employ the repressilator system (21) as a basic elementary circuit, and then investigate its dynamic consequences for extension and coupling.

The repressilator (21) is a synthetic construct of Escherichia coli designed to emulate the in vivo oscillatory behavior by using the components sequentially inhibiting the transcriptional activity of neighbor genes. It consists of three components: The protein LacI from E. coli inhibits the transcription of the second gene tetR from the tetracycline-resistance transposon Tn10, the protein product of which in turn inhibits the expression of the third gene cI from λ-phage. Finally, CI inhibits the lacI expression, completing the three-component feedback cycle. For example, LacI, TetR, and CI are represented as N1, N2, and N3 in Fig. 1 a, respectively. Thus, it makes up a negative feedback loop of transcriptional regulators, capable of generating oscillatory protein levels for all the three components (21). It has recently been utilized as a basis for possible realization of a multicellular clock (22).

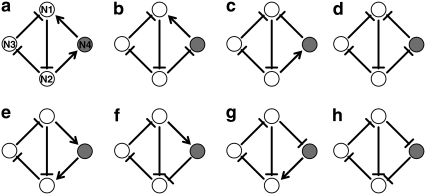
FIGURE 1.

Eight possible configurations of the repressilator with an additional regulator forming a coupled feedback structure. Open circles represent the elements of the original three-node repressilator and the solid circle denotes the additional element newly introduced. The arrow denotes activation and the blunted line indicates repression. Nodes are labeled from N1 to N4, as shown in panel a.

For continuous-value approximation, the basic kinetics of the repressilator is described by (21,23)

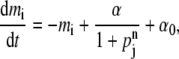(1a)

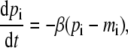(1b)

where i = (lacI, tetR, cI) and j = (cI, lacI, tetR), respectively. The variables m_i and p_i are the molecular concentrations of the mRNA and the protein product, respectively, of the gene i. The parameter α₀ is the basal activity, or leakage, of the promoter when fully repressed, and α + α₀ is its maximal activity in the absence of repressors; β is the ratio of the decay rate (i.e., inverse lifetime) of the protein to that of the corresponding mRNA; and n is the Hill coefficient. In Eq. 1, time is rescaled in units of the mRNA lifetime; protein concentrations are written in units of K_M, the number of repressors required to half-maximally repress a promoter; and mRNA concentrations are rescaled by the average number of proteins produced per each corresponding mRNA molecule. All of these parameters and scaling factors have to be set by experimental values but the current knowledge about the molecular details of them is rather limited. It has been demonstrated that Eq. 1 can reproduce sustained oscillations for a range of parameter values (21), and the existence of oscillatory solutions in Eq. 1 has been shown more rigorously (23). So, we assume that the mathematical representation in Eq. 1 provides us with a reasonable framework to study the essential feature of the system through deterministic continuous approximation.

To address our original question, we consider the in silico extension of the repressilator system where additional component(s) are introduced and interact with the original three-node repressilator system. Specifically, we focus on the cases in which the new components interact with the existing nodes (genes) to make up a coupled, or interlocked, feedback structure, and investigate the conditions under which sustained oscillations can survive.

THEORY AND METHODS

Equations for the regulation function

We use the deterministic continuous approximation analogous to Eq. 1 for the extended systems. Let us consider the situation where the new component (gene) interacts with two existing nodes to form an additional feedback loop. There are eight possible interaction patterns as shown in Fig. 1. We label the nodes of the original repressilator in Fig. 1 as N1, N2, and N3, clockwise from the top, ignoring the molecular identity of the three components as it is not essential for the generic approach here. The new node (denoted as a solid circle in Fig. 1) is labeled as N4. For this four-node system, Eq. 1 is modified into

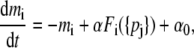(2a)

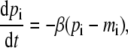(2b)

where the regulation function F_i depends on the molecular concentrations of the regulatory proteins {p_j}, whose form is determined by the characteristics of the system such as the number of regulators and the enhancing/inhibitory nature of those regulators as well as the combinatorial logic between them (4,5,24,25). In the presence of a single regulator, a Hill-type function

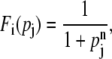(3)

can be used for the inhibition by the regulator j as in Eq. 1. Corresponding representation for the activating regulation is given by

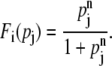(4)

When multiple proteins regulate the expression of a common target gene, such as for N1 by N3 and N4 in Fig. 1, a–d, and for N2 by N1 and N4 in Fig. 1, e–h, the form of F_i depends also on the combinatoric logic. To be specific, we consider the following specific forms of F_i.

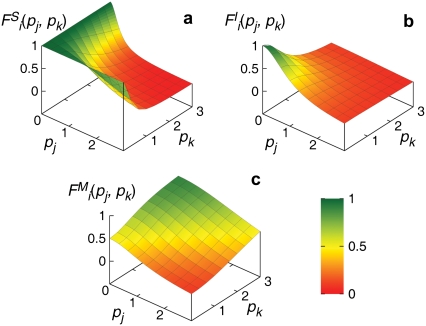
Let us first consider the case where both the regulators j and k are repressors (Fig. 1, c, d, f, and h). If the simultaneous binding of the two repressors is required to achieve the transcriptional repression of gene i, the regulation function can be modeled as

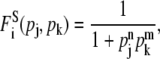(5)

where n and m are Hill coefficients of the protein j and k, respectively, which are not necessarily the same. The superscript S stands for “simultaneous.” On the other hand, if the binding of either of the two repressors is sufficient to inhibit the expression, the regulation function can be modeled as

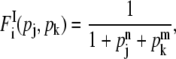(6)

where the superscript I stands for “independent.” The regulatory effect of these two schemes are depicted in Fig. 2, a and b. Next, if one regulator, say j, is an inhibitor and the other, k, is an activator (Fig. 1, a, b, e, and g), the expression of gene i can be maximal if the activator, but not the inhibitor, binds to the promoter region, and minimal if only the inhibitor binds there. For other cases, if both the regulators simultaneously bind or unbind to the promoter regions, the expression can be of an intermediate level. A simple form of the regulation function in this case can be modeled as

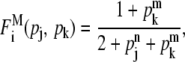(7)

where the superscript M stands for “mixed” (see Fig. 2 c).

FIGURE 2.

Plots of the multivariate regulation functions F_i used in this study, Eq. 5 (a), Eq. 6 (b), and Eq. 7 (c), with n = m = 2.

Numerical procedure and parameters used

For the original three-node repressilator system, the existence of an oscillatory solution has been attributed to the instability of a stationary solution (23,26). We follow this criterion to investigate the parameter space for sustained oscillations in the four-node extended systems. To this end, a stationary solution is identified and the Jacobian matrix is numerically evaluated at this point. The positivity of the maximum real part of its eigenvalues indicates the instability of the stationary solution. To find a parameter region inducing the sustained oscillations for different topologies of the extended system, we vary the two parameters, the maximum regulatory strength α and the relative inverse lifetime of protein to mRNA β, while fixing other parameters such as the Hill coefficients n = m = 2 and the leakage level α₀/α = 10⁻³, following Elowitz and Leibler (21). For larger values of the Hill coefficients, the system may exhibit more complex behaviors such as bistability. Excluding such exceptional cases, the results found in this study is at least qualitatively valid even for some larger Hill coefficients.

Oscillability and regulatory homogeneity

We define the oscillability of an extended system as the fraction of (α, β) parameter region for sustained oscillations in the original three-node repressilator in which the oscillation is maintained after the extension (the gray region within the dotted curve in Figs. 3 and 4). It quantifies the likelihood of preserving sustained oscillations after the coupling with other components, implicating the “robustness” of oscillations under the system extension. The regulatory homogeneity of a transcription factor with multiple targets is defined as the larger of the fractions of positive (activating) or negative (inhibitory) regulatory actions it has. For example, the regulatory homogeneity of N2 is 0.5 for Fig. 1 a and 1 for Fig. 1 b.

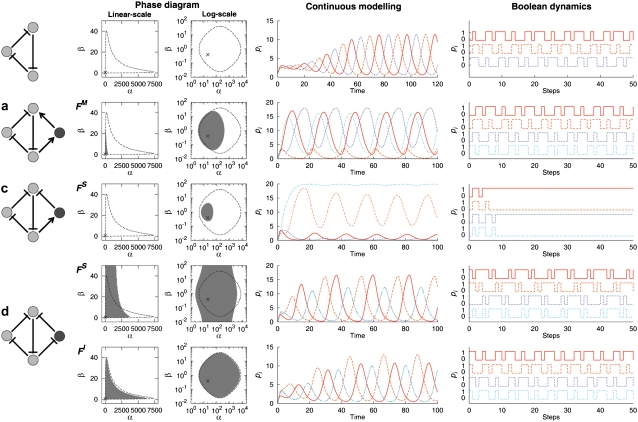
FIGURE 3.

Dynamic characteristics of the original three-node repressilator (top row) and the four-node extended repressilators a–d. The phase diagram in (α, β) parameter space with α₀/α = 10⁻³ and n = m = 2 is shown for each oscillable configuration and regulation function, both in linear and logarithmic scales, for clarity. Labeling of the panels follows that of Fig. 1. The configuration b is not shown since it does not support the sustained oscillations for any parameter set investigated. The configuration d is shown for each of the regulation functions of the form F^S (fourth row) and F^I (fifth row). The gray region in the phase diagram indicates the cases where the sustained oscillation occurs in the extended system and the region enclosed by the black-dotted curve denotes the cases where the sustained oscillation occurs in the original three-node repressilator, shown for comparison. Also shown is the temporal profile of the continuous modeling with the parameters α = 20 and β = 0.4 (marked by “×” in the phase diagram). Each curve shows the profile of the node N1 (red solid), N2 (orange dashed), N3 (blue dotted), and N4 (cyan dash-dotted), respectively. Note that trajectories of N3 and N4 overlap in d. Typical temporal profiles for the corresponding Boolean dynamics are shown in the rightmost column. The color-coding of the Boolean dynamic profiles follows that of the continuous modeling.

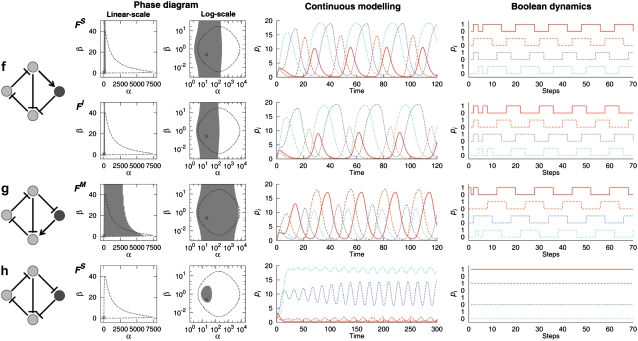
FIGURE 4.

Same as Fig. 3 for the four-node extended systems e–h. The configuration e is not shown since it does not show sustained oscillations. For the configuration f, both the cases with different regulation functions, F^S (first row) and F^I (second row), are shown. The color-coding of the curves follows that of Fig. 3.

Boolean dynamics

As the sigmoidal nonlinearity effect in the stimulus-response relationship increases, the continuous approximation can be simplified into a steplike regulatory response that can be modeled by Boolean dynamics (16,27), which can also be regarded as the case with n → ∞ in the continuous approximation. As the exact degree of nonlinearity in most of the real systems is not fully understood, we need to check how the system dynamics depends on such a degree of nonlinearity to draw a general conclusion. The Boolean dynamic rules we employed in this study are as follows. Each component (either mRNA or protein) can have one of the two states S(t) = 1 or S(t) = 0 where the state 1 (0) means that the mRNA or protein is present (absent). The state of a protein is determined by the state of the corresponding mRNA as

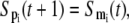(8)

that is, a protein is present only if the corresponding mRNA was present in the previous time step, otherwise, the protein degrades and vanishes. The corresponding rule for mRNA is slightly more complicated. If a gene is regulated by a single transcription factor p_j, the Boolean rule becomes

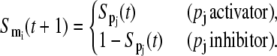(9)

When a gene is regulated by more than one transcription factor, the combinatorial rule has also to be considered. The Boolean rule corresponding to Eq. 5, the AND logic for the inhibitory effects, can be represented as

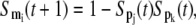(10)

while that for Eq. 6, the OR logic for the inhibition, can be represented as

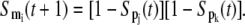(11)

Finally, when a gene is regulated by two regulators with opposite effects as in Eq. 7, the corresponding Boolean rule can be represented as

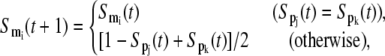(12)

that is, when the opposite effects compete, the state of the mRNA remains unchanged. To assess the capability of sustained oscillations for a given network configuration, we simulate the Boolean dynamics based on the above rules for all possible initial conditions (2⁸ initial conditions for four-node systems) and see if the oscillation is observed independent of initial conditions.

RESULTS

Our main results are presented in Figs. 3 and 4. We show in the figure, for each extended four-node configuration, the phase diagram in the (α, β) parameter space with α₀/α = 10⁻³ and n = 2. Among all possible configurations and regulation functions, only the cases showing sustained oscillations for some parameter region are considered. The combinatoric regulation function used is indicated beside the phase diagram. In the phase diagram, the gray region indicates the parameter range within which the sustained oscillation occurs after the extension. The region enclosed by the dotted line is the parameter range within which the sustained oscillation is observed in the original three-node repressilator system. Along with the phase diagrams, typical temporal profiles of the four-node systems with both continuous and Boolean dynamics are also shown.

Not all extended configurations can produce sustained oscillations

We first note that not all extended configurations in Fig. 1 are capable of exhibiting sustained oscillations. For example, the configurations in Fig. 1, b and e, do not exhibit sustained oscillations for any parameter sets investigated and therefore they do not appear in Figs. 3 and 4. We also note that the size of the parameter region in which the sustained oscillation occurs varies significantly across different configurations. To assess it, we measure the oscillability (see Theory and Methods). The oscillability 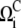of the configuration i with the regulation function F^C is measured for each configuration as

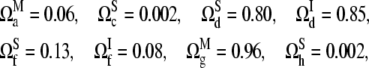(13)

where the oscillability of all other cases is zero. For the configurations c and h, we observe the sustained oscillations only for a particular type of the regulation function F^S, but not for F^I. Furthermore, the oscillability is measured to be smaller by at least an order of magnitude than other oscillable cases. This observation prompted us to examine these cases in more detail. We turn to the Boolean dynamics and found that these two cases do not show oscillatory behaviors for most of the initial conditions as shown in the rightmost column of Figs. 3 c and 4 h. On the other hand, for all other configurations that are found to be capable of sustained oscillations by the continuous modeling, the oscillatory behavior appears regardless of the initial conditions also in the Boolean dynamics. Thus, we suppose that the sustained oscillations rarely found for the configurations c and h may not represent the real observable oscillatory dynamics in which higher nonlinearity and complicated regulations may be involved. Thus, we disregard these two cases from the configurations that can produce sustained oscillations, leaving the four configurations a, d, f, and g as the oscillable extended configurations.

Each oscillable configuration exhibits a distinct temporal profile

The four configurations capable of sustained oscillations show distinct temporal patterns. Some typical patterns are shown in Figs. 3 and 4. In the original repressilator, three elements oscillate alternatively, with the peak in LacI concentration followed by the peak in TetR concentration, which in turn is followed by the peak in CI concentration (21). A simple pattern observed for the four-node extensions is that of d, in which the oscillating phase of three original elements is unchanged albeit with small changes in the oscillating amplitudes. The new element N4 shows the identical temporal profile as that of the node N3, which is expected from the symmetry in the configuration (Fig. 3 d). For the configuration g, the alternating pattern of the original three nodes is largely preserved as in d, but the oscillating profile of N4 is quite different and it oscillates almost in phase with the node N2 in this case (Fig. 4 g). In these two configurations, the oscillating pattern of the original repressilator is only slightly altered for nodes N1 and N2, and the changes for the node N3 can be seen as redistribution of the oscillating activity of node N3 in the original repressilator into those of nodes N3 and N4 in the extended configuration. Interestingly, we observe largest Ω for these two configurations than other cases (see Eq. 13).

For the other two configurations a and f, we observe more nontrivial changes in the oscillating pattern. For example, in a, although the alternating pattern is still present, the node N2 shows a suppressed oscillating amplitude, with the fourth element oscillating almost in phase with the node N1 (Fig. 3 a). In f, a different pattern appears in that the oscillating activity of node N1 is relatively suppressed and that of node N3, together with that of the new element N4, becomes enhanced, resulting in the oscillation with disproportionate active and inactive periods for each node (Fig. 4 f). As mentioned above, the oscillability of these two configurations are significantly smaller than that of the configurations d and g, for which the alteration of oscillating pattern is found to be weak.

Simple rules for sustained oscillations in extended circuits

We found that each extended configuration exhibits different dynamic characteristics, such as the capability of sustained oscillations and the different oscillabilities and temporal profiles. All these characteristics can be obtained by detailed mathematical modeling, which is, however, prohibitively impractical for larger systems. Thus it would be desirable if we could deduce some rules of thumb that enable us to pick out oscillable configurations without performing the detailed analysis. Such rules will help us not only prioritize the candidate patterns of molecular wirings where sustained oscillations play an important role, but also design synthetic circuits that can be embedded in the wild-type without interfering with the oscillatory functions.

To understand the condition under which the oscillation can survive, we note that the extended four-node system contains two feedback loops: One by the original repressilator, N1–N2–N3–N1, and the other by the nodes N1–N2–N4–N1 in a–d and N1–N4–N2–N3–N1 in e–h. In a, d, f, and g, the new feedback loop contains an odd number of inhibitory interactions (thus, its overall regulatory sign is negative), whereas in b, c, e, and h, it has an even number of inhibitions (thus, positive in sign). As the original repressilator forms a negative feedback loop, we call the former cases—a, d, f, and g—a coherent coupling, and the latter an incoherent coupling. The configurations with the coherent coupling coincide with those capable of sustained oscillations. For the incoherently coupled cases, on the other hand, since the positive feedback loop cannot support a sustained oscillation (23), the effects of two feedback loops, one negative and one positive, compete with each other. As a result, the oscillation is destroyed. Thus the coherence property of the coupling of feedback loops can discriminate the oscillable and nonoscillable configurations, implying that it plays an important role in the oscillatory dynamics.

The coherence of coupling alone cannot, however, explain the observed difference in oscillabilities displayed by, e.g., those of d and a. To understand the origin of this distinct oscillability property, we note the fact that, in d and g, where we have rather high oscillability, the element regulating two targets (N2 in d and N1 in g) has the same sign of regulation (inhibition, in this case) on both of the regulated targets. On the other hand, in a and f associated with small oscillabilities, such multi-target node acts as both the activator and the inhibitor. We call the former case a homogeneous regulation and the latter an inhomogeneous regulation. Thus the homogeneous regulation of multi-regulators might be another key ingredient for the oscillatory stability of the extended network in addition to the coherent coupling of feedback loops, and can be used as an indicator for high-oscillability configurations. It is interesting to note that we observe an enhanced propensity of such homogeneous regulations in the reconstructed transcriptional regulation network of the bacterium E. coli (28). In this network, 67 out of 77 (≈87%; empirical P = 10⁻⁴) multi-target transcription factors exhibit a perfectly homogeneous regulation activity. Such an enrichment in regulatory homogeneity (4) might be the consequence of selective pressure in favor of the homogeneous regulatory activity during the course of evolution as well as their physico-chemical properties such as the operon structures in E. coli, raising an interesting question on the connection between the biochemical regulatory functions and biological dynamic functions.

SUMMARY AND DISCUSSION

In summary, we have shown that upon the extension and coupling the capability of sustained oscillations for genetic oscillatory systems depends on the network topology. Different configurations yield different oscillabilities and temporal patterns. From the in silico experiments, we deduced two simple empirical rules—the coherent coupling and the homogeneous regulation. These can be used to discriminate the capability of sustained oscillations in extended configurations before detailed mathematical analysis or experiments. The rules may be interpreted as that the evolutionary pressure acts to minimize the incoherent interference at the coupling points at which the crosstalk between the feedback loops occur. Such biologically plausible interpretation guides us to study the underlying dynamics at the system level.

There are many examples of biological systems in which interacting feedback loop structures comprise key dynamic factors, ranging from the simple chemotactic responses of microorganisms such as Dictyostelium (29) to the cancer-related human systems involving the p53-Mdm2 feedback loops (18). One of the key challenges is to identify the underlying network wiring of molecular components that allows us to understand its functioning more accurately and to modulate it safely. It is, however, far from trivial to map the wiring of key components unambiguously (30) due to the complexity of molecular networks. In the engineering point of view, the repressilator represents one of the most successful demonstrations of the power and potential of synthetic biology (20), as it provides an experimental testbed for more precise understanding of cellular dynamics in a controllable manner. The repressilator currently works as a relatively independent module, using some components alien to the host organism. As one would ultimately like to use native components to engineer existing biological circuits, problems will then arise due to the evident connectivity of biological networks. The interplay between the network topology and biological function will thus be an increasingly important topic, representing a wide avenue for theoretical and experimental investigations in the future.