Quantum percolation in cuprate high-temperature superconductors

Abstract

Although it is now generally acknowledged that electron–phonon interactions cause cuprate superconductivity with T_c values ≈100 K, the complexities of atomic arrangements in these marginally stable multilayer materials have frustrated both experimental analysis and theoretical modeling of the remarkably rich data obtained both by angle-resolved photoemission (ARPES) and high-resolution, large-area scanning tunneling microscopy (STM). Here, we analyze the theoretical background in terms of our original (1989) model of dopant-assisted quantum percolation (DAQP), as developed further in some two dozen articles, and apply these ideas to recent STM data. We conclude that despite all of the many difficulties, with improved data analysis it may yet be possible to identify quantum percolative paths.

Percolation in strongly disordered materials cannot be treated analytically, and early discussions of percolation focused on lattice model simulations. Recent discussions are much more sophisticated, and include many off-lattice effects connected with nanoscale phase separation, especially in glassy materials (1–7). The case of cuprate electronic high-temperature superconductive (HTSC) glasses (disordered dopants in a crystalline host) is especially intriguing, as scanning tunneling microscopy (STM) measures local gaps directly. Long ago, we suggested (8) that the dopants (usually oxygen interstitials), added to the insulating host crystal to make it metallic, should not be regarded as donating carriers to the cuprate planes (the most common theoretical model in the early days), but should instead be regarded as electronic bridges connecting metallic nanodomains separated by insulating domain walls generated by planar lattice buckling. This model has several advantages: it recognizes the lattice instabilities that are ubiquitous in perovskite and pseudoperovskites, and the dopants can function as centers of strong electron–phonon interactions.

The foregoing dopant-assisted quantum percolation (DAQP) model, with its roots in materials science, initially enjoyed little popularity, because many theorists found more exotic models (not involving attractive electron–phonon interactions at all) more suitable (9–11). However, as we analyzed in many articles (12), the accumulation of data showing large strain effects (13) provided little support for exotic models. There is now a complete picture of the phase diagrams of lattice instabilities (pseudogaps) and superconductive gaps within the DAQP model (14). Nevertheless, the intriguing question of whether these percolation paths can actually be identified in cuprate planes studied by STM remains open. Why has this problem proved to be so difficult?

There are several answers to this question. Distinguishing between strain-related pseudogaps and superconductive gaps with only a local probe is difficult, because both gaps are pinned by the Fermi line, and both are intrinsically nonlocal. This means that studies with a local STM probe inevitably see only the projections of both gaps, and both of these projections have similar I–V characteristics and similar magnitudes near optimal doping. Moreover, the paths necessarily involve combining both lateral motion in the cuprate planes with vertical motion normal to them, and STM can observe only the former [a similar problem arises in angle-resolved photoemission scanning (ARPES)]. This means that the most important parts of the paths [the parts with the strongest attractive electron–phonon interactions (8, 12–14)] are unobservable directly; their presence must be inferred.

These difficulties would be insuperable with a small database, but Davis et al. assembled a very large area cuprate image (16,000 unit cells) in which they identified 600 well localized peaks in dI/dV centered at −0.96 eV in a slightly underdoped sample, which they assigned to interstitial oxygen dopants (15). One would not expect such a deep state, so far from the Fermi energy, favorably to affect either a pseudogap or a superconductive gap, because the latter are tied to the Fermi energy and are generally weakened by scattering from deep impurity states. However, consistently the data showed a 20% enhancement of mean gap amplitudes 〈Δ〉 near these interstitial sites (16). Enhanced electron–phonon interactions (as in the original DAQP model) are sufficient to explain this small local gap enhancement; the enhancement itself may be small, both because of nonlocality and because the observed gap is a mixture of pseudogaps and superconductive gaps, and the latter (which are combinations of specific lattice instabilities) are probably weakened by dopant scattering.

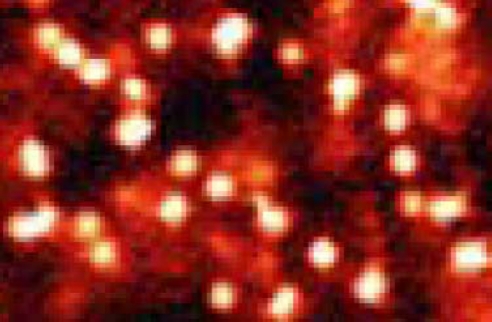
When one examines the constructions (15, 16) used to identify local gap enhancement 〈Δ(d)〉 and its decay with distance d from dopants, one is struck immediately by their circular symmetry. These constructions resemble Huygens wavelets (in 1678), which are a useful construction for identifying propagating wavefronts, but not percolative paths. Many numerical simulations of disordered materials (2–7, 17–21) have identified such paths by using more advanced algorithms. Here, many fragments of percolative paths are visible to the naked eye, typically consisting of chains of three to five evenly spaced dopants (see Fig. 1). The orientations of these fragments appear to be uncorrelated with the topographical superlattice modulations. The nearly even spacing may even reflect coherence waves of carriers pinned to these deep traps (14).

Fig. 1.

A snapshot of a small region (≈4 nm × 10 nm) of figure 1B of ref. 15, showing dopant chain segments [“pearls on a string” (13)], clearly illustrating the formation of a self-organized percolative dopant network.

Why are the chains so short? First, compared with a scatter-shot dopant distribution (which would be dominated by unevenly spaced pairs), the chains are not short. Second, chains in the surface layer can be terminated by percolative dopant bridging to the second and lower layers, as illustrated in many DAQP articles; in other words, one does not expect to see complete percolative paths confined to the surface layer. This situation (fragmentary percolation) has already been analyzed formally for random directed components (18). Note that the entire set of chain fragments is exponentially complex; it cannot be identified exhaustively in polynomial time, but its main qualitative features can still be recognized by studying channels defined by the neighborhoods of most of the chain fragments.

Here [where the dopants are organized by the energy gained by forming “wires” that screen internal ionic electric field (long-range) fluctuations] one might expect the analysis to be easy, but the doubly percolative mixture of pseudogap paths (lower normal state conductivities) with superconductive gap paths (higher conductivities, even in the normal state) greatly complicates the analysis. This is clear from careful study of figure 4 of ref. 16, especially comparing the mean gap 〈Δ(d)〉 (ref; 15, figure 4B) with the noisy gap histogram (ref. 16, figure 4C). The observation that along percolative paths there are two coordinates—parallel (z) and transverse (ρ) to the line segments connecting the dopants—suggests that histograms should be constructed with respect to these two coordinates, identified by hand. Except near chain ends, one would then expect to see 〈Δ(z,ρ)〉 depend weakly on z and strongly on ρ, perhaps even crossing over from a larger and broader pseudogap characteristic (curves 2–4 in the notation of figure 4D of ref. 16) for small ρ to a more superconductive gap (smaller and narrower) characteristic (curve 6) for large ρ.

Such a separation of gap distributions would in itself establish the doubly percolative nature of gaps. Moreover, by studying several samples with different dopant levels (ideally more underdoped), it might even become possible to identify two kinds of channels, and finally separate pseudogap from superconductive gap channels. One could also answer the question as to whether the deep interstitial states are markers for pseudogap wave packets only.

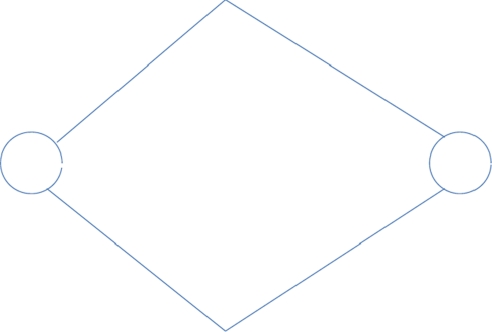
Curvilinear channels are probably an adequate (or even superior) alternative to the more elaborate construction shown in Fig. 2, which can be regarded as a kind of hybrid of Huygens wavelets (in 1678) and Voronoi tessellations (already used by Descartes in 1644). However, the construction shown in Fig. 2, which can be iterated, emphasizes the tendency of the dopants to be evenly spaced along the curvilinear channel [as “pearls on a string” (13)], thereby optimizing both electronic overlap and dopant–dopant strain energies.

Fig. 2.

A possible geometrical construction (hybrid Huygens–Descartes) for a channel between two dopants. For more dopants, these diamonds could be strung together, but because they represent only a first-order approximation to a self-organized pattern, simple curvilinear channel coordinates z,ρ centered on dopant chain segments would probably be an equally or even more effective partitioning. In principle, both constructions can be examined experimentally.

Separated gap distributions in apparently “homogeneous” (but still strongly disordered) surface areas would resolve a long-standing problem. It should be noted that since 1994 electron–phonon interactions have been observed in tunneling I–V fine structure, and that these are associated with superconductive gaps with large gap-to-T_c ratios (22, 23). Such observations are atypical, but they can be explained as associated with rare surface patches devoid of pseudogaps.

In conclusion, modern STM cuprate databases are so rich that much of their content still remains unexplored. By moving from seventeenth century Huygens models to modern DAQP models, we can expect to learn much about the complex mechanisms responsible for HTSC.

Postscript.

The recent discovery (24) of HTSC in layered and F doped (La₂O₂)(Fe₂As₂) provides further evidence [none was actually needed (8, 12–14)] for the DAQP mechanism. Here the metallic Fe₂As₂ layers are separated by insultating La₂O₂ layers. The latter can be doped by partially replacing O by F (nominal F content 5–12%), and the resulting samples are HTSC.

The authors suggest that layering is important in these materials as confinement “causes strong interactions among the electrons.” It is already known that planar confinement alone is not responsible for HTSC in the cuprates; indeed there the metallic elctron density in the cuprate planes is so low that such planes would not be superconductive in isolation, and this density is not significantly enhanced by doping. Instead, as we have often noted, it is the very cause large electron–phonon interactions at the interlayer interstitial O dopants that cause HTSC in the cuprates, and it appears that same mechnism applies here, with respect to interlayer F dopants. In fact, the difference between the metallic electron densities in cuprate and Fe₂As₂ metallic layers makes T_c^max in the cuprates higher than in Fe₂As₂ compounds, because the carriers that spend less time in metallic layers, spend more time near the interlayer dopants.

The interlayer F dopants replacing O can themselves be replaced by Sr replacing La, with similar transition temperatures (25). This shows that the key feature of the interlayer dopants is primarily their topological function as bridges, as was always assumed in the DAQP model. Unlike the cuprates, replacing La by other rare earths Ce (26) or Sm substantially enhances from 26K to 43K; apparently a size effect, as the ionic radii of Sm and Ce are similar and smaller than La.

It has recently been concluded theoretically, based on mean-field models (27), that superconductivity in these materials is not caused by electron–phonon interactions. This is an old story, based on the same kind of band models that led to similar conclusions for cuprates 20 years ago. The correct conclusion to be drawn from such results is that mean-field models cannot describe superconductivity in either doped cuprates or doped (La₂O₂)(Fe₂As₂). The entire phenomenon is percolative in nature, with superconductivity being driven by strong electron–phonon interactions at the interlayer dopant bridges.