Mechano-Coupling and Regulation of Contractility by the Vinculin Tail Domain

Abstract

Vinculin binds to multiple focal adhesion and cytoskeletal proteins and has been implicated in transmitting mechanical forces between the actin cytoskeleton and integrins or cadherins. It remains unclear to what extent the mechano-coupling function of vinculin also involves signaling mechanisms. We report the effect of vinculin and its head and tail domains on force transfer across cell adhesions and the generation of contractile forces. The creep modulus and the adhesion forces of F9 mouse embryonic carcinoma cells (wild-type), vinculin knock-out cells (vinculin −/−), and vinculin −/− cells expressing either the vinculin head domain, tail domain, or full-length vinculin (rescue) were measured using magnetic tweezers on fibronectin-coated super-paramagnetic beads. Forces of up to 10 nN were applied to the beads. Vinculin −/− cells and tail cells showed a slightly higher incidence of bead detachment at large forces. Compared to wild-type, cell stiffness was reduced in vinculin −/− and head cells and was restored in tail and rescue cells. In all cell lines, the cell stiffness increased by a factor of 1.3 for each doubling in force. The power-law exponent of the creep modulus was force-independent and did not differ between cell lines. Importantly, cell tractions due to contractile forces were suppressed markedly in vinculin −/− and head cells, whereas tail cells generated tractions similar to the wild-type and rescue cells. These data demonstrate that vinculin contributes to the mechanical stability under large external forces by regulating contractile stress generation. Furthermore, the regulatory function resides in the tail domain of vinculin containing the paxillin-binding site.

INTRODUCTION

Cell adhesion and cell-cell contacts determine cytoskeletal architecture and mechanical cell properties that in general are a prerequisite for proper metabolism, protein synthesis, and cell survival (1). An important group of adhesive transmembrane receptors that link the extracellular matrix with the cytoskeleton are integrins. These receptors are connected with the focal adhesion complex that consists of talin, vinculin, α-actinin, paxillin, zyxin, and other proteins (2). The formation of the focal adhesion complex is influenced by mechanical tension applied to the receptors either through external forces or internal forces associated with myosin II-driven cell contractility (3–7). The mechanisms that lead to force sensitivity are unknown. A currently debated mechanism considers force-induced structural and conformational changes of focal adhesion proteins that activate downstream signaling events (8).

A major component of the focal adhesion complex is vinculin that has been described as a mechano-coupler and an actin binding protein (9). It consists of 1066 amino acids, has a molecular weight of 117 kDa and, based on its protein structure, can be divided into a head region (residues 1–835) and a tail region (residues 896–1066) connected by a proline-rich region and a flexible hinge (residues 836–895) (10). Vinculin interacts directly with many focal adhesion (FA) proteins including talin, paxillin, α-actinin, and actin (11). Vinculin is involved in the formation of large focal adhesion complexes and is thought to provide mechanical coupling between the integrins and the cytoskeleton (6,12–14).

Given the abundance of vinculin in the cell, its multiple binding sites for other proteins, and its function as a mechano-coupler, experimental data of F9 vinculin knock-out (vinculin −/−) cells show only a surprisingly moderate reduction (25–50%) in cell stiffness compared to wild-type cells (9,13–16). Previous stiffness measurements were obtained under low forces and cell deformations such that cell mechanical properties remained in the linear range. In this work, we asked whether the mechano-coupling function of vinculin would be more relevant under higher forces or cell deformations, and whether the absence of vinculin would then lead to more dramatic effects. An aim of this study, therefore, was to measure cell mechanical behavior of wild-type and vinculin mutant cells under higher mechanical loads.

Another aim was to elucidate signaling functions of vinculin and vinculin domains that affect cell mechanical behavior. The absence of vinculin causes an ∼50% reduction in the cell spreading area, an ∼50% increase in the migration speed, a faster turnover of focal adhesion contacts, and the formation of fewer but longer filopodia (9,12,17,18). When fragments of vinculin (such as the head and tail domains) are transfected stably into vinculin −/− cells, the spreading characteristics of the wild-type cells are recovered partially (13).

Vinculin is implicated in a signaling cascade involving paxillin binding and subsequent inactivation of the extracellular signal-regulated kinase (ERK) and p21 GTPase–activated kinase (PAK) (17–19). In the absence of vinculin, paxillin associates with focal adhesion kinase (FAK) and activates ERK and PAK, both of which can phosphorylate and thereby inactivate myosin light chain kinase (MLCK) (20,21). We reasoned that the reduced activity of MLCK in vinculin deficient cells will result in a reduced actomyosin cycling and therefore a reduced tension generation. Furthermore, we expected that transfecting these cells with the vinculin tail domain, which harbors the paxillin binding site, will restore tension generation.

In this study, the mechano-coupling function of vinculin and its domains were examined using a high-force magnetic tweezer apparatus with force feedback control. Forces between 0.5 and 10 nN were applied to fibronectin-coated super-paramagnetic beads. The stability and the detachment forces of the fibronectin-integrin-cytoskeleton linkage were investigated, and the nonlinear cell mechanical properties were characterized. The tractions due to actomyosin-driven contractile forces that adherent F9 cells exerted on the extracellular matrix were measured to elucidate the mechano-regulating role of vinculin and its head and tail domains.

MATERIALS AND METHODS

Cell lines

F9 mouse embryonic carcinoma cells were a kind gift of Dr. E.D. Adamson (La Jolla, CA) and were originally generated and characterized by Coll et al. (22) and Xu et al. (23). F9 vinculin −/− cells were transfected with the full-length mouse vinculin cDNA (24). Coll et al. (22) constructed a pCNXN2 vector that expresses the following constructs:

1. Vinculin tail, which was composed of the entire vinculin sequence minus the talin and α-actinin binding sites, resulting in a sequence with only residues 811–1066.

2. Vinculin head, which was composed of the entire vinculin sequence minus the paxillin and actin binding sites, resulting in a sequence from residues 1 to 821.

3. Vinculin rescue, which was composed of the entire mouse vinculin sequence with an 83% vinculin expression level compared to wild-type.

The expression levels of these constructs were determined by Western blotting (22).

Cell culture

All chemicals were purchased from Sigma (Taufkirchen, Germany) unless otherwise indicated. Cells were maintained in low-glucose (1 g/L) Dulbecco's modified Eagle's medium (DMEM) supplemented with 10% fetal calf serum (low endotoxin), 2 mM L-glutamine, and 100 U/ml penicillin-streptomycin (DMEM complete medium, all from Biochrom, Berlin, Germany). Eighty-percent confluent, adherent cells were detached using Accutase (PAA Laboratories, Linz, Austria), seeded at a density of 2 × 10⁵ cells onto Ø 35 mm culture dishes (Nunclon Surface, Nunc, Wiesbaden, Germany) in DMEM complete medium and incubated at 37°C and 5% CO₂ overnight.

Cell spreading and actin staining

Cells were harvested using Accutase, and 10⁵ cells were seeded onto an 18 mm² cover slide (Menzel, Braunschweig, Germany) in a 3.5 cm well. After 24 h, the cells were fixed with 3% paraformaldehyde solution for 15 min at room temperature, washed twice with PBS buffer, and stained for 30 min with 66 nM Alexa Fluor 546 Phalloidin (Molecular Probes, Eugene, OR) in 3% paraformaldehyde solution containing 500 μg/ml L-α-lysophosphatidylcholine. After washing, cell nucleoli were stained with 1 mg/ml Hoechst dye 33342 for 5 min and then were embedded in 30 μl Vectashield mounting medium (Vector Laboratories, Burlingame, CA). The coverslips were sealed using nail polish, and 10–20 randomly selected fields of view were recorded at 20× magnification. The number of cells and their spreading area were computed using MatLab image analysis (MatLab; The MathWorks, Natick, MA).

The actin cytoskeleton was visualized by taking 100 z-sections (250 nm apart) with a 63× magnification, 1.35 NA objective. The images were deblurred with a no-neighbor algorithm and a maximum intensity projection was obtained from the series of images. To visualize the three-dimensional actin structure, each pixel was color-coded according to the z-position of the maximum intensity value.

Magnetic tweezers

The principle of the magnetic tweezer device has been described by Alenghat et al. (16) and Bausch et al. (25). Super-paramagnetic 4.5 μm epoxylated beads (Invitrogen, Karlsruhe, Germany) were coated with human fibronectin (100 μg/ml, Roche Diagnostics, Mannheim, Germany) in PBS at 4°C for 24 h. The beads were washed in PBS and stored at 4°C. Before measurements, the beads were sonicated and added to the cells (2 × 10⁵ beads/dish) and incubated for 30 min in 5% CO₂ at 37°C. A high magnetic field gradient was generated using a 2-cm-long, 1-cm-diameter solenoid (with 250 turns of a 0.4-mm diameter copper wire) with a needle-shaped core (HyMu80 alloy, Carpenter, Reading, PA). The needle tip was placed at a distance between 20 and 30 μm from a bead bound to a cell using a motorized micromanipulator (Injectman NI-2, Eppendorf, Hamburg, Germany). Bright-field images of the cell, the bead and the needle tip were taken by a charge-coupled device camera (ORCA ER, Hamamatsu, Hamamatsu City, Japan) at a rate of 40 frames per second. The bead position was tracked using an intensity-weighted center-of-mass algorithm. A preset force was maintained by continuously updating the solenoid current or by moving the solenoid such that the needle-tip to bead distance was kept constant. All measurements from all the beads in each well were performed at 37°C for 1 h, using a heated microscope stage on an inverted microscope at 40× magnification (NA 0.6 objective) in bright-field. To ensure that cells had not experienced any significant forces resulting from a previous measurement, the needle was moved at least 0.5 mm between any two measurements.

Force protocol and data analysis

When a force step with amplitude ΔF was applied to a bead, it moved toward the needle tip with a displacement d(t). The ratio d(t)/ΔF defines the creep response J(t), which, for all force amplitudes, is described by a power-law,

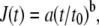(1)

where t₀ is a reference time (set to 1 s), a describes the elastic cell property in units of μm/nN and corresponds to a compliance (an inverse of stiffness), and the exponent b describes the dissipative (frictional) cell property and reflects the stability of the force-bearing structures of the cell that are connected to the bead (26). For example, a value for b = 1 indicates Newtonian viscous or fluidlike behavior, whereas b = 0 indicates an elastic, solidlike behavior (27). It is important to note that the parameters a and b change with the amplitude of the applied force, indicating a force-dependent nonlinearity of the creep modulus, such that a decreases with increasing force, whereas b shows diverging behavior.

The parameters a and b of the creep response were replaced by two arbitrary force-dependent functions a(F) and b(F) to describe the force-dependence of the creep response:

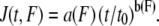(2)

The bead displacement d(t) resulting from an arbitrary force F(t) can be predicted from a nonlinear superposition principle:

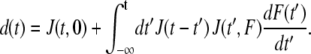(3)

The force-dependent, differential elastic modulus, 1/a(F), and the differential power-law exponent, b(F), can be easily evaluated at discrete forces if the force protocol follows a staircaselike pattern. A force protocol with nearly logarithmically spaced force steps according to 0.5, 1, 1.5, 2, 3, 4, 5, 6, 8, and 10 nN, where each force step lasted 1 s, was found to work best. Equation 3 was fitted to the bead displacement data, and for every force level a value for a(F) and b(F) was obtained.

Bead detachment

Some beads detached from the cell during force application. The fraction of beads that detached at a given force was used to quantify the bead binding strength to the cell.

Traction microscopy

Gels (4.7% acrylamide/0.24% bis-acrylamide) for traction experiments were cast on rectangular 75 × 25 mm nonelectrostatic silane-coated glass slides (Menzel) according to the procedure described by Wang and Pelham (28). The Young's modulus of the gels was measured with a magnetically driven plate rheometer and found to be 5.4 kPa (29). Yellow-green fluorescent 0.5 μm carboxylated beads (Molecular Probes) were suspended in the gels and centrifuged at 300 g toward the gel surface during polymerization at 4°C. These beads served as markers for gel deformations. The surface of the gel was activated with sulfo-SANPAH (Pierce Biotechnology, Rockford, IL) and coated with 50 μg/ml bovine collagen G (Biochrom). The cell suspension added on the gel was contained within a silicone ring (flexi-perm, In Vitro, Göttingen, Germany) attached to the glass slide. Cell tractions were computed from an unconstrained deconvolution of the gel surface displacement field measured before and after cell detachment with 8 μM Cytochalasin D and Trypsin/EDTA (0.25/0.02%) in PBS (30). During the measurements, the cells were maintained at 37°C in humidified atmosphere containing 5% CO₂. Gel deformations were estimated using a Fourier-based difference-with-interpolation image analysis (31).

RESULTS

Cell morphology

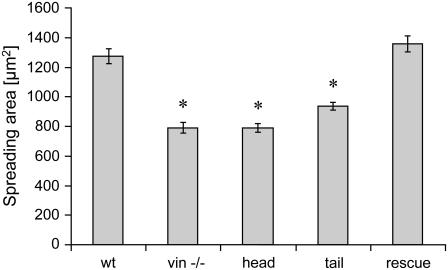
Compared to F9 vinculin wild-type cells, the spreading area of vinculin −/− and vinculin head cells were reduced to 62%, the spreading area of vinculin tail cells was reduced to 75%, and the spreading area of vinculin rescue cells was increased by 9%. These results are shown in Fig. 1 and confirm previous observations (9).

FIGURE 1.

Spreading area (mean ± SE) of F9 wild-type and vinculin mutant cell lines.

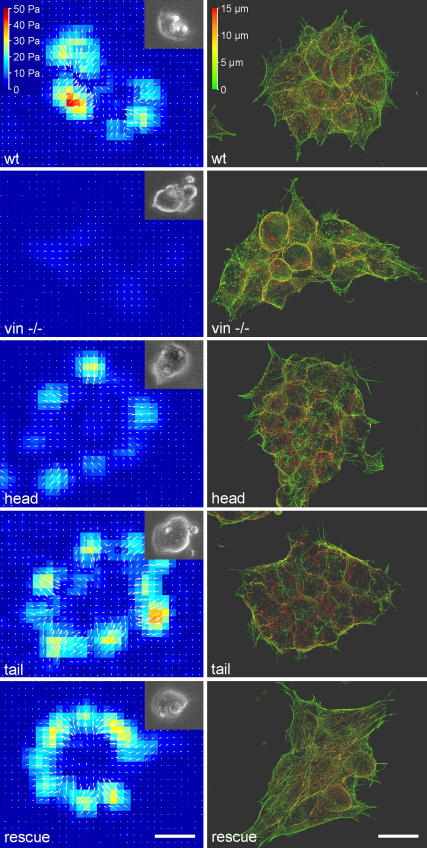
All cell lines formed cell clusters containing ∼10–20 cells. The cells were rounded and reached a height of ∼15 μm in wild-type and rescue cells and ∼20 μm in the other cell lines (Fig. 2). The actin cytoskeleton of all vinculin mutant cell lines was stained with fluorescently labeled phalloidin and visualized with a maximum intensity projection from multiple z-sections. The architecture of the actin cytoskeleton was similar in all mutant cell lines, with pronounced cortical actin and a few stress fibers. Actin fibers appeared somewhat shorter and more dispersed in the vinculin −/−, head, and tail cells, and domelike cell protrusions were frequently observed.

FIGURE 2.

(Left) Traction maps of a representative F9 wild-type cell cluster and of vinculin mutant cell clusters. The traction direction is indicated by white arrows. Insets show the bright-field view of the same cells. (Right) F-actin staining of F9 wild-type and vinculin mutant cells (maximum intensity projection of the z stacks). The color range represents the height from the basal cell surface. The scale bars are 20 μm.

Before staining, the cells were incubated for 30 min with fibronectin-coated beads. These beads were slightly autofluorescent, and their locations on or within the cells were observed under epifluorescence. At least half of the beads were internalized by the cells, regardless of the cell line used. The beads did not appear to induce local actin reorganization (Fig. 2).

Creep response

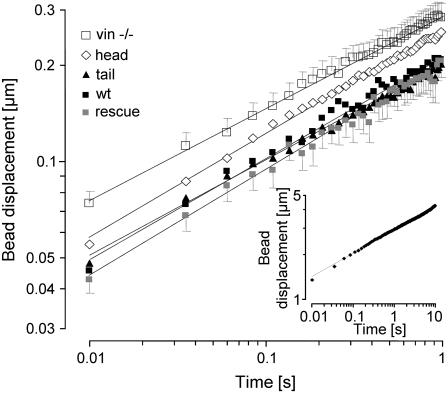
A normalized creep response J(t) was determined for each cell line as the ratio of bead displacement d(t) and the amplitude of the step force ΔF. The creep response of most cells followed a power-law relationship (Eq. 1 and Fig. 3).

FIGURE 3.

Creep response (geometric mean of bead displacement over time ± geometric SE) to a 0.5 nN force step. The creep response for all cells followed a power-law relationship over two time decades and differed between F9 wild-type and the vinculin mutant cell lines. Between 60 and 86 cells from each cell line were measured. (Inset) Creep response of a representative F9 wild-type cell measured over three time decades (0.01–10 s). The dotted lines show the power-law fit (Eq. 1) to the data.

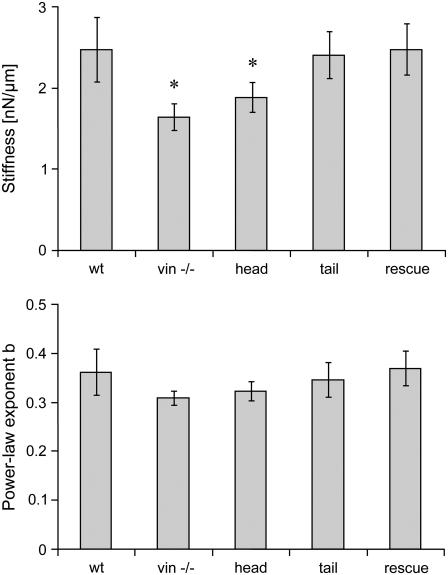
Equation 1 was fitted to the displacement of each bead in response to a 0.5 nN force step. From the fit, one value for cell stiffness (1/a) and one value for the power-law exponent (b) were obtained. For the vast majority of the beads, the quality of the fit was good (Fig. 3). The median deviation between the fit and the measured creep response was 3.7% (median correlation coefficient, r² = 0.97). Within any given cell line, the stiffness values of individual cells showed approximately a log normal distribution, and the power-law exponent showed a normal distribution (data not shown). To obtain the average response of a given cell line, the geometric mean of stiffness and the arithmetic mean of the power-law exponent, averaged over all cells, were computed. F9 wild-type, rescue, and tail cells all displayed nearly identical stiffness values, whereas the stiffness of vinculin −/− and head cells were 33% and 24% lower, respectively (Fig. 4). These differences were statistically significant (p < 0.05). However, the power-law exponent did not differ significantly between F9 wild-type and the four vinculin mutant cell lines (Fig. 4).

FIGURE 4.

Stiffness (top row) and power-law exponent (bottom row) in F9 wild-type and vinculin mutant cell lines obtained from the fit of Eq. 1 to the creep response to a 0.5 nN force step. Between 60 and 86 cells from each cell line were measured. (*p < 0.05.)

Bead binding strength

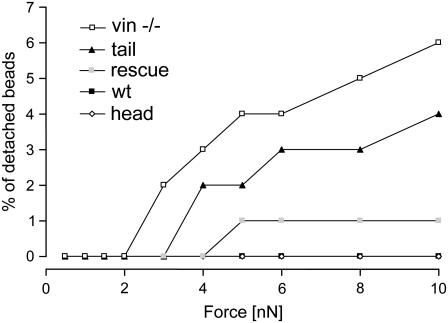
The binding strength between a bead and a cell was determined by applying a force to the bead that increased over time from 0.5 to 10 nN in a staircaselike fashion. The fraction of beads that detached at a given force level was a measure of the adhesion strength, or yielding force. Between 0.5 and 2 nN, no bead detached from any cell line (Fig. 5). With increasing force, marked differences between the vinculin mutant cell lines became apparent. At forces up to 10 nN, the bead detachment remained negligible for F9 wild-type, rescue, and head cells. At 10 nN, 4% of the beads on the tail cells and 6% of the beads on vinculin −/− cells became detached (Fig. 5).

FIGURE 5.

The percentage of detached beads versus force for the F9 wild-type and the vinculin mutant cell lines. Between 60 and 86 cells from each cell line were measured.

Nonlinear cell mechanical properties

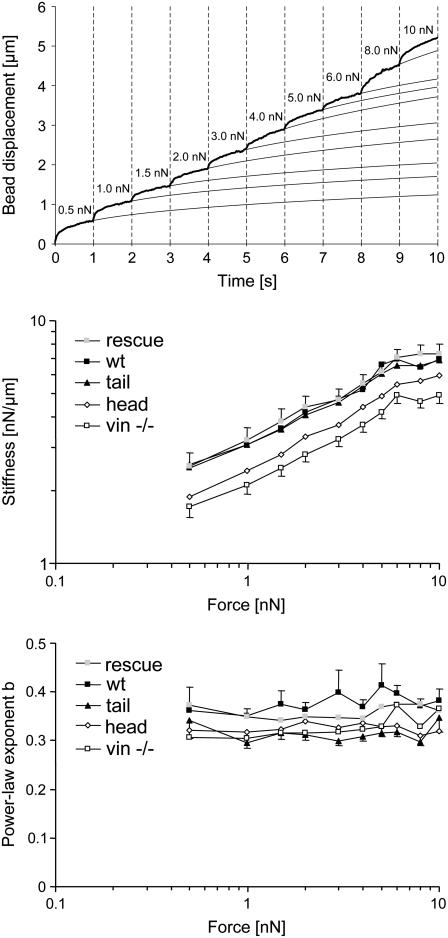
Using the same staircaselike force protocol as used above for measuring the bead binding strength, the differential creep modulus of those beads that remained attached to the cell throughout the measurement were evaluated (Fig. 6). Over the entire force range, the creep response showed highly nonlinear behavior. For most beads, the creep modulus decreased with increasing force, which is equivalent to stress stiffening. The power law exponent, or equivalently, the slope of the displacement curve after each incremental force step, remained approximately constant. However, a sudden increase in the slope was commonly observed with beads immediately before cell detachment (data not shown). For a quantitative analysis of these observations, Eq. 2 was fitted to the displacement curves (Fig. 6). For each bead and force step, one differential stiffness value 1/a and one differential power-law exponent b(F) was obtained. The median deviation between the fit of Eq. 2 to the data and the measured creep response was 0.54%, and the median correlation coefficient r² between the fit and the data was 0.99.

FIGURE 6.

Measurement of the nonlinear creep modulus. (Top) An example of the displacement of a bead on a F9 wild-type cell in response to a staircaselike force pattern. The measured displacement values are shown as a thick line, and the fits of Eq. 2 to the data are shown as thin lines. (Center) The differential cell stiffness (geometric mean ± geometric SE) increased with force by a similar factor in all the cell lines, as indicated by the nearly parallel lines of stiffness versus force in a log-log plot. (Bottom) The power-law exponent, b, was force-independent in all cell lines. (Note: the stiffness values and exponents at 0.5 nN are not identical with the values in Fig. 4 because detached beads were excluded from this analysis.)

To obtain the average response of a cell line for each force level, we computed the geometric mean of the differential stiffness, and the arithmetic mean of the differential power-law exponent, averaged over all beads that remained attached to the cell throughout the measurement. In all the cell lines, the differential stiffness increased with increasing force (Fig. 6). This force stiffening was similar in all cell lines. Cell stiffness at 10 nN had increased by threefold compared to the cell stiffness measured at 0.5 nN. The order of soft to stiff cell lines (Fig. 4, top) remained unchanged at all force levels (Fig. 6).

The average power-law exponent of F9 wild-type and the four vinculin mutant cell lines did not significantly change with force (Fig. 6). Similar to the data at 0.5 nN (Fig. 4, bottom), differences between the power-law exponents throughout the force range were not significantly different between the cell lines.

Cell tractions

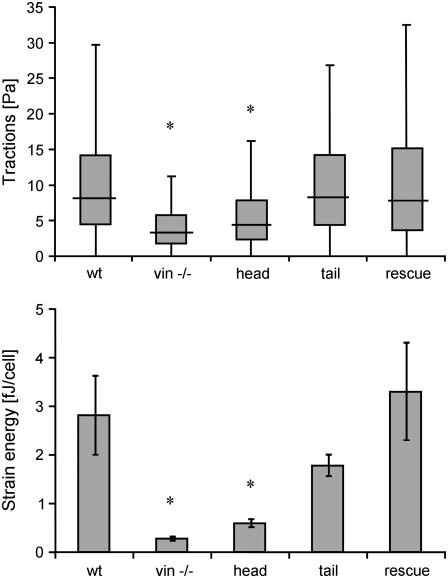
Cell aggregates consisting of between 10 and 20 cells generated tractions predominantly at the periphery. In general, the direction of the tractions pointed toward the aggregate center (Fig. 2). The traction “footprint” did not follow the shape or arrangement of any individual cell but rather that of the cell aggregate (Fig. 2). The 25–95th percentiles of the tractions of each cell aggregate were taken as an index of the force-generating potential. Regardless of the percentile, tractions were similar in F9 wild-type, rescue, and tail cells, but were significantly (p < 0.05) suppressed in vinculin −/− cells and head cells (Fig. 7, top).

FIGURE 7.

25th, 50th, 75th, and 95th percentile (mean) of the cell tractions within cell aggregates (top), and elastic strain energy (mean ± SE) stored in the extracellular matrix due to cell tractions (bottom). The number of cell aggregates analyzed were 31 (wt), 32 (vin −/−), 61 (head), 86 (tail), and 21 (rescue). Each cell aggregate consisted of between 10 and 20 cells. (*p < 0.05.)

The elastic strain energy stored in the polyacrylamide gel due to the cell tractions was calculated according to Butler et al. (30) as the product of local tractions and deformations, integrated over the spreading area of the cells. The strain energy was normalized by the number of cells in each aggregate, giving the elastic strain energy in units of femtoJoules per cell (Fig. 7, bottom). Compared to F9 wild-type cells, the elastic strain energy decreased to 11% in vinculin −/− cells, to 21% in head cells, and to 63% in tail cells; the strain energy in the vinculin rescue cells increased by 18%, but this increase was not statistically significant (p > 0.05). Compared to wild-type cells, the elastic strain energy of tail cells was significantly decreased, but this decrease was attributable to the smaller spreading area (see Fig. 1) and not to a decreased force-generating potential (see Fig. 7, top) of the tail cells.

DISCUSSION

Mechanical tension that is transmitted between the extracellular matrix and the cytoskeleton plays a critical role in determining cell structure and function. The forces generated by, and in, a cell have been shown to regulate many biological functions (8). In this study, we examined the mechano-coupling and regulating function of vinculin and its head and tail domains in F9 cells.

Cell stiffness

Cell stiffness is a measure of the number and the combined-bond elasticity of molecular interactions that transfer mechanical forces between the cell and the probe (e.g., a ligand-coated bead) (32,33). The stiffness depends on multiple factors including cell geometry, cell thickness below the probe, the degree of probe embedment in the cell, contact area between the probe and the cell, tensile stress generated in the cytoskeleton, the ligand concentration on the probe, the number of integrins, and the number of other focal adhesion and cytoskeletal proteins associated with the probe (33–38).

Cell stiffness in vinculin −/− cells was reduced and could be restored to F9 wild-type levels in rescue cells. This observation is consistent with previously published data on F9 wild-type, vinculin −/−, and rescue cells that have been obtained using a variety of different methods including atomic force microscopy, cell poking, plate rheometry, magnetic twisting cytometry, and magnetic tweezers (9,13–16,39). Transfecting vinculin −/− cells with the head domain of vinculin, which harbors the α-actinin and talin binding sites, showed only an insignificant increase in stiffness compared to vinculin −/− cells. This observation is also consistent with the previous studies. Transfecting vinculin −/− cells with the vinculin tail fragment, which harbors the actin and paxillin binding sites, showed a return of cell stiffness to the levels of F9 wild-type cells. This observation is conspicuously different to an earlier study that did not show a full recovery to F9 wild-type levels (14). In that study, an AFM probe was used that was not specifically bound to the integrin receptors and therefore the measurement may have been influenced by cell shape to a larger extent than in this study.

Given the many factors listed above that impact cell stiffness, the results in this study are insufficient to decide whether the reduced stiffness of vinculin −/− cells and head cells was entirely due to fewer molecular interactions within the focal adhesion complex (reduced mechano-coupling) as suggested by previous studies. Alternatively, vinculin-mediated signaling events may have affected cell shape, bead internalization, contractile stress, or the reorganization of force-transmitting structures. Further biochemical and biophysical studies are needed to clarify this detail.

Binding strength

Bead-binding strength is defined here as the force that is necessary to detach a bead from the cell. Similar to cell stiffness, it depends on the number of molecular interactions that transfer mechanical forces between the cell and the bead, i.e., between 1), the fibronectin-coated bead and the integrins; 2), the integrins and the FA proteins; and 3), the FA proteins and the cytoskeleton. Unlike cell stiffness, the binding strength also depends on the yielding force of those molecular interactions. Of all cell lines tested, vinculin −/− cells displayed the lowest binding strength to fibronectin-coated beads. With increasing pulling forces, more beads detached from vinculin −/− than from F9 wild-type or from rescue cells (Fig. 5). These results are consistent with cell stiffness measurements (Fig. 4), and are also consistent with the interpretation that vinculin is a force-transmitting component that strengthens the focal adhesion complex.

Vinculin −/− cells expressing the head domain displayed a higher binding strength than those expressing the tail domain. This observation is contrary to that found for mechanical stiffness, where tail cells were stiffer than head cells. A possible explanation is that the higher stiffness of tail cells is due to a higher cytoskeletal (contractile) tension generated by these cells, whereas the interactions formed between the vinculin tail domain and its binding proteins break at lower forces than interactions formed by the vinculin head domain and its binding proteins. This interpretation is consistent with the view that the vinculin tail can only bind to one type of structural protein, i.e., actin, while the head domain can connect talin (which binds to integrins) with α-actinin (which binds to actin) and thereby provide a mechanical clutch (10,40,41). Moreover, it is also possible that the binding of the vinculin head domain to talin may further activate the integrin receptors and increase its ligand binding affinity, although such a mechanism has not yet been demonstrated. Nonetheless, the fraction of beads that detached at the highest pulling force remained low even in vinculin −/− cells, indicating that vinculin is not an essential mechano-coupling protein.

Stress-stiffening

Another sensitive assay to detect yielding is the measurement of the differential cell stiffness at higher pulling forces. Stress-induced irreversible yielding decreases the cell stiffness, regardless of the exact nature of the yielding interactions (32). Cell stiffening at stress- and strain levels comparable to those used in this study have been described recently in microplate cell-stretch experiments (42). The molecular origin of stress- and strain-induced cell stiffening is not well understood. Most models consider as the main source of nonlinear cell mechanical behavior certain geometric nonlinearities that arise when cytoskeletal filaments bend or stretch under stress (42–46). Accordingly, the operating point of the stress-strain relationship in a network of cytoskeletal filaments is set by the prestress (the contractile tension) and can be sensitively modulated by actin crosslinking proteins (44–46). We observed nearly identical stiffening behavior in all cell lines (Fig. 6). The cell stiffness increased monotonically with force according to a power-law with a slope of ∼0.4. The presence or absence of the entire vinculin molecule or of the vinculin head and tail domains did not alter the stiffening response. This finding is consistent with the observation that the structure of the actin cytoskeleton was similar in all cell lines (Fig. 2), if one considers the stiffening response to be mostly due to the bending geometry and structure of the cytoskeleton. By the same argument, the nearly identical stiffening behavior in all cell lines suggests that vinculin is not a critical component of the force transmission pathway. Stress-induced yielding events do not seem to be intensified by the absence of vinculin.

Cell morphology and bead internalization

Vinculin −/−, head, and tail cell lines spread less than F9 wild-type and rescue cells. The results are similar to previously reported findings, despite the fact that not single cells but clusters of 10–20 cells were analyzed (13). F-actin staining of these cell lines revealed some subtle differences; for example, more scattered actin filaments and rounder appearance of the vinculin −/−, head, and tail cells. Nonetheless, all cell lines readily internalized fibronectin-coated after 30 min of bead incubation.

Power-law exponent of the creep modulus

Both the magnitude and the time dependence of the creep responses of F9 wild-type and the vinculin mutant cell lines differed widely between individual cells. In every instance, the creep response conformed to a weak power-law dependence of bead displacement against time according to Eq. 1. The observation of a power-law dependence of the creep response, or equivalently, the complex modulus of cell rheology, is consistent with the literature (26,33,35,37,47–49). As mentioned in Materials and Methods, the fit of Eq. 1 to the creep response of each bead yielded one value for cell stiffness (1/a) and one value for the power-law exponent (b). As discussed comprehensively in the literature, a higher power law exponent reflects a lower dynamic stability and hence a higher turnover of the molecular interactions that carry the mechanical stress during a creep measurement (26,27,32,33,35,37,47,48,50). At a pulling force of 0.5 nN, the power-law exponent did not differ between F9 wild-type cells and vinculin mutant cells. These results are surprising because vinculin −/− cells have been reported to exhibit a faster turnover of focal adhesions (17). This apparent conflict is explained by the duration of our creep measurements (of 1 s) that was too short to pick up a turnover of a significant fraction of focal adhesion proteins. Unfortunately, creep measurements are not suitable for measurements lasting substantially longer because active transport and cytoskeletal remodeling processes would interfere (51). At higher pulling forces up to 10 nN, the power-law exponent of the creep modulus also did not change significantly, indicating that no force-induced yielding or fluidization of stress-bearing structures occurred. These results are consistent with our findings from the bead binding strength and stress stiffening assays and again suggest that vinculin is not essential for the transmission of high forces between integrins and the cytoskeleton.

Cell tractions and their regulation by signaling pathways

Up to this point, the differences between F9 wild-type and vinculin mutant cell lines have been only small or moderate. However, the tractions exerted by these cells to the extracellular matrix differed markedly. Compared to F9 wild-type cells, vinculin −/− and head cells showed a marked reduction in traction generation, while the tractions generated by tail cells were not decreased (Figs. 2 and 7). These results illustrate that the contractile stress generation in F9 cells is dependent on the presence of the vinculin tail. Note, however, that the tractions of the F9 cell lines were very low compared to most other cell types (3,30,36,52,53), possibly due to the poorly developed stress fibers in F9 cells (Fig. 2).

Between cell lines, stiffness varied by only ∼50%, while the tractions varied considerably more (approximately twofold in maximum tractions, approximately ninefold in strain energy), suggesting that the differences in stiffness are not solely determined by the differences in cytoskeletal prestress. This finding does not necessarily stand in contrast to Wang et al. (54) who reported a proportionality between cell stiffness and prestress; as discussed above, an absolute value of cell stiffness is difficult to measure using bead-based techniques, while traction measurements are intrinsically quantitative. To investigate the extent to which the stiffness of vinculin mutant cell lines is determined by cytoskeletal prestress, one would need to pharmacologically alter cell tractions and simultaneously measure relative changes in cell stiffness.

Tension and contractile forces in cells are generated by actomyosin cycling that is initiated by myosin light chain phosphorylation from myosin light chain kinase (MLCK) and Rho-kinase (55). MLCK is phosphorylated and subsequently inhibited by extracellular-related kinases 1,2 (ERK1/2) and p21 GTPase-activated kinase (PAK) (20,21,56). The involvement of vinculin in ERK signaling has been described recently by Subauste (18) and Hong (17), both of whom showed that upon cell adhesion of vinculin −/− cells, ERK is activated through the following mechanism: vinculin competes with FAK for paxillin binding, with the paxillin-binding region located on the vinculin tail (18). Consequently, in the presence of the vinculin tail, FAK-paxillin binding is reduced, resulting in a reduced activation of ERK and PAK (18,57). Conversely, in the absence of the vinculin tail, an increase in complexed FAK-paxillin will activate both ERK1/2 (18) and PAK (57) that both inhibit MLCK. The hypothesis, then, would be that cells lacking the vinculin tail domain exhibit a reduced tension generation and reduced tractions. Our data (Fig. 7) support this hypothesis. This needs to be further investigated, e.g., by point mutations and pharmacology studies of the intimate paxillin-FAK and paxillin-vinculin interactions, and inhibition studies of the downstream ERK1/2 and PAK signaling pathways.

CONCLUSION

Our data demonstrate that vinculin contributes to, but is not essential, for the force transfer between integrins and the cytoskeleton at high forces. This function is mainly conferred by the vinculin tail domain. More strikingly, cells lacking vinculin showed a markedly suppressed contractility that was restored by transfecting the vinculin tail domain but not the head domain. Our data suggest that the mechano-coupling function of vinculin is not primarily due to a strengthened and direct mechanical linkage between focal adhesion and cytoskeletal proteins, but rather, that paxillin binding to the vinculin tail region activates actomyosin cycling by suppressing the paxillin-FAK-ERK and -PAK signaling cascade. Reduced actomyosin cycling in turn leads to decreased cytoskeletal tension and hence to the decreased stiffness that had been reported for vinculin-deficient cells.