A SIMPLIFIED MODEL FOR PREDICTING MALARIA ENTOMOLOGIC INOCULATION RATES BASED ON ENTOMOLOGIC AND PARASITOLOGIC PARAMETERS RELEVANT TO CONTROL

Abstract

Malaria transmission intensity is modeled from the starting perspective of individual vector mosquitoes and is expressed directly as the entomologic inoculation rate (EIR). The potential of individual mosquitoes to transmit malaria during their lifetime is presented graphically as a function of their feeding cycle length and survival, human biting preferences, and the parasite sporogonic incubation period. The EIR is then calculated as the product of 1) the potential of individual vectors to transmit malaria during their lifetime, 2) vector emergence rate relative to human population size, and 3) the infectiousness of the human population to vectors. Thus, impacts on more than one of these parameters will amplify each other’s effects. The EIRs transmitted by the dominant vector species at four malaria-endemic sites from Papua New Guinea, Tanzania, and Nigeria were predicted using field measurements of these characteristics together with human biting rate and human reservoir infectiousness. This model predicted EIRs (± SD) that are 1.13 ± 0.37 (range = 0.84–1.59) times those measured in the field. For these four sites, mosquito emergence rate and lifetime transmission potential were more important determinants of the EIR than human reservoir infectiousness. This model and the input parameters from the four sites allow the potential impacts of various control measures on malaria transmission intensity to be tested under a range of endemic conditions. The model has potential applications for the development and implementation of transmission control measures and for public health education.

INTRODUCTION

Complex mathematical models are often incomprehensible to non-specialists and few have been applied by anyone other than their original authors. The pitfalls of over-elaboration and tenuous assumptions in the modeling of malaria transmission have been summarized by Koella, “The qualitative predictions of simple models may be more biologically meaningful than the precise quantitative predictions of complex models involving many parameters.”¹ This is an especially important point in the context of disease control because the majority of those who might use such models come from medicine or public health backgrounds, rather than the basic sciences.¹ It is therefore essential that simple models are made available that are broadly accessible and conceptually straightforward, and that use input and output variables that are meaningful in the field.

The impact of malaria on mortality and morbidity are determined by vector-mediated transmission intensity^2–4 and post-inoculation factors that include pre-existing immunity, age, nutrition, genetic background, and access to anti-malarial drugs.^5–10 Ideally, mortality and morbidity should be the final outputs of malaria models.^2,11–13 The relationship between malaria transmission intensity and disease burden is poorly understood and recently has been a topic of considerable debate.^2–4,14 Nevertheless, available evidence indicates that malaria prevalence, incidence, morbidity, and mortality all increase with transmission intensity.^2–4,15 We propose that models should express the transmission component of this combination as the entomologic inoculation rate (EIR) because it is a direct index of human exposure to malaria parasites that can be measured directly in the field.^4,16,17 Unlike vectorial capacity or stability index, EIR is a direct determinant of malaria prevalence, parasite density, incidence, and mortality.^2–4,17,18 Furthermore, the impacts of control measures on these important outcomes of malaria exposure all depend on the baseline EIR of the area to which they are applied.^2,4,15

We describe the adaptation of a relatively simple cyclical model¹⁹ to allow the calculation of transmission intensity as a function of its three fundamental contributors: 1) the infectiousness of the human reservoir, 2) the capacity of individual mosquitoes to transmit malaria, and 3) the mosquito emergence rate relative to human population density. The model was used to predict the EIR of four disparate malaria endemic sites and found to be quite accurate at assessing the potential impact of malaria transmission control on EIR in endemic settings.²⁰

METHODS

Malaria transmission model framework

The major conceptual difference between previous models and the one presented here is the perspective. Malaria transmission is generally modeled from the starting perspective of individual humans and the vector biting densities they experience.^1,19,21 Here we model malaria transmission based on the life histories of individual mosquitoes, which when combined with mosquito emergence rates relative to human population size and infectiousness, define the transmission intensity experienced by any given human population. Thus, malaria transmission is resolved into three components that are conceptually easy to separate and are independently relevant to malaria epidemiology and control.

The model described is based on the principles of an existing cyclical model¹⁹ that has previously been used to measure vector infection and transmission parameters in the field^21,22 and to assess the potential of vaccines against the malaria parasite as tools to reduce malaria transmission.²³ This is a deterministic, cyclical model, meaning that estimates are calculated directly and that blood acquisition by mosquitoes occurs at fixed intervals during its lifetime rather opportunistically at a fixed rate.¹⁹ We have kept symbols and definitions as consistent with existing terminology as possible (Table 1). In addition to the rigorous descriptions in Table 1, we also present a schematic outline of the model structure and the role of its parameters in Figure 1. Like most others, our model assumes that the length of the feeding cycle (f), the probability of surviving per feeding cycle (P_f), the number of days required for parasite development (n), and the susceptibility of the vector to infection as well as ability to become infectious (κ) do not change with age. Mathematically, this means that f, P_f, n, and κ are independent of the number of feeding cycles a given mosquito has completed (i) and whether the mosquito is infected or not, at any cycle. This model also assumes that each vector feeds from a single host during each feeding cycle and that the vector and human populations mix homogeneously. Deviations from such assumptions and their quantitative importance have been discussed elsewhere.^1,18,24 The only major difference between this model and the cyclical form from which it was derived is that the first cycle starts at emergence rather than the first bloodmeal. This approach is consistent with the intended perspective of the model and allows the effects of control measures that act before the first bloodmeal to be modeled.

Table 1.

Symbols and definitions for the malaria transmission model

Symbol	Definition	Reference
bh	Mean number of human bites per emerging mosquito during its lifetime	This paper
β	Mean number of infectious human bites per emerging mosquito during its lifetime	This paper
δ	Number of previous bloodmeals that occurred too recently for ingested parasites to have become infectious	This paper
E	Rate of emergence of vectors from larval habitats within a discrete malaria transmission focus	This paper
EIR	Entomologic inoculation rate	4, 44
f	Interval between blood feeds	This paper
F	Mean number of feeding cycles required for parasite development	19
HBt	Rate at which individual human hosts are bitten	19
i	Number of feeding cycles completed since emergence (i = 0)	This paper
Ii	Probability of surviving to and being infectious by feeding cycle i	This paper
k	Probability of a vector becoming infected per bite on an infectious human	19
K	Probability of a vector becoming infected per human bite (K = xk)	19
κ	Probability of a vector becoming infectious per human bite, if it survives long enough (κ = Kv)	This paper
L	Lifetime transmission potential of individual vectors	This paper
n	Mean number of days required for parasite sporogonic development	19, 36, 45
Nh	Number of humans within a discrete malaria transmission focus	This paper
P	Probability of a mosquito surviving one day	36
Pf	Probability of surviving for one feeding cycle	19
Pi	Probability of surviving to feeding cycle i	This paper
Q	Proportion of bloodmeals taken from humans	19
S	Proportion of mosquitoes with infectious sporozoites in the overall population	19
Si	Proportion of mosquitoes with infectious sporozoites by feeding cycle i	This paper
v	Proportion of infected vectors that will become infectious if they survive long enough	19
x	Proportion of blood feeds upon human hosts that are infectious	36

Figure 1.

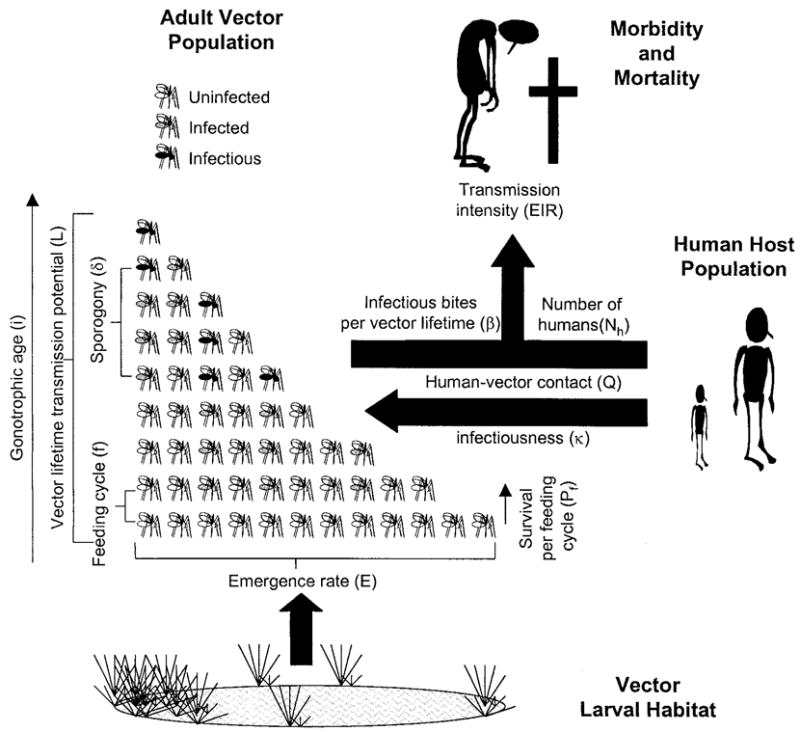
Schematic outline of the model and its major parameters. See Table 1 for definitions.

Modeling malaria transmission by individual mosquitoes

P_i, the probability of survival to any given feeding cycle (i), is defined either in terms of the daily survival parameter of classical models (P) and the mean interval between blood meals (f, the feeding cycle length) or in terms of the survivorship per feeding cycle (P_f) as defined previously:¹⁹

$${\text{P}}_{\text{i}}={(\text{P})}^{\text{fi}}={({\text{P}}_{\text{f}})}^{\text{i}}$$ (1)

Here we define b_h as the mean number of human blood-meals a vector will acquire during its lifetime. During its lifetime, a typical mosquito will bite humans in proportion to its probability of reaching each possible feeding cycle and Q, its preference for human hosts:^19,25

$${\text{b}}_{\text{h}}=\text{Q}\sum {({\text{P}}_{\text{f}})}^{\text{i}}\text{for i}=1,2,3\dots$$ (2)

The overwhelming proportion of the total bites on humans by mosquitoes are by those in the youngest age groups. Thus, b_h can be approximated by summing the probabilities of surviving to each feeding cycle, up to feeding cycle 20 or less and multiplying this sum by Q. Note that because the first cycle in our form begins at emergence rather than at recruitment to the human-feeding population, this differs fundamentally from equivalent forms of the original model in which terms are summed from the power of zero upwards (i = 0, 1, 2 …).¹⁹ A possible disadvantage of our approach is that the sums cannot be solved as simply and elegantly, as in the original model,¹⁹ using limits. However, the advantage of such an approach is that the impacts of control measures that occur before the first bloodmeal (e.g., bed nets) can be included in calculations. This approach and derived mathematical form is also more consistent with the intended perspective of the model and is applied throughout.

Assuming that multiple infections are negligible, the probability of a mosquito being infectious at a given feeding cycle is related directly to the number of infectious blood-meals taken from humans that have had sufficient time to allow infectious sporozoites to appear in the salivary glands (n). This interval is expressed as F, the mean number of feeding cycles required for sporogonic development of the parasite:

$$\text{F}=\text{n}/\text{f}$$ (3)

Clearly, no mosquito can be infectious unless they have survived at least F feeding cycles (S_i = 0 where i < F). Here we define δ as the number of previous bloodmeals that occurred too recently for any ingested parasites to have fully developed into infectious sporozoites. Mathematically, δ is simply the next integer less than F. The probability of becoming infected is directly related to the proportion of human hosts that are infectious (x), the susceptibility of the vectors to infection (k), and the proportion of vectors that progress from being infected to infectious if they live long enough (v). These three factors represent the probabilities of a vector feeding on an infectious host and of the ingested gametocytes successfully transforming to gametes, zygotes, ookinetes, oocysts, and then infectious sporozoites. The original model considered x, k, and v separately, but for the purposes of applying the model, x and k were treated together as K.^19,21 Also, v was assumed to be 1 and ignored because losses at these separate stages of vector infection and sporogony could not be resolved in the field.^19,21 Thus, we will refer only to the product of x, k, and v as κ, which reflects the overall capacity of a human reservoir to produce infectious vectors. Thus, if we assume that superinfections of mosquitoes are negligible, S_i, the probability of a mosquito being infectious after surviving to a given feeding cycle i, can be expressed as a function of the number of blood-meals it has taken which have the potential to result in infectious status:

$${\text{S}}_{\text{i}}=\kappa \text{Q(i}-\delta \text{)}\text{for i}-\delta =1,2,3\dots$$ (4)

Thus, for any given age group, i, the probability of a mosquito surviving from emergence and being infective (I_i) is the product of these two possible occurrences:

$${\text{I}}_{\text{i}}={\text{S}}_{\text{i}}{\text{P}}_{\text{i}}$$ (5)

The cyclical nature of this model allows the probable mean number of infectious bites transmitted by a typical emerging mosquito over the course of its lifetime (β) to be calculated as the product of the human biting preference and the sum of the probabilities being alive and infectious at each cycle:

$$\beta =\text{Q}\sum {\text{I}}_{\text{i}}\text{for i}-\delta =1,2,3\dots$$ (6)

However, as will be seen in the results, the contributions of individual age classes to overall transmission level peaks between the fourth and ninth feeding cycle, and does not increase indefinitely with i when modeled using field-based estimates for P_f, κ, Q, and F. Thus, it is only necessary to sum those feeding cycles which contribute significantly to transmission. For our purposes, we will only consider the first 20 cycles because these are the most quantitatively important (see Results). Furthermore, in field populations of mosquitoes, the assumption that survivorship is independent of age is not strictly true and as mosquitoes age and senesce, their mortality increases exponentially.²⁶ Although senescence usually has little impact on the relative abundance of earlier age groups, very few females live beyond their tenth feeding cycle²⁶ and the oldest reported field-collected vector mosquito that we are aware of is an Anopheles funestus female from Muheza, Tanzania, which completed 14 gonotrophic cycles.²⁷ For the purposes of examining its contributing factors, by substituting equation 4 into equation 5 and then equation 5 into equation 6, β can be expressed in more detail as

$$\beta =\text{Q}\sum \text{Q}\kappa (\text{i}-\delta ){({\text{P}}_{\text{f}})}^{\text{i}}\text{for i}-\delta =1,2,3\dots$$ (7)

which by rearrangement yields

$$\beta =\kappa {\text{Q}}^2\sum (\text{i}-\delta ){({\text{P}}_{\text{f}})}^{\text{i}}\text{for i}-\delta =1,2,3\dots$$ (8)

For the purpose of resolving malaria transmission by individual mosquitoes into two distinct contributing factors, this equation can be broken down into κ and L, a life–history function for the local vector population:

$$\beta =\kappa \text{L}$$ (9)

where

$$\text{L}={\text{Q}}^2\sum (\text{i}-\delta ){({\text{P}}_{\text{f}})}^{\text{i}}\text{for i}-\delta =1,2,3\dots$$ (10)

Thus, the transmission capacity of individual mosquitoes becomes the product of two separate variables with real meaning in the field. κ reflects the effective infectiousness of the human reservoir and the physiologic compatibility of the local vector and parasite populations. L reflects the ability of an individual vector to transmit malaria from infectious human hosts over its lifetime, based on its longevity (P_f) and blood-feeding habits (Q). Equation 9 allows the contributions of the infectious reservoir and the mosquito life–histories to be considered separately as two crucial determinants of overall transmission intensity. Note that L differs from individual vectorial capacity, a parameter derived for similar purposes,^19,22 in that it reflects the potential of a mosquito to transmit malaria per lifetime rather than per bite.

Modeling malaria transmission by vector populations in human communities

For both the immediate purpose of modeling individual sites under specific conditions, and for the longer-term aim of modeling malaria dynamics on larger scales, it is useful to treat malaria transmission foci as discrete entities. Malaria vectors, parasites, and human hosts occur predominantly as patchworks of quite distinct populations, such as towns or villages, with varying degrees of connectivity or exchange. Discrete populations can be reasonably modeled at the community level.^23,28,29 Furthermore, models of discrete foci may subsequently allow the interactions between such populations over larger scales to be studied as networks of inter-linked populations.³⁰ The importance of heterogeneities in malaria dynamics is well established^31–33 and models for studying interactions among patchworks of populations are being developed by ecologists.³⁰ The simplest definition of the EIR⁴ is the product of the human biting rate and the prevalence of sporozoites in the vector population:

$$\text{EIR}={\text{H}}_{\text{Bt}}\text{S}$$ (11)

However, this model offers an alternative form in which to calculate EIR. Intuitively, the EIR experienced by an individual person in such a discrete transmission focus is the product of the mean number of infections transmitted by individual mosquitoes over their lifetimes (β) and the mean rate at which vector mosquitoes emerge (E) divided by the number of humans available for them to feed upon (N_h):

$$\text{EIR}=\beta \text{E}/{\text{N}}_{\text{h}}$$ (12)

Expressed in terms that are meaningful to those concerned with controlling transmission, we substitute equation 9 into equation 12:

$$\text{EIR}=\kappa \text{LE}/{\text{N}}_{\text{h}}$$ (13)

Relating the model to entomologic measurements and estimating emergence rates

The proportion of Anopheles mosquitoes in wild populations that are infectious is usually measured as the sporozoite rate, by circumsporozoite protein ELISA, or by salivary gland dissection.⁴ The proportion of mosquitoes that are infectious at any given time fluctuates with emergence rate, reflecting changes in the age distribution of the mosquito population. However, over complete seasons or long periods of perennial transmission, such fluctuations are likely to balance themselves out so that S, the mean proportion of adult vectors which are infectious, reflects the proportion of bites that are infectious over the lifetime of an individual mosquito. Thus, S is equal to the number of infectious bites divided by the number of total bites for an individual mosquito over its lifetime:

$$\text{S}=\beta /{\text{b}}_{\text{h}}$$ (14)

This model also allows us to estimate emergence rates of vectors from the overall human biting rate (H_Bt) and average number of bites per lifetime (b_h). Combining equations 11 and 12:

$${\text{H}}_{\text{Bt}}\text{S}=\beta \text{E}/{\text{N}}_{\text{h}}$$ (15)

So by substituting equation 14 for S and rearranging:

$$\text{E}={\text{H}}_{\text{Bt}}{\text{N}}_{\text{h}}/{\text{b}}_{\text{h}}$$ (16)

and

$$\text{E}/{\text{N}}_{\text{h}}={\text{H}}_{\text{Bt}}/{\text{b}}_{\text{h}}$$ (17)

Thus it becomes possible to estimate the emergence rate of mosquitoes per human host or, where the human population size is known, for the whole site with relatively straightforward adult mosquito sampling and age-grading methods.

Modeling specific malaria endemic sites

Four Plasmodium falciparum-endemic sites, Kankiya and Kaduna in Nigeria, Namawala in Tanzania, and Butelgut in Papua New Guinea were identified in the literature where values for EIR, S, H_Bt, κ, Q, P_f, and F have all been either measured directly or where reported values for other parameters allow their calculation (Table 2). All of these sites are intense foci of P. falciparum transmission, morbidity, and mortality from the southwest Pacific and both sides of the African continent, spanning an approximately ten-fold range of annual EIR with varying degrees of seasonality. It is also noteworthy that the sampling and analytical methods used to study these four sites have been similarly disparate. Although other vector species do occur at these sites, for simplicity we consider only the dominant vector species of that area. Where these parameters have been measured for Anopheles gambiae sensu lato (Kaduna and Namawala), or where a complete set of parameters for the species complex can only be obtained by considering both An. gambiae sensu stricto and An. arabiensis (Namawala), these are treated as a single, homogenous population. Note also that at Butelgut, P. vivax is also quite prevalent and the methods used to estimate κ and F could not distinguish these species.²¹ Therefore the values output from this model for β, S, and EIR represent combined or mean estimates for the mixture of the two Plasmodium species. For the other three sites, these values pertain to P. falciparum only, although other parasite species are present at much lower levels.

Table 2.

Reported estimates of entomologic and parasitologic parameters used to model malaria transmission at individual sites

Site name	Kankiya	Kaduna	Namawala	Butelgut
Country	Nigeria	Nigeria	Tanzania	Papua New Guinea
Nh (persons)	Not reported	84646	1,21247	9848
Dominant vector species	Anopheles arabiensis49	A. gambiae s.l.50	A. gambiae s.l.51	A. punctulatus52
HBt (bites per person per year)	1,12949	2,48050	24,09051	15,33052
P (per day)	0.9449	0.9050	0.8353	0.86*
f (days)	3†	2†	2.722	3.748
Pf (per feeding cycle)	0.83‡	0.81‡	0.6222	0.5821
Mean or median temperature (°C)	26.849	25.650	25.622	27.554
n (days)	10.3§	11.6§	10.7¶ or 11.6§	8.3¶ or 9.6§
F (feeding cycles)	3.4#	5.8#	4.0** or 4.3#	2.321
δ (feeding cycles)	3	5	3 or 4††	2
Q (human bites per bite)	0.7549	0.9046	0.9555	0.7221
κ (infective bites per human bite)	0.02449‡‡	0.05546	0.01822, 53	0.07421

^*Back-calculated from f⁴⁸ and P_f.²¹

^†Assumed by original authors.

^‡P_f = (P)^f.

^§Calculated³⁸ from mean or median temperatures.

^¶Back-calculated from f⁴⁸ and F.²¹

^#F = n/f.

^**Calculated from P_f and (P_f)^F values, estimated from parity and from sporozoite and delayed oocyst rates, respectively.²²

^††The lower value was used in all calculations.

^‡‡Mean of values reported for peak and off-peak transmission periods.

RESULTS

Contributions of vector age classes to malaria transmission

Figure 2 shows the survival and infectious status probabilities of individual mosquitoes over their lifetimes at each of the four sites, as calculated using this model and the input parameter values for κ, P_f, F, and Q listed in Table 1. The probable number of infectious bites transmitted by a mosquito is clearly defined by the overlap of the two functions, mortality and infectiousness, over the course of its lifetime (Figure 2). The probability of infectious survival (I_i) peaks at feeding cycles 8, 10, 5, and 4 for Kankiya, Kaduna, Namawala, and Butelgut, respectively (Figure 2A, B, C, and D, respectively).

Figure 2.

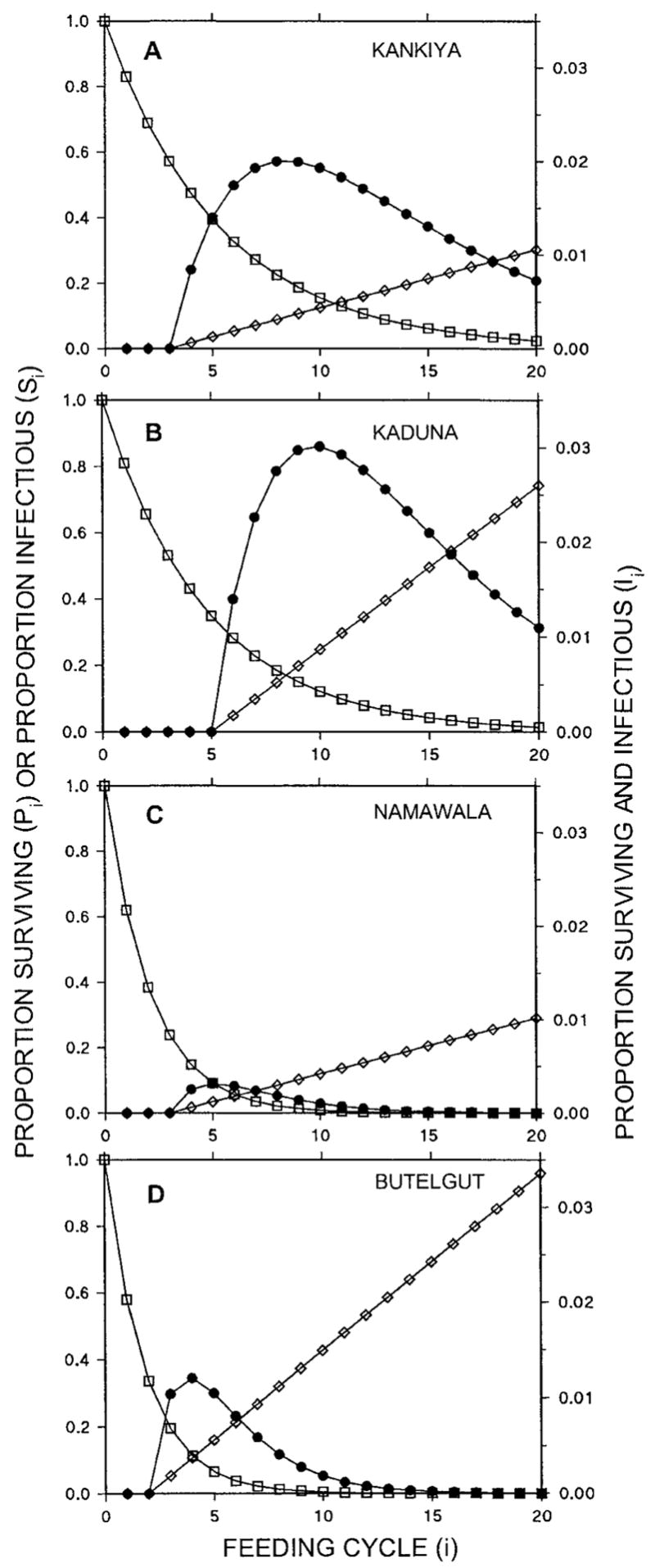
Predicted proportion of emerging mosquitoes that are alive (P_i; □), infectious (S_i; ◇) or both (I_i; ●) over the course of their lifetime, expressed in terms of the number of bloodmeals taken (i). See Table 1 for definitions.

The life-histories of mosquitoes in Butelgut (Figure 2D) and Namawala (Figure 2C) are particularly well suited to the simple model described here. Indeed, the predicted peak of I_i at Namawala (Figure 2C) is consistent with direct measurements of age–specific sporozoite rates in An. gambiae s.s. at other sites in Tanzania.²⁷ However, both sites from Nigeria, Kaduna in particular, diverge appreciably from the assumptions of this simple model. According to the calculations of this model, age classes as old as the twentieth feeding cycle contribute to transmission at both sites and, in the case of Kaduna, the high level of human reservoir infectiousness results in infectious probabilities of up to 70% in these older mosquitoes.

Predicted life history characteristics of malaria transmission by individual vectors

The greater longevity of vectors at both Nigerian sites result in higher numbers of infectious bites per mosquito (Table 3), even in Kankiya where the An. arabiensis vectors are only moderately anthropophilic and the human reservoir is less infectious than any of the other sites except Namawala (Table 2). This is also reflected in values for L, the lifetime transmission potential of individual vectors, indicating that vectors at the two Nigerian sites are approximately eight-fold more efficient than those at Namawala and Butelgut (Table 3). Note that L represents a more meaningful expression of the efficiency with which individual mosquitoes transmit malaria than individual vectorial capacity^19,22 because it represents the potential number of infective bites transmitted per lifetime rather than per bite (see equations 9 and 10). Examination of b_h, the lifetime biting potential of vectors at the four sites, shows just how much this can vary and how much it can contribute to the higher L values seen in Kankiya and Kaduna (Table 3). Predicted sporozoite rates (S) at all four sites compare reasonably well with published estimates (Table 3) ± SD, being 1.22 ± 0.38 (range = 0.69–1.60) of reported values from the literature, and not significantly different (degrees of freedom [df] = 3, t = −1.61, P = 0.21, by paired t-test). This is particularly encouraging, given that inspection of the predicted life–histories of vectors at Kaduna and Kankiya (Figure 2) indicates that lifetime infective bites and thus sporozoite rates are probably somewhat overestimated at these sites.

Table 3.

Modeled and reported (in parentheses) estimates of life history and malaria transmission parameters of vector populations at four field sites^*

Parameter	Equation	Kankiya	Kaduna	Namawala	Butelgut
bh (human bites per lifetime)	2	3.6	3.8	1.5	0.99
β (infectious human bites per lifetime)	8	0.18	0.29	0.017	0.042
S (infectious human bites per bite)	14	0.050 (0.03849†)	0.077 (0.04850)	0.011 (0.01622)	0.043 (0.03421,52)
L (infectious human bites per lifetime per proportion of bites on infective hosts)	10	7.7	5.3	0.97	0.57
E/Nh (new vectors per person per year)	17	320	660	15,500	15,300
E (new vectors per site per year)	16	ND	0.55 × 106	1.8 × 106	1.5 × 106
EIR (infectious bites per person per year)	12	56 (6749)	191 (12050)	272 (32951)	653(51721,52‡)

^*ND = not determined because an estimate of human population was not available. For definitions of other symbols, see Table 1.

^†Mean or combined value for peak and off-peak transmission periods.

^‡Calculated on the basis of S and H_Bt using equation 11, without using original authors’ correction factor for converting circumsporozoite protein prevalence to salivary gland sporozoite prevalence.

Predicted EIR values

Predictions of the annual EIR are also quite good (Table 3). The predicted EIR ± SD values are 1.13 ± 0.37 times (range = 0.84–1.59) and do not differ significantly from (df = 3, t = −0.81, P = 0.48, by paired t-test) those measured in the field. It is also noteworthy that by far the most deviant estimate (59% higher than field estimate) is Kaduna, the site that most clearly deviates from the assumptions of the model. For comparison, the same input parameters with classical models³⁴ predict EIRs that are 0.76 ± 0.30 (range = 0.39–1.15) of those measured in the field and do not differ significantly from those of this model (df = 3, t = −2.06, P = 0.13, by paired t-test).

Relative importance of contributing factors to malaria transmission intensity

The relative contributions of κ, L, and E/N_h to the EIR at each of the four sites modeled are presented graphically in Figure 3. There is greater between-site variation in L and E/N_h than in κ, their standard deviations being 95%, 108%, and 61% of their mean values, respectively. This suggests that the infectiousness of the human reservoir may be the least important factor in determining the level of transmission intensity in an area. Note also that the order of the sites in terms of L is approximately opposite to that in terms of the EIR, whereas the two sites with the highest EIR also have the highest E/N_h. This demonstrates how at Butelgut and Namawala moderately efficient vectors transmit extremely intense malaria by sheer weight of numbers, whereas at Kaduna and Kankiya small numbers of highly efficient vectors readily maintain intense, if somewhat lower, transmission.

Figure 3.

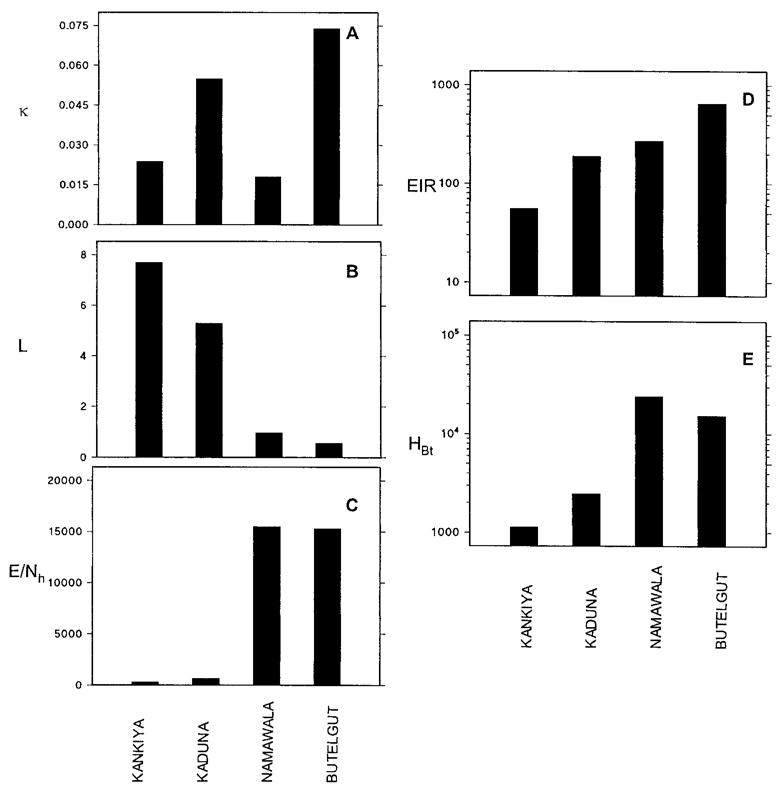
Between–site comparison of A, the infectiousness of the human reservoir; B, the lifetime malaria transmission capacity of individual vectors; C, their emergence rates relative to the size of the human populations; D, entomologic inoculation rates; and E, human biting rates. See Table 1 for definitions and Tables 2 and 3 for units and derivations.

DISCUSSION

The most important feature of this model is that EIR, the main output variable, is both meaningful and testable (Table 3). Other advantages of this model are the clarity with which it illustrates the role of different vector age classes in malaria transmission (Figure 2) and the relative importance of human reservoir infectiousness, vector life-history, vector emergence rates, and human population size as determinants of transmission intensity (Figure 3). The model has potential applications for the development and implementation of transmission control measures and for public health education.

The accuracy and precision of all malaria models are limited by the necessity to simplify the complex life cycle of the parasite, by the absence or inherent imprecision of field estimates, and by deviations from fundamental assumptions. Calculated infection rates at Kaduna and Kankiya deviate clearly from assumptions of the model and reality in the field. First, sporozoite rates exceed 20% among vector age classes contributing to transmission, indicating that super-infections are likely to occur and sporozoite rates in the older age groups are overestimated. Second, mosquitoes that have completed more than 10 feeding cycles contribute little to malaria transmission in the field because of increasing mortality caused by senescence.^26,35 It is noteworthy that Kaduna gives by far the most deviant estimate of EIR. This overestimation probably results from the assumption, rather than estimation, of a very short feeding cycle by the original authors, highlighting the importance of field estimates in malaria models. Despite these sources of error, this model predicts EIR quite accurately over the broad spectrum of epidemiologic circumstances that the four endemic sites represent. This indicates that the input parameters used can explain most of the heterogeneity of EIR in endemic areas and that research, implementation, and education in the malaria vector-control field should focus on the underlying determinants of these fundamental parameters.

The prediction of malaria transmission intensity as the EIR is clearly more useful than either vectorial capacity or reproductive number because this parameter is more meaningful as an epidemiologic predictor and is testable by measuring the EIR directly. This model predicts the EIR well and is slightly more accurate than previous classical Mc-Donald-Ross–type models.³⁴ Here, we have made reasonable estimates of the EIR transmitted by the dominant vector species at four very different endemic sites based on only five input parameters; κ, P_f, F, Q, and H_Bt. The expression of P_f, F, and Q as their combined function, L, the lifetime transmission potential of individual vectors (equation 10) can be clearly represented graphically (Figure 2). This allows the five input parameters to be simplified into only three determinants, each representing distinct targets for transmission control (equation 13). The structure of equation 13 implies that proportionately equivalent changes to any of these contributors will have the same impact on EIR and that, when combined, these can amplify each other’s effects. This implies that using a handful of modestly effective tools, in an integrated fashion, may result in considerable reductions of the EIR.

One of the primary uses of models is to predict the effects of specific intervention measures, based on assumed or measured impacts on the vector population or infectious reservoir.^1,2,23,36 For example, our predictions of the impact of bed nets on the sporozoite rate in intervention areas are consistent with observations in the field.²⁰ Such predictions may be useful for assessing the potential impacts of new transmission control tools³⁷ and for prioritizing research resources accordingly. New models need to be validated using a handful of sites that have been studied in considerable detail and that represent as diverse a cross-section of malaria-endemic settings as possible. Validated models can then assess control strategies across the spectrum of conditions that may be encountered in the field, using data from these sites. Additionally, the study of transmission foci in clusters may allow the application of metapopulation methods³⁰ that model patchworks of populations with respect to connectivity and stability. These ecologic methods could allow the flux of malaria parasites across larger scales to be modeled so that we gain quantitative insights into the difference between local elimination of malaria and its suppression over larger areas.

Compared to such ambitious goals, this is a very simple model that allows EIR to be estimated by addition, subtraction, multiplication, and division using any commercially available spreadsheet program or even a pocket calculator. Nevertheless, a striking feature of the literature is just how few sites exist from which all of the necessary parameters (κ, P_f, F, Q, and H_Bt) have been reported. We could only identify four sites that could be modeled and two of these (Kaduna and Kankiya) required us to assume or calculate values for the length of the feeding cycle and the sporogonic incubation period because direct estimates were unavailable. Standard methods for measuring P_f and Q are well established and are discussed in detail elsewhere.^19,21,25 However, the length of the sporogonic cycle in relation to that of the feeding cycle is an important input for this model that has rarely been measured in the field. Given that this extrinsic incubation period of the parasite can strongly influence transmission intensity and can vary seasonally¹⁶ or with longer term climate cycles,^38,39 this represents a considerable gap in our knowledge base for future modeling studies. Also, the infectiousness of the human reservoir remains a relatively difficult parameter to measure in the field²² and it is unclear whether determination of κ by direct feeding methods is satisfactory or whether entomologic methods are necessary.²¹ In summary, it seems that obtaining good estimates of these five input parameters is a large task, which can only be justified at a limited number of research sites, for the purposes outlined in the previous paragraph.

The usefulness of this and other models are very much dependent on the resources available to those who could use them. For the purpose of vector-control implementation rather than research, measuring these parameters for every endemic site is impossible. This is particularly true in malaria-endemic countries, which cannot afford a fraction of the resources applied to basic weather forecasts in developed nations. This limitation may be overcome in the future as submodels for predicting such primary input parameters from climatologic and hydrologic measurements become more refined.^{11,38,40–42} However, direct measurements of the EIR remains the gold standard for the quantification of transmission intensity so we emphasize that the EIR should be measured directly in epidemiologic studies.^4,16

Nevertheless, this model does have potential as a decision-making tool for vector-control planning.²⁰ Vector-control program managers need to know what impact they can expect to see on EIR for a given expenditure of resources. Additionally, the detailed modeling studies of control interventions in representative study sites may provide a sufficient set of scenarios for the tailoring of control programs in comparable settings. This principle has already been applied to the testing of bed nets and vaccines in a number of settings which span a wide range of EIR levels.^15,43 However, this model only represents a rough guide with which to assess practically feasible combinations of transmission control measures with respect to their impact on the EIR. As such, its predictions are only as good as the educated guesses of what can be practically achieved under local conditions. We also emphasize that, in reality, malaria transmission distribution is quite heterogeneous within even small communities, and that control should be appropriately targeted.³³

This simple model demonstrates how the intensity of malaria transmission is largely explained by a few fundamental determinants: human population size and infectiousness, vector emergence rate, longevity, feeding cycle length and human blood index, and the sporogonic incubation time of the parasite. The distribution of malaria transmission among older vectors can be easily visualized and the probable number of infectious bites transmitted by individual vectors can be readily appreciated as a function of the area under these curves (Figure 2). Classical continuous models¹ and existing simulation models^23,28,29 require either calculus or considerable computer processing, respectively, to complete the equivalent of some of these tasks. This model therefore represents a promising tool for teaching public health and medical professionals about the underlying determinants of malaria transmission intensity. In this context, the feeding cycle-by–feeding cycle spreadsheet approach, as outlined here, may be more instructive than classical and cyclical models that have more elegant solutions and summarize entire mosquito life spans with single equations.