Solving structures of protein complexes by molecular replacement with Phaser

Four case studies in using maximum-likelihood molecular replacement, as implemented in the program Phaser, to solve structures of protein complexes are described.

Abstract

Molecular replacement (MR) generally becomes more difficult as the number of components in the asymmetric unit requiring separate MR models (i.e. the dimensionality of the search) increases. When the proportion of the total scattering contributed by each search component is small, the signal in the search for each component in isolation is weak or non-existent. Maximum-likelihood MR functions enable complex asymmetric units to be built up from individual components with a ‘tree search with pruning’ approach. This method, as implemented in the automated search procedure of the program Phaser, has been very successful in solving many previously intractable MR problems. However, there are a number of cases in which the automated search procedure of Phaser is suboptimal or encounters difficulties. These include cases where there are a large number of copies of the same component in the asymmetric unit or where the components of the asymmetric unit have greatly varying B factors. Two case studies are presented to illustrate how Phaser can be used to best advantage in the standard ‘automated MR’ mode and two case studies are used to show how to modify the automated search strategy for problematic cases.

1. Introduction  

MR involves the rigid-body placement (both the orientation and position) of a search model (the structure of an identical or structurally similar protein) in the asymmetric unit of the target crystal so as to minimize the r.m.s. deviation between the search model and the target structure. The best placement is identified by the agreement between the calculated and observed structure factors, measured by one of a number of different MR search functions (e.g. Rossmann & Blow, 1962 ▶; Crowther, 1972 ▶; Fujinaga & Read, 1987 ▶; Navaza & Vernoslova, 1995 ▶; Read, 2001 ▶; Storoni et al., 2004 ▶; McCoy et al., 2005 ▶). The success of the method depends predominantly on two factors: the fraction of the asymmetric unit for which there is a suitable model(s) and the r.m.s. deviation (after optimal superposition) between the model and target structures. The r.m.s. deviation generally increases with decreasing sequence identity, so good models generally have high sequence identity with the target structure. If the sequence identity between the model and the target is less than ∼50%, the signal from the MR search can be improved by some judicious editing of the model structure (Schwarzenbacher et al., 2004 ▶). Since MR involves the rigid-body placement of the model, it is important to model conformational changes or to split the model into rigid domains and search for the domains separately. However, if an unanticipated conformational change has occurred between the model and target structures and hence there is a systematic deviation in atomic positions between model and target, MR will fail outright.

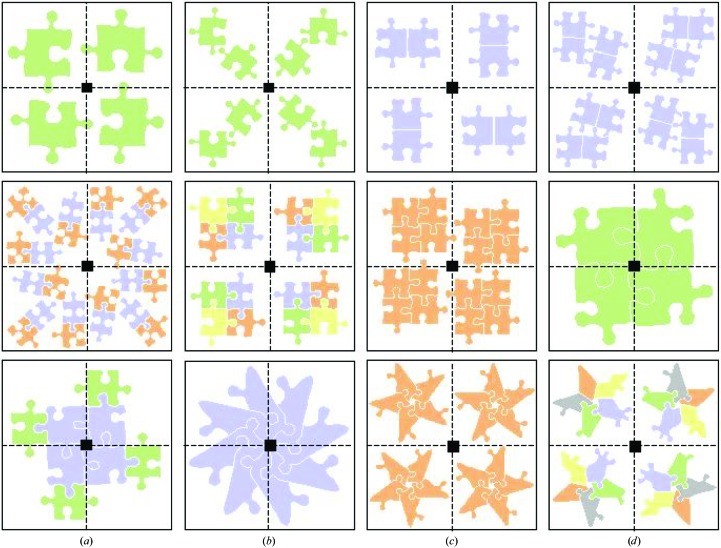
Although the availability of a good model is a prerequisite for MR, the quality of the target functions and search strategy are also important for success, particularly when there is an excellent model available but high symmetry, tight packing and/or multiple search components in the asymmetric unit complicate the problem. These complicating factors are often present when the target structure is a ‘biological’ protein complex (i.e. the complex is present in vivo). ‘Biological’ protein complexes can either be homo- or hetero-oligomers. The search models for hetero-oligomers are often the uncomplexed proteins, previously solved separately, and for homo-oligomers the search models are often proteins that are structurally homologous but do not form the same oligomeric association. Many combinations of crystallographic and noncrystallographic symmetry relationships between the proteins are possible. Homodimers, homotrimers, homotetramers and homohexamers may crystallize with one monomer in the asymmetric unit, with the complex generated by a crystallographic two-, three-, four- or sixfold. Hetero-oligomers or homo-oligomers in which the number of subunits is not a multiple of two, three, four or six must crystallize with at least one whole complex in the asymmetric unit. Fibres (infinite chains) must be generated by crystallographic symmetry (and may or may not also have noncrystallographic symmetry). Fig. 1 ▶ shows a schematic representation of a catalogue of possible asymmetric unit contents for a series of homo- and hetero-oligomeric protein complexes. It is important to note that the relationship between the contents of the asymmetric unit and the ‘biological’ oligomer need not be simple.

Figure 1.

Catalogue of some possible contents of the unit cell for a crystal of space group P4. The contents of the asymmetric unit are as follows: top row, (a) one monomer, (b) two monomers, (c) biological homodimer, (d) two biological homodimers; middle row, (a) three biological heterodimers, (b) biological heterotetramer, (c) biological homotetramer, (d) one monomer of a biological homotetramer; bottom row, (a) one heterodimer of a biological hetero-octamer, (b) two monomers of a biological homo-octamer, (c) biological homopentamer, (d) biological heteropentamer.

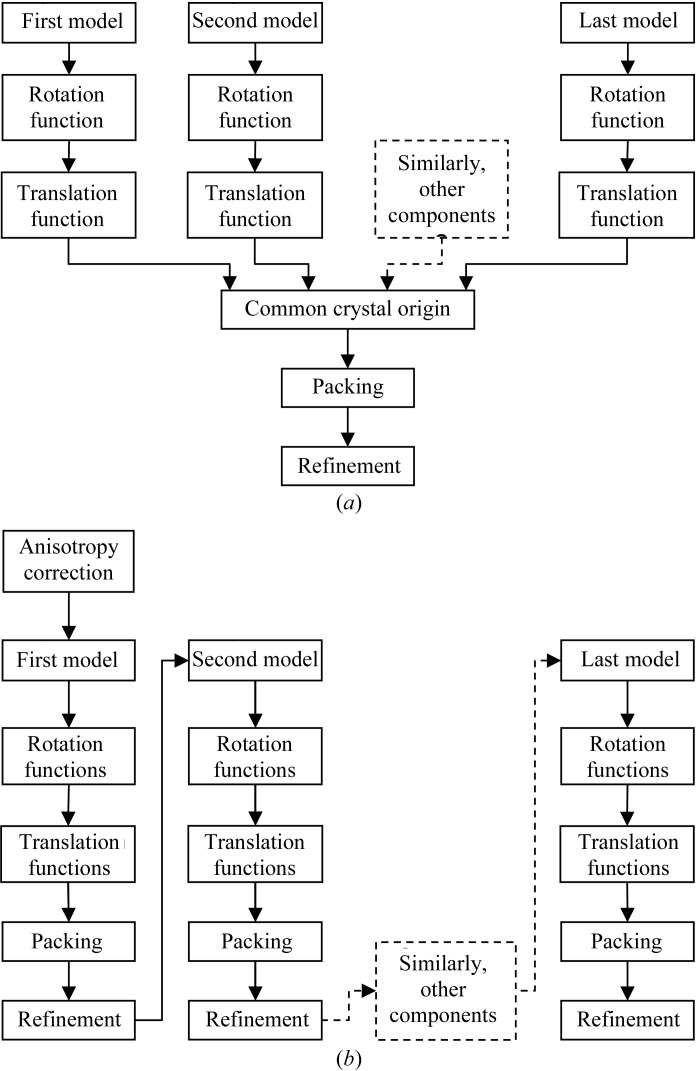
In order to solve the structures of protein complexes by MR, it is usually necessary to orient and position all the model components in the asymmetric unit, although sometimes small components can be traced in electron density generated only with phases from the larger components. Large numbers of components in the asymmetric unit are particularly problem­atic for traditional MR algorithms, where each component of the asymmetric unit is found independently (Fig. 2 ▶ a). When there is a large number of components, the fraction of the total scattering contributed by each component is low and so the signal in the searches for individual components is often non-existent. Maximum-likelihood MR (for a review, see McCoy, 2004 ▶), as implemented in the program Phaser (Read, 2001 ▶; Storoni et al., 2004 ▶; McCoy et al., 2005 ▶), significantly improves the success rate in cases where there are multiple search components in the asymmetric unit, because it has more discriminating (maximum-likelihood) rotation and translation functions than other methods and these functions also enable information about the orientation and position of one component to be used to increase the signal-to-noise ratio of both the rotation and translation search for other components (Fig. 2 ▶ b). I describe here how maximum likelihood improves the success rate of MR for protein complexes using four illustrative cases.

Figure 2.

Flow diagrams for solving structures of protein complexes by MR. (a) Traditional MR, where each search component must be found separately and then combined to assemble the asymmetric unit. (b) Maximum-likelihood MR, where placement of the first component is used to aid the search for the second and subsequent components; the complete asymmetric unit is generated by the addition of search components one at a time.

2. Automated MR in Phaser  

Most structures that can be solved by MR with Phaser can be solved with the ‘automated MR’ mode, which consists of six distinct steps: anisotropy correction, model generation (ensembling), rotation function, translation function, packing function and rigid-body refinement. The ‘automated MR’ mode links these six steps iteratively to enable searches for multiple components in the asymmetric unit with a ‘tree search with pruning’ algorithm.

2.1. Anisotropy correction  

Where a crystal diffracts to different effective resolution limits along different directions in reciprocal space, the crystal is said to diffract anisotropically. The anisotropic variation in intensity restricts the sensitivity of MR functions, particularly maximum-likelihood MR functions. Before undertaking maximum-likelihood MR, it is thus important to computationally remove the anisotropic variation in intensity by applying an anisotropic B-factor correction. This can be thought of as up-weighting the observed structure factors (F _obs) in the direction of weak diffraction and/or down-weighting them in the direction of strong diffraction. Strictly, the correction is not applied directly to the F _obs, but via the reflection-wise normalization factors, Σ_N, that are used to calculate the E values (normalized structure factors) used for all calculations. The low F _obs/σ(F _obs) [E _obs/σ(E _obs)] ratio in the direction of weakest diffraction is accounted for by increasing the sigma of these reflections accordingly. The degree of anisotropy is measured as the difference between the B factors in the directions of strongest and weakest diffraction.

2.2. Model generation (ensembling)  

The coordinates of an MR model are converted to calculated structure factors for comparison with the observed data. In Phaser, this procedure (called ‘ensembling’, as it can be performed with a structurally aligned ‘ensemble’ of homologous models) uses the estimated r.m.s. deviation between the model and the target in the calculation of the structure factors. The initial estimate of the r.m.s. deviation is made via the formula of Chothia & Lesk (1986 ▶), which relates the r.m.s. deviation of C^α atoms to the fraction sequence identity (f _identity),

In Phaser the minimum r.m.s. deviation is increased to 0.8 Å, so for a fraction sequence identity of higher than 63% the r.m.s. deviation is 0.8 Å rather than the lower value given by the formula. A fraction sequence identity of 50% corresponds to an r.m.s. deviation of C^α atoms of 1.0 Å. In the limit of 0% sequence identity the formula would give a maximum r.m.s. deviation of C^α atoms of 2.6 Å. However, if the r.m.s. deviation estimated from fraction sequence identity is a severe underestimate of the true r.m.s. deviation, MR may fail. In Phaser, the correct MR solution may be rescued by manually entering an increased r.m.s. deviation estimate.

2.3. Rotation function  

In a ‘brute-force’ rotation function, the target function (which ‘scores’ the rotations) is calculated on a grid of orientations and the orientations with the highest score are selected for the next step in MR (which, in Phaser’s ‘automated MR’ mode, is a translation function). ‘Brute-force’ rotation functions are very slow when the target function is the maximum-likelihood rotation function (MLRF). A significant speed improvement is achieved in Phaser by the calculation of an approximation to the full MLRF, the likelihood-enhanced fast rotation function (LERF), via fast-Fourier transform (which is very fast). The LERF is the first term in the Taylor series expansion of the full MLRF and can be thought of as a scaled and variance-weighted version of the Patterson overlap function used in the traditional Crowther RF. The full MLRF contains many (an infinite number of) additional terms, the physical interpretation of which in terms of Patterson functions is more difficult. For example, part of the second term in the Taylor series expansion can be thought of as a ‘Patterson of a Patterson’, with the other part including cross-terms between symmetry-related models with different symmetry operations. For an intuitive interpretation of the full MLRF, it is far easier to consider a random walk of structure factors in reciprocal space rather than trying to find an interpretation in real (Patterson) space (see McCoy, 2004 ▶). The highest peaks from the fast but poorer scoring LERF are then re-scored with the full MLRF, which gives better discrimination of the correct orientation (Storoni et al., 2004 ▶). Apart from being more sensitive to the correct solution, the MLRF is also able to easily include knowledge of partial structure, so that MR components that have already been placed can be used to even further improve the sensitivity of the search under way. Inclusion of partial structure information in the rotation function has previously only been possible using Patterson subtraction techniques, i.e. using coefficients |F _o|² − |F _c|² (Nordman, 1994 ▶; Zhang & Matthews, 1994 ▶) or coefficients (|F _o| − |F _c|)² (Dauter et al., 1991 ▶), which suffer from the problem of achieving correct relative scaling between F _o and F _c and consequently have only ever been attempted in a few specialized cases.

2.4. Translation function  

The full maximum-likelihood translation function (MLTF) is the same function as the maximum-likelihood refinement function. As for the MLRF, the MLTF is slow to compute when used as the target function of a ‘brute-force’ search. A speed improvement is achieved in Phaser in the same way as for the MLRF, i.e. an approximation to the full MLTF, the likelihood-enhanced fast translation function (LETF) is calculated by fast Fourier transform and then the top peaks are re-scored with the full MLTF (McCoy et al., 2005 ▶). The MLTF also makes good use of partial structure information to enhance the signal from the search under way.

2.5. Packing function  

The packing of potential solutions is checked using a C^α clash test. Each C^α position is tested for the presence of any C^α from another model that is within 2 Å (a clash). The search includes other components in the asymmetric unit, their symmetry-related copies and symmetry-related copies of the model under consideration. Only potential solutions that have a number of clashes less than the user-specified number (default zero) are accepted for the next step (in Phaser’s ‘automated MR’ mode, refinement). The number of accepted clashes should be increased when the search model has low sequence identity with the target or has large flexible loops that could adopt an alternative conformation. However, it is best to edit the model so as to remove flexible loops and allow only a small number of clashes, as packing provides a very powerful constraint on the translation function.

2.6. Refinement  

Rotation-function and translation-function searches are on a grid of orientations and positions. However, the best orientation and position need not (and in general will not) lie exactly on this grid. In addition, for the rotation function, the true orientation may be a shoulder of a peak in the rotation search rather than exactly where the peak maximum indicates. Therefore, a rigid-body refinement is performed to optimize the orientation and position of a model. This can greatly improve the likelihood score for a given solution from marginally above the noise level to a solution with a significant signal-to-noise ratio.

2.7. Tree search with pruning  

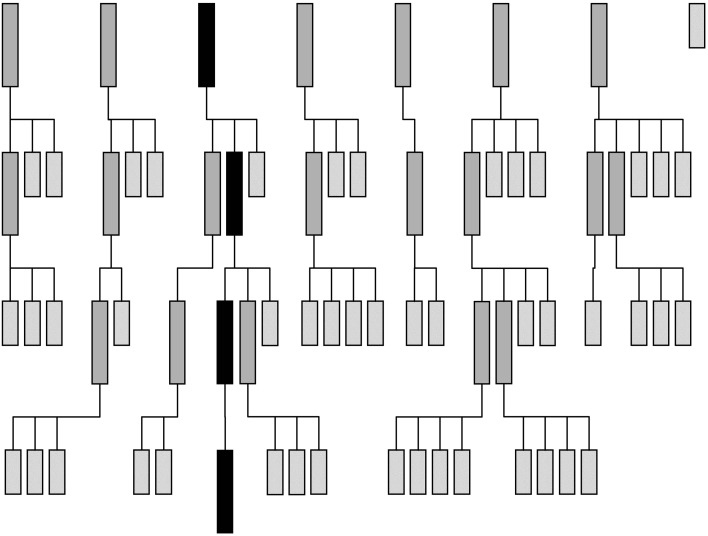
Maximum-likelihood rotation and translation functions can include partial structure information. Partial structure information increases the signal-to-noise ratio of the search for the second and subsequent components of the asymmetric unit and enables a ‘tree search with pruning’ search strategy (flow diagram shown in Fig. 3 ▶). In this strategy, all potential placements for the first component are used as the ‘background’ for the search for the second component, branching the search at each of these first component placements. Placing the second molecule correctly increases the signal of the correct placement (of the two components together) and so the correct (combined) placement will be high in the list of potential placements. The lowest placements can thus be pruned away without losing the correct placement. This process is repeated for as many components as are present. Ideally, at the end of the search strategy there will be a single branch (solution) with high signal-to-noise ratio containing placements for all the components. By default, Phaser prunes away solutions that have a log-likelihood gain that is less than 75% of the value of the difference between the highest log-likelihood gain and the mean log-likelihood gain (other selection criteria, using Z scores or saving a defined number of solutions, are also possible).

Figure 3.

Tree search with pruning MR search strategy for a crystal with four search components in the asymmetric unit. Row 1 represents the results of the search for the first component, where seven of eight solutions meet the selection criteria. Row 2 represents the results from the search for the second component. The search is performed using the seven possible placements for the first component as the background for seven separate searches for the second component. 13 of the 22 results of the seven searches that do not meet the selection criteria are pruned from the search tree. At the end of this step, two of the four components have been placed in nine potential solutions. Row 3 represents the results from the search for the third component. As the percentage of the total scattering being modelled increases so does the signal-to-noise ratio of the search and there is better discrimination of the best solution in this step, where 17 of 23 branches are pruned. Row 4 represents the results of searching for the fourth and final component. The correct solution, which includes placements for all four components, stands out well above the noise. The history of this solution can be traced through the search tree (shown in black)

The order of the search is important in the ‘tree search with pruning’ approach. The fastest way to obtain a solution is to search for the components that explain the highest fraction of the scattering first, since these will have the highest signal-to-noise ratio in their searches. The best component to search for first is usually the component with the highest molecular weight; however, if the component is more disordered than other components, its fraction scattering is reduced. It may be better to search with a smaller but more highly ordered component first. A solution will still likely be obtained for a search in the ‘wrong’ order provided that the correct placement of the first component (with weak scattering) has a likelihood value that is sufficiently high that it is not pruned from the list of potential placements and so survives to the next search step. This may, however, require the use of less stringent pruning criteria.

3. Case studies  

The algorithmic and automation methods implemented in Phaser are illustrated here with the following four test cases: BETA–BLIP, ROP four-helix bundle, V_κ antibody fibre and AP2 complex. In all four cases, the models for use in MR were the uncomplexed structures or a structure with only a few point mutations, so that the difficulty in finding a solution was not the result of using structures with low sequence identity as MR models. BETA–BLIP illustrates how some of the maximum-likelihood algorithms enable the BLIP component to be found with ease. The ROP four-helix bundle illustrates how the ‘tree search with pruning’ approach can be used to search for four helices. The V_κ antibody fibre is used to show how to short-circuit Phaser’s ‘automated MR’ protocol when searching for multiple copies of the same component in the asymmetric unit. The AP2 complex is an example of how to account for B-factor differences in the model, which is currently a limitation of the Phaser algorithms. Crystallographic details of the problems are given in Table 1 ▶.

Table 1. Summary of crystallographic data for the four test cases.

Test case	Space group	Unit-cell parameters (, )	Solvent content (%)	Model(s)	Molecular weight (kDa)	Content of ASU	Resolution ()
BETABLIP	P3221	a = 75, b = 75, c = 133, = 90, = 90, = 120	49	BETA/BLIP	29/18	1/1	3.0
ROP four-helix bundle	C2	a = 92, b = 24, c = 64, = 90, = 130, = 90	44	Poly-Ala helix	2	4	2.9
V antibody fibre	P6422	a = 192, b = 192, c = 197, = 90, = 90, = 120	60	V	12	15	2.7
AP2 complex	P42212	a = 166, b = 166, c = 160, = 90, = 90, = 90	58	AP2	188	1	3.1

3.1. BETA–BLIP  

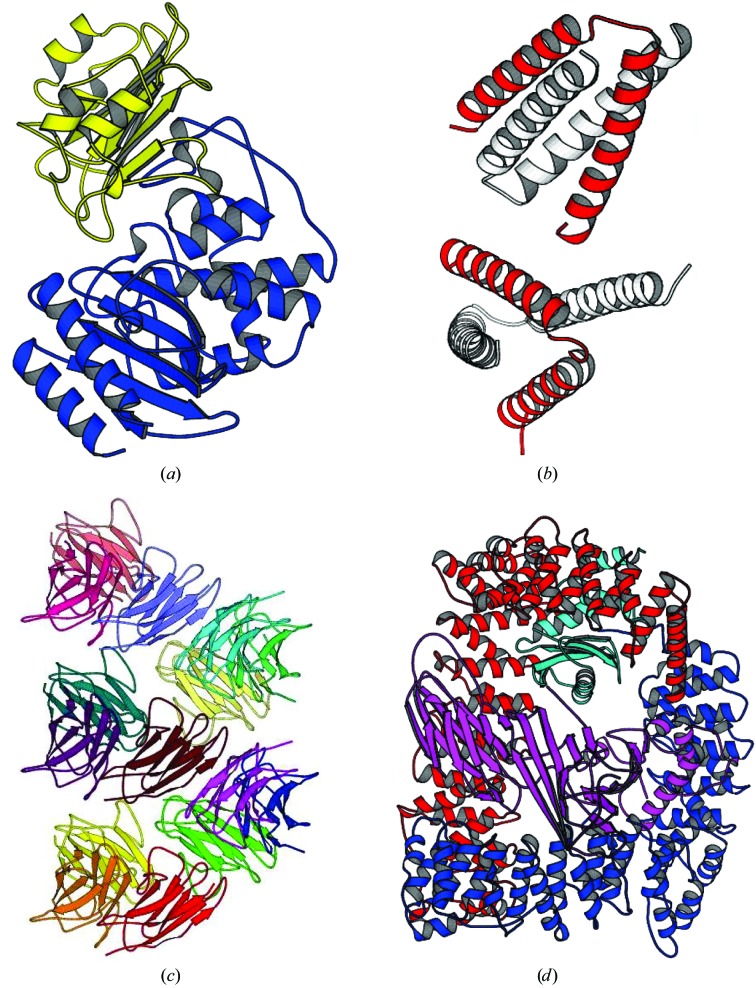
The case of β-lactamase (BETA)–β-lactamase inhibitor (BLIP) has been used repeatedly as a test case for Phaser (Storoni et al., 2004 ▶; McCoy et al., 2005 ▶) because the original structure solution by MR using AMoRe (Navaza, 1994 ▶) was difficult even though good models were available (the structures of both components had already been solved in isolation; Strynadka et al., 1996 ▶; Fig. 4 ▶ a). The difficult part of the MR solution was placing BLIP.

Figure 4.

(a) Structure of the β-lactamase (BETA)–β-lactamase inhibitor (BLIP) complex. BETA is in blue and BLIP is in yellow. (b) Structure of the ROP four-helix bundle structure. The asymmetric unit is shown in red and crystallographically related molecules are shown in white. Together, they form two four-helix bundles. The search model was a 26-residue polyalanine helix. (c) The 15 molecules in the asymmetric unit for the V_κ antibody fibre. The molecules form a continuous fibre along the 6₄ axis in the crystals (space group P6₄22). (d) The AP2 complex of four proteins. The α subunit (a superhelix of α-helices) is shown in red, the β2 subunit in blue (a similar superhelix of helices), the σ2 subunit in cyan (mixed α-helix/β-sheet structure) and the μ2 subunit in magenta (which consists of an N-­terminal domain structurally homologous to the σ2 subunit and a larger C-terminal mixed α-­helix/β-sheet structure).

The command script for the solution of BETA–BLIP using the ‘automated MR’ mode of Phaser is shown in Appendix A1. The search order is given as BETA and then BLIP. This is because BETA, with 62% of the molecular weight, would be expected to have the highest fraction scattering (and indeed it does, as the B factors for BETA and BLIP are comparable). Phaser rapidly produces a correct solution for the complex. This previously difficult structure solution becomes trivial because of two algorithms implemented in Phaser. The first is the anisotropy correction; there is significant anisotropy in the data (the maximum B-factor difference in different directions is 32 Ų). The second is the improved rotation-function target in MLRF, particularly in that the solution for BETA can be used to find the correct rotation-function solution for BLIP. Using the traditional Crowther (1972 ▶) fast rotation function, the Z score for the correct BLIP placement is 3.8 and the top Z score of 4.4 corresponds to an incorrect placement. Using MLRF and the prior knowledge about the placement of BETA, the correct placement of BLIP has a Z score of 6.5 and is the highest score in the search. (These results are for data that have had the anisotropy correction applied, to illustrate the improvement given by the MLRF alone.)

This example is illustrative of the case where one component of the asymmetric unit is easy to find in isolation and another is difficult or impossible to find. Knowledge of the partial structure of the component that is easy to find, introduced using the maximum-likelihood algorithms, enables the complex to be easily built up by addition.

3.2. ROP four-helix bundle  

The A31P mutant of ROP forms a helix–turn–helix motif that homodimerizes to form a four-helix bundle. The asymmetric unit contains two copies of the helix–turn–helix motif (Glykos & Kokkinidis, 2003 ▶; Fig. 4 ▶ b). The structure was originally solved with a 26-residue polyalanine single helix as the model and an extremely computationally intensive 23-dimensional Monte-Carlo search implemented in the program Queen of Spades (Glykos & Kokkinidis, 2001 ▶).

The command script for the solution of the ROP four-helix bundle using the ‘automated MR’ mode of Phaser is shown in Appendix A2. The r.m.s. deviation for ROP is given as 1.0 Å, since the sequence identity of the polyalanine helix is not a valid estimation of the r.m.s. deviation between the polyalanine helix and the backbone atoms of the ROP structure. The r.m.s. deviation value of 1.0 Å is a reasonable guess. Phaser produces eight solutions after a tree search with hundreds of branches, especially in the search for the second of the four helices. The eight solutions are nearly identical, differing only in the registration of the model to the structure helices (i.e. the C^α residues slip up or down the helix). All eight solutions generate a complete structure after model building with ARP/wARP (Perrakis et al., 2001 ▶). Although many potential solutions are stored in the intermediate stages of the search, the search itself is not computationally intensive.

This example is illustrative of the case where there are multiple components of the asymmetric unit and a poor signal for each component in isolation. The correct solution for placing the first few components was only found after placing the last component. After the search for first few components, there were a large number of branches on the tree and it was not apparent that a solution would eventually be found. However, the ‘tree search with pruning’ strategy, when left to run to completion, found the correct solution with the placement of the last model, when the signal of the correct solution finally became significant.

3.3. V_κ antibody fibre  

Unlike the previous two examples, other MR software had not solved this example of an aggregation-prone antibody variable domain of the kappa subgroup (V_κ) prior to structure solution with Phaser (James et al., 2006 ▶). Structures of antibody domains are of course well known; it was the association of the domains in the aggregate that was of interest in this structure. The aggregation-prone V_κ antibody domain crystallized in space group P6₄22 in a unit cell such that the Matthews coefficient (Matthews, 1966 ▶) indicated that there were most probably 18 molecules in the asymmetric unit. The search model had 98% sequence identity to the target structure, i.e. three point mutations, which give it the tendency to aggregate.

The first command script for the solution of the V_κ antibody domain using the ‘automated MR’ mode of Phaser is shown in Appendix A 3.1. In this step, only one of the potential 18 molecules in the asymmetric unit was searched for, the aim being to determine whether or not there was any signal in the search for a single molecule. Rather surprisingly, this step produced two placements with much higher Z scores than all the others. In this case, the signal from the single component was significant because subsets of V_κ domains had similar orientations and so there was a signal for these orientations in the rotation function. Using this clear rotation-function signal, the top Z score from the translation function was 19.2 and the second was 16.0. This indicated that the problem was solvable by short-cutting the automated MR job. The structure was therefore solved by manually editing the output ‘solution’ files from Phaser and checking the packing of the resulting solutions with Phaser’s ‘packing’ mode, as described below.

Since the first step produced two clear solutions, the two solutions were combined into a single solution by editing the ‘solution’ file as described in Appendix A 3.2. However, before proceeding to the searches for more molecules, it was necessary to check the packing of the two components in the solution by running Phaser’s ‘packing’ mode (Appendix A 3.3) and only accepting the subset of placements that had no clashes. The packing test showed that the two placements packed with no clashes and thus no placements needed to be deleted. This ‘solution’ was then used as the background of the search for the next molecule (Appendix A 3.4). Three more rounds of searching, manual editing of the solution files and checking of the packing gave a solution with 15 molecules in the asymmetric unit (Fig. 4 ▶ c). The noncrystallographic symmetry of the 15 molecules and the crystallographic symmetry along the 6₄ axis form a continuous chain of V_κ antibody domains, showing that the aggregation assembly is a fibre structure.

This example is illustrative of the case where there are multiple copies of the same component in the asymmetric unit and there is a signal from the search for individual components. The ‘tree search with pruning’ strategy is suboptimal in this case because the tree has multiple branches, each with a subset of the complete solution. The solutions only converge onto one branch (solution) with the placement of the last component on each of the branches. In this case the optimal search strategy is to add multiple components at each search step (rather than branching at each search step), but this search strategy must currently be performed semi-manually as described above. If there is no signal from the search for individual components, it is necessary to perform the search using the full tree search with pruning strategy as described in test case 2 (ROP four-helix bundle).

3.4. AP2 complex  

The structure of the endocytic AP2 complex was originally solved in space group P3₁21 (Collins et al., 2002 ▶). The AP2 complex consists of four proteins (α, β2, σ2 and μ2; Fig. 4 ▶ d). The μ2 protein has two distinct domains separated by a flexible polypeptide linker. Both of these μ2 domains and the σ2 subunit are compact mixed α-helix/β-sheet folds. The α and β2 proteins are superhelices of α-helices with a hinge approximately one third of the way between the N- and C-termini. The complex thus has seven separate rigid domains in total.

A new crystal form of AP2 was obtained in space group P4₂2₁2. The first attempt to solve the new structure by MR with Phaser, using the whole AP2 complex as a model, all data (resolution 3.1 Å) and the r.m.s. deviation estimated from a sequence identity of 100% (i.e. 0.8 Å), failed to find a solution. It thus appeared that AP2 had undergone a conformational change between the old and new crystal forms in which the subunits moved with respect to one another. The second attempt at obtaining an MR solution was to search for the seven rigid domains using the ‘tree search with pruning’ strategy. However, only the α, σ2 and C-terminal μ2 domains could be found using this strategy because the ‘tree search with pruning’ strategy assumes that the domains have similar B factors (which turns out not to be the case). Structure solution thus required that the conformational change be accounted for, while avoiding the B-factor problem.

The command script for the solution of the AP2 complex using the ‘automated MR’ mode of Phaser is shown in Appendix A 4.1. The conformational change in AP2 is accounted for in this script by increasing the r.m.s. deviation, decreasing the resolution to 5 Å and increasing the number of allowed clashes to above that used in the initial unsuccessful script. With these parameters, the correct solution was easily obtained. However, this solution did not model the domain movements of the conformational change that made the structure solution difficult in the first place. To model these domains movements, the ‘solution’ PDB file (the structure in original conformation) was split into seven PDB files, one for each of the seven rigid domains predicted from inspection of the AP2 structure, and a rigid-body refinement was performed (Appendix A 4.2). The domains refined away from their initial orientations and positions by up to 16° and 4 Å (see Table 2 ▶ for a complete description of the conformational changes). After further all-atom refinement with REFMAC (Murshudov et al., 1997 ▶), the average refined B factors of the atoms in the seven domains were markedly different. The lowest B factors were in the N- and C-terminus of α (95 and 80 Ų, respectively), σ2 (88 Ų) and the C-terminus of μ2 (90 Ų), which agrees with the observation that these were the components that could be found when searched for as separate models. However, the B factors for atoms in the N-terminus of μ2 and the N-terminus of β2 were on average much higher (155 and 185 Ų respectively). The differences in B factors between the most ordered and least ordered components (around 60 and 90 Ų, respectively) are less significant at 5 Å than at 3 Å, which is why decreasing the resolution was a factor in the successful structure solution.

Table 2. Conformational changes in AP2.

Deviation in angles between best superposition of the domains for the whole AP2 complex and best superposition of the seven domains allowing for the conformational change.

Domain	()	()	()	x ()	y ()	z ()
N-	+16	2	+3	0	2	+1
C-	2	+4	8	1	+1	0
N-2	+1	+4	+3	0	+1	+3
C-2	0	+8	+1	0	1	1
2	7	+4	+10	0	0	1
N-2	+1	0	0	0	+2	+2
C-2	3	+1	2	1	+2	+1

This example is illustrative of the case where a small conformational change has occurred between the model and the target structures and the components of the target structure have very different B factors. Performing searches with the whole structure (in a different conformation to the target structure) and lowering the resolution, increasing the r.m.s. value and increasing the number of allowed clashes may result in a structure solution despite the conformational change. A suitable set of resolution and r.m.s. values is found by running similar scripts searching a grid of resolution (e.g. 4–6 Å in 0.5 Å steps) and r.m.s. values (e.g. 1.5–3 Å in 0.5 Å steps), with a generous allowance for the number of clashes. If successful, this method will find the ‘average’ placement of the model structure with respect to the target structure. Rigid-body minimization (if the placement is within the convergence radius of the refinement) or local rotation/translation searches can then be used to optimize the placement of the different components.

4. Summary  

The maximum-likelihood MR functions implemented in Phaser (current version 1.3.2) have enabled many previously intractable MR problems to be solved (e.g. Jaskólski et al., 2006 ▶). The ‘automated MR’ mode will solve most structures that can be solved with Phaser. However, in some cases it is necessary, or at least better, to diverge from the ‘automated MR’ procedure. Where there are many copies of the same component in the asymmetric unit, manual editing of the solution files and packing checks can be used to short-circuit the automated script and speed up structure solution. Where different components of the asymmetric unit have different B factors, the r.m.s. deviation and resolution of the search can be altered to avoid the problem. The development of alternative automated scripts and new algorithms in future versions of Phaser should overcome these shortcomings of Phaser v.1.3.2.

Appendix A. Example scripts for Phaser for the test cases

Documentation for the Phaser scripting language is provided at http://www-structmed.cimr.cam.ac.uk/phaser.

A1. BETA–BLIP  

The script for running the ‘automated MR’ mode of Phaser to obtain a solution for the BETA–BLIP complex test case is shown below.

A2. ROP four-helix bundle  

The script for running the ‘automated MR’ mode of Phaser to obtain a solution for the ROP four-helix bundle test case is shown below.

A3. V_κ antibody domain  

Solution of the V_K antibody domain was achieved by short-circuiting the automated MR mode of Phaser as described in the text.

A3.1. Round 1  

The script for running the ‘automated MR’ mode of Phaser to search for one copy of the V_κ domain in the asymmetric unit is shown below. Two placements with high Z scores were found from this search. The ‘solution’ file output by this script has the name round1.sol.

A3.2. Solution file from the ‘round 1’ script  

 

A3.3. Edited ‘solution’ file from the ‘round 1’ script  

The two solutions given in the round1.sol file were combined into a single solution by editing the file to remove the second SOLUTION SET line; in Phaser, SOLUTION SET commands delineate separate solutions.

A3.4. Packing  

The packing of the two placements in the edited solution file was checked using the script below, which uses Phaser’s @ pre-processor command to include the data from the edited round1.sol file.

A3.5. Round 2  

The script for running the ‘automated MR’ mode of Phaser to search for one copy of the V_K domain in the asymmetric unit in the presence of the two molecules found in the round 1 search is shown below. The solutions found from this run of Phaser were added to the solution set as described and the search continued until no more molecules could be found.

A4. AP2  

A4.1. Solution  

The script for running the ‘automated MR’ mode of Phaser to obtain a solution for the AP2 test case is shown below.

A4.2. Refinement  

The script for running the ‘automated MR’ mode of Phaser to obtain a solution for the AP2 test case is shown below. Since the coordinates used for the seven ensembles (models) in this job were those of the structure in the correct placement (as determined by the search with the whole complex), the initial orientation and translation values for the seven domains prior to refinement were the origin (entered as EULER 0 0 0 FRAC 0 0 0).