Skip to main content
PMC home page
Acta Crystallographica Section D: Biological Crystallography logoLink to Acta Crystallographica Section D: Biological Crystallography
. 2007 Jan 16;63(Pt 2):188–196. doi: 10.1107/S0907444906045793

Ab initio molecular-replacement phasing for symmetric helical membrane proteins

Pavel Strop a, Michael R Brzustowicz a, Axel T Brunger a,*
PMCID: PMC2483470  PMID: 17242512

An ab initio molecular-replacement method for phasing X-ray diffraction data for symmetric helical membrane proteins has been developed. The described method is based on generating all possible orientations of idealized transmembrane helices and using each model in a molecular-replacement search.

Keywords: ab initio phasing, membrane proteins, MscL, ion channels

Abstract

Obtaining phases for X-ray diffraction data can be a rate-limiting step in structure determination. Taking advantage of constraints specific to membrane proteins, an ab initio molecular-replacement method has been developed for phasing X-ray diffraction data for symmetric helical membrane proteins without prior knowledge of their structure or heavy-atom derivatives. The described method is based on generating all possible orientations of idealized transmembrane helices and using each model in a molecular-replacement search. The number of models is significantly reduced by taking advantage of geometrical and structural restraints specific to membrane proteins. The top molecular-replacement results are evaluated based on noncrystallographic symmetry (NCS) map correlation, OMIT map correlation and R free value after refinement of a polyalanine model. The feasibility of this approach is illustrated by phasing the mechanosensitive channel of large conductance (MscL) with only 4 Å diffraction data. No prior structural knowledge was used other than the number of transmembrane helices. The search produced the correct spatial organization and the position in the asymmetric unit of all transmembrane helices of MscL. The resulting electron-density maps were of sufficient quality to automatically build all helical segments of MscL including the cytoplasmic domain. The method does not require high-resolution diffraction data and can be used to obtain phases for symmetrical helical membrane proteins with one or two helices per monomer.

1. Introduction

Obtaining high-resolution structures of integral membrane proteins is one of the grand challenges in structural biology. Many processes important to the cell, such as electrochemical, immunological and signalling functions, occur at the membrane. Not surprisingly, membrane proteins are extremely attractive pharmacological targets. Modern biomedical research builds upon high-resolution structural information and the demand for membrane-protein structures is clearly increasing (Dahl et al., 2002 ▶), yet relatively few membrane-protein structures are known (Tusnady et al., 2004 ▶). Low expression, poor stability in the absence of the lipid bilayer, the presence of detergents and difficulty in forming well ordered crystals are some of the problems that account for the slow progress in membrane-protein structure determination. Even after crystals have been obtained, obtaining phases for X-ray diffraction data can be the next bottleneck.

In the past century, several methods have been developed to circumvent the phase problem in protein crystallography. Heavy-atom substitution (Robertson, 1935 ▶), direct methods and molecular replacement (Hoppe, 1957 ▶; Rossmann & Blow, 1962 ▶) are the most common ways to obtain approximate initial phases for electron-density calculation. Heavy-atom methods rely on the availability of numerous well diffracting crystals for soaking experiments and on the ability of the soaked compounds to bind at discrete locations within the protein. Such conditions can be sometimes difficult to achieve for membrane proteins (Bass et al., 2002 ▶). Membrane proteins expressed in eukaryotic expression hosts further suffer from difficulties in expressing selenomethionine-substituted protein.

If one can make a reasonable ‘guess’ as to the structure (for example, from a homologous protein), molecular replacement is the method of choice since no further experimental effort is required. Indeed, as the number of structures in the Protein Data Bank (PDB) increases (Berman et al., 2000 ▶; Sussman et al., 1998 ▶), molecular-replacement methods have become increasingly more popular. However, relative to soluble proteins (∼1030 folds), the number of known membrane-protein folds (∼40 folds) is very low (Berman et al., 2000 ▶; http://scop.mrc-lmb.cam.ac.uk/scop/; Tusnady et al., 2004 ▶). Although the total number of membrane-protein folds might be smaller than the number for soluble proteins, the small numbers of presently known membrane-protein folds render molecular replacement unlikely to succeed for many cases. However, membrane proteins have the advantage that their orientation is restricted in the lipid bilayer. By surveying known α-helical membrane-protein structures, it is possible to obtain constraints on helical arrangements such as the maximum helix tilt angle, helix–helix distances and helix-packing preferences (Bowie, 1997 ▶, 1999 ▶; Spencer & Rees, 2002 ▶; Strop et al., 2003 ▶). Additionally, the number of membrane-spanning helices can be often accurately predicted from the primary sequence (Cserzo et al., 1997 ▶; Krogh et al., 2001 ▶). Taking advantage of these constraints, we have developed an ab initio molecular-replacement method for phasing X-ray diffraction data for symmetric helical membrane proteins (Fig. 1 ▶). After generating an exhaustive ensemble of plausible models, each model is subjected to a molecular-replacement search. The top molecular-replacement models are evaluated based on noncrystallographic symmetry (NCS) map correlation, OMIT map correlation and free R value after simulated-annealing refinement. As a test case, we successfully obtained phases for the mechanosensitive channel of large conductance (MscL; Chang et al., 1998 ▶) without any prior structural knowledge other than the number of transmembrane helices.

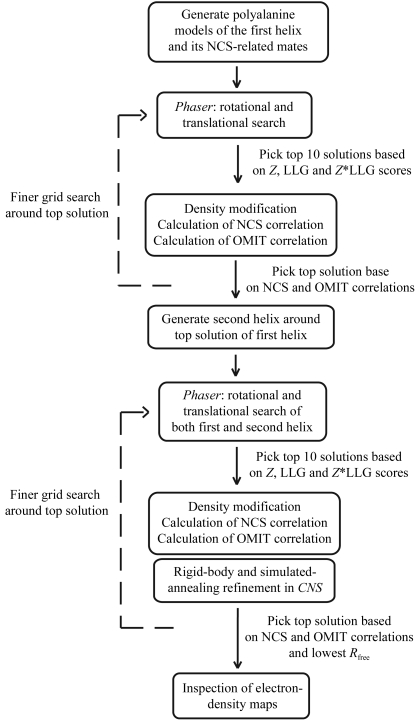
Figure 1.

Figure 1

Open in a new tab

Schematic of the ab initio molecular-replacement method. Dashed lines indicate optional fine grid searches.

2. Materials and methods

2.1. Model generation

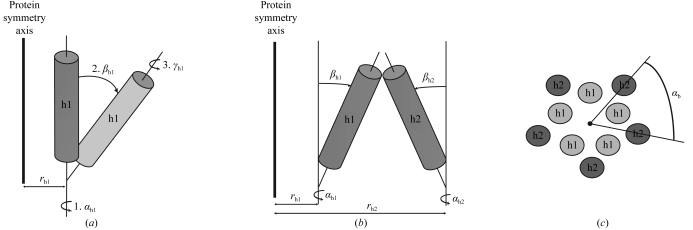
Idealized Cα traces of helical assemblies with n-fold symmetry were generated using an implementation of the algorithm in MATHEMATICA (Wolfram, USA). The geometric quantities are defined in Fig. 2 ▶(a), where the distance from the bundle symmetry axis to the projection of the first Cα atom on the helix axis is designated r hi and the rotation angle of the helix tilting plane αhi, the helix tilt βhi and the helix axial rotation γhi are the Euler angles according to Arfken for a helix in bundle i (Arfken & Weber, 1995 ▶). The symmetrical assembly of helices is defined such that the origin of each helical coordinate system (i.e. the helical axes; Fig. 2 ▶) lie evenly spaced about the circumference of a circle of radius r h. A helical bundle may also undergo a collective rotation about the bundle symmetry axis with angle αb (Fig. 2 ▶ c). Each helix was constructed with a 1.45 Å rise per residue, 3.76 residues per turn and an Cα helix radius of 2.58 Å (Kleywegt, 1999 ▶), producing an overall length of l h = (n r −1) × 1.45 Å, where n r is the number of residues. Thus, the variable parameters in generating all of the models are r hi, αhi and βhi. The helical orientation (N- to C-terminal direction) and rotation along the individual helical axes (γhi) are not considered in the search. Although helix rotation might have a small effect on the quality of the molecular-replacement solution even at low resolutions, i.e. 5–6 Å, we use this approximation to limit the size of the calculation. The effect of helix rotation is also reduced by the use of polyalanine models and by helix translation in the subsequent molecular-replacement search.

Figure 2.

Figure 2

Open in a new tab

Geometric description of the parameters used to generate the helical models. Constraints and limits are given in §2 and Table 1 ▶. Parameters of the helices in the inner bundle are subscripted h1, while the parameters of the outer helical bundle are subscripted h2. (a) The first helix is rotated with Euler angles αh1, βh1 and γh1. The resulting new helix orientation is shown in a lighter shade of gray. (b) The second helix is rotated with Euler angles αh2, βh2 and γh2 and a distance from the protein symmetry axis r h2. (c) αb is the rotation of the outer helical bundle about the inner helical bundle.

Several important restrictions were considered in creating the ensemble of structures. The restraints for r h1 are calculated from r h1 = d/[2sin(π/n)], where d is the side length of an n-­sided polygon. The minimum r h1 is the smallest radius possible for an n-fold symmetric helical bundle with helices that have a diameter of 9 Å (an approximate diameter of a typical membrane-protein helix with its side chains). The maximum r h1 for the inner bundle occurs when an outer bundle would be intercalated into the inner bundle, equivalent to a 2n-sided polygon (for a protein with two transmembrane helices per monomer). Here, n is replaced with 2n in the preceding equation. 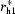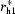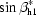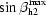When constructing the outer helical bundle, r h2 is subjected to the restraint Inline graphic ≤ r h2 ≤ Inline graphic + l h1 Inline graphic + l h2 Inline graphic. The asterisks indicate the chosen models from the inner bundle search. The maximum r h2 occurs when βh1 and βh2 are at their maximum values (Table 1 ▶) and the inner and outer helical bundles are still in contact (Fig. 2 ▶ b). In all cases, to ensure that helical space was sampled equivalently, we utilized the relation Δαh = s/(l hsinβh) such that the increment Δαh decreases with increasing βh, where s is the distance between the helical axes (at the last Cα positions) in the ensemble. In other words, the number of αh angles is calculated by dividing the circumference described by the end of the tilted helix by the helical spacing s.

Table 1. Parameters used for model building according to the geometry indicated in Fig. 2 ▶ .

The increment of the αhi angle is dependent on the tilting angle βhi and is calculated by dividing the circumference described by the end of the tilted helix by the helical spacing s as described in the methods.

  Coarse Fine
  Range Increment Range Increment
Inner        
  rh1 (Å) 8–14 2 9–11 1
 αh1 (°) 0–360 s = 4.5 Å 90–130 s = 2 Å
 βh1 (°) 0–45 7.5 20–40 2.5
Outer        
 αb (°) 0–72 7.2 10–25 2.5
  rh2 (Å) 10–44 2 20–25 1
 αh2 (°) 0–360 s = 4.5 Å 100–140 s = 2 Å
 βh2 (°) 0–45 7.5 25–35 2.5
Open in a new tab

Each generated model was checked for steric clashes (models where the minimum inter-axial distance between any helices was less than 9 Å were eliminated). Additionally, models where the minimum inter-axial distance between inner and outer bundle helices was greater than 10.5 Å were also eliminated to ensure that the outer helical bundle would come into contact with the inner bundle. From this restrained ensemble, idealized polyalanine helix models including all main-chain and side-chain atoms were created with MOLEMAN and LSQMAN (Kleywegt, 1999 ▶).

2.2. Molecular replacement

Molecular-replacement phasing was performed with Phaser (McCoy et al., 2005 ▶). All models were searched against an MscL data set (Chang et al., 1998 ▶) limited to 15–5.0 Å resolution, 40% identity and no allowed Cα clashes. Peak-selection criteria were set to 80% in order to optimize the calculations. The top molecular-replacement models were assessed with the Z score (Z) and log-likelihood gain (LLG) statistics (McCoy et al., 2005 ▶). Ten solutions with the highest Z score, ten solutions with the highest LLG score and ten solutions with the highest Z*LLG scores were selected for further scoring by NCS and OMIT map correlations, although other alternative ways of selecting top solutions are possible. All molecular replacements for the inner helical bundle (305 models) were completed in approximately 80 CPU hours utilizing a 2.8 GHz Intel Xeon P4 processor. The secondary search for the combined inner/outer helical bundles (1050 models) was completed in 130 CPU hours. The entire procedure is easily adaptable to parallel processing since each molecular-replacement search is independent.

2.3. NCS map correlation, OMIT map correlation and refinement

The NCS map correlation scoring takes advantage of the fact that if the position of a model in the asymmetric unit is correct then the NCS axis of the search model will coincide with the crystal’s NCS axis. In such cases, the NCS map correlation between the five monomers should be higher than if they were incorrectly placed within the asymmetric unit. Density modification including solvent flattening and NCS averaging with phase extension was performed in DM (Collaborative Computational Project, Number 4, 1994 ▶) prior to NCS map correlation calculation. The NCS mask for monomer A was calculated in NCSMASK from the coordinates of monomer A with a radius of 15 Å, removing any overlaps. NCS operators were obtained from the oriented model with LSQMAN (Kleywegt, 1999 ▶).

Independent of the NCS map correlation calculation, segments of five residues were omitted from each helix in the top molecular-replacement solutions and the maps generated from these models were subjected to prime-and-switch density modification with fivefold NCS averaging in the program RESOLVE (Terwilliger, 2000 ▶). After density modification, the map correlation for the omitted residues was computed with OVERLAPMAP (Branden & Jones, 1990 ▶), where the correlation coefficient is calculated as CC = (〈xy〉 − 〈x〉〈y〉)/[(〈x 2〉 − 〈x〉2)1/2(〈y 2〉 − 〈y〉2)1/2]. The product of the OMIT and NCS correlation scores (NCS*OMIT) was used to delineate the top molecular-replacement models. The resulting polyalanine models were subjected to rigid-body and torsion-angle simulated-annealing refinement with the MLF maximum-likelihood target function as implemented in CNS (Brünger et al., 1998 ▶).

3. Results and discussion

Our method is summarized in Fig. 1 ▶. The molecular-replacement search for MscL was split into two independent searches for the inner and combined inner/outer helical bundles. Firstly, all possible models of the inner helical bundle were constructed and used as models in molecular-replacement searches. The top solutions from the molecular-replacement searches were further evaluated based on NCS map correlation and OMIT map correlation. At this point, the process was repeated with finer parameter variation in order to achieve a more precise model. Next, the top solution was ‘fixed’ in place and all possible conformations of the outer helical bundle were constructed. The resulting models were again subjected to molecular-replacement searches and the top solutions were scored based on NCS and OMIT map correlation. Once again, the process was repeated on a finer grid in order to achieve a more precise model.

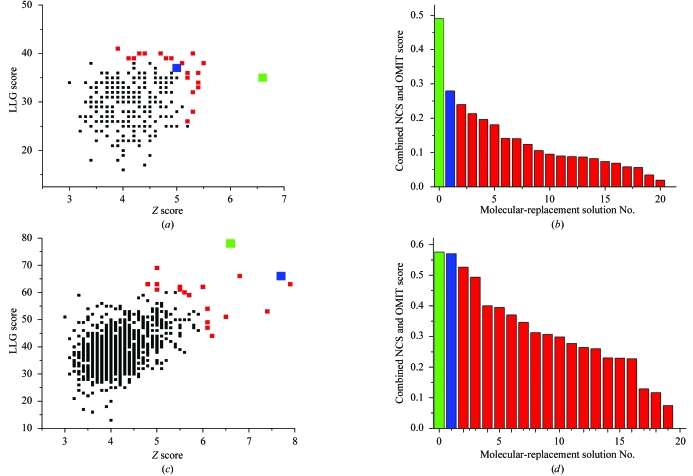
The molecular replacement for the inner helical bundle (five helices) representing the inner transmembrane core of MscL was performed with a coarse set of 305 models (Table 1 ▶). The resolution range of the diffraction data was restricted to 15.0–5.0 Å in order to exclude high-resolution detail missing from our polyalanine helical models. The molecular-replacement results were represented as a scatter plot of Z versus LLG scores (Fig. 3 ▶ a). Since the inner helical bundle is a small fragment of the asymmetric unit, distinguishing the correct solution from incorrect solutions is difficult. To circumvent this problem, we assessed the models with the highest Z, LLG and Z*LLG scores (shown in red and blue in Fig. 3 ▶ a) with NCS map correlation and OMIT map correlation coefficients. The ‘best’ model, i.e. that with the largest product of NCS and OMIT map correlation, yielded the parameters r h1 = 10 Å, αh1 = 115° and βh1 = 30° (coloured blue in Figs. 3 ▶ a and 3 ▶ b). In order to obtain a higher accuracy solution for the inner helical bundle, a second finer search was performed around the top coarse solution. After repeating the process with the ‘finer’ parameters (Table 1 ▶), the resulting molecular-replacement models were again subjected to scoring by NCS and OMIT map correlation. The resulting best model yielded the parameters r h1 = 11 Å, αh1 = 120° and βh1 = 40°.

Figure 3.

Figure 3

Open in a new tab

Molecular replacement results. (a), (c) Z versus LLG scatter plot from coarse molecular replacement searches of inner (a) and outer (c) helical bundle ensembles. Each black square represents the top solution of one model. (b), (d) NCS*OMIT product scores resulting from coarse search for inner (b) and outer (d) helical bundle ensembles. In all panels, the top ten Z, LLG and Z*LLG scores are shown in red, the best solution from a coarse search is shown in blue, and the best solution from a fine grid search is shown in green. For clarity, the best coarse and fine search solutions are also shown as large squares in panels (a) and (c).

After the solution for the first (inner) helical bundle was found, an ensemble of second (outer) ring helices was constructed around the fixed geometry of the inner bundle. Roughly 1040 models composed of two transmembrane helices per monomer (ten helices in total) were subjected to another round of molecular-replacement searches (Table 1 ▶). The top results were again evaluated by NCS and OMIT map correlations (Figs. 3 ▶ c and 3 ▶ d), revealing the best solution with parameters r h2 = 23 Å, αh2 = 131°, βh2 = 30° and αb = 14°. A finer grid search (see Table 1 ▶) around the top solution was also performed, producing r h2 = 21 Å, αh2 = 122°, βh2 = 30° and αb = 10°.

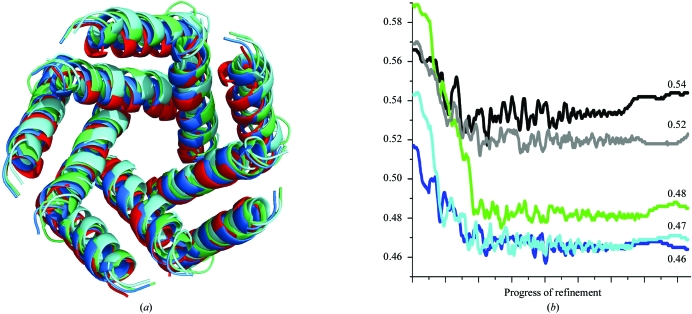
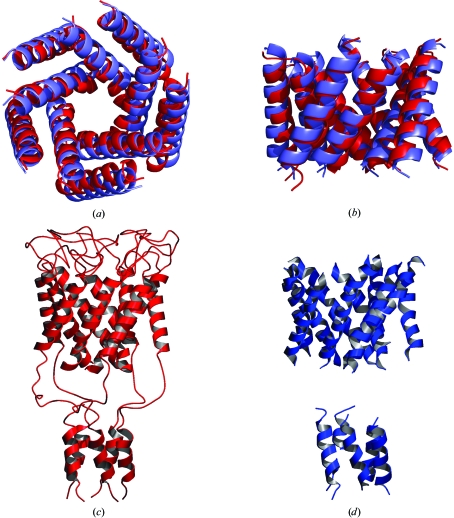
The correct solution was further distinguished from incorrect models by rigid-body and torsion-angle simulated-annealing refinement with a maximum-likelihood target function (Adams et al., 1999 ▶). The top five models were subjected to refinement and evaluated with the R free statistic (Fig. 4 ▶ a). Three models converged to approximately the same structure with an R free of 0.46–0.48 (Fig. 4 ▶ b). The two incorrect models are thus easily distinguisheable by their higher R free values (0.52–0.54). The final model found by ab initio molecular replacement and the known structure of MscL are qualitatively in good agreement (Figs. 5 ▶ a and 5 ▶ b).

Figure 4.

Figure 4

Open in a new tab

Comparison of (a) structure and (b) R free statistic for the top five converging (light blue, dark blue and green) and nonconverging (black and gray) models after torsion-angle simulated-annealing refinement with a maximum-likelihood target function. The known transmembrane structure of MscL (red) is shown for reference.

Figure 5.

Figure 5

Open in a new tab

(a) Comparison of the known transmembrane helical structure of MscL (red) and the model derived from ab initio molecular replacement (blue). (b) View perpendicular to the membrane normal. (c) Ribbon representation of the known MscL structure. (d) Ribbon representation of the transmembrane and cytoplasmic helices built by ARP/wARP HelixBuild into electron density computed with phases from ab initio molecular replacement. This figure was prepared with PyMOL (DeLano Scientific, San Carlos, CA, USA) and POVSCRIPT (Fenn et al., 2003 ▶; Kraulis, 1991 ▶)

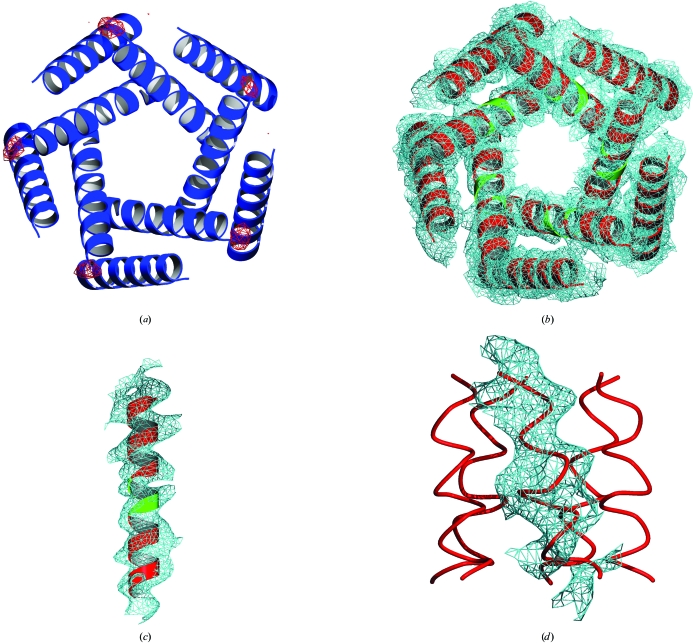
To further validate the correctness of the final model, we calculated an anomalous difference electron-density map of an MscL gold derivative (Chang et al., 1998 ▶) with phases derived solely from the ab initio molecular-replacement searches. The resulting map contoured at 4σ is shown in Fig. 6 ▶(a) and clearly shows the symmetrical positions of the Au atoms. Anomalous difference maps calculated with incorrect models were not symmetrical and yielded no significant peaks at the known gold positions. We have also omitted a region of the inner helix (in all five monomers) and subjected the maps from this omitted model to a prime-and-switch density-modification protocol (Terwilliger, 2000 ▶). The resulting 2F o − F c OMIT maps contoured around the helices are shown in Figs. 6 ▶(b) and 6 ▶(c).

Figure 6.

Figure 6

Open in a new tab

(a) Anomalous difference electron-density map (red) contoured at 4σ computed for a gold derivative using the phases obtained from ab initio molecular replacement. 2F o − F c map contoured at 1σ computed from ab initio phases with omitted residues shown in green for (b) the complete transmembrane ensemble, (c) for a single transmembrane helix and (d) for the cytoplasmic domain (for clarity, the electron density is shown for only one cytoplasmic helix).

Crucial questions are whether the resulting electron-density maps provide new features that are not part of the search model and whether they are sufficient for model building. Remarkably, in addition to the electron density of the transmembrane region, there is also a visible density for the cytoplasmic helical bundle (Fig. 6 ▶ d). This extra-membranous region was not included in the molecular-replacement searches, demonstrating the presence of ‘new’ information in the electron-density maps. Automated construction of helical fragments with ARP/wARP (Perrakis et al., 1997 ▶) successfully built main-chain atoms for all ten helices in the transmembrane region as well as the five helices in the cytoplasmic region (Figs. 5 ▶ c and 5 ▶ d). While the ARP/wARP helix builder has been reported to work down to 3.5 Å resolution (http://www.embl-hamburg.de/ARP/), tracing of side chains and loops requires higher resolution data sets (at least 2.6 Å; http://www.embl-hamburg.de/ARP/). Therefore it is not surprising that ARP/wARP did not succeed in automatically building side-chain and loop regions using the 4.0 Å resolution data set. However, the new helical model generated in ARP/wARP followed by crystallographic refinement reduced R free to 41.5%, improving electron-density maps for manual model building.

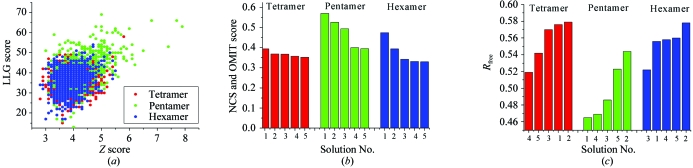
The native oligomerization state of membrane proteins is not always apparent from biochemical studies. It is often difficult to distinguish between closely related oligomerization states (such as tetramer, pentamer or hexamer). In many cases, only an approximate oligomerization state can be experimentally deduced. To address whether it is necessary to know the oligomerization state of the protein prior to using ab initio molecular replacement, we have also performed the entire procedure assuming incorrect fourfold and sixfold symmetry. The Z versus LLG plot for molecular replacements of models with fourfold (red), fivefold (green) and sixfold (blue) symmetries is shown in Fig. 7 ▶(a). The correct fivefold-symmetric model scored much higher than either the fourfold or sixfold symmetric models in the molecular-replacement searches. This distinction is also supported by the NCS*OMIT product scores (Fig. 7 ▶ b) and is even more pronounced in the R free statistics after refinement of the top models (Fig. 7 ▶ c). Therefore, it appears that for MscL it is not necessary to know the oligomerization state. In situations where the oligomerization state is unknown, our ab initio molecular-replacement method could thus be used to determine the molecular symmetry.

Figure 7.

Figure 7

Open in a new tab

Determination of the oligomeric state from X-ray diffraction data by ab initio molecular replacement. (a) Z versus LLG scatter plot from molecular replacement for models with fourfold (red), fivefold (green) and sixfold (blue) symmetry. (b) NCS and OMIT scores for fourfold, fivefold and sixfold assemblies. (c) Refinement progress monitored with R free statistics of the top five models from each symmetry group. Colours are as in (a).

4. Conclusions

One limitation of all molecular-replacement methods is that finding a correct solution becomes increasingly difficult as the fractional amount of scattering mass present in the search model decreases. In the case of MscL, we were able to find the correct solution with as little as 15% of the scattering mass, corresponding to one idealized transmembrane helix per monomer (the crystal structure of MscL consists of 3954 atoms, while the search model consisted of five polyalanine helices with a total of 575 atoms). Finding a molecular-replacement solution with such a low percentage of the asymmetric unit was probably aided by the high solvent content of the MscL crystals (85%). Additional algorithms such as generalized molecular replacement of flexible elements (Brünger, 1991 ▶) or normal-mode analysis (Suhre & Sanejouand, 2004 ▶) might be useful for these difficult molecular-replacement searches. In many cases, it may therefore be necessary to perform the molecular-replacement searches with a larger fraction of the asymmetric unit. However, as the number of helices in the model increases, the number of necessary models grows significantly. For example, if both helices of MscL were used together, the search would increase approximately 200-fold.

Our search method benefited greatly from reducing the total number of possible helical arrangements by utilizing geometrical and structural restraints. For larger helical assemblies, additional restraints or constraints limiting the number of models would be advantageous. Such restraints can come from experimental evidence of disulfide bonds, disulfide scanning experiments, chemical cross-linking (Faulon et al., 2003 ▶) or electron paramagnetic resonance (EPR) spectroscopy (Perozo et al., 2001 ▶, 2002 ▶). Additional reduction of the number of models can be achieved through the use of global search methods. Global search methods have been successful in some cases in predicting oligomeric membrane-protein structures (Adams et al., 1995 ▶, 1996 ▶; Arkin et al., 1994 ▶) and could be used to decrease the parameter space of the ab initio molecular-replacement searches. In some cases it may be possible to locate the NCS axis using a self-rotation function, although this was not possible for MscL. Restraining the orientation of the NCS axis could then simplify the molecular-replacement searches and thus significantly speed up the procedure. In cases where the number of models is too large to consider, statistical search tools such as genetic algorithms can provide an alternative approach. Although genetic algorithms are nondeterministic, they can be used to find approximate solutions to search problems and have been successful in many applications including molecular-replacement phasing (Kissinger et al., 1999 ▶).

Presently, our ab initio molecular-replacement method is applicable mainly to symmetrical membrane proteins. Although it is difficult to estimate how many symmetrical membrane proteins are present in the genomes, one can obtain a rough estimate by examining known membrane-protein structures. Currently, there are 44 known α-helical membrane-protein families in the Protein Data Bank (Raman et al., 2006 ▶). 52% of these membrane-protein families form homo-oligomeric structures. Furthermore, in 31% of α-helical membrane-protein families the association of monomers forms the region responsible for the functionality of the protein. For example, in many ion channels the ion-conducting pathway coincides with its symmetry axis. Although these statistics might not hold in the future, there is a significant chance that many new membrane-protein structures will be symmetric.

Achieving a high-resolution structure of a membrane protein is a formidable task. Once the barrier of producing quality diffracting crystals has been overcome, the next hurdle is the phase problem. We have shown that membrane proteins can provide sufficient constraints in the placement of α-helices to make ab initio molecular replacement possible. Therefore, our ab initio molecular-replacement method should be an important tool for phasing membrane proteins.

Acknowledgments

We thank Doug Rees, Paul Adams and Tim Fenn for helpful discussions. Support by the NIH to ATB is gratefully acknowledged (MH63105).

References

  1. Adams, P. D., Arkin, I. T., Engelman, D. M. & Brünger, A. T. (1995). Nature Struct. Biol.2, 154–162. [DOI] [PubMed] [Google Scholar]
  2. Adams, P. D., Engelman, D. M. & Brünger, A. T. (1996). Proteins, 26, 257–261. [DOI] [PubMed] [Google Scholar]
  3. Adams, P. D., Pannu, N. S., Read, R. J. & Brunger, A. T. (1999). Acta Cryst. D55, 181–190. [DOI] [PubMed] [Google Scholar]
  4. Arfken, G. B. & Weber, H. J. (1995). Mathematical Methods for Physicists. San Diego: Academic Press.
  5. Arkin, I. T., Adams, P. D., MacKenzie, K. R., Lemmon, M. A., Brünger, A. T. & Engelman, D. M. (1994). EMBO J.13, 4757–4764. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Bass, R. B., Strop, P., Barclay, M. & Rees, D. C. (2002). Science, 298, 1582–1587. [DOI] [PubMed] [Google Scholar]
  7. Berman, H. M., Westbrook, J., Feng, Z., Gilliland, G., Bhat, T. N., Weissig, H., Shindyalov, I. N. & Bourne, P. E. (2000). Nucleic Acids Res.28, 235–242. [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bowie, J. U. (1997). J. Mol. Biol.272, 780–789. [DOI] [PubMed] [Google Scholar]
  9. Bowie, J. U. (1999). Protein Sci.8, 2711–2719. [DOI] [PMC free article] [PubMed] [Google Scholar]
  10. Branden, C. & Jones, T. (1990). Nature (London), 343, 687–689.
  11. Brünger, A. T. (1991). Acta Cryst. A47, 195–204. [DOI] [PubMed] [Google Scholar]
  12. Brünger, A. T., Adams, P. D., Clore, G. M., DeLano, W. L., Gros, P., Grosse-Kunstleve, R. W., Jiang, J.-S., Kuszewski, J., Nilges, M., Pannu, N. S., Read, R. J., Rice, L. M., Simonson, T. & Warren, G. L. (1998). Acta Cryst. D54, 905–921. [DOI] [PubMed] [Google Scholar]
  13. Chang, G., Spencer, R. H., Lee, A. T., Barclay, M. T. & Rees, D. C. (1998). Science, 282, 2220–2226. [DOI] [PubMed] [Google Scholar]
  14. Collaborative Computational Project, Number 4 (1994). Acta Cryst. D50, 760–763. [Google Scholar]
  15. Cserzo, M., Wallin, E., Simon, I., von Heijne, G. & Elofsson, A. (1997). Protein Eng.10, 673–676. [DOI] [PubMed] [Google Scholar]
  16. Dahl, S. G., Kristiansen, K. & Sylte, I. (2002). Ann. Med.34, 306–312. [DOI] [PubMed] [Google Scholar]
  17. Faulon, J. L., Sale, K. & Young, M. (2003). Protein Sci.12, 1750–1761. [DOI] [PMC free article] [PubMed] [Google Scholar]
  18. Fenn, T. D., Ringe, D. & Petsko, G. A. (2003). J. Appl. Cryst.36, 944–­947. [Google Scholar]
  19. Hoppe, W. (1957). Acta Cryst.10, 750–751.
  20. Kissinger, C. R., Gehlhaar, D. K. & Fogel, D. B. (1999). Acta Cryst. D55, 484–491. [DOI] [PubMed] [Google Scholar]
  21. Kleywegt, G. J. (1999). Acta Cryst. D55, 1878–1884. [DOI] [PubMed] [Google Scholar]
  22. Kraulis, P. J. (1991). J. Appl. Cryst.24, 946–950. [Google Scholar]
  23. Krogh, A., Larsson, B., von Heijne, G. & Sonnhammer, E. L. (2001). J. Mol. Biol.305, 567–580. [DOI] [PubMed] [Google Scholar]
  24. McCoy, A. J., Grosse-Kunstleve, R. W., Storoni, L. C. & Read, R. J. (2005). Acta Cryst. D61, 458–464. [DOI] [PubMed] [Google Scholar]
  25. Perozo, E., Cortes, D. M., Sompornpisut, P., Kloda, A. & Martinac, B. (2002). Nature (London), 418, 942–948. [DOI] [PubMed] [Google Scholar]
  26. Perozo, E., Kloda, A., Cortes, D. M. & Martinac, B. (2001). J. Gen. Physiol.118, 193–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
  27. Perrakis, A., Sixma, T. K., Wilson, K. S. & Lamzin, V. S. (1997). Acta Cryst. D53, 448–455. [DOI] [PubMed] [Google Scholar]
  28. Raman, P., Cherezov, V. & Caffrey, M. (2006). Cell. Mol. Life Sci.63, 36–51. [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Robertson, J. M. (1935). J. Chem. Soc., pp. 615–621.
  30. Rossmann, M. G. & Blow, D. M. (1962). Acta Cryst. A15, 24–31.
  31. Spencer, R. H. & Rees, D. C. (2002). Annu. Rev. Biophys. Biomol. Struct.31, 207–233. [DOI] [PubMed] [Google Scholar]
  32. Strop, P., Bass, R. & Rees, D. C. (2003). Adv. Protein Chem.63, 177–­209. [DOI] [PubMed] [Google Scholar]
  33. Suhre, K. & Sanejouand, Y. H. (2004). Acta Cryst. D60, 796–799. [DOI] [PubMed] [Google Scholar]
  34. Sussman, J. L., Lin, D., Jiang, J., Manning, N. O., Prilusky, J., Ritter, O. & Abola, E. E. (1998). Acta Cryst. D54, 1078–1084. [DOI] [PubMed] [Google Scholar]
  35. Terwilliger, T. C. (2000). Acta Cryst. D56, 965–972. [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Tusnady, G. E., Dosztanyi, Z. & Simon, I. (2004). Bioinformatics, 20, 2964–2972. [DOI] [PubMed] [Google Scholar]

Articles from Acta Crystallographica Section D: Biological Crystallography are provided here courtesy of International Union of Crystallography

RESOURCES