Interpretation of ensembles created by multiple iterative rebuilding of macromolecular models

Heterogeneity in ensembles generated by independent model rebuilding principally reflects the limitations of the data and of the model-building process rather than the diversity of structures in the crystal.

Abstract

Automation of iterative model building, density modification and refinement in macromolecular crystallography has made it feasible to carry out this entire process multiple times. By using different random seeds in the process, a number of different models compatible with experimental data can be created. Sets of models were generated in this way using real data for ten protein structures from the Protein Data Bank and using synthetic data generated at various resolutions. Most of the heterogeneity among models produced in this way is in the side chains and loops on the protein surface. Possible interpretations of the variation among models created by repetitive rebuilding were investigated. Synthetic data were created in which a crystal structure was modelled as the average of a set of ‘perfect’ structures and the range of models obtained by rebuilding a single starting model was examined. The standard deviations of coordinates in models obtained by repetitive rebuilding at high resolution are small, while those obtained for the same synthetic crystal structure at low resolution are large, so that the diversity within a group of models cannot generally be a quantitative reflection of the actual structures in a crystal. Instead, the group of structures obtained by repetitive rebuilding reflects the precision of the models, and the standard deviation of coordinates of these structures is a lower bound estimate of the uncertainty in coordinates of the individual models.

1. Introduction

X-ray diffraction analysis of the crystal structure of a macromolecule normally yields an electron-density map that is subsequently interpreted in terms of a simplified atomic model. Although the atomic models used in macromolecular crystallography provide a wealth of detailed and highly valuable structural information, the models are well known to be imperfect and to have varying degrees of accuracy depending on many factors including resolution, data quality, the methods used to determine the structure and the limitations of a single-model representation of a crystal structure (Lattman, 1996 ▶; Kleywegt, 2000 ▶). A major contribution to the inadequacy of macromolecular models is thought to be the presence of many slightly different conformations and arrangements of the macromolecules within the crystal itself (Kuriyan et al., 1986 ▶; Gros et al., 1990 ▶; Burling et al., 1996 ▶; Burling & Brünger, 1994 ▶; Clarage & Phillips, 1994 ▶; Pellegrini et al., 1997 ▶; Chen & Chapman, 2001 ▶; Vitkup et al., 2002 ▶; DePristo et al., 2004 ▶). If these arrangements could be described adequately as harmonic displacements, then a single model with isotropic or anisotropic displacement parameters could be used to fully represent a macromolecule in a crystal structure (Jensen, 1997 ▶). This appears to rarely be the case. The agreement between amplitudes of structure factors calculated from the single-model representations typically used for macromolecules and those obtained from experiment normally differ by about 20%, which is greater than the typical experimental uncertainty of about 5% (Vitkup et al., 2002 ▶).

The use of a single model to describe a crystal structure that actually contains many closely related structures creates significant complications for the interpretation of the structure. In particular, the single-structure representation itself is not well defined in this case. It is unclear what a single-structure representation of a crystal that contains many structures should look like even if the multiple structures that are present in the crystal were known. An average structure, for example, will probably have non-ideal geometry. Nonetheless, if the differences in conformation among the structures in a crystal are small compared with the data resolution, the average structure will yield better agreement with the experimental data than any one structure actually in the crystal. On the other hand, if the conformational differences among structures in a crystal are large, a single conformation from this group may give better agreement with the data than the average structure (some atoms of which may not actually lie in density). Carrying this a step further, the uncertainty in coordinates in a model representing a group of structures is also not well defined, as there is no single ‘correct’ set of coordinates to be compared with, even if the structures in the crystal were known precisely.

In practice, macromolecular models are normally constructed in a way that yields molecular geometries (e.g. bond angles and distances) that are close to ideal and that yield as close as possible a fit of the model to the electron density (or of calculated and experimental structure-factor amplitudes). The very good agreement between model and experimental density that can be obtained for most parts of many macromolecular models suggests that the use of a single-model representation may often be adequate. On the other hand, the very poor agreement for some parts of almost all models further suggests that some other representation is also necessary. In an ideal macromolecular structure, methods assuming small errors in coordinates can be used to estimate overall as well as individual coordinate errors (Luzzati, 1952 ▶; Cruickshank, 1965 ▶; Read, 1986 ▶; Jensen, 1997 ▶; Murshudov & Dodson, 1997 ▶; Sheldrick & Schneider, 1997 ▶; Tickle et al., 1998 ▶). As emphasized by DePristo et al. (2004 ▶), these methods are not well suited for structures where a single model cannot fully represent what is in the crystal, however, so another approach for estimating errors is needed for at least part of most macromolecular structures.

A number of elegant multiple-model representations of macromolecular crystal structures have been developed, but all have given at best a small improvement in the free R factor, the best available measure of overall model quality (Gros et al., 1990 ▶; Burling & Brünger, 1994 ▶; Clarage & Phillips, 1994 ▶; Pellegrini et al., 1997 ▶; Chen & Chapman, 2001 ▶). The fundamental difficulty in this approach is that the number of experimental observations is typically far too small to uniquely specify a detailed multiple-model representation of a macromolecular structure.

Recently, a number of methods for full or nearly full automation of iterative model building and refinement in macromolecular crystallography have been developed, making it straightforward to carry out the entire process multiple times (Perrakis et al., 1999 ▶; Terwilliger, 2003b ▶; DePristo et al., 2005 ▶; Ondráček, 2005 ▶). Besides the useful ability to carry out structure determination rapidly, automation allows a group of models to be generated, for example by repeating the process using different random seeds each time. It is found empirically that a heterogeneous group of models can be generated in this fashion, each approximately equally compatible with experimental data (DePristo et al., 2004 ▶; Ondráček, 2005 ▶; Ondráček & Mesters, 2006 ▶). DePristo et al. (2004 ▶) carried out iterative rebuilding of protein structures taken from the PDB and have demonstrated that models differing from each other by an r.m.s.d. of as much as 0.53 Å for main-chain atoms can fit experimental data at a resolution of 2.3 Å about as well as the original structure from the PDB. Ondráček (2005 ▶) and Ondráček & Mesters (2006 ▶) use ‘hip-hop’ refinement, in which alternative water-molecule placement generates diversity in a group of models built to represent a structure in order to generate a set of structures that are compatible with the data.

The interpretation of the heterogeneity in models that are compatible with a set of experimental X-ray diffraction data is not entirely clear (Furnham et al., 2006 ▶; de Bakker et al., 2006 ▶). It is generally expected that the heterogeneity at least in part reflects the precision with which the model can be defined (DePristo et al., 2004 ▶; de Bakker et al., 2006 ▶; Ondráček & Mesters, 2006 ▶). It has also been suggested that the heterogeneity may reflect the heterogeneity and dynamics of the structures in the crystal itself (DePristo et al., 2004 ▶; de Bakker et al., 2006 ▶) or that the models could reflect some combination of these possibilities (Furnham et al., 2006 ▶). This situation in which more than one model of a structure is compatible with available experimental data is related to the situation routinely encountered in NMR structure determination, although the variation among models is typically much smaller in the case of X-ray structure determination compared with that in NMR work. In NMR structure determination it is recognized that since it is not possible to generate all models compatible with a set of NMR restraints, the variability among the members of an NMR ensemble represents an estimate of the precision of the resulting structures rather than an estimate of the accuracy (Zhao & Jardetzky, 1994 ▶).

In this work, we continue within the constraints of the single-model representation of a macromolecular crystal structure, but extend the work of DePristo et al. (2004 ▶) and Ondráček (2005 ▶) by using synthetic data to examine the relationship between the ensemble of models that fit a set of structure factors and the underlying structures in the crystal and examine how such an ensemble can represent what is known and not known about a structure.

2. Methods

2.1. Iterative model rebuilding, density modification and refinement

The AutoBuild wizard in the PHENIX macromolecular crystallographic package was used to carry out iterative model rebuilding, density modification and refinement (Adams et al., 2002 ▶). Key software routines used in this Wizard include the PHENIX refinement package (phenix.refine; Afonine et al., 2005b ▶), RESOLVE density modification and model building (Terwilliger, 2000 ▶, 2003a ▶) and crystallographic libraries from cctbx (Grosse-Kunstleve et al., 2004 ▶) and CCP4 (Collaborative Computational Project, Number 4, 1994 ▶). The starting model in each case was the refined structure from the PDB corresponding to the data set used.

The overall process for model rebuilding was to create 100 initial rebuilt models, to recombine these models in groups of five using the best-fitting parts of the five models and then to remove all solvent molecules and refine the resulting recombined models, yielding a total of 20 final recombined models with no solvent or ligands.

The rebuilding scheme used to create the 100 initial models was the ‘rebuild-in-place’ option of the PHENIX AutoBuild wizard. In this scheme, the starting map was a σ_A-weighted (2mF _o − DF _c)exp(iϕc) map (Read, 1986 ▶) based on the starting model, and the map used in subsequent cycles was a density-modified map in which the density modification included information from the current model as well as density histograms and solvent flattening (Terwilliger, 2003b ▶). Noncrystallographic symmetry was not used in density modification or refinement in these tests, even when present in the crystal, as this has not yet been automated in the AutoBuild wizard, although its use is planned for future versions. This could result in some overfitting of the data that might not be detected by the free R factor. In each cycle, the model from the previous cycle was rebuilt in segments, the rebuilt segments were combined and the model was refined, including a bulk-solvent model and automatically placed solvent molecules (Afonine et al., 2005a ▶), to yield a new initial model for this cycle. The overlapping segments of a chain were rebuilt in segments of ten residues, with the rebuilt segments overlapping by five residues. For the first and last residues in the segment, only the side chains were rebuilt. For the eight residues in the middle, the chain was traced into the current electron-density map forwards using the second amino acid in the segment as an anchor and backwards from the ninth amino acid in the segment, joining them where they overlap, provided there was an amino acid where the N, C^α and C atoms from the two overlap with an r.m.s.d. of less than a set cutoff (typically 0.8 Å). A random seed was used to apply a slight randomization (typically 10°) to the orientations of the second and ninth residues in each segment, generating a slightly different chain tracing each time. Five tracings in each direction were typically constructed and the best-fitting rebuilt segment was kept. If the segment could not be rebuilt using this algorithm, then the original main-chain coordinates were kept. This procedure can therefore yield some main-chain coordinates that are artificially close to the coordinates used to initiate the rebuilding in cases where the density is especially poor. Side chains for the initial model for this cycle were rebuilt and the resulting model was refined. The initial and side-chain-optimized models were then recombined as described below, where the model for each residue that had the best real-space correlation coefficient was chosen and the recombined model was then refined to yield the final model for this cycle. Two to five cycles of this rebuilding in place were carried out for each of the 100 models constructed.

Recombination steps were carried out using the ‘cross’ option in RESOLVE model building. In this procedure, two closely related models are considered in relation to a single electron-density map and a new model is created by splicing together segments from the two input models. Crossovers between the two models were considered at all corresponding C^α positions that were within a specified distance of each other (typically 0.2–0.5 Å). The difference between the residue-based correlation coefficients for the two models, smoothed with a window of typically five residues, was used to decide which of the two models was to be used at each position. A protein chain was started with whichever model had the higher smoothed correlation coefficient at the N-terminus and was continued with the same model until a C^α position was found where crossover was allowed as defined above and where the other model had the higher smoothed correlation coefficient. This process was repeated until the end of the chain. To merge members of a group of more than two models, the process was repeated iteratively by combining the two models and then combining the resulting composite model with the next model until all models were used in the recombination step.

2.2. Generation of synthetic data and calculation of r.m.s. differences between structures

Synthetic data were created in which a crystal structure was modelled as a set of ‘perfect’ structures. Beginning with the refined structure of initiation factor 5A (IF5A) from Pyrobaculum aerophilum (Peat et al., 1998 ▶), a set of 20 models was created by iterative rebuilding as described above using experimental data to a resolution of 4 Å. The resulting ensemble of models was quite heterogeneous, with an overall coordinate standard deviation (SD) of 1.31 Å (0.75 Å for main-chain and 1.75 Å for side-chain atoms). Atomic displace­ment (B) factors for the atoms in these models ranged from 12 to 114 Ų, with a mean of 26 Ų and an SD of 10 Ų.

Structure factors including a bulk-solvent model (Afonine et al., 2005a ▶) were calculated individually for each model in the ensemble. A composite structure factor was then created by averaging the complex structure factors for the individual models. The amplitudes of these averaged structure factors were obtained and a Gaussian random ‘experimental error’ with an SD of 10% of the value of the structure-factor amplitude was added to yield the final ‘experimental’ amplitudes for the synthetic data set. A ‘mean perfect structure’ was also created using the simple arithmetic mean of all coordinates of all the models in the ensemble. This mean perfect structure differed from the starting model of IF5A by an r.m.s.d. of 1.05 Å (0.63 Å for main-chain and 1.37 Å for side-chain atoms).

In the process of calculating r.m.s. differences among models and in averaging the coordinates of multiple models, the identification of which atoms are ‘equivalent’ and therefore to be compared or averaged was not always straightforward. This was the case, for example, when a side chain such as tyrosine, phenylalanine, glutamate, aspartate or arginine has more than one equivalent orientation (a 180° rotation places the C^δ1 and C^∊1 atoms of tyrosine in the locations of the C^δ2 and C^∊2 atoms, for example). Other residues are nearly symmetric except for exchange among C, N and O atoms (e.g. glutamine, asparagine and histidine). All these residues were aligned in the following way for the purpose of calculating r.m.s. differences between models. An arbitrary model was chosen as a standard for comparison. In any model to be averaged or compared, all the side chains with multiple equivalent orientations were oriented so as to place corresponding atoms as close as possible to those in the standard model (minimizing the r.m.s.d. among corresponding atoms) and the coordinates were then averaged or compared.

2.3. Convergence of the model-building process

The models that are produced using our automated process have gone through multiple cycles of rebuilding and refinement; however, it is possible that if more extensive refinement procedures were applied, the heterogeneity within ensembles would be reduced. A simple test was carried out to examine this possibility. The first two models in the ensemble created at a resolution of 1.75 Å (see Table 3 below) were re-refined, carrying out 100 cycles of refinement either with or without simulated annealing (Afonine et al., 2005b ▶), and the r.m.s.d. between these two models before and after refinement was compared. The two models originally differed by an r.m.s.d. of 0.09 Å for main-chain atoms and 0.49 Å for side-chain atoms. After re-refinement without simulated annealing they differed by very similar r.m.s.d.s of 0.09 Å for main-chain atoms and 0.50 Å for side-chain atoms. With simulated annealing these values were again very similar (0.10 Å for main-chain atoms and 0.50 Å for side-chain atoms). The free R values of all the models were in the range 0.304–0.311. This test indicates that the differences among the models produced by our procedure cannot readily be reduced by extensive refinement.

As another test of the convergence of the model-building process, the two models examined above were also rebuilt manually using the interactive model-building program MAIN 2006 (http://www-bmb.ijs.si/). The model rebuilding consisted of fitting side chains, followed by peptide-bond orientation fitting. In this process, models 1 and 2 were rebuilt independently of each other. In each rebuilding cycle the parts with the most unfavorable nonbonded interactions were manually rebuilt. The two models diverged from each other after each cycle of model rebuilding, whereas the subsequent refinement cycle brought the structures closer, but did not overcome the differences introduced during the model-rebuilding process (the r.m.s.d. between C^α atoms was 0.98 Å between models 1 and 2 in the ensemble created at a resolution of 1.75 Å; after manual rebuilding it was 0.14 Å, after refinement it was reduced to 0.13 Å, after an additional rebuilding step it was 0.15 Å and after additional refinement it was 0.14 Å). Apart from the variability in the positioning in side chains, the two rebuilt models differed principally in the orientations of a few peptides. This interactive rebuilding, in which the two rebuilt models remained different from each other, suggests that final conformation of the refined models is even at relatively high resolution in part a result of the procedures used to establish them.

2.4. Structures and data from the Protein Data Bank

The X-ray structures used in this work were taken from the Protein Data Bank (Bernstein et al., 1977 ▶; Berman et al., 2000 ▶) and are shown in Table 1 ▶. For the present study, all solvent molecules and ligands were removed from these structural models and X-ray diffraction data (structure-factor amplitudes) were used to the resolution available. In order to have a consistent refinement procedure for the ‘starting’ model and for the models rebuilt as described above, each model without solvent and ligands was refined with phenix.refine from the PHENIX crystallographic package (Adams et al., 2002 ▶). The working and test sets for each structure were taken from the deposited data sets in the PDB. The free R factors for these structures reported in Fig. 3 are those obtained from PHENIX refinement.

Table 1. X-ray structural data used in this study.

PDB code	dmin (Å)	R/Rfree	Mean ADP (Å2)	Total chains	Total residues	Reference
1a0j	1.70	0.17/0.22	22.9	2	892	Kishan et al. (1997 ▶)
1a3n	1.80	0.17/0.22	16.2	4	572	J. Tame & B. Vallone, unpublished work
1bmb	1.80	0.19/0.22	22.5	2	106	Ettmayer et al. (1999 ▶)
1aof	2.00	0.16/0.20	25.8	2	1074	Williams et al. (1997 ▶)
1c2t	2.10	0.23/0.26	31.7	1	418	Greasley et al. (1999 ▶)
1uyi	2.20	0.18/0.22	28.3	1	209	Wright et al. (2004 ▶)
1rg5	2.50	0.16/0.18	52.9	3	824	Roszak et al. (2004 ▶)
1p4t	2.55	0.23/0.26	39.1	1	155	Vandeputte-Rutten et al. (2003 ▶)
1cqp	2.60	0.19/0.26	36.2	2	364	Kallen et al. (1999 ▶)
1c1z	2.88	0.24/0.24	55.3	1	326	Schwarzenbacher et al. (1999 ▶)

3. Results and discussion

3.1. Repetitive rebuilding of models from the PDB

Iterative model rebuilding, density modification and refinement was carried out on ten macromolecular structures from the PDB that had deposited structure-factor amplitudes and had test and working sets defined. These structures were first edited to remove all solvent molecules and ligands and were re-refined with the PHENIX refinement protocol to have a consistent procedure for refinement; the re-refined models were then used as starting points for model rebuilding. A different random seed was used for each repetition of the model-rebuilding procedure. The principal impact of this random seed was to generate diversity in the models built using RESOLVE model building (Terwilliger, 2003a ▶). Two to five cycles of model rebuilding, density modification and refinement were carried out to create 100 initial rebuilt models for a structure. These initial models were then merged in groups of five into composite structures that contained the best-fitting parts of the component initial rebuilt models. The 20 composite models were refined and used as the ensemble of models for that structure.

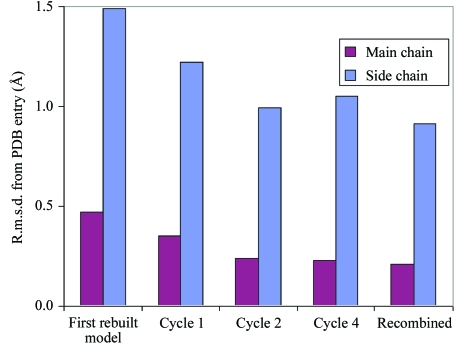
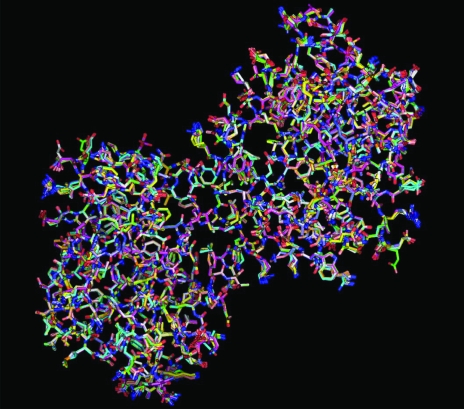
Fig. 1 ▶ illustrates the progress of rebuilding for one of the 20 models obtained for structure 1cqp at a resolution of 2.6 Å (Kallen et al., 1999 ▶). The model obtained after initial rebuilding of the 1cqp structure differs significantly from the starting model (0.47 Å for main chain, 1.49 Å for side chains), but subsequent iterations of rebuilding, including the recombination of five independently built models, reduces this difference to 0.21 Å for main-chain atoms and 0.91 Å for side-chain atoms. The starting free R factor in the first cycle of rebuilding was 0.42 and for the final rebuilt model it was 0.27; the corresponding value for the structure 1cqp from the PDB, re-refined with phenix.refine after removal of ligands and solvent, was 0.26. [The free R factor reported for this structure (Kallen et al., 1999 ▶) with all ligand and solvent was also 0.26]. The improvement in free R during the rebuilding process and the return of the structure towards the model in the PDB indicates that the rebuilding process generates diversity in the initial rebuilding of the model and then improves the agreement with the data during subsequent rounds of rebuilding, density modification and refinement. Fig. 2 ▶ illustrates the final 20 models obtained from rebuilding 1cqp. Most of the diversity among models is in the side chains and most of the heterogeneous side chains are on the surface of the protein. The SD of the coordinates of models is 0.12 Å for main-chain atoms and 0.53 Å for side-chain atoms. These models differ from the 1cqp model (after re-refinement with phenix.refine without waters or ligands; Kallen et al., 1999 ▶) by an r.m.s.d. of 0.18 Å for main-chain atoms and 0.93 Å for side-chain atoms. The maximum-likelihood estimate of overall coordinate uncertainty for the 1cqp model is 0.41 Å (Read, 1986 ▶; Lunin et al., 2002 ▶).

Figure 1.

Progress of model rebuilding for 1cqp. The r.m.s.d.s of refined models from the deposited coordinates of 1cqp are plotted for the first, second and fourth cycles of iterative model rebuilding, density modification and refinement and after the final recombination of five models to produce one of the 20 models of 1cqp.

Figure 2.

PyMOL view (DeLano, 2002 ▶) of the overlay of 20 models of 1cqp obtained by repetitive model rebuilding, density modification and refinement.

Table 2 ▶ lists maximum-likelihood estimates of the overall coordinate uncertainties for each deposited model from the PDB, the average SD of coordinates of the models in the ensembles (precision of the models) for each of the structures, the average r.m.s.d. among the models in the ensembles and the average r.m.s.d. of these ensemble structures from the deposited model. The average SD of coordinates of models in the ensembles and the average r.m.s.d. among the models in the ensembles are related by a constant factor of 2^1/2. They are both shown because the SD of coordinates of models in the ensembles is a useful estimate of the precision of the models, while the average r.m.s.d. among the models in the ensembles can be directly compared with the average r.m.s.d. between the ensemble structures and the (re-refined) deposited model. The average r.m.s.d. between models in the ensembles is in most cases quite similar to the average r.m.s.d. between these models and the corresponding PDB entry. This suggests that the models deposited in the PDB are not systematically different from the models in our ensembles, but rather are (on average) within the range of variation of the models in the ensembles.

Table 2. Characteristics of multiple rebuilt models.

			SD of models (precision, Å)		R.m.s.d. among models (Å)		R.m.s.d. between models and re-refined PDB entry (Å)
PDB code	dmin (Å)	ML estimate of coordinate error (Å)	Main chain	Side chain	Main chain	Side chain	Main chain	Side chain
1a0j	1.70	0.28	0.05	0.47	0.07	0.66	0.10	0.95
1a3n	1.80	0.35	0.03	0.38	0.04	0.54	0.06	0.68
1bmb	1.80	0.29	0.05	0.42	0.07	0.59	0.07	0.71
1aof	2.00	0.31	0.05	0.38	0.07	0.54	0.10	0.66
1c2t	2.10	0.41	0.13	0.56	0.18	0.79	0.19	0.98
1uyi	2.20	0.38	0.08	0.43	0.11	0.61	0.12	0.84
1rg5	2.50	0.44	0.14	0.44	0.20	0.62	0.18	0.62
1p4t	2.55	0.40	0.27	0.57	0.38	0.81	0.36	0.84
1cqp	2.60	0.41	0.12	0.53	0.17	0.75	0.18	0.93
1c1z	2.88	0.48	0.62	1.50	0.88	2.12	0.80	2.15

Although the model-rebuilding process used here is quite effective, it does not yet produce models that have all the characteristics desired of a final refined model of a structure. In particular, the 20 models produced for each structure do not have geometry that is fully regularized, nor have the models been examined in detail in the context of a difference map to identify all discrepancies between the model and experimental data. Nevertheless, these models have good geometry in general (the 1cqp models produced in Fig. 1 ▶ have r.m.s. deviations for bond angles of 0.7° and of bond distances of 0.005 Å, for example) and their free R factors are comparable to those corresponding to final refined models (see below).

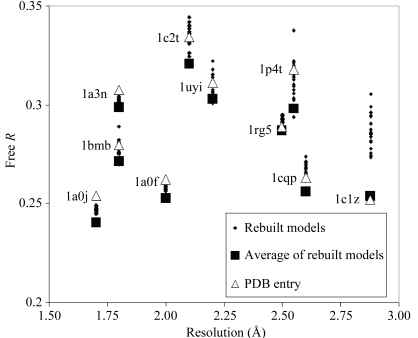
3.2. Free R factors of multiple models

Fig. 3 ▶ shows the free R factors for the 20 models obtained for each of the ten PDB entries that were rebuilt. The structures are arranged according to their high-resolution limits and the free R factor for each rebuilt model is illustrated. The free R factor for the original PDB entry (after refinement without solvent and ligands) is also shown. In the cases of all the structures rebuilt at resolutions higher than 2.5 Å, at least some of the rebuilt models had a free R factor for the rebuilt models at least as low as that of the original (re-refined) structure, indicating that the rebuilding process can produce models of very high quality. For three structures at lower resolution (1rg5, 1cqp, 1c1z), the free R factor of the original structure was lower than any of those for a rebuilt model, however, suggesting that the rebuilding process may be less effective compared with manual building at low resolution than it is at higher resolutions.

Figure 3.

Free R factors for rebuilt models, re-refined original models and composites of rebuilt models. Free R factors for each of the 20 rebuilt models for each structure from the PDB are illustrated as small diamonds. The free R factor for the original PDB entry, after refinement without solvent or ligands, is indicated by a large open triangle. The free R factor of a composite model corresponding to simple averaging of density from the 20 rebuilt models (including an implicit solvent model obtained as part of the refinement process) and calculated by simple averaging of complex structure factors based on all the component structures is indicated by a large filled square.

Fig. 3 ▶ also shows the free R factor obtained for each ensemble of 20 rebuilt models by simple averaging of the complex structure factors corresponding to all the models. With two exceptions (1rg5 and 1p4t), these free R factors are lower than the free R factors of any of the individual 20 rebuilt models. This means that the average of the density for the models in the ensemble is closer to the density in the crystal than that of any individual model. Furthermore, with just one exception (1rg5), these free R factors are lower than those of the original PDB entry (after re-refinement without ligands and solvent to improve comparability as described above). On average, the free R factor based on the average density for 20 rebuilt models is 0.8% lower than that of the re-refined original PDB entry. The interpretation of the small improvement in free R based on average density compared with the individual models will be addressed below, following an analysis of synthetic data.

3.3. Analysis of synthetic data

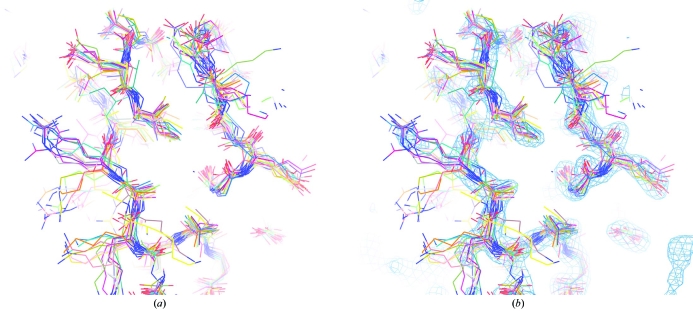
As mentioned above, the interpretation of ensembles of models created by repetitive model building, density modification and refinement procedures such as those used here is currently an open question (Furnham et al., 2006 ▶; de Bakker et al., 2006 ▶). In particular, it is not known whether the heterogeneity among these models reflects the contents of the crystal itself or whether it instead reflects the precision to which a particular model can be specified or some combination of these. To address this question, synthetic data were created based on the structure of initiation factor 5A from P. aerophilum in which the contents of the ‘crystal’ are known exactly. The contents of a crystal were modelled as a collection of 20 structures with an r.m.s.d. of 1.5 Å from the refined IF5A structure, model structure factors were calculated based on these structures (including a bulk-solvent model), 10% random error was added and the resulting structure factors were used as ‘experimental’ data. Fig. 4 ▶ illustrates a portion of this ensemble of ‘perfect’ structures and the model electron-density map calculated from their average. The models are quite heterogeneous, but the resulting electron-density map looks much like a real electron-density map that might be obtained at a resolution of about 2–2.5 Å.

Figure 4.

Models used to create synthetic ‘crystal’. (a) PyMOL view (DeLano, 2002 ▶) of 20 ‘perfect’ models in the ensemble used to create a synthetic data set. (b) Perfect models and perfect electron density corresponding to those models.

The same repetitive rebuilding process used for the structures from the PDB was applied to this synthetic data. Additionally, however, the process was repeated using data to various resolutions to examine the effect of having more or fewer data. One might question whether truncated data are representative of real crystals that diffract to lower resolution. The attainable resolution will be limited by two effects: the internal mobility of the molecules making up the crystal and lattice disorder in the crystal packing. By truncating data at different resolutions, we mimic part of each of these effects. This procedure does not mimic the effect of mobility and lattice disorder on the overall decrease in scattering with resolution (the overall B factor of the data) and a more comprehensive study could be undertaken in which this is modelled by generating ‘perfect’ ensembles with different amounts of variability.

Table 3 ▶ lists the mean free R factors obtained for the rebuilt ensembles of IF5A at each resolution, along with the r.m.s. deviation of these models from the ‘mean perfect structure’ (the average coordinates of the 20 structures in the model crystal used to generate the data) and the SD of coordinates among the models in the ensemble. The free R factors are in the range 0.22–0.40, similar to those of the real data sets from the PDB analyzed above. This rebuilding process not only generated diversity in the resulting models, but also improved the quality of the model, at least at resolutions finer than 4 Å (Table 3 ▶). The starting model had an r.m.s.d. from the ‘mean perfect structure’ of 0.63 Å for main-chain atoms, for example, while the resulting models built at a resolution of 1.75 Å had an r.m.s.d. of only 0.39 Å from the ‘mean perfect structure’. This improvement is important because it shows that the iterative rebuilding procedure does not simply introduce random diversity into the structures; rather, it obtains a group of structures that have diversity yet for which each structure is improved over the starting model.

Table 3. Ensembles built using synthetic data.

		SD of models (precision, Å)		R.m.s.d. from ‘mean perfect structure’ (Å)
Resolution (Å)	Mean free R factor	Main chain	Side chain	Main chain	Side chain
1.75	0.24	0.19	0.68	0.39	1.15
2.0	0.23	0.20	0.63	0.39	1.11
2.5	0.22	0.22	0.75	0.39	1.17
3.0	0.26	0.32	0.81	0.49	1.26
3.5	0.26	0.48	1.07	0.61	1.43
4.0	0.31	0.76	1.78	0.84	1.93
4.5	0.40	1.01	2.44	1.17	2.81

3.4. Does the heterogeneity among multiple rebuilt models reflect heterogeneity and dynamics in the crystal?

The models obtained from synthetic data were examined in order to test the two possibilities for the interpretation of the diversity among the rebuilt models. We first considered whether the diversity among the coordinates of the rebuilt models might reflect the actual diversity among coordinates of the structures in the model crystal. Table 3 ▶ lists the SD of the coordinates of rebuilt models as a function of the resolution of the data included in the iterative rebuilding process. All the experiments using synthetic data are based on the same ‘crystal’ and therefore all of the multiple models that were obtained represent exactly the same object.

Table 3 ▶ shows that the SD of coordinates for both main-chain and side-chain atoms in rebuilt models strongly increases as a function of the high-resolution cutoff of the data used. For main-chain atoms, this SD increases from 0.19 Å at a resolution of 1.75 Å to 1.01 Å at a resolution of 4.5 Å. As the SD of coordinates of rebuilt models varies strongly with the resolution of the data used, while the crystal itself is unchanged in these tests, we conclude that the heterogeneity of the rebuilt models cannot possibly by itself be a quantitative indicator of the heterogeneity of structures in the crystal.

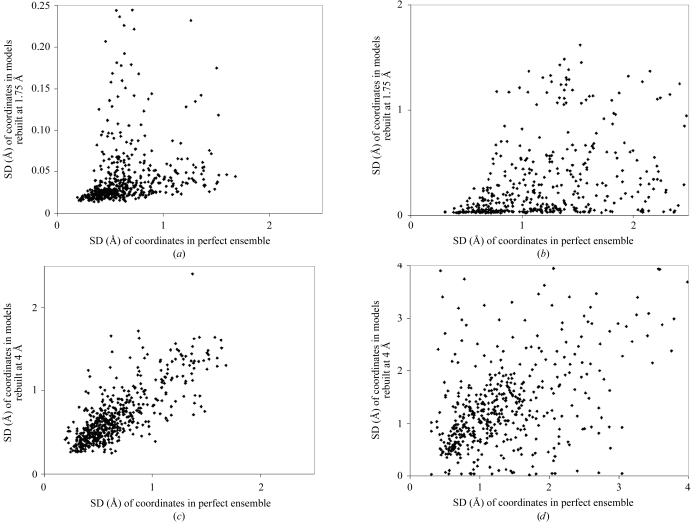
Despite this conclusion, we expect that the heterogeneity in a crystal does contribute to diversity among multiple rebuilt models, perhaps even on an atom-by-atom or residue-by-residue basis. For example, it seems likely that those parts of a structure that have a high degree of heterogeneity will typically be rebuilt with less reproducibility than those that are more uniform. The analysis in Table 3 ▶ simply shows that the variability among rebuilt models is dominated by the effects of the amount of data available and that the variability among rebuilt models is not necessarily even on the same scale as the heterogeneity among structures in the crystal. Fig. 5 ▶ illustrates this relationship. In Fig. 5 ▶(a), the SD of main-chain coordinates among models rebuilt at a resolution of 1.75 Å is plotted as a function of the SD of coordinates in the ‘perfect’ models used to construct the synthetic ‘crystal’. There is some correlation of the heterogeneity in the two cases, but the scale of variation in the rebuilt models is much smaller than that of the original perfect models. Fig. 5 ▶(b) shows a similar result for side-chain atoms. Figs. 5 ▶(c) and 5 ▶(d) show the same relation as Figs. 5 ▶(a) and 5 ▶(b), except that the models rebuilt at a resolution of 4 Å are considered. In this case, the scale of variation in the rebuilt models is similar to that of the original perfect models. A consideration of Figs. 5 ▶(c) and 5 ▶(d) alone might lead to the conclusion that there is a general relationship between ensembles of rebuilt models and the contents of the crystal. However, considering that Figs. 5 ▶(c) and 5 ▶(d) differ from Figs. 5 ▶(a) and 5 ▶(b) only in the truncation of the data to a resolution of 4 Å, it is clear that there is no such general relationship. A more likely interpretation of Figs. 5 ▶(c) and 5 ▶(d) is that the heterogeneity in the ‘crystal’ in some locations leads to a map with relatively poor definition in those locations and thereby to a set of rebuilt models with higher heterogeneity in those locations. The extent of heterogeneity of the rebuilt models, however, depends strongly on the resolution of the data used to create the map, so that the heterogeneity in the rebuilt models is not a quantitative indicator of the heterogeneity in the crystal.

Figure 5.

SD of coordinates of rebuilt models (precision) compared with SD of coordinates of perfect models used to create synthetic crystal. (a) Main-chain atoms of models rebuilt at a resolution of 1.75 Å. (b) Side-chain atoms of models rebuilt at a resolution of 1.75 Å. (c) Main-chain atoms of models rebuilt at a resolution of 4.0 Å. (d) Side-chain atoms of models rebuilt at a resolution of 4.0 Å.

In fact, we should probably not expect multiple models, refined individually, to display the same degree of heterogeneity as the multiple structures in the crystal. As shown in Fig. 4 ▶, much of the variation is local and of a size that is relatively small compared with the resolution. Such local variation will spread out the electron density in a manner very similar to the harmonic displacements represented by a B factor, so the density in these cases can be represented fairly well by single atoms and isotropic B factors. The uncertainty in locating the center of a Gaussian distribution is not the same as the standard deviation of that Gaussian, so we should expect higher precision in locating the mean positions of atoms than the r.m.s. displacements of individual copies of those atoms.

3.5. Does the heterogeneity among multiple rebuilt models reflect the precision of the model-building process?

A second interpretation of the heterogeneity among multiple models built by repeated iterative model building, density modification and refinement is that this heterogeneity specifies the precision of the rebuilt models (DePristo et al., 2004 ▶; de Bakker et al., 2006 ▶; Ondráček & Mesters, 2006 ▶). As all the rebuilt models for any one data set tend to have relatively good geometries and similar free R factors (Fig. 3 ▶), it is difficult to identify any one of them that is significantly ‘better’ than any other one, particularly in the absence of any global indicator of ‘quality’ of a macromolecular model. All of these models are generated by essentially the same calculation (differing only in a random seed). The differences among the rebuilt models therefore reflect the reproducibility of the entire rebuilding process and in effect specify the precision of the resulting models. Although this interpretation is somewhat trivial, the concept can have significant utility because the precision of a model defines a lower limit on the uncertainty in coordinates of that model. Furthermore, if the precision (reproducibility) of the models is quantitatively similar to some measure of the accuracy (deviation from a true value) of the models, then the precision as estimated from repetitive rebuilding may have even more utility.

As discussed above, the accuracy of a single model that represents a crystal containing many structures is difficult to define. However, a crude approximation to the ‘mean’ structure in a crystal might be the arithmetic mean of all the structures present. In this analysis of synthetic data, we have used this approach to define the ‘mean perfect structure’. In this context, it is possible to define the accuracy of the rebuilt models as the deviation between the coordinates of the rebuilt models and those of the mean perfect structure.

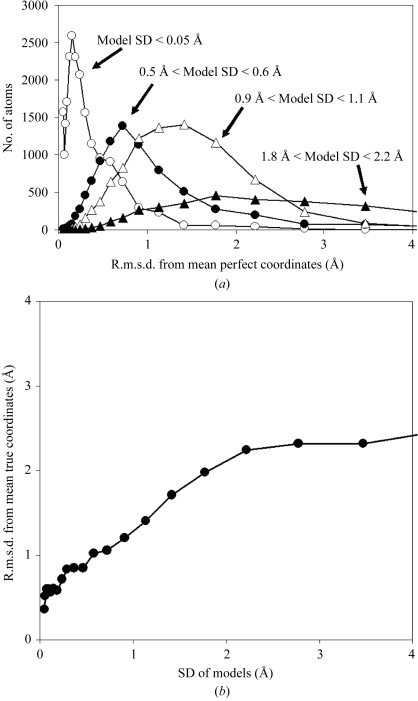
Fig. 6 ▶ illustrates the relationship between the precision of model building (as determined from the SD of coordinates of the rebuilt models) and a rough measure of the accuracy of model building (as determined from the r.m.s.d. between rebuilt models and the mean perfect structure) for the synthetic data sets in Table 3 ▶. Fig. 6 ▶(a) shows that for those atoms that have high precision (very low SD) in coordinates among rebuilt models, the rebuilt models have high accuracy (coordinates that are very close to those of the mean perfect structure). Correspondingly, those atoms that have low precision (high SD of coordinates of rebuilt models) are typically inaccurate (they are further from those of the perfect structure). Fig. 6 ▶(b) illustrates this quantitatively, showing that the relationship between the SD for coordinates of rebuilt models and the r.m.s.d. between rebuilt models and the mean perfect structure is nearly linear over a wide range. There is a clear bias in this relationship, however, in which the r.m.s.d. from the mean perfect model is systematically higher than the SD of model coordinates. As discussed above, it is difficult to define the accuracy of a model that represents a collection of structures, so it is not entirely clear whether the differences between the precision and accuracy of these structures are significant. Overall, Fig. 6 ▶ indicates that the SD of coordinates in a group of rebuilt models can be a reasonable, but not perfect, indicator of the accuracy of those models.

Figure 6.

SD of coordinates of rebuilt models (precision) compared with r.m.s.d. between rebuilt models and mean perfect structure (a rough measure of accuracy) in a synthetic data set. (a) Histograms of the number of atoms in models rebuilt at all resolutions (Table 3 ▶) with each value of r.m.s.d. from the mean true structure, grouped according to the SD of coordinates of rebuilt models. Open circles, atoms with SD of coordinates of rebuilt models of <0.05 Å; solid circles, 0.5 Å < SD < 0.6 Å; open triangles, 0.9 Å < SD < 1.1 Å; closed triangles, 1.8 Å < SD < 2.2 Å. (b) R.m.s.d. from mean true structure as a function of the SD of coordinates of rebuilt models. Atoms are grouped in bins as a function of the SD of coordinates of the rebuilt models and the mean r.m.s.d. from the mean true structure for each group is shown.

3.6. Reproducibility of the ensemble-generation process using different starting models

It would be useful if the characteristics of the ensembles resulting from our process did not depend strongly on the starting model that is used. The reproducibility of the ensemble-generation process was tested based on the synthetic data considered above but using a series of different starting models and rebuilding each time using data to a resolution of 1.75 Å. The starting models used were the models produced from the rebuilding process described above (Table 3 ▶) using data from various resolutions ranging from 1.75 to 4.5 Å. For example, the starting model for ensemble 1 was one of the models in the ensemble obtained at a resolution of 1.75 Å (Table 3 ▶) and was similar to the ‘mean perfect structure’ (main-chain r.m.s.d. of 0.38 Å). The starting models for ensembles 2–7 had r.m.s.d.s of 0.22–1.12 Å, respectively, for main-chain atoms from the starting model for ensemble 1. These starting models differed from the mean perfect structure by r.m.s.d.s of 0.38–1.11 Å, respectively, for main-chain atoms.

Table 4 ▶ lists the characteristics of models rebuilt in this way. The ensembles obtained using starting models 1–6 were all very similar and were different from the ensemble obtained using starting model 7. For the ensembles based on starting models 1–6, the mean free R values were all about the same (0.24). These ensembles were obtained using starting models that had an r.m.s.d. of main-chain atom coordinates to the starting model for ensemble 1 of less than 1.0 Å. Importantly, for this set of ensembles the r.m.s.d. among models in an ensemble (mean of 0.20 Å for main-chain atoms) was only slightly smaller than the r.m.s.d. between models in different ensembles (mean of 0.25 Å). This similarity indicates that this set of ensembles consists of a set of samples from very similar parent distributions.

Table 4. Ensembles built using synthetic data at a resolution of 1.75 Å, beginning from different starting models.

			R.m.s.d. among models in ensemble (Å)		R.m.s.d. between models and models in ensemble 1 (Å)
Ensemble	Main-chain r.m.s.d. of starting model from ensemble 1 (Å)	Mean free R factor of structures in ensemble	Main chain	Side chain	Main chain	Side chain
1	0.00	0.24	0.19	0.72	—	—
2	0.22	0.24	0.21	0.65	0.24	0.75
3	0.31	0.24	0.19	0.66	0.20	0.74
4	0.43	0.24	0.18	0.78	0.22	0.88
5	0.58	0.24	0.24	0.72	0.30	0.84
6	0.87	0.24	0.16	0.65	0.27	0.86
7	1.12	0.27	0.49	1.21	0.51	1.35

In contrast, the one ensemble which was obtained using a starting model that had a high main-chain r.m.s.d. from the mean perfect structure (1.1 Å, ensemble 7) was considerably different from the others, with much higher variability amongst structures (0.49 Å compared with 0.16–0.24 Å) and a higher r.m.s.d. from the models in ensemble 1 (0.51 Å for main-chain atoms). Additionally, the structures in this ensemble had a somewhat higher mean free R value (0.27 compared with 0.24). The observation that the ensemble based on the starting model that was most different from the ‘mean true structure’ had a high variability and relatively poor free R factor suggests that this starting model was too different from the mean true structure to be successfully rebuilt.

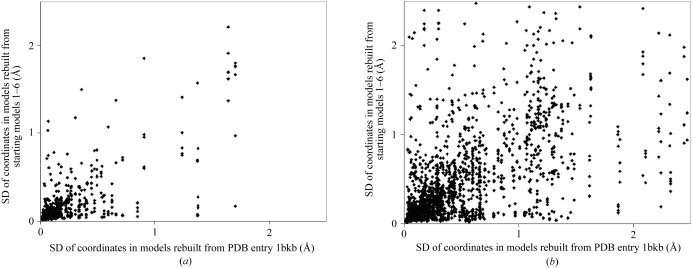
The reproducibility of the estimates of precision obtained from ensembles of models rebuilt at a resolution of 1.75 Å was also examined. Fig. 7 ▶ compares the precision of the models, atom by atom, estimated from ensembles 1–6 in Table 4 ▶, with the precision estimated from the single ensemble generated in the separate analysis at a resolution of 1.75 Å in Table 3 ▶. Fig. 7 ▶(a) compares the SD of coordinates for main-chain atoms and Fig. 7 ▶(b) for side-chain atoms. While the SDs of the coordinates in the two cases are not identical, they are similar, with an overall correlation coefficient of 0.73 for main-chain atoms and 0.65 for side-chain atoms.

Figure 7.

SD of coordinates of rebuilt models (precision) estimated using ensembles with different starting models in a synthetic data set. The ordinates are the SD of coordinates in the single ensemble obtained by rebuilding at a resolution of 1.75 Å listed in Table 3 ▶. The abscissas are the SD of the coordinates of the corresponding atoms in the six ensembles (1–6) in Table 4 ▶, rebuilt at the same resolution but using different starting models. (a) Main-chain atoms. (b) Side-chain atoms.

As starting models differing by an r.m.s.d. of main-chain atoms of up to 1 Å yield similar ensembles and related estimates of precision in this test case, we conclude that the characteristics of the ensembles of models that are generated by our process are not strongly dependent on the starting model used.

3.7. Interpretation of the precision of rebuilt models

The precision (reproducibility) of an ensemble of rebuilt models has a simple meaning and care should be taken not to extrapolate this meaning beyond an appropriate range of applications. An ensemble of models generated by a standard process from one set of data, varying only in randomization steps, gives an indication of the range of models that could have been obtained in any one structure determination using this process. In a sense, this is the precision of the resulting models and a measure of the reproducibility of the procedure. It is reasonable to use this precision as a lower bound estimate of the accuracy of the models, as the models cannot be any more accurate, as a group, than their precision. As shown above, this precision may even be a reasonably good estimate of the accuracy, not simply a lower bound, but this observation seems likely to be highly dependent on the procedures used.

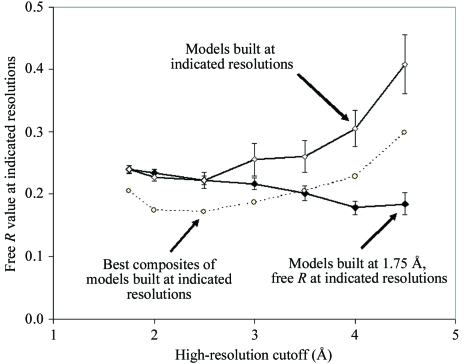
The precision of a set of models does not, however, necessarily have anything to do with the accuracy of a model that can be produced by some other procedure based on the same data. To illustrate this point, an analysis of the ensembles of models produced from synthetic data (Table 3 ▶) was carried out. Fig. 8 ▶ compares the free R values of the models produced using the data truncated at various resolutions with those of models produced by using all the data but then only considering the data to these various resolutions in calculating the free R value. Fig. 8 ▶ shows that the models produced at a resolution of 1.75 Å have much better free R values at low resolution than the models that were built at low resolution. This is not particularly surprising, as it is well known that the fit to X-ray data at moderate resolution can be improved by obtaining higher resolution data and using it to improve the model and its fit at moderate (as well as high) resolution (Lattman, 1996 ▶). Fig. 8 ▶ confirms, however, that the models that are obtained using data to low resolution (e.g. 4.0 Å) are not the best possible models that could be obtained using this data. The 1.75 Å models all have lower free R values than any of the 4.0 Å models, considering just the data to 4.0 Å. This means that the quality of the models in the ensemble generated at a resolution of 4.0 Å is in part a sampling problem in which the model-building algorithm is not able to test all possible models and some of the best ones are never examined. None of the 1.75 Å models were ever considered during the generation of the 4.0 Å models. If they had been, then they would have been identified (based on R or free R values) as clearly superior to the 4.0 Å models that the procedure generated. We examined this point further by determining whether the ensemble of models generated using data to various resolutions contained accurately placed atoms, but simply never together in the same model. For each ensemble represented in Fig. 8 ▶, we created a composite ‘structure’ by breaking each structure in the ensemble into segments five residues long and choosing for each segment the one that had the lowest r.m.s.d. to the mean true structure. The dotted line in Fig. 8 ▶ shows that the free R values of these composite models are consistently somewhat lower than the mean free R values of the individual models in the ensembles. This suggests that the sampling problem might be partially overcome by recombination among multiple models of a structure, provided a method for choosing the best example of each segment can be developed.

Figure 8.

Comparison of free R values of models built at varying resolutions with models built at a resolution of 1.75 Å. The open diamonds indicate the mean of the free R values of the models built at varying resolutions as described in Table 3 ▶. The closed diamonds show the mean of the free R values of the models built at a resolution of 1.75 Å, but only using data to the indicated resolutions to calculate the free R values. The error bars are ±1 SD. The open circles indicate the free R value of composite models constructed as described in the text from the ensemble of models built at varying resolutions.

The results in Fig. 8 ▶ indicate that the heterogeneity among the models produced at low resolution reflects the procedure used to generate the models as well as the intrinsic information contained in the data. It seems likely that this conclusion would apply to any ensemble of models created using procedures similar to those described here. We would expect, therefore, that as procedures for automated model building are improved and yield more accurate structures, the heterogeneity in models obtained using a particular set of data is likely to decrease.

3.8. Interpretation of the free R factor of averaged rebuilt models

We noticed above that using experimental data, the free R factor based on structure factors constructed as the simple complex average of structure factors for each of the models in an ensemble of rebuilt models was in almost all cases slightly lower than the free R factor of any of the individual models in the ensemble and also slightly lower than the free R factor of the model taken from the PDB (after refinement without solvent and ligands in a comparable fashion). As in the overall analysis of multiple models described above, there are several possible interpretations of this observation. One interpretation would be that the multiple models reflect what is in the crystal. According to this interpretation, the density averaged over all models is more similar to what is in the crystal than any individual model because the crystal contains a group of structures that are similar to the models in the ensemble. Our analysis of synthetic data indicates that this interpretation is unlikely to be correct, however, as the multiple models in that case were shown not to quantitatively reflect what is in the crystal.

A more likely interpretation is that the individual models in the ensemble represent a variety of equally plausible interpretations of the data. In this interpretation, the density averaged over all models is more similar to what is in the crystal than any individual model because all the individual models have errors and these errors are partially independent and can therefore be reduced by averaging. This interpretation is similar to the interpretation of the multiple models created in the ARP/wARP procedure (Perrakis et al., 1999 ▶), in ‘kicked’ OMIT maps (Guncar et al., 2000 ▶) and in a multi-start refinement procedure (Rice et al., 1998 ▶). In each of these procedures a (weighted) set of models yields a map that is superior to the maps corresponding to any individual model, presumably because each model contains errors that are different from the errors in the other models.

4. Conclusions

The principal conclusion from our work is that it is possible to estimate the precision of a macromolecular model by carrying out the entire model-building process multiple times, introducing some sampling differences in steps that involve randomization and creating an ensemble of models that all agree with the data about equally well. This precision forms a lower bound on the uncertainty in coordinates and in our test case it was quantitatively similar to, although smaller than, the error in coordinates based on comparisons with a ‘mean perfect structure’ consisting of the average of all models in the synthetic crystal.

We expect that an important use of the multiple models that can be created in this fashion will be to define the range of structures that are compatible with available data (Furnham et al., 2006 ▶; Ondráček & Mesters, 2006 ▶). As all of the structures in an ensemble of this type are of about equal quality, a calculation based on the atomic coordinates of one structure in an ensemble is about as likely to be correct as one based on any other model in the ensemble. A quantitative lower bound estimate of the uncertainty in a calculation based on atomic coordinates can therefore be obtained by performing the calculation on each of the models and determining the mean and standard deviation of these calculations (Furnham et al., 2006 ▶).

It is important to note that the multiple models that are generated with one process for model rebuilding do not necessarily have a direct bearing on the interpretation of a structure produced with another technique. As an extreme example, if a structure of very high quality is produced by careful analysis by a human experimenter, a set of models of lower quality and higher variability subsequently produced using some other procedure based on this starting model would not imply that the hand-built structure was inaccurate. The structure 1c1z (Fig. 3 ▶) could represent such a case, as the models built by our procedure are considerably poorer than the model deposited in the PDB. Conversely, a low variability among a set of models produced using a technique that cannot generate substantial diversity would not imply that the structures are highly accurate.

The experimental data used to determine a set of models should be the same data that were used to determine the original structure. In particular, if experimental phases are available, then these should be included in the rebuilding process so as to ensure that the models reflect the same information as that used to obtain the original structure. In general, the creation of an ensemble of structures should be carried out with the same algorithm and all the same parameters as the actual determination of the structure, with the only change being a different random seed. In this case, the structures in the ensemble represent the range of structures that could have been obtained with this algorithm and they therefore represent a lower bound on both the precision and accuracy that can be obtained in structure determination with this algorithm.

There are many possible techniques that can be used to generate ensembles of structures that are compatible with the experimental data. Those used already include conformational sampling (DePristo et al., 2004 ▶), ‘hip-hop refinement’ (Ondráček, 2005 ▶; Ondráček & Mesters, 2006 ▶), multi-start simulated-annealing refinement (Rice et al., 1998 ▶) and iterative model rebuilding with random seeds as discussed here, but other methods, including parallel building of several structures compatible with the data as made possible in MAIN 2006 (http://www-bmb.ijs.si/), could also be used.

The process we use to generate an ensemble of models is a sampling of the space of models that are highly and approximately equally compatible with experimental data. There is no guarantee that the best possible single model will lie within this space of models and no guarantee that our sampling will adequately cover this space. If a technique for generating multiple models is to be used as an estimate of accuracy (as opposed to a lower bound on accuracy), then this technique must be able to sample plausible structures relatively thoroughly (de Bakker et al., 2006 ▶) and it must be able to generate models that are of high quality. We show here that in our test example our procedure for iterative model building, density modification and refinement yields ensembles with free R factors that are similar to those of refined structures from the PDB and with good geometries, although they are not yet ‘final’ models. The coordinate standard deviations obtained with synthetic data are quantitatively similar to the ‘errors’ in these coordinates (the r.m.s.d. between the coordinates and those of the ‘mean perfect structure’), although there is a small but systematic underestimation of the errors. Furthermore, the technique is not very sensitive to the starting model. These observations indicate that the procedure generates high-quality models and ensembles with sufficient diversity to represent much of the uncertainty in the structures. We suggest that procedures proposed for generation of error estimates be examined in a similar fashion so that their characteristics can be identified.

As mentioned above, the models produced by our automated iterative rebuilding process are not ‘finished’; however, improvements in this and other software are likely to lead to essentially final models in the near future. We hope that as this software becomes robust it will become general practice to carry out model building and refinement or perhaps even the complete structure-determination process multiple times so as to define a lower bound on the uncertainties in coordinates and other parameters of the models obtained. In this case, an ensemble of models could be a routine part of PDB deposition (Furnham et al., 2006 ▶) for a structure. We emphasize, however, that a group of models can represent either of two very different things. One is the range of single-model structures that are compatible with the data, as discussed here. The other is the set of structures that is actually present in a crystal. Such a set of structures is not addressed in this work; it could be addressed more appropriately by a procedure in which all the structures are refined as a group against the crystallographic data. It is important that in any depositions of multiple-model representations of proteins it be made abundantly clear what this set of models represents: uncertainty (lack of knowledge) in a single-model description or knowledge about the multiple structures actually present in the crystal.