The CCP13 FibreFix program suite: semi-automated analysis of diffraction patterns from non-crystalline materials

FibreFix integrates various programs for the analysis of non-crystalline diffraction patterns into a single user-friendly package. The main features of FibreFix are outlined and some of its applications are illustrated.

Abstract

The extraction of useful information from recorded diffraction patterns from non-crystalline materials is non-trivial and is not a well defined operation. Unlike protein crystallography where one expects to see well behaved diffraction spots in predictable positions defined by standard space groups, the diffraction patterns from non-crystalline materials are very diverse. They can range from uniaxially oriented fibre patterns which are completely sampled as Bragg peaks, but rotationally averaged around the fibre axis, to fibre patterns that are completely unsampled, to either kind of pattern with considerable axial misalignment (disorientation), to liquid-like order and even to mixtures of these various structure types. In the case of protein crystallography, the specimen is generated artificially and only used if the degree of order is sufficient to yield a three-dimensional density map of high enough resolution to be interpreted sensibly. However, with non-crystalline diffraction, many of the specimens of interest are naturally occurring (e.g. cellulose, rubber, collagen, muscle, hair, silk) and to elucidate their structure it is necessary to extract structural information from the materials as they actually are and to whatever resolution is available. Even when synthetic fibres are generated from purified components (e.g. nylon, polyethylene, DNA, polysaccharides, amyloids etc.) and diffraction occurs to high resolution, it is rarely possible to obtain perfect uniaxial alignment. The CCP13 project was established in the 1990s to generate software which will be generally useful for analysis of non-crystalline diffraction patterns. Various individual programs were written which allowed separate steps in the analysis procedure to be carried out. Many of these programs have now been integrated into a single user-friendly package known as FibreFix, which is freely downloadable from http://www.ccp13.ac.uk. Here the main features of FibreFix are outlined and some of its applications are illustrated.

1. Introduction

Diffraction studies of non-crystalline materials have had a rich history and have made profound contributions to our knowledge of the world around us (Arnott, 1999 ▶; Stubbs, 1999 ▶; Squire, 2000 ▶). The structures of silks, cellulose, rubber, collagen, DNA, α-helices, oriented crystalline synthetic polymers, muscle, hair and so on, have all been determined by a variety of applications of fibre diffraction, and studies of mixed crystalline and amorphous phases have made a large impact in the understanding of, for example, the behaviour of materials manufactured from synthetic polymers. Apart from having different underlying molecular architectures, all of these different kinds of materials give rise to diffraction patterns with a variety of degrees of three-dimensional order and alignment, and the resolution achievable can vary from the quasi-atomic level (∼0.1 nm) to hundreds of nanometres (Fig. 1 ▶). Just as in protein crystallography, where there are elegant software packages designed to extract useful intensity data from the recorded data sets (see http://www.ccp4.ac.uk), so in non-crystalline diffraction (NCD) it is necessary to achieve the same kind of result. But, whereas in the former, one is usually dealing with reasonably well defined diffraction spots whose positions for a given camera geometry can be defined in terms of known space groups, in the case of NCD patterns there is, by definition, less information available than from a crystal, the pattern may be sampled or unsampled or sometimes a mixture of both, and the peak shape may vary substantially across the diffraction pattern in a way that makes analysis non-trivial but at the same time carries useful information. In addition, the information required from an NCD pattern may not be a structure determination in the conventional sense, but may involve, for example, estimation of the degree of crystallinity or of the texture (degree of alignment) in a polymer sample. Clearly, alternative software packages are necessary to extract the maximum amount of useful information from these non-crystalline diffraction patterns. In addition, recent rapid advances in computer processing power enable analysis approaches to be tried which were previously impossible.

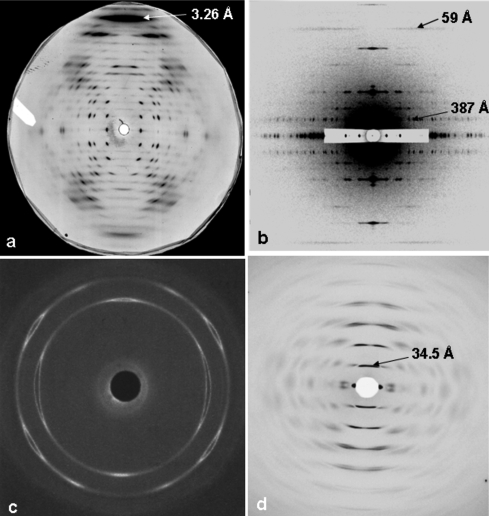
Figure 1.

Sample diffraction patterns from non-crystalline materials. (a) A well aligned polycrystalline specimen of E-DNA [poly(I-I-T).poly(A-C-C) (from Leslie et al., 1980 ▶)]. (b) A low-angle X-ray diffraction pattern from insect flight muscle, showing excellent sampling and d spacings in the range 48–387 Å with a c-axis repeat of 2320 Å (from AL-Khayat et al., 2004 ▶). (c) Wide-angle X-ray diffraction pattern from a sample of a diblock copolymer of oxyethylene (E) and oxybutylene (B) as E₇₆B₃₈ (where the subscripts denote the average numbers of repeat units) that had been crystallized after shearing in the melt (Fairclough et al., 2000 ▶). (d) High-angle X-ray diffraction pattern from magnetically oriented sols of PotatoVirus X, showing a helical repeat of about 34.5 Å (Stubbs et al., 2005 ▶).

2. The BSL program and early CCP13 developments

The Collaborative Computing Project (CCP13) in Fibre Diffraction and Solution Scattering was established in the early 1990s, with the aid of funding from the UK BBSRC and EPSRC (SERC in the early years), both to generate new software for tackling the analysis of diffraction patterns from non-crystalline materials and also to collate existing programs which had been developed in individual laboratories across the UK and elsewhere. Early developments, particularly by Denny (Denny, 1993 ▶, 1994 ▶, 1995a ▶,b ▶, 1996 ▶; Denny et al., 1998 ▶; Denny & Shotton, 1999 ▶; Shotton et al., 1998 ▶; Shotton & Denny, 1999 ▶), implementing much of the analysis of Fraser et al. (1976 ▶), were based on the need to complement and build on the BSL program updated by J. Bordas and G. Mant at the UK Synchrotron Radiation Source (SRS) at Daresbury, UK, from the initial work of Koch & Bendall (1981 ▶). The standard BSL image file name format is X00000.ABC, where X is always a letter followed by five numbers, the first two of which can be chosen by the user, and the extension ABC can be any three characters or numbers. A set of standard files consists of a header file and one or more binary files. BSL data files from the NCD experimental stations at the Daresbury Laboratory SRS are of the form:

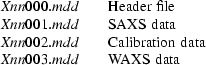where the first letter refers to the experimental session and the next two digits to the number of the individual experiment. This number increases by one after each experiment until the 100th experiment, after which the number returns to zero. The Xnn format can be used to identify any experiment in a session. The next three digits refer to the type of information contained in the file. The 000 file is the header file and is in ASCII or readable form. It contains information such as the sample title, the number of frames in the file, and the names of the intensity and calibration data files. The 001 file contains the raw SAXS (small-angle X-ray scattering) data in binary (unreadable) format. The 002 file contains calibration information, again in binary format. The 003 file (if present) contains raw WAXS (wide-angle X-ray scattering) data, also in binary format. The mdd extension gives the date on which the data were recorded, the first digit being the duodecimal month and the other digits the date (e.g. Xnn000.807 was recorded on August 7th, Xnn000.A24 on October 24th). For more general purposes (not involving Daresbury experimental stations) the file name details are at the user’s choice as long as the general X00000.ABC format is adhered to.

The original BSL program incorporated a set of operations to be carried out on the recorded diffraction patterns. Some of these operations are discussed later (Table 2) since they are now incorporated into the new FibreFix package.

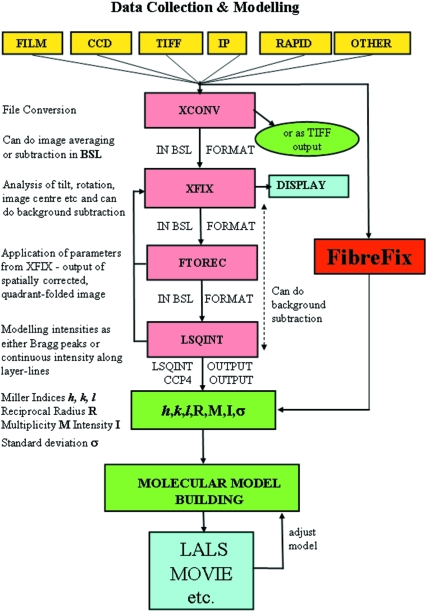
In the early 1990s Denny and colleagues produced a set of Unix-based stand-alone programs to process BSL format data files. The logic of the process is illustrated in Fig. 2 ▶ (Squire et al., 2003 ▶). The XCONV program could convert data with different image (detector) formats into the standard BSL format. XFIX was designed to carry out manipulations on this BSL image; for example, to find the centre of the pattern and the rotation from vertical of a pattern showing preferred orientation. FTOREC was designed to remap data from detector space into reciprocal space. LSQINT was designed for analysis of polycrystalline fibre patterns by fitting two-dimensional shapes to the observed peaks. At the XFIX and LSQINT stages it was also possible to try to fit and remove the unwanted ‘background’ in the diffraction patterns.

Figure 2.

Schematic diagram showing the logic of analysis of non-crystalline diffraction patterns, particularly those from fibres with uniaxial orientation. For details see text. (Modified from Squire et al., 2003 ▶.)

Initially, the CCP13 programs, as well as BSL itself, although excellent in their execution, were not GUI (graphical user interface)-driven and were rather difficult to use. For this reason, these programs have now been integrated by CCP13 into a single user-friendly GUI-driven package and additional features have been incorporated. The new program, FibreFix (He et al., 2004 ▶; Rajkumar et al., 2005 ▶), incorporates and links BSL, XCONV, XFIX, FTOREC and LSQINT into a single Windows-based application (Fig. 2 ▶). Here we describe the main features of FibreFix and illustrate how it can be used.

3. The FibreFix window

Non-crystalline diffraction patterns are generally recorded on planar two-dimensional detectors (e.g. film, image plates, CCDs, multiwire detectors etc.). In other cases, diffraction data are recorded on flat or curved one-dimensional detectors. In some cases, the output from analysis of two-dimensional detectors is also best presented and processed as one-dimensional intensity profiles. The present FibreFix application takes in two-dimensional detector data and transforms them into whatever is the most useful form of intensity representation (e.g. Bragg peak data or one-dimensional radial, circumferential or linear profiles) for the particular analysis needed for that kind of specimen.

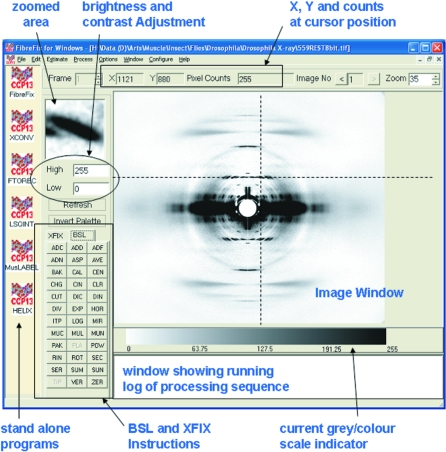
Once FibreFix has been installed and opened (from http://www.ccp13.ac.uk), a window appears as in Fig. 3 ▶. This shows: a series of drop-down menus at the top; a central image frame showing a cursor and beneath which is the current grey or colour scale being used for the image; a selected image area (top left) enlarging details in a small box centred around the cursor; text boxes to control the contrast and brightness; and a window at the bottom carrying a running text log of the processing that has been carried out. All of the functionality of XCONV, XFIX, FTOREC and LSQINT has been integrated into this single FibreFix package, but these programs can, if desired, be used independently by opening them from the list to the left of the window, to which the modelling programs HELIX (Knupp & Squire, 2004 ▶) and MusLABEL (Squire & Knupp, 2004 ▶) are also linked.

Figure 3.

The FibreFix window with its main features highlighted. The diffraction pattern from live resting Drosophila flight muscle recorded on the BioCAT beamline at the Argonne Photon Source, Illinois, USA, was kindly provided by Professor T. C. Irving.

As in the original Unix programs, the standard file format throughout FibreFix is the BSL format. The first need of FibreFix is therefore to take in an image file from any of the standard kinds of detector currently in use, convert it to BSL format, display it and, if the user requires, save it. FibreFix now opens files automatically, if they are in a supported format, either by using the ‘Open’ command on the ‘File’ drop-down menu (Fig. 3 ▶, top left) or simply by dragging and dropping the file name from an ‘Explorer’ directory directly into the image window of FibreFix. The input images can be saved as BSL, TIFF or TEXT format files. The many detector formats accepted by FibreFix are listed in Table 1 ▶.

Table 1. Detector/image formats accepted by FibreFix .

float	Float
int	Unsigned int
short	Unsigned short
char	Unsigned char
smar	Small MAR image plate (1200 × 1200)
bmar	Big MAR image plate (2000 × 2000)
fuji	Fuji image plate (2048 × 4096)
fuji2500	BAS2500 Fuji image plate (2000 × 2500)
rax2	R-Axis II image plate
psci	Photonics Science CCD
riso	RISO file format
tiff	TIFF (8-, 12-, 16-bit greyscale with all compression types)
ESRF Id2	ESRF data format (KLORA)
LOQ 1D	One-dimensional ASCII data files recorded at LOQ
LOQ 2D	Two-dimensional ASCII data files recorded at LOQ
SMV	Used by ADSC CCD detectors (8-bit unsigned, 16-bit unsigned, 32-bit signed integer, 32-bit float)
ESRF Id3	ESRF data format
BRUKER	Area-detector frame format Siemens/Bruker file format (8, 16, or 32 bits per pixel)
Mar345	MAR345 image plate (file extension mar1200, mar1800, mar1600, mar2400, mar2000, mar3000, mar2300, mar3450)
BSL	The BSL file format is described in the BSL manual
ILL_SANS	ILL-SANS treated data formats
rax4	R-Axis IV image plate
Mar225	MAR225 format

Once the file has been opened and displayed, the brightness, contrast, size and colour palette of the image can be changed at will by the user. The operations to be carried out on the image can be controlled from the lower left sets of instructions in the FibreFix window which can be toggled between the BSL set of operations (seen in Fig. 3 ▶) or the XFIX set (Fig. 4 ▶ a). The BSL instructions (Table 2 ▶) are similar to those of the old UNIX BSL program, although several algorithms have been improved and some new ones have been added. Some individual BSL operations are discussed below.

Figure 4.

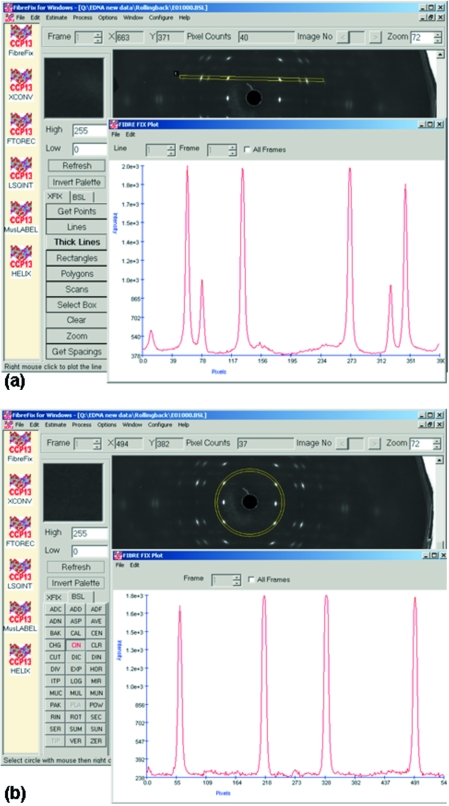
Applications of FibreFix (a) using the XFIX group of operations, in this case to plot the intensity along a ‘thick line’ across the diffraction peaks along a layer-line in a pattern from E-DNA (Fig. 1 ▶ a), and (b) plotting a circumferential intensity plot in the same pattern as (a), but here with inverted contrast.

Table 2. Operations under BSL in FibreFix .

ADC	Add a constant to a selected range in spectrum
ADD	Weighted addition of two images
ADF	Add multiple frames together
ADN	Add and normalize image using a calibration file
ASP	Apply aspect ratio
AVE	Average a series of images
BAK	Background subtraction of an image and correct background image using a calibration file
CAL	Normalize calibration file for exposure time
CEN	Estimate centre from four points or centre the image by adding extra columns and rows
CHG	Change a selected value in an image
CIN	Integrate around a circle
CLR	Clear screen drawing
CUT	Cut part of an image into a smaller image
DIC	Divide a selected region of an image by a constant
DIN	Divide and normalize image using a calibration file
DIV	Weighted division of two images
EXP	Exponentiate data values
HOR	Perform a horizontal integration in a selected region
ITP	Interpolate a two-dimensional image
LOG	Calculate natural or base10 log of image
MIR	Mirror the four quadrants of an image
MUC	Multiply a selected region of an image by a constant
MUL	Weighted multiplication of two images
MUN	Multiply and normalize image using a calibration file
PAK	Pack an image into smaller dimensions by averaging and/or merge several small frames into one large image file
PLA	Play movie of time series
POW	Raise image to specified power
RIN	Radial scan and integration
ROT	Rotate an image
SEC	Perform sector integration
SER	Make time series of image
SUN	Subtract and normalize image using a calibration file
SUM	Sum a series of images
TIP	Time series intensity plot
VER	Perform a vertical integration in a selected region
ZER	Set all negative values in an image equal to 0.0

4. Preliminary processing of non-crystalline diffraction patterns

Whatever the source of a two-dimensional non-crystalline diffraction pattern, it is usually essential to carry out preliminary processing of the recorded image before meaningful analysis can take place. Sometimes this might mean adding together many images from separate experiments, for example where the exposure time in each experiment was limited by radiation damage. In some cases, with patterns showing preferred orientation, it is necessary to align the individual exposures before adding them. In addition, it is common practice to record a ‘specimen-free’ diffraction pattern as a record of the camera background that can be subtracted from the recorded image after suitable weighting. All of these operations can be carried out using the BSL and XFIX commands in FibreFix. For example, the centre of the pattern can be determined using the ‘Get Points’ operation in XFIX, either from arced reflections or from sampled peaks, by selecting equivalent points on the pattern with the cursor (with exact positioning aided by the enlarged ‘zoom’ window) and then opening a dialogue box, selecting the required parameter to be estimated (e.g. centre or rotation) and applying them if required. Another way of selecting points which may not be regularly shaped is to use the ‘Rectangles’ or ‘Polygons’ options in XFIX, where one can draw around several chosen peaks and the program will estimate their centres of mass (intensity) and use these to determine the required parameter. Note that the standard BSL image file name format is automatically extended and saved with the applied operation extension when FibreFix operations are carried out. By this means the history of any particular file is clear. For example, a rotated file would be X00000.ABC.ROT. After processing with FTOREC (see below) it would be X00000.ABC.ROT.FTR, and so on.

If a reflection of known spacing is present in the diffraction pattern (e.g. a calibration ring) then this can be used to estimate the camera length once the appropriate calibration spacing has been supplied. This and all other operations carried out on a pattern are automatically saved as a log file.

5. Real-time applications

A major application of a program like FibreFix is to be able to establish quickly, while an experiment is running, whether appropriate and useful results are being obtained. For this reason it is very helpful to have the ability to produce virtually instant plots of intensity profiles in any direction across the diffraction pattern. Under the XFIX set of operations, it is possible to select an area of interest to enlarge in the image window (‘Select Box’) and/or to obtain plots along a line running in any direction across the image, or along a strip of chosen width in any direction, or scanned around an arc or full circle of chosen radial extent about a chosen centre. Examples of linear and circular plots are shown in Figs. 4 ▶(a) and 4 ▶(b), respectively. If, for instance, it is the degree of preferred orientation in a polymer sample that is of interest, then a plot like Fig. 4 ▶(b) can be very informative. Under BSL, horizontal and vertical linear plots can be generated with the added feature that the exact coordinates of the box of integration can be defined by the user. This is especially useful if different, previously aligned, patterns are to be compared. Finally, BSL will carry out a radial plot of the intensity in the two-dimensional image, as needed in solution scattering, once the centre of the pattern has been defined. Quick look radial and circular scans can also be carried out in XFIX using the ‘Scans’ operation.

6. Background subtraction and separation of overlapping patterns

It is usually the case in diffraction patterns from non-crystalline materials that there is a substantial background under any Bragg peaks of interest. Estimation of the background can be carried out in XFIX using several possible algorithms. In some cases, the observed intensity distribution is a mixture of patterns from more than one kind of structure; perhaps one is sampled and the other continuous. In this case, once any recorded camera background has been removed, it is possible to fit, remove and store the remaining smoothly varying part of the pattern as a ‘background’, although it is actually the unsampled transform, and to leave the sampled part of the pattern as the extracted final image. Thus both parts of such a mixed pattern can be estimated. Note that background fitting can also be carried out in XFIX on a pattern showing preferred orientation after the FTOREC process has been applied (see below). Alternatively or in addition the background can be fitted and refined as part of the LSQINT process.

7. Processing of fibre diffraction patterns

7.1. Estimating fibre tilt

In the case of diffraction patterns with preferred orientation, especially those from polycrystalline fibres, XFIX can be used to estimate the size and shape of the unit cell (Fig. 5 ▶). In order to do this computation and to plot the predicted points correctly, it is necessary for the pattern centre and rotation to have been determined. In addition, in the case of a tilted fibre, it is also necessary to provide an estimate of the specimen tilt. A uniaxially oriented system tilted to the beam will give a pattern which is asymmetrical top to bottom (assuming the fibre axis is ‘vertical’). The degree of tilt can be assessed under XFIX by using ‘Get Points’ to select four equivalent reflections, and then using the ‘Estimate Tilt’ option. Once this has been done, the expected peak positions can be plotted on the pattern using the ‘Cells’ dialogue box under the ‘Edit’ drop-down menu. Here the estimated unit-cell parameters can be inserted as well as the space group. If the camera length has already been determined using a reflection of known spacing, or by direct measurement, and is present in the ‘Parameters’ list under ‘Edit’, then estimation of the order of magnitude of the unit cell sides is made relatively easy by inspection of the main equatorial peaks (related to a and b) and the mean layer-line spacing (related to c). The values of these spacings can be estimated by using the ‘Get Spacings’ option in XFIX where the Bragg spacing (d) of a peak is shown, as well as the real space estimates of the radial (1/R) and axial (1/Z) positions of the peak. These values appear in the text box at the bottom of the FibreFix window. With the possible unit-cell parameters determined from these measured spacings and entered into the cell dialogue box (Fig. 5 ▶ a), clicking on ‘Generate’ causes the theoretical positions of the predicted lattice peaks to be drawn onto the diffraction pattern. Because at this stage the pattern has not been remapped into reciprocal space, the plotted layer-lines and row-lines are curved (Fig. 5 ▶ a), often in complicated ways, both due to the detector being flat and to the tilt of the fibre. Plotting the predicted points in this way is usually a very sensitive indicator not only of whether the chosen lattice spacings are reasonable, but also of whether the pattern is properly centred, and the estimated rotation and tilt angles are accurate. It is therefore advisable to go through this process a few times until satisfactory results are obtained before attempting to remap the data into reciprocal space using FTOREC. Note that refinement of the unit-cell parameters can be carried out in the LSQINT process (see below).

Figure 5.

(a) Fitting peak positions after estimation of the unit-cell parameters and their insertion into the ‘Cell Dialog’ box. Determination of the pattern centre, rotation, tilt and the camera length is needed first. Selecting ‘Generate’ in the ‘Cell Dialog’ box plots the predicted peaks on layer-lines and row-lines as shown here as small yellow circles. (b)–(g) Stages in the fitting of intensities using FTOREC and LSQINT. (b) is the FTOREC, quadrant-folded, image from (a), and (c) and (d) are the fitted background and original minus background from (b). (f) is the NOFIT image from LSQINT, which just fits the peak shapes and positions, but not their intensities. (g) is the final set of peak intensities fitted by LSQINT to the profiles in (f). A test of whether all is well is shown in (e), which is the sum of the fitted peaks in (g) and the background in (c). It can be compared directly with the original FTOREC image in (b).

7.2. Remapping into reciprocal space (FTOREC)

In the case of diffraction data from materials with a preferred orientation (e.g. fibres, or liquid crystals) it is usually necessary either to obtain layer-line profiles (such as in Fig. 4 ▶ a) or to model Bragg peaks properly, allowing for variations in peak shape and size across the pattern. To obtain either set of intensity data, it is necessary to remap the image format into reciprocal space. If the centre, rotation, camera length and specimen tilt have already been determined, then the conversion to reciprocal space can be carried out using the FTOREC function listed under the ‘Process’ drop-down menu at the top of the FibreFix window. The parameters already generated in XFIX are automatically carried forward into the FTOREC control window. The remapped image will appear as a single (lower right) quadrant of the diffraction pattern (i.e. centre now top left; Fig. 5 ▶ b) which is a weighted average of the data in the four quadrants of the original pattern. As well as the FTOREC image, a second image is also produced which shows the standard deviations between the intensities at equivalent points in the quadrants that are being merged. It is usually clear from inspection of both images whether the remapping process has been carried out satisfactorily (e.g. for example if the centre, rotation and tilt are correct). The plotting of theoretical peak positions using the cell dialogue box can also be carried out on the FTOREC image as a final check that all is in order and the unit-cell parameters are optimal.

7.3. Fitting and refining peaks and background (LSQINT)

The final process for patterns from polycrystalline fibres is to model the Bragg peaks to yield reliable values for their integrated intensities. This is achieved using LSQINT (Denny, 1993 ▶). LSQINT will model peak shapes and sizes without at this stage attempting to determine their integrated intensities in what is called the NOFIT operation (Fig. 5 ▶ f). This includes inputting estimates relating to the beam size in the horizontal and vertical directions, the degree of arcing in the pattern, the required parameter step sizes for refinement and so on. Achieving appropriate values for some of these parameters can be difficult and time-consuming, but appropriate values for particular kinds of specimen are given in the FibreFix ‘Tutorials’ on the CCP13 website (http://www.ccp13.ac.uk). As well as the NOFIT plot of peak shapes, LSQINT can be used for background fitting (Fig. 5 ▶ c) using a variety of alternative procedures. Also, with the peak shapes defined, the fitting of the Bragg peak intensities, together with refinement of the unit-cell parameters and the background, can all be processed together to give an estimated optimal fit to the data (Fig. 5 ▶ g). The sum of the fitted peaks (Fig. 5 ▶ f) and fitted background (Fig. 5 ▶ c) gives a test of the reliability of the analysis (Fig. 5 ▶ e). The final integrated intensity values can be output as an LSQINT-format list showing h, k, l, R, M, I, σ, where h, k, l are the Miller indices of the peak, R is its radial position in reciprocal space, M is the multiplicity of the peak (number of overlapping reflections), I is its integrated intensity and σ is the standard deviation of the intensity (Fig. 2 ▶). Alternatively, the data can be output in a format suitable for direct input into programs such as FXPLOR (Denny et al., 1997 ▶; Wang & Stubbs, 1993 ▶).

8. Intensity time courses

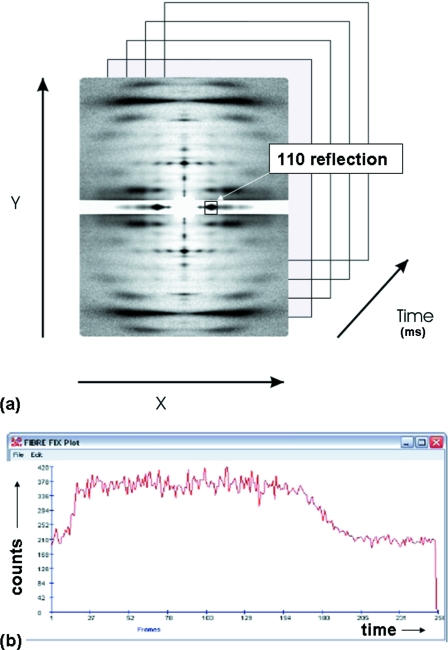
As a further application of FibreFix, this time to multiframe time-resolved diffraction data, for example from contracting muscle (Fig. 6 ▶ a; Squire et al., 2003 ▶), a number of procedures can now be carried out automatically to prepare the time-resolved data for further analysis. For example, in some experiments it is convenient for different frames in the series to have different exposures. The recorded time frames therefore need to be normalized for exposure if meaningful intensity time courses are to be plotted (see Rajkumar et al., 2006 ▶). It also can happen that the fibre axis rotates a little at different stages of the time series. This variable rotation can also be dealt with semi-automatically using the ROT function in BSL. Fig. 6 ▶(b) shows that a quick look at the intensity change of a given reflection through the time series can be plotted by using the TIP function in BSL. This can be very helpful in assessing experimental results in real time as the experiment progresses.

Figure 6.

Application of FibreFix to time-resolved experiments. Data files are recorded as intensities across a detector area defined by X and Y positional coordinates and through a series of time frames. The intensity of a particular part of the pattern, in this case the equatorial 110 reflection from contracting fish muscle at a defined X, Y value, can be plotted as a function of time (b) using the TIP operation in BSL to give the intensity time course.

9. Multiple frames and repeated exposures

Multiple files can be loaded together into FibreFix using the ‘Open’ function under the ‘File’ menu or by highlighting several files in an ‘Explorer’ window and dragging and dropping them into the image window. These files will then be treated as successive ‘frames’ of data which can be saved as a single file, or can all be processed together as required. Note that if they are short exposures which need to be added together to generate sufficient total counts in the final image then the BSL instruction ADF will add the files together between specified frame numbers (see Rajkumar et al., 2006 ▶). Alternatively the frames can be shown as a tiled array of patterns, with appropriate array numbers in the X and Y directions, as might be needed for example after scanning across a specimen in a microfocus X-ray experiment (Riekel, 2000 ▶). In addition, a time series can be shown as a movie by using the PLA instruction in BSL, which automatically cycles through the frames one by one.

10. Modelling of non-crystalline structures

Once a satisfactory set of intensity data has been extracted from the observed non-crystalline diffraction pattern, whether it is of Bragg peak intensities, continuous layer-line profiles, radial intensity distributions or annular intensity distributions, it is often necessary to simulate these intensities by Fourier transform computations from model structures. A number of programs exist to help users to do this. In the case of oriented polycrystalline materials and high-resolution data, the programs LALS (Arnott & Wonacott, 1966 ▶; Arnott et al., 1969 ▶; Okada et al., 2003 ▶) and FXPLOR (Denny et al., 1997 ▶; Wang & Stubbs, 1993 ▶) can be used to refine and test plausible molecular structures. Modelling of helical macromolecular assemblies can be carried out using MOVIE (Hudson et al., 1997 ▶; AL-Khayat et al., 2004 ▶). A preliminary quick look at the kind of diffraction pattern that helical structures of plausible symmetry and dimensions might produce can be obtained from the HELIX program (Knupp & Squire, 2004 ▶). Ideas about diffraction from muscle structures can be obtained from the MusLABEL program (Squire & Knupp, 2004 ▶). Theoretical aspects of fibre diffraction are described by, for example, Holmes & Blow (1965 ▶), Wang & Stubbs (1993 ▶), Harford & Squire (1997 ▶), Squire (1998 ▶, 2000 ▶), Millane (2001 ▶). In the case of SAXS data from polymer samples, macromolecular ordering information can be extracted by programs such as CORFUNC (correlation function analysis; see http://www.ccp13.ac.uk; Ryan, 1994 ▶; King & Flannery, 2005 ▶) after initial processing and sector integration using FibreFix/BSL.

11. Conclusion

In this short paper it has only been possible to highlight a small selection of the features of the FibreFix program suite. However, we hope that this will have demonstrated some of the strengths of the program and will tempt new users to explore the capabilities of FibreFix and to apply it to their own NCD data. Particular applications of FibreFix, for example in fitting polycrystalline diffraction data from oriented fibres, in processing continuous layer-line data, in analysing time-resolved diffraction data, and in analysing limited order fibre patterns (e.g. from amyloid) are detailed in the FibreFix tutorials on the CCP13 website (http://www.ccp13.ac.uk). In the future, we hope to add to this list of tutorials for other kinds of applications. FibreFix is an evolving software suite which will be developed further as our own ideas and those of users are gradually incorporated. We hope that users will feel free to contact us (contact details are at http://www.ccp13.ac.uk) to learn more about applying FibreFix to their own experimental results, to suggest new operations to incorporate into FibreFix, and to describe novel applications of the software which others may find helpful.