Denoising based on spatial filtering

Abstract

We present a method for removing unwanted components of biological origin from neurophysiological recordings such as magnetoencephalography (MEG), electroencephalography (EEG), or multichannel electrophysiogical or optical recordings. A spatial filter is designed to partition recorded activity into stimulus-related and stimulus-unrelated components, based on a criterion of stimulus-evoked reproducibility. Components that are not reproducible are projected out to obtain clean data. In experiments that measure stimulus-evoked activity, typically about 80% of noise power is removed with minimal distortion of the evoked response. Signal-to-noise ratios of better than 0 dB (50% reproducible power) may be obtained for the single most reproducible spatial component. The spatial filters are synthesized using a blind source separation method known as Denoising Source Separation (DSS), that allows the measure of interest (here proportion of evoked power) to guide the source separation. That method is of greater general use, allowing data denoising beyond the classical stimulus-evoked response paradigm.

I Introduction

Magnetoencephalography (MEG) measures magnetic fields produced by brain activity using sensors placed outside the skull. The fields to be measured are extremely small, and they compete with strong fields from environmental noise sources (electric power lines, vehicles, etc.), sensor noise, and unwanted physiological sources (muscle activity, heart, eyeblinks, background brain activity, etc.).

Many methods have been proposed to combat noise (see Hämäläinen et al., 1993; Cutmore and James, 1999; Croft and Barry, 2000; Vrba, 2000; Volegov et al., 2004; Rong and Contreras-Vidál, 2006 for reviews). We recently proposed two new methods to target environmental noise (de Cheveigné and Simon, 2007) and sensor noise (de Cheveigné and Simon, 2008). In this paper we present a third method that deals with biological noise that those previous methods did not address. The method involves spatial filtering, that is, replacing the recorded data by a set of linear combinations such that sources of interest are preserved and unwanted components are suppressed. Spatial filtering is involved in many MEG or EEG signal analysis techniques, such as beamforming or independent component analysis (ICA). We cast the problem in terms of denoising and to offer a rational and flexible method for synthesizing the appropriate spatial filters.

Denoising involves a partition of the data into desirable components (signal) and undesirable components (noise). This is conceptually easier than the more ambitious task of analyzing the data into individual sources, such as performed for example by ICA. Separating the data into two parts requires milder assumptions than a complete analysis of all sources present. Validation is easier than for more general techniques, and the tools require less expertise and pose less risk of misuse by inexperienced practitioners. Denoised data have the same format as raw data, so that standard analysis tools may be applied to them, the only difference with raw data being better sensitivity and reduced risk that results are affected by noise.

In spatial filtering, each output channel ${\tilde{s}}_{k\prime }(t)$ is the weighted sum of input channels:

$${\tilde{s}}_{k^{\prime }}(t)={\displaystyle \sum _{n=1}^K{a}_{k{k}^{\prime }}{s}_k}(t)$$ (1)

where t is time, S(t) = [s₁(t),⋯, s_K(t)]^T represents the K channels of raw data, $\tilde{\mathbf{S}}(t)={[{\tilde{s}}_1(t),\cdots ,{\tilde{s}}_{K\prime }(t)]}^{\mathrm{T}}$the filtered data, and A = [a_kk′] the filtering matrix. Spatial filtering can be described in matrix format as:

$$\tilde{\mathbf{S}}(t)=\mathit{A}\mathbf{S}(t).$$ (2)

Spatial filtering subsumes a wide range of operations. The simplest is to select an individual sensor channel (all a_kk′=0 except one), as in classic descriptions of EEG data using standardized electrode nomenclature, or a group of channels known to be sensitive to the phenomenon of interest (all a_kk′=0 except for k within the group) (e.g. Poeppel et al. 1996). More complex spatial filtering techniques are signal space projection (SSP) (Uusitalo and Ilmoniemi 1997), signal space separation (SSS) (Taulu et al. 2005), spatiotemporal signal space separation (tSSS) (Taulu and Simola 2006), beamforming (Sekihara 2001, 2006), principal component analysis (PCA) (e.g. Kayser and Tenke 2003), independent component analysis (ICA) (e.g. Makeig et al. 1996; Vigário et al. 1998), the surface laplacian (e.g. Bradshaw and Wikswo 2001), and other linear processing schemes (Parra et al. 2005; James and Gibson, 2003; Barbati et al., 2004; Cichocki, 2004; Tang et al., 2004; Delorme and Makeig, 2004; Nagarajan et al., 2005; Gruber et al., 2006). The spatial filter (or set of filters) enhances activity of interest and/or suppresses unwanted activity. Spatial filtering takes advantage of the spatial redundancy of high-density MEG or EEG systems, and is complementary with temporal filtering which takes advantage of the spectral structure of target and/or noise.

Our method belongs to the spatial filtering family. To synthesize the filter we rely on a recently-proposed method for semi-blind source separation known as Denoising Source Separation (DSS) (Särelä and Valpola, 2005). In DSS, the K-channel sensor data are first spatially whitened by applying PCA and normalized to obtain a data set with spherical symmetry, i.e. with no privileged direction of variance in K-dimensional space. The whitened data are then submitted to a bias function (which Särelä and Valpola, 2005 call “denoising function”) followed by a second PCA that determines orientations that maximize the bias function. This second PCA produces a transformation matrix that is finally applied to the whitened (but not biased) data. The result of DSS analysis is a set of components ordered in terms of decreasing susceptibility to bias. Throughout this paper the bias function is chosen to be the proportion of epoch-averaged (evoked) activity. However, other bias functions may be used and the DSS method is of wider applicability than described here.

Our focus here is denoising rather than data analysis. The method that we propose is intended to complement, by use as a denoising preprocessor, other techniques for brain source analysis and source modeling.

II Methods

Signal Model

Sensor signals S(t) = [s₁(t),⋯, s_K(t)]^T include interesting “target” activity and uninteresting “noise” activity:

$$\mathbf{S}(t)={\mathbf{S}}_B(t)+{\mathbf{S}}_N(t).$$ (3)

The first term results from the superposition of sources of interest B(t) = [b₁(t),⋯, b_J(t)]^T within the brain:

$${\mathbf{S}}_B(t)={\mathbf{A}}_{\mathrm{B}}\mathbf{B}(t)$$ (4)

where A_B is a mixing matrix. The second term results from the superposition of various noise sources N(t) = [n₁(t),⋯, n_J′(t)]^T in the environment, sensors, and subject’s body:

$${\mathbf{S}}_N(t)={\mathbf{A}}_{\mathbf{N}}\mathbf{N}(t)$$ (5)

where A_N is a second mixing matrix. Our aim is to attenuate S_N(t) and thereby improve our observation of S_B(t). We suppose that environmental and sensor noise sources (power line and machinery) have already been suppressed (de Cheveigné and Simon 2007, 2008), and so we are dealing mainly with physiological noise sources within the subject’s body and brain, such as heart activity, eye-blinks, and “uninteresting” ongoing brain activity. The distinction between interesting and non-interesting obviously depends on the experiment or application. Here we focus on stimulus-driven responses, for which “interesting” is defined as activity reproducibly triggered by presentation of a stimulus.

A typical stimulus-response experiment may include M distinct stimulus conditions, each involving N_m repetition of that stimulus. During the experiment, stimuli of all conditions are typically pooled and presented in random order, while magnetic fields are recorded continuously from K sensors around the subject’s brain. Sensor data S(t) are then temporally divided into peristimulus segments (epochs) and the trials grouped by condition, forming a set of M of three-dimensional matrices {S^m(t)}, each with dimensions N_m (trials), K (number of channels) and T (duration of an epoch in samples).

Bias function

Our operational definition of “interesting” is implemented as a bias function usable by DSS. As we are interested in evoked activity, we will define bias as the function F that to data {S^m(t)} associates the set $\left\{{\overline{S}}^m(t)\right\}$ of averages over epochs, one average for each condition:

$$F[\{{\mathbf{S}}^m(t)\}]=\{(1/N_m){\displaystyle \sum _{n=1}^{N_m}{\mathbf{S}}^{mn}(t)\}}$$ (6)

where S^mn(t) designates epoch n of condition m. Stimulus-evoked activity is reinforced by averaging whereas stimulus-unrelated activity and noise are not, so the norm of F [{S^m(t)}] is greater for evoked activity than for noise.

Algorithm

The following steps are performed:

1. Each data channel is normalized (divided by its norm).

2. Data are submitted to a PCA and components with negligible power are discarded.

3. The time series corresponding to the remaining L principal components are normalized to obtain a set of orthonormal, “spatially whitened”, vectors.

4. The bias function defined in Eq. 6 is applied to these data, and the biased data are submitted to a second PCA.

5. The rotation matrix produced by the second PCA is applied to the whitened data from step 3.

6. The set of L time series produced by steps 1 to 5, ordered by decreasing bias score, is partitioned into “signal” components, which are retained, and “noise” components, which are discarded.

7. Signal components are projected back into sensor space to obtain “clean” MEG data.

The combined effect of these steps can be recapitulated in matrix format:

$$\tilde{\mathbf{S}}(t)=\mathbf{P}\mathbf{Q}{\mathbf{R}}_{\mathbf{2}}{\mathbf{N}}_{\mathbf{2}}{\mathbf{R}}_{\mathbf{1}}{\mathbf{N}}_{\mathbf{1}}\mathbf{S}(t)$$ (7)

where N₁ represents the initial normalization, R₁ the first PCA rotation , N₂ the second normalization (whitening), R₂ the second PCA rotation matrix, Q the criterion-based selector, and P the projection matrix back to sensor space. The initial normalization is not critical: its aim is to give equal weight to each sensor regardless of its gain. In step 2, components with power below some arbitrary (non critical) threshold are discarded to save computation and avoid numerical problems. The selection criterion of step 6 (number of components retained) constitutes the single important parameter of the method. It can be set directly, or determined indirectly for example based on a threshold applied to the bias score. The algorithm produces a set of components that are (a) mutually orthogonal, and (b) ordered by decreasing evoked-to-total power ratio.

Equation 7 defines a spatial filter in sensor space: each sensor channel is modified by adding a weighted sum of other channels. The filter may be applied to the recorded data, and the filtered data then averaged over trials to produce evoked responses that are more reproducible and less noisy than those obtained by simple averaging (see below). Alternatively, once the filter has been designed (a process that requires multiple trials) it can be applied to enhance the quality of single trial data, but this lies outside the main focus of the present paper. A more intuitive explanation of why the method is effective is given in the Discussion.

Implementation

The algorithm was implemented in Matlab. The implementation involves standard matrix operations, but several issues are worth discussing. (1) In experiments that involve multiple conditions, processing must be applied uniformly to all conditions, so as to avoid introducing differences that might masquerade as experimental effects. The matrices of Eq. 7 are calculated from pooled data from all conditions, and then applied to each condition individually. This complicates the implementation, and multiple processing passes may be required if the data are too large to fit in memory. (2) It is important to prevent outliers and artifacts from dominating the solution (the solution depends on sums of squares that are easily dominated by high-amplitude values). Outliers are detected automatically in several steps. First, sensor channels with consistently large or constant values are flagged as bad. Second, samples with absolute values larger than a threshold (e.g. 2000 fT), or that exceed the average power for that channel by a second threshold (e.g. 1000 %), are marked as outliers. If a sample is marked as outlier in one channel, all channels are similarly marked, and their values at that time are ignored (given zero weight) in all calculations (averages, PCA, projection matrices, etc.). Third, trials with power relative to the mean greater than a threshold (e.g. 1.4) are marked as outlier trials and likewise ignored in all calculations. Thresholds are not critical: the goal is to exclude severe outliers while retaining a sufficient proportion of data (e.g. >80%) to constrain the solution. Although outlier data are excluded from the denoising matrix calculations, they may be denoised together with the non-outlier data so that no data are lost. (4) In steps involving PCA, it is useful to ignore components with relative power below a threshold (e.g. 10⁻⁶), to save computation and avoid numerical problems. Taking these considerations into account, calculation of the filter matrix takes approximately real time on a personal computer for MEG data sampled at 500 Hz.

MEG data

MEG data used to illustrate the algorithm were acquired from a 160-channel, whole-head MEG system, with 157 axial gradiometers sensitive to brain sources, and 3 magnetometers sensitive to distant environmental sources (KIT, Kanazawa, Japan, Kado et al., 1999). Subject and system were placed within a magnetically shielded room. Data were filtered in hardware with a combination of highpass (1 Hz), notch (60 Hz) and antialiasing lowpass (200 Hz) filters before acquisition at a rate of 500 Hz. Acquired data were then filtered in software by convolution with a square window of size 16.67 ms to attenuate higher-frequency components and suppress 60 Hz and harmonics. Remaining environmental noise was suppressed using the TSPCA algorithm (de Cheveigné and Simon, 2007), and sensor noise was suppressed by the SNS algorithms (de Cheveigné and Simon, 2008). These pre-denoised data were used as a baseline to evaluate the amount of additional noise reduction offered by the present method.

The MEG data were borrowed from an auditory MEG study (Chait et al., in preparation). They were recorded in response to presentations of a 200-ms noise burst randomly interspersed between tonal stimuli. Subjects performed a task on the tonal stimuli, but no task was associated with the noise bursts. The MEG signal was divided into epochs spanning from −400 ms to +600 ms relative to the noise onset. The denoising matrix was calculated based on the −200 ms to +400 ms interval. Data shown are from one subject. There were 229 stimulus presentations, but the results presented here are from a subset of 100 trials.

Evaluation statistics

The effect of denoising is quantified in terms of power of the data or of individual components or groups of components (before vs after denoising), and variance across stimulus repetitions. For the average over trials (evoked response) for which we have only one observation, variability is calculated using bootstrap resampling (Efron and Tibshirani 1993).

III Results

Figure 1(a) shows the percentage of power carried by each DSS component before (black) and after (red) averaging. In both cases the values are normalized to add up to 100%. For the raw signal (black) all components have roughly the same order of magnitude, but for the evoked signal (red) the low-order components carry most of the power. Figure 1(b) shows the percentage of power that would be retained if the component series were truncated beyond a given component before (red) and after (black) averaging. Evoked power asymptotes rapidly at close to 100%, whereas total power increases much more slowly. For example, if the series were truncated beyond the 10th component (dotted line), 96% of evoked power would be retained, but only about 13% of power in the original, unaveraged signal. Figure 1(c) shows the percentage of evoked power carried by each component (blue), or by all components up to a given rank (green). The first component by itself is about 60% reproducible (the part of the response that is the same in each trial amounts to 60% of the power). If more components are retained, their collective reproducibility is less (about 20% for 10 components).

Fig. 1.

(a) Power carried by each DSS component, expressed as a percentage of the total power over components. Black: raw data, red: average over trials (evoked power). (b) Power over subsets of components as a function of the rank of the last component (cumulative power). (c) Ratio between evoked power (reproducible over trials) and total power for each component (blue) or for all components up to a given rank (green). The vertical dotted line separates components retained as signal (see text) and those discarded as noise.

It is clear from these plots that the algorithm has succeeded to decompose the data into a first small set of components that are highly reproducible (stimulus-driven), and a second larger set that are less so. Denoising proceeds by discarding the second set and projecting the first back to sensor space, to obtain “clean” data. Figure 1(b) (red) suggests that very little is lost in the process, in terms of power of the evoked response pattern. In other words: if we were concerned that the denoising operation might have eliminated some important component together with the noise, we can be reassured that that subtle component accounted for at most 6% of the evoked pattern (for 10 components retained). The choice of cutoff involves a tradeoff: a more stringent value (more components rejected) suppresses more noise power at the risk of distorting the evoked response. This requires a decision on behalf of the researcher, but we note that there is a wide range of “safe” values with both substantial noise reduction and negligible distortion of evoked activity (Fig. 1b). One could argue that, if denoising does not change the response pattern it cannot offer much benefit. We address this question below.

A common way to summarize the time course of the evoked MEG response is to plot the root-mean-square (RMS) over channels and trials. Figure 2 (a) shows the RMS evoked response calculated from our data before (red) and after (blue) denoising. The typical “M100” response occuring approximately 100 ms from the onset of an acoustic stimulus is visible in both plots. However the background level is lower and the peak is more salient for the denoised data. The gray bands represent ±2 standard deviations of the bootstrap resampling over trials, and give an idea of the reliability of the RMS response (i.e. to what degree it might differ if calculated over a different set of trials). The denoised response is much more reliable. For this plot, the RMS before denoising was calculated, as is common, from the 10 “best” channels in terms of reproducibility, whereas the RMS of the denoised data was calculated from all channels (but only the 10 best DSS components were retained).

Fig. 2.

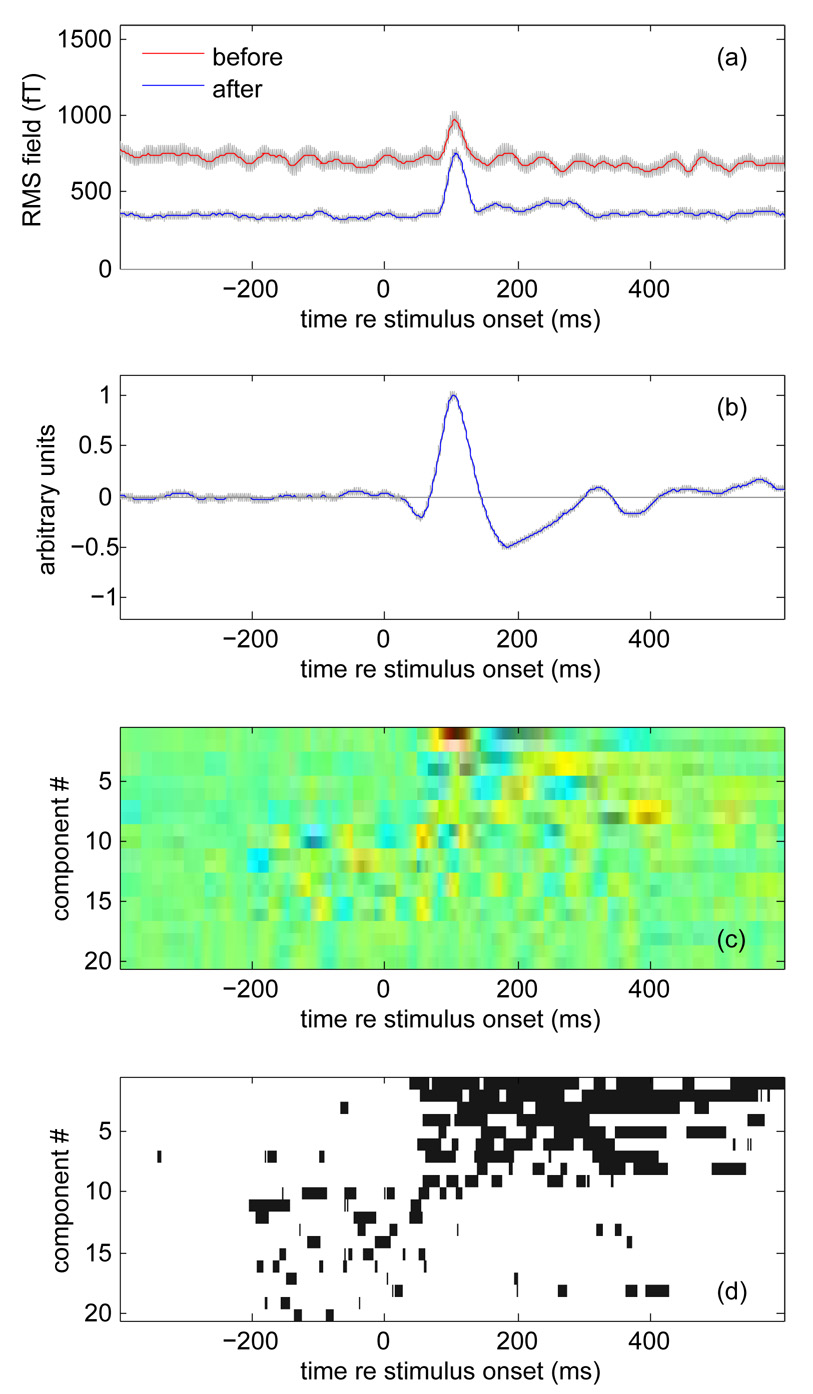
Effect of denoising on MEG responses to repeated auditory stimuli (200 ms noise bursts). (a) RMS over channels and trials before (red) and after (blue) denoising. Gray bands indicate ±2 standard deviations of the bootstrap-resampled mean. (b) Time course of best (most reproducible) component averaged over trials. The gray band (hardly visible) indicates ±2 standard deviations of the bootstrap-resampled mean. (c) Time-course of the first 20 components averaged over trials, coded as color. Each component was normalized and then multiplied by the square root of its power. (d) Map of time intervals for which each component differs from 0 by more than 4 times the standard deviation of the bootstrap-resampled mean. Intervals for which this plot is white are unlikely to represent stimulus-evoked activity, as are intervals that precede stimulus onset.

If the goal is to summarize the evoked response by a single function of time, an alternative to RMS is to use the first DSS component. It can be understood as the best (most reproducibly stimulus-driven) linear combination of channels, and as such it is a reasonable candidate for a summary statistic. This component is plotted in Fig. 2b. The gray band (hardly visible) indicates ±2 standard deviations of the bootstrap resampling: this response is extremely reliable.

Figure 2c plots the time courses of the first 20 components. Each is weighted by the square root of its share of total power (hence the differences in salience). The first few components (1 to 9) appear to be silent before the stimulus onset, consistent with their interpretation as stimulus-evoked. Subsequent components (10 to 20) are more active before stimulus onset, suggesting that the spatial filters associated with these components are not effective to isolate stimulus-driven activity. Figure 2d indicates (in black) which portions of the previous plot were in absolute value greater than 4 times the standard deviation of the bootstrap. Components beyond the 10th tend to have fewer such samples, consistent with the notion that they are not reliably stimulus driven, justifying the choice of 10 as a cutoff for denoising.

The left column of Fig. 3 shows the field distribution associated with each of the first three components. These were calculated from rows of the pseudoinverse of the denoising matrix (equivalently, the field map for a component can be calculated by cross-correlating its time series with each of the sensor waveforms). The field map for the first component has a characteristic “auditory” shape (a dipole over each auditory cortex). Those for subsequent components are less easily interpreted (see below). The second column shows a map of the estimated signal-to-noise ratio of each component (power ratio between that component and all other components combined, both signal and noise). The rightmost column shows the coefficients of the spatial filters associated with each component. The remarkable differences between filter maps (right) and field maps (left) is discussed below

Fig. 3.

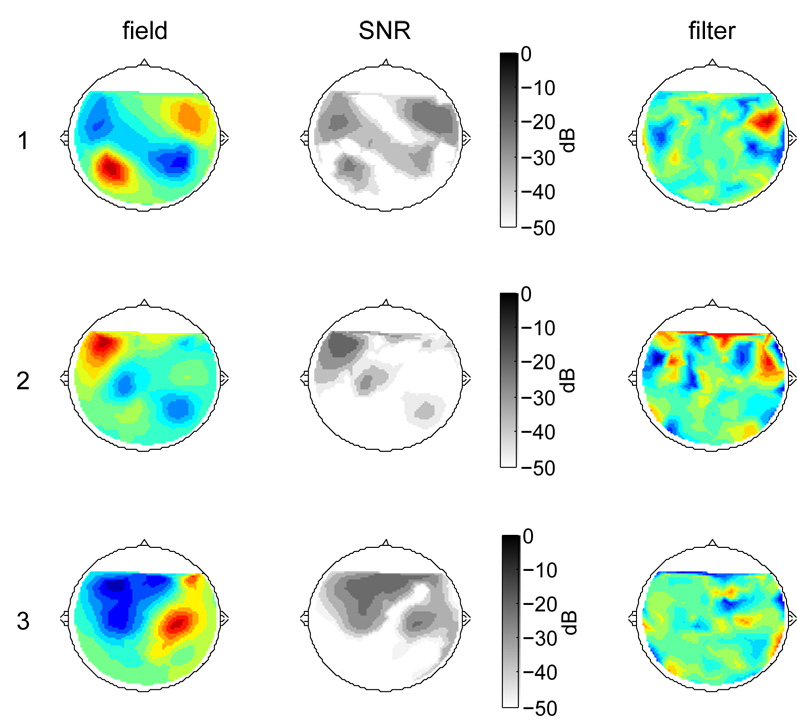
Topography of magnetic field (left), signal-to-noise ratio (center), and filter coefficients (right) for the three components with greatest evoked-to-total power ratio.

We stress that no claim is made that each individual component corresponds to a meaningful source within the brain. What can be said with some confidence is that, collectively, the components retained carry most of the power of the repeatable activity, probably all that can be extracted based on spatial filtering. Analysis into meaningful physiological sources requires further analysis (using ICA, beamforming, source models, etc.). That analysis should be greatly facilitated as a result of denoising because it does not need to modeld large noise components. Note that the number of components retained at the denoising stage sets an upper limit on the dimensionality of the data, i.e. the number of distinct sources that can be analyzed. More sources may exist within the brain, but the data cannot resolve them (to resolve more sources might require more sensors and/or less noise) (Ahonen et al 1993).

The first component might reasonably be attributed to a particular source if, as here, it accounts for a large proportion of the evoked power. Averaged over trials, the time course of this component (the most reproducible linear combination of sensors) is a good candidate for a statistic to summarize concisely the time course of the multichannel stimulus-evoked response. In this role it is competitive with commonly used quantities such as the RMS, or the time course of a particular sensor.

To summarize, our new denoising method suppresses sources of activity that do not contribute consistently to evoked responses. Removing those components allows a more reliable observation of the stimulus-evoked brain activity. The new method usefully complements the panoply of tools available to reduce noise (Hämälainen et al. 1993; Vrba, 2000; Baillet et al. 2001; de Cheveigné and Simon 2007; 2008). As the method produces clean data in sensor space, it should be easy to combine with standard methods of brain response analysis and modeling.

Comparison with other denoising techniques

Our method may be compared to other spatial filtering techniques. Figure 4 plots the ratio between the power of the evoked response averaged over 100 trials, and the variance of this power (estimated by bootstrap with 200 iterations) for several common techniques applied to our data set.

Fig. 4.

Ratio of evoked response power to variance of evoked response (based on 200 repetitions of a bootstrap resampling), for various noise reduction schemes. A: selection of single channel with best SNR. B: average of 20 channels with best SNR. C: matched filter (coefficients as in Fig. 4, top, center). D: matched filter with coefficients weighted by SNR. E: first PCA component. F: best PCA component (greatest evoked-to-total power ratio). G: best ICA component (RUNICA). H: best ICA component (AMUSE). I: our method.

The simplest form is the time-honored practice of selecting one sensor channel with best SNR (e.g. Sharbrough 1991). Supposing that we are interested in the brain activity that gives rise to the most reproducible spatial component (Fig. 3, top), the SNR plot in that figure suggests that we should select a sensor located in the right temporal region. However the value of SNR at that sensor (about −17 dB) is much smaller than the estimated SNR of component 1 (about 1.5 dB). Other drawbacks of channel selection are that it requires expert intervention, the observations reflect multiple brain sources in unknown proportions, and it does not take advantage of the redundancy of multiple sensors. The power / variance ratio of the best channel is shown in Fig. 4 (column A).

Selecting a group of sensor channels (e.g. Poeppel et al. 1996) hopefully improves SNR by drawing data from multiple sensors, for example 10 per hemisphere in an auditory experiment. The selected channels may be summarized by their root-mean-square (RMS) field. RMS is a robust statistic, relatively insensitive to sensor placement and independent of any particular model, but it discards information about polarity, and it is potentially sensitive to baseline shifts such as induced by spectral or spatial filtering. Here, to ease comparison with other methods, we instead averaged over channels (flipping the polarity of any channel negatively correlated with the mean). The power/variance ratio is shown in Fig. 4 column B).

A different approach is to design a spatial filter based on the topography of a component of interest (for example measured at some time when competing components are less active). This is the idea behind signal space projection (Uusitalo and Ilmoniemi 1997). Drawbacks are (a) the choice of spatial filter requires expert intervention, (b) the filter is component-specific and thus does not address the case of multicomponent responses. Surprisingly the outcome (Fig. 4 column C) is no better than the best-channel approach, presumably because the activity pattern extends over regions of rather low SNR (Fig. 3, column 2). Weighting the component topography by its SNR (product of columns 1 and 2 of Fig. 3) provides some improvement (Fig. 4 column D).

PCA produces a set of components that are mutually orthogonal (uncorrelated), ordered by decreasing power. It can be used for denoising on the assumption that low-order components (with strong power) represent activity of interest and higher-order components noise. Denoising then involves discarding PCs beyond a certain rank. Obviously this assumption may fail, particularly when the SNR is unfavorable (Fig. 4 column E). A different way of applying PCA, closer to the spirit of our algorithm, is to suppose that principal components map to distinct brain sources. A measure of evoked-to-total power ratio is applied to each PC, and PCs with poor scores are discarded. Unfortunately PCs often do not map to individual sources, and indeed results are disappointing (Fig. 4, F).

In contrast to PCA, ICA produces components that are statistically independent rather than uncorrelated. ICs are usually held to be more likely than PCs to correspond to distinct brain sources, on the assumption that distinct sources in the brain follow unrelated time courses. The name “ICA” actually covers a range of distinct algorithms. Certain algorithms can give different results at each run (not a serious problem as long as the algorithm distinguishes useful activity from noise). After ICA, ICs with small evoked-to-total power ratio may be discarded. Figure 4 (columns G and H) show results for algorithms ’RUNICA’ and ’AMUSE’ as implemented in EEGLAB (Delorme and Makeig, 2004). Scores are better than for PCA but not as good as our method (column I).

Our method is related to ICA. Indeed, Särelä and Valpola (2005) claim that most ICA techniques can be understood (or implemented) as special cases of DSS. Equivalently DSS may be understood as a reformulation of earlier techniques (Green et al 1988; Parra and Sadja 2003; Särelä 2004). In our opinion, the appeal of our method over ICA is that (a) separation is guided by the measure of interest (here evoked-to-total power ratio) rather than a general measure of statistical independence, (b) components are ordered according to this measure, and as a result selecting signal and/or noise components is straightforward. The method is also relatively fast. The multiplicity of different “ICA” methods, the fact that some are non-deterministic (the outcome depends on a randomized initialization), and the fact that ICs are not ordered makes ICA a difficult tool to use.

Our method does not compete with approaches that it can be combined with, such as spectral filtering and averaging over trials. To summarize, our method is competitive with other noise-suppression methods that involve spatial filtering, and complementary with other standard techniques such as averaging over trials. in order

Testing with other data

So far the algorithm has been tested with data from a number of MEG and EEG systems, and also with data from intrinsic optical imaging of auditory cortex. In each case it greatly reduced non-reproducible activity, leading to clearer estimates of stimulus evoked activity (not shown).

IV Discussion

The method reduces noise effectively in stimulus-evoked response paradigms.

How it works

A formal description was given in the Methods section, here we give a more intuitive account. Two things need explaining. The first is how our spatial filter is more effective than simple schemes such as channel selection or a matched filter. A plausible matched filter might be shaped as one of the field maps in column 1 of Fig. 3. The filter that we use is shaped instead as in column 3. Comparing it to the first, an intruiguing feature is that the filter comprises non-zero coefficients in regions that appear to lack activity for that component. The explanation is that those excentric coefficients are needed to observe noise components that contaminate sensors close to the source of interest (here auditory cortex), so as to subtract them. Those observations may themselves be noisy, requiring subtraction of additional components from other regions, and so on. The filter thus samples activity from all over cortex, cancelling out most of it in a delicate “balancing act” in order to get the best possible estimate of the source of interest. The method resembles in this beamforming (e.g. Sekihara 2001), that also cancels unwanted sources in a data-dependent manner. This explains the widespread distribution of filter coefficients.

The second thing that needs explaining is how this filter is determined automatically from the data. The reader is referred to Särelä and Valpola (2005), and references therein, for a clear detailed explanation of how DSS works. In brief, the initial PCA and normalization transform the multichannel MEG data into a set of points in signal space that is spherical, that is, free to rotate in any direction. The bias function (average over trials) has the effect of distorting this set so that it is no longer spherical, increasing the variance in some directions of greater bias, and reducing it in directions of lesser bias. The second PCA aligns these particular directions with the axes of a new basis, the vectors of which are the DSS components. By construction, the first component is the best linear combination to maximize the bias. Each subsequent component is the best linear combination orthogonal to the previous components.

Caveats and cautions

The method as described works for paradigms that focus on evoked responses to repeated stimuli. This is the case of a large proportion of studies. It would be unwise to use the evoked-response method described here to enhance, say, induced activity, as components that carry that activity may well have been discarded as noise. It is possible to adjust the method to handle such a situation, but this is outside the scope of the present paper (see below).

Powerful noise components are removed by adjusting sensor coefficients to cancel them out and reveal the weaker signal components. Obviously, any change to this delicate balance (for example head movement) could compromise the outcome. If the mismatch occurred in one condition but not others, it could masquerade as an experimental effect and lead to erroneous conclusions. This situation is common in experimental sciences, but given the sensitivity of this method it is worth pointing out. Suggested precautions are (a) examine attentively the noise components for leakage of useful activity, (b) ensure that data collection and analysis are uniform across conditions (did the subject move between blocks?), (c) check variability using the bootstrap. For example head movement within a block is likely to result in a much larger variance of the mean for that block (as evaluated by bootsrap). Head movements may conceivably be compensated by techniques such as spatiotemporal signal space segregation (tSSS) (Medvedovsky et al 2007; Uutela et al 2001).

At each step of the algorithm, solutions are found by minimizing sums of squares involving data samples. These are very sensitive to large-value outliers, for example glitches or peaks of noise that have escaped previous denoising stages. To avoid the solutions being shaped by these pathological data samples, they should be excluded from analysis. This may be done automatically, but it is important to check that all major artifacts are addressed. Things to look for are: bad channels, bad trials, temporally or spatially localized outlier samples, narrow-band noise, large-amplitude physiological events. This is important for the quality of the outcome. Note, however that the samples excluded from the calculation of the denoising matrix may nevertheless be retained when that matrix is applied to obtain denoised data.

The method involves a large number of free parameters (K², where K is the number of sensors), and thus it is susceptible to over-fitting: even within a random data set it may discover linear combinations that yield repeatable patterns. For example, in Fig. 2d, some components with ranks ≥10 seem to show robust activation before stimulus onset (e.g. component 11 around −200 ms): such activation obviously cannot be stimulus-evoked. The investigator should parry this possibility using stringent tests and cross-validation. For example, the outcome of analysis may be validated by including the denoising stage within the resampling loop of a bootstrap procedure (Efron and Tibshirani 1993).

Field maps for each component (left column of Fig. 3) are subject to spurious correlations between the component of interest and noise components. When fitting a field map to a model (for example a dipole model) it may be useful to weight the map by SNR (center column of Fig. 3). To summarize these caveats: this method is critically dependent on several assumptions: reproducible brain activity, stationary mixing matrix between brain sources and sensors. If the data does not fit the model, or if its parameters are no longer correct (e.g. head motion) denoising may fail or produce misleading results. It is also susceptible to overfitting: patterns revealed by denoising should be cross-validated.

To analyze or to denoise?

Tools such as ICA are in principle capable of denoising and analysis in the same process. In contrast, we focus on the two-way partition between noise and target. This less ambitious goal is easier to attain than the multi-way partition involved in ICA. It is also easier to validate. Once validated, denoising schemes may be cascaded, each step removing some aspect of the noise. For example in this study the methods TSPCA, SNS and the present method were cascaded to remove in sequence environmental, sensor and biological noise sources respectively. To the extent that denoising does not distort brain activity, it may be combined with the many existing analysis tools, while relieving them from the burden of resolving low power brain sources in the context of high power noise. Denoising and analysis fit together neatly as modules. Denoising is attractive as a processing step that can (with appropriate care) “do no harm”.

Observing single trial and ongoing activity

Could the method be used to design a spatial filter to observe single-trial or ongoing brain activity? This can be divided into two questions: (a) does such a filter exist? and (b) how can we design it? As visible from the leftmost data point in Fig. 1c, about 60% of the power of each trial response is the same as other responses, so this component is reproducibly stimulus-driven. This is also obvious from Fig. 5 that shows the time course of individual trial responses. This shows that an effective filter does exist, at least for this data set, and if that filter had been known in advance we could have observed each trial as it appeared, in real time. However the filter was derived after observation of the data. We believe that in many cases a similar filter can be derived in advance, in a data-adaptive fashion, but proof requires extensive testing that is beyond the scope of this paper. The issue is of interest in the context of brain-machine interface applications.

Fig. 5.

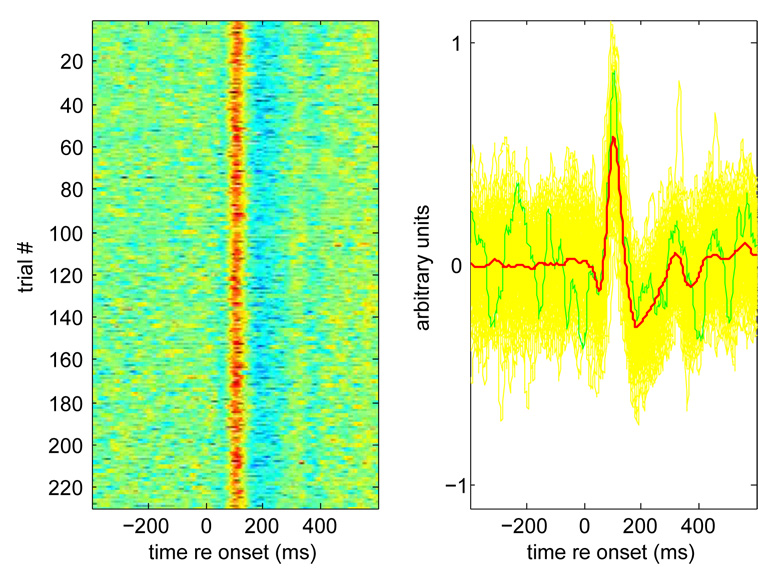
Single-trial responses for component with greatest evoked-to-total power ratio. (a) Raster plot of responses over successive trials. (b) Yellow: responses over all trials, green: response over one trial, red: average over all trials.

Beyond denoising

We intentionally limited this paper to denoising, mainly because it is a relatively simple task that is universally useful. However the technique that we use for that purpose (DSS) is much more powerful. Särelä and Valpola (2005) suggest that DSS may be used with a wide range of bias functions, including non-linear functions of the data. Indeed, we have found it useful to investigate other responses such as the induced response, and to further analyze the multidimensional denoised response into meaningful sources. The investigation of these possibilities is beyond the scope of this paper.

What next?

Brain activity is expected to be of high dimensionality, much greater than the number of sensors on any typical machine. The fact that, even after denoising, the data occupy a much smaller space (in our example less than 10 dimensions) suggests that we are still far from a detailed observation of brain activity. How can this be improved? Systems with large, high-density sensor arrays are sometimes criticized on the account that they go beyond the limits imposed by the spread of fields or currents produced by brain sources. We would argue that a major benefit of high-density arrays is to increase the leverage of algorithms such as ours. Following the same logic, additional sensor modalities (EEG, EOG, EMG, ECG, etc.) may help by offering observations of artifacts that can then be factored out from brain activity.

This paper concludes a series of three papers on denoising methods. The previous two methods, TSPCA (de Cheveigné and Simon 2007) and SNS (de Cheveigné 2008) addressed environmental and sensor noise respectively. Together, the three methods offer a toolkit to improve the quality of electrophysiological recording techniques such as MEG. To give a quantitative idea of the benefit of each processing step, let us define arbitrarily the “signal” as the average over trials of the first DSS component, and measure its signal-to-noise ratio at each stage. The SNR of the final denoised, averaged component was estimated from its bootstrap resampling, the SNR at other stages was calculated as (signal power) / (data power minus signal power). The values are plotted in Fig. 6 (thick full line) together with similar values for data recorded from other systems. The step that provides the largest improvement is usually the time-honored average over trials, but each other step contributes to reduce the noise, sometimes significantly. These values should not be taken as a norm, as noise levels and processing benefits vary greatly between systems and data sets.

Fig. 6.

Estimated signal-to-noise ratio (SNR) at each step of processing. The ’signal’ here is defined here as the trial-by-trial replication of the average over trials of the best DSS component. The SNR after processing (rightmost data point) is calculated based on bootstrap resampling. The SNR for other steps is calculated as (signal power) / (total power − signal power). Dataset 1: the 157-channel MEG data used to illustrate this study (100 trials). Dataset 2: data from a 208-channel MEG system (28 trials). Dataset 3: data from a 440-channel MEG system (30 trials). Dataset 4: data from a 151-channel MEG system (89 trials). Dataset 5: data from a 4788-channel intrinsic optical imaging system recording from auditory cortex (10 trials).