Propagators and Time-Dependent Diffusion Coefficients for Anomalous Diffusion

Abstract

Complex diffusive dynamics are often observed when one is investigating the mobility of macromolecules in living cells and other complex environments, yet the underlying physical or chemical causes of anomalous diffusion are often not fully understood and are thus a topic of ongoing research interest. Theoretical models capturing anomalous dynamics are widely used to analyze mobility data from fluorescence correlation spectroscopy and other experimental measurements, yet there is significant confusion regarding these models because published versions are not entirely consistent and in some cases do not appear to satisfy the diffusion equation. Further confusion is introduced through variations in how fitting parameters are reported. A clear definition of fitting parameters and their physical significance is essential for accurate interpretation of experimental data and comparison of results from different studies acquired under varied experimental conditions. This article aims to clarify the physical meaning of the time-dependent diffusion coefficients associated with commonly used fitting models to facilitate their use for investigating the underlying causes of anomalous diffusion. We discuss a propagator for anomalous diffusion that captures the power law dependence of the mean-square displacement and can be shown to rigorously satisfy the extended diffusion equation provided one correctly defines the time-dependent diffusion coefficient. We also clarify explicitly the relation between the time-dependent diffusion coefficient and fitting parameters in fluorescence correlation spectroscopy.

INTRODUCTION

In systems where particles or molecules diffuse freely via Brownian dynamics, the mean-square displacement (MSD) of the particles in n-dimensional space is proportional to time, written as 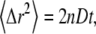where D and t represent the diffusion coefficient and time, respectively. In contrast, diffusion within complex media such as within living cells may be hindered by various factors that can inhibit mobility, such as interactions with obstacles, transient binding events, or molecular crowding. In such cases, the mobility of the molecules is often anomalous, indicating a distribution of diffusion times, and the MSD does not increase linearly with time. Anomalous diffusion has been observed in a wide variety of experimental systems, and detailed characterization of the nature and origin of such observations is of widespread interest (1,2). A number of experimental tools are available to measure diffusion dynamics within complex environments, and we here focus on the use of fluorescence correlation spectroscopy (FCS) (3,4) to investigate anomalous mobility. Analysis of FCS data showing anomalous diffusion is complicated by several factors. First, there is significant confusion in the field regarding the mathematical validity of the widely used model for anomalous diffusion in FCS (5–7) as well as confusion about the physical significance of the model parameters. Second, additional confusion is introduced by differing procedures in reporting the fitting parameters recovered from FCS analysis. Last, although FCS curves provide significant information content when correct fitting models are used for data analysis, individual FCS curves can typically be well fit by a variety of physical models, which can make model discrimination challenging. Efforts to identify appropriate fitting models and thus the underlying physical and chemical basis for the anamolous mobility therefore require careful analysis of how experimentally recovered parameters vary as the experimental system and/or measurement conditions are systematically manipulated. Comparing experimental parameters recovered with varied measurement conditions requires a clear understanding of the physical significance of the fitting parameters used in curve-fitting models. This article aims to clarify the mathematical basis for anomalous diffusion fitting models and the physical significance of the fitting parameters. We suggest that a detailed understanding of this model can play an important role in further investagations aimed at better understanding the underlying causes of anomalous diffusion in different experimental systems.

THEORY AND RESULT

A variety of theoretical approaches have been introduced to model complex diffusive dynamics based on various assumptions about the underlying physical basis for the anomalous mobility (8). We here focus exclusively on the most widely used model for anomalous diffusion in FCS, for which the MSD versus time is assumed to exhibit power law scaling (1) with

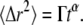(1)

The magnitude of the anomalous exponent, α, determines whether the mobility is called anomalous subdiffusion 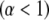or superdiffusion 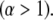The constant prefactor Γ is usually referred to as the transport factor and has dimensions of length-squared per fractional time. We show below that with appropriate definitions for the time-dependent diffusion coefficient, the propagator associated with this power law scaling is mathematically sound and that the model parameters can be rigorously understood in terms of the physical parameters of the sample and measurement system.

The physical properties of diffusive motion are conveniently characterized by a density distribution function, 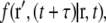also called the propagator. The propagator solves the diffusion equation and specifies the probability that a particle located at position r at time t, will be found at position r′ at time 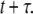For normal Brownian motion the propagator is a Gaussian distribution (9). In general, the standard diffusion coefficient defined by Fick's law, and the corresponding diffusion equation cannot describe the nonlinear time dependence of the MSD, and there is no simple comparable propagator for anomalous diffusion, although many sophisticated approaches have been introduced to model anomalous dynamics (2,10). A mathematically simplified approach that is commonly used to model anomalous diffusion defines a time-dependent diffusion coefficient D(t) (11) based on the partial power-law dependence of the MSD as in Eq. 1. Assuming no spatial heterogeneity in D(t), one can then obtain an extended diffusion equation from Fick's first law and the continuity equation as (6,11)

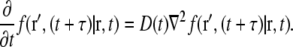(2)

The most commonly published form of the time-dependent diffusion coefficient, which we will refer to as the apparent diffusion coefficient, is defined as 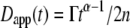such that the MSD can then be written as 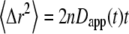(11). The apparent diffusion coefficient (Fig. 1) is proportional to the slope of the line that connects the origin with the MSD for a particular time point. The quantity 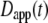specifies the diffusion coefficient that would produce the observed MSD at a given diffusion time if the dynamics followed free diffusion and thus represents the time-averaged mobility.

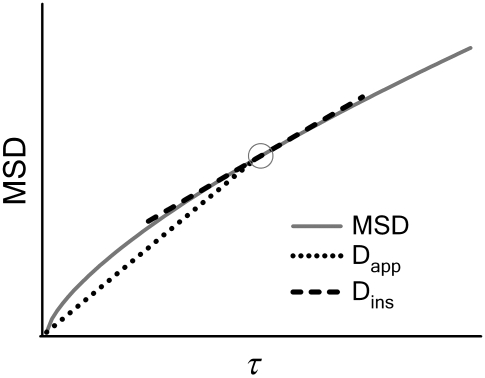
FIGURE 1.

Commonly used definition for D(τ) (11) is the apparent diffusion coefficient 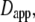which is found at time τ from the slope of a straight line between the origin and MSD(τ) (dotted line). The slope of the line is 2nD_app. The instantaneous diffusion coefficient 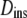is determined by the local slope of MSD(τ) at time τ (dashed line), with slope 2nD_ins.

A previously published propagator based on the extended diffusion equation and the apparent diffusion coefficient, 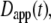does correctly capture the power law scaling for different values of the anomalous exponent (5,6). However, the published propagator is problematic in that it does not appear to solve the extended diffusion equation, resulting in widespread confusion regarding its validity and also leading to inconsistencies between published fitting functions for analysis of FCS data and anomalous diffusion models (6,12).

We suggest that much of the confusion regarding published propagators for anomalous diffusion lies in the definition of the time-dependent diffusion coefficient. In particular, the extended diffusion equation is meant to describe the temporal behavior of the diffusive density distribution function, and D(t) in Eq. 2 should represent the instantaneous time dependence of the MSD rather than the time-average quantity represented by 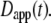Thus, a more physically correct value to describe the anomalous diffusion temporal evolution and to use for D(t) in Eq. 2 is the instantaneous diffusion coefficient (Fig. 1), defined in terms of the time-dependent slope of the MSD versus time, with (13)

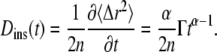(3)

Importantly, this definition for D(t) differs from 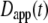by a factor α.

If 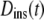is used for D(t) in Eq. 2, the anomalous diffusion propagator is easily obtained by standard methods, yielding

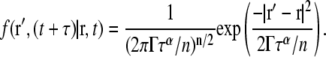(4)

This format for the propagator is similar to that published elsewhere (5,6). Significantly, however, by using 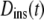in Eq. 2 it becomes straightforward to demonstrate that Eq. 4 both rigorously solves the extended diffusion equation and produces the correct power law scaling of MSD versus time, removing widespread confusion regarding whether or not this propagator can be used legitimately for data analysis. Furthermore, this exact solution to the extended diffusion equation allows precise clarification of the definition of the FCS diffusion time and its relation to the anomalous exponent and transport factor. Additionally, with this exact solution, the correct constant factors for diffusion in two (n = 2) or three (n = 3) dimensions are easily determined. We note that the formal validity of this propagator does not necessarily imply that it can correctly describe the dynamics of a particular experimental system, which will in each case require careful investigation.

FCS has become an important tool for measuring molecular mobility, concentrations, and chemical kinetics (4,14,15). FCS fitting models are derived using a model for the observation volume (16,17) and an appropriate physical representation of the underlying molecular dynamics. In FCS with one- or two-photon excitation, the volume profile is typically modeled as a three-dimensional Gaussian function of the form 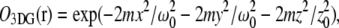with radial and axial beam waists 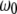and 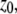respectively. The index m specifies one- (m = 1) or two-photon (m = 2) excitation.

With the propagator (Eq. 4), one can then easily derive the autocorrelation function for anomalous diffusion as (9,18):

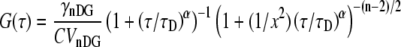(5)

Here the characteristic time τ_D is defined in dimensions of time for m-photon excitation with n-dimensional motion as

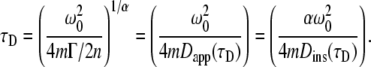(6)

The volume and gamma factors (9,19) are 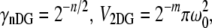and 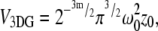and the structure factor, x, is defined as 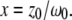Contrary to some reports, the structure factor does not have an exponent of α in Eq. 5. The variable C specifies the molecular concentration. We note that although Eq. 5 has the same visual format as previously published versions (5,7,12), the clarifications introduced above allow demonstration that this equation is consistent with a rigorous solution to Eq. 2 for both two and three dimensions, and the values of τ_D can now be defined unambiguously in terms of physical variables.

The precise definitions for fitting parameters in terms of physical variables as shown here allow for some clarification in assigning physical significance to recovered parameters and interpreting mobility measurements. This capability will be important in designing research approaches aimed at uncovering the fundamental mechanisms underlying the anomalous dynamics in a particular system. FCS curves and the MSD report only on low-order properties of the propagator, and therefore, as noted above, it is unlikely that curve fitting alone will generally be capable of resolving the applicability of different physical models. Instead it will be important to measure the anomalous dynamics on different length scales or timescales and to couple the analysis of how experimental parameters change with predictions from different mechanistic models. With imprecise parameter definitions, this type of analysis is not possible, and the clarifications introduced above can be of significant importance for future investigations of anomalous dynamics.

One further issue that warrants discussion is parameter reporting in measurement of anomalous diffusion. In principle, the parameters Γ and α contain all the experimental information on various length scales or timescales and are therefore valuable to report directly. On the other hand, it is complicated to compare mobility using Γ parameters directly when the α-values are not the same because Γ has different dimensions for different α-values (19). Additional methods to report the diffusion parameters are thus also warranted. In many publications, the molecular mobility has been reported in terms of τ_D. However, its meaning has not always been clearly defined, and it cannot be easily compared between experiments because the value of τ_D depends on the experimental configuration. With the clarifications introduced above, it becomes more feasible to unambiguously report mobility data in terms of either a well-defined diffusion time or, alternatively, as time-dependent diffusion coefficients. Diffusion coefficients may be easier to compare intuitively, and one may compare either 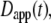which reports the average diffusion coefficient on a particular length scale, or 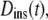and both may be of interest in answering particular experimental questions. Comparing time-dependent diffusion coefficients, whether instantaneous or apparent, does require selection of a common length scale or timescale. This scale selection would ideally be dictated by the properties of the sample but in some cases may also be defined or limited by the measurement apparatus. If α-values are essentially the same, then the choice of scale is of minimal importance for comparing the mobility of different diffusing entitites. On the other hand, if α-values are significantly different, then the relative magnitudes of apparent diffusion coefficients may depend strongly on the choice of scale. In such cases, it may be most helpful to plot the MSD versus time, which provides a complete representation of the mobility over all timescales or length scales.

SUMMARY

This work is intended to clarify the parameter definitions in fitting functions widely used for data analysis of mobility measurements and to demonstrate that, when properly interpreted, these fitting models are based on physical assumptions that can rigorously satisfy the extended diffusion equation. There are many sophisticated theoretical approaches to understanding anomalous diffusion (2,10) that attempt to link molecular-level phenomena with the observed power law behaviors. The discussion presented here has no direct bearing on the underlying mechanisms leading to the anomalous behavior. However, using FCS and other techniques to investigate anomalous mobility (11,20,21) certainly requires a thorough understanding of the theoretical basis of fitting models and the physical significance of associated fitting parameters. By attempting to clarify some of the confusion regarding the use of these fitting models, we hope to further advance the capability to understand anomalous behavior in terms of fundamental mechanisms by facilitating more precise interpretation of experimental data acquired under different experimental conditions, thereby facilitating the comparison of experimental measurements with different theoretical models.