Molecular Simulations of Lipid-Mediated Protein-Protein Interactions

Abstract

Recent experimental results revealed that lipid-mediated interactions due to hydrophobic forces may be important in determining the protein topology after insertion in the membrane, in regulating the protein activity, in protein aggregation and in signal transduction. To gain insight into the lipid-mediated interactions between two intrinsic membrane proteins, we developed a mesoscopic model of a lipid bilayer with embedded proteins, which we studied with dissipative particle dynamics. Our calculations of the potential of mean force between transmembrane proteins show that hydrophobic forces drive long-range protein-protein interactions and that the nature of these interactions depends on the length of the protein hydrophobic segment, on the three-dimensional structure of the protein and on the properties of the lipid bilayer. To understand the nature of the computed potentials of mean force, the concept of hydrophilic shielding is introduced. The observed protein interactions are interpreted as resulting from the dynamic reorganization of the system to maintain an optimal hydrophilic shielding of the protein and lipid hydrophobic parts, within the constraint of the flexibility of the components. Our results could lead to a better understanding of several membrane processes in which protein interactions are involved.

INTRODUCTION

For complex biological systems, questions concerning their functioning should be answered from the principle that their properties are not only related to the individual behavior of each component but also to the interactions between them. This is particularly true for biological membranes and hence it is important to invoke the collective nature of the system for the study of membrane processes. An important membrane process that received increasing attention over the last years is the lipid-mediated interaction between integral membrane proteins. The results from a number of investigations have pointed out that the composition of the lipid membrane and the hydrophobic matching between the lipid bilayer hydrophobic thickness and the hydrophobic length of the transmembrane proteins are important physical properties that regulate the mechanism of lipid-protein interaction in biomembranes. Moreover, a protein-induced bilayer deformation could interact with a bilayer deformation due to one or several other proteins and this could result in indirect lipid-mediated protein interactions (1). These could play a greater part in protein topology, protein activity, and membrane processes than is presently supposed. Proteins or other membrane inclusions, like, e.g., cholesterol, affect the lipid metabolism and transport, which have a role in diseases (2). On the other hand, lipids influence the distribution and the function of the proteins (3).

The insertion of a protein in a membrane is mostly done with the help of a translocon and, to a lesser extent, spontaneously. Both experiments and thermodynamic considerations lead to the conclusion that an increasing side-chain hydrophobicity of a membrane protein drives the equilibrium toward a bilayer insertion (4). Once inserted, the proteins fold and associate in a certain topology. The driving force behind the first step of the protein folding, i.e., from an unfolded protein toward a more compact, sometimes helical, molten globule, is primarily driven by hydrophobic-hydrophilic interactions. Although the translocon plays an important role in determining the protein topology, it is observed that the length of the protein hydrophobic segment could partly determine the topology and hence the function of the membrane protein (4,5).

The changing nature of the lipid bilayer in the Golgi apparatus has been proposed as an agent for protein segregation in the membrane so that they are excluded from budding vesicles (6–8). Cornelius et al. (9,10) report that the hydrophobic matching is a crucial parameter in regulating optimal Na, K-ATPase activity. Moreover, the activation entropy and enthalpy of Na, K-ATPase and Na-ATPase reactions together with the temperature dependence of the Na, K-ATPase activity as well as of the Na-ATPase reactions depend not only on the amount of cholesterol present in the membrane but also on the lipid chain lengths. Hinderliter et al. (11) suggests that the enormous lipid variety present in the eukaryotic membrane could play an important role in signal transduction as proteins are observed to interact preferentially with a specific lipid type. Of particular interest are the G-protein-coupled receptors (GPCR), which are essential components of cellular signaling pathways, as they represent by far the largest class of targets for therapeutic agents. With the help of the fluorescence resonance energy transfer technique, more and more GPCRs are detected in homo- or heteromeric complexes. Because GPCRs are major pharmacological targets, the existence of oligomers should have important implications for the development of new drugs, which until now have been designed with the assumption that these receptors are monomeric (12,13). Previous studies using electron microscopy have shown that bacteriorhodopsin aggregates in bilayers only when there is a very large hydrophobic mismatch (14). It was also determined by x-ray diffraction that bacteriorhodopsin monomers form a very tight trimeric unit and that the contact between the trimers in the membrane plane is almost exclusively mediated by lipids (15). Botelho et al. (16) showed, using the fluorescence resonance energy transfer technique, that the hydrophobic mismatch is the main physical mechanism that regulates the oligomerization of rhodopsin in membranes and that hydrophobic matching indirectly modulates the activity of rhodopsin. Previously, Brown (17) observed that the lipid bilayer modulates the rhodopsin function because the bilayer has a direct influence on the energetics of the conformational states of rhodopsin. Similar results were obtained by Kota et al. (18) and Mansoor et al. (19).

There is very little information regarding the thermodynamic stability, quantitatively described by the interaction free energy, of transmembrane protein-protein interactions in a biological membrane. Most free energies of helix-helix dissociation have been measured in detergent micelles (e.g., the work of Fisher et al. (20), Fleming et al. (21)); however, a first approach that allows quantitative measurements of α-helical membrane protein interactions has recently been proposed (22). A method to quantify the helix-helix binding affinities in both micelles and lipid bilayers has been developed by Lomize et al. (23). Several continuous models have been developed to calculate quantitatively the indirect lipid-mediated interactions between intrinsic membrane proteins. Among them are approaches based on statistical-mechanics integral equation theories developed for dense liquids (24,25), chain packing theory (26), elasticity theory (27), and elasticity theory combined with director field theory (28).

In the last decade, the first articles in which molecular dynamics (MD) simulations were applied to better understand the nature of several membrane processes have been published. Petrache et al. (29) performed MD simulations of both the dimer and monomer form of glycophorin A in lipid bilayers with different bilayer thickness, which they found to be the most relevant property on which the helix tilt angle, the helix crossing angle, and the helix-accessible volume depend. With the help of extended MD simulations, Deol et al. (30) studied the interactions of several membrane proteins with phosphatidylcholine bilayers. Nielsen et al. (31) used MD to study a coarse-grained model of a protein embedded in a mixed lipid bilayer and found peptide-induced lipid domain formation as an effect arising solely from hydrophobic mismatch. The MD simulations of Smeijers et al. (32) showed that coarse-grained membrane proteins with hydrophobic mismatch aggregate and that the size of the aggregates depends both on the hydrophobic mismatch and on the protein shape. Hénin et al. (33) estimated the free energy of α-helix dimerization of the transmembrane region of glycophorin A by using MD simulations. The coupling between the retinal conformational change and the large-scale rhodopsin conformational change which results in G-protein activation and signal amplification throughout the cell has also been studied by MD simulation (34). This study points out that the efficiency of the coupling has, most likely, a strong dependence on the nature of the lipid bilayer.

However, because most of the described membrane processes happen at the mesoscopic length and timescale, i.e., greater than 1–1000 nm, ns, and involve the collective nature of the system, atomistic simulation methods are still too computationally expensive. Hence, mesoscopic models of the phospholipids and the embedded proteins have been developed and studied by molecular dynamics and dissipative particle dynamics (DPD) techniques (reviewed in Venturoli et al. (35)). Venturoli et al. studied the protein induced bilayer deformations and the lipid induced protein tilting for proteins with a different hydrophobic length (36). Their results show that the protein induced bilayer perturbation is a function of the hydrophobic mismatch between the protein hydrophobic length and the pure lipid bilayer hydrophobic thickness and that proteins may tilt when embedded in too thin a bilayer. Recently, Periole et al. (37) developed a mesoscopic model to investigate how the physicochemical properties of a phospholipid bilayer affect the self-assembly of rhodopsin.

We have adopted the DPD simulation method and the previously developed model for lipid bilayers with embedded proteins (36) to study the mechanism by which hydrophobic mismatch induces lipid-mediated protein-protein interactions.

The article is structured as follows. In Model and Simulation Methods, we describe the mesoscopic model for lipid bilayers with embedded proteins, the DPD simulation technique, and the method to compute the potential of mean force (PMF) as a function of the distance between two proteins. In Results and Discussion we present the calculated PMF profiles and we explain the concept of hydrophilic shielding by introducing the hydrophilic shielding parameter. We use this to illustrate how the nature of the protein-protein interactions reflects the rearrangements of the system to insure an optimal hydrophilic shielding of the protein and lipid hydrophobic parts, within the constraint of the flexibility of the system components. The results of our simulation studies and their implications are summarized in the concluding section.

MODEL AND SIMULATION METHODS

Mesoscopic model

In this work, we adopt a mesoscopic representation of the molecular components of the system, namely water, lipids, and proteins, in which each molecule is coarse-grained by a set of beads. The following types of beads are considered: a waterlike bead, labeled w; a hydrophilic bead, labeled h, which models a part of the headgroup of either the lipid or the protein; and a hydrophobic bead, labeled either t_L or t_P, depending on whether it refers to a part of the lipid hydrocarbon tail or to the hydrophobic region of the protein, respectively. The waterlike bead represents three water molecules and the hydrophobic beads have the size of approximately three CH₂ groups (or two CH₂ groups and one CH₃ group). The model lipid we use in this study is aimed to represent dimyristoylphosphatidylcholine (DMPC) and is built by connecting three hydrophilic h beads to form the headgroup to which two hydrophobic tails of equal length (five t_L beads each) are connected. Previous simulation studies have shown that this lipid model forms a stable bilayer and displays the typical temperature phase behavior of lipid bilayers (35,38).

A transmembrane protein is modeled by linking together N_p amphipathic chains into a cylindrical bundle. The N_p amphipathic chains are linked to the neighboring ones by springs, thus forming a relatively rigid object with no appreciable internal flexibility. Each amphipathic chain consists of n_tp hydrophobic beads t_P, to the ends of which are attached three headgroup h beads. The distance spanned by a bead is approximately equal to that spanned by a helix turn. Simulation studies of lipid bilayers with these model proteins embedded were able to correctly describe the lipid bilayer deformation and protein tilt induced by hydrophobic mismatch (35,36).

In this work, we considered proteins of three different sizes: N_p = 4 (diameter D = 7.8 Å), N_p = 7 (diameter D = 12.3 Å) and N_p = 43 (diameter D = 30.4 Å). The smallest protein could represent an α-helical synthetic peptide (diameter D = 4–7 Å), the intermediate one a β-helix protein like gramicidin A (diameter D = 11–27 Å), and the biggest one a bacteriorhodopsin protein (consisting of seven α-helical peptides associated into a bundle, diameter ≈45 Å).

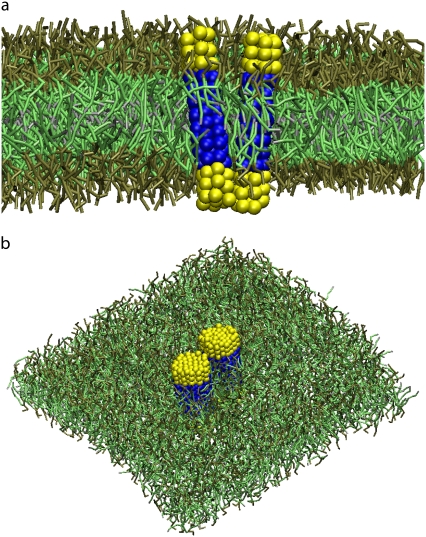
Fig. 1 shows a snapshot of two of the systems we studied: 1), two proteins of size N_p = 7 and n_tp = 8 embedded in the lipid bilayer; and 2), two proteins of size N_p = 43 and n_tp = 8 embedded in the lipid bilayer. The water particles are not shown for clarity.

FIGURE 1.

Snapshot of the lipid bilayer with two embedded proteins of size N_p = 7 (a) and N_p = 43 (b). The hydrophilic and the hydrophobic beads of the proteins are depicted in yellow and in blue, respectively. The lipid headgroups are depicted in brown, the lipid tails in green and the terminal beads of the lipid tails in gray.

Because we are interested in addressing the question of whether hydrophobic mismatch may induce lipid-mediated protein interactions, we performed simulations with proteins of different hydrophobic length (n_tp = 4, 6, and 8) with the hydrophobic mismatch, Δd, defined as

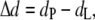(1)

where d_P is the protein hydrophobic length and d_L is the mean hydrophobic thickness of the unperturbed pure lipid bilayer. In the bilayer considered here, d_L = (23.6 ± 0.2) Å and the values of d_p for each value of n_tp are reported in Table 1, together with the corresponding hydrophobic mismatch Δd.

TABLE 1.

ntp	dP (Å)	Δd (Å)
4	13.6	−10.0 ± 0.2
6	22.6	1.0 ± 0.2
8	31.7	8.1 ± 0.2

Values of the protein hydrophobic thickness d_P and the corresponding mismatch Δd (Eq. 1) for different numbers of protein hydrophobic beads n_tp per aliphatic chain.

Dissipative particle dynamics

The mesoscopic model described in the previous section is studied with the dissipative particle dynamics (DPD) simulation technique (39). In DPD, pairwise-additive and momentum conserving dissipative and random forces are added to the pairwise additive conservative force, to obtain the correct hydrodynamic behavior. The total force, f_i, acting on bead i, is thus expressed as a sum over all other beads, j, which are within a certain cutoff radius R_c from bead i,

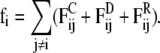(2)

The conservative force 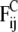comprises two contributions. The first contribution represents nonbonded interactions and is chosen in such a way as to model the hydrophobic interaction between every two beads by a soft-repulsive potential (39),

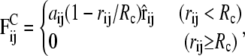(3)

where the coefficients a_ij > 0 represent the maximum repulsion strength, r_ij = r_i – r_j is the distance between beads i and j, and R_c is the cutoff radius, which gives the range of the interaction. The second contribution takes into account bonded interactions and contains an elastic contribution, F_spring, which describes the harmonic force used to tie two beads which are bonded in the chains of either the lipid or the protein, and a bond-bending force, F_θ, between consecutive bonds to control the chain flexibility,

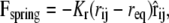(4)

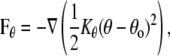(5)

where K_r and K_θ are the elastic and the bending constants, and r_eq and θ_o are the equilibrium values of the distance between two bonded beads and of the angle between two consecutive bonds, respectively.

The other two forces in Eq. 2 are a drag force (F^D) and a random force (F^R), which are expressed as

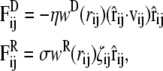(6)

where v_ij = v_i – v_j is the velocity difference between particles i and j, η is the friction coefficient, and σ is the noise amplitude. The value ζ_ij is a white noise, which is chosen from a uniform random distribution with zero mean and unit variance, and in an independent manner for each pair of particles. The combined effect of the dissipative and the random forces acts as a thermostat, which preserves the (angular) momentum, and thus provides the correct hydrodynamic behavior, at least for sufficiently long timescales and large system sizes.

If the weight functions and coefficients of the drag and random forces are chosen so to satisfy a fluctuation dissipation theorem, then the equilibrium distribution (in the limit of small timestep) of DPD is the Boltzmann-Gibbs distribution (40) and only the conservative part of the force determines the equilibrium averages of the system observables. In this way, DPD can be seen as a momentum-conserving thermostat for MD simulations. The functional form of w^R(r_ij) can be chosen to have the same dependence on the interparticle distance r_ij as the conservative force 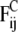(39), i.e.,

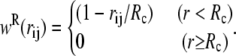(7)

The resulting equations of motion were integrated using a modified version of the velocity Verlet algorithm (39).

Computational details and model parameters

Because unconstrained lipid bilayers are essentially in a tensionless state (41), we reproduced this condition by simulating the system in the NγVT ensemble, where γ is the surface tension of the lipid bilayer. To do so we used a hybrid scheme which combines the DPD and the Monte Carlo (MC) simulation methods. The DPD method is used to evolve the positions of the beads and the MC method to impose a given value to the surface tension of the bilayer (35,42), and in particular the value γ = 0.

Within the DPD approach, reduced units are usually adopted. The reduced unit of energy is k_BT = 1 (k_B is the Boltzmann constant and T the dimensionless temperature) and the unit of length is the cutoff radius R_c. The number of atoms or molecules represented by a DPD bead is the renormalization factor for expressing the cutoff radius R_c in physical units. By representing three water molecules as one coarse-grained bead and considering that a water molecule has approximately a volume of 30 Ų, one obtains R_c = 6.46 Å at the considered bead density ρ = 3.

The numerical values of the repulsion parameters (see Eq. 3) for the interaction between bead types are the same used in Venturoli et al. (36), and are reported in Table 2.

TABLE 2.

aij	w	h	tL	tP
w	25	15	80	120
h	15	35	80	80
tL	80	80	25	25
tP	120	80	25	25

Repulsion parameters a_ij (Eq. 3) used for the interactions between the different bead-types: w represents a waterlike bead, h a hydrophilic bead, and t_L and t_P a hydrophobic lipid and protein bead, respectively.

The parameters for the elastic contribution to the interaction energy (Eq. 4) have the values r_eq = 0.7 R_c and K_r = 100 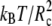for both the lipids and the proteins and the parameters for the bond-bending force (Eq. 5) are K_θ = 6 k_BT and θ_o = 180° for the angle formed by consecutive bonds in the lipid tails, K_θ = 3 k_BT and θ_o = 90° for the angle between the bonds connecting the last head-bead to the first beads in the lipid tails, and K_θ = 100 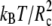and θ_o = 180° for each consecutive pair of bonds in the protein (36).

To avoid finite size effects, a sufficiently large bilayer patch should be simulated. Based on the calculation of the decay length of single protein bilayer perturbations (36), we have chosen a bilayer of area 635 nm², which contains a ∼2000 lipids. To assure sufficient hydration, 25 water beads per lipid were considered, for a total of 50,000 water beads. The volume of the simulation box is chosen such that the overall bead density is ρ = 3. The simulations were performed at the dimensionless temperature of 0.7 (∼60°C), i.e., when the DMPC bilayer is well in the fluid phase (36).

Influence of hydrophobic mismatch

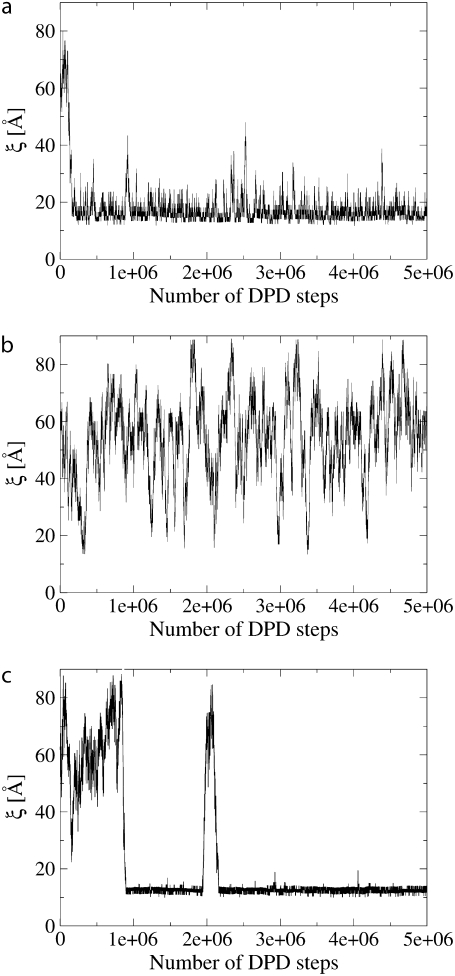
To investigate whether hydrophobic mismatch can induce lipid-mediated protein-protein interactions, DPD simulations of three different bilayer systems with two embedded proteins, both of size N_p = 7 (D = 12.3 Å), at negative, Δd = (−10 ± 0.2) Å, negligible, Δd = (1 ± 0.2) Å, and positive, Δd = (8 ± 0.2) Å, mismatch conditions were performed. The two proteins were initially inserted in the membrane at a distance of 63 Å from each other. Fig. 2 shows the time evolution of the distance between the protein centers of mass during the simulation. Fig. 2 a, which represents the time evolution of the distance between two proteins with negative mismatch, suggests that both proteins freely diffuse in the lipid bilayer until they are at a distance of 40–45 Å from each other. From this point, they appear to be strongly attracted to each other, and, once together, they remain in each other's neighborhood, without forming a stable physical dimer. Here we use the term “stable physical dimer” to indicate that the proteins are at close contact, i.e., no lipids are present between the proteins. Fig. 2 b shows that the motion of proteins with zero mismatch is a free diffusion in the lipid bilayer, and no attraction is observed. Proteins with positive mismatch (Fig. 2 c), diffuse freely up to a distance of 35–40 Å, after which they are strongly attracted to each other and form a stable dimer. Since the cutoff R_c of all acting forces is set to 6.64 Å in the model, no direct interaction can take place between the proteins if they are located at a distance >6.64 Å. Moreover, since the degree of protein mismatch is the only difference between the three systems described, these results suggest that hydrophobic mismatch is a major driving force in lipid-mediated protein-protein interactions.

FIGURE 2.

Time-series (in DPD-steps) of the distance between two proteins with size N_p = 7 with negative (a), zero (b), and positive (c) mismatch.

Potential of mean force calculation

To quantitatively describe the lipid-mediated interactions between the proteins, we performed free energy calculations, focusing on the interaction between two equal proteins embedded in the lipid bilayer. We express the free energy of protein-protein interactions with respect to the collective variable ξ(X_p, Y_p), which represents the distance in the xy-plane (i.e., the plane parallel to the lipid bilayer) between the centers of mass of the proteins. X_p and Y_p are the coordinates of the centers of mass of the proteins in the bilayer plane. Since the motion of the proteins in the direction perpendicular to the membrane plane is small and supposed not to be important in the description of protein-protein interactions, it is reasonable to restrict the collective variable to the membrane plane. The potential of mean force was computed in two steps.

First, an initial guess of the PMF as function of ξ(X_p, Y_p) was obtained using umbrella sampling with an harmonic biasing potential centered on different values of the collective variable. The data generated by umbrella sampling calculations were unbiased and combined using the weighted histogram analysis method (WHAM) (43,44). According to Roux (45), this is the most accurate approach for calculating free energy curves from biased distribution functions. During the umbrella sampling, simulations were performed in windows centered around N_W successive values of the reaction coordinate ξ_i (i = 1,···,N_W; ξ = iΔξ) with the potential of the unbiased system V₀(R) replaced by a modified potential V_i(R) of the form

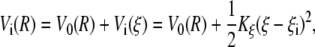(8)

where R represents the coordinates of all the beads in the system. These simulations were performed in the NVT ensemble. To correctly recombine the different windows, the values of ξ_i and of the harmonic constant K_ξ should be chosen in such a way that consecutive windows overlap. We found that the values K_ξ = 10 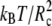and Δξ_i = 0.2 R_c satisfy this requirement. The average unbiased total distribution function, P^ub(ξ), is obtained by solving the coupled WHAM equations,

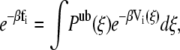(9)

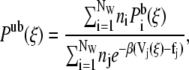(10)

where f_i is the (initially unknown) free energy due to the biasing potential, n_i is the number of samples made in the i^th window, 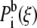is the biased distribution of ξ in the i^th window, and β = 1/k_BT. Equations 9 and 10 are solved self-consistently, starting from an initial guess of f_i, until convergence is reached.

Because the PMF only provides a measure of the difference in free energy between two states, we imposed the PMF to evolve toward zero at large distances between the proteins. The potential of mean force was then directly calculated from the reversible work theorem (46):

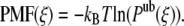(11)

It should be noted that Eq. 11 is only exact in the limit of zero protein density. For a system containing a finite protein density, correction terms should be added (47). However, as we consider only two proteins, Eq. 11 should hold.

In the second step of the PMF calculation, we used umbrella sampling, during which simulations were performed around N_W successive values of the reaction coordinate ξ_i (i = 1,···,N_W) with a biasing potential V_i(ξ) of the form

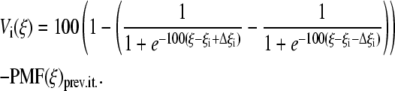(12)

The first term in Eq. 12 is a deep potential well that forces the system to sample in the distance interval [ξ_i – Δξ_i, ξ_i + Δξ_i] with Δξ_i = 1.3 R_C, while PMF(ξ)_prev.it. is the PMF calculated at the previous iteration. By using this approach, we were able to reduce the number of windows by a factor of 10, compared with the harmonic biasing potential case. These simulations were performed in the NγVT ensemble, with γ = 0. The unbiased distribution function, from which the PMF is calculated, was again obtained by solving the WHAM equations. This step was repeated, updating the PMF, until all the individual histograms of the windows showed a uniform distribution.

We observed that the extremely time-consuming second step did not significantly change the PMF computed in the first step. Therefore, for some of the PMFs presented here, the second step was not applied.

The proteins were manually inserted in the equilibrated pure lipid bilayer. For every protein distance (window), we first performed 20,000 DPD-MC cycles to equilibrate the system at zero surface tension. In each cycle, it was chosen, with a probability of 70%, whether to perform a number of DPD steps. Otherwise an attempt was made to change the box aspect-ratio according to the imposed surface tension value (γ = 0). Data to calculate the PMF were collected after the equilibration period.

The WHAM equations were solved self-consistently starting from an initial value of the free energy constants f_i = 0. The iterations were repeated until

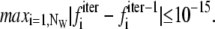RESULTS AND DISCUSSION

Potentials of mean force

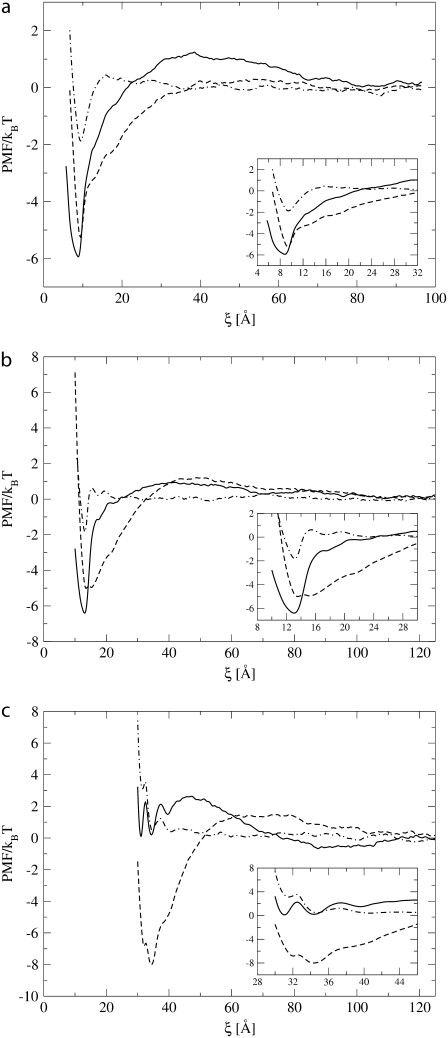
The PMFs as a function of the distance between the centers of mass of the protein pairs of size N_p = 4, N_p = 7, and N_p = 43 are shown in Fig. 3, a–c, for proteins with negative, Δd = −10 Å; negligible, Δd = 1 Å; and positive, Δd = 8 Å, hydrophobic mismatch conditions, respectively.

FIGURE 3.

Potential of mean force as a function of the distance between two proteins of size N_p = 4 (a), N_p = 7 (b), and N_p = 43 (c) with negative (dashed line), zero (dot-dashed line), and positive (solid line) mismatch.

No mismatch

For a protein pair with zero or negligible hydrophobic mismatch (dot-dashed lines), the PMF is essentially zero, except at short distances between the two proteins, which means that there are no long-range lipid-mediated interactions between the two proteins. At short distance, three minima occur in the free energy profiles of the protein pairs of size N_p = 7 and N_p = 43. These minima are at distances ξ = D, ξ = D + 0.7 R_c, and ξ = D + 1.4 R_c (where D is the protein diameter). As 0.7 R_c is approximately the diameter of a coarse-grained lipid bead, we can, based on geometric arguments, assign these oscillations in the PMF to the free energy needed to remove the lipids that are in between the two proteins.

Interestingly, the number of minima depends on the diameter of the protein. For the protein pair of size N_p = 4 there is only one minimum, at position D, corresponding with the physical dimer configuration. Our results suggest that the bigger the diameter of the protein, the more difficult it becomes to expel the lipid beads from between the two proteins and to form a physical dimer. This effect is comparable with the two-dimensional crystallization of molecules located between two parallel surfaces (48). For the protein pair of size N_p = 43, the physical dimer configuration is very unstable and does not correspond to the absolute minimum of the free energy curve, as is instead the case for proteins of size N_p = 4 and N_p = 7, and a rather high free energy barrier (∼3 k_BT) needs to be crossed to go from the configuration with one lipid in between to the physical dimer. From this analysis of the PMF curves we can conclude that two proteins with zero mismatch diffuse randomly in the lipid bilayer and that, when they approach each other, they temporarily associate, but only if their size is sufficiently small (N_p = 4 and N_p = 7). However, the free energy in this dimer configuration is not sufficiently low to stabilize the dimer against thermal fluctuations (see also Fig. 2 b).

Negative mismatch

Proteins with negative mismatch interact with each other over a broad range of distances, with their PMFs (dashed lines) displaying a repulsive barrier at intermediate interprotein distances, followed by a broad and deep attractive minimum as the proteins get closer (but still at several R_c apart). At this point, it is important to recall that there are no long-range interactions explicitly included in the direct protein-protein interaction potential. In fact, all interactions are short-range and repulsive. Comparison with the case of zero hydrophobic mismatch shows that the long-range attractive interactions observed in the PMF are therefore induced solely by the hydrophobic mismatch. The negative mismatch causes a perturbation of the lipid bilayer. If the proteins are close to each other, the net perturbation of the surrounding lipids is less than the corresponding perturbation when the proteins are far from each other, explaining the long-range attractions between the proteins. Interestingly, the deformation of the lipid membrane at intermediate distances between the proteins results in an unfavorable configuration. In Hydrophilic Shielding, we discuss the nature of these interactions in more detail as we introduce the concept of hydrophilic shielding. The height of the repulsive barrier increases slightly with increasing protein diameter (≈0.2 k_BT for N_p = 4, ≈1 k_BT for N_p = 7, and ≈1.5 k_BT for N_p = 43) while the range of the attractive interaction does not depend significantly on the protein diameter. This also holds for the range of the repulsive interactions.

The PMF of the protein pair of size N_p = 4 is characterized by one absolute minimum of −5.2 k_BT corresponding to the dimer configuration, and two “shoulders” at interprotein distance of D + 0.7 R_c and D + 1.4R_c corresponding to two proteins with respectively one and two lipids in between. The PMF of the protein pair of size N_p = 7 displays two local minima of value ≈−5.0 k_BT. The first one corresponds to the physical dimer configuration. The second one most likely corresponds to the two proteins with one lipid bead in between, although this lipid bead cannot be situated on the axis linking the two centers of mass of the proteins because the distance between the two minima is much shorter than 0.7 R_c. The separation of these two minima by only a small barrier (≈0.1 k_BT) and the broadness of the attractive region of the PMF reflect the instability of the physical dimer. Thermal fluctuations are sufficient to allow lipid beads to slip in between the proteins, thus breaking the physical dimer. The same considerations hold for the protein pair of size N_p = 43, with the only difference that the absolute minimum (−8.0 k_BT) no longer corresponds to the physical dimer configuration and the physical dimer configuration (−6.8 k_BT) is unstable.

To summarize, our results show that, due to lipid-mediated interactions, two proteins with negative mismatch experience a short- and intermediate-range strong attraction and a soft repulsion at larger interprotein distance.

Positive mismatch

In the case of positive mismatch, the PMFs (solid lines) show that the protein pairs of size N_p = 4 and N_p = 7 behave in a completely different manner than the protein pair of size N_p = 43. The PMFs of the protein pairs of size N_p = 4 and N_p = 7 are both characterized by a long-range weak repulsion with a barrier of ∼1.0 k_BT, followed by an intermediate- and short-range strong attraction toward a very stable physical dimer. The width, relative to the protein diameter, of the attractive part of the PMF decreases as the protein diameter increases. The physical dimer formed by the protein pair of size N_p = 7 is slightly more stable than the dimer of the protein pair of size N_p = 4, because a higher energy barrier has to be crossed to go from the dimer configuration to the configuration of two proteins with one lipid in between. Furthermore, the minimum corresponding to the physical dimer of the protein pair of size N_p = 7 is slightly deeper (−6.5 k_BT) than the corresponding minimum for the protein pair of size N_p = 4.

The PMF curve of the protein pair of size N_p = 43 reveals a completely different behavior. A broad attractive region appears at interprotein distances between 88 and 105 Å, with a depth of ∼−0.6 k_BT. This long distance attraction is also present for the protein pair of size N_p = 4, albeit much narrower and shallower. A high repulsive energy barrier is present at interprotein distances between 47 and 88 Å, followed by an attraction as the distance between the proteins further decreases. The formation of the physical dimer is clearly hindered by the removing of the last two lipids in between the proteins, shown by the three minima at D and D + 0.7 R_c and D + 1.4 R_c. Hence, three energy barriers have to be crossed to reach the physical dimer configuration; first, the barrier of height 3.2 k_BT, separating the minimum at long distance from the configuration with two lipids in between the proteins, then the barrier between D + 1.4 R_c and D + 0.7 R_c of height 0.6 k_BT, and finally the barrier between D + 0.7 R_c and D, of height 2.0 k_BT. The three barriers to be crossed for dissociation are 2.2 k_BT, 2.0 k_BT, and 1.2 k_BT, respectively. As these barriers are relatively easy to cross, none of the free energy minima in this region is stable.

From these results, we can conclude that the interaction of a protein pair with positive mismatch strongly depend on the diameter of the proteins. Proteins that are rather small (N_p = 4, N_p = 7) repel each other slightly before forming a very stable physical dimer. Larger proteins (N_p = 43) are slightly attracted when they are relatively far from each other toward an interprotein distance of 88 Å (i.e., two times the diameter), but a short-distance repulsive interaction hinders the formation of the physical dimer configuration.

DISCUSSION OF PREVIOUS MODELS

The free energy profiles shown in Fig. 3 clearly indicate the presence of lipid-mediated protein-protein interactions, whose characteristics depend on the degree of mismatch and on the protein diameter. In an attempt to understand the relations among the nature of the protein-protein interactions, the mismatch condition, and the protein diameter, it is instructive to compare our results with those obtained by other theoretical models.

Lagüe et al. (24,25) applied the hypernetted chain integral equation formalism for liquids to different lipid bilayers and studied the lipid-mediated interactions between two hard repulsive cylinders. Their results show that a cylindrical inclusion induces a perturbation of the average radial lipid density over a distance of ∼30 Å from the surface of the inclusion and that the characteristics of this perturbation depend on the type of lipid bilayer and on the diameter of the inclusion. For their model of a DMPC lipid bilayer, which is what our model represents, these authors observed a depletion layer close to the inclusion, where the lipid density is lower than in the bulk, followed by a lipid-enriched region. The density in the depleted region decreases with increasing inclusion diameter. In the enriched region, the density increases with increasing inclusion diameter. However, while the relative range of the depletion decreases with increasing inclusion diameter, the absolute range of the perturbation remains the same. By calculating the PMF as a function of the distance between the two inclusions, these authors find that two inclusions first experience a repulsive interaction followed by an attraction at closer distances and that it is the perturbation of the average hydrocarbon density around the proteins that gives rise to lipid-mediated protein interactions. Although in our simulations the absolute number of lipid beads as a function of the distance from the protein surface shows the presence of a depletion layer, we did not observe a decrease in lipid density since the membrane thickness around the protein is also changing, resulting in a constant density.

According to the theoretical model of Bohinc et al. (28), which combines elasticity theory with director field theory, the deformation of the lipid bilayer due to embedded rigid proteins showing mismatch induces an increase of the membrane elastic energy. The dimerization of two proteins showing positive or negative mismatch leads to a gain in this elastic free energy. Considering only membrane elastic effects leads to a membrane elastic free energy as a function of the distance between the two proteins which depends on the degree of mismatch, but not on the type of mismatch, i.e., PMF(ξ, Δd) = PMF(ξ, −Δd). The PMF then displays only an intermediate distance attraction, whose range is independent of the degree of mismatch and with a minimum which becomes deeper with increasing mismatch. Including director field theory in the free energy computation leads to long-range interactions, characterized by repulsion-attraction for the case of negative mismatch and only attraction for the case of positive mismatch. The proteins studied by Bohinc et al. (28) have a diameter of 14 Å and the cross-sectional area of their model lipids is 32.5 Ų, hence their results can be compared with our results for N_p = 7 (Fig. 2 b) (although our model DMPC gives an area per lipid of 60.4 Ų (36)). For proteins with negative mismatch and N_p = 7, we also obtain repulsive-attractive interactions. However, according to our simulations, for the case of positive mismatch, the repulsive part, although smaller than in the case of negative mismatch, does not entirely disappear.

Hydrophilic shielding

In this section we interpret and explain the features of the PMF curves shown in Fig. 3 in terms of hydrophobic and hydrophilic interactions. Due to the soft repulsive interactions, whose strength is given by the parameters a_ij in our model, the water beads, the lipids, and the proteins tend to reorganize so that the hydrophobic beads of the proteins and the lipids are shielded from the water beads by the hydrophilic beads of the proteins and the lipid headgroups in the most optimal way. This regrouping is, however, constrained by the internal flexibility of the proteins and the lipids, i.e., by their bond-bending rigidity.

To characterize the degree of screening of the hydrophobic parts of the lipids and the peptides from the polar environment of the solvent, we introduce the concept of hydrophilic shielding. For this purpose, we define the lipid head fraction as the average number of lipid head beads at a given position in the plane of the lipid bilayer in which the protein is embedded, divided by the average number of lipid head beads of a pure bilayer without embedded proteins. The lipid tail fraction is defined in an analogous way for the lipid tail beads. The hydrophilic shielding parameter, defined at every position in the plane of a lipid bilayer, is the ratio of the lipid head fraction and the lipid tail fraction, and it is a measure for the relative number of hydrophilic beads shielding the hydrophobic tail beads from the water at a given position. This parameter is one at sufficient distances from a protein. When the hydrophilic shielding parameter is >1, the density of the lipid heads shielding the lipid tails is higher than in the pure lipid bilayer.

Hydrophilic shielding around one protein

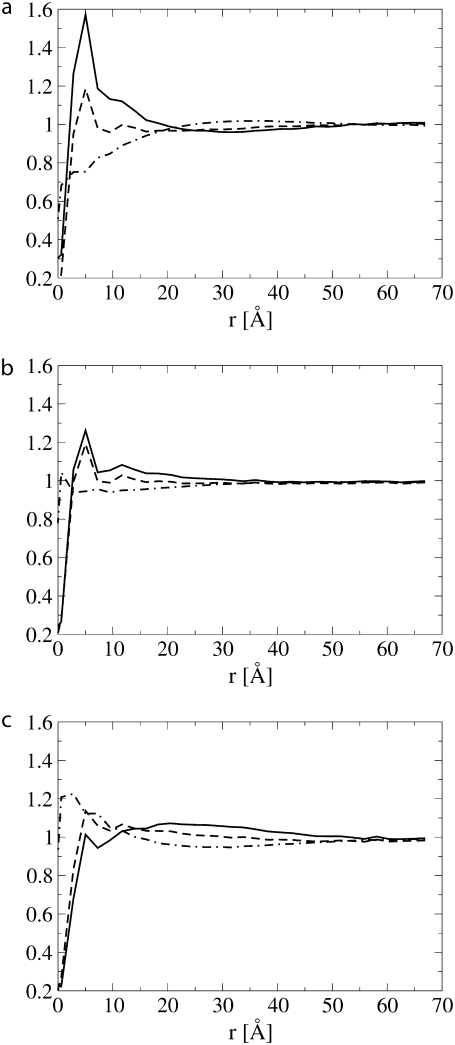
Fig. 4 shows the lipid head and tail fraction and the hydrophilic shielding parameter as a function of the distance from a single protein embedded in the lipid bilayer. Three different proteins were considered, all of size N_p = 43, but with negative (Fig. 4 a), zero (Fig. 4 b), and positive (Fig. 4 c) mismatch. In an unperturbed pure lipid bilayer the lipid head and tail fraction and the hydrophilic shielding parameter are on average one at every point in the bilayer plane. Fig. 4 shows that the presence of a protein perturbs the surrounding lipid organization and indicates how the lipids reorganize around the protein as function of the hydrophobic mismatch.

FIGURE 4.

Lipid tail fraction (dot-dashed line), lipid head fraction (dashed line), and hydrophilic shielding (solid line) as a function of the distance from one protein of size N_p = 43 with negative (a), zero (b), and positive (c) mismatch.

Around a protein with negative mismatch (Fig. 4 a), the lipids reorganize by increasing the density of the lipid heads close to the protein surface, while the lipid tails point away from the protein surface. This region of high lipid head fraction is followed by a region of low lipid head fraction. Because the tails of the lipids close to the protein are pointing away from the protein, the region of low lipid head fraction contains a high lipid tail fraction. This results in a hydrophilic shielding parameter which is high in the vicinity of the protein (up to 1.6 at 5 Å) but which decreases to a minimum value of 0.96 at a distance of 31 Å from the protein surface. The shielding parameter then goes to one at larger distances. Around a protein with positive mismatch (Fig. 4 c), the lipids reorganize in the opposite way. An undershielded region appears in the vicinity of the protein surface because the lipid heads regroup at a certain distance from the protein surface while the lipid tails point in the direction of the protein surface. The undershielded region of the bilayer is followed by a well-shielded region. The hydrophilic shielding parameter reaches a maximum value of 1.07 at a distance of 20 Å, after which it decreases toward one. When the lipids reorganize around a protein with zero mismatch (Fig. 4 b), the lipid heads regroup close to the protein, resulting in a higher shielding in the vicinity of the protein. This effect is, however, smaller than in the case of negative mismatch. The overshielded region is not followed by a large undershielded region and the hydrophilic shielding parameter decays to one at shorter distance from the protein.

The reorganization of the lipids also leads to a change of the lipid bilayer thickness (36) and thus of the structure parameter (49). The lipid tail fraction as a function of the distance from the protein surface shows the same trend as the change in hydrophobic bilayer thickness around the protein as calculated in Venturoli et al. (36). This implies that the reorganization of the lipids around a protein does not result in long-range lipid tail density fluctuations. This was confirmed by our simulations (data not shown).

It is very important to note that the way the lipids reorganize around a protein in an optimal way may also strongly depend on the three-dimensional structure of the protein. Hence, the results presented here are only valid for cylindrical proteins.

Hydrophilic shielding around two proteins

In this section we explain how the lipid reorganization around a protein can determine the nature of the interactions between two or more proteins. When the distance between two proteins embedded in a lipid bilayer is decreased from an initial to a final protein-protein distance, three different scenarios may arise. A first possibility is that the approaching of the two proteins allows for a reorganization of the other components of the system which results in an increase of the hydrophilic shielding. As this is energetically favorable, the free energy curve displays an attractive region over this distance interval, which means that the aggregation process occurs spontaneously. In a second scenario, the position of the proteins within the distance interval does not influence the capability of the system to shield its hydrophobic regions. The total shielding then remains constant, and this is reflected by a flat free energy profile over the distance interval and thus in an absence of lipid-mediated protein-protein interactions. The third possibility is that, as the proteins get closer, the lipids cannot reorganize to optimize the hydrophilic shielding. This then results in a repulsive interaction, which is reflected in the PMF by a barrier in the considered distance interval.

In the following part of this section, we compare the calculated shielding parameter profiles against these possibilities.

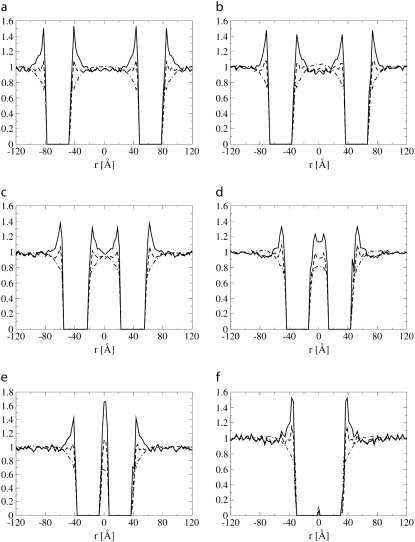
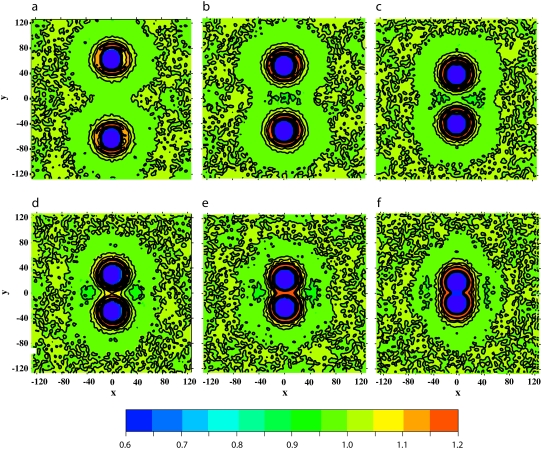
Negative mismatch. Fig. 5 shows the lipid head and tail fraction and the hydrophilic shielding parameter along the axis linking the centers of mass of two proteins of size N_p = 43 and with negative mismatch, at different distances from each other: ξ = 126 Å (a), 103 Å (b), 78 Å (c), 58 Å (d), 45 Å (e), and 32 Å (f). Fig. 6 shows, for the same systems as in Fig. 5, the hydrophilic shielding parameter profile in the bilayer plane. From Fig. 5 a it can be observed that when the two proteins are sufficiently far apart, the lipids regroup around each protein in a similar way as if each protein were isolated, i.e., several lipid heads cluster close to the protein surface while the lipid tails point away from the protein surface (compare with Fig. 4 a). As the interprotein distance decreases (Fig. 5 b), the hydrophilic shielding between the two proteins becomes <1, showing that the lipids cannot rearrange to ensure an optimal shielding. Indeed, a badly shielded hydrophilic region appears (Fig. 6 b) between the proteins where the hydrophobic tails of the lipids pointing away from one protein meet the lipid tails pointing away from the second protein. Thus, the PMF between ξ = 126 Å and ξ = 103 Å is repulsive. Further decrease of the interprotein distance to ξ = 78 Å involves an important reorganization of the surrounding lipids, whose tails now point away from both proteins, toward the notches in the direction perpendicular to the axis linking the two proteins. This results in an increase of the hydrophilic shielding in the region between the proteins (Figs. 5 c and 6 c). Because the lipid heads regroup close to, and the lipid tails point away from, a protein with negative mismatch, a further approach of the proteins increases the interprotein lipid head fraction and decreases the interprotein lipid tail fraction, and hence increases the interprotein hydrophilic shielding (Fig. 5, d and e, and Fig. 6, d and e). Thus, the proteins spontaneously aggregate, and the PMF is attractive over this distance interval. Finally, the two proteins form a stable physical dimer (Figs. 5 f and 6 f), which allows the most optimal regrouping of the lipids with respect to the hydrophilic shielding, and hence corresponds with the absolute minimum of the PMF curve. The absolute minimum in the PMF is relatively broad compared to the corresponding minima of proteins with positive mismatch because the well shielded region attracts the surrounding lipids.

FIGURE 5.

Lipid head (dashed line), tail (dot-dashed line) fraction, and hydrophilic shielding parameter (solid line) along the axis linking the centers of mass of two proteins of size N_p = 43 embedded in the lipid bilayer with negative mismatch at different interprotein distances: ξ = 126 Å (a), 103 Å (b), 78 Å (c), 58 Å (d), 45 Å (e), and 32 Å (f).

FIGURE 6.

Hydrophilic shielding parameter in the plane of the bilayer in which two proteins of size N_p = 43 and with negative mismatch are embedded at different interprotein distances: ξ = 126 Å (a), 103 Å (b), 78 Å (c), 58 Å (d), 45 Å (e), and 32 Å (f).

With this mechanism for protein interactions in mind, one can now make reasonable predictions about many-protein interactions. The aggregation of a third protein to a protein dimer is unlikely in the direction perpendicular to the interprotein axis (Fig. 6 f) because of the unfavorable interaction with the undershielded regions in the notches of the physical dimer. It is thus more likely that the third protein will approach the dimer along the direction parallel to the interprotein axis. However, because the undershielded notches are energetically unfavorable, the trimer should reorganize such that the number of notches becomes minimal. Hence, the optimal final configuration is triangular rather than linear. These predictions are supported by preliminary simulation studies.

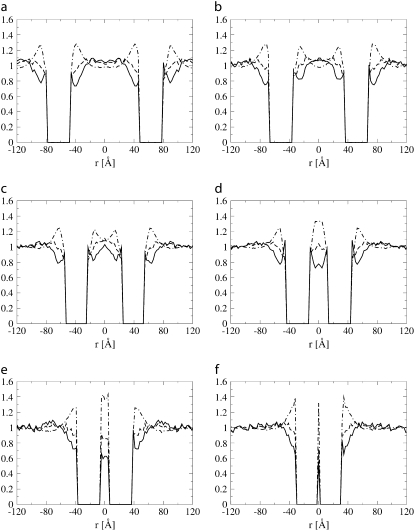
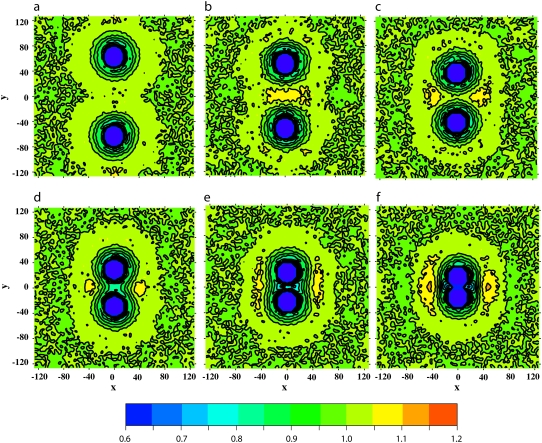
Positive mismatch. Fig. 7 shows the lipid head and tail fraction and the hydrophilic shielding parameter along the axis linking the centers of mass of two proteins of size N_p = 43 and with positive mismatch, at different distances from each other: ξ = 126 Å (a), 103 Å (b), 78 Å (c), 58 Å (d), 45 Å (e), and 32 Å (f). For the same system, the average hydrophilic shielding parameter in the bilayer plane is shown in Fig. 8. Fig. 7 a shows that at large protein separations the lipids reorganize around each protein in a way similar to the case of one isolated protein of the same size and mismatch (Fig. 4 c), i.e., by regrouping their heads at a certain distance of, and with the tails pointing toward, the protein surface. When the proteins are at a distance of 103 Å (Fig. 7 b), a well-shielded region forms in between the proteins, due to the interaction of the lipid heads regrouped at a certain distance from both proteins. This explains the attractive region in the PMF between ξ = 126 Å and ξ = 103 Å. A further approach of the proteins to a distance of ξ = 78 Å involves an important reorganization of the interprotein lipids, whose heads now regroup in the notches between the proteins, while their tails point toward the interprotein region depleted of lipid headgroups (Figs. 7 c and 8 c). Hence, further approach of the proteins decreases the interprotein lipid head fraction and increases the interprotein lipid tail fraction, thus decreasing the interprotein hydrophilic shielding (Fig. 7, d and e, and Fig. 8, d and e). As a result, the protein-protein interaction is strongly repulsive over the corresponding distance interval. However, once the repulsive barrier is crossed, the proteins form a physical dimer which allows an optimal regrouping of the lipids with respect to hydrophilic shielding (Fig. 8 f), and hence corresponds with the absolute minimum of the PMF curve. The stability of the physical dimer is discussed in Influence of the Protein Diameter.

FIGURE 7.

Lipid head (dashed line) and tail (dot-dashed line) fraction and hydrophilic shielding parameter (solid line) along the axis linking the centers of mass of two proteins of size N_p = 43 embedded in the lipid bilayer with positive mismatch, at different interprotein distances: ξ = 126 Å (a), 103 Å (b), 78 Å (c), 58 Å (d), 45 Å (e), and 32 Å (f).

FIGURE 8.

Hydrophilic shielding parameter in the plane of the bilayer in which two proteins of size N_p = 43 and with positive mismatch are embedded, at different interprotein distances: ξ = 126 Å (a), 103 Å (b), 78 Å (c), 58 Å (d), 45 Å (e), and 32 Å (f).

In Hydrophilic Shielding Around One Protein, we noted that the lipid tail fraction follows the same trend as the hydrophobic bilayer thickness. Therefore, the values of the lipid tail fraction between two proteins at different distance, as shown in Figs. 5 and 7, also give us a measure of the corresponding bilayer hydrophobic thickness.

Influence of the protein diameter

When a protein with a small diameter, N_p = 4 or 7, subjected to positive mismatch is embedded in the bilayer, the mismatch is compensated for with a bilayer deformation as well as by a tilt of the protein, so that its hydrophobic section is shielded from the water (36,50,51). Hence, the thickening of the lipid bilayer is not as pronounced as in the case of a protein with a larger diameter (N_p = 43), for which the tilting is instead very small. The different mechanisms of hydrophilic shielding, namely the thickening of the lipid bilayer or the tilt, result in different protein-protein interactions. This explains the difference between the free energy curve for proteins with positive mismatch and of size N_p = 43 on the one hand and the free energy curve for proteins with size N_p = 4 or 7 on the other hand.

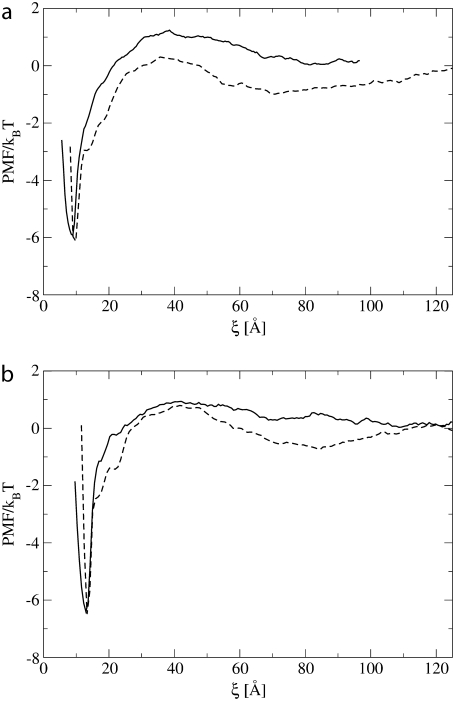
To investigate the influence of tilting on the PMF, we computed the PMF for the protein pair of size N_p = 4 and the protein pair of N_p = 7 with positive mismatch condition, with the additional constraint that both proteins are not allowed to tilt, and hence remain parallel to the bilayer normal. In Fig. 9, we compare the resulting PMFs with the PMFs obtained when the proteins are free to tilt. For both the protein pairs of size N_p = 4 and N_p = 7, the PMF now shows a shallow and rather broad minimum at large protein separation. At intermediate separation a repulsive region appears, which is followed by two metastable states and a deep and narrow minimum, corresponding with the two proteins with respectively two and one lipid bead in between and with the physical dimer configuration. A comparison of the PMF obtained when the proteins are not allowed to tilt (Fig. 9), with the PMF for the protein pair of size N_p = 43 and with positive mismatch (Fig. 3 c), shows that both have the same characteristics at intermediate and long distance, while they differ at short distance. Our results indicate that, in the case of positive mismatch, the long-range interaction between two proteins is influenced by the degree of protein tilt.

FIGURE 9.

Comparison of the potential of mean force as function of the distance between two proteins of size N_p = 4 (a) and N_p = 7 (b) with positive mismatch in the case when the proteins are allowed (solid line) or not allowed (dashed line) to tilt.

The different shape and depth of the PMF minimum at short distance for the large protein pair (N_p = 43) and the small ones (N_p = 4, 7) at positive mismatch conditions can be explained by looking at Fig. 8, e and f. Indeed, as shown in this figure, the dimerization of two proteins with size N_p = 43 reduces the number of badly shielded lipids between the two proteins, but induces two new regions of badly shielded lipids in the notches of the eight-shaped configuration of the dimer. Hence, the dimerization does not bring a significant improvement of the overall hydrophilic shielding. However, when two proteins with a much smaller diameter (N_p = 4, 7) aggregate, the badly shielded region in between them disappears without the formation of new undershielded regions. This difference can be attributed to the different curvature of the small and large proteins. When two large proteins, which have a pronounced curvature, come in close contact, they form an eight-shaped interface with the lipids. This shape creates the very unfavorable undershielded notches, which are not present in the case of smaller proteins, whose physical dimer has a more rectangular shape.

COMPARISON WITH RELEVANT EXPERIMENTAL OBSERVATIONS

The presence of specific lipid-mediated protein-protein interactions, which depend on the biophysical properties of the lipid bilayer, on the protein diameter, or more generally, on the three-dimensional structure of the protein, and on the type and the degree of mismatch, could have several consequences on the stability and the size of protein oligomers, as discussed in the introduction of this article. In this section we will attempt to link our simulation results to relevant experimental observations. In making this comparison we have to assume that our model gives a reasonable description of the experimental system. Whereas we can make a very reasonable estimate of the effective sizes of the molecules, we have to assume that the specific nature of, for example, electrostatic interactions or hydrogen bonds, is less important for a general understanding of the protein-protein interactions.

Gramicidin A (D = 18 Å, d_P = 22 Å) was observed to spontaneously form spherical clusters containing 50–100 proteins when embedded in a DMPC lipid bilayer in the fluid phase (d_L = 28 Å) (52). For this system there is a negative hydrophobic mismatch of Δd = −6 Å. Our results show that, for proteins with negative mismatch, the nature of the PMF does not significantly depend on the protein diameter. Hence, for the case of negative mismatch our model also predicts clustering of the proteins (i.e., the short-range interaction remains attractive as the cluster size grows).

The aggregation behavior of WALP-23 peptides (D = 10 Å, d_P=33 Å) has been investigated in three bilayers with a different hydrophobic thickness: C14:1c-PC (d_L = 23 Å), C18:1c-PC (d_L = 30 Å), and C22:1c-PC (d_L = 37 Å) (1). When embedded in the C18:1c-PC bilayer (Δd = 3 Å), the WALP-23 peptides diffuse randomly in the bilayer without forming stable oligomers. However, aggregation of the WALP-23 peptides was observed when inserted in the C14:1c-PC (Δd = 10 Å) bilayer or in the C22:1c-PC (Δd = −4 Å) bilayer. Accordingly, for proteins with size N_p = 7, our model predicts the attraction between proteins with both positive and negative mismatch conditions, and free diffusion of proteins with negligible mismatch.

Our simulation results support the hypothesis that hydrophobic interactions could influence the protein organization in the bilayer. Indeed, our simulations show that, e.g., for the case of two proteins with positive mismatch, the height of the intermediate range repulsive barrier increases with increasing protein diameter, while the short-range attractive minimum deepens with decreasing protein diameter. Hence, it is likely that several smaller proteins could aggregate and form oligomers of increasing size, until the clusters reach a critical size, after which the interactions between the oligomers become dominantly repulsive. Relevant experiments (14) have been performed with bacteriorhodopsin (D = 45 Å, d_P = 34 Å). Bacteriorhodopsins inserted in bilayers with different hydrophobic thickness, namely lecithins with acyl chains ranging from di-10:0 to di-24:1, were observed to remain dispersed when the bilayer hydrophobic region was <4 Å thicker or >10 Å thinner than the bacteriorhodopsin hydrophobic length. Aggregation of bacteriorhodopsin was observed when the hydrophobic mismatch was >10 Å or <−4 Å. A related experiment (16) showed organization of bacteriorhodopsin in big clusters when embedded in a bilayer with hydrophobic mismatch Δd = −5 Å, no aggregation for Δd = −2 to 2 Å, and the formation of small oligomers for Δd = 5–10 Å, with the size of the oligomers slightly increasing with increasing positive mismatch. Considering that the diameter of rhodopsin is comparable to the diameter of our model protein with N_p = 43, our results for this protein in the case of negative mismatch also predict clustering. In the case of positive mismatch no aggregation is observed, unless the hydrophobic mismatch is strong. Indeed, strong positive mismatch induces an increase in tilt, which promotes aggregation.

CONCLUSION

In this article we presented a simulation study of a mesoscopic model of a hydrated DMPC bilayer with embedded protein pairs of different diameters and at different mismatch conditions. The only direct interactions considered in our model are the short-range soft repulsive interactions between different bead-types, representing hydrophobic and hydrophilic forces, and the internal rigidity of the proteins and the lipids. Despite its simplicity, our model provides a framework to gain insight into the mechanism by which hydrophobic and hydrophilic interactions induce a reorganization of all the components of the system (water, lipids, and proteins) after the insertion in the bilayer of one or more proteins. Specific long-range attractive and repulsive protein-protein interactions were found to spontaneously emerge during the dynamic reorganization of the components of the system to improve the hydrophilic shielding of the hydrophobic parts of the proteins and the lipids. The nature of the protein-protein interactions was quantitatively described by calculating the potential of mean force as a function of the distance between two proteins and it was found to depend on the degree of hydrophobic mismatch and on the size of the proteins.