Analysis of Phosphatidylinositol-4,5-Bisphosphate Signaling in Cerebellar Purkinje Spines

Abstract

A 3D model was developed and used to explore dynamics of phosphatidylinositol-4,5-bisphosphate (PIP2) signaling in cerebellar Purkinje neurons. Long-term depression in Purkinje neurons depends on coincidence detection of climbing fiber stimulus evoking extracellular calcium flux into the cell and parallel fiber stimulus evoking inositol-1,4,5-trisphosphate (IP3)-meditated calcium release from the endoplasmic reticulum. Experimental evidence shows that large concentrations of IP3 are required for calcium release. This study uses computational analysis to explore how the Purkinje cell provides sufficient PIP2 to produce large amounts of IP3. Results indicate that baseline PIP2 concentration levels in the plasma membrane are inadequate, even if the model allows for PIP2 replenishment by lateral diffusion from neighboring dendrite membrane. Lateral diffusion analysis indicates apparent anomalous diffusion of PIP2 in the spiny dendrite membrane, due to restricted diffusion through spine necks. Stimulated PIP2 synthesis and elevated spine PIP2 mediated by a local sequestering protein were explored as candidate mechanisms to supply sufficient PIP2. Stimulated synthesis can indeed lead to high IP3 amplitude of long duration; local sequestration produces high IP3 amplitude, but of short duration. Simulation results indicate that local sequestration could explain the experimentally observed finely tuned timing between parallel fiber and climbing fiber activation.

INTRODUCTION

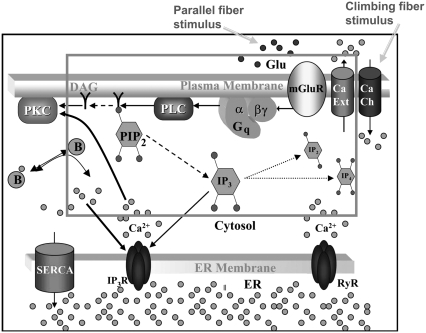
Phosphatidylinositol-4,5-bisphosphate (PIP2) is the most common doubly phosphorylated phosphoinositide in the plasma membrane of mammalian cells (1). It is a central member of the phosphoinositide pathway, and is involved in cell migration (2), signal transduction (3), actin cytoskeleton mobilization (4), endocytosis and exocytosis (5), and ion channel regulation (6,7). Hydrolysis of PIP2 by phospholipase C (PLC) yields diacylglycerol (DAG) and inositol-1,4,5-trisphosphate (IP3) that activate protein kinase C (PKC) and calcium mobilization from endoplasmic reticulum (ER) stores, respectively (8) (Fig. 1). This pathway is particularly important in Purkinje cells of the cerebellum, because of its role in neuronal integration and synaptic plasticity. The major type of synaptic plasticity in the cerebellum that may underlie some forms of motor learning is long-term depression (LTD) (9). Long-term depression in Purkinje cells was proposed in the 1960s and 1970s by Marr and Albus (10,11) and shown experimentally in the 1980s by Ito et al. (12). Other cell types achieve long-term depression via NMDA receptors, but NMDA receptors are not present in the mature Purkinje cell (13). Instead, the Purkinje cell mediates long-term depression via concurrent stimulation by multiple parallel fibers and a single climbing fiber. Coincident activation of the Purkinje cell by parallel fibers and a climbing fiber leads to an increase in cellular IP3 levels at the same time that voltage-gated calcium channels are opened in the plasma membrane (12). Calcium that enters the cytosol through these voltage-gated channels binds the IP3 receptor on the membrane of the endoplasmic reticulum, modulating the open probability of the receptor (14). IP3 also binds its receptor, thus synergizing a large flux of calcium from ER stores into the cytosol. Cytosolic calcium, along with DAG, activates protein kinase C (PKC) (15). PKC phosphorylates submembrane substrates that ultimately internalize AMPA receptors from the plasma membrane. This internalization of AMPA receptors depresses the response of the Purkinje cell to stimulus by parallel fibers (16).

FIGURE 1.

Membrane and cytoplasmic events involved in parallel fiber-stimulated calcium release in the Purkinje neuron spine. On PF stimulation of the Purkinje neuron spine, the neurotransmitter Glu binds its G-protein coupled glutamatergic metabotropic receptor (mGluR) on the spine surface membrane. 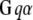separates from its partner 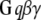and activates the enzyme PLC. PLC cleaves the membrane phospholipid PIP2 to give two products: DAG that remains in the membrane, diffuses away and activates PKC; and IP3 that diffuses away in the cytosol to bind its calcium channel-coupled receptor on the ER membrane. IP3 in the cytoplasm is rapidly degraded to IP2 and IP4. Calcium is released from ER stores into the cytoplasm and also activates PKC. Calcium in the cytoplasm is sequestered and dissociated from various buffers (B). Some calcium is pumped back into the ER by SARCO/endoplasmic reticulum calcium-ATPase (SERCA) on the ER membrane. Some of the remaining calcium is pumped out of the cell by a calcium exchanger; calcium also may enter the cell via a calcium channel. The highlighted rectangular area roughly encloses the portion of the diagram included in the 1D and 3D Virtual Cell models described in this study: cleavage of PIP2 to form IP3 and DAG on stimulation of the Purkinje neuron spine by PF via the neurotransmitter glutamate. The compartmental model in this study then examines the consequences of the patterns of IP3 on the ability of the spine to generate a calcium response.

Insult to the cerebellum usually damages or obliterates Purkinje cells, thus disrupting neuronal integration and long-term depression. As a result, motor coordination, motor learning, and conditioned reflexes are all compromised. The resulting lack of motor coordination is medically termed ataxia (17). Cerebellar ataxia affects ∼150,000 Americans; a handful of more common hereditary ataxias are linked in some way to the phosphoinositide pathway. The most direct link between hereditary ataxias and the phosphoinositide pathway seems to involve spinocerebellar ataxia 15 and 16 (SCA15 and SCA16). Families with these two classes of ataxia possess mutations in the gene that codes for IP3R1, the IP3 receptor isoform that is enriched in the cerebellum (18,19). Furthermore, autopsies of human brains from individuals with various forms of ataxia show reduced immunostaining of IP3R1 in the cerebellum (20,21). In addition, mice with mutations in the gene that encodes IP3R1 exhibit an ataxic phenotype identical to that in SCA15 individuals (18). Pathophysiology involving the IP3R1 receptor provides a direct connection between ataxia and the phosphoinositide signaling pathway.

Our laboratory previously published a compartmental model (i.e., a model based on ordinary differential equations) that focuses on calcium signaling in the Purkinje cell, taking into account increased abundance and decreased sensitivity of the Purkinje cell IP3 receptor to IP3 relative to other cell types. In that model, we investigated the influence of Purkinje cell geometry and biochemistry on IP3 and calcium transients (22). We included tetanic production of IP3, calcium influx resulting from depolarization, and the downstream effects leading to calcium release. The model was able to recapitulate experimental measurements on the localized release of calcium in a single spine by multiple synaptic activations of the metabotropic glutamate receptor, which is mediated by large local IP3 signals (23,24). The model was also able to reproduce and elucidate the experimentally observed supralinear calcium response when both calcium influx, mediated by climbing fiber (CF) activation, and calcium release from the ER, mediated by parallel fiber (PF) activation, are triggered together (25). But we did not address the question of where sufficient PIP2 comes from to produce the large levels of IP3 required for these mechanisms. In this study, we present a 3D spatial model that explores the upstream events involving phosphoinositide turnover leading to IP3 production, explicitly defining the interactions among phosphatidylinositol (PI), phosphatidylinositol-4-phosphate (PIP), PIP2, and PLC, as well as IP3 in Purkinje cells. In addition, we carried out simulations in an adapted version of the compartmental model to study the dependence of calcium transients on the shape and amplitude of the IP3 signals that were outputs from our 3D spatial models.

Our objective was to develop a physiological model of PIP2 signaling in the Purkinje cell to study the cellular mechanisms leading to neuronal integration and long-term depression in this cell type. Previously, Xu et al. (26) investigated the upstream events leading to IP3 production in N1E-115 neuroblastoma cells, and explored hypotheses of sources of sufficient PIP2 in this cell type. We draw on parameters in this previous set of experiments and the resultant model from these neuronal cells to develop our 3D spatial model of PIP2 signaling in the Purkinje neuron. Simulation results indicate that basal levels of free PIP2 in the internal layer of the plasma membrane are not sufficient to produce the required IP3. We set out to explore the feasibility of different mechanisms for the source of PIP2 to produce enough IP3. The IP3 mechanisms that we explored are: lateral diffusion of PIP2 into the spine from the neighboring dendrite membrane; stimulated synthesis of PIP2 during synaptic activation; and locally high concentrations of PIP2 at the synapse, possibly via a PIP2 sequestering protein.

MODEL FEATURES

We created 3D models of PIP2 signaling in cerebellar Purkinje spines using the Virtual Cell software (http://www.vcell.org) (27,28). The models consist of parameters (Table 1) and equations based largely on experimental data for neuronal cells and Purkinje neurons, as well as previous modeling efforts. The 3D models described here and the previously published models that are referred to in this study are all accessible via the Virtual Cell modeling database at http://www.vcell.org.

TABLE 1.

Parameter and initial condition values used in 3D simulations

Parameter	Description	Value	Comments
IP3_basal	Basal IP3 concentration	0.16 μm	(30)
k_PIP2hyd	Rate of PIP2 hydrolysis by PLC_act_PM	1.188 s−1	Appropriate for IP3 production
kBasalSynPIP	Rate of basal synthesis of PIP	0.0015 s−1	Similar to Xu et al. (26)
kBasalSynPIP2	Rate of basal synthesis of PIP2	0.045 s−1	Similar to Xu et al. (26)
Kf	Forward rate of PIP2 binding to sink protein	0.003 s−1	Appropriate for IP3 production
KfPLCact	Forward rate of PLC activation	10 s−1	Appropriate for PIP2 hydrolysis
kIP3deg	IP3 degradation rate	0.14 s−1	(30)
Kr	Reverse rate of PIP2 binding to sink protein	1 s−1	Appropriate for IP3 production
krPLCact	Reverse rate of PLC activation	2 s−1	Appropriate for PIP2 hydrolysis
kStimSynPIP	Rate of stimulated synthesis of PIP	3 s−1	Appropriate for IP3 production
kStimSynPIP2	Rate of stimulated synthesis of PIP2	150 s−1	Appropriate for IP3 production
PIP_basal	Basal PIP concentration	2857 mol/μm2	(26)
PIP2_basal	Basal PIP2 concentration	4000 mol/μm2	(26)
PIP2syndecay	Decay rate factor for PIP2 synthesis	0.8 s	Appropriate for PIP2 synthesis
PIPsyndecay	Decay rate factor for PIP synthesis	0.8 s	Appropriate for PIP synthesis
stimdecay	Decay rate factor for PLC_act_PM	0.8 s	Appropriate for PIP2 hydrolysis
τ0	Time at which stimulation is introduced	0.1 s
τPIP2syn	Time at which stimulation is introduced	0.1 s
τPIPsyn	Time at which stimulation is introduced	0.1 s
DAG_PM_init	Initial DAG concentration	2000 mol/μm2	Model from Xu et al. (26)
IP3_Cyt_init	Initial IP3 concentration	0.16 μm	(30)
PI_PM_init	Initial PI concentration	142,857 mol/μm2	(30)
PIP_PM_init	Initial PIP concentration	2857 mol/μm2	(30)
PIP2_bound_PM_init	Initial amount of sink protein bound to PIP2	36,003 mol/μm2	Appropriate for IP3 production
PIP2_PM_init	Initial PIP2 concentration	4000 mol/μm2	(26)
PIP2Sink_PM_init	Initial amount of PIP2 sink protein	2997 mol/μm2	Appropriate for IP3 production
PLC_act_PM_init	Initial concentration of activated PLC	0 mol/μm2	(26)
PLC_PM_init	Initial concentration of inactive PLC	100 mol/μm2	(26)

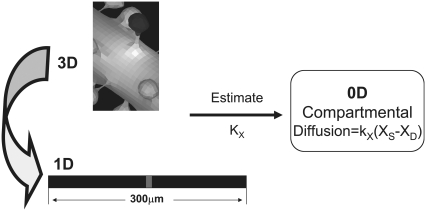
Spatial and compartmental models have their respective virtues. Spatial models require a geometry, whether a constructed analytical geometry or a geometry derived from experiment, and can be implemented in 1D, 2D, or 3D. Diffusion within a spatial model is treated explicitly. Compartmental models attempt to abstract the geometrical features by accounting for compartment volumes and surface areas and consider each species to be uniformly distributed within each compartment (i.e., rapid diffusion). In compartmental models, diffusion of molecules or species from one cellular region to another can be modeled implicitly via a rate equation such as

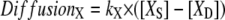(1)

as shown in Fig. 2, where [X_S] and [X_D] represent the concentrations of the various diffusible species, X (such as IP3, PIP2, Ca²⁺, calcium buffers, and so on), in the spine and adjacent dendrite, respectively. Fig. 2 shows the three geometrical models used in this study: 3D, 1D, and 0D. For the 1D and the nonspatial 0D geometries, average values (calculated in Virtual Cell from the experimentally derived geometry) or values that fall in ranges reported in literature (29) can be used for spine head radii and spine neck lengths and radii (Table 2) to derive the appropriate parameter k_X in Eq. 1. Simulations run most efficiently with 0D compartmental models, permitting a thorough exploration of the sensitivity of the system to various parameters. On the other hand, models with more complex, experimentally derived geometries are required to assess the role of diffusion on both the membrane surface and in the cytosol.

FIGURE 2.

Relationships between 3D, 1D, and 0D models. 3D models consider diffusion in all regions, including on the membrane surface, explicitly. In a 1D geometry (straight line), diffusion down the dendrite can be modeled explicitly within a long linear geometry and diffusion between spine and dendrite is modeled implicitly according to Eq. 1. Various segments of the straight line in 1D can be designated by x coordinates to span a single activated spino-dendritic unit, highlighted in gray in the center of the straight line. The 0D (compartmental) model uses ordinary differential equations to mathematically describe a single spino-dendritic unit where the geometries are taken into account by considering the relative volumes and surface to volume ratios of the spine and dendrite compartments. Again, the diffusion of species between spine and dendrite must be modeled by Eq. 1 and an additional term is also included for the decay of the dendritic species due to the equilibration between the region just under the activated spine and the steady state concentration further way in the dendritic shaft (see Hernjak et al. (22) for full details of the structure of the compartmental model).

TABLE 2.

Additional parameter and initial condition values for 1D simulations

Parameter	Description	Value	Comments
D_DAG	Diffusion coefficient for DAG	10 μm2/s	Similar to D_PIP2
D_IP3	Diffusion coefficient for IP3	283 μm2/s	(64)
D_PI	Diffusion coefficient for PI	10 μm2/s	Adapted from Haugh et al. (33)
D_PIP	Diffusion coefficient for PIP	10 μm2/s	Adapted from Haugh et al. (33)
D_PIP2	Diffusion coefficient for PIP2	10 μm2/s	Adapted from Haugh et al. (33) and Wagner and Tamm (34)
DAGd_PM_init	Initial DAG concentration	2000 mol/μm2	Model from Xu et al. (26)
DAGs_PM_init	Initial DAG concentration	2000 mol/μm2	Model from Xu et al. (26)
IP3d_Cyt_init	Initial IP3 concentration	0.16 μm	(30)
IP3s_Cyt_init	Initial IP3 concentration	0.16 μm	(30)
PId_PM_init	Initial PI concentration	142,857 mol/μm2	(26)
PIP2d_PM_init	Initial PIP2 concentration	4000 mol/μm2	(26)
PIP2s_PM_init	Initial PIP2 concentration	4000 mol/μm2	(26)
PIPd_PM_init	Initial PIP concentration	2857 mol/μm2	(26)
PIPs_PM_init	Initial PIP concentration	2857 mol/μm2	(26)
PIs_PM_init	Initial PI concentration	142,857 mol/μm2	(26)
To fit constructed 3D geometry
L_neck	Spine neck length	0.33 μm	Adapted from Harris and Stevens (29)
n	Spine density	14 μm−1	(29)
r_d	Dendrite radius	0.63 μm
r_neck	Spine neck radius	0.0418 μm	Adapted from Harris and Stevens (29)
r_spine	Spine head radius	0.34 μm	Adapted from Harris and Stevens (29)
stim_PM	Linear description of single spine in 1D	(x < 0.0367)*	Calculated
To fit experimentally derived 3D geometry
l_neck	Spine neck length	0.37 μm	Calculated
n	Spine density	11 μm−1	Calculated
r_d	Dendrite radius	0.6 μm	Calculated
r_neck	Spine neck radius	0.02 μm	Calculated
r_spine	Spine head radius	0.34 μm	Calculated
stim_PM	Linear description of single spine in 1D	(x < 0.0454)*	Calculated

*See ID geometries in “Purkinje ID” located under the user name “Brown” in the Virtual Cell database.

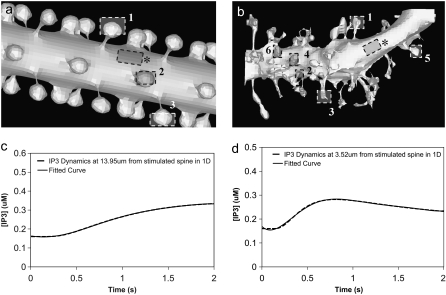
Unless otherwise specified, all the 3D spatial model simulations were implemented using our constructed 3D geometry (Fig. 3 a). The constructed 3D geometry uses a cylinder to represent the dendrite with spherical spines connected to the dendrite via cylindrical necks; we used values for a representative Purkinje neuron dendrite with a diameter of 2 μm, various spine head radii, and spine neck radii and lengths. To compare simulation results with an actual experimentally determined geometry, we reconstructed the image of a Purkinje cell dendrite (Fig. 3 b) in Virtual Cell from a 3D stack of electron micrograph images, kindly provided by Maryanne Martone, Mark Ellisman, and Masako Terada of the National Center for Microscopy and Imaging Research (San Diego, CA).

FIGURE 3.

3D Purkinje dendrite geometries and the derivation of boundary conditions. (a) Constructed geometry with spines that have uniformly spherical heads and narrow, wide, and medium-sized necks; created using values for spine parameters that fall within ranges obtained from Harris and Stevens (29). The dendrite branchlet is 20 μm long and 2 μm in diameter. Spine 1 is used for most of the simulations. Spines 2 and 3 and the patch of dendrite (*) are used in the PIP2 lateral diffusion studies. (b) Experimentally derived geometry with spines of various shapes and sizes that have narrow, wide, and medium-sized necks; reconstructed in Virtual Cell from a 3D stack of electron microscope images courtesy of Maryanne Martone, Mark Ellisman, and Masako Terada of the National Center for Microscopy and Imaging Research (San Diego, CA). Spine 1 is used in most of the simulations with the experimentally derived geometry. Spines 3 and 6 are used in the PIP2 lateral diffusion studies; and spines 2, 4, and 5 are also stimulated in the stimulated PIP2 synthesis model. (c) IP3 concentration time course at 13.95 μm from the stimulated spine in the 1D model that is used to set a time-varying boundary condition for the constructed 3D geometry (13.95 μm represents the edge of the geometry relative to the stimulated spine at the center of the geometry). The central spine is excited 12 times in succession beginning at t = 0.1 s. Each excitation follows the last by 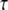= 0.012 s. A fitted curve with equation y = −3E-14x⁶ + 2E-11x⁵ − 4E-09x⁴ + 3E-07x³ + 6E-06x² − 0.0003x + 0.1618 is superimposed on the simulation results. (d) IP3 concentration at ∼3.52 μm from the stimulated spine in the 1D model that is used to set a time-varying boundary condition for the 3D geometry (3.52 μm represents the edge of the geometry relative to the stimulated spine at the center of the geometry). The central spine is excited 12 times in succession beginning at t = 0.1 s. Each excitation follows the last by = 0.012 s. A fitted curve with equation y = 2E-13x⁶ − 2E-10x⁵ + 4E-08x⁴ − 5E-06x³ + 0.0003x² − 0.0047x + 0.1744 is superimposed on the simulation results.

To determine IP3 boundary conditions for the edges of our 3D geometries, we created a 1D model (“Purkinje 1D”) of a long 300 μm dendrite, similar to the approach described by Hernjak et al. (22). To create a 1D model that fit the average constructed geometry, we used values for Purkinje spine head radius and spine neck radius and length that fall within ranges obtained from electron micrograph studies by Harris and Stevens (29). A short length of the 1D geometry (Fig. 2, gray) was set to represent a dendritic segment that spans a single spine compartment where PLC activation and consequently PIP2 hydrolysis (and synthesis or release from the sink protein) occur. To determine the value of this length, we referred to studies by Harris and Stevens (29), which found an average of ∼14 spines/μm of dendrite. Thus, we determined that 1/14 = 0.071 μm represents the equivalent of a dendritic segment that spans one spine in the 1D model fit to the average constructed 3D geometry. In Virtual Cell, an average of ∼11 spines/μm of dendrite was determined for the experimentally derived 3D geometry. Thus, 1/11 = 0.091 μm was used in 1D to represent the equivalent of a dendritic segment that spans the stimulated spine from the experimentally derived 3D geometry. We represented diffusion from each implicit spine compartment into the 1D dendrite according to Eq. 1.

Membrane surfaces are represented in Virtual Cell as the boundary between two volumes. Therefore, to implement membrane events in our 1D model, we needed to input two layers into our Virtual Cell Geometry. The top layer represents the extracellular medium; the bottom layer represents the cytoplasm. As a result, our 1D model actually uses a 2D Virtual Cell geometry with a membrane between two 1D layers, thereby permitting the model to account for diffusion in both the plasma membrane and cytoplasm, as well as transport between them (as when PIP2 is hydrolyzed to IP3). Because 1D simulations were very efficient, we could use sufficiently long dendrites so that the boundary conditions at the edges of the 1D dendrite could be safely set at the basal levels of the various species. We then used the simulation results at a length away from an activated spine that corresponded to the edge of the dendritic segment in the 3D models to derive time-dependent boundary conditions for the 3D simulations. For example, for IP3 (Fig. 3 c) at 13.95 μm from a spine stimulated 12 times in succession (13.95 μm represents the edge of our constructed 3D geometry relative to the stimulated spine in the center of the geometry), the boundary condition used was the following polynomial fit:

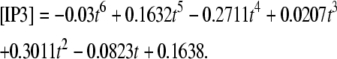(2)

Our 1D model with average values (calculated in Virtual Cell by measuring spine parameters) fit to our experimentally derived 3D geometry displayed time-dependent behavior of IP3 (Fig. 3 d) at ∼3.52 μm from the spine activated 12 times in succession (3.52 μm represents the edge of our experimentally derived 3D geometry relative to the activated spine roughly in the center of the geometry) modeled by

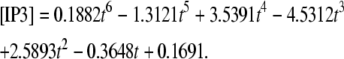(3)

The respective boundary condition for each 3D geometry was also used in simulations with four excitations of the central spine. The relatively small changes in IP3 concentration (Fig. 3, c and d) at the edge of each geometry over the 2-s time course would minimally affect IP3 kinetics in the central spine. Consequently, the same boundary conditions described by Eqs. 2 and 3 were used for IP3 produced in the various spines with both 4 and 12 PF stimuli in the 3D models.

A simple rate expression for PIP2 hydrolysis connects PIP2 to DAG in the plasma membrane and IP3 in the cytoplasm. The reaction rate equation includes concentration of PIP2, as well as concentration of activated PLC:

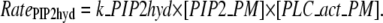(4)

PLC activation is modeled as the difference between the forward and the reverse rates:

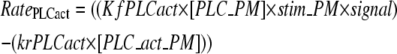(5)

Two new terms are added to the forward PLC rate reaction: stim_PM and signal; signal characterizes the nature and duration of the activation:

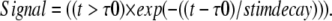(6)

Stim_PM is a variable that is reserved for localizing signals to a single spine in the spatial models. For example, to activate a central spine in the constructed 3D geometry, the stim_PM variable is set to the following expression in the x, y, and z coordinates:

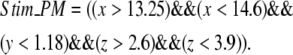(7)

The region in which this rectangular solid intersects the membrane, indicated in Fig. 3 a, would then correspond to the spine that experiences PLC activation.

A local sequestering protein or “sink” was also added to the model to represent local PIP2 sequestration. For stimulated synthesis, PIP2 precursors PIP and PI were both placed in the membrane, and the synthesis of both PIP from PI and subsequently PIP2 from PIP were localized using the variable stim_PM. IP3 output from 3D models using our constructed 3D geometry was fed into the compartmental model, which has two compartments: the spine cytoplasm and the dendrite cytoplasm. IP3 in the spine is designated IP3s; dendritic shaft IP3 is designated IP3d, to model the diffusion of IP3 from the spine to the dendrite, as well as down the length of the dendrite, in 1D. Each IP3 species was given two separate reactions. One reaction models its conversion from spine to dendrite or vice versa. The other models its creation (in the case of IP3s, hydrolysis of PIP2) and degradation (for both IP3s and IP3d):

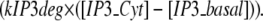(8)

Calcium release was implemented in only the compartmental (0D) model, originally described by Hernjak et al. (22), but with parameters for IP3 dynamics that were derived from the various 3D simulations carried out in this study. This allowed us to test how the various scenarios for the delivery of PIP2 to the stimulated spine affect the downstream calcium signal that is a prerequisite for LTD.

All of the compartmental (0D), 1D, and 3D models can be accessed in Virtual Cell by logging onto www.vcell.org, then clicking on “Published Models”. In the biomodel public domain, the compartmental model (“Purkinje Compartmental–adapted from Hernjak et al.”), as well as the 1D and 3D models (“Purkinje 1D”, “Purkinje 3D–12 PF Stimuli”, “Purkinje 3D–4 PF Stimuli”, “Purkinje 3D Several Spines–12 PF Stimuli”, and “PIP2 Diffusion 1D and 3D”) are located under the user name “Brown”.

RESULTS

Basal levels of PIP2 are not adequate for IP3 production

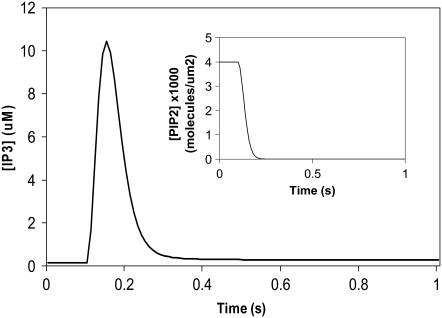
We had determined previously a basal level of 4000 PIP2 molecules/μm² on the inner leaflet of the plasma membrane in differentiated neuroblastoma cells (26). This is a reasonable, but high, estimate based on the percentage of membrane phospholipids composed of PIP2 (<1%) (1). We used this basal level of PIP2 in our 3D spatial Purkinje cell model. On stimulation of the Purkinje cell by a train of parallel fiber inputs, using either our constructed or experimentally derived 3D Purkinje dendrite geometries (Fig. 3, a and b, spine 1), PIP2 levels fell rapidly from 4000 to 0 mol/μm² in under 0.2 s (Fig. 4 inset for data from constructed geometry). The resulting IP3 concentration rose to a peak of ∼10 μM in ∼0.2 s (Fig. 4) before returning close to basal levels. Basal synthesis of PIP2 leads to slightly increased amounts of IP3 above the basal concentration of 0.16 μM even up to 1 s, because PLC activation has not completely decayed by 1 s (Fig. 5 a, right inset). Normally, IP3 diffuses freely in cytoplasm with a coefficient of 283 μm² s⁻¹, but through the spine neck the diffusion rate is effectively:

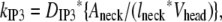(9)

where D_IP3 is the diffusion coefficient for bulk diffusion of IP3 in cytoplasm, A_neck is the cross-sectional area of the spine neck, l_neck is the length of the spine neck, and V_head is the volume of the spine head, giving an effective diffusion rate of 132 s⁻¹ for a typical spine. The spine neck effectively decreases the rate of diffusion from the spine by a factor of ∼10. The parameters used to calculate this rate are taken from the model published by Hernjak et al. (22). Even with the restricted diffusion posed by the spine neck, the rate of IP3 diffusion out of the spine neck is much greater than the rate of degradation of IP3, 0.14 s⁻¹, which was taken from an earlier study on neuroblastoma cells (30). Thus, even if this value for the IP3 degradation rate in Purkinje cells is greatly underestimated, it would not significantly change the overall IP3 decay in the spine.

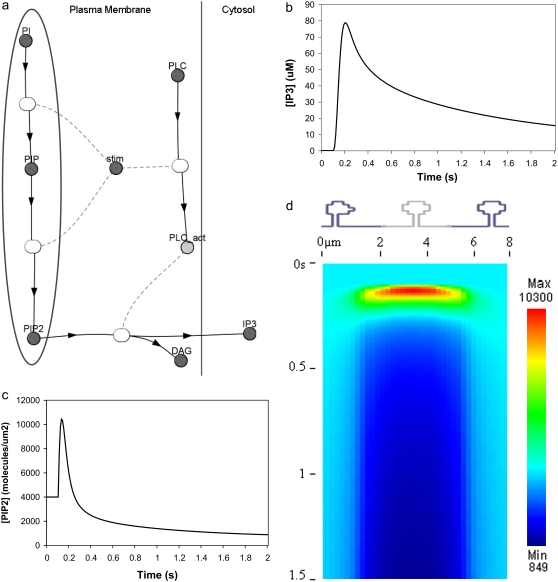
FIGURE 4.

IP3 concentration in constructed 3D geometry for central spine stimulated 12 times in succession beginning at t = 0.1 s. IP3 concentration results from cleavage of PIP2, which is rapidly depleted. Each excitation follows the last by 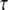= 0.012 s. (Inset) Corresponding PIP2 concentration at central spine in constructed 3D geometry. The results show that calculated basal levels of PIP2 in the Purkinje neuron spine membrane (4000 mol/μm²) are not sufficient to produce large amounts of IP3.

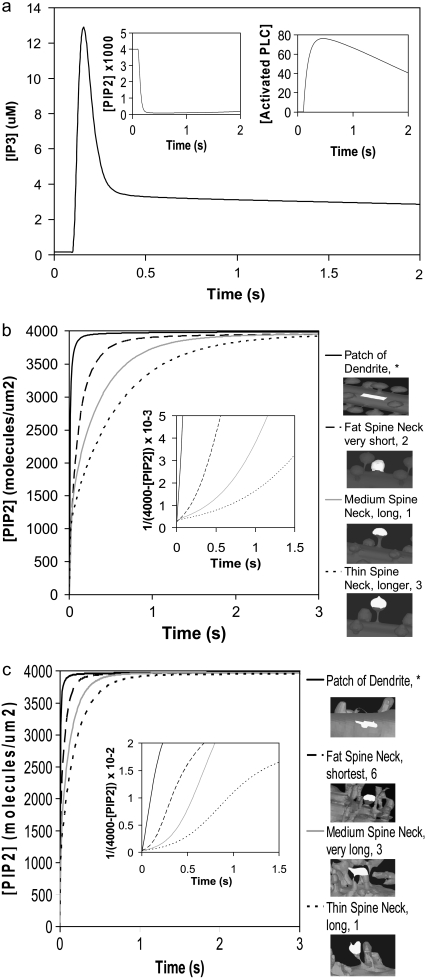
FIGURE 5.

(a) IP3 concentration for central spine stimulated 12 times at the central spine in constructed 3D geometry as in Fig. 4, but allowing for lateral diffusion of PIP2. (Inset) Corresponding PIP2 and activated PLC concentrations. Recovery of PIP2 in the presence of lateral diffusion begins soon after depletion. (b) PIP2 diffusion for spine necks of varying diameter and length in our 3D model using the constructed geometry (Fig. 3 a, spines 1–3). PIP2 was depleted instantaneously in a patch of dendrite membrane and portions of spine heads. PIP2 laterally diffused into the patch of dendrite and into the spine heads at different rates. The pattern of diffusion varies with the geometry of the spine necks. The PIP2 concentration in the patch of dendrite and in the spine heads recovers to an equilibrium value of 4000 mol/μm². (Inset) Analysis of PIP2 diffusion in constructed geometry. For simple diffusion, time ∝ 1/(4000-[PIP2]), where 4000 mol/μm² is the surface density of PIP2 at t = ∞. The patch of dendrite yields a straight line indicating simple diffusion, whereas each spine gives a different curve, but not a straight line, indicating apparent anomalous diffusion. (c) PIP2 diffusion with time for spine necks of varying diameter and length in our 3D model using the experimentally derived geometry (Fig. 3 b, spines 1, 3, 6). PIP2 was instantaneously depleted in a patch of dendrite and portions of spine heads and the patterns of recovery are similar to those observed for the idealized geometry of Fig. 3 a. (Inset) Analysis of PIP2 diffusion in the experimental geometry, as in b.

This suggests that the calculated basal level of PIP2 in the Purkinje cell spine in its resting state can produce only up to ∼10 μM of IP3. However, studies have indicated that Purkinje cells can produce IP3 concentrations significantly higher than 10 μM (e.g., 23) and that, indeed, concentrations in the range of 20–30 μM are required before any calcium release can be detected (31). Various experimental studies use a range of synaptic inputs when activating parallel fiber-Purkinje synapses. Finch and Augustine (23) obtain small calcium responses using 12 PF stimuli at 80 Hz (periodicity of 0.012 s), but do not correlate this with IP3 concentration. They indicate that 16 PF stimuli correspond to uncaging of 10–20 μM IP3 in the Purkinje dendrite, but they do not measure the IP3 concentration within the spine, where the IP3 concentration must achieve much higher levels because of the restriction to diffusion through the spine neck. In our model by Hernjak et al. (22), we generated 70 μM IP3 in the Purkinje neuron spine using 12 PF stimuli. Indeed, uncaged IP3 concentrations of 80–160 μM in the Purkinje dendrite yield calcium signals with short latency, fast rise times, and large amplitudes (23). But if basal levels of PIP2 cannot produce such large amounts of IP3, where does the additional IP3 come from? Three candidate sources of sufficient PIP2 are considered in the following sections: lateral diffusion, high spine membrane PIP2, and stimulated synthesis. Our Discussion section also considers the possibility that our calculated value of 4000 PIP2 mol/μm² on the inner plasma membrane of neuroblastoma cells may underestimate the level of PIP2 in cerebellar Purkinje spines.

Lateral diffusion of PIP2

We considered whether sufficient PIP2 could be provided by lateral diffusion from the surrounding dendrite into the stimulated spine head. To simulate lateral diffusion on these convoluted surfaces, we used a novel lateral diffusion algorithm (32) that allows for coupling between the diffusing membrane species (e.g., PIP2) and species in their adjoining volumes (e.g., IP3). We added lateral diffusion of PIP2 into our model, using a diffusion coefficient of D = 10 μm² s⁻¹; this is at least a factor of 10 greater than measured PIP2 diffusion coefficients (33,34), and was deliberately chosen to provide as rapid replenishment by this mechanism as might be physiologically possible. The resulting IP3 concentration rose to ∼13 μm (Fig. 5 a), a small increase above 10 μM obtained without lateral diffusion (Fig. 4) in the central spine of the constructed 3D geometry (Fig. 3 a, spine 1). Note that the IP3 signal decayed more slowly with lateral diffusion of PIP2 from surrounding dendrite into the spine head and maintained a basal level of ∼3 μM after the decay of the initial burst (Fig. 5 a). This results from the convolution of lateral PIP2 diffusion with the decay rate of PLC activation (Fig. 5 a, right inset), the rate of degradation of IP3 and the diffusion of IP3 out of the activated spine. Fig. 5 a (left inset) displays the dynamics of the PIP2 signal in the presence of lateral diffusion through the spine neck. The figure shows that PIP2 descends to very low levels but is never completely depleted and begins to slowly recover as PLC becomes inactivated (Fig. 5 a, right inset). In contrast, Fig. 4 shows that without lateral diffusion, PIP2 is completely depleted and that basal rates of PI and PIP phosphorylation are insufficient to replenish PIP2. In fact, in the absence of lateral diffusion, PIP2 recovery starts only 5 s after the cells is stimulated, and even after 30 s, only a little under one quarter of the basal level of PIP2 has been replenished (data not shown). Simulations using a diffusion coefficient of D = 1 μm² s⁻¹ give similar qualitative results for IP3 production; PIP2 is almost completely depleted and does not recover as quickly as with D = 10 μm² s⁻¹. The results from these simulations can be accessed in Virtual Cell in the biomodel titled “Purkinje 3D–12 Stimuli”, located under the user name “Brown”.

To determine why lateral diffusion did not replenish PIP2 and to investigate the dynamics of PIP2 on the membranes of our 3D geometries, we carried out detailed analyses of lateral diffusion of PIP2 in the spiny Purkinje dendrite. In our constructed 3D geometry, we simulated recovery from depletion of PIP2 molecules in single spines of varying neck lengths and radii (Fig. 3 a, spines 1-3), as well as in a patch of dendrite (Fig. 3 a, asterisk) (see Movie S1, Data S1, for one spine included in the Supplementary Material). Fig. 5 b shows that for the patch of dendrite, the PIP2 concentration recovers rapidly in <1 s, rising from 0 mol/μm² to an equilibrium concentration of 4000 mol/μm². This corresponds to rapid lateral diffusion of PIP2 from the surrounding dendritic shaft into the selected patch of dendrite. In the spines, the PIP2 concentration rises rapidly at first, but then slows. Because the depleted patch of membrane corresponded to only ∼80% of each spine head, PIP2 from the remaining 20% redistributed throughout the entire spine head very quickly, represented by the initial rapid rise in PIP2, with the remaining recovery funneling from the dendrite membrane through the spine neck. Fig. 5, b and c, show that the restricted lateral diffusion of PIP2 varies with different neck lengths and radii. Narrow spine necks restrict diffusion more than wide spine necks; short spine necks allow faster diffusion than long spine necks. As a result, the rate of lateral diffusion of PIP2 from the adjoining dendritic shaft through spine necks into spine heads seems to be a function of both spine neck length and radii, similar to the rate of volumetric diffusion of molecules between the spine and dendrite (Eq. 9).

For simple diffusion, time is proportional to the mean-square displacement. For lateral diffusion along a surface, this relationship corresponds to proportionality between time and the inverse of the surface density of the diffusing molecule. Therefore, for simple lateral diffusion we should obtain a straight line if we plot 1/[4000-PIP2] versus time. This is the case for PIP2 lateral diffusion into the patch of dendrite, as illustrated in the inset of Fig. 5 b. The linear plot for the patch of dendrite indicates conventional lateral diffusion of PIP2. However, if we follow recovery of PIP2 in spines, the corresponding plots are nonlinear. The wider and shorter the spine neck, the more closely the curve approaches linearity, whereas the narrower and longer the spine neck, the more the curve diverges from linearity. This departure from linearity reflects a deviation from conventional diffusion that is usually referred to as “anomalous” diffusion. Anomalous volume diffusion has been shown for cytosolic molecules such as calcium, IP3, and fluorescein dextran along spiny Purkinje dendrites (35), but anomalous lateral diffusion along spiny Purkinje dendrites has not been studied previously for surface molecules like PIP2. Strictly speaking, these results are not truly reflective of anomalous diffusion, but rather diffusion in the presence of barriers. True anomalous diffusion would be manifested as a linear relation between time and a displacement raised to a power other than 2; the behavior in Fig. 5 b reflects simple diffusion, but with effective diffusion coefficients that change in different spatial scales. The information presented here provides new insight into the influence of dendritic spine geometry on surface molecule diffusion in Purkinje neurons. Similar results are obtained using both our constructed 3D geometry and our experimentally derived 3D geometry (Fig. 3 b, spines 1, 3, and 6) (Fig. 5 c), and can be explained by the small surface of the spine neck, which produces an effective barrier to diffusion from the dendrite membrane.

We have shown in this section that “anomalous” lateral diffusion through the spine neck restricts diffusion of PIP2 into the spine head from surrounding dendrite. This restricted diffusion limits the ability of lateral diffusion to provide sufficient PIP2 in the spine during intense synaptic activity. The pattern of the effect of spine geometry on diffusion suggests that wider spine necks may allow more PIP2 to diffuse into the spine head, but it is important to note that IP3 would also diffuse more rapidly out of the spine head, limiting its peak concentration in the spine. Some studies have described slower PIP2 diffusion coefficients in various cell types (36,37); this would further diminish the ability of lateral diffusion to supply sufficient PIP2.

Stimulated synthesis

Because lateral diffusion cannot supply sufficient PIP2 for IP3 production, we investigated whether stimulated synthesis could deliver the requisite quantity of this key lipid. Our group previously discovered stimulated synthesis of PIP2 in neuroblastoma cells as a required mechanism for IP3 production during bradykinin receptor stimulation (26). Local synthesis was also considered by McLaughlin et al. (1) as a possible means of creating locally increased concentrations of PIP2. We added stimulated synthesis to our model, specifically via activated phosphorylation of phosphoinositide precursors, PI and PIP (Fig. 6 a). The phosphorylation rates were adjusted to achieve an IP3 amplitude similar to the levels required for calcium release (22). We included lateral diffusion of PIP2, but, as discussed above, this does not significantly influence the amplitude or duration of the IP3 increase. Fig. 6 b shows that the resulting IP3 increases from a basal level of 0.16 μM to almost 80 μM in <0.1 s in the central spine of the constructed 3D geometry (Fig. 3 a, spine 1). The signal is sustained for more than 2 s, in keeping with predicted IP3 curves (22) that produce robust calcium transients. Thus, based on parameters adapted from our neuroblastoma cell study (26), stimulated synthesis yields adequate IP3 amplitude and duration. Stimulated synthesis could therefore be a physiological source for sufficient PIP2 during stimulation of Purkinje cells by parallel fibers.

FIGURE 6.

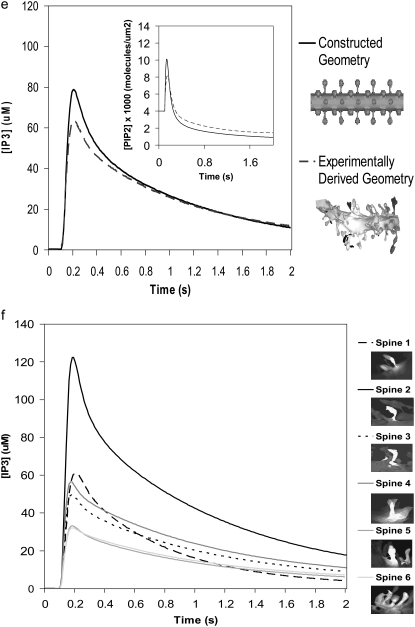
(a) Virtual Cell Reaction scheme for activation of PLC, cleavage of PIP2, and stimulated synthesis of PIP2 via phosphorylation of its precursors. The gray oval encloses the section of the reaction scheme representing stimulated PIP2 synthesis. The dark shaded circles represent species or variables and the lightly shaded ovals represent reactions; in the Virtual Cell software; doubleclicking a shaded oval shows an editable reaction rate law. The variable stim is set to an expression in the spatial coordinates that localizes PLC activation and stimulated PIP2 synthesis to a single spine in the 1D and 3D geometries. PI is converted to PIP and PIP is converted to PIP2. A species with an arrow going away from it is described as a reactant; a species with an arrow coming toward it is described as a product; a species with dotted lines is considered a modifier that is not depleted or created during the course of the reaction (e.g., a catalyst or a variable such as stim that serves to localize a reaction). (b) IP3 concentration for central spine stimulated 12 times at 80 Hz beginning at t = 0.1 s, with both stimulated PIP2 synthesis and lateral diffusion of PIP2 added to the model using the constructed 3D geometry. The large IP3 concentration results from cleavage of high amounts of PIP2 produced by stimulated synthesis. (c and d) Corresponding PIP2 concentration at the central spine in the constructed 3D geometry. The results show that stimulated PIP2 synthesis with a small contribution from PIP2 lateral diffusion produces a transient increase in PIP2 concentration before depletion. The kymograph (d), spanning a distance of 8 μm along the Purkinje dendrite flanking the stimulated spine, illustrates that the PIP2 concentration peaks in the stimulated central spine before depletion and stays relatively constant in the adjacent dendrite. (e) Comparison of IP3 concentration curves for stimulated PIP2 synthesis in the central spine in the constructed and the experimentally derived 3D geometries. (Inset) Corresponding PIP2 concentrations for stimulated synthesis and lateral diffusion in the central spine in both the constructed and the experimentally derived 3D geometries. Both geometries give similar curves. (f) IP3 concentration for several spines in experimentally derived 3D geometry stimulated as above. Each IP3 concentration curve corresponds to a unique spine in the experimentally derived geometry. Variations in IP3 concentration exhibited for each spine is solely due to the geometry of the spine; ∼80% of each spine head was stimulated.

We now turn to consideration of the PIP2 dynamics. Fig. 4 showed that with only basal levels of synthesis, PIP2 falls rapidly from a calculated basal level of 4000 mol/μm² to 0 mol/μm² in our model of the Purkinje neuron spine. With stimulated synthesis added to the model, PIP2 levels increase before depletion (Fig. 6 c). The peak in PIP2 concentration occurs at a little over 10,000 mol/μm² in <0.1 s from the start of the simulation and before the peak in IP3 concentration. The PIP2 concentration response in Purkinje neuron spines in our simulations with stimulated synthesis is remarkably similar to the PIP2 response in neuroblastoma cells (26), even with the very different geometries for each cell type. This reflects the relatively small effect of lateral diffusion of PIP2 on these timescales.

The kymograph in Fig. 6 d displays the PIP2 dynamics in the plasma membrane of our constructed 3D geometry with stimulated synthesis and lateral diffusion. The kymograph spans the length of the stimulated spine as well as a short length of dendrite directly adjacent to the spine; the region from ∼1.8 μm to 5.2 μm corresponds to the stimulated spine membrane. After PLC activation at 0.1 s, PIP2 rises from basal levels and peaks, then returns to basal levels, before falling to very low levels reflecting depletion. Outside the spine region, the kymograph indicates that PIP2 in the adjacent dendrite increases or decreases only in the very small area of dendrite directly adjacent to the spine neck. Beyond this region, PIP2 remains at basal levels, suggesting that PIP2 concentrations in the rest of the dendritic shaft and the surrounding spines are not affected. Thus, restricted PIP2 diffusion through the narrow neck of the stimulated spine effectively isolates the stimulated spine membrane. The time plots in Fig. S1 a in the Supplementary Material also show that the majority of the PIP2 response occurs in the stimulated spine head, with very little change in PIP2 concentration in the dendritic shaft adjacent to the stimulated spine, and no change at all in the dendrite shaft ∼3 μm from our stimulated spine.

Similar IP3 responses were obtained in the stimulated spine using both our constructed 3D geometry and our experimentally derived geometry (Fig. 3 b, spine 1) (Fig. 6 e). In our experimentally derived geometry, IP3 increases from a basal level of 0.16 μM to ∼60 μM. The shape of the IP3 curve is very similar to that obtained using our constructed 3D geometry. The PIP2 increase, return to baseline, and subsequent depletion (see Movie S2, Data S1, included in the Supplementary Material) are also similar to those obtained using our constructed 3D geometry (Fig. 6 e, inset). One result notably different between the two geometries involves the boundary condition for PIP2. We first assumed in our simulations zero flux of PIP2 in the plasma membrane at the edges of both our constructed and experimentally derived geometries. If PIP2 diffusion is restricted through the spine neck, then PIP2 levels in the dendritic shaft far away from the spine neck should be relatively unaffected. This zero flux boundary condition for PIP2 in the plasma membrane at the edges of the constructed 3D geometry yields PIP2 and IP3 curves identical to those obtained from assuming a fixed basal value of 4000 PIP2 mol/μm² at the edges of the geometry (Fig. 6, e and f). Yet in the experimentally derived 3D geometry, these two assumptions (zero flux and fixed value) give slightly different PIP2 and IP3 curves (Fig. S1, b and c), suggesting that PIP2 has not yet equilibrated at the edges of the experimentally derived 3D geometry. At the edge of the experimentally derived 3D geometry, PIP2 is still laterally diffusing inward, albeit at very low levels, toward the stimulated spine. As low levels of PIP2 in the plasma membrane leave the edge of the geometry, they are replenished by PIP2 theoretically beyond the edges of the geometry, further along the dendritic shaft of the Purkinje neuron. The unexpected lack of equilibration at the edges of the geometry is presumably due to the shorter length of the experimentally derived 3D geometry, ∼7 μm long, versus 20 μm for the constructed 3D geometry. In general then, a fixed value boundary condition for PIP2 and other surface molecules seems to be a better approximation for both constructed and experimentally derived geometries, regardless of length.

We investigated the increase in PIP2 and IP3 in various spines of the experimentally derived geometry (Fig. 3 b, spines 1–6) (see Movie S3, Data S1, included in Supplementary Material). We stimulated ∼80% of each spine head. However, because lateral diffusion within the spine head occurs rapidly, all PIP2 present in the entire spine head will be used up quickly once the spine is stimulated. In addition, each spine has its unique neck geometry, resulting in various degrees of restricted lateral diffusion. Fig. 6 f shows that spines with short, wide spine necks retain less IP3 in their spine heads than narrow, crooked spines. This shows that the IP3 concentration in each spine head is also a function of the spine neck geometry. The complexity of the experimentally derived geometry indicates that different spines will experience different accumulations of IP3 when the Purkinje dendrite branchlet is stimulated. This suggests that spines with different geometries, yet on the same dendrite branchlet, can produce differing patterns of synaptic plasticity in response to identical input patterns.

Local sequestration

McLaughlin et al. (1) consider local sequestration as a means of producing locally increased levels of PIP2 in areas of the plasma membrane of any cell type. They suggest that basic proteins may serve as buffers for PIP2. MARCKS, CAP23, and GAP43 are among such proteins and have been termed pipmodulins (38). However, none of these proteins has been localized in the Purkinje cell by immunostaining (39,40). Further, binding of PIP2 by the MARCKS protein shields PIP2 from hydrolysis by PLC (41,42). It is unlikely that the so-called pipmodulins are sequestering PIP2 in the Purkinje neuron spine. PDZ domains of some proteins also bind PIP2 (43,44) and could possibly sequester the phospholipid locally. Homer, a PDZ scaffolding protein, coimmunoprecipitates with PLCβ, mGluR1, and IP3R1 in cerebellar Purkinje cells (45–47), and could bind PIP2 via its PDZ domain (if the PDZ domain is not already bound to mGluR1) or some other domain, bringing clusters of PIP2 into close proximity with PLC, the enzyme that cleaves PIP2. This would effectively increase the local concentration of PIP2 available to PLC for cleavage. In addition to these proteins, there are many uncharacterized proteins in the postsynaptic density (47–49), one or more of which may help to locally sequester PIP2 in the cerebellar Purkinje spine perisynapse.

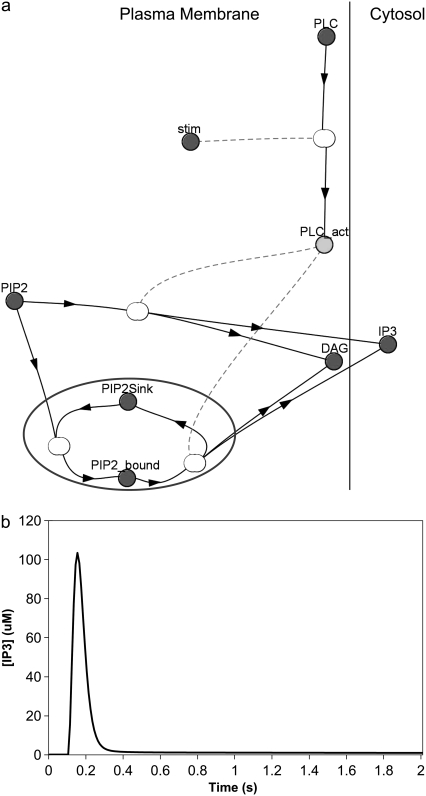
We incorporated local sequestration into our model in the form of a PIP2-binding protein or “sink” (Fig. 7 a) with a surface density of binding sites that is 10 times the basal concentration of PIP2. In our model, binding of PIP2 to these sites does not shield it from hydrolysis by activated PLC, so that bound and unbound PIP2 can both be cleaved to produce IP3 and DAG (Fig. 7 a). Fig. 7 b shows the resulting IP3 dynamics in the central spine of the constructed 3D geometry (Fig. 3 a, spine 1). IP3 rises from a basal level of 0.16 μM to a high amplitude of ∼105 μM in 0.05 s. Its concentration then rapidly returns nearly to baseline after 0.1 s. The IP3 increase therefore has large amplitude, but limited duration, compared with the lasting duration of the IP3 signal produced by stimulated synthesis of PIP2 (Fig. 6 b). This important characteristic of large amplitude, but limited duration can help experimentalists distinguish between local sequestration and stimulated synthesis as possible sources of sufficient PIP2 for IP3 production. The fast kinetics reflected in the curve in Fig. 6 b corresponds to a sequestering protein that rapidly releases PIP2, making it readily available for cleavage by PLC to produce IP3. Note that, in vivo, PIP2 could be bound to some buffering protein that shields it from PLC; but if the off-rate of PIP2 is sufficiently rapid, the bound PIP2 would become available for hydrolysis by activated PLC. Even in the context of local sequestration, free PIP2 can diffuse laterally in the phospholipid membrane. Adding lateral diffusion to our local sequestration simulation does not significantly increase the amplitude or duration of the IP3 increase (data not shown). It follows, therefore, that the local sequestration mechanism should produce IP3 dynamics essentially identical to a model that simply postulates increased PIP2 basal levels.

FIGURE 7.

(a) Virtual Cell Reaction scheme for activation of PLC, cleavage of bound and unbound PIP2, and local sequestration of PIP2 by a binding protein or “sink”. The gray circle encloses the section of the reaction scheme representing local sequestration. PLC is allowed to cleave free PIP2 as well as PIP2 bound to the “sink” protein or complex. Other details are similar to Fig. 6 a. (b) IP3 concentration for central spine stimulated 12 times at 80 Hz beginning at t = 0.1 s, with local sequestration of PIP2 added to the model using the constructed 3D geometry. The IP3 concentration results from cleavage of both free PIP2 and PIP2 bound to a binding protein or “sink”.

Calcium signals from local sequestration versus stimulated synthesis

The amplitude and shape of calcium signals in the spine result from a confluence of four factors: IP3-dependent calcium release from the endoplasmic reticulum, calcium entry into the cell through voltage-gated calcium channels in the membrane, calcium diffusion through the spine neck, and the association-dissociation of calcium with cytosolic buffers, including the fluorescent indicator. Having established the contrasting pattern of IP3 dynamics arising from the sequestration and stimulated synthesis mechanisms in our 3D spatial models, we apply these IP3 dynamics to explore the patterns of calcium signaling.

Stimulated synthesis gives large IP3 amplitude and long duration, whereas high spine PIP2 sequestration gives large amplitude but limited duration. To investigate the calcium transients obtained with local sequestration or stimulated synthesis of PIP2, we adapted the compartmental model previously published by our laboratory (22). In this model, Hernjak et al. (22) use the following equation to produce four pulses of IP3 (to represent 4 PF stimuli) to compare results from the model to experimental data by Wang et al. (25):

(10)

where J_S represents the pulse amplitude, n is the number of pulses, 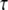is the time period between each pulse, K_S controls the rate of decay of the pulse, and K_deg is the degradation rate of IP3; Diffusion_IP3 is the diffusion rate for IP3 from the spine to the adjacent dendrite, as given by Eq. 1, where k_IP3 depends on the geometry of the spine that is activated. Hernjak et al. (22) use a pulse amplitude, J_S, of 80 μM.s⁻¹, a pulse decay rate, K_S, of 1.188 s⁻¹ and n = 4, corresponding to 4 PF stimulations, to produce a calcium transient comparable to results from Wang et al. (25). The IP3 concentration reaches a peak of ∼25 μM under these circumstances (Fig. S2 in the Supplementary Material). These IP3 dynamics, when coupled with coincident calcium influx through voltage dependent channels in the plasma membrane, generally recapitulate the changes in fluorescence of a calcium indicator measured in the Wang et al. (25) experiment.

The activation that had been used in Figs. 4–7 was equivalent to the 12 pulses at 80 Hz used in experimental studies of the IP3 signals in the absence of coincident calcium influx (23). We therefore adjusted the parameters in the models with the constructed 3D geometry to produce a peak IP3 of 25 μM. This corresponded to the weaker activation used in the coincidence detection experiments (25). To see how these mechanisms might affect calcium signaling in the spine, we adjusted J_S and K_S in our compartmental model to reproduce the corresponding IP3 dynamics.

To reproduce an IP3 peak concentration of ∼25 μM, we adjusted the rate of stimulated synthesis of PIP2 in our 3D spatial model by varying the parameter kStimSynPIP2 (Table 1, Fig. S2), which determines the rate at which PIP is converted to PIP2 by phosphatidylinositol-4-phosphate 5-kinase type 1 (PIP5K1). A kStimSynPIP2 of 4 gives a reasonable fit for both the desired amplitude and rate of decay of the IP3 signal. In the compartmental model, this corresponds approximately to the original parameters used in the Hernjak et al. (22) model where J_S = 80 μM.s⁻¹, and K_S = 1.188 s⁻¹ (Fig. 8 a). The resultant fluorescence transient predicted by the compartmental model, for the calcium indicator Magnesium Green used by Wang et al. (25), is shown as the solid curve in Fig. 8 b. This simulation corresponded to activation of the PF inputs (i.e., IP3 generation) at 0.1 s and the activation of climbing fiber (CF)-induced depolarization (i.e., calcium influx) at 0.15 s, which terminates 5 ms later. The initial spike in calcium concentration reflects this rapid transient influx. The initial spike is followed by a secondary peak that results from the calcium-induced calcium release from the endoplasmic reticulum. The initial spike is likely missed in the experiments, because they typically measure the average calcium concentrations over time windows much greater than the 5 ms duration of the calcium influx.

FIGURE 8.

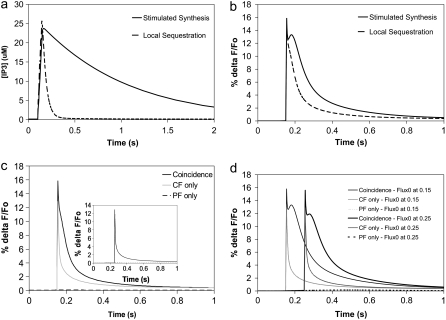
(a) IP3 concentration for 4 PF stimuli at 80 Hz beginning at t = 0.1 s in the adapted compartmental model. The parameters were chosen to fit the spine IP3 dynamics for local PIP2 sequestration (dashed curve) and stimulated PIP2 synthesis (solid curve) in our 3D model using the constructed geometry. Local sequestration and stimulated synthesis are able to produce similar amplitudes of IP3, but with different durations. (b) Ca transients for coincident activation of Purkinje neuron spine by 4 PF stimuli beginning at t = 0.1 s and 1 CF stimulus at 0.15 s in the adapted compartmental models produced by parameters corresponding to local PIP2 sequestration (dashed curve) and stimulated PIP2 synthesis (solid curve). (c) Ca transients for 4 PF stimuli only (dashed line), 1 CF stimulus only (shaded line), or coincident activation by 4 PF stimuli and 1 CF stimulus (solid line) in the adapted compartmental model with parameters corresponding to local PIP2 sequestration. The train of 4 PF stimuli begins at 0.1 s; the CF stimulus occurs at 0.15 s. (Inset) As above, but with calcium influx at 0.25 s. (d) Timing dependence for the stimulated synthesis mechanism. Ca transients for 4 PF stimuli only (partially dashed line), 1 CF stimulus only (lightly shaded line), or coincident activation by 4 PF stimuli and 1 CF stimulus (solid line). The train of 4 PF stimuli begins at 0.1 s; the CF stimulus occurs at 0.15 s for the curves on the left and at 0.25 s for the curves on the right.

To reproduce an IP3 peak concentration of ∼25 μM in our model with local sequestration, we adjusted the initial concentration of the variable PIP2_bound (representing the sequestered PIP2, Table 1) to 4500 mol/μm². Although the amplitude of the resultant IP3 signal attains 25 μM, its duration is short (data not shown, but as in Fig. 8 a). The duration of the IP3 signal in the compartmental model therefore had to be decreased for comparison. We adjusted the values of the pulse amplitude, J_S, and the pulse decay rate, K_S, in the compartmental model, to produce an IP3 curve with an amplitude of 25 μM, but with limited duration. A pulse amplitude, J_S, of 150 μM.s⁻¹ and a pulse decay rate, K_S, of 25 s⁻¹ in the compartmental model were thus used to simulate IP3 production by local sequestration (Fig. 8 a). Fig. 8 b shows that the initial spike in the calcium transient from local sequestration of PIP2 is identical to the spike in the calcium transient from stimulated PIP2 synthesis. It is important to note, however, that the secondary peak in the calcium transient from stimulated PIP2 synthesis is depressed in the calcium transient from local sequestration of PIP2. Although the brief 5 ms influx of calcium at 0.15 s occurs at a point in time where the IP3 is near its peak in the local sequestration model, the duration of the IP3 is limited.

Both the local sequestration and the stimulated synthesis mechanisms produce calcium signals that display the characteristics of supralinearity. Fig. 8 c illustrates this for local sequestration and Fig. 8 d shows this for stimulated synthesis. The figures show virtually no fluorescence change for PF stimulation (i.e., IP3 generation and calcium release from intracellular stores) alone and a very short transient spike for CF stimulation (i.e., calcium entry from extracellular stores) alone. Taken together, however, both mechanisms are able to produce a fluorescence change that is much greater than the sum of the individual signals, similar to the experimentally measured results (25).

Although the calcium signals from our two models are similar when the calcium influx follows the initiation of IP3 production by 50 ms, changing the timing between PF and CF inputs in our two models produces starkly different results. Fig. 8 c inset shows that when the climbing fiber is stimulated 150 ms after the parallel fiber, the local PIP2 sequestration mechanism produces a calcium transient reflective of only the calcium influx with no significant contribution from IP3-mediated calcium release. This is because the calcium influx transient has missed the narrow peak of the IP3 signal. Thus, duration of the IP3 concentration increase becomes important when the timing of the climbing fiber stimulus relative to the parallel fiber stimulus is varied. Because the duration of the IP3 signal is much longer in our model with stimulated synthesis, timing in this context should not be an issue. This is borne out by Fig. 8 d in which an almost identical large supralinear calcium response was obtained for CF activation at either 50 ms or 150 ms after PF activation. This is presumably due to the maintenance of a stable high IP3 amplitude for several hundred ms (Fig. 8 a). At 50 ms after the parallel fiber stimulus, IP3 concentration has risen to 23 μM; at 150 ms after the parallel fiber stimulus, IP3 concentration has fallen only to 22 μM. The IP3 signal from stimulated synthesis of PIP2 therefore produces large calcium transients with a generous allowance for timing differences between climbing fiber and parallel fiber stimuli.

DISCUSSION

In our modeling studies, we established that presumed basal levels of plasma membrane PIP2 are insufficient to produce the requisite high concentrations of IP3 for calcium release when the Purkinje cell spine is stimulated through its metabotropic glutamate receptor. We explored sources of sufficient PIP2 in the Purkinje neuron spine and investigated PIP2 dynamics in the plasma membrane. We found that the geometry of the spine influences lateral diffusion of PIP2, which does not follow the linear relationship between displacement and the square root of time that describes simple diffusion. Our results show that spines with longer and thinner spine necks exhibit apparent anomalous lateral diffusion more dramatically than short, large spines with wide necks. Santamaria et al. (35) showed that the geometry of the Purkinje dendrite spine neck creates a volume diffusion barrier for calcium, fluorescence calcium indicators, and IP3, as well as the inert molecule fluorescein dextran, but the effect of the spine geometry on the lateral diffusion of surface molecules has not previously been studied. Due to this restriction on PIP2 diffusion through the spine neck, it is not possible for PIP2 laterally diffusing into the stimulated spine head from the surrounding dendrite to provide enough substrate for hydrolysis by PLC when the Purkinje neuron spine is stimulated.

Our findings indicate that stimulated synthesis can provide sufficient PIP2 to produce high concentrations of IP3 with lasting duration. Unlike basal resynthesis, which maintains lipid levels homeostatically and operates over timescales of minutes, stimulated synthesis is postulated to involve the direct activation of PIP2 replenishment through a mechanism that may share some of the elements involved in signaling its hydrolysis. Thus, in this view, activation of the spine synapse stimulates phosphorylation of PI to PIP by phosphatidylinositol-4-kinase and PIP to PIP2 by PIP5K1, before or concurrent with activation of PLC (26). In our simulations, this results in IP3 concentrations of high amplitude and long duration, as well as large calcium transients, and is consistent with studies that have shown increases in IP3 significantly exceeding decreases in PIP2 on stimulation of various cell types (26,50).

We also compared the PIP2 and IP3 dynamics in our constructed 3D geometry, which we used for most of our simulations, to those obtained using a geometry derived from electron microscopy of serial sections from a Purkinje cell dendrite. The results were comparable and highlight how the different geometries of the spines can strongly modulate the amplitude and duration of the IP3 signals (Fig. 6, e and f). Thus, the geometry of the spine represents another level at which synaptic integration can be regulated.

Local sequestration of PIP2 also produces large calcium transients in the adapted compartmental model. This suggests that if PIP2 is sequestered in the perisynapse, this could serve as a local source of sufficient PIP2. This may involve a PIP2-binding protein or some other mechanism maintaining PIP2 in tight clusters, whether in lipid rafts, pools, or microdomains. Thus, there may be pools of locally sequestered PIP2 bound to basic proteins similar to MARCKS, GAP43, and CAP23 that sequester PIP2 in plasma membranes of some neuronal cell types (38–40). Local sequestration effectively produces locally high concentrations of PIP2 in the spine membrane, resulting in high amplitudes of IP3 with limited duration. (It is worth noting that equivalent behavior would result if our estimate of the basal level of PIP2 in the Purkinje cell was significantly too low.) Interestingly, the short duration could contribute to the ability of the synapse to detect coincidence between PF and CF activation, thereby integrating synaptic inputs from different brain regions. Local sequestration gives a very short timeframe during which CF stimulus can coincide with high IP3 amplitude. These results suggest that the sequestration hypothesis could explain the finely tuned timing between parallel fiber and climbing fiber stimuli during coincident activation of the Purkinje neuron spine (25).

Various neuronal cell types may use different methods to produce sufficient PIP2 for hydrolysis when the cell is stimulated. Both local sequestration and stimulated synthesis are prime candidates for abundant PIP2 supply, but which cell types use either method still remains unclear. In neuroblastoma cells, stimulated synthesis seems to be the selected method (26). Our studies indicate that Purkinje cells may use local sequestration, to finely tune the timing of coincident activation by parallel fiber and climbing fiber stimuli.

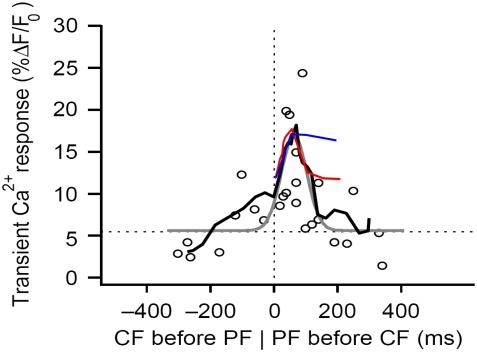
To determine whether results from either mechanism are consistent with experimental observations, we can compare our model predictions to the measurements by Wang et al. (25). In that study, Purkinje cells were filled with the calcium indicator Magnesium Green and whole-cell patch clamp was used to control membrane potential, mimicking the depolarization associated with climbing fiber activation, to investigate the timing dependence of supralinear spine calcium transients (25). Wang et al. (25) found that the largest peak calcium transients were obtained with parallel fiber preceding climbing fiber stimulus by 50–100 ms. We carried out similar simulations with local PIP2 sequestration and stimulated PIP2 synthesis peak calcium transients (plotting the amplitude of the initial spike against the timing difference between the 4 PF stimuli and 1 CF stimulus; Fig. 8, c and d) and compared our resulting curves to data from Wang et al. (25) (Fig. 9). We found that the local sequestration curve (Fig. 9, red) was almost superimposable with the experimental curve (Fig. 9, black) as far as peak pattern and timing are concerned for timing differences of 0–100 ms. This indicates that local sequestration may be the physiological means by which Purkinje cells produce sufficient PIP2 for IP3 production on stimulation by parallel fibers. A similar curve for stimulated synthesis peak calcium transients (Fig. 9, blue) superimposes with data from Wang et al. (25) (Fig. 9, black) for a timing difference of 0–50 ms, but not for 50–100 ms. This suggests that the maintenance of a stable IP3 amplitude resulting from stimulated synthesis precludes the sharp drop in the peak calcium transient pattern observed experimentally. Thus, stimulated synthesis may not be the physiological means that the Purkinje cell uses to produce sufficient PIP2 on stimulation of a spine by a parallel fiber. In cerebellar synaptic plasticity, a key feature of the synaptic coincidence detection mechanism is the ability to detect the precise relative timing of the PF and CF stimuli. Based on experiments with photolysis of caged IP3 in Purkinje neuron spines in a very recent publication, Sarkisov and Wang (51) propose that the timing window depends on the kinetics of calcium removal and IP3 unbinding from IP3R. Our study suggests that the timing window in Purkinje neuron spines may also depend on the duration of the IP3 increase, which is determined largely by the source of sufficient PIP2. In the case of uncaging, the duration of the IP3 increase depends, in large part, on the time course of the UV flash used to uncage IP3. Their published time window for enhanced calcium transients from pairing uncaged IP3 with 1 CF stimulus is 50–200 ms, a wider range than that observed for enhanced calcium transients from pairing 4 PF stimuli with 1 CF stimulus, as in the previous study from their laboratory (Fig. 9, black traces). The increased time window suggests that in the case of uncaging, the spine is exposed to increased IP3 for a longer duration than when the spine is stimulated by 1 CF and 4 PF stimuli.

FIGURE 9.

Comparing simulation results to experimental data for spine coincidence detection. Peak calcium transient patterns from the adapted compartmental model produced by parameters corresponding to stimulated PIP2 synthesis (blue) and local PIP2 sequestration (red) are superimposed on the peak calcium transient pattern published by Wang et al. (25) based on their experimental results (black) (adapted by permission from Macmillan Publishers: Nature Neuroscience (25), copyright 2000). The peak calcium transient refers to the amplitude of the calcium transient obtained from coincident activation by 4 PF stimuli and 1 CF stimulus. Timing, on the horizontal axis, is calculated as Time of CF stimulus − Time of initial PF stimulus. The curves show that local PIP2 sequestration provides a peak calcium transient pattern that qualitatively fits the experimental results.

Further experiments need to be done to tease out these mechanisms in the cerebellar Purkinje cell, as well as to address several questions that derive from our results. Phosphoinositol (PI), the precursor for all other phosphoinositides, is the most abundant phosphoinositide in neuronal cells (26) and is present in amounts far exceeding basal PIP2 concentrations. The PI pool is sufficient to produce large amounts of PIP2 on stimulation of the Purkinje cell spine, if phosphorylation of PI by PI(4)K, the rate-limiting enzyme for PIP2 synthesis, is activated concurrently with or before PIP2 hydrolysis by PLC. Alternatively, the next step in the PIP2 synthesis pathway could be activated on Purkinje cell stimulation. The phosphoinositide kinase isoform PIP5K1γ87 is highly expressed in Purkinje cells (52) and has been extensively investigated in HeLa cells (53). This isoform phosphorylates the 5′-position on PI4P to produce PI45P2 and is responsible for the G-protein coupled receptor (GPCR)-responsive pool of PIP2 in HeLa cells. Although other PIPK1 isoforms are present in this cell type, the α- and β-isoforms seem to be responsible for maintaining total PIP2 mass, but do not have much effect on the GPCR-responsive PIP2 pool (53). This has significant implications for our study. If stimulated synthesis is the physiological method that the Purkinje cell uses to provide sufficient levels of PIP2 when a spine is activated by a parallel fiber, then PIP5K1γ could be the enzyme that is activated instead of phosphatidylinositol-4-kinase, concurrent with PLC activation.

Candidates that may mediate the stimulated synthesis of PIP2, via phosphorylation of precursors PI and PIP, include the 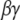subunit of the metabotropic glutamate receptor (mGluR1) and small G proteins. Both have been found previously to interact with various phosphoinositide kinases (54,55), but their interaction with PIP5K1γ87 has not been studied. McLaughlin et al. (1) state that even if local synthesis of PIP2 is stimulated, PIP2 diffuses away very quickly and cannot accumulate locally in a hypothetical spherical cell. However, they suggest that if there is a means of “sequestering” the newly produced PIP2, then the synthesis and “sequestration” together can facilitate increased local concentration of PIP2. The effect of “sequestration” in this context will be to effect low mobility of PIP2 in the plasma membrane. In Purkinje cell spines, the low lateral mobility of PIP2 is created by the geometry of the spine necks, which restricts lateral diffusion, as described in the section on anomalous lateral diffusion. Thus, PIP2 synthesized locally when the spine is activated by parallel fibers would remain concentrated within the spine head and be available locally and immediately for hydrolysis by PLC to produce high levels of IP3. Gamper and Shapiro (56) suggest that the lateral mobility of PIP2 may depend on cell type. Indeed, the geometry of the cell in consideration may influence the lateral mobility of PIP2 due to anomalous lateral diffusion, as we have shown. We deliberately chose an overestimate for the diffusion coefficient in our simulations to assure that replenishment of PIP2 via diffusion through the spine neck would not be significant on the timescale of synaptic activity. Likewise, if PIP2 were produced in the spine membrane during activation, it would not have sufficient time to diffuse away and would therefore be available for hydrolysis to IP3 on this timescale.

The local sequestration mechanism described by McLaughlin et al. (1) involves electrostatic interactions between PIP2 and the MARCKS family of proteins containing a basic effector domain. However, the MARCKS family of proteins does not seem to be present in cerebellar Purkinje cells. If local sequestration does exist in the Purkinje cell, some other method must be at play. We suspect that the PDZ scaffolding protein Homer helps to sequester PIP2 in close proximity to PLCβ, mGluR1, and IP3R1; the latter three coimmunoprecipitate with Homer. Homer also coimmunoprecipitates with Shank, an adaptor protein that seems to link proteins such as Homer to PSD-95, another PDZ-domain scaffold protein found in the postsynaptic density (57,58). Shank and PSD-95 may therefore play specific roles in the local sequestration of PIP2. Lupu et al. (59) have shown that IP3R1 itself forms a complex with PIP2. Thus, IP3R1 could sequester PIP2 on its own, bringing it into close proximity with PLCβ, because IP3R1 and PLCβ are linked in the same signaling complex by Homer. Further, because IP3R1 is involved in these signaling complexes, this could allow for locally increased concentrations of IP3, even if the average IP3 in the spine is low.

Our model has not accounted for the calcium-sensitivity of PLCβ, the PLC isoform enriched in Purkinje neurons. Calcium activates PLCβ, and could therefore change the PLC signal. However, high levels of calcium are achieved after initial peaks in IP3 concentration, and if all the available PIP2 in the spine has been used up, subsequent enhanced activation of PLC would be futile. Another consideration that has not been included in our model involves the effect of synaptic activity on spine geometry. Bloodgood and Sabatini (60) and Biess et al. (61) have suggested that the cross-sectional area and the length of the spine neck, respectively, can be regulated in response to synaptic activity. It is unlikely that the geometry of the spine will change on the small timescale for IP3 production (0.1–0.2 s), but changes that occur beyond 0.1 s or 0.2 s can affect downstream calcium signaling, by trapping calcium in the spine and excluding further diffusion of PIP2. This can be especially important in the context of synaptic plasticity.

In a recent review article, Hilgemann (62) concluded that PIP2 densities presumably in both leaflets of the surface membrane of various nonneuronal cell types (cell cultures from hamster ovary, hamster kidney, human embryonic kidney, mouse intestine, and human cervix) are on the order of 20,000 mol/μm², five times higher than the value we used in our simulations for PIP2 density on the inner leaflet of the surface membrane, calculated by Xu et al. (26) for human neuronal cells. Hilgemann's estimate is based on the assertion that essentially all the PIP2 in cells must reside on the inner leaflet of the plasma membrane, based on studies by Horowitz et al. (63) in mouse mammary adenocarcinoma and Chinese hamster ovary cell cultures. As noted above, a higher estimate of basal PIP2 would behave essentially equivalently to the mechanism involving local PIP2 sequestration. This is because the diffusion of high levels of PIP2 into the spine membrane through the spine neck would be too slow to replenish the supply of PIP2 and would thereby be unable to lengthen the short duration of the IP3 transient (Fig. 7 b).

In conclusion, this study has shown that both stimulated PIP2 synthesis and locally high PIP2 concentration can serve as mechanisms to assure that PLCβ receives sufficient substrate for the requisite IP3 production during synaptic activation of Purkinje cell spines. On the other hand, lateral diffusion of PIP2 is too slow on the timescale of synaptic activity and the pool of spine PIP2 is effectively isolated from the large reservoir of this lipid in the adjacent dendrite membrane. For strong multiple synaptic activations, as in the protocols used by Finch and Augustine (23) and Takechi et al. (24), both the stimulated synthesis and the local sequestration scenarios provide sufficient IP3 for calcium release in the spine. Both mechanisms also display supralinear calcium signals observed by Wang et al. (25) when PF stimulation (i.e., calcium release through the IP3 receptor) is closely coupled to CF stimulation (i.e., calcium influx through voltage dependent channels). However, only the short duration of the IP3 signals that result from the local sequestration mechanism provides a natural mechanism for well tuned coincidence detection (25) between CF and PF inputs to the Purkinje cell.

SUPPLEMENTARY MATERIAL

To view all of the supplemental files associated with this article, visit www.biophysj.org